इस पृष्ठ पर
ऑर्गेनिक रूलेट प्रयोग
परिचय
सितंबर 2016 में, मैंने एक आरोप सुना कि इंटरब्लॉक द्वारा निर्मित ऑर्गेनिक रूलेट मशीनें, व्हील-क्लॉकिंग खिलाड़ियों के खिलाफ आक्रामक प्रतिकारात्मक उपाय कर रही हैं। निष्पक्ष और ईमानदार जुए के समर्थक होने के नाते, इस विषय ने मेरा ध्यान आकर्षित किया। छह महीनों में, मैंने इस विषय पर कई बैठकों में भाग लिया और हज़ारों स्पिन डेटा एकत्र किए। यह पृष्ठ उस जाँच की कहानी बताता है।
खेल
ऑर्गेनिक रूलेट मशीन लास वेगास के कई कैसिनो में मिल जाएगी। यह टेबल गेम की तरह ही काम करती है। खिलाड़ी के पास दांव लगाने के लिए लगभग 30 सेकंड का समय होता है। आमतौर पर, जब खिलाड़ी के पास दांव लगाने के लिए 1 से 5 सेकंड बचे होते हैं, तब गेंद बाहर निकल जाती है। दांव बंद होने के बाद भी, गेंद को ज़मीन पर आने में कुछ सेकंड और लगेंगे। फिर जीतने वाले दांव का भुगतान किया जाएगा और पूरी प्रक्रिया दोहराई जाएगी। शुरुआत से अंत तक इसमें एक मिनट से थोड़ा ज़्यादा समय लगता है।
आरोप
अगर गेंद छोड़ने और सट्टा बंद होने के बीच पर्याप्त समय हो, तो खेल को हराना संभव है। सट्टा बंद होने से पहले गेंद और पहिये की गति का विश्लेषण किया जा सकता है। व्हील क्लॉकर गेंद की गति, पहिये और लॉन्च के समय पहिये की स्थिति का अनुमान लगाकर यह अनुमान लगा सकते हैं कि गेंद पहिये पर कहाँ गिरेगी।
मैं उस खिलाड़ी का नाम श्री एस रखूँगा जिसने इस मुद्दे को मेरे ध्यान में लाया। उनके अनुसार, मनोरंजनात्मक खिलाड़ियों को शायद एक निष्पक्ष खेल मिलता, जहाँ प्रत्येक संख्या के जीतने की संभावना 38 में से 1 होती। हालाँकि, अगर कुछ लाल झंडे उठाए जाते, तो खेल उस स्थिति में पहुँच जाता जिसे उन्होंने "संकटग्रस्त मोड" कहा। व्हील क्लॉकर के लिए लाल झंडों की परिकल्पना इस प्रकार की गई थी:
- बड़े दांव। यह स्पष्ट नहीं था कि "बड़ा" कितना बड़ा होना चाहिए, लेकिन कुल मिलाकर 20 डॉलर पर्याप्त माने गए।
- देर से लगाए गए दांव। विशेष रूप से, गेंद के लॉन्च और समय की समाप्ति के बीच के पाँच सेकंड।
- अनुभागीय दांव। पहिये पर एक-दूसरे के निकट स्थित एकल संख्याओं पर दांव लगाना।
खेल को खतरा महसूस होने पर, कथित तौर पर मशीन आक्रामक जवाबी कार्रवाई करती थी। इन जवाबी कार्रवाई का उद्देश्य गेंद को व्हील क्लॉकर द्वारा निर्धारित सेक्शन से दूर गिराना था। यह कैसे किया जाता था, यह स्पष्ट नहीं था, लेकिन श्री एस के पास कुछ सिद्धांत थे, जिन्हें उन्होंने मुझे साझा न करने के लिए कहा।
श्री एस ने मुझे अपना डेटा और उसका विश्लेषण बताया, जो निश्चित रूप से मेरी उत्सुकता बढ़ाने के लिए काफ़ी था। हालाँकि, श्री एस ने मुझसे अनुरोध किया कि मैं इसके बारे में कोई भी विशिष्ट जानकारी साझा न करूँ।
ग्लोबल गेमिंग एक्सपो
इस खेल से जुड़ने के शुरुआती दौर में, मैं लास वेगास में 2016 ग्लोबल गेमिंग एक्सपो में गया था। इंटरब्लॉक वहाँ एक बहुत बड़ा और प्रमुख स्थान रखता था। श्री एस की अनुमति से, मैंने इंटरब्लॉक बूथ पर एक इंजीनियर से बात करने का अनुरोध किया। जिस सेल्सवुमन से मैंने शुरुआत में बात की थी, उसे एक इंजीनियर मिला जो मेरे पास आया और अपना परिचय दिया। मैं ऑर्गेनिक रूलेट जैसी ही एक मशीन पर बैठा था, जिसमें गेंद निकलने के बाद भी खिलाड़ी को दांव लगाने के लिए लगभग पाँच सेकंड का समय दिया जाता था। परिचय के बाद, बातचीत कुछ इस प्रकार हुई, और मैं इसे संक्षेप में प्रस्तुत कर रहा हूँ:
- शेकलफोर्ड: मैंने इस मशीन पर देखा है कि बेटिंग बंद होने से कई सेकंड पहले गेंद छोड़ दी जाती है।
- इंटरब्लॉक: और?
- शेकलफोर्ड: क्या आपको नहीं लगता कि यह व्हील-क्लॉकिंग टीमों के लिए असुरक्षित होगा?
- इंटरब्लॉक: हम इस मुद्दे से अच्छी तरह परिचित हैं।
उनके शरीर की भाषा और लहजे से लग रहा था कि वे अब और कुछ नहीं कहेंगे, इसलिए मैंने उन्हें समय देने के लिए धन्यवाद दिया और अपनी राह पर चल दिया।
उस बातचीत का आप जो चाहें अर्थ निकालें।
पहला प्रयोग
श्रीमान एस द्वारा प्रस्तुतीकरण प्राप्त करने के बाद, मैं निश्चित रूप से जानने को उत्सुक था कि क्या हो रहा है। पहले चरण के रूप में, मैंने एक अन्य इच्छुक व्यक्ति, जिसे मैं श्रीमान सी कहूँगा, के साथ मिलकर 299 स्पिन का डेटा एकत्र किया। हमारी सट्टेबाजी की विधि पाँच लगातार संख्याओं पर $2-$2 का दांव लगाना था। श्रीमान एस को यकीन नहीं था कि कुल $10 का दांव खेल को खतरे में डालने के लिए पर्याप्त होगा, लेकिन उन्हें लगा कि प्रयोग करते समय खेल को नाराज़ करने और बहुत ज़्यादा पैसा न गँवाने के बीच यह एक अच्छा संतुलन था।
न तो श्रीमान सी और न ही मैं व्हील क्लॉकर हैं, इसलिए हम एक व्यवस्थित तरीके से दांव लगाते थे जिसमें आर्क बेट का केंद्र दो स्पिन पीछे जीतने वाला नंबर होता था। हमारा लक्ष्य यह देखना था कि व्हील पर जीतने वाली स्थिति हमारे बेटिंग आर्क के केंद्र से कितनी मेल खाती है।
ग्राफ 1 और तालिका 1 हमारी केंद्र सट्टेबाजी स्थिति और जीतने वाली संख्या के बीच प्रत्येक ऑफसेट की आवृत्ति को दर्शाते हैं।
png" />तालिका नंबर एक
| ओफ़्सेट | टिप्पणियों | अपेक्षाएं |
|---|---|---|
| -18 | 5 | 7.87 |
| -17 | 9 | 7.87 |
| -16 | 13 | 7.87 |
| -15 | 7 | 7.87 |
| -14 | 11 | 7.87 |
| -13 | 12 | 7.87 |
| -12 | 7 | 7.87 |
| -11 | 10 | 7.87 |
| -10 | 8 | 7.87 |
| -9 | 10 | 7.87 |
| -8 | 6 | 7.87 |
| -7 | 8 | 7.87 |
| -6 | 9 | 7.87 |
| -5 | 10 | 7.87 |
| -4 | 3 | 7.87 |
| -3 | 7 | 7.87 |
| -2 | 7 | 7.87 |
| -1 | 6 | 7.87 |
| 0 | 8 | 7.87 |
| 1 | 4 | 7.87 |
| 2 | 4 | 7.87 |
| 3 | 8 | 7.87 |
| 4 | 7 | 7.87 |
| 5 | 4 | 7.87 |
| 6 | 18 | 7.87 |
| 7 | 6 | 7.87 |
| 8 | 9 | 7.87 |
| 9 | 6 | 7.87 |
| 10 | 8 | 7.87 |
| 11 | 4 | 7.87 |
| 12 | 13 | 7.87 |
| 13 | 3 | 7.87 |
| 14 | 8 | 7.87 |
| 15 | 12 | 7.87 |
| 16 | 6 | 7.87 |
| 17 | 7 | 7.87 |
| 18 | 9 | 7.87 |
| 19 | 7 | 7.87 |
| कुल | 299 | 299.00 |
एक काई-स्क्वेयर्ड गुडनेस-ऑफ-फिट परीक्षण का परिणाम 37 डिग्री स्वतंत्रता के साथ 45.29 का काई-स्क्वेयर्ड आँकड़ा प्राप्त होता है। एक यादृच्छिक खेल द्वारा इससे अधिक विषम परिणाम प्राप्त करने की संभावना 16.5% है।
तालिका 2 पहले प्रयोग में केंद्र संख्या दांव के आसपास केंद्रित विभिन्न चाप आकारों पर एक गॉसियन परीक्षण के परिणाम दर्शाती है। हमने जिस पाँच-संख्या चाप को कवर किया है, उसके लिए एक निष्पक्ष पहिये पर जीत की अपेक्षित संख्या 39.3 होगी। हमारे पास केवल 29 थे। एक निष्पक्ष खेल में इतने बुरे या उससे भी बदतर परिणामों की संभावना 3.84% है।
तालिका 2
| चाप का आकार | टिप्पणियों | अपेक्षाएं | आकार मानक विचलन | संख्या मानक विचलन | संभावना |
|---|---|---|---|---|---|
| 1 | 8 | 7.87 | 2.77 | 0.05 | 0.518957 |
| 3 | 18 | 23.61 | 4.66 | -1.20 | 0.114658 |
| 5 | 29 | 39.34 | 5.85 | -1.77 | 0.038417 |
| 7 | 44 | 55.08 | 6.70 | -1.65 | 0.049187 |
| 17 | 124 | 133.76 | 8.60 | -1.14 | 0.128074 |
हालाँकि हमारे नतीजे उम्मीदों से कम थे, फिर भी यह आसानी से एक सामान्य दुर्भाग्य भी हो सकता था। हालाँकि, मैंने हिसाब लगाया कि अगर मैं इसी दर से हारता रहा, तो अनुचित खेल का मामला बनाने के लिए बस बड़े नमूने की ज़रूरत होगी। कई बैठकों और ईमेल के बाद, दूसरे प्रयोग के साथ आगे बढ़ने का फैसला किया गया।
दूसरा प्रयोग
किसी कैसीनो गेम के निष्पक्ष न होने का एक वैध मामला बनाने के लिए, उसे साबित करने के लिए एक प्रयोग को दोहराया जाना चाहिए। काफी विचार-विमर्श के बाद, पाँच अंकों वाले आर्क में प्रत्येक संख्या पर $5 का दांव लगाकर जीत की कमी का परीक्षण करने का निर्णय लिया गया। यह निर्णय लिया गया कि तीन अलग-अलग पहियों पर 1,000 चक्करों के लिए ऐसा किया जाएगा। श्रीमान एस के खेलने के अलावा, हमेशा कम से कम एक गवाह मौजूद रहता था, या तो मैं या श्रीमान सी। यह तय किया गया कि खेल पूरा होने के बाद, हम आँकड़ों की जाँच करेंगे और तय करेंगे कि आगे क्या करना है। अगर हमें कोई गैर-यादृच्छिक खेल दिया जा रहा है, तो किसी भी उचित संदेह से परे, हमने अपने सबूत सार्वजनिक करने की योजना बनाई।
इस कहानी के अंत तक हमारे पास 1,204 स्पिन डेटा थे। हमें पता था कि नतीजे उम्मीदों से थोड़े कम होंगे, लेकिन श्री एस के अनुसार, ज़्यादातर समय गेम बेतरतीब ढंग से चल रहे थे और कुछ समय के लिए ही "खतरे" की स्थिति में थे।
आंकड़ों की इस समीक्षा के आधार पर, हमें लगा कि हम इतनी अधिक हार नहीं रहे हैं कि हमें खेलना जारी रखना पड़े।
दूसरे प्रयोग के परिणाम और विश्लेषण निम्नलिखित हैं। शुरुआत करने के लिए, निम्नलिखित ग्राफ़ और तालिका 3, आर्क बेट के केंद्र और गेंद के गिरने की जगह के बीच प्रत्येक ऑफसेट की आवृत्ति दर्शाते हैं।
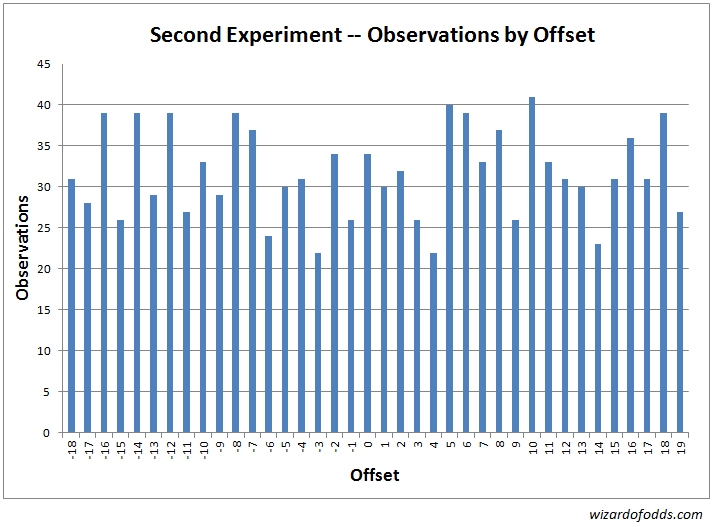
टेबल तीन
| ओफ़्सेट | टिप्पणियों | अपेक्षाएं |
|---|---|---|
| -18 | 31 | 31.68 |
| -17 | 28 | 31.68 |
| -16 | 39 | 31.68 |
| -15 | 26 | 31.68 |
| -14 | 39 | 31.68 |
| -13 | 29 | 31.68 |
| -12 | 39 | 31.68 |
| -11 | 27 | 31.68 |
| -10 | 33 | 31.68 |
| -9 | 29 | 31.68 |
| -8 | 39 | 31.68 |
| -7 | 37 | 31.68 |
| -6 | 24 | 31.68 |
| -5 | 30 | 31.68 |
| -4 | 31 | 31.68 |
| -3 | 22 | 31.68 |
| -2 | 34 | 31.68 |
| -1 | 26 | 31.68 |
| 0 | 34 | 31.68 |
| 1 | 30 | 31.68 |
| 2 | 32 | 31.68 |
| 3 | 26 | 31.68 |
| 4 | 22 | 31.68 |
| 5 | 40 | 31.68 |
| 6 | 39 | 31.68 |
| 7 | 33 | 31.68 |
| 8 | 37 | 31.68 |
| 9 | 26 | 31.68 |
| 10 | 41 | 31.68 |
| 11 | 33 | 31.68 |
| 12 | 31 | 31.68 |
| 13 | 30 | 31.68 |
| 14 | 23 | 31.68 |
| 15 | 31 | 31.68 |
| 16 | 36 | 31.68 |
| 17 | 31 | 31.68 |
| 18 | 39 | 31.68 |
| 19 | 27 | 31.68 |
| कुल | 1204 | 1204.00 |
एक काई-स्क्वेयर्ड गुडनेस-ऑफ-फिट परीक्षण का परिणाम 37 डिग्री स्वतंत्रता के साथ 34.79 का काई-स्क्वेयर्ड आँकड़ा प्राप्त होता है। एक यादृच्छिक खेल द्वारा इससे अधिक विषम परिणाम प्राप्त करने की संभावना 57.32% है।
तालिका 4 केंद्र संख्या बेट के आसपास केंद्रित विभिन्न चाप आकारों पर गॉसियन परीक्षण के परिणाम दर्शाती है। सभी चाप आकार सामान्य सीमा के भीतर ही हैं।
तालिका 4
| चाप का आकार | टिप्पणियों | अपेक्षाएं | आकार मानक विचलन | संख्या मानक विचलन | संभावना |
|---|---|---|---|---|---|
| 1 | 34 | 31.68421053 | 5.55 | 0.42 | 0.661637 |
| 3 | 90 | 95.05263158 | 9.36 | -0.54 | 0.294599 |
| 5 | 156 | 158.4210526 | 11.73 | -0.21 | 0.418235 |
| 7 | 204 | 221.7894737 | 13.45 | -1.32 | 0.092997 |
| 17 | 536 | 538.6315789 | 17.25 | -0.15 | 0.439385 |
संयुक्त परिणाम
पहले और दूसरे प्रयोगों के संयुक्त आँकड़े निम्नलिखित हैं। शुरुआत करने के लिए, निम्नलिखित ग्राफ़ और तालिका 5, आर्क बेट के केंद्र और गेंद के गिरने की जगह के बीच प्रत्येक ऑफसेट की आवृत्ति दर्शाते हैं।
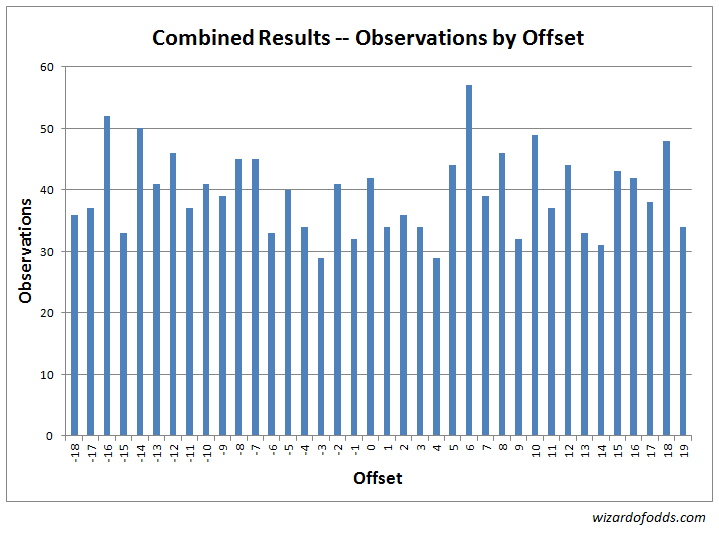
तालिका 5
| ओफ़्सेट | टिप्पणियों | अपेक्षाएं |
|---|---|---|
| -18 | 36 | 39.55 |
| -17 | 37 | 39.55 |
| -16 | 52 | 39.55 |
| -15 | 33 | 39.55 |
| -14 | 50 | 39.55 |
| -13 | 41 | 39.55 |
| -12 | 46 | 39.55 |
| -11 | 37 | 39.55 |
| -10 | 41 | 39.55 |
| -9 | 39 | 39.55 |
| -8 | 45 | 39.55 |
| -7 | 45 | 39.55 |
| -6 | 33 | 39.55 |
| -5 | 40 | 39.55 |
| -4 | 34 | 39.55 |
| -3 | 29 | 39.55 |
| -2 | 41 | 39.55 |
| -1 | 32 | 39.55 |
| 0 | 42 | 39.55 |
| 1 | 34 | 39.55 |
| 2 | 36 | 39.55 |
| 3 | 34 | 39.55 |
| 4 | 29 | 39.55 |
| 5 | 44 | 39.55 |
| 6 | 57 | 39.55 |
| 7 | 39 | 39.55 |
| 8 | 46 | 39.55 |
| 9 | 32 | 39.55 |
| 10 | 49 | 39.55 |
| 11 | 37 | 39.55 |
| 12 | 44 | 39.55 |
| 13 | 33 | 39.55 |
| 14 | 31 | 39.55 |
| 15 | 43 | 39.55 |
| 16 | 42 | 39.55 |
| 17 | 38 | 39.55 |
| 18 | 48 | 39.55 |
| 19 | 34 | 39.55 |
| कुल | 1503 | 1503.00 |
एक काई-स्क्वेयर्ड गुडनेस-ऑफ-फिट परीक्षण का परिणाम 37 डिग्री स्वतंत्रता के साथ 41.75 का काई-स्क्वेयर्ड आँकड़ा प्राप्त होता है। एक यादृच्छिक खेल द्वारा इससे अधिक विषम परिणाम प्राप्त करने की संभावना 27.19% है।
तालिका 6 केंद्र संख्या दांव के आसपास केंद्रित विभिन्न चाप आकारों पर एक गॉसियन परीक्षण के परिणाम दिखाती है। सभी परीक्षण एक निष्पक्ष खेल के लिए एक उचित सीमा के भीतर आते हैं।
तालिका 6
| चाप का आकार | टिप्पणियों | अपेक्षाएं | आकार मानक विचलन | संख्या मानक विचलन | संभावना |
|---|---|---|---|---|---|
| 1 | 42 | 39.55263158 | 6.21 | 0.39 | 0.653346 |
| 3 | 108 | 118.6578947 | 10.45 | -1.02 | 0.153986 |
| 5 | 185 | 197.7631579 | 13.11 | -0.97 | 0.165050 |
| 7 | 248 | 276.8684211 | 15.03 | -1.92 | 0.027374 |
| 17 | 660 | 672.3947368 | 19.28 | -0.64 | 0.260114 |
पहले और दूसरे प्रयोगों के परिणामों के बीच सहसंबंध गुणांक 0.153853 है। सीधे शब्दों में कहें तो, इसका मतलब है कि थोड़ा-बहुत सहसंबंध था, लेकिन यह दो यादृच्छिक डेटा सेटों से अपेक्षित सीमा के भीतर था।
निष्कर्ष
मुझे यह कहने से पहले कि कोई भी खेल निष्पक्ष खेल की स्वाभाविक संभावनाओं के अनुसार नहीं खेला जा रहा है, बहुत उच्च स्तर के प्रमाणों की आवश्यकता है। इस मामले में, वह मानक पूरा नहीं हुआ। दूसरे शब्दों में, मेरे पास यह आरोप लगाने का कोई औचित्य नहीं है कि ऑर्गेनिक रूलेट मशीनें अनुचित तरीके से खेल रही हैं।
जवाब
मैंने श्री एस को इस पृष्ठ को आम जनता के सामने प्रकाशित करने से पहले उसका पूर्वावलोकन करने का अवसर दिया। उन्होंने कई अच्छे सुझाव और सुधार दिए। अंततः, उन्हें मेरे शब्दों पर अभी भी कुछ आपत्तियाँ थीं। इसलिए, मैंने उन्हें एक प्रतिक्रिया प्रकाशित करने का अवसर दिया, जो उन्होंने प्रकाशित की। इसका शीर्षक है, "श्री एस द्वारा इंटरब्लॉक प्रयोग के परिणामों पर एक और दृष्टिकोण"।
मैं हमेशा अंतिम शब्द कहना पसंद करता हूं, इसलिए मैंने एक प्रति-प्रतिक्रिया प्रकाशित की जिसका शीर्षक था, माइकल शेकलफोर्ड द्वारा लिखित ऑर्गेनिक रूलेट प्रयोग पर श्री एस. की प्रतिक्रिया का उत्तर ।



