रूले - अक्सर पूछे जाने वाले प्रश्न
अगर आप इस तरह रूलेट खेलें तो आपका क्या होगा - 0 और 00 दोनों पर $5 का दांव लगाएँ, और दो स्तंभों पर $15 का दांव लगाएँ। क्या आपको जीतने की 70% संभावना नहीं होगी?
आपके पास $140 जीतने की 2/38 संभावना, $5 जीतने की 24/38 संभावना और $40 हारने की 12/38 संभावना होगी। कुल अपेक्षित रिटर्न [(2/38)*140 + (24/38)*5 + (12/38)*-40]/40 = -5.26% है। डबल-ज़ीरो रूलेट में हर दांव पर समान हाउस एज (0-00-1-2-3 संयोजन को छोड़कर, जो 7.89% है)।
मान लीजिए मैं किसी कसीनो में जाकर रूलेट में 2-1 के भुगतानों में से दो पर दांव लगाता हूँ, जैसे 1-12 पर $100 और 13-24 पर $100। एक बार के सौदे में, क्या मेरे $100 जीतने की संभावना 63% नहीं है? मैं लंबी अवधि की बात नहीं कर रहा हूँ; बस एक बार के दांव की बात कर रहा हूँ।
आप सही कह रहे हैं, जीतने की संभावना 24/38, यानी लगभग 63% है। हालाँकि, आपको केवल $100 जीतने के लिए $200 का जोखिम उठाना होगा। अगर आप अपनी जीत की संभावना और बढ़ाना चाहते हैं, तो किसी भी 35 नंबरों पर दांव लगाएँ। जीतने की संभावना 92% होगी।
क्या रूलेट में दांवों को मिलाकर अपनी जीत की संभावना को अधिकतम करने का कोई तरीका है? उदाहरण के लिए, एक दर्जन दांव पर 2 से 1 का भुगतान होता है। अगर मैं दो दर्जन दांव लगाता हूँ, मान लीजिए 12 के पहले और दूसरे सेट पर, तो मेरे पास जीत की 63.16% संभावना है। ये दांव किसी साधारण लाल/काले, सम/विषम, या उच्च/निम्न दांव से बेहतर हैं। हालाँकि मुझे वास्तव में 2 से 1 के बजाय केवल 1 से 1 का लाभ होता है (यदि मैं जीत जाता हूँ, क्योंकि मेरे दांव का कुछ हिस्सा हारना ही है क्योंकि विजेता संख्या बारह के पहले और दूसरे दोनों सेट में नहीं हो सकती), दो दांवों को मिलाकर मेरे पक्ष में दांवों की संभावना थोड़ी बदल गई है। क्या इस प्रकार के संयोजनों पर दांवों की संभावनाएँ निर्धारित की गई हैं? यदि निर्धारित की गई हैं, तो मैं उन्हें कहाँ पा सकता हूँ?
जब तक आप 0-00-1-2-3 के संयोजन से दूर रहते हैं, तब तक किसी भी दांव के संयोजन पर हाउस एज हमेशा ठीक 1/19, या 5.26% होता है। जीतने की संभावना बढ़ाने के कई तरीके हैं, लेकिन इसकी कीमत यह होगी कि आप अपने कुल दांव के मुकाबले कम जीतेंगे।
मैं कल रात "मार्टिंगेल" पद्धति से रूलेट खेल रहा था, जिसमें पहली हार के बाद दो बार दांव दोगुना हो जाता है। बेवकूफी है, मुझे पता है, लेकिन मैं आमतौर पर ज़्यादा नहीं हारता और लंबे समय तक जुआ खेलता हूँ। खैर, मेरे लिए खेल का अंत यह हुआ कि मैं बराबरी का दांव लगा रहा था, और चार बार घुमाने पर तीन बार 9 आया। इसकी संभावना क्या है? क्या यह संदिग्ध लगता है? वैसे, क्या कैसीनो कभी धोखाधड़ी करते हुए पकड़े गए हैं?
किसी भी संख्या के 4 में से तीन बार आने की प्रायिकता 38*4*(1/38) 3 *(37/38) = 1/5932 है। हालाँकि, अगर आप काफी देर तक खेलते हैं, तो आप इस तरह की असामान्य घटनाओं को देखे बिना नहीं रह सकते। यह संदेह के स्तर तक नहीं पहुँचता। असली कैसिनो में धोखाधड़ी होती है। आमतौर पर कोई धोखेबाज डीलर ही कैसिनो सुरक्षाकर्मियों द्वारा पकड़ा जाता है। ऑनलाइन कैसिनो के खिलाफ धोखाधड़ी के कुछ गंभीर मामले दर्ज किए गए हैं, लेकिन जहाँ तक मुझे पता है, किसी भी सरकारी प्राधिकरण ने कभी किसी को दोषी नहीं ठहराया है।
क्या एक ही दांव के दौरान अंदर की कई संख्याओं पर दांव लगाना (जैसा कि ज़्यादातर खिलाड़ी करते हैं) रूलेट सट्टेबाजी की एक और भी बुरी रणनीति नहीं है, बजाय एक ही नंबर पर लगातार अलग-अलग दांव लगाने के? उदाहरण के लिए, अगर किसी के पास $100 हों, तो "8" नंबर पर $10 के 10 दांव लगाने पर, एक ही बार में 10 नंबरों पर $10 दांव लगाने से कम नुकसान होगा? मुझे लगता है कि "हेजिंग" सिर्फ़ इस बात की गारंटी देती है कि कुछ (ऊपर दिए गए मामले में 9 दांव) हमेशा हारेंगे? क्या आप अपने पेज पर "हेजिंग" का ज़िक्र नहीं करते?
मैंने सिस्टम्स पर आपका पेज पढ़ा है और मैं सालों से लोगों को यही बताता आ रहा हूँ! मैं एक कसीनो में रूलेट खेलता हूँ और मैंने कभी न कभी सभी सिस्टम्स देखे हैं। मैंने एक ऐसा सिस्टम देखा है जो कंप्यूटर सिमुलेशन पर भले ही काम न करे (शायद काम न करे), लेकिन असल ज़िंदगी में "काम करता हुआ" "लगता" है। इसका मतलब है कि मैंने इसे हार से ज़्यादा जीतते देखा है।
यह इस तरह काम करता है कि एक खिलाड़ी 1 से 18 तक के अंकों पर $75, तीसरे 12 पर $50 और 0-00 के बंटवारे पर $10 लगाता है, यानी कुल $135। यह छह अंकों (19 से 22 तक) को छोड़कर बाकी सभी पर लागू होता है और जब भी गेंद उन छह अंकों से चूकेगी, तो $15 का भुगतान होगा, सिवाय इसके कि जब 0 या 00 आए, तो यह $40 होगा। मुझे पता है कि यह अजीब लग रहा है!!! लेकिन यकीन मानिए, मैं आपको बता रहा हूँ कि मैंने इसे हार से ज़्यादा जीतते देखा है। यह उल्टा भी काम करता है (अरे वाह)। मुझे इस सिस्टम के असली ऑड्स जानने में बहुत मज़ा आएगा, लेकिन किसी को यह बताना मुश्किल है कि यह काम नहीं करता, जब वह मेरी टेबल से दो हज़ार डॉलर ज़्यादा अमीर होकर जा रहा हो :-)
$15 जीतने के 30 तरीके हैं, $135 हारने के 6 तरीके हैं, और $45 जीतने के 2 तरीके हैं (न कि $40)। इस दांव संयोजन का अपेक्षित प्रतिफल ((30/38)*15 + (6/38)*-135 + (2/38)*(45))/135 = -.0526, या 5.26% है, जो किसी भी एक दांव या दांवों के संयोजन पर हाउस एज है, बशर्ते कि खतरनाक 0-00-1-2-3 संयोजन से बचा जाए। आपके अवलोकन में, आपने संभवतः अपेक्षा से कम 19-24 बार ऐसा होते देखा होगा, जिससे यह भ्रम पैदा होता है कि यह तरीका जीत रहा है।
मान लीजिए, जादूगर, मैं रूलेट के बारे में सोच रहा था। बॉस मीडिया सॉफ्टवेयर के साथ, आप बिना दांव लगाए ही पहिया घुमा सकते हैं। क्या यह खिलाड़ी के पक्ष में नहीं है? मैंने कुछ रूलेट सट्टेबाजी प्रणालियाँ देखी हैं, जैसे मार्टिंगेल, जहाँ हारने पर आप दुगुना दांव लगा सकते हैं। क्या आप बिना दांव लगाए बस पहिया नहीं देख सकते और पिछले घुमावों के आधार पर अपना दांव नहीं लगा सकते? एक उदाहरण यह होगा कि दांव लगाने से पहले पहिया को पाँच बार घुमाएँ। मान लीजिए कि सभी संख्याएँ विषम हैं। क्या सम संख्या पर दांव लगाकर पहिया खेलना शुरू करना समझदारी नहीं होगी? मुझे पता है कि यह जुआरी के भ्रम को दर्शाता है और पहिया को इस बात की परवाह नहीं होती कि आखिरी घुमाव क्या था, लेकिन हर घुमाव के साथ विषम संख्या आने की संभावना भी कम होती जाती है। क्या मैं सही कह रहा हूँ या बस किसी पुराने सिद्धांत पर चल रहा हूँ?
आप बस जुआरी के भ्रम को दोहरा रहे हैं। अगर गेंद लगातार 100 बार सम संख्या में आती है, तो अगले चक्कर के सम होने की संभावना हर चक्कर के बराबर ही रहेगी, दोहरे शून्य वाले पहिये पर 47.37%। इसलिए बिना दांव लगाए घूमने से कोई फायदा नहीं है। गेंद की कोई याददाश्त नहीं होती।
हालाँकि रूलेट को संयोग से नहीं हराया जा सकता, मैंने सुना है कि भौतिकी इसे दो तरीकों से (सिद्धांत रूप में) हरा सकती है। पहला तरीका: एक उच्च तकनीक वाला उपकरण, जो पहिये के वेग के विरुद्ध गेंद के वेग को मापता है और पहिये के परिणामी क्षेत्र का लगभग 40% सटीकता से अनुमान लगाता है। दूसरा तरीका: पहिये का बायस। ज़ाहिर है, खिलाड़ी को बराबरी पर लाने के लिए पहिये का बायस कम से कम 5.26% होना चाहिए। सवाल यह है कि जादूगर, अगर कोई बायस है, तो उसे निर्धारित करने के लिए आपको कितने चक्कर लगाने होंगे?
मैंने इन दोनों तकनीकों के इस्तेमाल के बारे में सुना है। मुझे पहियों को घड़ी की तरह चलाने वाले उपकरणों के बारे में ज़्यादा जानकारी नहीं है, सिवाय इसके कि ये मौजूद हैं और समय-समय पर इस्तेमाल किए जाते हैं। यहाँ नेवादा में ऐसा उपकरण बेहद गैरकानूनी होगा। पक्षपाती पहियों का फ़ायदा उठाने के बारे में मैंने काफ़ी सुना है। ऐसा कई बार किया गया है। मुझे लगता है कि पुराने पहियों वाले कैसीनो सबसे असुरक्षित लक्ष्य हैं। मैं सालों से कह रहा हूँ कि अर्जेंटीना इसके लिए एक उपयुक्त लक्ष्य है।
मार्टिंगेल डबल-अप सिस्टम में सिंगल-ज़ीरो रूलेट व्हील के विरुद्ध किसी भी सम संभावना पर खेलते समय, मैंने अनुमान लगाया था कि आप हर 248 सत्रों में एक बार हारेंगे। यानी एक सत्र जो या तो एक यूनिट की जीत या 255 यूनिट की हार के साथ पूरा होता है। क्या मैं सही अनुमान लगा रहा हूँ? अगर नहीं, तो क्या आप कृपया सही ऑड्स बता सकते हैं?
यदि अधिकतम हानि 255 यूनिट है, तो आप 8 बार तक दांव लगा सकते हैं। लगातार आठ बार हारने की संभावना (19/37) 8 = .004835 है। इसलिए, आपके पास एक यूनिट जीतने की 99.52% संभावना है, और 255 यूनिट हारने की 0.48% संभावना है।
औसतन, एकल-शून्य रूलेट में, 36 चक्करों के दौरान एक संख्या कितनी बार दोहराई जाएगी (उदाहरण के लिए, एक पंक्ति में दो 8)?
आप संख्याओं के हर 37 जोड़ों में एक बार दोहराव की उम्मीद कर सकते हैं। तो, 36 संख्याओं के साथ हमारे पास संख्याओं के 35 जोड़े हैं। इसलिए, दोहराव की अपेक्षित संख्या 35/37 = 0.9459 है।
हर कोई कहता है कि गणितीय प्रणालियों से रूलेट को लंबे समय तक नहीं हराया जा सकता। लेकिन, आप इस तथ्य को कैसे समझाएँगे कि कुछ पेशेवर जुआरी भी हैं जो रूलेट से अपना गुज़ारा करते हैं? मुझे नहीं लगता कि यह सिर्फ़ शेखी बघारने की बात है। दरअसल, रोज़ाना खेलने से वे जितना हारते हैं, उससे कहीं ज़्यादा जीतते हैं।
मुझे कोई ऐसा दिखाओ जो रूलेट के निष्पक्ष खेल में जीत रहा हो, और मैं तुम्हें कोई ऐसा दिखाऊँगा जो बस भाग्यशाली है, और शायद सब कुछ हार जाएगा। आप रूलेट को केवल लाभप्रद खेल से ही कुशलता से हरा सकते हैं, जैसे पक्षपाती पहिये का फायदा उठाना, या पहिये को घुमाना।
मैंने रूलेट के बारे में आपकी सारी बातें पढ़ ली हैं, लेकिन रूलेट स्पिनरों के बारे में कुछ नहीं देखा। पिट बॉस की चौकस निगाह में, रूलेट स्पिनर घर की संभावनाओं को बेहतर बनाने के लिए "सेक्शन" फेंकता है। स्पिनर जो ग्रीन्स फेंक सकता है, हर बार नहीं, लेकिन समय के अच्छे प्रतिशत के साथ, शायद 7 या 8 में से एक जब वह किसी बड़े प्रोग्रेसिव बेटर को खत्म करना चाहता है।
कैसीनो को जीतने के लिए ऐसी तरकीबें अपनाने की ज़रूरत नहीं है। इसके अलावा, कैसीनो को प्रगतिशील सट्टेबाजों से डरने की कोई ज़रूरत नहीं है। ज़्यादातर प्रगतिशील सट्टेबाज ही जीतते हैं, लेकिन जो कुछ लोग अपनी बैंकरोल सीमा तक पहुँच जाते हैं, वे सभी विजेताओं के लिए भुगतान करते हैं और फिर कैसीनो के लिए कुछ और भी। इसके अलावा, किसी गेंद को जानबूझकर किसी खास हिस्से में घुमाने के लिए बहुत कौशल की ज़रूरत होती है। मुझे नहीं लगता कि यह किसी भी हद तक सटीकता से किया जा सकता है।
हाय विज़ार्ड, आपकी साइट बहुत बढ़िया है। डबल 0 रूलेट में, मुझे पता है कि सभी दांवों का हाउस एज एक जैसा होता है, लेकिन मैं अभी एक सांख्यिकी पाठ्यक्रम पूरा कर रहा हूँ और मुझे लगता है कि सभी दांव अपने मानक विचलन के कारण बिल्कुल समान नहीं होते। उदाहरण के लिए, लाल पर $1 के दांव का मानक विचलन 1.012019 है, जबकि मेरी गणना के अनुसार, किसी एकल संख्या पर $1 के दांव का मानक विचलन 5.839971 है। इस प्रकार, 1, 100 और 10000 परीक्षणों में आगे निकलने की अपेक्षित संभावना क्रमशः सम-धन दांव के लिए 0.4793, 0.3015 और 0.0000 है, और एकल संख्या दांव के लिए 0.4964, 0.4641 और 0.1837 है। क्या मेरा विश्लेषण सही है? (मैंने सामान्यता मान ली थी) धन्यवाद!
तारीफ़ के लिए शुक्रिया। सबसे पहले, किसी भी सम संख्या वाले दांव पर मानक विचलन 0.998614 है और एकल संख्या पर 5.762617 है। 1, 100 और 10000 स्पिन पर सम संख्या वाले दांव पर फ्लैट बेटिंग करके आगे निकलने की संभावना क्रमशः 0.473684, 0.265023 और 0.00000007 है। 1, 100 और 10000 स्पिन पर एकल संख्या वाले दांव पर फ्लैट बेटिंग करके आगे निकलने की संभावना क्रमशः 0.0263158, 0.491567 और 0.18053280 है। ऐसा लगता है कि आप यह तर्क देने की कोशिश कर रहे हैं कि एकल संख्या वाले दांव बेहतर होते हैं क्योंकि कई दांवों पर आगे निकलने की संभावना ज़्यादा होती है। यह सच है, हालाँकि, बड़े नुकसान की संभावना भी कहीं ज़्यादा होती है। एक सत्र में अपेक्षित परिणाम हमेशा बेल कर्व पर कहीं न कहीं आते हैं। लाल या काले जैसे कम अस्थिरता वाले दांवों के साथ, यह बेल कर्व स्पष्ट होता है और छोटे नुकसान से ज़्यादा दूर नहीं जाता। एकल संख्याओं जैसे उच्च अस्थिरता वाले दांवों के साथ, यह बेल कर्व चौड़ा होता है, जिससे अच्छे और बुरे, दोनों तरह के शुद्ध परिणामों की एक व्यापक श्रृंखला प्राप्त होती है।
मेरा सहकर्मी डी. ज़ोर देकर कहता है कि उसने रूलेट में लगातार जीतने का एक तरीका खोज निकाला है। मुझे यकीन नहीं हो रहा। क्या वह सिर्फ़ किस्मत वाला है या कोई और तरीका है जो काम करता है?
वह तो बस किस्मत वाला है। जैसा कि मैंने हज़ारों बार कहा है, कोई भी सट्टेबाजी प्रणाली समय की कसौटी पर खरी नहीं उतर सकती।
मैंने रूलेट में मार्टिंगेल विधि पर आपका विषय पढ़ा। मैंने कंप्यूटर पर यह विधि कई बार आज़माई है और मुझे $500 का फायदा हुआ है। फिर मैं कसीनो गया और $1000 से ज़्यादा हार गया। क्योंकि काला लगातार 8 बार आया। लेकिन मैं अभी बैकारेट सीखना शुरू कर रहा हूँ। मैं इसे कंप्यूटर पर आज़मा रहा था और बैंकर पर दांव लगाकर मुझे फिर से $500 का फायदा हुआ। $20 से शुरू होकर, फिर $40, फिर $80 और इसी तरह। हर हाथ पर 5% देकर भी मुझे $500 का फायदा हुआ। क्या आपको लगता है कि यह विधि कसीनो में काम करेगी? मैंने सोचा कि मैं जाने से पहले पूछ लूँगा और $1000 और हार जाऊँगा। जैसा कि मैंने कहा, काला लगातार 8 बार आया। लेकिन क्या आपको लगता है कि खिलाड़ी का हाथ लगातार 8 बार जीतेगा? इसके अलावा, यह खेल अच्छा है क्योंकि बराबरी एक धक्का है, जबकि रूलेट में 0 या 00 हार है।
मार्टिंगेल हर खेल में खतरनाक होता है और लंबे समय में कभी जीत नहीं दिलाएगा। हालाँकि, बैकारेट में रूलेट की तुलना में इसका इस्तेमाल करना बेहतर है, क्योंकि इसमें हाउस एज कम होता है। खिलाड़ी के लगातार 8 बार जीतने की संभावना 0.493163^8 = 286 में 1 है। यह भी ध्यान रखें कि आप सीरीज़ के आखिर में एक हाथ जीत सकते हैं और फिर भी कमीशन के कारण पीछे रह सकते हैं। उदाहरण के लिए, अगर आपने $1 की बाजी से शुरुआत की और आप सातवें हाथ में जीत गए, तो आप $60.80 ($64*95%) जीतेंगे, जो पिछले $63 के नुकसान की भरपाई नहीं करेगा।
नमस्ते। आप कहते हैं कि सभी सट्टेबाजी प्रणालियाँ विफल हो जाएँगी। अगर आप रूलेट खेलते हैं और 1-12 नंबर पर एक यूनिट और 13-24 नंबर पर 2 यूनिट दांव लगाते हैं, तो क्या आपके जीतने या बराबरी करने की संभावना 66.66% नहीं होगी?
बिल्कुल नहीं। आपके पास 3 यूनिट जीतने की 12/38 संभावना, बराबरी पर आने की 12/38 संभावना और 3 यूनिट हारने की 14/38 संभावना होगी। अपेक्षित मान [(12/38)*3 + (12/38)*0 + (14/38)*-3]/3 = (-6/38)/3 = -2/38 = -5.26% है। यह दांवों के किसी भी संयोजन पर लागू होगा, बशर्ते आप खतरनाक 5 नंबरों के संयोजन (0/00/1/2/3) से बचें। अगर आप सिर्फ़ एक स्पिन के लिए खेलते हैं और अपनी जीत की संभावना को अधिकतम करना चाहते हैं, तो 35 नंबरों पर बराबर दांव लगाएँ। आपके पास 1 यूनिट जीतने की 92.11% संभावना और 35 यूनिट हारने की 7.89% संभावना होगी।
नमस्ते। मैं पिछले कुछ सालों से रूलेट का शौकीन जुआरी रहा हूँ और पहली बार मैं रूलेट सिस्टम आज़माने के बारे में सोच रहा हूँ... अब मुझे पता चल गया है कि आप इन तथाकथित "सिस्टम्स" और इनके पीछे के धोखेबाज़ों के बारे में कैसा महसूस करते हैं, और यकीन मानिए, मैं भी ऐसा ही महसूस करता हूँ, लेकिन मुझे दो ऐसे सिस्टम मिले हैं जिन्हें नज़रअंदाज़ नहीं किया जा सकता...
पहली रणनीति आरडी एलिसन की पुस्तक "गैम्बल टू विन: रूलेट" में पाई जाने वाली 3q/A-रणनीति है, जिसकी सत्यापित जीत दर 7.94% (7500 स्पिन) है। इस प्रणाली का परीक्षण और विकास फ्रैंक स्कोबलेट द्वारा "स्पिन रूलेट गोल्ड" और एरिक सेंट जर्मेन द्वारा "रूलेट सिस्टम टेस्टर" के साथ मिलकर किया गया था।
दूसरा है डॉन यंग का रूलेट सिस्टम, जिसे ज़ुम्मा पब्लिशिंग के रूलेट सिस्टम टेस्टर (15000 स्पिन) से मात देने के लिए सत्यापित किया गया है।
अब, मुझे कहना होगा कि मैं अभी भी इन सिस्टम्स पर पैसा खर्च करने को लेकर थोड़ा संशय में हूँ, लेकिन चूँकि इन्होंने लंबे समय में खुद को साबित किया है, इसलिए मुझे ऐसा कोई कारण नहीं दिखता कि मुझे ऐसा क्यों नहीं करना चाहिए। मेरा मतलब है, इन टेस्टबुक्स को मात देने का कुछ तो मतलब होगा...
इन प्रणालियों के बारे में आपकी क्या राय है? और क्या आपको लगता है कि मुझे इन्हें आज़माना चाहिए?
बहुत बहुत धन्यवाद! आपका दिन शुभ हो। शुभकामनाएँ
7500 स्पिन? बस इतना ही? अगर कोई आक्रामक तरीके से दांव लगाए, तो 7500 स्पिन से ज़्यादा में कोई भी कुल दांव पर लगाई गई रकम का 7.94% मुनाफ़ा दिखा सकता है। 15000 स्पिन के बारे में भी यही बात लागू होती है। ज़्यादातर सिस्टम छोटी-छोटी जीत और कम संख्या में बड़े नुकसान के लिए डिज़ाइन किए गए हैं। एक ऐसा सिस्टम जिसके लिए बहुत ज़्यादा बैंकरोल की ज़रूरत होती है, वह आसानी से 15000 स्पिन तक जा सकता है और मुनाफ़ा दिखा सकता है। आखिरकार नुकसान तो होगा ही और यह समय की कसौटी पर खरा नहीं उतरेगा। शुरुआत में भी बड़े नुकसान हो सकते हैं। किसी सिस्टम को परखने का सही तरीका है उसे अरबों बार आज़माना। इन सिस्टम के बारे में मेरी राय बाकी सभी सिस्टम जैसी ही है, ये बेकार हैं। मुझे आपके इन्हें आज़माने से कोई दिक्कत नहीं है, लेकिन मुझे इस बात से दिक्कत है कि कोई इन्हें बेचने वालों की जेब में एक पैसा भी डाल दे।
नोट: इस प्रश्न का अनुवर्ती उत्तर अगले कॉलम में देखें।
प्रिय महोदय, एकल शून्य रूलेट गेम में, जीतने की संभावना बढ़ जाती है यदि आप अधिक स्पिन के लिए कम नंबरों पर अपने पैसे का एक हिस्सा लगाते हैं, बजाय प्रति स्पिन अधिक संख्याओं को कवर करने के, एक उदाहरण: यदि आप 250 डॉलर जीतने के लिए 500 डॉलर का जोखिम उठाने को तैयार हैं तो आप यह कर सकते हैं: विकल्प (ए): दो दर्जन में से किसी पर 250 डॉलर लगाएं और यदि आप जीतते हैं तो आप 250 डॉलर जीतेंगे। ऐसा होने की संभावना 24/37 = (.648648) है। विकल्प (बी): किसी एक दर्जन पर 125 लगाएं और यदि आप जीतते हैं तो आप 250 डॉलर जीतेंगे और चले जाएंगे। हालांकि, अगर आप हार जाते हैं तो आप अब उसी दर्जन पर 187.5 डॉलर का दांव लगा सकते हैं और यदि आप जीतते हैं तो आप 375 डॉलर जीतेंगे अब अगर आप दोनों स्पिन में हार जाते हैं तो आपके पास खेलने के लिए 187.5$ हैं और आप किसी भी नौ नंबर पर 20.833333$ लगा सकते हैं और अगर आप जीतते हैं तो आपको 750$ मिलेंगे जो आपकी 500 मूल पूंजी के बराबर है और साथ ही जीतने पर 250$ मिलेंगे जो आपका लक्ष्य था। ऐसा होने की संभावना, जिसका मतलब है कि तीन स्पिन में कम से कम एक बार एक दर्जन या नौ नंबरों पर हिट होना, [1-(25/37)x(25/37)x(28/37)]=0.65451 के बराबर है। इसलिए, समान पूंजी और समान भुगतान के लिए आप विकल्प (B) की तरह अपनी सफलता की संभावना बढ़ा सकते हैं यदि आप कम पैसों से कम संख्याएं खेलते हैं लेकिन शायद ज़्यादा स्पिन के लिए। (क्योंकि आप पहले स्पिन में जीत सकते हैं) आप अपनी संभावना को और भी बेहतर बना सकते हैं यदि आप एक बार में केवल छह नंबरों पर खेलते हैं और 250$ जीतने की कोशिश करते हैं मैं आपको अपना सर्वोच्च सम्मान देता हूं और आपके उत्तर की प्रतीक्षा में हूं।
आप सही हैं कि विकल्प B में सफलता की संभावना ज़्यादा है, हालाँकि लक्ष्य और पूँजी समान हैं। इसका कारण यह है कि विकल्प B में दांव की औसत राशि कम होती है, इसलिए आपका पैसा हाउस एज से कम प्रभावित होता है, जिससे जीतने की संभावना बढ़ जाती है। विकल्प A में दांव की राशि हमेशा $500 होती है। विकल्प B में दांव की औसत राशि (12/37)*125 + (25/37)*(12/37)*(125+187.5)+ (25/37)*(25/37)*(125+187.5+187.5) = 337.29 है।
जब मैं वेगास चैलेंज में था, तो कुछ ही मिनट बचे थे, मेरे पास लगभग $8,000 थे और मुझे कम से कम $24,000 तक पहुँचना था। इसलिए मैंने अपने बैंकरोल को $2000 के चार ढेरों में बाँट दिया और हर एक पर चार अंकों के संयोजन पर दांव लगाया, जिससे मुझे $22,000 मिलते। इस तरह मैं अपनी पूरी हिस्सेदारी हाउस एज पर नहीं लगा रहा था, जिससे मेरे जीतने की संभावना बढ़ गई।
रूलेट पर सभी 38 संख्याओं पर दांव लगाने से थोड़े समय के लिए भी बाधाओं को पार करना असंभव हो जाएगा, और प्रति संख्या $1 की शर्त के साथ पहिये के प्रत्येक घुमाव पर $2 की हानि होगी। (0, 00 पहिया, सम धन दांव के लिए लाभप्रद नियमों के बिना) क्या यह उचित प्रतीत होगा कि आंकड़ों के आधार पर दांव लगाने के लिए संख्याओं की एक इष्टतम सीमा होनी चाहिए?
मैं किसी दांव के मूल्य को जीतने की संभावना से नहीं, बल्कि अपेक्षित प्रतिफल से मापता हूँ। इसलिए सभी 38 नंबरों पर दांव लगाने पर 2/38 = 5.26% का हाउस एज होता है, जो एक नंबर या किसी भी संख्या पर दांव लगाने के समान है। हालाँकि सभी 38 नंबरों पर दांव लगाने पर शुद्ध जीत की संभावना 0% होती है, लेकिन इसका नकारात्मक पक्ष यह है कि आप अपने कुल दांवों का केवल 5.26% ही हारते हैं। यदि आपको दांव लगाने के लिए मजबूर किया जाता है और आप विचरण को कम करना चाहते हैं, तो आपको सभी 38 नंबरों पर दांव लगाना चाहिए। एक व्यावहारिक उदाहरण यह है कि यदि आपके पास प्रमोशनल चिप्स हैं जिन पर आपको दांव लगाना है और आप उनसे अपना सटीक अपेक्षित मूल्य प्राप्त करने के लिए दांव नहीं लगाना चाहते हैं। तो आपके प्रश्न का उत्तर देने के लिए, संख्याओं की कोई इष्टतम सीमा नहीं है। सभी सीमाएँ अपेक्षित मूल्य में समान हैं।
आज एक ब्रिटिश व्यक्ति की कहानी है जो अपनी ज़िंदगी भर की जमा-पूंजी एक रूलेट रोल पर दांव पर लगा देता है। मैं और मेरा दोस्त इस बात पर बहस कर रहे हैं कि इस तरह के दांव के लिए सबसे अच्छा कैसीनो दांव कौन सा है। अगर आप सिर्फ़ एक ही दांव लगा सकते हैं, और अपनी जीत की संभावना बढ़ाना चाहते हैं, तो कौन सा खेल खेलना सबसे अच्छा है और कौन सा दांव सबसे अच्छा है?
सबसे पहले, मैं यह कहना चाहूँगा कि यह आदमी मूर्ख था। उसने एक सामान्य अमेरिकी रूलेट व्हील पर $138,000 का दांव लगाया, जिसमें दो शून्य होते हैं और हाउस एज 5.26% होता है। इससे उसे $7,263 का अपेक्षित नुकसान हुआ। हालाँकि, अगर वह बेलाजियो, मिराज या अलादीन तक 10 मिनट की सवारी करता, तो वह एक शून्य वाले व्हील पर दांव लगा सकता था, जो यूरोपीय नियम के अनुसार है कि अगर गेंद शून्य पर आती है तो उसे आधा सम राशि का दांव वापस मिलता है। उसने वैसे भी सम राशि का दांव लगाने की योजना बनाई थी। इसलिए, पूरे यूरोपीय नियमों वाले इन व्हील पर उसका हाउस एज केवल 1.35% होता, और उसे केवल $1865 का अपेक्षित नुकसान होता।
आपके प्रश्न का उत्तर देने के लिए, यदि मुझे केवल एक समान धन प्रकार का दांव लगाने के लिए मजबूर किया जाता, तो मैं बैकारेट में 1.06% हाउस एज के साथ बैंकर दांव चुनता।
रूलेट में निम्नलिखित सट्टेबाजी पैटर्न के साथ मेरे बर्बाद होने का जोखिम क्या है?
बर्बादी के जोखिम वाले सवाल गणितीय रूप से जटिल हैं। जब तक कि यह एक साधारण जीत/हार का खेल न हो, मैं कंप्यूटर पर एक यादृच्छिक सिमुलेशन करने की सलाह दूँगा।
मैं अटलांटिक सिटी से लगभग दो घंटे उत्तर में न्यू जर्सी में रहता हूँ। क्या आपको पता है कि मेरे देश के किसी हिस्से में सबसे नज़दीकी यूरोपियन रूलेट व्हील कहाँ है?
अटलांटिक सिटी में ढेरों सिंगल ज़ीरो व्हील हैं। वहाँ के ज़्यादातर कैसिनो में ये उपलब्ध हैं, लेकिन कम से कम 25 डॉलर में।
मैं कैसीनो ऑन नेट पर था। मैं रूलेट खेल रहा था। मैं सुरक्षित दांव लगा रहा था, सिर्फ़ पहले 12 (L), दूसरे 12 (M) और तीसरे 12 (H) पर ही दांव लगा रहा था। मैंने बिना दांव लगाए पहिया 5 बार घुमाया, इस उम्मीद में कि किसी एक सेट का पैटर्न न आए ताकि मैं उस पर दांव लगा सकूँ, इस उम्मीद में कि इससे मेरे पक्ष में आने की संभावना बदल जाएगी। 5 चक्करों के बाद L नहीं दिखा। मैं L पर ही दांव लगाता रहा, मुझे लगा कि 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 या 12 नंबर 12 चक्करों के अंदर आ जाएँगे ताकि मैं कम से कम अपना पैसा वापस पा सकूँ... लेकिन ऐसा नहीं हुआ। टेबल पर लगातार 17 चक्कर बिना किसी कम नंबर के चले गए और मैं $258 से $0.00 पर पहुँच गया... खैर, यह बोनस मनी थी। यह 3 भागों वाला प्रश्न है:
- क्या कम संख्या के बिना 5 स्पिन तक प्रतीक्षा करने से वास्तव में L आने की संभावना बढ़ गई?
- इसकी क्या संभावना है कि कोई निम्न संख्या लगातार 16 बार नहीं दिखाई देगी?
- इसकी क्या संभावना है कि कोई निम्न संख्या लगातार 17 बार नहीं दिखाई देगी?
धन्यवाद, मैं आपको ब्लैकजैक गाइड के लिए भी धन्यवाद देना चाहता हूं, मैंने आपकी विधि का उपयोग करके $5.00 को $100.00 में बदल दिया।
- नहीं
- कैसीनो ऑन नेट पर एक एकल-शून्य पहिया का उपयोग किया जाता है। इसलिए, शून्य के साथ 16 बार जाने की संभावना (25/37) 16 = 0.1887% है।
- (25/37) 17 = 0.1275%.
रूलेट व्हील के 10 चक्करों में डीलर द्वारा 5 समान संख्याएं प्राप्त करने की संभावना क्या है?
डबल-जीरो रूलेट गेम में किसी भी संख्या के 10 स्पिन में ठीक 5 बार आने की संभावना को 38* संयोजन (10,5)*(1/38) 5 *(37/38) 5 = 359275 में 1 के द्वारा करीब से अनुमानित किया जा सकता है।
एक बेहतरीन साइट के लिए बधाई। मैं ब्लैकजैक में 6 से 5 के भुगतान के फैलाव पर आपके गुस्से को पूरी तरह समझता हूँ, लेकिन मुझे यह जानने की उत्सुकता है कि अमेरिकी बिना किसी तर्क के 00 रूलेट को क्यों स्वीकार कर लेते हैं। यह रूलेट लगभग अपराध है और इसे केनो और स्लॉट्स के साथ रैंक किया जाना चाहिए।
धन्यवाद। आपने बिलकुल सही बात कही है। सामान्य नियमों के तहत 6 से 5 ब्लैकजैक में हाउस एज 1.44% है, जबकि डबल ज़ीरो रूलेट में यह 5.26% है। यह 3.7 गुना ज़्यादा है। हालाँकि, मैंने वर्षों में यह सीखा है कि खिलाड़ियों को उनके पसंदीदा खेल से दूर करना लगभग असंभव है, चाहे हाउस एज कितनी भी कम क्यों न हो। इसलिए मैं बस यही कर सकता हूँ कि उन्हें सलाह दूँ कि वे अपनी पसंद का खेल कैसे खेलें। ब्लैकजैक खिलाड़ियों के लिए अभी भी 3 से 2 खेलों की कोई कमी नहीं है। 6 से 5 खेलने से कैसीनो को बिना किसी कारण के 0.8% का अतिरिक्त लाभ मिल रहा है। अगर आप रूलेट खिलाड़ी हैं, तो मैं सिंगल-ज़ीरो रूलेट पर भी ध्यान देने की ज़रूरत पर ज़ोर देता हूँ। इसलिए मुझे कोई असंगति नज़र नहीं आती।
क्या आप मुझे समझा सकते हैं कि रूलेट के लिए टेबल लिमिट कैसे काम करती है और व्यक्तिगत नंबर और टेबल के लिए न्यूनतम लिमिट में क्या अंतर है? हो सके तो कृपया उदाहरण भी दें।
रूलेट में आमतौर पर दो न्यूनतम राशियाँ होती हैं। उदाहरण के लिए: बाहर $5, अंदर $1। बाहरी दांव सभी सम राशि वाले दांव, स्तंभ दांव और दर्जन दांव होते हैं। अंदर के दांव 2, 3, 4, 5 और 6 के समूहों वाली संख्याओं पर होते हैं। इस स्थिति में, बाहर के दांव पर न्यूनतम राशि $5 और अंदर के दांव पर $1 होती है। हालाँकि, आपको अंदर के दांव पर कम से कम $5 का दांव लगाना होगा या बिल्कुल भी नहीं लगाना होगा।
मैं एक कसीनो में काम करता हूँ और मेरे पास एक शर्त है कि रूलेट डीलर रोल के नतीजे को प्रभावित नहीं कर सकता। निश्चित रूप से कुछ लोग हैं जो सोचते हैं कि ऐसा किया जा सकता है। बेशक, कुछ लोगों के लिए नहीं, लेकिन शायद पहिये के एक हिस्से के लिए। डीलर ने नतीजों को प्रभावित किया है या नहीं, यह यथोचित रूप से निर्धारित करने के लिए आप कौन सा परीक्षण अच्छा मानेंगे? यह मानते हुए कि हमारे लिए प्रयासों की संख्या उचित है, मैं ख़ुशी से परिणाम साझा करूँगा।
मैं आपके पक्ष में हूँ। अगर ऐसा हो पाता, तो डीलर आसानी से खिलाड़ियों के साथ साज़िश रचकर मुनाफ़े में हिस्सा ले सकते थे। फिर भी, मैंने ऐसा होते कभी नहीं सुना। एक अच्छा परीक्षण यह होगा कि किसी ऐसे व्यक्ति को ढूँढा जाए जो रोल को प्रभावित करने का दावा करता हो और उसे 100 चक्करों में जितनी बार हो सके, पहिये के एक खास हिस्से में गेंद डालने का प्रयास करने को कहा जाए। वह जितनी ज़्यादा बार ऐसा करेगा, उसका दावा उतना ही ज़्यादा मज़बूत होगा। नीचे दी गई तालिका 50 से 70 सफल स्पिनों की संभावना दर्शाती है। उदाहरण के लिए, 60 या उससे ज़्यादा सफल स्पिनों की संभावना 2.8444% है। सांख्यिकी में सामान्य विश्वास सीमाएँ 90%, 95% और 99% के स्तर हैं। 90% विश्वास परीक्षण को पास करने के लिए, जिसमें दिए गए यादृच्छिक स्पिनों में असफल होने की संभावना 90% है, सफल स्पिनों की संख्या 57 या उससे ज़्यादा होनी चाहिए। 95% परीक्षण को पास करने के लिए संख्या 59 या उससे ज़्यादा होनी चाहिए, और 99% पर यह संख्या 63 या उससे ज़्यादा होनी चाहिए।
कम से कम 50 से 70 सफल रूलेट स्पिन की संभावना
| जीत | संभावना |
| 70 | 0.000039 |
| 69 | 0.000092 |
| 68 | 0.000204 |
| 67 | 0.000437 |
| 66 | 0.000895 |
| 65 | 0.001759 |
| 64 | 0.003319 |
| 63 | 0.006016 |
| 62 | 0.010489 |
| 61 | 0.0176 |
| 60 | 0.028444 |
| 59 | 0.044313 |
| 58 | 0.066605 |
| 57 | 0.096674 |
| 56 | 0.135627 |
| 55 | 0.184101 |
| 54 | 0.242059 |
| 53 | 0.30865 |
| 52 | 0.382177 |
| 51 | 0.460205 |
| 50 | 0.539795 |
www.ccc-casino.com पर कोई शून्य रूलेट नहीं है जिसे वे सुपर चांस रूलेट कहते हैं। क्या कोई ऐसी प्रणाली है जो प्रभावी हो क्योंकि शून्य है ही नहीं? शून्य के बिना क्या कोई एक ही समय में काला और लाल दोनों खेल सकता है क्योंकि शून्य का कोई डर नहीं है?
मैंने उस खेल को ढूँढ़ने की कोशिश की, लेकिन जब मैंने जाँच की तो साइट बंद थी। हालाँकि, मान लीजिए कि ऐसा कोई खेल मौजूद है, तो जवाब है नहीं। किसी भी सिस्टम से लंबे समय तक उसे हराने या उससे हारने की उम्मीद नहीं की जा सकती। हर सिस्टम का अपेक्षित मान बिल्कुल शून्य होगा।
सिंगल 0 रूलेट। किसी एक संख्या (0-36) के लगातार तीन चक्करों में एक से ज़्यादा बार आने की क्या संभावना है? अपना समय देने के लिए धन्यवाद!
पहली संख्या चाहे जो भी हो, केवल दूसरे स्पिन के उससे मेल खाने की संभावना (1/37)*(36/37) है। केवल तीसरे स्पिन के उससे मेल खाने की संभावना (36/37)*(1/37) है। किसी भी स्पिन के मेल न खाने की संभावना, लेकिन दूसरे और तीसरे स्पिन के एक-दूसरे से मेल खाने की संभावना (36/37)*(1/37) है। दूसरे और तीसरे दोनों स्पिन के उससे मेल खाने की संभावना (1/37)*(1/37) है। इन सबको जोड़ने पर आपको 3*(1/37)*(36/37)+ (1/37)*(1/37) = 7.962% मिलता है।
मुझे लगता है कि आपको इसमें रुचि हो सकती है। मैं यहाँ यूके में Betfair का इस्तेमाल करता हूँ। मुझे यकीन है कि अमेरिका में आप जैसे अच्छे लोगों को किसी कारण से इसका इस्तेमाल करने की अनुमति नहीं है, फिर भी अगर आप इससे परिचित नहीं हैं तो betfair.co.uk पर जाकर देख लीजिए। यह एक सट्टेबाजी एक्सचेंज है, बुकमेकर नहीं। खैर, मेरा सवाल यह है। वे अब बिना किसी शून्य के रूलेट की पेशकश कर रहे हैं, हाँ, बिना किसी शून्य के। यह वास्तव में असली है। क्या आप कोई अच्छी रणनीति बता सकते हैं जिसका इस्तेमाल किया जा सके, और अगर हाँ, तो क्या आप इसे अपने तक ही सीमित रखेंगे? शुभकामनाएँ, जोनाथन। पुनश्च: वे बिना किसी हाउस एज वाले अन्य कैसीनो गेम भी प्रदान करते हैं।
मैंने इसकी जाँच करने के लिए वहाँ एक खाता बनाने की कोशिश की, लेकिन उन्होंने अमेरिकी खिलाड़ियों को ब्लॉक कर दिया। मुझे बताया गया है कि न्यूनतम दांव £2 और अधिकतम £50 है। यहाँ तक कि नो-ज़ीरो रूलेट जैसे ज़ीरो हाउस एज गेम में भी, कोई भी सट्टेबाजी प्रणाली 0% के आंकड़े से ऊपर या नीचे नहीं पहुँचती। आप चाहे जो भी करें, जितना ज़्यादा आप करेंगे, वास्तविक हाउस जीत 0% के उतने ही करीब पहुँचेगी।
आप कहते हैं कि रूलेट में जीतने का कोई सिस्टम नहीं होता। गोंजालो गार्सिया-पेलायो और उनके परिवार ने दुनिया भर के कई कैसीनो में खूब पैसा जीता। उन्होंने एक किताब भी प्रकाशित की है और बताया है कि उन्होंने यह कैसे किया। आपकी क्या राय है?
मैंने एक बार उनके बारे में एक टेलीविज़न शो देखा था, और मैं उनके काम की सराहना करता हूँ। मैं जिसे "सिस्टम" कहता हूँ, वह एक सट्टेबाजी पैटर्न है, जैसे मार्टिंगेल , जो किसी ऐसे खेल पर लागू होता है जिसमें हाउस एडवांटेज हो, जैसे कि एक निष्पक्ष रूलेट गेम। गोंजालो गार्सिया-पेलायो ने जो सफलतापूर्वक किया, वह यह सर्वेक्षण करना था कि गेंद कितनी बार प्रत्येक संख्या पर गिरती है, ताकि पक्षपाती रूलेट पहियों को ढूंढा जा सके और उनका फायदा उठाया जा सके। मैं इसे एक रणनीति कहूँगा, न कि एक सिस्टम। कैसीनो को हराने के लिए कई लाभदायक रणनीतियाँ हैं, लेकिन कोई भी लाभदायक सट्टेबाजी प्रणाली नहीं है।
यदि मैं आपको रूलेट का ऐसा खेल दिखाऊं जिसमें कोई शून्य न हो और सभी सामान्य रूलेट नियम लागू हों, तो क्या 100% जीतना संभव है?
नहीं।
मैं आपके न्यूज़लेटर का लंबे समय से ग्राहक हूँ और अब भी आपकी वेबसाइट को पसंद करता हूँ। मुझे एक कैसीनो वेबसाइट मिली जो रूलेट खेलती है जिसमें पहिये में कोई शून्य नहीं होता। इसमें सिर्फ़ 1-36 तक की संख्याएँ होती हैं, और सभी मानक रूलेट नियम लागू होते हैं। क्या आपको इसका फ़ायदा उठाने का कोई तरीका नज़र आता है? मुझे पता है कि आपको सट्टेबाजी के सिस्टम पसंद नहीं हैं, लेकिन इस मामले में कोई हाउस एज नहीं है। कोई ऐसा मनी मैनेजमेंट सिस्टम ज़रूर होना चाहिए जो इन टेबल लिमिट के साथ मुनाफ़े में काम कर सके। किसी भी सलाह का स्वागत है।
आपके दयालु शब्दों के लिए धन्यवाद। मुझे लगता है कि मैंने इसका उत्तर पहले भी दिया है, लेकिन नहीं, शून्य हाउस एज के साथ भी, कोई भी सट्टेबाजी प्रणाली लंबे समय तक जीत नहीं सकती।
नमस्ते, ज़ाहिर है, अगर आप मेरा नाम किसी के साथ साझा न करें, तो मैं आपकी सराहना करूँगा। जिस कैसीनो में मैं काम करता हूँ, वहाँ रूलेट डीलरों के बीच इस बात पर लगभग एकमत है कि वे "स्पिन को नियंत्रित" कर सकते हैं और पहिये के कुछ हिस्सों को आसानी से हिट कर सकते हैं या जानबूझकर कुछ हिस्सों को छोड़ सकते हैं। रूलेट में गेंद के घूमने के सभी कारकों को देखते हुए, जिसमें किनारे पर लगे उभार (बम्प्स), गेंद की दिशा और पहिये की गति आदि शामिल हैं - क्या आपको लगता है कि इसमें कोई दम है? क्या यह पर्याप्त होगा कि एक धोखेबाज डीलर किसी खिलाड़ी को बड़े हाउस एडवांटेज से उबरने में मदद कर सके?
यह पहली बार नहीं है जब मैंने यह दावा सुना है, और मुझे इस पर बहुत संदेह है। ज़्यादातर डीलर भी इस मिथक पर यकीन करते हैं कि एक खराब थर्ड-बेसमैन ब्लैकजैक में दूसरे खिलाड़ियों को हार का कारण बनेगा, इसलिए एक समूह के रूप में वे ज़्यादा संदेह करने वाले समूह नहीं हैं। मुझे लगता है कि हो यह रहा है कि उन्हें वे मौके याद रहते हैं जब वे स्पिन को नियंत्रित करने की कोशिश में सफल रहे थे, और वे आसानी से भूल जाते हैं जब वे असफल रहे थे। ठीक वैसे ही जैसे उन्हें वे मौके याद रहते हैं जब थर्ड-बेसमैन ने डीलर का बस्ट कार्ड लिया था, लेकिन वे वे मौके भूल जाते हैं जब उसने टेबल को बचा लिया था।
अगर डीलर वाकई ऐसा कर पाते, तो किसी कॉन्फ़ेडरेट को खेल में शामिल करना आसान होता, जिससे वह जीत जाता और दूसरे खिलाड़ी हार जाते, और इसकी भरपाई हो जाती। जब तक वे स्पिन के लिए उचित प्रक्रियाओं का पालन करते और कॉन्फ़ेडरेट के साथ सार्वजनिक रूप से नहीं दिखाई देते, तब तक यह सब पूरी तरह से वैध लगता। फिर भी, आपने ऐसा होते कभी नहीं सुना होगा। मुझे लगता है कि विश्वास करने वाले कह सकते हैं कि ऐसा करने वाले बस अपनी पहचान छिपा रहे हैं, लेकिन बेकार सट्टेबाजी प्रणालियों में विश्वास करने वाले भी यही कहते हैं। अगर यह उतना आसान होता जितना आपके कार्यस्थल पर रूलेट डीलर दावा करते हैं, तो परिणामस्वरूप धोखाधड़ी की समस्या बहुत बढ़ जाती।
डबल-जीरो रूलेट में, क्या संभावना है कि 200वें स्पिन तक कोई संख्या नहीं आएगी?
किसी भी दी गई संख्या के हिट न होने की संभावना (37/38) 200 = 0.48% है।
38 संख्याओं के साथ, हम गलत तरीके से कह सकते हैं कि उनमें से किसी एक के हिट न होने की संभावना 38 × (37/38) 200 = 18.34% है।
यह गलत है क्योंकि यह उन दो संख्याओं की दोहरी गणना करता है जो नहीं टकराईं। इसलिए हमें उन संभावनाओं को घटाना होगा। कुल 38 में से 2 संख्याओं के 703 सेट हैं। किसी भी दो दी गई संख्याओं के न टकराने की संभावना (36/38) 200 = 0.000020127 है। हमें दोनों संख्याओं से बचने की संभावना घटानी होगी। तो हम यहाँ हैं:
38×(37/38) 200 - संयोजन(38,2)×(36/38) 200 = 16.9255%।
हालाँकि, अब हमने तीन संख्याओं के न आने की प्रायिकता को रद्द कर दिया है। तीन संख्याओं के किसी भी दिए गए समूह के लिए, हमने किसी एक संख्या के न आने की प्रायिकता को तीन गुना गिना। फिर हमने तीन में से दो संख्याएँ चुनने के प्रत्येक तरीके के लिए तीन गुना घटाया, जिससे तीनों संख्याओं के न आने की प्रायिकता शून्य रह गई। ऐसे संयोजन (38,3) = 8,436 समूह हैं। उन्हें वापस जोड़ने पर अब हम इस पर पहुँचते हैं:
38×(37/38) 200 - कॉम्बिन(38,2)×(36/38) 200 + कॉम्बिन(38,3)×(35/38) 200 = 16.9862%।
फिर भी, अब हमने चार संख्याओं के न आने की संभावना को ज़्यादा गिन लिया है। चार संख्याओं के प्रत्येक संयोजन (38,4) = 73,815 समूहों के लिए, मूल रूप से प्रत्येक की चौगुनी गणना की गई थी। फिर हमने संयोजन (4,2) = 6 के प्रत्येक समूह में से 2 को घटाया। फिर हमने 4 में से 3 के 4 समूहों को वापस जोड़ा। इस प्रकार, चार संख्याओं के प्रत्येक संयोजन के लिए, इसे 4 − 6 + 4 = 2 बार गिना गया। दोहरी गणना को समायोजित करने के लिए हमें प्रत्येक समूह के लिए घटाना होगा। उन्हें घटाने पर अब हम इस पर पहुँचते हैं:
38×(37/38) 200 - कॉम्बिन(38,2)×(36/38) 200 + कॉम्बिन(38,3)×(35/38) 200 - कॉम्बिन(38,4)×(34/38) 200 = 16.9845%।
इस प्रक्रिया को जारी रखते हुए, हम बारी-बारी से जोड़ते और घटाते रहेंगे, जब तक कि 37 संख्याएँ छूट न जाएँ। इस प्रकार, कम से कम एक संख्या के कभी न मिलने की प्रायिकता है:
योग i=1 से 37 [(-1) (i+1) × संयोजन(38,i) × ((38-i)/38) 38 ] = 16.9845715651245%
यहां ऐसे 126,900,000 200-स्पिन प्रयोगों के यादृच्छिक सिमुलेशन के परिणाम दिए गए हैं।
200 रूलेट स्पिन में हिट हुए नंबर
| संख्या हिट | टिप्पणियों | अनुपात |
|---|---|---|
| 31 या उससे कम | 0 | 0 |
| 32 | 1 | 0.00000001 |
| 33 | 33 | 0.00000026 |
| 34 | 1812 | 0.00001428 |
| 35 | 68845 | 0.00054251 |
| 36 | 1577029 | 0.01242734 |
| 37 | 19904109 | 0.15684877 |
| 38 | 105348171 | 0.83016683 |
| कुल | 126900000 | 1 |
कम से कम एक संख्या के हिट न होने की बारंबारता का अनुपात 0.169833 था।
मेरा एक दोस्त है जो एक कसीनो स्टाफ का हिस्सा था और रूलेट टेबल पर नज़र रखता था, और उसने मुझे बताया कि जब लोग जीतने लगते हैं तो कसीनो क्रुपियर बदल देता है। मैंने स्टाफ के एक सदस्य को क्रुपियर से रूलेट व्हील को अलग गति से घुमाने के लिए कहते भी देखा है। क्या इसका मतलब यह नहीं है कि कसीनो को यकीन है कि क्रुपियर संख्याओं की एक गैर-यादृच्छिक श्रृंखला प्रकट कर सकता है? क्या इसका मतलब यह नहीं है कि एक जुआरी एक "भाग्यशाली" टेबल की तलाश कर सकता है जहाँ नियमित रूप से घुमाव करने वाले क्रुपियर के जीतने की संभावना बढ़ जाती है?
दुख की बात है कि अज्ञानता सीढ़ी पर बहुत ऊपर तक जा सकती है। मैं इस बात से इनकार नहीं करता कि एक विशेषज्ञ बहुत धीमी गति से घूमते हुए भी पहिये को घुमा सकता है। हालाँकि, इस मुद्दे को छोड़ दें, डीलर बदलने से संभावनाएँ नहीं बदलतीं। कोई भाग्यशाली या बदकिस्मत डीलर जैसी कोई चीज़ नहीं होती। अंधविश्वास को छोड़ना मुश्किल होता है। जैसा कि मैंने कई बार कहा है, कोई भी मान्यता जितनी बेतुकी होती है, उतनी ही दृढ़ता से उस पर विश्वास किया जाता है।
प्रिय महोदय, मैंने एक स्वचालित सिंगल-ज़ीरो रूलेट गेम में 8672 बार "घूमा" है। मेरा पूर्वनिर्धारित नंबर आश्चर्यजनक रूप से 278 बार आया। मैंने यह नंबर जेब की घिसावट के कारण चुना था। मुझे क्या यकीन है कि इस नंबर की संभावना 1/37 से ज़्यादा है?
अगर मेरी शब्दावली सही है, तो "व्हील क्लॉकिंग" का मतलब गेंद की गति, गेंद की स्थिति और पहिये की गति के आधार पर गेंद के गिरने की जगह का अनुमान लगाना है। ऐसा लगता है कि आप एक पक्षपाती पहिये का फायदा उठा रहे हैं, जो एक अलग तरह का फ़ायदा उठाने वाला खेल है। जब तक हम इस विषय पर हैं, एक तीसरा फ़ायदा उठाने वाला खेल "डीलर के हस्ताक्षर" का फायदा उठाना है, जहाँ क्रुपियर इतना स्थिर रहता है कि गेंद और पहिये की गति हर स्पिन में लगभग एक जैसी रहती है। इससे खिलाड़ी गेंद की स्थिति और पिछले परिणामों के आधार पर गेंद के गिरने की जगह का अनुमान लगा सकता है।
आपके प्रश्न का उत्तर देने के लिए, आपके द्वारा अपने नंबर पर अपेक्षित बार हिट होने की संख्या 8672/37 = 234.38 है। विचरण 8672×(1/37)×(36/37) = 228.04 है। मानक विचलन विचरण का वर्गमूल है, या 15.10 है। आपके द्वारा अपेक्षित हिट से 278-234.38 = 43.62 अधिक हिट हुए। यानी (43.62-0.5)/15.10 = 2.8556 मानक विचलन। 0.5 घटाने का कारण स्पष्ट करना कठिन है। इतना कहना पर्याप्त है कि यह एक असतत फलन का अनुमान लगाने के लिए एक सतत फलन का उपयोग करने हेतु एक समायोजन कारक है। गॉसियन सन्निकटन का उपयोग करते हुए, आपके नंबर पर इतनी बार या उससे अधिक बार हिट होने की संभावना 0.21% है। इसलिए, इस बात की अच्छी संभावना है कि आपको एक पक्षपाती पहिया मिला हो। हालाँकि, अभी भी 466 में से 1 संभावना है कि यह सिर्फ अच्छी किस्मत थी।
जापानी हाई-रोलर, काशीवागी, और डोनाल्ड ट्रम्प के बीच 20 साल पहले हुई एक फ्रीज़-आउट प्रतियोगिता की कहानी बहुत मशहूर है। काशीवागी को बैकारेट में प्रति हाथ 2 लाख डॉलर से ज़्यादा दांव लगाने की अनुमति नहीं थी। खेल तब खत्म होता जब कैसीनो या खिलाड़ी 1.2 करोड़ डॉलर से आगे होता। मान लीजिए कि काशीवागी हमेशा बैंकर पर सबसे ज़्यादा दांव लगाता था। काशीवागी के जीतने की क्या संभावना है?
अगर वह खिलाड़ी पर दांव लगाता है तो गणित ज़्यादा आसानी से हल हो जाता है। मैं अपनी mathproblems.info साइट पर रूलेट में इसी तरह की एक समस्या हल करता हूँ, समस्या संख्या 116। सम राशि के दांवों के लिए, सामान्य सूत्र ((q/p) b -1)/((q/p) g -1) है, जहाँ:
b = इकाइयों में प्रारंभिक बैंकरोल.
g = इकाइयों में बैंकरोल लक्ष्य.
p = किसी भी शर्त को जीतने की संभावना, बराबरी की गिनती नहीं।
q = किसी भी शर्त के हारने की संभावना, टाई की गिनती नहीं।
यहाँ खिलाड़ी $12 मिलियन, यानी $200,000 की 60 इकाइयों से शुरुआत करता है, और तब तक खेलता रहेगा जब तक कि वह 120 इकाइयों तक नहीं पहुँच जाता या बस्ट नहीं हो जाता। इसलिए खिलाड़ी के दांव के मामले में समीकरण के मान इस प्रकार हैं:
बी = 60
जी = 120
पी = 0.493175
क्यू = 0.506825
तो उत्तर है ((0.506825/0.493175) 60 -1)/(( 0.506825/0.493175) 120 -1) = 16.27%.
बैंकर बेट पर यह 5% कमीशन के कारण कहीं अधिक जटिल है। इससे खिलाड़ी के अपने लक्ष्य से आगे निकल जाने की पूरी संभावना हो जाती है। अगर हम यह नियम जोड़ दें कि अगर जीतने वाली बेट से खिलाड़ी अपना लक्ष्य हासिल कर लेता है, तो वह केवल उतना ही दांव लगा सकता है जितना $12 मिलियन तक पहुँचने के लिए ज़रूरी हो, तो मेरा अनुमान है कि उसकी सफलता की संभावना 21.66% होगी।
बैंकरोल को दोगुना करने की संभावना के लिए एक सरल सूत्र 1/[1+(q/p) b] है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
औसतन, 38-संख्या रूलेट में किसी भी संख्या के दोहराए जाने से पहले आपको कितनी बार प्रयास करने की आवश्यकता होगी?
पहले परीक्षण की गणना करते हुए, मैं दिखाता हूँ कि माध्य 8.408797 है, माध्यिका 8 है, और बहुलक 7 है।
दो संख्याओं के बिना दोहराए जाने की संभावना 37/38 = 97.37% है।
बिना दोहराए तीन संख्याओं की संभावना (37/38) × (36/38) = 92.24% है।
चार संख्याओं के बिना दोहराए जाने की संभावना (37/38) × (36/38) × (35/38) = 84.96% है।
इस पैटर्न का अनुसरण करते हुए, 8 संख्याओं में कोई दोहराव न होने की संभावना (37/38) × (36/38) × (35/38) ×... × (31/38) = 45.35% है।
अतः 8 संख्याओं के भीतर पुनरावृत्ति की संभावना 100% - 45.35% = 54.65% है।
मुझे लगता है कि ज़्यादातर लोग अनुमान लगाएँगे कि 8 संख्याओं के भीतर किसी संख्या के दोहराने की संभावना इससे कम होगी। अगर आप अपने गणित में कमज़ोर दोस्तों का फ़ायदा उठाने से नहीं हिचकिचाते, तो शर्त लगाएँ कि कम से कम एक संख्या दोहराने के लिए 8 या उससे कम संख्याएँ लगेंगी। इस तरह आप 8 या उससे कम पर दांव लगाएँगे, और आपका दोस्त 9 या उससे ज़्यादा पर। अगर वह मना कर दे, तो 7 या उससे ज़्यादा पर दांव लगाने की पेशकश करें, जिससे जीतने की संभावना 55.59% होगी। मूलतः, जो भी पक्ष 8 के मध्यमान को कवर करेगा, उसके जीतने की संभावना ज़्यादा होगी।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
डिस्कवरी चैनल पर प्रसारित होने वाले "हसलिंग द हाउस" शो में $30 को $1,000 में बदलने के सबसे बेहतरीन तरीके पर एक लंबा खंड दिखाया गया था। इसमें एंडी ब्लोच कहते हैं, "अगर आपकी जेब में $30 हैं और आप उन्हें $1,000 में बदलना चाहते हैं, तो रूलेट ही आपका एकमात्र खेल है।" एंडी ने आगे बताया कि एक ही नंबर पर पूरे $30 का दांव लगाना, सम-धन के दांव को पाँच बार लगाने से बेहतर क्यों है।
क्या एंडी सही है कि $30 को $1,000 में बदलने का सबसे अच्छा तरीका रूलेट में पूरे $30 को एक ही नंबर पर लगाना है?
नहीं, वह सही नहीं है। एंडी की एकल दांव रणनीति की संभावना 1/38 = 2.6316% है।
काफी प्रयास और त्रुटि के बाद, मैंने अपनी "हेल मैरी" रूलेट रणनीति तैयार की, जिससे $30 को $1,000 में बदलने की संभावना 2.8074% तक बढ़ जाएगी।
रूलेट के लिए जादूगर की "हेल मैरी" रणनीति:
यह रणनीति मानती है कि दांव $1 की वृद्धि में होने चाहिए। सभी दांव गणनाओं में, नीचे की ओर पूर्णांकित करें।
होने देना:
b = आपका बैंकरोल
g = आपका लक्ष्य
- यदि 2*b >=g, तो किसी भी सम राशि वाले दांव पर (gb) दांव लगाएं।
- अन्यथा, यदि 3*b >=g, तो किसी भी कॉलम पर (gb)/2 का दांव लगाएं।
- अन्यथा, यदि 6*b >=g, तो किसी भी छह लाइन (छह संख्या) पर (gb)/5 का दांव लगाएं।
- अन्यथा, यदि 9*b >=g, तो किसी भी कोने (चार संख्या) पर (gb)/8 का दांव लगाएं।
- अन्यथा, यदि 12*b >=g, तो किसी भी स्ट्रीट (तीन नंबर) पर (gb)/11 का दांव लगाएं।
- अन्यथा, यदि 18*b >=g, तो किसी भी विभाजन (दो संख्या) पर (gb)/17 का दांव लगाएं।
- अन्यथा, किसी भी एक नंबर पर (gb)/35 का दांव लगाएं।
दूसरे शब्दों में, अगर हो सके तो हमेशा एक ही दांव लगाकर लक्ष्य तक पहुँचने की कोशिश करें, बिना लक्ष्य से ज़्यादा खर्च किए। अगर ऐसा करने के कई तरीके हैं, तो उस तरीके को चुनें जिसमें जीतने की संभावना सबसे ज़्यादा हो।
आप पूछ सकते हैं कि दूसरे खेलों के बारे में क्या? डिस्कवरी चैनल के वॉयस-ओवर वाले के अनुसार, "हर कोई इस बात पर सहमत है कि कैसीनो में रूलेट सबसे जल्दी अमीर बनने का सबसे अच्छा तरीका है।" खैर, मैं नहीं मानता। आम खेलों और नियमों तक ही सीमित रहकर भी, मुझे क्रेप्स ज़्यादा बेहतर लगता है। खासकर, पास न होने पर दांव लगाना और ऑड्स लगाना।
क्रेप्स के लिए मेरी हेल मैरी रणनीति (नीचे बताई गई है) के अनुसार, $30 के $1,000 में बदलने की संभावना 2.9244% है। यह मानकर चला जाता है कि खिलाड़ी पॉइंट की परवाह किए बिना 6x ऑड्स लगा सकता है (ऐसा तब होता है जब 3x-4x-5x ऑड्स लेने की अनुमति हो)। सफलता की यह संभावना रूलेट के लिए मेरी हेल मैरी रणनीति से 0.117% ज़्यादा और एंडी ब्लॉक रणनीति से 0.2928% ज़्यादा है।
एंडी शायद यह तर्क दे कि मेरा उपरोक्त तर्क न्यूनतम $1 के दांव की धारणा पर आधारित है, जो वेगास में लाइव डीलर गेम में मिलना मुश्किल है। यह उम्मीद करते हुए कि कोई ऐसा कहेगा, मैंने दोनों गेम न्यूनतम $5 के दांव के अनुमान और $5 की वृद्धि में दांव लगाकर खेले। उस स्थिति में, मेरी हेल मैरी रणनीति का उपयोग करके सफलता की संभावना रूलेट में 2.753% और क्रेप्स में 2.891% है। दोनों ही मामलों में, एंडी ब्लोच रणनीति के तहत 2.632% से अधिक है।
सच कहूँ तो, डिस्कवरी चैनल ने कभी भी ऊपर दी गई बेतुकी बातें प्रसारित नहीं की होंगी और निश्चित रूप से कुछ ऐसा सरल तरीका खोज रहा था जो आम जनता को समझ में आए। एंडी निश्चित रूप से उन्हें कुछ ऐसा दे रहे थे जो वे सुनना चाहते थे। उनकी सलाह का मूल आधार यह है कि अगर आप किसी खास लक्ष्य तक पहुँचना चाहते हैं, तो हिट-एंड-रन रणनीति, हाउस एज के कारण कई दांव लगाने से कहीं बेहतर है। यह बिल्कुल सच है और मैं पिछले 17 सालों से इसी बात का प्रचार कर रहा हूँ।
क्रेप्स के लिए जादूगर की "हेल मैरी" रणनीति।
इस रणनीति में यह माना जाता है कि दांव $1 के हिसाब से लगने चाहिए और जीत की राशि को निकटतम डॉलर तक पूर्णांकित किया जाएगा। दांव की गणना करते समय, कभी भी इतना दांव न लगाएँ कि आप लक्ष्य से आगे निकल जाएँ। साथ ही, कभी भी दांव की राशि इतनी न रखें कि आपको गोल में ही जीत मिल जाए।
होने देना:
b = आपका बैंकरोल
g = आपका लक्ष्य
- पास न होने पर अधिकतम ($1, न्यूनतम(b/7,(gb)/6)) दांव लगाएं।
- अगर कोई पॉइंट आता है और आपके पास पूरी ऑड्स वाली शर्त के लिए पर्याप्त राशि है, तो पूरी ऑड्स लगाएँ। अन्यथा, जितना हो सके, लगाएँ।
तो, मुझे उम्मीद है कि एंडी और डिस्कवरी चैनल खुश होंगे। मैंने उन्हें ग़लत साबित करने के लिए कई दिन सिमुलेशन चलाए हैं।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।
रूलेट में 4, 5, 6, 7, 8, या 9 चक्करों में गेंद के 1, 2, और 3 पर उतरने की संभावना क्या है?
सामान्य सूत्र है:
Pr(गेंद 1 में गिरती है) + Pr(गेंद 2 में गिरती है) + Pr(गेंद 3 में गिरती है) - Pr(गेंद 1 और 2 में गिरती है) - Pr(गेंद 1 और 3 में गिरती है) - Pr(गेंद 2 और 3 में गिरती है) + Pr(गेंद 1, 2 और 3 में गिरती है)।
डबल-जीरो रूलेट में, n स्पिनों के लिए, यह 3*(1-(37/38)^n)-3*(1-(36/38)^n)+(1-(35/38)^n) आता है।
निम्नलिखित तालिका एकल और दोहरे शून्य रूलेट के लिए 3 से 100 तक विभिन्न स्पिनों के लिए सभी तीन संख्याओं के आने की संभावना को दर्शाती है।
रूले प्रश्न
| स्पिन | अकेला शून्य | दोहरा शून्य |
|---|---|---|
| 3 | 0.000118 | 0.000109 |
| 4 | 0.000455 | 0.000420 |
| 5 | 0.001091 | 0.001009 |
| 6 | 0.002094 | 0.001939 |
| 7 | 0.003518 | 0.003261 |
| 8 | 0.005404 | 0.005016 |
| 9 | 0.007785 | 0.007234 |
| 10 | 0.010684 | 0.009937 |
| 15 | 0.033231 | 0.031066 |
| 20 | 0.068639 | 0.064476 |
| 25 | 0.114718 | 0.108254 |
| 30 | 0.168563 | 0.159750 |
| 35 | 0.227272 | 0.216265 |
| 40 | 0.288292 | 0.275379 |
| 45 | 0.349548 | 0.335089 |
| 50 | 0.409453 | 0.393835 |
| 55 | 0.466865 | 0.450467 |
| 60 | 0.521017 | 0.504191 |
| 65 | 0.571445 | 0.554501 |
| 70 | 0.617922 | 0.601122 |
| 75 | 0.660393 | 0.643951 |
| 80 | 0.698930 | 0.683016 |
| 85 | 0.733693 | 0.718435 |
| 90 | 0.764897 | 0.750386 |
| 95 | 0.792791 | 0.779086 |
| 100 | 0.817638 | 0.804773 |
मेक्सिको के कुछ कसीनो में रूलेट में पहिये की जगह पासे का इस्तेमाल होता है। नियम ये हैं:
- चार पासे हैं - दो हरे, एक लाल और एक नीला।
- यदि दोनों हरे पासे एक ही स्थान पर आते हैं, तो "स्पिन" का परिणाम शून्य होगा।
- यदि दोनों हरे पासे छह पर आते हैं, तो "स्पिन" का परिणाम दोहरा शून्य होगा।
- यदि हरे पासे के साथ कोई अन्य परिणाम आता है, तो लाल और नीले पासे के 36 संभावित परिणामों को "स्पिन" का प्रतिनिधित्व करने के लिए संख्या 1 और 36 से मैप किया जाएगा।
पारंपरिक रूलेट की तुलना में इससे बाधाओं में क्या परिवर्तन होता है?
0 और 00 के जीतने की संभावना 1/36 होगी। अगर इन नतीजों पर दांव लगाने वालों को सामान्य 35 से 1 का भुगतान मिलता है, तो हाउस एज ठीक 0% होगा।
किसी भी अन्य संख्या के जीतने की संभावना (34/36)*(1/36) = 2.62% होगी। इसकी तुलना पारंपरिक डबल-ज़ीरो रूलेट में 1/38 = 2.63% से करें। 1 से 36 तक की संख्याओं पर किसी भी दांव पर हाउस एज 5.56% होगा। इसकी तुलना पारंपरिक डबल-ज़ीरो रूलेट में 5.26% से करें। इस खेल में मेरी सलाह है कि केवल शून्य और डबल-ज़ीरो पर ही दांव लगाएँ।
यदि कोई इन नियमों की पुष्टि या खंडन कर सकता है और भुगतान कर सकता है, तो कृपया मुझे बताएं।
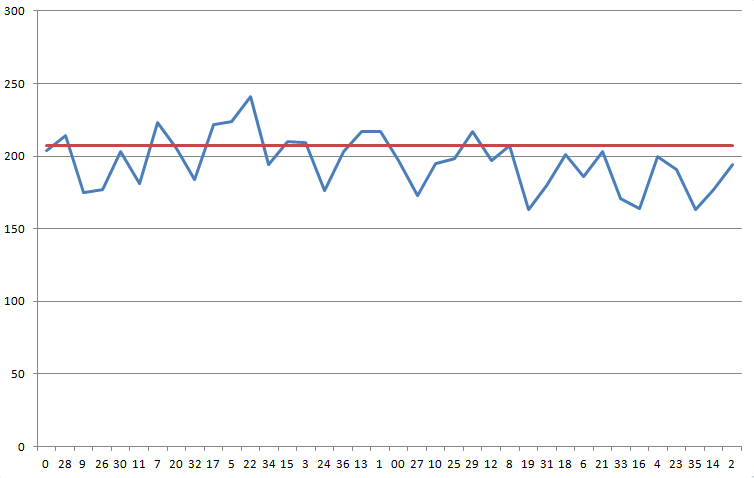
मैंने रूलेट में 7,456 स्पिन रिकॉर्ड किए। परिणाम इस प्रकार हैं। मुझे संदेह है कि पहिया पक्षपाती है, लेकिन मुझे यकीन नहीं है कि डेटा इसे खेलने के लिए पर्याप्त निर्णायक है या नहीं।
रूलेट डेटा
| जीत संख्या | पुनरावृत्तियां |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| कुल | 7456 |
निम्नलिखित ग्राफ़ आपके परिणामों को पहिये पर क्रमिक क्रम में दर्शाता है। नीली रेखा आपके परिणाम दिखाती है। लाल रेखा वह संख्या है जिसकी आपको 5.26% हाउस एज को पार करने के लिए आवश्यकता है, 207.11।
इस वितरण पर काई-स्क्वेयर परीक्षण से 37 डिग्री स्वतंत्रता के साथ 68.1 का आँकड़ा प्राप्त होता है। इस विषम या उससे अधिक परिणाम की संभावना 725 में 1 है।
मुझे नहीं लगता कि इस स्थिति के लिए काई-स्क्वेयर्ड सही परीक्षण है क्योंकि यह परिणामों के क्रम पर विचार नहीं करता, लेकिन मुझे इससे बेहतर कोई परीक्षण नहीं पता। कुछ लोगों ने कोल्मोगोरोव-स्मिरनोव परीक्षण का सुझाव दिया है, लेकिन मुझे नहीं लगता कि वह उपयुक्त है। अगर कोई और उपयुक्त परीक्षण हैं, तो मैं पूरी तरह तैयार हूँ।
मैं कह सकता हूँ कि अगर आपने 5 नंबर के आसपास 3-अंकीय चाप पर दांव लगाया होता, तो आपको अपने रिकॉर्ड किए गए स्पिन पर 10.57% का लाभ होता। हालाँकि, अगर आपने इसे 7-अंकीय चाप तक बढ़ा दिया, तो यह लाभ घटकर 2.84% रह जाता है।
अगर मुझे सीधे-सादे अंग्रेजी में जवाब देने के लिए मजबूर किया जाए, तो मैं कहूँगा कि पहिया इस बात का सबूत ज़रूर देता है, लेकिन किसी भी तरह के संदेह से परे कोई सबूत नहीं कि पहिया पक्षपाती है। हालाँकि, यह पक्षपात शायद हाउस एज पर पूरी तरह से और आत्मविश्वास से काबू पाने के लिए पर्याप्त नहीं है। यह मानते हुए कि कैसीनो टेबलों के बीच पहियों को नहीं बदलता, मैं कहूँगा कि बड़ी रकम दांव पर लगाने से पहले ज़्यादा जानकारी इकट्ठा कर लेनी चाहिए। मुझे खेद है कि यह जवाब इतना अस्पष्ट है।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
एकल-शून्य रूलेट में, प्रत्येक संख्या के कम से कम एक बार प्रकट होने के लिए आवश्यक स्पिनों की औसत और मध्यिका संख्या क्या है?
माध्य का उत्तर देना ज़्यादा आसान है, इसलिए हम इसी से शुरुआत करेंगे। आइए इसे चरण दर चरण समझते हैं:
- पहला स्पिन निश्चित रूप से एक नया नंबर होगा।
- दूसरे प्रक्षेप में एक नई संख्या प्राप्त होने की प्रायिकता 36/37 होगी। यदि किसी घटना की प्रायिकता p है, तो उसके घटित होने के लिए अपेक्षित प्रयासों की संख्या 1/p है। इस स्थिति में, दूसरी संख्या प्राप्त करने के लिए अपेक्षित प्रयासों की संख्या 37/36 = 1.0278 है।
- दो संख्याओं के देखे जाने के बाद, अगले स्पिन में नई संख्या आने की संभावना 35/37 है। इस प्रकार, दूसरी संख्या के बाद तीसरी संख्या देखने के लिए अपेक्षित स्पिनों की संख्या 37/35 = 1.0571 है।
- इस तर्क के अनुसार, प्रत्येक संख्या को देखने के लिए स्पिन की औसत संख्या 1 + 37/36 + 37/35 + 37/34 + ... + 37/2 + 37/1 = 155.458690 है।
माध्यिका कहीं अधिक जटिल है। सटीक उत्तर प्राप्त करने के लिए, यादृच्छिक सिमुलेशन के बजाय, मैट्रिक्स बीजगणित का भरपूर उपयोग करना पड़ता है। मैंने अन्य Ask the Wizard प्रश्नों में इसी तरह की समस्याओं को हल करने के तरीके पर चर्चा की है, इसलिए मैं फिर से विवरण में नहीं जाऊँगा। इसी तरह के एक प्रश्न का उदाहरण लगातार तीन बार 6-6 जोड़ी होल में आने का प्रश्न है, जैसा कि Ask the Wizard #311 में चर्चा की गई है। इतना कहना पर्याप्त है कि 145 चक्करों में प्रत्येक संख्या को देखने की प्रायिकता 0.49161779 है, और 146 चक्करों में 0.501522154 है। इस प्रकार, माध्यिका 146 है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
यदि रूलेट में पिछले 20 चक्करों में गेंद लाल रंग में आई है, तो अगली बार काले रंग में आने की क्या संभावना है?
लाल के समान, दोहरे शून्य पहिये पर 47.37%, 18 काली संख्याओं को 38 कुल संख्याओं से विभाजित किया गया।
मुझे लगता है कि आप पिछले प्रश्न के बारे में गलत हैं। लगातार 21 लाल कार्ड आने की संभावना (18/38) है। 21 = 6,527,290 में 1। संभावनाएँ काले कार्ड के पक्ष में होनी चाहिए।
यह सच है, लेकिन इससे कोई फ़र्क़ नहीं पड़ता। 20 लाल कार्ड के बाद एक काला कार्ड आने की संभावना भी यही है। सच तो यह है कि रूलेट जैसे स्वतंत्र परीक्षणों वाले खेलों में अतीत कोई मायने नहीं रखता।
मैंने रूलेट में कैसिनो को हराने का एक तरीका सोच लिया है! किसी भी सम-धन वाली बाजी, जैसे लाल या काली, पर एक छोटा सा दांव लगाकर शुरुआत करो। अगर हार हो जाए, तो उसी बाजी पर दांव दोगुना करो। फिर जीत मिलने तक दोगुना करते रहो। जीत का नतीजा आखिरकार आना ही है और जब ऐसा होगा, तो मैं अपने मूल दांव का मुनाफ़ा कमा लूँगा। फिर दोहराओ। तुम्हारी क्या राय है? और, कृपया किसी को मत बताना।
यह शायद सभी सट्टेबाजी प्रणालियों में सबसे लोकप्रिय है, जिसे मार्टिंगेल के नाम से जाना जाता है। जुआरी अनादि काल से इसकी कल्पना और उपयोग करते आ रहे हैं। सभी सट्टेबाजी प्रणालियों की तरह, यह न केवल घर के लाभ को कम नहीं करता, बल्कि उसे नुकसान भी नहीं पहुँचाता। इसका कारण यह है कि जुआरी अंततः एक बुरी हार का सिलसिला शुरू कर देता है, जहाँ उसका बैंकरोल एक और डबल बनाने के लिए पर्याप्त नहीं होता।
अपने पिछले उत्तर में, आपने बताया था कि मार्टिंगेल क्यों काम नहीं करता। तो फिर इसके उलट, हर जीत के बाद अपनी बाजी दोगुनी करते रहना, जब तक कि मनचाहा लक्ष्य न मिल जाए, कैसा रहेगा?
इसे एंटी-मार्टिंगेल कहते हैं और यह भी उतना ही बेकार है। जब आपका बैंकरोल पूरी तरह से खत्म हो जाएगा, तो लक्ष्य हासिल करने पर मिलने वाली जीत की रकम उससे ज़्यादा होगी। आप चाहे कोई भी सट्टेबाजी प्रणाली अपनाएँ, या बिल्कुल भी न लगाएँ, आप जितना ज़्यादा खेलेंगे, डबल-ज़ीरो रूलेट में आपके दांव पर लगे पैसों के मुकाबले आपके खोए हुए पैसों का अनुपात उतना ही ज़्यादा 5.26% के करीब पहुँच जाएगा।
रूलेट में लगातार पांच लाल या पांच काले कार्ड देखने के लिए अपेक्षित स्पिन की संख्या क्या है?
[स्पॉइलर] उत्तर है 3872789/118098 =~ 32.79301089 स्पिन. [/स्पॉइलर]
यहां मेरा समाधान (पीडीएफ) है।
रूलेट में "थर्ड्स का नियम" क्या है?
"तिहाई का नियम" कहता है कि यदि आप पहिये पर प्रत्येक संख्या के लिए रूलेट पहिये को एक बार घुमाते हैं, तो लगभग 1/3 संख्याएं कभी नहीं आएंगी।
1/3 वाकई एक बहुत ही खराब अनुमान है। इससे बेहतर अनुमान 1/e =~ 36.79% होगा। डबल-ज़ीरो रूलेट में असली प्रतिशत 36.30% है।
निम्नलिखित तालिका डबल-जीरो रूलेट के 38 स्पिनों में 1 से 38 अलग-अलग संख्याओं के देखे जाने की संभावना को दर्शाती है।
थर्ड्स का नियम - डबल-ज़ीरो रूलेट
| विशिष्ट नंबर | संभावना |
|---|---|
| 1 | 0.000000000 |
| 2 | 0.000000000 |
| 3 | 0.000000000 |
| 4 | 0.000000000 |
| 5 | 0.000000000 |
| 6 | 0.000000000 |
| 7 | 0.000000000 |
| 8 | 0.000000000 |
| 9 | 0.000000000 |
| 10 | 0.000000000 |
| 11 | 0.000000000 |
| 12 | 0.000000000 |
| 13 | 0.000000005 |
| 14 | 0.000000124 |
| 15 | 0.000001991 |
| 16 | 0.000022848 |
| 17 | 0.000191281 |
| 18 | 0.001186530 |
| 19 | 0.005519547 |
| 20 | 0.019434593 |
| 21 | 0.052152293 |
| 22 | 0.107159339 |
| 23 | 0.169042497 |
| 24 | 0.204864337 |
| 25 | 0.190490321 |
| 26 | 0.135436876 |
| 27 | 0.073211471 |
| 28 | 0.029838199 |
| 29 | 0.009063960 |
| 30 | 0.002020713 |
| 31 | 0.000323888 |
| 32 | 0.000036309 |
| 33 | 0.000002742 |
| 34 | 0.000000132 |
| 35 | 0.000000004 |
| 36 | 0.000000000 |
| 37 | 0.000000000 |
| 38 | 0.000000000 |
| कुल | 1.000000000 |
तालिका दर्शाती है कि सबसे संभावित परिणाम 24 अलग-अलग संख्याएँ हैं, जो 20.49% है। औसत 24.20656478 है।
कुछ धोखेबाज़ यह तर्क देते हैं कि खिलाड़ी को पहले नौ अलग-अलग परिणामों को देखना चाहिए और फिर उन पर दांव लगाना चाहिए, इस गलत धारणा के तहत कि उनके होने की संभावना अन्य संख्याओं की तुलना में ज़्यादा है। यह बिल्कुल सच नहीं है! पहिये और गेंद की कोई स्मृति नहीं होती। निष्पक्ष पहिये पर, हर संख्या समान रूप से संभावित होती है और अतीत मायने नहीं रखता।