इस पृष्ठ पर
ब्लैकजैक में डेक की संख्या क्यों मायने रखती है?
परिचय
ब्लैकजैक पर कोई भी सम्मानित स्रोत यह ज़रूर बताएगा कि ब्लैकजैक में इस्तेमाल होने वाले डेक की संख्या और हाउस एज के बीच, बाकी सभी चीज़ें समान होने पर, एक सकारात्मक संबंध होता है। दूसरे शब्दों में, जितने कम डेक होंगे, मनोरंजन करने वाले खिलाड़ी के लिए जीतने की संभावना उतनी ही बेहतर होगी। यह तथ्य ब्लैकजैक खिलाड़ियों के बीच आम है, जो कम से कम इतना तो जानते ही हैं कि अच्छे नियमों वाले खेल की तलाश कर सकें। हालाँकि, मैंने कभी इस बात का गहराई से विश्लेषण नहीं देखा कि यह सच क्यों है। इस लेख का उद्देश्य इसी प्रश्न पर प्रकाश डालना है।
शुरू करने से पहले, मैं कुछ बुनियादी नियम बता दूँ। ये नियम 2020 में इस लेख के लिखे जाने के समय ब्लैकजैक की परिस्थितियों को देखते हुए यथासंभव यथार्थवादी होने के लिए चुने गए हैं:
- डीलर ने सॉफ्ट 17 मारा।
- ब्लैकजैक 3 से 2 का भुगतान करता है।
- डीलर दस या इक्का के साथ ब्लैकजैक के लिए झांकता है।
- खिलाड़ी किसी भी दो कार्ड पर दोगुना कर सकता है।
- खिलाड़ी आत्मसमर्पण नहीं कर सकता.
- खिलाड़ी विभाजन के बाद दोगुना हो सकता है।
- खिलाड़ी किसी भी जोड़ी (इक्के सहित) को अधिकतम तीन बार पुनः विभाजित कर सकता है।
- निरंतर शफलर का प्रयोग (प्रत्येक हाथ के बाद कार्डों को फेरबदल किया जाता है)।
- खिलाड़ी बुनियादी रणनीति का उपयोग करता है.
मेरा ब्लैकजैक हाउस एज कैलकुलेटर इन नियमों के तहत इंगित करता है कि डेक की संख्या के अनुसार हाउस एज निम्नानुसार है:
डेक द्वारा ब्लैकजैक हाउस एज
| डेक्स | हाउस एज |
|---|---|
| 1 | 0.014% |
| 2 | 0.341% |
| 4 | 0.499% |
| 6 | 0.551% |
| 8 | 0.577% |
ये आँकड़े ब्लैकजैक के अन्य सम्मानित स्रोतों से बिल्कुल मेल नहीं खा सकते। मेरा मानना है कि कोई भी अंतर या तो कटे हुए कार्ड के इस्तेमाल या खिलाड़ी द्वारा इष्टतम संयोजन-निर्भर रणनीति के इस्तेमाल के कारण होगा। तुलनात्मक रूप से, मेरा मानना है कि हर हाथ के बाद कार्डों को फेरबदल किया जाता है और खिलाड़ी हमेशा कुल-निर्भर बुनियादी रणनीति का पालन करता है।
ध्यान दें कि आठ डेक और एक डेक के बीच हाउस एज में 0.563% का अंतर होता है। यह लेख इस प्रश्न का उत्तर देने का प्रयास करेगा कि डेक की संख्या का ऑड्स पर इतना महत्वपूर्ण प्रभाव क्यों पड़ता है।
संतुलित खेल
शुरुआत के तौर पर, मैं एक सरलीकृत ब्लैकजैक गेम पर विचार करता हूँ, जिसमें खिलाड़ी और डीलर दोनों के लिए नियम बिल्कुल एक जैसे होते हैं, जिसके परिणामस्वरूप डेक की संख्या चाहे कितनी भी हो, हाउस एज 0% रहता है। फिर मैं धीरे-धीरे एक-एक करके वास्तविक ब्लैकजैक नियम जोड़ता हूँ और जाँचता हूँ कि डेक की संख्या के आधार पर वे हाउस एज को कैसे प्रभावित करते हैं।
प्रारंभिक काल्पनिक सरलीकृत ब्लैकजैक खेल के नियम वही होंगे जो पहले बताए गए हैं, सिवाय इसके:
- खिलाड़ी “डीलर की नकल” रणनीति का पालन करता है।
- ब्लैकजैक जीतने पर भी पैसा मिलता है।
- यदि खिलाड़ी और डीलर दोनों बस्ट हो जाते हैं, तो परिणाम पुश होता है।
इस संतुलित खेल में हाउस एज स्पष्ट रूप से 0.000% है, क्योंकि प्रत्येक नियम दोनों तरफ समान रूप से लागू होता है।
डीलर स्थितिगत लाभ
ब्लैकजैक में जब खिलाड़ी और डीलर दोनों बस्ट हो जाते हैं तो कौन जीतता है? डीलर ही जीतता है। दूसरे शब्दों में, डीलर को स्थितिगत लाभ मिलता है क्योंकि जो पहले बस्ट होता है वह हार जाता है और खिलाड़ी को पहले कदम उठाना पड़ता है। यही कारण है कि डीलर को लाभ मिलता है, भले ही कई नियम खिलाड़ी के रास्ते में बाधा डालते हों। इस नियम को बैलेंस गेम में जोड़ने और इसे एक और आठ डेक के लिए सिमुलेशन के माध्यम से चलाने पर खिलाड़ी के लिए निम्नलिखित अपेक्षित रिटर्न प्राप्त होते हैं।
नियम परिवर्तन द्वारा अपेक्षित मान
| नियम | एक डेक | आठ डेक | अंतर |
|---|---|---|---|
| डीलर की स्थितिगत लाभ | -8.237% | -8.157% | -0.079 % |
ऊपर दी गई तालिका दर्शाती है कि आठ डेक की तुलना में एक डेक वाले इस काल्पनिक खेल में खिलाड़ी के लिए संभावनाएँ कम होती हैं। ऐसा इसलिए है क्योंकि जैसे-जैसे डेक की संख्या कम होती जाती है, बस्ट होने की संभावना बढ़ती जाती है। इस "डीलर की नकल करो" खेल में बस्ट होने की संभावना इस प्रकार है, यह मानते हुए कि डीलर अपना हाथ खेलता है, भले ही खिलाड़ी पहले बस्ट हो जाए।
- एक डेक = 27.333%
- आठ डेक = 27.209%
ऊपर दिए गए उदाहरण से पता चलता है कि एक-डेक वाले खेल में किसी भी पक्ष के बस्ट होने की संभावना आठ-डेक वाले खेल की तुलना में 0.124% ज़्यादा होती है। दोनों पक्षों के बस्ट होने के बीच कुछ संबंध होता है, तो आइए खिलाड़ी और डीलर के बस्ट होने के सभी चार संयोजनों पर नज़र डालें:
बस्ट संभावनाएं
| खिलाड़ी बस्ट | डीलर बस्ट | एक डेक | आठ डेक | अंतर |
|---|---|---|---|---|
| नहीं | नहीं | 44.096% | 44.468% | -0.372% |
| नहीं | हाँ | 19.095% | 19.051% | 0.044% |
| हाँ | नहीं | 19.095% | 19.051% | 0.044% |
| हाँ | हाँ | 8.237% | 8.157% | 0.079% |
| कुल | 90.524% | 90.728% | -0.204% |
संभावनाओं का योग 100% नहीं होने का कारण यह है कि टेबल उन हाथों की गिनती नहीं करता है जहाँ किसी भी पक्ष के पास ब्लैकजैक है और हाथ अन्यथा नहीं खेला गया है। "हाँ हाँ" पंक्ति उन स्थितियों को दिखाती है जहाँ दोनों पक्ष बस्ट होते हैं, जिसके परिणामस्वरूप डीलर जीत जाता है। यह दर्शाता है कि आठ डेक की तुलना में एकल-डेक गेम में यह 0.080% अधिक बार होता है। क्यों? यदि कोई भी पक्ष बस्ट होता है, तो यह 12 से 16 अंकों के हार्ड हैंड को मारने के बाद हुआ होगा। इस हाथ में कम से कम दो कार्ड होने चाहिए। इस बीच, यदि किसी भी पक्ष के पास दो उच्च मूल्य के कार्ड हैं, तो वह खड़ा होगा। दूसरे शब्दों में, हिटिंग आम तौर पर उन हाथों के साथ होती है जिनमें औसत-मूल्य के कार्ड से छोटे होते हैं। हिटिंग स्थितियों में छोटे कार्डों को हटाने से शेष कार्डों में उच्च कार्डों की अधिकता हो जाती है
ब्लैकजैक 3 से 2 का भुगतान करता है
अगला नियम जो हम संतुलित खेल में जोड़ेंगे वह यह होगा कि ब्लैकजैक जीतने वाला खिलाड़ी 3 से 2 का भुगतान करता है। मेरे सिमुलेशन में उस नियम को जोड़ने से निम्नलिखित संचयी खिलाड़ी अपेक्षित रिटर्न प्राप्त होता है।
- एक डेक = -5.912%
- आठ डेक = -5.894%
इस नियम को जोड़ने के लिए एक पंक्ति जोड़ने वाली सिमुलेशन परिणाम तालिका है:
नियम परिवर्तन द्वारा अपेक्षित मान
| नियम | एक डेक | आठ डेक | अंतर |
|---|---|---|---|
| डीलर की स्थितिगत लाभ | -8.237% | -8.157% | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | -5.912% | -5.894% | -0.018% |
दो पंक्तियों के बीच का अंतर लेने से 3 से 2 का भुगतान करने वाले विजेता ब्लैकजैक के खिलाड़ी को लाभ पता चलता है:
- एक डेक = 2.325%
- आठ डेक = 2.263%
- अंतर = 0.062%
गणितीय रूप से इसकी पुष्टि इस प्रकार आसानी से की जा सकती है। मान लीजिए d = डेक की संख्या। एक्सेल संकेतन का उपयोग करते हुए, ब्लैकजैक जीतने की प्रायिकता है: प्रायिकता (खिलाड़ी ब्लैकजैक) * (1-प्रायिकता (डीलर ब्लैकजैक)) = (16*d)*(4*d)/कॉम्बिनेशन(52*d,2) * [1-(16*d-1)*(4*d-1)/कॉम्बिनेशन(52*d-2,2)
ब्लैकजैक जीतने की संभावना
| डेक्स | संभावना |
|---|---|
| 1 | 4.649% |
| 2 | 4.578% |
| 4 | 4.544% |
| 6 | 4.532% |
| 8 | 4.527% |
जैसा कि ऊपर देखा गया है, जीतने वाले ब्लैकजैक की संभावना बढ़ जाती है क्योंकि डेक की संख्या कम हो जाती है। यह केवल हटाने के प्रभावों के कारण है। उदाहरण के लिए, मान लें कि पहला खिलाड़ी कार्ड कोई भी 10-मूल्य का कार्ड है। डेक की संख्या के बावजूद, इसकी संभावना 4/13 है। यह देखना आसान है कि एकल-डेक गेम में दूसरे कार्ड के रूप में इक्का मिलने की संभावना 4/51 = 7.843% है। आठ-डेक गेम में यह संभावना 32/415 = 7.711% है, जो एकल-डेक गेम की तुलना में 0.123% कम है। सरल अंग्रेजी में, एकल-डेक गेम में इक्का मिलने की संभावना अधिक होने का कारण यह है कि 10 को हटाने के बाद डेक इक्कों से समृद्ध होता है। यदि पहला कार्ड इक्का है तो भी यही सच है; शेष कार्ड एकल-डेक गेम में दहाई से समृद्ध होंगे।
इसके अलावा, यदि खिलाड़ी को ब्लैकजैक मिलता है, तो डीलर को ब्लैकजैक मिलने की संभावना डेक की संख्या कम होने के साथ कम हो जाती है। ऐसा इसलिए है क्योंकि एकल-डेक गेम में खिलाड़ी द्वारा डेक से इक्का और 10 हटाने से डीलर के लिए आठ-डेक गेम की तुलना में ब्लैकजैक प्राप्त करना अधिक कठिन हो जाता है। विशेष रूप से, डीलर ब्लैकजैक की संभावना, यह मानते हुए कि खिलाड़ी के पास पहले से ही एक है, एक डेक के साथ 3.673% और आठ डेक के साथ 4.605% है। खिलाड़ी हर जीतने वाले ब्लैकजैक के साथ एक अतिरिक्त आधी इकाई जीतता है। हमारे काल्पनिक संतुलित गेम में एक जीतने वाले ब्लैकजैक के 3-2 का भुगतान करने का मूल्य प्राप्त करने के लिए, एक जीतने वाले ब्लैकजैक की संभावना लें और हर बार उस अतिरिक्त आधी इकाई के लिए 0.5 से गुणा करें
ब्लैकजैक जीतने से खिलाड़ी की बढ़त
| डेक्स | खिलाड़ी बढ़त |
|---|---|
| 1 | 2.325% |
| 2 | 2.289% |
| 4 | 2.272% |
| 6 | 2.266% |
| 8 | 2.263% |
ध्यान दें कि विजेता खिलाड़ी द्वारा ब्लैकजैक में अतिरिक्त आधी इकाई का भुगतान करने के गणितीय रूप से परिकलित लाभ, एकल- और आठ-डेक के लिए पहले दिखाए गए सिमुलेशन परिणामों से मेल खाते हैं।
नीचे दी गई तालिका में अब तक विश्लेषित नियमों की सूची तथा आठ डेक की तुलना में एकल डेक खिलाड़ी के लिए उनके लाभ को दर्शाया गया है:
नियमों का प्रभाव
| नियम | एकल-डेक लाभ |
|---|---|
| डीलर की स्थितिगत लाभ | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | 0.062% |
| कुल | -0.018% |
इसके बाद, आइए 12 से 16 के हार्ड टोटल पर खड़े होने की अनुमति से खिलाड़ी को होने वाले लाभ का विश्लेषण करें। इस श्रेणी में कुल-निर्भर बुनियादी रणनीति किसी भी संख्या में डेक के लिए समान है, इस प्रकार:
- कुल 12 के साथ, डीलर के खिलाफ 4 से 6 तक खड़े रहें, अन्यथा हिट करें।
- कुल 13 से 16 के साथ, डीलर 2 से 6 के खिलाफ खड़े हों, अन्यथा हिट करें।
इस रणनीति को सिमुलेशन में जोड़ने पर खिलाड़ी को निम्नलिखित अपेक्षित रिटर्न प्राप्त होता है:
- एक डेक = -2.209%
- आठ डेक = -2.625%
नीचे दी गई सिमुलेशन परिणाम तालिका में इस नियम को जोड़ने के लिए एक पंक्ति शामिल है:
नियम परिवर्तन द्वारा अपेक्षित मान
| नियम | एक डेक | आठ डेक | अंतर |
|---|---|---|---|
| डीलर की स्थितिगत लाभ | -8.237% | -8.157% | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | -5.912% | -5.894% | -0.018% |
दूसरी और तीसरी पंक्ति के बीच का अंतर यह दर्शाता है कि खिलाड़ी की हार्ड 12 से 16 पर खड़े होने की स्वतंत्र इच्छा का क्या प्रभाव पड़ता है।
- एक डेक = 3.703%
- आठ डेक = 3.270%
- अंतर = 0.433%
इन दोनों आंकड़ों के अंतर को देखते हुए, यह पता चलता है कि इस नियम परिवर्तन का प्रभाव आठ डेक वाले खेल की तुलना में एकल डेक वाले खेल में खिलाड़ी के लिए 0.433% अधिक है। आम धारणा के विपरीत, यही कारण है कि एकल डेक वाला खेल आठ डेक वाले खेल की तुलना में खिलाड़ी के लिए 0.563% अधिक लाभदायक है।
यदि हम इस बात पर अधिक गहराई से विचार करें कि क्या होता है, जब खिलाड़ी 12 से 16 के कठोर योग पर खड़ा होता है, जबकि डीलर ऐसा नहीं कर सकता - तो यह तालिका विभिन्न घटनाओं से खिलाड़ी को होने वाले लाभ को दर्शाती है, जो खिलाड़ी द्वारा कम कठोर योगों को मारने के कारण बदलती हैं, जिसके परिणामस्वरूप कम खिलाड़ी बस्ट होते हैं, और अधिक डीलर बस्ट होते हैं, साथ ही डीलर अधिक फेस-ऑफ हारता है:
जब खिलाड़ी हार्ड 12 से 16 पर खड़ा होता है तो संभावित परिणाम
| आयोजन | एक डेक | आठ डेक | अंतर |
|---|---|---|---|
| केवल खिलाड़ियों के लिए कम बस्ट | 6.282% | 6.271% | 0.010% |
| अधिक डीलर-केवल बस्ट | 4.228% | 4.171% | 0.057% |
| दोनों बस्ट कम | 4.228% | 4.172% | 0.055% |
| खिलाड़ी कम फेस-ऑफ जीतता है | -1.914% | -2.039% | 0.125% |
| डीलर अधिक फेस-ऑफ जीतता है | -9.121% | -9.306% | 0.185% |
| कुल | 3.703% | 3.270% | 0.433% |
डीलर के अधिक बार बस्ट होने और अधिक फेस-ऑफ हारने के कारण अधिक जीतने के लाभ को दिखाने के लिए उसी तालिका को सरल बनाया गया है:
जब खिलाड़ी हार्ड 12 से 16 पर खड़ा होता है तो संभावित परिणामों का सारांश
| आयोजन | एक डेक | आठ डेक | अंतर |
|---|---|---|---|
| खिलाड़ी को कम लाभ पहुँचाना | 14.738% | 14.615% | 0.123% |
| आमने-सामने की हार | -11.035% | -11.345% | 0.310% |
| कुल | 3.703% | 3.270% | 0.433% |
सरल भाषा में कहें तो, सिंगल-डेक गेम में, 12 से 16 के हार्ड टोटल के साथ बुनियादी रणनीति का पालन करके, खिलाड़ी डीलर की तुलना में 14.738% कम बार बस्ट होगा। हालाँकि, ऐसे हाथों में, 75% बार डीलर बस्ट नहीं होगा, जिसके परिणामस्वरूप 16 या उससे कम के खिलाड़ी के हाथ के साथ फेस-ऑफ़ में डीलर जीत जाएगा, जो जीत नहीं सकता। सभी हाथों की तुलना में, खिलाड़ी कम बस्ट करके 14.738% बचाता है, लेकिन अधिक फेस-ऑफ़ नुकसान के रूप में 11.035% वापस देता है, जिससे सिंगल-डेक गेम में 3.703% का शुद्ध लाभ होता है।
आठ डेक वाले खेल में यह लाभ केवल 3.270% है। कुल मिलाकर, 12 से 16 डेक पर रणनीतिक स्थिति का लाभ, आठ डेक वाले खेल की तुलना में एकल डेक वाले खेल में खिलाड़ी के लिए 0.433% अधिक होता है।
एक डेक बनाम आठ डेक में रणनीतिक स्टैंडिंग अधिक मूल्यवान क्यों है? इसका उत्तर उसी तरह है जैसे एकल-डेक गेम में डीलर का स्थितिगत लाभ अधिक महत्वपूर्ण क्यों होता है। एकल-डेक गेम में अधिक बस्टिंग होती है। हालांकि अधिक बस्टिंग दोनों तरफ नुकसान पहुंचा सकती है, यह खिलाड़ी के खिलाफ अधिक नुकसान पहुंचाती है क्योंकि जब दोनों पक्ष ब्रेक करते हैं तो वह हार जाता है। जब खिलाड़ी स्टैंड पर होता है तो 12 से 16 का योग संभवतः बड़े की तुलना में अधिक छोटे कार्डों से बना होता है। इससे डेक में खिलाड़ी के बस्ट होने के लिए अधिक बड़े कार्ड बच जाते हैं। खिलाड़ी को अपने हाथ को बेहतर बनाने के लिए इन कम कार्डों को हटाने के प्रभाव एकल-डेक गेम में आठ डेक की तुलना में अधिक महंगे होते हैं। दूसरे शब्दों में, एकल-डेक गेम में स्टिफ्स मारना अधिक खतरनाक होता है
यहां प्रत्येक नियम परिवर्तन की लागत/लाभ की अद्यतन तालिका दी गई है:
नियमों का प्रभाव
| नियम | एकल-डेक लाभ |
|---|---|
| डीलर की स्थितिगत लाभ | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | 0.061% |
| खिलाड़ी हार्ड 12 से 16 पर खड़ा हो सकता है | 0.433% |
| कुल | 0.415% |
खिलाड़ी दोगुना कर सकता है
अब, आइए खिलाड़ी को दोगुना करने की अनुमति मिलने से होने वाले लाभ का विश्लेषण करें। प्रभाव का अध्ययन करने के लिए, मैंने सिमुलेशन को दी गई डेक की संख्या के लिए उपयुक्त दोहरीकरण रणनीति अपनाने को कहा, जिसका विवरण लेख में आगे दिया गया है। इस रणनीति को सिमुलेशन में जोड़ने पर खिलाड़ी को निम्नलिखित अपेक्षित लाभ प्राप्त होते हैं:
- एक डेक = -0.556%
- आठ डेक = -1.245%
इस सिमुलेशन परिणाम तालिका में इस नियम को जोड़ने के लिए एक पंक्ति शामिल है:
नियम परिवर्तन द्वारा अपेक्षित मान
| नियम | एक डेक | आठ डेक | अंतर |
|---|---|---|---|
| डीलर की स्थितिगत लाभ | -8.237% | -8.157% | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | -5.912% | -5.894% | -0.018% |
| खिलाड़ी हार्ड 12 से 16 पर खड़ा हो सकता है | -2.209% | -2.625% | 0.415% |
| खिलाड़ी दोगुना कर सकता है | -0.556% | -1.245% | 0.689% |
तीसरी और चौथी पंक्ति के बीच का अंतर खिलाड़ी की दोगुनी करने की स्वतंत्र इच्छा के प्रभाव को दर्शाता है, जो इस प्रकार है:
- एक डेक = 1.653%
- आठ डेक = 1.380%
- अंतर = 0.273%
इन दोनों आंकड़ों के अंतर को देखते हुए, यह पता चलता है कि इस नियम परिवर्तन का प्रभाव आठ डेक वाले खेल की तुलना में एकल डेक वाले खेल में खिलाड़ी के लिए 0.273% अधिक है। यह इस बात का एक और महत्वपूर्ण पहलू भी बताता है कि आठ डेक वाले खेल की तुलना में एकल डेक वाला खेल खिलाड़ी के लिए 0.563% अधिक क्यों है।
एकल-डेक खेल में दोगुना करना ज़्यादा महत्वपूर्ण क्यों है? ज़्यादातर खिलाड़ी जब दोगुना करता है तो वह 9 से 11 अंकों के हार्ड टोटल पर होता है। दोगुना करना दो पत्तों से किया जाता है, इसलिए 9 से 11 के कम टोटल में जोड़ने के लिए औसत से छोटे दो पत्तों की ज़रूरत होती है। अगर ताश के पत्तों की एक ही डेक से दो छोटे पत्ते हटा दिए जाते हैं, तो अगले पत्ते के दहाई होने की संभावना 32.00% होती है, जो हार्ड टोटल पर दोगुना करने पर स्पष्ट रूप से अच्छा है। वहीं, अगर आठ-डेक के जूते से दो छोटे पत्ते हटा दिए जाते हैं, तो हटाने का प्रभाव उतना ज़्यादा नहीं होता, जिससे अगले पत्ते के दहाई होने की संभावना घटकर 30.92% रह जाती है।
यहाँ प्रत्येक नियम परिवर्तन की लागत/लाभ की एक अद्यतन तालिका दी गई है। ध्यान दें कि 0.689% का कुल लाभ अंतिम हाउस एज अंतर से अधिक है। ऐसा इसलिए है क्योंकि हमने अभी तक विभाजन के प्रभाव पर विचार नहीं किया है।
नियमों का प्रभाव
| नियम | एकल-डेक लाभ |
|---|---|
| डीलर की स्थितिगत लाभ | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | 0.061% |
| खिलाड़ी हार्ड 12 से 16 पर खड़ा हो सकता है | 0.433% |
| खिलाड़ी दोगुना कर सकता है | 0.273% |
| कुल | 0.689% |
खिलाड़ी विभाजित हो सकता है
इसके बाद, मैंने स्प्लिट करने की अनुमति मिलने से खिलाड़ी को होने वाले लाभ का विश्लेषण किया। प्रभाव का अध्ययन करने के लिए, मैंने सिमुलेशन को दी गई डेक की संख्या के लिए उपयुक्त स्प्लिटिंग रणनीति अपनाने को कहा, जिसका विवरण लेख में आगे दिया गया है। इस रणनीति को जोड़ने पर हम पूरी मूल रणनीति पर पहुँच जाते हैं। स्प्लिटिंग जोड़ने के बाद खिलाड़ी और डीलर के बीच अध्ययन करने के लिए कोई अन्य नियम अंतर नहीं हैं। पूरी मूल रणनीति से खिलाड़ी को अपेक्षित लाभ इस प्रकार हैं:
- एक डेक = -0.012%
- आठ डेक = -0.575%
इस नियम को जोड़ने के लिए एक पंक्ति सहित सिमुलेशन परिणाम तालिका है:
नियम परिवर्तन द्वारा अपेक्षित मान
| नियम | एक डेक | आठ डेक | अंतर |
|---|---|---|---|
| डीलर की स्थितिगत लाभ | -8.237% | -8.157% | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | -5.912% | -5.894% | -0.018% |
| खिलाड़ी हार्ड 12 से 16 पर खड़ा हो सकता है | -2.209% | -2.625% | 0.415% |
| खिलाड़ी दोगुना कर सकता है | -0.556% | -1.245% | 0.689% |
| खिलाड़ी विभाजित हो सकता है | -0.012% | -0.575% | 0.563% |
चौथी और पांचवीं पंक्ति का अंतर खिलाड़ी की स्वतंत्र इच्छा के प्रभाव को दर्शाता है।
- एक डेक = 0.544%
- आठ डेक = 0.669%
- अंतर = -0.125%
इन दोनों आंकड़ों के अंतर को देखते हुए यह पता चलता है कि आठ डेक की तुलना में एकल डेक गेम में इस नियम परिवर्तन का प्रभाव खिलाड़ी पर 0.125% कम पड़ता है।
आठ डेक वाले खेल में, एक डेक वाले खेल की तुलना में, स्प्लिटिंग ज़्यादा फ़ायदेमंद होती है, क्योंकि पहले दो पत्तों में एक जोड़ी मिलने की संभावना ज़्यादा होती है। एक्सेल शब्दावली का इस्तेमाल करें तो, आठ डेक के साथ, संभावना 13*कॉम्बिन(4*8,2)/कॉम्बिन(52*8,2) = 7.470% है। एक डेक के साथ, संभावना 13*कॉम्बिन(4*1,2)/कॉम्बिन(52*1,2) = 5.882% है।
यह भी याद रखें कि खेल के मूल नियम तीन बार या चार हाथों तक पुनः-विभाजन की अनुमति देते हैं। यदि एक ही डेक से समान रैंक के दो पत्ते हटा दिए जाते हैं, तो अगले पत्ते पर उसी रैंक के पत्ते आने की संभावना 2/50 = 4.000% है। वहीं, आठ-डेक वाले जूते के लिए, यह संभावना 30/414 = 7.246% है। एकल-डेक वाले खेल में कम विभाजन और पुनः-विभाजन होने के कारण, कुल मिलाकर विभाजन का मूल्य कम होता है। यही कारण है कि आठ से एक डेक पर जाने पर विभाजन का लाभ कम हो जाता है।
एकल डेक खेल में विभाजन के नकारात्मक प्रभाव को जोड़ने से आठ डेक की तुलना में एकल डेक खेल के लाभ पर विभिन्न नियमों के प्रभाव की हमारी तालिका पूरी हो जाती है।
नियम एकल डेक लाभ डीलर स्थितिगत लाभ -0.079% विजेता खिलाड़ी ब्लैकजैक 3 से 2 का भुगतान करता है 0.061% खिलाड़ी हार्ड 12 से 16 पर खड़ा हो सकता है 0.433% खिलाड़ी दोगुना कर सकता है 0.273% खिलाड़ी विभाजित कर सकता है -0.125% कुल 0.563%ध्यान दें कि निचले दाएँ सेल में 0.563% का योग लेख की शुरुआत में उद्धृत हाउस एज कैलकुलेटर द्वारा दिए गए अंतर से मेल खाता है। यहाँ प्रभाव के क्रम में वही तालिका दी गई है:
नियमों का प्रभाव
| नियम | एकल-डेक लाभ |
|---|---|
| डीलर की स्थितिगत लाभ | -0.079% |
| विजेता खिलाड़ी को ब्लैकजैक में 3 से 2 का भुगतान किया जाता है | 0.061% |
| खिलाड़ी हार्ड 12 से 16 पर खड़ा हो सकता है | 0.433% |
| खिलाड़ी दोगुना कर सकता है | 0.273% |
| खिलाड़ी विभाजित हो सकता है | -0.125% |
| कुल | 0.563% |
बुनियादी रणनीति तालिकाएँ
निम्नलिखित तालिका दिए गए नियमों और एक डेक के लिए उपयुक्त बुनियादी रणनीति दिखाती है।
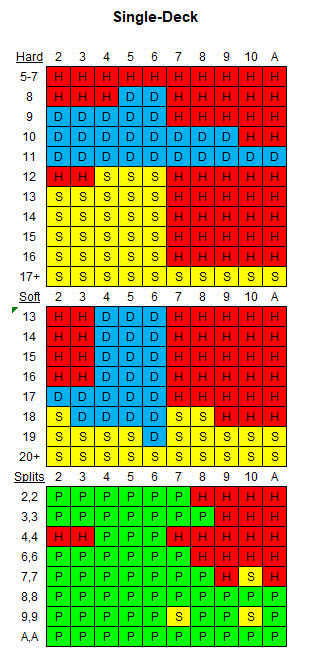
निम्नलिखित तालिका दिए गए नियमों और आठ डेक के लिए उपयुक्त बुनियादी रणनीति दर्शाती है।
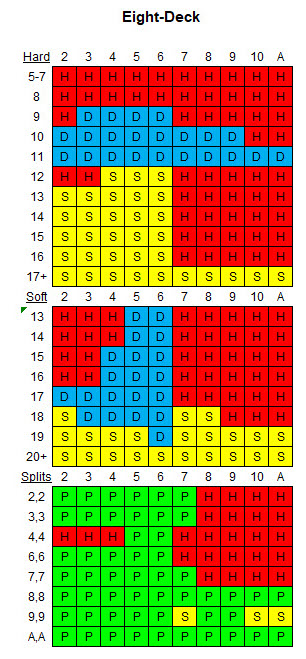
अपेक्षित मूल्य तालिकाएँ
निम्न तालिका एकल-डेक खेल में प्रत्येक प्रारंभिक हाथ के अपेक्षित मूल्य को दर्शाती है। ऊपरी पंक्ति डीलर के अप कार्ड को दर्शाती है। अपेक्षित मूल्यों को डीलर द्वारा ब्लैकजैक की जाँच करने से पहले मापा जाता है। कुल स्तंभ हाथ प्राप्त करने की संभावना के अनुसार प्रत्येक पंक्ति में अपेक्षित मूल्यों का भारित औसत दर्शाता है। निचला दायाँ कक्ष समग्र खेल का अपेक्षित मूल्य दर्शाता है।
सिंगल-डेक गेम में अपेक्षित मान
एक डेक के साथ खिलाड़ी के हाथ बनाम डीलर के अप कार्ड द्वारा अपेक्षित मान
| खिलाड़ी | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ऐस | कुल |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1278 | -0.0968 | -0.0379 | 0.0227 | 0.0403 | -0.1191 | -0.1805 | -0.2624 | -0.3654 | -0.5443 | -0.2169 |
| 6 | -0.1477 | -0.1037 | -0.0519 | 0.0104 | 0.0371 | -0.1640 | -0.2343 | -0.3046 | -0.4015 | -0.5713 | -0.2469 |
| 7 | -0.1120 | -0.0701 | -0.0119 | 0.0528 | 0.0683 | -0.0690 | -0.2232 | -0.2948 | -0.3863 | -0.5765 | -0.2211 |
| 8 | -0.0174 | 0.0199 | 0.0826 | 0.1407 | 0.1498 | 0.0921 | -0.0565 | -0.2135 | -0.3136 | -0.5144 | -0.1286 |
| 9 | 0.1124 | 0.1923 | 0.2837 | 0.3753 | 0.3799 | 0.1951 | 0.1111 | -0.0519 | -0.2165 | -0.4146 | 0.0151 |
| 10 | 0.4262 | 0.4908 | 0.5494 | 0.6276 | 0.6241 | 0.4458 | 0.3145 | 0.1644 | -0.0528 | -0.2991 | 0.2316 |
| 11 | 0.5428 | 0.5922 | 0.6516 | 0.7176 | 0.7198 | 0.4785 | 0.3417 | 0.2240 | 0.0670 | -0.1848 | 0.3268 |
| 12 | -0.2518 | -0.2255 | -0.1915 | -0.1364 | -0.1194 | -0.2273 | -0.2925 | -0.3639 | -0.4175 | -0.5824 | -0.3131 |
| 13 | -0.2879 | -0.2411 | -0.1816 | -0.1344 | -0.1208 | -0.2861 | -0.3461 | -0.3764 | -0.4590 | -0.6106 | -0.3415 |
| 14 | -0.2900 | -0.2391 | -0.1835 | -0.1342 | -0.1209 | -0.3442 | -0.3612 | -0.4192 | -0.4957 | -0.6356 | -0.3644 |
| 15 | -0.2803 | -0.2379 | -0.1837 | -0.1388 | -0.1266 | -0.3590 | -0.4133 | -0.4703 | -0.5397 | -0.6677 | -0.3893 |
| 16 | -0.2863 | -0.2446 | -0.1872 | -0.1435 | -0.1450 | -0.3760 | -0.4254 | -0.4797 | -0.5482 | -0.6739 | -0.3978 |
| 17 | -0.1568 | -0.1216 | -0.0712 | -0.0445 | -0.0306 | -0.1217 | -0.3976 | -0.4154 | -0.4562 | -0.6560 | -0.2947 |
| 18 | 0.1072 | 0.1359 | 0.1538 | 0.1983 | 0.2031 | 0.3887 | 0.0956 | -0.1961 | -0.2242 | -0.4527 | -0.0185 |
| 19 | 0.3763 | 0.3774 | 0.3965 | 0.4449 | 0.4364 | 0.6101 | 0.5769 | 0.2642 | 0.0125 | -0.1586 | 0.2644 |
| ए,2 | 0.0402 | 0.0711 | 0.1174 | 0.2130 | 0.2455 | 0.1074 | 0.0392 | -0.0141 | -0.1454 | -0.3991 | -0.0057 |
| ए,3 | 0.0184 | 0.0447 | 0.1127 | 0.2042 | 0.2391 | 0.0605 | 0.0349 | -0.0602 | -0.1781 | -0.4205 | -0.0308 |
| ए,4 | -0.0103 | 0.0237 | 0.0892 | 0.1753 | 0.2191 | 0.0339 | -0.0354 | -0.1136 | -0.2226 | -0.4533 | -0.0697 |
| ए,5 | -0.0298 | -0.0019 | 0.0667 | 0.1490 | 0.2327 | -0.0239 | -0.0842 | -0.1666 | -0.2760 | -0.4900 | -0.1094 |
| ए,6 | 0.0142 | 0.0743 | 0.1549 | 0.2805 | 0.2630 | 0.0597 | -0.0646 | -0.1348 | -0.2383 | -0.4810 | -0.0586 |
| ए,7 | 0.1279 | 0.1867 | 0.3091 | 0.3482 | 0.3623 | 0.4118 | 0.1209 | -0.0873 | -0.1926 | -0.4433 | 0.0459 |
| ए,8 | 0.3953 | 0.4157 | 0.4100 | 0.4593 | 0.4666 | 0.6146 | 0.6078 | 0.2882 | -0.0009 | -0.1938 | 0.2686 |
| ए,9 | 0.6525 | 0.6415 | 0.6507 | 0.6810 | 0.6730 | 0.7732 | 0.7848 | 0.7656 | 0.4594 | 0.0943 | 0.5871 |
| ए,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.4081 | 1.0409 | 1.4449 |
| ए,ए | 0.6384 | 0.6863 | 0.7417 | 0.8075 | 0.8289 | 0.6277 | 0.4865 | 0.3605 | 0.2080 | -0.1580 | 0.4744 |
| 2,2 | -0.0349 | 0.0396 | 0.1235 | 0.3014 | 0.3378 | 0.0137 | -0.1412 | -0.2224 | -0.3355 | -0.5246 | -0.1145 |
| 3,3 | -0.1082 | -0.0209 | 0.1607 | 0.3049 | 0.3395 | -0.0448 | -0.2232 | -0.3100 | -0.3986 | -0.5715 | -0.1646 |
| 4,4 | -0.0136 | 0.0268 | 0.1354 | 0.2680 | 0.2980 | 0.1104 | -0.0549 | -0.2063 | -0.3069 | -0.5065 | -0.0991 |
| 5,5 | 0.4441 | 0.5075 | 0.5870 | 0.6933 | 0.7084 | 0.4663 | 0.3227 | 0.1738 | -0.0510 | -0.2978 | 0.2444 |
| 6,6 | -0.0963 | 0.0132 | 0.1456 | 0.2786 | 0.1992 | -0.1933 | -0.3222 | -0.3862 | -0.4366 | -0.5989 | -0.2245 |
| 7,7 | -0.0546 | 0.0494 | 0.1879 | 0.2244 | 0.2396 | -0.0524 | -0.3804 | -0.4744 | -0.5556 | -0.6790 | -0.2508 |
| 8,8 | 0.1165 | 0.1873 | 0.2245 | 0.3287 | 0.3508 | 0.3040 | -0.0599 | -0.4017 | -0.4929 | -0.6389 | -0.1224 |
| 9,9 | 0.2052 | 0.2156 | 0.3070 | 0.4064 | 0.4080 | 0.4011 | 0.2067 | -0.0986 | -0.2041 | -0.4520 | 0.0666 |
| 10,10 | 0.6220 | 0.6323 | 0.6402 | 0.6718 | 0.6683 | 0.7647 | 0.7832 | 0.7440 | 0.4539 | 0.1383 | 0.5803 |
| कुल | 0.1021 | 0.1388 | 0.1860 | 0.2391 | 0.2471 | 0.1473 | 0.0551 | -0.0435 | -0.1712 | -0.3891 | -0.0001 |
आठ-डेक गेम में अपेक्षित मान
आठ डेक के साथ खिलाड़ी के हाथ बनाम डीलर के अप कार्ड द्वारा अपेक्षित मान
| खिलाड़ी | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ऐस | कुल |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1258 | -0.0929 | -0.0562 | -0.0175 | 0.018 | -0.1196 | -0.1871 | -0.266 | -0.3663 | -0.5291 | -0.2191 |
| 6 | -0.1389 | -0.1042 | -0.0677 | -0.0287 | 0.0085 | -0.1534 | -0.2192 | -0.2941 | -0.3902 | -0.5469 | -0.2395 |
| 7 | -0.1094 | -0.0760 | -0.0391 | -0.0004 | 0.0349 | -0.0689 | -0.2121 | -0.2866 | -0.3731 | -0.5526 | -0.2164 |
| 8 | -0.0234 | 0.0076 | 0.0427 | 0.0774 | 0.1079 | 0.0831 | -0.0595 | -0.2104 | -0.3079 | -0.4931 | -0.1316 |
| 9 | 0.0743 | 0.1277 | 0.1921 | 0.2580 | 0.3141 | 0.1745 | 0.0998 | -0.0522 | -0.2180 | -0.3962 | -0.0071 |
| 10 | 0.3653 | 0.4176 | 0.4704 | 0.5253 | 0.5723 | 0.3990 | 0.2895 | 0.1469 | -0.0535 | -0.2865 | 0.2056 |
| 11 | 0.4786 | 0.5264 | 0.5759 | 0.6271 | 0.6718 | 0.4653 | 0.3496 | 0.2271 | 0.0864 | -0.2297 | 0.3097 |
| 12 | -0.2535 | -0.2331 | -0.2041 | -0.1613 | -0.1208 | -0.2146 | -0.2741 | -0.3430 | -0.4273 | -0.5746 | -0.3146 |
| 13 | -0.2867 | -0.2461 | -0.2030 | -0.1611 | -0.1210 | -0.2713 | -0.3264 | -0.3858 | -0.4682 | -0.6049 | -0.3447 |
| 14 | -0.2870 | -0.2456 | -0.2034 | -0.1612 | -0.1211 | -0.3240 | -0.3707 | -0.4295 | -0.5059 | -0.6328 | -0.3694 |
| 15 | -0.2858 | -0.2456 | -0.2033 | -0.1616 | -0.1217 | -0.3683 | -0.4162 | -0.4715 | -0.5422 | -0.6597 | -0.3927 |
| 16 | -0.2866 | -0.2463 | -0.2038 | -0.1622 | -0.1236 | -0.4103 | -0.4547 | -0.5057 | -0.5721 | -0.6820 | -0.4128 |
| 17 | -0.1565 | -0.1205 | -0.0819 | -0.0461 | -0.0090 | -0.1085 | -0.3842 | -0.4223 | -0.4633 | -0.6636 | -0.2958 |
| 18 | 0.1098 | 0.1379 | 0.1648 | 0.1953 | 0.2211 | 0.3982 | 0.1045 | -0.1847 | -0.2394 | -0.4626 | -0.0208 |
| 19 | 0.3780 | 0.3949 | 0.4138 | 0.4372 | 0.4513 | 0.6153 | 0.5918 | 0.2848 | -0.0149 | -0.1753 | 0.2569 |
| ए,2 | 0.0458 | 0.0737 | 0.1041 | 0.1376 | 0.2024 | 0.1207 | 0.0523 | -0.0350 | -0.1703 | -0.3789 | -0.0269 |
| ए,3 | 0.0224 | 0.0507 | 0.0827 | 0.1366 | 0.2010 | 0.0769 | 0.0155 | -0.0733 | -0.2024 | -0.4031 | -0.0533 |
| ए,4 | -0.0006 | 0.0294 | 0.0641 | 0.1328 | 0.1986 | 0.0368 | -0.0282 | -0.1123 | -0.2357 | -0.4281 | -0.0803 |
| ए,5 | -0.0211 | 0.0088 | 0.0611 | 0.1301 | 0.2004 | -0.0070 | -0.0689 | -0.1507 | -0.2691 | -0.4532 | -0.1057 |
| ए,6 | -0.0006 | 0.0558 | 0.1220 | 0.1933 | 0.2513 | 0.0545 | -0.0721 | -0.1479 | -0.2563 | -0.4626 | -0.0792 |
| ए,7 | 0.1160 | 0.1749 | 0.2418 | 0.3000 | 0.3560 | 0.4014 | 0.1074 | -0.0990 | -0.2075 | -0.4205 | 0.0270 |
| ए,8 | 0.3800 | 0.3993 | 0.4157 | 0.4389 | 0.4621 | 0.6159 | 0.5953 | 0.2878 | -0.0164 | -0.1795 | 0.2579 |
| ए,9 | 0.6371 | 0.6455 | 0.6562 | 0.6699 | 0.6778 | 0.7732 | 0.7909 | 0.7591 | 0.4379 | 0.1070 | 0.5752 |
| ए,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.3874 | 1.0388 | 1.4309 |
| ए,ए | 0.6072 | 0.6561 | 0.7062 | 0.7588 | 0.8058 | 0.6277 | 0.5001 | 0.3629 | 0.2059 | -0.1511 | 0.4411 |
| 2,2 | -0.0797 | -0.0089 | 0.0697 | 0.1700 | 0.2643 | 0.0087 | -0.1576 | -0.2385 | -0.3430 | -0.5115 | -0.1430 |
| 3,3 | -0.1305 | -0.0482 | 0.0500 | 0.1502 | 0.2425 | -0.0518 | -0.2189 | -0.2946 | -0.3899 | -0.5465 | -0.1859 |
| 4,4 | -0.0225 | 0.0080 | 0.0441 | 0.1066 | 0.2027 | 0.0857 | -0.0595 | -0.2096 | -0.3070 | -0.4921 | -0.1212 |
| 5,5 | 0.3676 | 0.4201 | 0.4748 | 0.5324 | 0.5814 | 0.4012 | 0.2910 | 0.1477 | -0.0534 | -0.2863 | 0.2074 |
| 6,6 | -0.1947 | -0.0972 | 0.0043 | 0.1075 | 0.1900 | -0.2189 | -0.2775 | -0.3453 | -0.4295 | -0.5767 | -0.2426 |
| 7,7 | -0.1233 | -0.0335 | 0.0669 | 0.1569 | 0.2508 | -0.0485 | -0.3765 | -0.4361 | -0.5129 | -0.6382 | -0.2497 |
| 8,8 | 0.0720 | 0.1452 | 0.2171 | 0.3005 | 0.3753 | 0.3195 | -0.0276 | -0.3893 | -0.5170 | -0.6660 | -0.1329 |
| 9,9 | 0.1943 | 0.2506 | 0.3196 | 0.3925 | 0.4551 | 0.3996 | 0.2308 | -0.0801 | -0.2369 | -0.4624 | 0.0585 |
| 10,10 | 0.6334 | 0.6442 | 0.6549 | 0.6688 | 0.6770 | 0.7723 | 0.7907 | 0.7566 | 0.4373 | 0.1124 | 0.5745 |
| कुल | 0.0927 | 0.1262 | 0.1628 | 0.2025 | 0.2390 | 0.1453 | 0.0585 | -0.0403 | -0.1727 | -0.3712 | -0.0058 |
अपेक्षित मूल्य में अंतर (% में)
निम्नलिखित तालिका प्रतिशत के आधार पर एकल-डेक खेल में आठ-डेक खेल को घटाकर अपेक्षित मूल्य दर्शाती है।
खिलाड़ी के हाथ बनाम डीलर के अप कार्ड द्वारा अपेक्षित मूल्यों में परिवर्तन (x100)
| खिलाड़ी | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ऐस | कुल |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.196 | -0.383 | 1.834 | 4.02 | 2.229 | 0.05 | 0.664 | 0.361 | 0.087 | -1.52 | 0.22 |
| 6 | -0.8770 | 0.0480 | 1.5840 | 3.9030 | 2.8630 | -1.0640 | -1.5170 | -1.0490 | -1.1320 | -2.4330 | -0.7380 |
| 7 | -0.2560 | 0.5920 | 2.7210 | 5.3240 | 3.3400 | -0.0070 | -1.1090 | -0.8160 | -1.3150 | -2.3840 | -0.4720 |
| 8 | 0.6060 | 1.2300 | 3.9870 | 6.3300 | 4.1900 | 0.9040 | 0.3020 | -0.3070 | -0.5740 | -2.1370 | 0.2910 |
| 9 | 3.8080 | 6.4600 | 9.1610 | 11.7320 | 6.5770 | 2.0670 | 1.1320 | 0.0300 | 0.1480 | -1.8380 | 2.2220 |
| 10 | 6.0970 | 7.3170 | 7.8980 | 10.2270 | 5.1830 | 4.6820 | 2.4980 | 1.7530 | 0.0720 | -1.2510 | 2.6040 |
| 11 | 6.4200 | 6.5830 | 7.5650 | 9.0560 | 4.8030 | 1.3220 | -0.7900 | -0.3170 | -1.9460 | 4.4940 | 1.7050 |
| 12 | 0.1670 | 0.7540 | 1.2640 | 2.4890 | 0.1350 | -1.2760 | -1.8390 | -2.0880 | 0.9840 | -0.7830 | 0.1460 |
| 13 | -0.1260 | 0.5070 | 2.1460 | 2.6670 | 0.0210 | -1.4780 | -1.9700 | 0.9410 | 0.9190 | -0.5660 | 0.3180 |
| 14 | -0.2970 | 0.6510 | 1.9930 | 2.6980 | 0.0150 | -2.0210 | 0.9460 | 1.0330 | 1.0240 | -0.2860 | 0.5000 |
| 15 | 0.5560 | 0.7690 | 1.9570 | 2.2820 | -0.4950 | 0.9270 | 0.2900 | 0.1190 | 0.2470 | -0.7990 | 0.3400 |
| 16 | 0.0300 | 0.1700 | 1.6680 | 1.8640 | -2.1330 | 3.4380 | 2.9220 | 2.6000 | 2.3870 | 0.8060 | 1.4950 |
| 17 | -0.0300 | -0.1100 | 1.0720 | 0.1630 | -2.1630 | -1.3190 | -1.3380 | 0.6910 | 0.7130 | 0.7580 | 0.1060 |
| 18 | -0.2560 | -0.2000 | -1.0990 | 0.2950 | -1.7950 | -0.9490 | -0.8890 | -1.1420 | 1.5210 | 0.9900 | 0.2340 |
| 19 | -0.1730 | -1.7470 | -1.7360 | 0.7660 | -1.4910 | -0.5200 | -1.4980 | -2.0590 | 2.7370 | 1.6770 | 0.7460 |
| ए,2 | -0.5660 | -0.2590 | 1.3280 | 7.5340 | 4.3080 | -1.3290 | -1.3120 | 2.0900 | 2.4910 | -2.0210 | 2.1220 |
| ए,3 | -0.4090 | -0.6000 | 3.0040 | 6.7580 | 3.8040 | -1.6410 | 1.9440 | 1.3040 | 2.4300 | -1.7440 | 2.2470 |
| ए,4 | -0.9750 | -0.5720 | 2.5100 | 4.2580 | 2.0490 | -0.2980 | -0.7230 | -0.1290 | 1.3080 | -2.5210 | 1.0610 |
| ए,5 | -0.8730 | -1.0720 | 0.5650 | 1.8950 | 3.2330 | -1.6930 | -1.5280 | -1.5890 | -0.6930 | -3.6740 | -0.3690 |
| ए,6 | 1.4820 | 1.8480 | 3.2870 | 8.7240 | 1.1650 | 0.5180 | 0.7480 | 1.3090 | 1.7920 | -1.8340 | 2.0600 |
| ए,7 | 1.1920 | 1.1830 | 6.7250 | 4.8180 | 0.6310 | 1.0410 | 1.3420 | 1.1640 | 1.4890 | -2.2860 | 1.8940 |
| ए,8 | 1.5370 | 1.6390 | -0.5690 | 2.0370 | 0.4540 | -0.1320 | 1.2540 | 0.0390 | 1.5550 | -1.4310 | 1.0640 |
| ए,9 | 1.5370 | -0.3990 | -0.5560 | 1.1160 | -0.4780 | 0.0020 | -0.6060 | 0.6480 | 2.1530 | -1.2700 | 1.1970 |
| ए,10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0730 | 0.2070 | 1.3970 |
| ए,ए | 3.1200 | 3.0230 | 3.5450 | 4.8720 | 2.3070 | 0.0000 | -1.3620 | -0.2430 | 0.2140 | -0.6920 | 3.3340 |
| 2,2 | 4.4790 | 4.8510 | 5.3790 | 13.1380 | 7.3480 | 0.4980 | 1.6370 | 1.6100 | 0.7540 | -1.3140 | 2.8470 |
| 3,3 | 2.2320 | 2.7290 | 11.0750 | 15.4710 | 9.7010 | 0.7020 | -0.4300 | -1.5380 | -0.8700 | -2.4920 | 2.1250 |
| 4,4 | 0.8840 | 1.8800 | 9.1320 | 16.1400 | 9.5290 | 2.4760 | 0.4550 | 0.3380 | 0.0090 | -1.4460 | 2.2100 |
| 5,5 | 7.6550 | 8.7410 | 11.2230 | 16.0940 | 12.6990 | 6.5150 | 3.1720 | 2.6130 | 0.2380 | -1.1510 | 3.7020 |
| 6,6 | 9.8410 | 11.0360 | 14.1250 | 17.1060 | 0.9170 | 2.5610 | -4.4720 | -4.0910 | -0.7110 | -2.2180 | 1.8060 |
| 7,7 | 6.8730 | 8.2850 | 12.1030 | 6.7540 | -1.1240 | -0.3840 | -0.3830 | -3.8370 | -4.2660 | -4.0800 | -0.1170 |
| 8,8 | 4.4530 | 4.2080 | 0.7370 | 2.8160 | -2.4470 | -1.5490 | -3.2240 | -1.2460 | 2.4110 | 2.7050 | 1.0500 |
| 9,9 | 1.0910 | -3.5070 | -1.2560 | 1.3820 | -4.7120 | 0.1480 | -2.4060 | -1.8530 | 3.2860 | 1.0450 | 0.8060 |
| 10,10 | -1.1490 | -1.1970 | -1.4750 | 0.2960 | -0.8740 | -0.7630 | -0.7510 | -1.2620 | 1.6580 | 2.5910 | 0.5780 |
| कुल | 0.9370 | 1.2510 | 2.3110 | 3.6590 | 0.8050 | 0.1970 | -0.3390 | -0.3210 | 0.1480 | -1.7900 | 0.5620 |
अग्रिम पठन
पीटर ग्रिफिन द्वारा लिखित 'द थ्योरी ऑफ़ ब्लैकजैक' इस लेख के विषय पर अब तक का सबसे बेहतरीन विवरण प्रस्तुत करता है। उन्होंने अध्याय 8 में इस विषय पर चर्चा की है, जिसका शीर्षक है: "कई डेक और अलग-अलग नियम", जो नियमों के एक अलग आधारभूत सेट का उपयोग करता है और एक डेक और अनगिनत डेक के बीच के अंतर की गणना करता है। वह हमेशा हर चीज़ के लिए सटीक संख्याएँ नहीं देते, लेकिन अपनी मान्यताओं के आधार पर 0.69% अंतर के विभाजन को इस प्रकार व्यक्त करते हैं:
- दोगुना वृद्धि: 0.69% का लगभग आधा
- खिलाड़ी ब्लैकजैक: 0.07%
- स्प्लिटिंग: ब्लैकजैक के लाभ से कहीं अधिक
- 12 से 16 पर खड़े होकर: “संभवतः शेष विसंगति।”
ग्रिफिन ने एक डेक और अनंत डेक दोनों के तहत विभिन्न नियम परिवर्तनों के लाभ की सूची दी है।
स्वीकृतियाँ
मैं इस लेख के विश्लेषण और प्रूफरीडिंग पर उनके बुद्धिमान परामर्श के लिए डॉन स्लेसिंगर को धन्यवाद देना चाहूंगा।


