खेल - अक्सर पूछे जाने वाले प्रश्न
वर्गास और क्वार्टी के बीच मुक्केबाजी मैच के लिए वर्तमान ऑड्स वर्गास के लिए -240 और क्वार्टी के लिए +190 हैं। अगर मैं वर्गास के लिए $100 या क्वार्टी के लिए $100 लगाऊँ तो यह कैसे काम करेगा?
वर्गास पर $240 का दांव लगाने पर $100 का इनाम मिलेगा। क्वार्टी पर $100 का दांव लगाने पर $190 का इनाम मिलेगा। बेशक, आप कितनी भी राशि का दांव लगा सकते हैं, लेकिन जीत का अनुपात समान ही रहेगा। अगर आप वर्गास पर $100 का दांव लगाते हैं, तो आप $100 × (100/240) = $41.67 जीतेंगे।
मुझे लगता है कि स्प्रेड के विरुद्ध खेलों में सट्टेबाज़ी में, जीतने वाला 10% कमीशन देता है, हारने वाला नहीं। मैं क्या भूल रहा हूँ?
आप इसे दोनों तरह से देख सकते हैं। उदाहरण के लिए, मान लीजिए कि आप किसी खेल में $10 जीतने के लिए $11 का दांव लगाते हैं।
हारने वाला भुगतान करता है: यह एक सम-धन वाली शर्त है, जिसमें जीतने पर $1 का शुल्क वापस मिलता है। इसलिए, केवल हारने वाले को ही शुल्क देना पड़ता है।
विजेता भुगतान करता है: एक निष्पक्ष सम-धन वाली शर्त पर $11 की शर्त पर $11 की जीत होगी। हालाँकि, अगर शर्त जीत जाती है, तो विजेता को केवल $10 मिलते हैं। छूटे हुए डॉलर को कमीशन या शुल्क के रूप में देखा जा सकता है।
व्यक्तिगत रूप से, मैं इसे 4.54% हाउस एज के रूप में भुगतान के रूप में देखता हूं, यह मानते हुए कि जीतने की संभावना 50% है।
क्या नेवादा के अलावा कोई अन्य राज्य है, जहां बेसबॉल और फुटबॉल जैसे पेशेवर खेलों पर दांव लगाना कानूनी है?
नेवादा के अलावा, खेलों पर सट्टा लगाने वाला एकमात्र राज्य डेलावेयर है। उस राज्य में यह लॉटरी के ज़रिए होता है, इसलिए संभावनाएँ काफ़ी कम हैं।
मैं हाल ही में एक फुटबॉल पूल देख रहा था जो चल रहा था। यह उनमें से एक था जहाँ 100 बॉक्सों का एक ग्रिड था और 0-9 तक के अंक X और Y अक्षों पर चलते थे और स्कोर के अंतिम अंक के अनुरूप थे। मैं फुटबॉल का प्रशंसक नहीं हूँ और मैंने इस पूल पर दांव नहीं लगाया था, लेकिन मैं एक जुआरी हूँ और मुझे नहीं लगता कि यह कोई बहुत अच्छा दांव है।
मैं यह मानकर चल रहा हूँ कि आप उस पूल के प्रकार को जानते हैं जिसकी मैं बात कर रहा हूँ। प्रत्येक बॉक्स की कीमत $5 है और भुगतान प्रत्येक तिमाही में होता है। अगर आपका बॉक्स जीतता है, तो आप $125 जीतेंगे और अगर आखिरी संख्याएँ समान रहती हैं, तो सभी 4 तिमाहियाँ जीतना संभव है, यानी $500 जीतना, यानी 100 से 1 का भुगतान।
शर्त लगाने वाला व्यक्ति मुझे यह बताने की कोशिश कर रहा था कि 500 डॉलर जीतने की संभावना 100 से 1 है। मैं इससे सहमत नहीं हूँ। सबसे पहले, जिस बॉक्स में 0 + 7 है, उसके जीतने की संभावना 2 + 9 वाले बॉक्स से कहीं ज़्यादा है। हालाँकि, पूरे खेल में आखिरी 2 नंबर 0 + 7 रहने की संभावना ज़्यादा होनी चाहिए। अगर आपके लिए बॉक्स यादृच्छिक प्रक्रिया से चुने जाते हैं, तो क्या आप मुझे 500 डॉलर का इनाम जीतने की अनुमानित संभावना बता सकते हैं?
यह मानते हुए कि ग्रिड में सेल यादृच्छिक रूप से चुने गए हैं, किसी एक तिमाही में जीतने की संभावना 1/100 होगी। यह मानते हुए कि प्रत्येक तिमाही एक स्वतंत्र घटना थी, जो कि नहीं है, सभी चार तिमाहियों में जीतने की संभावना (1/100) 4 = 100 मिलियन में 1 होगी।
अभी-अभी आपका नवीनतम 'जादूगर से पूछो' अनुभाग पढ़ा। आपने कहा था कि खेलों पर सट्टा लगाना जीविकोपार्जन का एक ज़रिया हो सकता है। क्या आप इसे थोड़ा विस्तार से बता सकते हैं? क्या इसमें सट्टेबाज़ों पर वैसी ही बढ़त है जैसी कार्ड काउंटिंग वाले ब्लैकजैक में कैसीनो पर है? धन्यवाद।
दुर्भाग्य से मैं ज़्यादा विस्तार से नहीं बता सकता। खेल सट्टेबाजी मेरी खासियत नहीं है, हालाँकि समय मिलने पर मैं इसके बारे में और जानने की योजना बना रहा हूँ। मैं कहूँगा कि खेल सट्टेबाजी के मुनाफ़े की तुलना कार्ड गिनने से करना मुश्किल है। कार्ड गिनना बहुत तकनीकी और नियम-कायदे से किया गया काम है। खेल सट्टेबाजी से पैसा कमाने के लिए ज़्यादा सोच-विचार की ज़रूरत होती है और यह ज़्यादातर राय पर निर्भर करता है। खेल सट्टेबाजी से पैसा कमाने के लिए कई तरह की रणनीतियाँ अपनाई जा सकती हैं, उदाहरण के लिए, अलग-अलग कैसिनो में अलग-अलग पॉइंट स्प्रेड पर दोनों पक्षों को चुनकर खेलों में मध्यस्थता करना, असामान्य प्रस्ताव दांव का फ़ायदा उठाना, या सहसंबद्ध पार्ले का इस्तेमाल करना। खेल सट्टेबाजी में जीत के बारे में ज़्यादा जानकारी के लिए मैं स्टैनफोर्ड वोंग की 'शार्प स्पोर्ट्स बेटिंग' की सलाह दूँगा।
मैंने कई NFL हैंडीकैपर्स को अपनी जीत के प्रतिशत के बारे में शेखी बघारते देखा है। किसी रैंडम पिकर को 1, 3 और 5 सीज़न में 50%, 55% और 60% जीतने की क्या संभावना है?
निम्नलिखित तालिका 1 से 5 सीज़न तक प्रत्येक सीज़न में 1% की वृद्धि के साथ, 50% से 60% तक प्रत्येक प्रतिशत प्राप्त करने की संभावना दर्शाती है। यह 259 खेलों वाले सीज़न पर आधारित है। मैं यह भी मानता हूँ कि कुल प्रतिशत को नीचे की ओर पूर्णांकित किया गया है। उदाहरण के लिए, यदि किसी हैंडीकैपर ने 50.97% प्रतिशत के लिए 259 खेलों में से 132 चुने, तो उसे केवल 50% चुनने का श्रेय मिलेगा, क्योंकि उसने 51% तक पूरी तरह से नहीं पहुँचा। मुझे आश्चर्य नहीं होगा यदि ये शेखी बघारने वाले हैंडीकैपर अपने पक्ष में पूर्णांकित कर रहे हों।
एनएफएल में हैंडीकैपिंग प्रतिशत की संभावना
| अनुपात | 1 सीज़न | 2 सीज़न | 3 सीज़न | 4 सीज़न | 5 सीज़न |
| 0.5 | 0.5 | 0.517523 | 0.5 | 0.512393 | 0.5 |
| 0.51 | 0.354641 | 0.314437 | 0.282985 | 0.257059 | 0.234993 |
| 0.52 | 0.267178 | 0.178085 | 0.125486 | 0.101366 | 0.074229 |
| 0.53 | 0.160065 | 0.086589 | 0.049447 | 0.025155 | 0.015098 |
| 0.54 | 0.106982 | 0.035817 | 0.013066 | 0.004959 | 0.001926 |
| 0.55 | 0.053095 | 0.012519 | 0.002569 | 0.000687 | 0.000152 |
| 0.56 | 0.023385 | 0.00282 | 0.000373 | 0.000051 | 0.000007 |
| 0.57 | 0.012645 | 0.00067 | 0.000053 | 0.000003 | 0 |
| 0.58 | 0.00453 | 0.000133 | 0.000004 | 0 | 0 |
| 0.59 | 0.00213 | 0.000022 | 0 | 0 | 0 |
| 0.6 | 0.000617 | 0.000003 | 0 | 0 | 0 |
मैं NFL पूल पर आपकी राय जानना चाहता/चाहती हूँ। प्रत्येक टिकट की कीमत $25 है और इसमें तीन यादृच्छिक टीमें, एक निश्चित क्रम में, शामिल हैं। हर हफ़्ते, सही क्रम में, सबसे ज़्यादा तीन स्कोर करने वाली टीमों वाला टिकट धारक $1000 जीतता है। प्रत्येक टिकट का वास्तविक मूल्य क्या है?
एनएफएल सीज़न में 17 नियमित हफ़्ते होते हैं और 32 टीमें होती हैं। किसी भी हफ़्ते जीतने की संभावना 32*31*30 में 1 = 29760 है। प्रत्येक टिकट का अपेक्षित मूल्य $1000*17/29760 = 57.12 सेंट है। इसलिए अपेक्षित रिटर्न 2.28% है, यानी हाउस एज 97.72%!
जैसा कि आपके वेब पेज पर कहा गया है, आपको परेशान करने के लिए क्षमा करें, लेकिन क्या आपने खेल सट्टे पर बाधाओं में विसंगतियों को खोजने के लिए अपने गणितीय कौशल का उपयोग किया है, या उस जानकारी के आधार पर गारंटीकृत रिटर्न प्राप्त करने का कोई तरीका निकाला है?
पिछले कुछ सालों से मैं खेल सट्टेबाजी में काफ़ी समय बिता रहा हूँ, किसी भी अन्य प्रकार के जुए से कहीं ज़्यादा। जब तक आप दो खेल सट्टेबाजी को अलग-अलग लाइनों के ज़रिए एक-दूसरे के ख़िलाफ़ नहीं खेल सकते, जो कि एक बहुत ही दुर्लभ अवसर है, खेल सट्टेबाजी से पैसे कमाने के कोई गारंटीशुदा जीतने के तरीके नहीं हैं। अभी कोई राज़ खोलना जल्दबाजी होगी, लेकिन मैं खिलाड़ी के फ़ायदे वाले किसी भी संभावित दांव पर नज़र रखता हूँ और फिर अपना दांव लगाता हूँ। आपको मेरे खेल सट्टेबाजी परिशिष्ट 2 में हाल ही में दी गई कुछ जानकारी देखना पसंद आएगा।
यदि किसी विश्वविद्यालय की फुटबॉल टीम के पास खेल 1 जीतने की 10% संभावना है और खेल 2 जीतने की 30% संभावना है, तथा दोनों खेल हारने की 65% संभावना है, तो उनके एक बार जीतने की संभावना क्या है?
अगर हम मान लें कि दोनों खेल स्वतंत्र हैं, तो दोनों में हारने की संभावना 90%*70%=63% होगी। लेकिन चूँकि आप कह रहे हैं कि दोनों में हारने की संभावना वास्तव में 65% है (जो कि 63% से ज़्यादा है), इसका मतलब है कि दोनों घटनाएँ परस्पर संबंधित हैं। अगर दोनों में हारने की संभावना 65% है और सिर्फ़ दूसरा खेल हारने की संभावना 70% है, तो पहला खेल जीतने और दूसरा खेल हारने की संभावना 5% होनी चाहिए। इसी तर्क से, पहला खेल हारने और दूसरा खेल जीतने की संभावना 25% होनी चाहिए। यानी दोनों खेल जीतने की संभावना केवल 5% बचती है। इसलिए ठीक एक बार जीतने की संभावना 25%+5% = 30% है।
मेरा सवाल आज रात होने वाले सोमवार के फ़ुटबॉल मैच (डलास बनाम वाशिंगटन) के बारे में था। वाशिंगटन में पिछले कुछ घंटों से बारिश हो रही है। यह बारिश मैच के दौरान और अगले दिन भी जारी रहेगी। मैं जानना चाहता था कि बारिश का ओवर/अंडर NFL बेट पर क्या असर होगा? क्या आप मुझे कोई ट्रेंड या कोई और सलाह दे सकते हैं?
मुझे बारिश का कुल योग पर क्या असर पड़ता है, यह तो नहीं पता। हालाँकि, मुझे इतना ज़रूर पता है कि तेज़ हैंडीकैपर मौसम को बहुत गंभीरता से लेते हैं और तापमान, वर्षा, हवा की गति वगैरह को ध्यान में रखते हुए रेखा को आगे-पीछे करते हैं।
हाय विज़, मान लीजिए मैं एक खेल सट्टेबाजी प्रणाली बनाता हूँ जिसमें $1,000 के दांव से $80,000 प्रति वर्ष का रिटर्न मिलता है। इस रिटर्न के लिए प्रति वर्ष लगभग 250-300 दांव लगाने पड़ते हैं। क्या खेल सट्टेबाजी वाले अंततः मुझे भी उसी तरह प्रतिबंधित कर देंगे जैसे कैसीनो कार्ड काउंटरों पर प्रतिबंध लगाते हैं? क्या आप खुलेआम एक सफल खेल सट्टेबाज बन सकते हैं, या आपको कार्ड काउंटर की तरह चुपचाप घूमना होगा?
सबसे पहले, मुझे शक है कि कोई भी 1 हज़ार के दांव और सिर्फ़ 250-300 के बैंकरोल से 80 हज़ार कमा सकता है। और "सिस्टम" शब्द के बारे में तो बात ही मत कीजिए। आपके सवाल का जवाब देने के लिए, ज़्यादातर बेहतरीन खेल सट्टेबाज़ खुलेआम सट्टेबाजी करते हैं। अगर कोई खेल सट्टेबाजी की किताब किसी पेशेवर खिलाड़ी के दांव लगाने पर रोक लगा भी दे या उन्हें संपत्ति से वंचित कर दे, तो भी किसी और से सट्टेबाजी करवाना आसान होगा। फिर एक बार मैं एक पेशेवर जुआरी, फेज़िक द्वारा आयोजित सुपर बाउल प्रस्ताव सट्टे के सेमिनार में गया था, और उसने हैलोवीन मास्क पहनकर अपनी प्रस्तुति दी थी।
क्या आपके पास सुपर बाउल पूल में अंतिम अंक चुनने के लिए कोई सलाह है?
मैंने जिन ऑफिस पूल्स को देखा है, वे हर पंक्ति और कॉलम को एक यादृच्छिक अंक देकर तालिकाओं को यादृच्छिक बनाते हैं। हालाँकि, अगर आप वास्तविक अंतिम अंक चुन सकते हैं, तो नीचे दी गई तालिका 1983 से 2003 तक के हर NFL खेल के आधार पर, किसी भी टीम के अंतिम स्कोर के लिए प्रत्येक अंतिम अंक की आवृत्ति दर्शाती है।
प्रति पक्ष एनएफएल टर्मिनल अंक
अंक | आवृत्ति | संभावना |
0 | 1887 | 17.75% |
1 | 1097 | 10.32% |
2 | 348 | 3.27% |
3 | 1382 | 13.00% |
4 | 1608 | 15.13% |
5 | 396 | 3.73% |
6 | 848 | 7.98% |
7 | 1945 | 18.30% |
8 | 631 | 5.94% |
9 | 488 | 4.59% |
कुल | 10630 | 100% |
अतः यह तालिका दर्शाती है कि 7 सर्वोत्तम विकल्प है, उसके बाद 0, 4 और 3 हैं।
मुझे आपके "एनएफएल पिक्स" संख्यात्मक मॉडल के बारे में और विस्तार से जानना अच्छा लगेगा। अगर आप इसका इस्तेमाल वास्तव में दांव लगाने के लिए करने लगें, तो क्या इसे "सट्टेबाजी प्रणाली" नहीं कहा जाएगा?
उनमें से कुछ मुझे दूसरों से ज़्यादा पसंद हैं। मेरा मॉडल हर खेल में एक उचित फैलाव का अनुमान लगाता है और मैं उन खेलों को सूचीबद्ध करता हूँ जिनमें एक निश्चित संख्या से ज़्यादा अंकों का अंतर होता है। व्यक्तिगत रूप से, मैं ज़्यादा अंतर वाले खेलों पर ज़्यादा दांव लगाता हूँ। हालाँकि, जब तक मैं यह साबित नहीं कर देता कि मेरे चुनाव सही हैं, मुझे लगता है कि आत्मविश्वास की डिग्री पोस्ट करना दिखावा होगा।
आपके एनएफएल चयनों के संबंध में, क्या उन सभी का भार समान है, अर्थात्, क्या आपके मॉडल के अनुसार कोई भी चयन अन्य की तुलना में अधिक मजबूत है?
उनमें से कुछ मुझे दूसरों से ज़्यादा पसंद हैं। मेरा मॉडल हर खेल में एक उचित फैलाव का अनुमान लगाता है और मैं उन खेलों को सूचीबद्ध करता हूँ जिनमें एक निश्चित संख्या से ज़्यादा अंकों का अंतर होता है। व्यक्तिगत रूप से, मैं ज़्यादा अंतर वाले खेलों पर ज़्यादा दांव लगाता हूँ। हालाँकि, जब तक मैं यह साबित नहीं कर देता कि मेरे चुनाव सही हैं, मुझे लगता है कि आत्मविश्वास की डिग्री पोस्ट करना दिखावा होगा।
क्या आप दिल से पैकर्स के प्रशंसक हैं? मैं हूँ। ऐसा लग रहा है कि आप दिल से दांव लगा रहे हैं और पैकर्स आपके बेहतरीन एनएफएल पिक्स को बर्बाद कर रहे हैं। पैकर्स के न आने के बावजूद भी यह प्रतिशत बहुत अच्छा है। बस सोचा कि शायद आपको यह अवलोकन पसंद आएगा।
इसका कारण टीम की वफादारी से कोई लेना-देना नहीं है। मेरे प्रोग्राम ने 2004 सीज़न के अंत में उन्हें पाँचवीं सर्वश्रेष्ठ टीम का दर्जा दिया था, और मैं उस पावर रेटिंग को 2005 सीज़न में भी जारी रखूँगा। हालाँकि, हो सकता है कि हाल के इतिहास पर प्रतिक्रिया देने में यह बहुत धीमा हो। यह मेरे लिए सोचने वाली बात है।
मैंने देखा कि कोई व्यक्ति 100 खेलों में 57% स्प्रेड चुनने वाले खिलाड़ी के खिलाफ 2-1 का दांव लगा रहा था। हालाँकि मुझे लगता है कि 57% एक मुश्किल संख्या है, लेकिन छोटे सैंपल साइज़ को देखते हुए मुझे लगता है कि यह एक अच्छा दांव हो सकता है। मेरा सवाल यह है - अगर कोई बेटर 50% लाइफटाइम पिकर होता, विग और टाई (यानी सिक्का उछालने की स्थिति) को नज़रअंदाज़ करते हुए, तो क्या यह एक अच्छा दांव होगा? अगर नहीं, तो पिकर के लिए इसे एक अच्छा सौदा बनाने के लिए कुल कितने प्रतिशत की ज़रूरत होगी?
2 से 1 वाले दांवों के लिए, सबसे बड़ा नमूना आकार जिसमें यह एक अच्छा दांव है, 14 गेम हैं। यादृच्छिक रूप से चुनने पर, आपके पास 57% या उससे बेहतर, या 8 या उससे अधिक सही चुनने की 39.5264% संभावना होगी। इसे एक अच्छा दांव बनाने के लिए आपके पास 33.3333% से बेहतर संभावना होनी चाहिए। 21 लगभग उचित है, लेकिन संभावना 33.1812% पर थोड़ी कम है। जितने अधिक चयनों की आवश्यकता होगी, आवश्यक प्रतिशत उतना ही कम होना चाहिए। उदाहरण के लिए, यदि 1000 चयनों की आवश्यकता है, तो जीतने की 1/3 से अधिक संभावना के लिए आवश्यक अधिकतम संख्या 507 होगी। 1000 चयनों में 507 या उससे अधिक सही होने की संभावना 34.05% है।
मैं लंबे समय से फ़ुटबॉल का प्रशंसक और जुआरी हूँ। मुझे फ़ुटबॉल के लिए आपके संख्यात्मक मॉडल में बहुत दिलचस्पी है और मैं अपना खुद का मॉडल बनाने की कोशिश कर रहा हूँ क्योंकि मुझे पहले से ही पता है कि मैं सिर्फ़ अपने ज्ञान के आधार पर फ़ुटबॉल पर सट्टा नहीं जीत सकता (मैंने कोशिश की है)। इसलिए मैंने एक सांख्यिकीय दृष्टिकोण आज़माने का सोचा। मैं सांख्यिकीय प्रोग्राम SPSS का उपयोग कर रहा हूँ। मेरा आपसे प्रश्न है कि आप अपने मॉडल में किन चरों का उपयोग कर रहे हैं?
इस मॉडल में सिर्फ़ स्कोर और घरेलू मैदान का फ़ायदा ही शामिल होता है। कभी-कभी मैं बड़ी चोटों पर बाहरी राय लेता हूँ, जैसे कि छठे हफ़्ते में बेन रोथ्लिसबर्गर की चोट, या न्यू ऑरलियन्स का सैन एंटोनियो में घरेलू मैच खेलना।
जादूगर, आपका स्वागत है। अब आप सिर्फ़ Wizard of Odds ही नहीं, बल्कि अपने प्रदर्शन के आधार पर NFL पिक्स के भी जादूगर हैं। मैं कैसीनो पूल में सिर्फ़ 51.7% पर हूँ। मेरा एक छोटा सा अनुरोध है। क्या हर हफ़्ते सभी खेलों के लिए अपनी पसंद की सूची बनाना संभव है, अगर इसमें आपका ज़्यादा समय न लगे?
धन्यवाद। आपने शायद यह चौथे हफ़्ते से पहले भेजा था, जो मेरे लिए एक बुरा हफ़्ता था। अब, पाँच हफ़्तों के बाद मेरा रिकॉर्ड 17 और 13 है, यानी 56.7% औसत, जो अच्छा तो है, लेकिन बहुत अच्छा नहीं। मुझे लगता है कि अपने न्यूज़लेटर पाठकों के लिए एक बोनस के तौर पर मैं सभी खेलों पर अपने विचार ज़रूर दूँगा।
चूँकि अब आप फ़ुटबॉल खेल रहे हैं, इसलिए मेरे मन में पार्लेज़ के बारे में एक सवाल है। मैंने हाल ही में एक शर्त लगाई थी जिसमें मैंने स्टीलर्स/चार्जर्स एमएनएफ गेम के चारों क्वार्टर में ओवर/अंडर चुना और जीत गया। (सिर्फ़ क्वार्टर, हाफ या टोटल नहीं।) अब स्पोर्ट्स बुक भुगतान नहीं करेगी क्योंकि उनके अनुसार इसमें सहसंबंध है -- यानी एक क्वार्टर जीतने से दूसरे क्वार्टर जीतने की संभावना ज़्यादा हो जाती है। मेरा मानना है कि खेल का हर क्वार्टर परस्पर अनन्य होता है, लेकिन वे इस बात से सहमत नहीं हैं। जादूगर क्या सोचता है?
पहला, जिसने भी यह शर्त स्वीकार की है, उसे सिद्धांततः इसका सम्मान करना चाहिए। एक सज्जन व्यक्ति अपने ऋणों का सम्मान करता है, खासकर जुए के ऋणों का। दूसरा, हालाँकि मैंने इसका अध्ययन नहीं किया है, मुझे लगता है कि तिमाहियों का वास्तव में नकारात्मक सहसंबंध हो सकता है। उदाहरण के लिए, यदि पहले क्वार्टर का कुल योग कम है, तो यह अधिक संभावना है कि दूसरे क्वार्टर की शुरुआत में किसी भी टीम की फ़ील्ड स्थिति अच्छी होगी, और इस प्रकार दूसरे क्वार्टर में उच्च स्कोरिंग होने की संभावना होगी, और इसके विपरीत।
जादूगर, एनएफएल पिक्स के लिए मेरे "असली" जीत प्रतिशत के बारे में मेरा एक सवाल है। मैं अपने दोस्तों को बताता हूँ कि पिछले 5 सालों से मेरा कोई भी सीज़न हार का नहीं रहा है (जो कि सच है), मैं हफ़्ते 3-16 तक औसतन 2-3 पिक्स के साथ सट्टा लगाता हूँ। मेरी बात यह है कि मुझे खेलों की अच्छी समझ है और मैं उन खेलों में काफ़ी ज़्यादा दांव लगाता हूँ जहाँ मुझे लगता है कि ऑड्स मेरे पक्ष में हैं। उदाहरण के लिए, मैंने इस साल 9 दांव लगाए हैं, जिनमें से 4 $55 के थे, और उनमें से 3 पिक्स पर जीत हासिल की है। मैंने $110 के 3 दांव लगाए हैं, जिनमें से 1 में जीत हासिल की है। लेकिन मुझे दो खेल बहुत पसंद आए, जिनमें मैंने एक पर $330 और एक पर $600 (सम रेखा) का दांव लगाया, और दोनों में जीत हासिल की। बिल्कुल, मेरे 9 में से 6 दांव 66% क्लिप के लिए हैं, लेकिन चूँकि मैंने उन खेलों पर दांव लगाया जिनके बारे में मुझे ज़्यादा यकीन था, इसलिए यह वास्तव में लगभग 80% क्लिप (पैसे के हिसाब से) दर्शाता है। क्या यह आपको समझ में आता है? पिछले 5 सालों में मैंने मोटे तौर पर यही किया है, जब मैंने इसकी गणना की (चुनावों में 60-70%, लेकिन दांव पर लगाई गई राशि को ध्यान में रखते हुए लगभग 80%)। क्या आप मुझे दांव की राशि को ध्यान में रखने का कोई आसान तरीका बता सकते हैं, और क्या मैं अपनी धारणाओं में सही हूँ? बहुत-बहुत धन्यवाद।
मैं हाल ही में इस बारे में काफ़ी सोच रहा हूँ। मेरी राय में, जीत प्रतिशत का हर मैच में बराबर वज़न होना चाहिए। आपके पास अपने निवेश पर कुल रिटर्न का एक अलग आँकड़ा भी होना चाहिए, हालाँकि किसी भी आँकड़े के साथ टीम, तारीख, लाइन स्रोत, पॉइंट स्प्रेड और ऑड्स (आमतौर पर -110) की सूची होनी चाहिए। एक और मुद्दा जो आप नहीं उठाते, वह यह है कि अगर आपको 3 या 7 पॉइंट स्प्रेड पर -120 लगाना पड़े तो क्या करें। अगर आप अपनी पसंद के दांवों में ऐसे दांव लगाएँ तो अच्छा जीत प्रतिशत हासिल करना आसान होगा। इसलिए मेरा मानना है कि फ्लैट बेटिंग के बावजूद भी निवेश पर रिटर्न का आँकड़ा रखा जाना चाहिए। एक और बात जो मुझे कुछ दूसरे हैंडीकैपर्स के बारे में परेशान करती है, वह यह है कि वे ऐसी लाइनें बताते हैं जो कहीं दिखाई नहीं देतीं। मुझे लगता है कि थोड़ा इधर-उधर देखना ठीक है, लेकिन बताई गई लाइनें ढूँढ़ना मुश्किल नहीं होना चाहिए। मैं मानता हूँ कि मैं इस सीज़न में इनमें से कुछ चीज़ें खुद नहीं कर रहा हूँ, क्योंकि शुरुआत में मैंने इनके बारे में नहीं सोचा था। अगले साल, अगर मैं फिर से ऐसा करूँगा, तो मैं अपने नतीजों को भी एक निवेश के रूप में दर्ज करूँगा।
क्या आप अपने एनएफएल चयनों पर मनी लाइन या स्प्रेड खेलने की सलाह देते हैं या इससे कोई फर्क नहीं पड़ता?
दांव लगाने का कारण चाहे जो भी हो, सामान्य तौर पर, धन रेखा पर कमजोर पक्ष पर तथा प्रसार के विरुद्ध पसंदीदा पक्ष पर दांव लगाना बेहतर होता है।
मैं हमेशा से खुद NFL हैंडीकैपिंग करना चाहता था, लेकिन मुझे टीम के अनुसार ऐतिहासिक डेटा डाउनलोड करने के लिए कोई वेबसाइट, शायद मुफ़्त, ढूँढ़ने में मुश्किल हो रही है। कोई सुझाव? डाउनलोड करने योग्य फ़ाइलें मेरी प्राथमिकता होंगी क्योंकि वेब पेज से काटकर पेस्ट करना व्यावहारिक नहीं है, लेकिन ज़रूरत पड़ने पर मैं ऐसा करने को तैयार हूँ। इसके अलावा, मौसम और मैदान की स्थिति जैसी जानकारी भी बहुत मददगार होगी।
निजी तौर पर, मैं मिस्टर एनएफएल का एनएफएल एक्सेस डेटाबेस इस्तेमाल करता हूँ, जिसकी कीमत 99 डॉलर है। अगर इससे कम कीमत में भी कोई चीज़ इतनी अच्छी है, तो मुझे उसकी जानकारी नहीं है।
ऐसा लगता है कि आपके NFL चयनों का सिस्टम कमज़ोर टीम पर ज़्यादा ज़ोर दे रहा है। 49 में से सिर्फ़ 8 खेलों में ही आप पसंदीदा टीम चुनते हैं। एक में आप बराबरी की स्थिति वाली टीम चुनते हैं। क्या यह आपके सिस्टम की खामी है या लोग पसंदीदा चुनने में ज़्यादा रुचि रखते हैं और आपका सिस्टम उनकी इसी प्रवृत्ति का फ़ायदा उठाने की कोशिश कर रहा है? मैंने कोई विश्लेषण नहीं किया, लेकिन मेरे अवलोकन से ऐसा लगता है कि स्प्रेड रेंज में बहुत कम दांव बिना टीम के वास्तव में गेम जीते ही जीत जाते हैं।
ऐतिहासिक रूप से देखा जाए तो अंडरडॉग्स ज़्यादा बेहतर दांव होते हैं। 1983 सीज़न की शुरुआत से लेकर 2005 सीज़न के 10वें हफ़्ते तक खेले गए हर मैच के नतीजे यहां दिए गए हैं।
पसंदीदा खिलाड़ी स्प्रेड के विरुद्ध जीतता है: 2554 गेम
अंडरडॉग स्प्रेड के खिलाफ जीतता है: 2724 गेम
खेल ठीक उसी समय समाप्त होता है जब प्रसार 150 गेम होता है
इसलिए तय किए गए दांवों में, कमज़ोर पक्ष 51.61% बार जीतता है। यह भी सर्वविदित है कि वर्गाकार दांव लगाने वाले पसंदीदा पर दांव लगाना पसंद करते हैं, जिससे कमज़ोर पक्ष पर मूल्य बनता है।
इस साल हमारे "फुटबॉल बेट टेकर" ने ओवर/अंडर बेट्स पर जूस को 10% से बढ़ाकर 20% कर दिया है, और पार्लेज़ पर 10% जूस हटा दिया है। इसलिए इस साल दो अलग-अलग ओ/यू बेट्स लगाने के बजाय, मैं 2.5 से 1 के पेऑफ़ पर दोनों बेट्स पर पार्लेज़ कर रहा हूँ। क्या यह एक अच्छी रणनीति है?
स्ट्रेट बेट्स पर अपेक्षित रिटर्न (0.5*1 + 0.5*(-1.2))/1.2 = -8.33% होगा। पार्ले पर अपेक्षित रिटर्न 0.25*2.5 + 0.75*-1 = -12.5% होगा। हालाँकि, अगर मुझे सिर्फ़ दो गेम पर दांव लगाना हो और मैं जीतना चाहता हूँ या कोशिश में हारना चाहता हूँ, तो मैं पार्ले ही चुनूँगा। इससे भी ज़रूरी बात यह है कि मैं सैद्धांतिक रूप से इस सट्टेबाज़ का बहिष्कार करूँगा, क्योंकि मैंने पहले कभी स्ट्रेट बेट्स पर -120 लगाने के बारे में नहीं सुना।
अपनी साइट के दो अलग-अलग खंडों में, आपने उल्लेख किया है कि आम तौर पर मनी लाइन के मुक़ाबले पसंदीदा टीमों की बजाय कमज़ोर टीमों पर दांव लगाना बेहतर होता है। हालाँकि, जैसा कि आपने अपने स्पोर्ट्स बेटिंग परिशिष्ट 3 में बताया है, पसंदीदा टीम पर दांव लगाने पर मनी लाइन हाउस एज कम होता है। क्या यह विरोधाभास नहीं है? क्या किसी भी प्रकार के दांव के लिए सबसे कम हाउस एज की तलाश करना सही नहीं है?
अच्छी बात है। इस पर थोड़ा विचार करने के बाद, मैंने अपने खेल सट्टेबाजी परिशिष्ट 3 को हटाने का फैसला किया है। यह इस धारणा पर आधारित था कि फेयर लाइन दो मनी लाइनों के ठीक बीच में होती है। उदाहरण के लिए, पिछले सुपर बाउल में मनी लाइन आम तौर पर सिएटल +160 और पिट्सबर्ग -180 थीं। मेरा परिशिष्ट इस अवास्तविक धारणा पर आधारित था कि फेयर मनी लाइन +/- 170 होगी। वास्तव में मनी लाइन बाजार द्वारा संचालित होती हैं। मनी लाइन पर चौकोर कार्रवाई पसंदीदा के पक्ष में होती है, जिससे अंडरडॉग पर मूल्य बनता है। पिट्सबर्ग को 4-पॉइंट पसंदीदा के रूप में मानना उचित था, ऐतिहासिक डेटा बताता है कि 4-पॉइंट पसंदीदा के जीतने की लगभग 61% संभावना होती है। इससे सिएटल पर फेयर मनी लाइन +156 और पिट्सबर्ग पर -156 हो जाती। आपको याद दिला दूँ कि ज़्यादातर कैसीनो में मनी लाइन +160/-180 पर थी। बेशक इस बार पिट्सबर्ग ने गेम जीत लिया, लेकिन ऐतिहासिक रूप से, मुझे यकीन है कि आप मनी लाइन पर पसंदीदा की तुलना में अंडरडॉग पर बेहतर दांव लगा पाएँगे।
मैं एनएफएल स्क्वेयर्स पूल में हूँ और मुझे बहुत अच्छे नंबर मिले हैं। पिट्सबर्ग के लिए 7 और 4, और सिएटल के लिए 4 और 0। मैं सोच रहा था कि इस साल मेरे जीतने की क्या संभावना है?
मेरे पाठकों के लिए, जो शायद प्रश्न को समझ नहीं पा रहे हों, सुपर बाउल पूल में 10 गुणा 10 का ग्रिड होता है। खिलाड़ी एक निश्चित राशि देकर खाने खरीदेंगे और प्रत्येक खाने पर खरीदार का नाम लिखेंगे। सभी 100 खाने खरीद लेने के बाद, पंक्तियों और स्तंभों को 0 से 9 तक बेतरतीब ढंग से शीर्षक दिए जाने चाहिए। यह 10 गुणा 10 की गुणन तालिका जैसा है, बस पंक्ति और स्तंभ के शीर्षक बेतरतीब ढंग से फेरबदल किए जाने चाहिए। फिर विजेता का निर्धारण करने के लिए प्रत्येक टीम के स्कोर के अंतिम अंक का उपयोग किया जाएगा। फेरबदल का कारण यह है कि कुछ अंतिम अंक दूसरों की तुलना में अधिक संभावित होते हैं, जैसा कि आप नीचे देखेंगे। उदाहरण के लिए, जिसके पास सिएटल 0, पिट्सबर्ग 1 वाला खाना होगा, वह पूल जीत जाएगा, क्योंकि अंतिम स्कोर सिएटल 10, पिट्सबर्ग 21 था।
निम्नलिखित तालिका 1983 से 2005 सीज़न तक प्रत्येक NFL खेल में प्रत्येक संयोजन की आवृत्ति दर्शाती है। यह ध्यान देने योग्य है कि 2-पॉइंट रूपांतरण नियम लगभग 1998 में आया था, जिससे वितरण को थोड़ा सुचारू करने में मदद मिली।
एनएफएल में टर्मिनल अंक - घर से दूर कुल योग
| दूर की टीम | घरेलू टीम | कुल | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 126 | 104 | 34 | 160 | 138 | 37 | 99 | 237 | 64 | 32 | 1031 |
| 1 | 73 | 40 | 17 | 41 | 103 | 21 | 36 | 117 | 67 | 31 | 546 |
| 2 | 25 | 15 | 1 | 20 | 30 | 9 | 13 | 33 | 9 | 12 | 167 |
| 3 | 194 | 69 | 33 | 66 | 102 | 40 | 102 | 132 | 43 | 40 | 821 |
| 4 | 122 | 133 | 27 | 78 | 108 | 27 | 48 | 215 | 59 | 35 | 852 |
| 5 | 32 | 12 | 12 | 21 | 21 | 9 | 13 | 36 | 22 | 5 | 183 |
| 6 | 91 | 47 | 17 | 75 | 57 | 7 | 28 | 57 | 25 | 39 | 443 |
| 7 | 217 | 115 | 35 | 135 | 195 | 47 | 65 | 125 | 69 | 47 | 1050 |
| 8 | 43 | 59 | 12 | 24 | 41 | 23 | 20 | 38 | 15 | 7 | 282 |
| 9 | 48 | 28 | 17 | 33 | 40 | 14 | 29 | 33 | 14 | 7 | 263 |
| कुल | 971 | 622 | 205 | 653 | 835 | 234 | 453 | 1023 | 387 | 255 | 5638 |
अगली तालिका उपरोक्त तालिका के योग के आधार पर प्रत्येक संयोजन की संभावना दर्शाती है।
एनएफएल में टर्मिनल अंक - घर से दूर होने की संभावना
| दूर की टीम | घरेलू टीम | कुल | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 0.0223 | 0.0184 | 0.006 | 0.0284 | 0.0245 | 0.0066 | 0.0176 | 0.042 | 0.0114 | 0.0057 | 0.1829 |
| 1 | 0.0129 | 0.0071 | 0.003 | 0.0073 | 0.0183 | 0.0037 | 0.0064 | 0.0208 | 0.0119 | 0.0055 | 0.0968 |
| 2 | 0.0044 | 0.0027 | 0.0002 | 0.0035 | 0.0053 | 0.0016 | 0.0023 | 0.0059 | 0.0016 | 0.0021 | 0.0296 |
| 3 | 0.0344 | 0.0122 | 0.0059 | 0.0117 | 0.0181 | 0.0071 | 0.0181 | 0.0234 | 0.0076 | 0.0071 | 0.1456 |
| 4 | 0.0216 | 0.0236 | 0.0048 | 0.0138 | 0.0192 | 0.0048 | 0.0085 | 0.0381 | 0.0105 | 0.0062 | 0.1511 |
| 5 | 0.0057 | 0.0021 | 0.0021 | 0.0037 | 0.0037 | 0.0016 | 0.0023 | 0.0064 | 0.0039 | 0.0009 | 0.0325 |
| 6 | 0.0161 | 0.0083 | 0.003 | 0.0133 | 0.0101 | 0.0012 | 0.005 | 0.0101 | 0.0044 | 0.0069 | 0.0786 |
| 7 | 0.0385 | 0.0204 | 0.0062 | 0.0239 | 0.0346 | 0.0083 | 0.0115 | 0.0222 | 0.0122 | 0.0083 | 0.1862 |
| 8 | 0.0076 | 0.0105 | 0.0021 | 0.0043 | 0.0073 | 0.0041 | 0.0035 | 0.0067 | 0.0027 | 0.0012 | 0.05 |
| 9 | 0.0085 | 0.005 | 0.003 | 0.0059 | 0.0071 | 0.0025 | 0.0051 | 0.0059 | 0.0025 | 0.0012 | 0.0466 |
| कुल | 0.1722 | 0.1103 | 0.0364 | 0.1158 | 0.1481 | 0.0415 | 0.0803 | 0.1814 | 0.0686 | 0.0452 | 1 |
हालाँकि सुपर बाउल में एक औपचारिक घरेलू टीम होती है, मुझे लगता है कि हम इसे नज़रअंदाज़ कर सकते हैं। आइए दोनों टीमों के बारे में सब कुछ नज़रअंदाज़ करें और ऊपर दिए गए ऐतिहासिक औसतों पर ही पूरी तरह से अमल करें। अंत में, इस तथ्य को नज़रअंदाज़ करें कि सुपर बाउल बराबरी पर समाप्त नहीं हो सकता, जिससे 4/4 जैसे मैच के जीतने की संभावना थोड़ी कम हो जाएगी। तो आइए एक औसत निकालें जब अंतिम अंक अलग हों। उदाहरण के लिए, आपके पिट्सबर्ग 7, सिएटल 4 वर्ग की प्रायिकता, अवे 7, होम 4 के औसत के बराबर होगी; और अवे 4, होम 7 के औसत के बराबर होगी। ऐसा करने से आपके प्रत्येक वर्ग के लिए निम्नलिखित प्रायिकता प्राप्त होगी।
पिट्स 7, सी 4: (0.0346+0.0381)/2 = 0.0364
पिट्स 7, सी 0: (0.0385+0.0420)/2 = 0.0403
पिट्स 4, सागर 4: 0.0192
पिट्स 4, सी 0: (0.0216+0.0245)/2 = 0.0231
तो इनमें से एक जीतने की आपकी कुल संभावना 11.90% है। यह मानते हुए कि आपने केवल 4% वर्ग ही अच्छे से कवर किए हैं।
हालाँकि आपने स्पष्ट रूप से नहीं पूछा, फिर भी यहाँ बताया गया है कि प्रत्येक टर्मिनल अंक कितनी बार आया। इससे पता चलता है कि कुल मिलाकर सबसे अधिक बार आने वाला क्रम 7043168952 है।
एनएफएल में टर्मिनल अंक - दूर और घरेलू कुल योग
| टर्मिनल अंक | दूर की टीम | घरेलू टीम | कुल |
|---|---|---|---|
| 0 | 1031 | 971 | 2002 |
| 1 | 546 | 622 | 1168 |
| 2 | 167 | 205 | 372 |
| 3 | 821 | 653 | 1474 |
| 4 | 852 | 835 | 1687 |
| 5 | 183 | 234 | 417 |
| 6 | 443 | 453 | 896 |
| 7 | 1050 | 1023 | 2073 |
| 8 | 282 | 387 | 669 |
| 9 | 263 | 255 | 518 |
अंत में, यहां प्रत्येक टर्मिनल अंक की संभावना दी गई है।
एनएफएल में टर्मिनल अंक - दूर और घरेलू संभावनाएं
| टर्मिनल अंक | दूर की टीम | घरेलू टीम | कुल |
|---|---|---|---|
| 0 | 0.1829 | 0.1722 | 0.1775 |
| 1 | 0.0968 | 0.1103 | 0.1036 |
| 2 | 0.0296 | 0.0364 | 0.033 |
| 3 | 0.1456 | 0.1158 | 0.1307 |
| 4 | 0.1511 | 0.1481 | 0.1496 |
| 5 | 0.0325 | 0.0415 | 0.037 |
| 6 | 0.0786 | 0.0803 | 0.0795 |
| 7 | 0.1862 | 0.1814 | 0.1838 |
| 8 | 0.05 | 0.0686 | 0.0593 |
| 9 | 0.0466 | 0.0452 | 0.0459 |
इस विषय पर अधिक जानकारी के लिए, फुटबॉल स्क्वेयर्स गणितीय और सांख्यिकीय रणनीति पर जाएं।
लोगों को यह गलतफहमी है कि वेगास में खेलों पर सट्टेबाज़ी की सीमाएँ बहुत ऊँची हैं, जो मेरे अनुभव में सिर्फ़ फ़ुटबॉल पर ही लागू होती है और हमेशा नहीं। क्या आप मुझे वेगास की खेल पुस्तकों में चार प्रमुख खेलों पर अनुमानित सीमाएँ बता सकते हैं? आपके समय के लिए धन्यवाद।
मैं हॉकी को कोई बड़ा खेल नहीं मानता क्योंकि इसमें बहुत कम खेल होते हैं। मुझे बताया गया है कि कोस्ट के कैसिनो में सबसे ज़्यादा सीमाएँ होती हैं। जहाँ तक मुझे पता है, कोई निश्चित सीमा नहीं है, लेकिन वे हर मामले के आधार पर बड़े दांव लगाते हैं। मुझे लगता है कि वे शायद एक औसत खेल के लिए यही सीमाएँ लेते होंगे।
एनएफएल पक्ष: $50,000
एनएफएल कुल: $5000
एमएलबी मनी लाइन: $10,000
एमएलबी कुल: $2000
एनबीए पक्ष: $10,000
एनबीए कुल: $2,000
कई ऑनलाइन किताबें हाफटाइम सट्टेबाजी की पेशकश करती हैं, इसलिए मैं "डचिंग" पर आपकी राय जानना चाहूँगा। कभी-कभी यह स्पष्ट होता है, लेकिन आप हाफटाइम में अपने खेल दांव के विपरीत दांव लगाने पर कब विचार करेंगे? और, अगर आपको अनुकूल स्थिति मिले तो आप कितनी राशि पर विचार करेंगे?
मुझे लगता है कि "डचिंग" से आपका मतलब हेजिंग से है। जुए के बारे में मेरी दस आज्ञाओं में से छठी आज्ञा है, "अपने दांव हेज मत करो।" मैं केवल तभी अपवाद करूँगा जब हेज दांव का अपेक्षित मूल्य सकारात्मक हो, या जीवन बदल देने वाली बड़ी रकम दांव पर लगी हो।
वेगास के किसी कैसीनो में कॉलेज फ़ुटबॉल पर दांव लगाकर आप अधिकतम कितनी राशि जीत सकते हैं, और टिकट निकालते समय कैसीनो को अपनी व्यक्तिगत जानकारी भी नहीं देनी पड़ेगी? मैं जानना चाहता/चाहती हूँ कि मैं (प्रति दांव) कितनी राशि जीत सकता/सकती हूँ और फिर भी वे बिना कोई सवाल पूछे मुझे नकद भुगतान कर सकते हैं।
$10,000. $10,000 से ज़्यादा के नकद लेन-देन के लिए, चाहे वह खेल से जुड़ा हो या नहीं, CTR (नकद लेनदेन रिपोर्ट) ज़रूरी होगी। आप चिप्स में भुगतान की मांग भी कर सकते हैं, हालाँकि जब आप उन्हें भुनाएँगे तो वही CTR जनरेट होगा।
निःशुल्क साइटों के अलावा, क्या आप मुझे कोई ऐसी साइट सुझा सकते हैं जहां मैं मासिक शुल्क या जीत के प्रतिशत पर पेशेवर खेल हैंडीकैपिंग प्राप्त कर सकूं।
नहीं, मैं किसी दलाल का समर्थन नहीं करता।
आपने एनएफएल में अंडरडॉग्स पर अपनी सट्टेबाजी के बारे में बात की है। क्या आपने हर बार सिर्फ़ घरेलू अंडरडॉग पर ही दांव लगाया था या यह उससे कहीं ज़्यादा जटिल था? और सबसे ज़रूरी बात, कौन सी लाइन तय करती थी कि घरेलू डॉग है... शुरुआती लाइन या खेल से ठीक पहले वाली लाइन। धन्यवाद।
मैं बिना सोचे-समझे अंडरडॉग्स पर दांव नहीं लगाता, भले ही मुझे -105 ही क्यों न लगाना पड़े, जैसा कि इस सीज़न में लास वेगास के डाउनटाउन प्लाजा में हुआ। अगर मुझे किसी खेल के दांव पर थोड़ा सा भी फायदा नज़र आता है, तो मैं उस पर दांव नहीं लगाऊँगा। खेलों में मैं हमेशा एक निश्चित त्रुटि सीमा मानता हूँ, क्योंकि आखिरकार लोग खेल खेलते हैं, आँकड़े नहीं। हालाँकि, अगर मुझे बाज़ार की रेखा से बेहतर कोई दांव मिल जाए, या कोई टीम किसी विश्वसनीय हैंडीकैपर की सिफ़ारिश के साथ आए, तो मुझे दांव लगाने में खुशी होगी।
शानदार वेबसाइट के लिए धन्यवाद! मेरे पिताजी और मेरे बीच दांव हेजिंग को लेकर बहस चल रही है और हमें आपकी मदद की ज़रूरत है! यह मामला सुपर बाउल पर लगे दांव से जुड़ा है। सीज़न शुरू होने से पहले (मेरे पिताजी को साल याद नहीं है) मेरे चाचा ने शर्त लगाई थी कि न्यू इंग्लैंड सुपर बाउल जीतेगा। इस दांव पर 60 से 1 का भुगतान हुआ। सुपर बाउल (जिसमें न्यू इंग्लैंड खेल रहा था) से ठीक पहले, मेरे चाचा ने अपनी शर्त हेज कर ली (पिताजी को विवरण याद नहीं है) और $6,000 की संभावित कमाई छोड़ दी, लेकिन इसके बदले $3,000 की गारंटी दे दी। मुझे पूरा यकीन है कि यह एक बेवकूफी भरा दांव था, लेकिन मेरे पिताजी मेरी बात नहीं सुनेंगे। मैं तर्क दे रहा हूँ कि इस मौके पर हेजिंग करके वे अपेक्षित मूल्य छोड़ रहे थे और एक समझदार सट्टेबाज ऐसा कभी नहीं करता। मेरे पिताजी तर्क दे रहे हैं कि अपेक्षित मूल्य छोड़ देना ठीक है क्योंकि इसमें बहुत पैसा लगता है और यह दांव अक्सर नहीं लगता, ठीक वैसे ही जैसे आप अपने घर का बीमा करवाते हैं। बेशक, मेरा मानना है कि घर का मालिक होना खेल सट्टेबाजी से स्वाभाविक रूप से अलग है, क्योंकि एक से तो बचा जा सकता है, जबकि दूसरे से बिल्कुल नहीं। आपके क्या विचार हैं? कृपया इस मामले को सुलझाने में हमारी मदद करें!
जुए के बारे में मेरी दस आज्ञाओं में से सातवीं आज्ञा है, "तुम्हें अपनी बाजी नहीं लगानी चाहिए।" हालाँकि, अपनी टिप्पणी में मैं यह भी जोड़ता हूँ, "ज़िंदगी बदल देने वाली रकम का बीमा करने के लिए अपवाद बनाए जा सकते हैं।" इसलिए अगर $3,000 का समर्पण मूल्य उसके लिए ज़िंदगी बदल देने वाली रकम है, और जीतने की संभावना 50% से ज़्यादा नहीं होती, तो मुझे उसके फ़ैसले पर कोई आपत्ति नहीं होती। हालाँकि, अगर यह 2002 में न हुआ होता, तो न्यू इंग्लैंड के जीतने की संभावना 50% से कहीं ज़्यादा थी। बाकी दो साल, 2004 और 2005 में जब वे सुपर बाउल में खेले, तो वे 7 अंकों के पसंदीदा थे। मेरा अनुमान है कि दोनों ही सालों में जीतने की संभावना लगभग 71% थी। एक उचित समर्पण मूल्य 0.71 × $6100 (उसकी मूल बाजी वापस सहित) = $4,331 होता। प्रस्ताव पर हाउस एज, जो दूसरी टीम पर सम राशि के दांव के बराबर था, 29%-71% = 42% था। इसलिए, अगर मैं इस साल के बारे में सही हूँ, तो उसने बहुत गलत फैसला लिया। वह दूसरी टीम पर मनी लाइन पर दांव लगाकर खुले बाजार में कहीं बेहतर ऑड्स पा सकता था। जिसने भी केवल $3,000 की पेशकश की, वह या तो खेल से पूरी तरह अनभिज्ञ था या उसने अनुचित लाभ उठाया। दिलचस्प बात यह है कि न्यू इंग्लैंड ने अपने हाल के तीनों सुपर बाउल तीन अंकों से जीते।
एनएफएल खेल के बराबरी पर समाप्त होने की संभावना क्या है?
1983 से 2007 के सीज़न तक, खेले गए 5,901 नियमित सीज़न मैचों में 10 बार बराबरी हुई। नियमों के अनुसार, सीज़न के बाद कोई भी मैच बराबरी पर समाप्त नहीं हो सकता। इसलिए, ऐतिहासिक मैचों के आधार पर, इसकी संभावना 0.17%, यानी लगभग 590 में से 1 होगी।
किसी एनएफएल खेल में दो टीमों के बीच अंतिम अंक अंतर और उस खेल के पॉइंटस्प्रेड के बीच अंतर का मानक विचलन क्या है?
अन्य पाठकों की सुविधा के लिए, आइए पिछले सुपर बाउल का एक उदाहरण देखें, ताकि आप जो पूछ रहे हैं उसे स्पष्ट किया जा सके। पैट्रियट्स 12 अंकों के प्रबल दावेदार थे, लेकिन 3 अंकों से हार गए। इसलिए खेल पॉइंट स्प्रेड से 15 अंक पीछे रह गया। अगर मैं प्रश्न को सही ढंग से समझ रहा हूँ, तो आप इस अंतर के मानक विचलन के बारे में पूछ रहे हैं। अध्ययन की गई प्रत्येक लीग के लिए औसत अंतर लगभग शून्य था। मानक विचलन के लिए मुझे जो मिला, वह इस प्रकार है:
एनएफएल 13.31 (2000 से 2007 सीज़न पर आधारित)
कॉलेज फ़ुटबॉल 15.72 (1993 से 2007 सीज़न पर आधारित)
एनबीए 11.39 (1987 से 2003 सीज़न पर आधारित)
तो, 2008 का सुपर बाउल 15/13.31 = 1.13 मानक विचलन के साथ उम्मीदों से दूर रहा। मैं चीजों को यथासंभव सरल रखने के लिए, असतत वितरण के समायोजन कारक को अनदेखा कर रहा हूँ। किसी भी दिशा में, उम्मीदों से 1.13 मानक विचलन या उससे अधिक होने की संभावना 25.85% है। इसे एक्सेल में 2 × normdist(-1.13) सूत्र का उपयोग करके ज्ञात किया जा सकता है।
एक ऐसे खेल सट्टेबाज के रूप में, जो अंडरडॉग्स पर दांव लगाना पसंद करता है, और जो लाइनों के लिए इधर-उधर खरीदारी करना पसंद करता है, मैं हर एक अतिरिक्त आधा अंक पाने की कीमत जानता हूँ। आपके सामान्य NFL या NBA खेल में, आपके लिए प्रत्येक आधा अंक कितना मूल्यवान है? मुझे पता है कि फेयर लाइन पर -110 पर दांव लगाने वाले जुआरी को ब्रेक-ईवन के लिए 52.4% तक पहुँचना होगा। मुझे पता है कि लाइनें बाज़ार द्वारा तय की जाती हैं, लेकिन आप क्या कहेंगे कि प्रत्येक आधे अंक का वास्तविक मूल्य क्या है? यदि आप प्रत्येक खेल में फेयर लाइन पर आधा अंक अतिरिक्त प्राप्त कर सकें, तो क्या इससे आपका ब्रेक-ईवन अंक वास्तव में 50% हो जाएगा? क्या इसकी गणना करने का कोई तरीका है? धन्यवाद।
जैसा कि मैंने NBA में अपने पेज पर दिखाया है, आधा पॉइंट खरीदने पर जीत की संभावना 51.01%, हार की संभावना 47.01% और पुश की संभावना 1.98% होती है, बशर्ते कि सट्टेबाज 0 या -1 के स्प्रेड पर आधा पॉइंट कभी न खरीदे, जो उसे नहीं करना चाहिए। अगर आपको अतिरिक्त आधा पॉइंट के लिए केवल 110 लगाना होता, तो अपेक्षित रिटर्न (0.5101 - 1.1×0.4701)/1.1 = -0.64% होता। इसलिए, एक मुफ़्त आधा पॉइंट हाउस एज को पार करने के लिए पर्याप्त नहीं होगा।
ऐसा नहीं है कि आपने पूछा, लेकिन अगर आप 120 लगाते हैं, तो आप ज़्यादातर स्पोर्ट्स बुक पर आधा पॉइंट खरीद सकते हैं। अगर आप किसी भी तरह से स्प्रेड के ख़िलाफ़ किसी खेल पर दांव लगाने को तैयार हैं, तो क्या अतिरिक्त आधा पॉइंट एक अच्छा मूल्य है? 110 लगाने पर, किसी रैंडम पिकर के लिए हाउस एज 4.45% है, जिसमें टाई भी शामिल है। 120 लगाने पर, आधे पॉइंट के साथ हाउस एज 4.50% है। इसलिए, आधा पॉइंट खरीदना थोड़ा भी उचित नहीं है।
फ़ुटबॉल में आधा पॉइंट खरीदने का मूल्य काफ़ी हद तक पॉइंट स्प्रेड पर निर्भर करता है, क्योंकि कुछ जीत के अंतर दूसरों की तुलना में ज़्यादा संभावित होते हैं। NFL में आधा पॉइंट खरीदना सिर्फ़ 3 पॉइंट स्प्रेड पर ही फ़ायदेमंद होता है। दुर्भाग्य से, स्पोर्ट्स बुक्स भी यह जानते हैं, और ज़्यादातर समय आपको 3 पॉइंट स्प्रेड पर ऐसा करने की इजाज़त नहीं देते।
यह जानते हुए कि टीम A प्रति गेम औसतन 1.5 गोल करती है, और टीम B प्रति गेम औसतन 1.2 गोल करती है, क्या संभावना है कि A और B के बीच एक गेम में:
1) A, B से अधिक अंक प्राप्त करेगा
2) B, A से अधिक अंक प्राप्त करेगा
3) खेल बराबरी पर समाप्त हुआ।
क्या प्रदान की गई जानकारी प्रत्येक परिणाम की संभावनाओं की गणना करने के लिए पर्याप्त है?
इसमें इस बात पर ध्यान नहीं दिया गया है कि व्यक्तिगत स्कोर कुछ हद तक नकारात्मक रूप से सहसंबद्ध होने चाहिए, और प्रत्येक टीम द्वारा दिए गए औसत अंक भी उतने ही महत्वपूर्ण हैं जितने कि औसत अंक। अगर हम मान लें कि खेल में 1.5 और 1.2 अंक अपेक्षित हैं, जिसमें आक्रामक और रक्षात्मक दोनों पहलुओं को ध्यान में रखा गया है, और सहसंबंध कारक को नज़रअंदाज़ कर दें, तो हम आपकी तीनों संभावनाओं का एक अच्छा अनुमान लगा सकते हैं। इस तरह के कई सुपर बाउल प्रॉप्स हैं, लेकिन ये इस पर आधारित हैं कि कौन ज़्यादा टचडाउन, फ़ील्ड गोल, इंटरसेप्शन आदि स्कोर करेगा।
पहला कदम पॉइसन बंटन का उपयोग करके प्रत्येक टीम के लिए गोलों की संख्या की प्रायिकता का अनुमान लगाना है। सामान्य सूत्र यह है कि किसी टीम के g गोल होने की प्रायिकता, जिसका माध्य m है, e -m × m g /g! है। एक्सेल में, आप पॉइसन(g,m,0) सूत्र का उपयोग कर सकते हैं। निम्न तालिका इस सूत्र का उपयोग करके दोनों टीमों के 0 से 10 गोलों की प्रायिकता दर्शाती है।
प्रत्येक टीम के लिए 0 से 8 गोल की संभावनाएं
| लक्ष्य | टीम ए | टीम बी |
| 0 | 0.223130 | 0.301194 |
| 1 | 0.334695 | 0.361433 |
| 2 | 0.251021 | 0.216860 |
| 3 | 0.125511 | 0.086744 |
| 4 | 0.047067 | 0.026023 |
| 5 | 0.014120 | 0.006246 |
| 6 | 0.003530 | 0.001249 |
| 7 | 0.000756 | 0.000214 |
| 8 | 0.000142 | 0.000032 |
अगला चरण काफी सामान्य है, लेकिन आपको प्रत्येक टीम के लिए 0 से 8 अंकों के सभी 81 संभावित संयोजनों का एक मैट्रिक्स बनाना होगा। यह ऊपर दी गई तालिका से टीम A के x अंकों और टीम B के y अंकों की प्रायिकता को गुणा करके किया जाता है। नीचे दी गई तालिका 0-0 से 8-8 तक प्रत्येक अंक संयोजन की प्रायिकता दर्शाती है।
अगली तालिका प्रत्येक गोल संयोजन के अनुसार विजेता को दर्शाती है, जहां T बराबरी को दर्शाता है।
दोनों टीमों के लिए विजेता संयोजन
| गोल टीम ए | गोल टीम बी | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | टी | बी | बी | बी | बी | बी | बी | बी | बी |
| 1 | ए | टी | बी | बी | बी | बी | बी | बी | बी |
| 2 | ए | ए | टी | बी | बी | बी | बी | बी | बी |
| 3 | ए | ए | ए | टी | बी | बी | बी | बी | बी |
| 4 | ए | ए | ए | ए | टी | बी | बी | बी | बी |
| 5 | ए | ए | ए | ए | ए | टी | बी | बी | बी |
| 6 | ए | ए | ए | ए | ए | ए | टी | बी | बी |
| 7 | ए | ए | ए | ए | ए | ए | ए | टी | बी |
| 8 | ए | ए | ए | ए | ए | ए | ए | ए | टी |
अंत में, आप एक्सेल में sumif फ़ंक्शन का उपयोग करके दांव के तीनों संभावित परिणामों के लिए संगत कक्ष जोड़ सकते हैं। इस स्थिति में संभावनाएँ इस प्रकार हैं:
A जीतता है = 44.14%
B जीतता है = 30.37%
टाई = 25.48%
स्टैनफोर्ड वोंग द्वारा लिखित शार्प स्पोर्ट्स बेटिंग के परिशिष्ट C में इस तरह के दांवों के लिए जीत/हार/बराबरी की संभावनाएँ दी गई हैं। इस मामले में, उन्होंने 44%, 30% और 25% की संभावनाएँ बताई हैं। अगर किसी को इस तरह की समस्या का कोई सरल सूत्र पता हो, तो मैं सुनने के लिए तैयार हूँ।
अनुवर्ती: मुझे बॉब पी. का एक ईमेल मिला, जो गणित के मामले में मुझे हमेशा सतर्क रखते हैं। उन्होंने जो लिखा, वह यहाँ है।
दो असंबद्ध पॉइसन के बीच अंतर का वितरण देखा। यह एक स्केलम है (मेरे लिए नया)।वैसे भी, प्रश्न को P(Z=0), P(Z>0) और P(Z<0) के रूप में प्रस्तुत किया जा सकता है, जहां Z एक स्केलम है जिसके पैरामीटर 1.5 और 1.2 हैं।
यदि आपने अभी तक ऐसा नहीं किया है, तो आपको यह जानकर खुशी होगी
पी(टाई) = पी(जेड=0) = .254817
P(A, B को हराता है) = P(Z>0) = .441465
P(B, A को हराता है) = P(Z<0) = 1 - .254817 - .441465 = .303718
लगभग आपके उत्तरों के समान।
स्केलम के लिए विकिपीडिया प्रविष्टि में बेसेल फ़ंक्शन का ज़िक्र था, जो कैलकुलस में उस बिंदु के बारे में है जहाँ मुझे आगे जाने में डर लगता है। इसलिए, मैं इस मामले में बॉब की बात मानूँगा।
मुझे उन टीमों के साथ दांव लगाने में अच्छी किस्मत मिली है जिन्होंने लगातार 5 हार का सामना किया है और उन टीमों के खिलाफ भी जिन्होंने लगातार 5 जीत हासिल की हैं। मेरा मानना है कि पासे और रूलेट के विपरीत, जहाँ आप कहते हैं कि पासे या गेंद की कोई याददाश्त नहीं होती, एक पेशेवर खेल टीम अंतहीन रूप से जीत या हार नहीं सकती। मैंने यह विश्लेषण करने के बाद कि बदलाव कब ज़्यादा बार होगा, लगातार 5 हार का चयन किया। मेरे लिए यह मायने नहीं रखता कि वे कहाँ खेल रहे हैं या शुरुआती पिचर कौन है, चोटें वगैरह। क्या आपको लगता है कि मैं अपने विचारों में सही हूँ?
मुझे लगता है कि ये अच्छे दांव हैं, लेकिन आपके बताए कारण से नहीं। सिद्धांततः, एक खेल टीम अंतहीन रूप से हार सकती है। वैसे भी, ये अच्छे दांव इसलिए हैं क्योंकि ये ज़्यादातर समय बड़ी अंडरडॉग टीमों पर लगाए जाएँगे, और अंडरडॉग टीमें आमतौर पर पसंदीदा टीमों से ज़्यादा मज़बूत दांव होती हैं। एक और कारण यह है कि इन परिस्थितियों में आमतौर पर स्क्वायर बेटर्स दूसरी तरफ़ दांव लगाते हैं, जिससे आपके पक्ष में मूल्य बनता है।
मैं एक एनएफएल हैंडीकैपिंग प्रतियोगिता में छह लोगों में से एक हूँ। हम सभी को एक प्रमुख इंटरनेट स्पोर्ट्स बुक, जिसकी लाइन 20 सेंट की है, में सीज़न के दौरान 70 गेम चुनने हैं। अन्य प्रतिभागियों में से एक ने सीज़न के अंत में उच्चतम स्कोर पर ओवर/अंडर प्रॉप की पेशकश की। उसकी लाइन 8.5 यूनिट के लाभ की थी। मान लीजिए कि सीज़न अभी शुरू नहीं हुआ है, और प्रतिभागी अनुभवी स्पोर्ट्स बेटर हैं। आप उस लाइन के बारे में क्या सोचते हैं, और आप इसका विश्लेषण कैसे करेंगे?
इस तरह के प्रोप के साथ खुद से पूछने वाला बड़ा सवाल यह है कि किसी दिए गए पिक के जीत, हार या पुश में समाप्त होने की संभावना क्या है। एनएफएल पर दांव लगाने वाले मेरे सेक्शन से, हम देख सकते हैं कि 2.8% गेम सीधे लाइन पर आते हैं। इसे सरल रखने के लिए हम केवल 3% मान लेते हैं। मान लीजिए कि शर्त हल हो गई है, तो हम जीत की संभावना को p कहते हैं। पूरी तरह से यादृच्छिक चयनकर्ता के लिए, p स्पष्ट रूप से 50% होगा। केवल अंडरडॉग्स को चुनकर इसमें सुधार करना आसान है। जैसा कि मेरे पहले उल्लेखित पेज से पता चलता है, 25 सीज़न से अधिक फ्लैट अंडरडॉग्स पर दांव लगाने से 51.5% की जीत दर होती। सामान्य तौर पर बाजार के खिलाफ सबसे नरम लाइनों को चुनकर इसमें थोड़ा और सुधार करना भी आसान है।
अतः, यह मानते हुए कि हल किए गए दांवों में से 52% जीतते हैं, समग्र संभावनाएं हैं:
जीत: 50.44%
ड्रा: 3.00%
हानि: 46.56%
बुनियादी आँकड़ों का उपयोग करके, यह देखना आसान है कि -110 पर प्रत्येक पिक की अपेक्षित जीत -0.0078 है। प्रत्येक पिक का मानक विचलन 1.0333 है। 70 पिक पर अपेक्षित जीत -0.5432 है, और मानक विचलन 70 1/2 × 1.0333 = 8.6452 है। 8.5 इकाइयों की जीत, अपेक्षा से 9.0432 इकाई अधिक है, या गॉसियन वक्र पर अपेक्षा के दाईं ओर 9.0432/8.6452 = 1.0460 मानक विचलन है। मुझे लगता है कि हम पुश के कारण असतत वितरण के समायोजन को अनदेखा कर सकते हैं, और कुछ गेम जो -110/-110 नहीं हैं, 0.05 इकाइयों के कारक से नीचे एक काफी सुचारू वक्र का परिणाम देंगे।
इसलिए, किसी एक खिलाड़ी के उम्मीद से 1.046 मानक विचलन से अधिक अंक प्राप्त करने की संभावना 14.77% है। यह आँकड़ा गॉसियन वक्र की किसी भी तालिका में, या एक्सेल में सूत्र =1-normsdist(1.046) से प्राप्त किया जा सकता है। सभी छह खिलाड़ियों के 1.046 से कम अंक प्राप्त करने की संभावना (1-0.1477) 6 =38.31% है। इस प्रकार, कम से कम एक खिलाड़ी के 1.046 मानक विचलन से ऊपर अंक प्राप्त करने की संभावना 61.69% है। इससे ओवर -110 पर एक ठोस दांव लगता है। मैं दिखाता हूँ कि यह -161 पर उचित है।
निम्नलिखित तालिका p के विभिन्न मानों पर 8.5 से अधिक के जीतने की संभावना दर्शाती है। संभवतः प्रॉप सेट करने वाला व्यक्ति p के लिए 51% के करीब मान मान रहा था।
एनएफएल हैंडीकैपिंग प्रॉप
| संभवतः सही चयन | संभवतः जीत पर |
| 50.0% | 41.16% |
| 50.5% | 46.18% |
| 51.0% | 51.33% |
| 51.5% | 56.53% |
| 52.0% | 61.69% |
| 52.5% | 66.72% |
| 53.0% | 71.52% |
आप उस पैट्रियट के पहले डाउन पर जाने के फैसले के बारे में क्या सोचते हैं, जबकि वे अपनी ही 28 गज की लाइन पर चौथे डाउन पर हैं—और वे 6 अंकों से आगे चल रहे हैं?! ऐसी स्थिति में पहले डाउन पर पहुँचने की संभावना क्या है, और आप क्या करते?
अन्य पाठकों की जानकारी के लिए, यह 15 नवंबर, 2009 के एक खेल का संदर्भ है जिसमें पैट्रियट्स, कोल्ट्स से छह अंकों से आगे थे। चौथे क्वार्टर में 1:57 मिनट बचे थे, यह चौथा डाउन था और लगभग 1.5 गज की दूरी पर था, और गेंद पैट्रियट्स की 28 गज की लाइन पर थी। पैट्रियट्स के कोच बिल बेलिचिक ने जीत पक्की करने और चौथे और छोटे डाउन पर पहला डाउन लेने का अब विवादास्पद निर्णय लिया, बजाय इसके कि आगे बढ़कर पंट किया जाए।
लास वेगास रिव्यू जर्नल में इस बारे में एक अच्छा कॉलम है। इसमें पेशेवर जुआरी और साथी एक्चुअरी स्टीव फेज़िक के हवाले से कहा गया है कि ऑड्स पहले डाउन के पक्ष में थे। मैं पूरी तरह सहमत हूँ। सामान्य तौर पर, मुझे लगता है कि दूसरे कोच बहुत ज़्यादा दांव लगाते हैं और जोखिम लेने से बहुत डरते हैं। अपनी बात पर ज़ोर देने के लिए मैंने साथी गणित विशेषज्ञ और खेल सट्टेबाज़ जोएल बी. से पूछा, जो खेल के बीच में फ़ुटबॉल ऑड्स का विश्लेषण करने में मुझसे कहीं बेहतर हैं। उन्होंने निम्नलिखित ऑड्स दिए:
- पैट्रियट के पहले डाउन करने की संभावना: 60%
- पैट्रियट की जीत की संभावना, बशर्ते कि वे पहला डाउन करें: 100%
- पैट्रियट की जीत की संभावना, बशर्ते कि वे पहला डाउन चूक जाएं: 50%
- पैट्रियट की जीत की संभावना, बशर्ते कि वे दांव लगाएँ: 75%
तो, पहले डाउन पर जीतने की संभावना 60%×100% + 40%×50% = 60% + 20% = 80% है। यह पंटिंग की 75% संभावना से ज़्यादा है।
सोमवार सुबह के क्वार्टरबैक बेलिचिक को जितना चाहें उतना बुरा-भला कह सकते हैं, लेकिन मैं उनके फैसले की सराहना करता हूँ। उनका मूल्यांकन खेल के नतीजे से नहीं, बल्कि इस आधार पर किया जाना चाहिए कि उस समय उनके प्रदर्शन के हालात उनके पक्ष में थे या नहीं। मुझे पूरा यकीन है कि वे सही थे। एक हफ्ते बाद रेवेन्स/स्टीलर्स के मैच में रेवेन्स ने चौथे और पाँचवें ओवर में दांव लगाया और जीत हासिल की। हालाँकि यह एक अलग तरह की स्थिति थी, लेकिन मैंने अभी तक किसी को भी उस फैसले पर पुनर्विचार करते नहीं सुना।
निष्पक्षता के हित में, मैं विपरीत दृष्टिकोण रखने वाले एक लेख का लिंक प्रदान कर रहा हूँ, जिसका शीर्षक है बेलिचिक का चौथा और लापरवाह, बिल सिमंस द्वारा ESPN.com पर लिखा गया है।
मान लीजिए दो फ़ुटबॉल मैच हैं जिनमें मुझे लगता है कि एक खिलाड़ी को फ़ायदा है। मान लीजिए कि दोनों में से किसी एक के जीतने की संभावना 55% है, और मुझे 110 का दांव लगाना है। कौन सा ज़्यादा फ़ायदेमंद है, दोनों मैचों पर सीधा दांव लगाना या एक ही पार्ले के रूप में?
अच्छा सवाल है। सीधे शब्दों में कहें तो, प्रति दांव लाभ 0.55×(10/11) - 0.45 = 0.05 है। पार्ले के रूप में, लाभ (0.55) 2 ×((21/11) 2 -1)-(1-(0.55) 2 ) = 10.25% है। इसलिए, ऐसा लगता है कि लाभ को अधिकतम करने के लिए पार्ले ही एकमात्र रास्ता है।
हालाँकि, पार्ले के रूप में विचरण अधिक होता है। यदि आप केली मानदंड का पालन कर रहे हैं, तो आपको पार्ले के लिए अपने बैंकरोल को एक छोटे दांव से सुरक्षित रखना होगा। इस उदाहरण में, यदि दोनों गेम ओवरलैप होते हैं, तो इष्टतम केली स्ट्रेट अप दांव बैंकरोल का 5.48% है, यदि आपका पहला गेम दूसरे गेम पर दांव लगाने से पहले समाप्त हो जाता है, तो 5.50% है, और पार्ले के लिए 3.88% है। दांव को लाभ से गुणा करने पर, हमें स्ट्रेट अप (5.50% लाभ के आधार पर) 0.00275 और पार्ले के लिए 0.00397 प्राप्त होता है। इस प्रकार, पार्ले से अधिक लाभ होता है।
मैंने इस तरह के प्रश्न के सामान्य मामले पर विचार किया, जिसमें 3-टीम और 4-टीम पार्ले और मनी लाइन दांवों पर भी विचार किया गया। सभी दांवों के लिए एक छोटे से लाभ को मानते हुए, एक सामान्य नियम के रूप में, यदि प्रत्येक घटना के जीतने की संभावना 33% से कम है, तो आपको सीधे दांव लगाना चाहिए। यदि प्रत्येक संभावना 33% और 52% के बीच है, तो आपको 2-टीम पार्ले करना चाहिए। यदि प्रत्येक संभावना 52% और 64% के बीच है, तो आपको 3-टीम पार्ले करना चाहिए। यदि प्रत्येक संभावना 64% से अधिक है, तो आपको 4-टीम पार्ले करना चाहिए। यदि आप सीधे दांव लगा रहे हैं, तो आप 2-टीम या 3-टीम पार्ले करने में लगभग समान रूप से बेहतर हैं, यह मानते हुए कि आपके पास शुरुआत में एक फायदा है।
मैं इस बात पर जोर देना चाहूंगा कि यदि आप एक मनोरंजनात्मक जुआरी हैं और हाउस एज के विरुद्ध खेल रहे हैं (कौन सा खेल सट्टेबाज इसे स्वीकार करेगा?), तो सीधे दांव लगाने से हाउस एडवांटेज कम हो जाता है।
एनएफएल में 2-पॉइंट रूपांतरण की संभावना क्या है?
2000 से 2009 के एनएफएल सीज़न में, 2009 के पोस्ट-सीज़न को छोड़कर, 2-पॉइंट रूपांतरण के 567 असफल प्रयास और 318 सफल प्रयास हुए। इस हिसाब से, सफलता की संभावना 318/(567+318) = 35.9% है।
मुझे आपकी विज़ार्ड ऑफ़ वेगास साइट पर मौजूद बेहतरीन संक्षिप्त गाइड बहुत पसंद हैं। स्पोर्ट्स बेटिंग गाइड के बारे में भी मेरा एक सवाल है। तस्वीर में दिख रहे बोर्ड पर कुछ खेलों के लिए कोई टोटल या मनी लाइन नहीं है, इसलिए मुझे लगता है कि कैसीनो उन बेट्स की पेशकश नहीं कर रहा था। क्या यह पॉइंट स्प्रेड के आकार से संबंधित है या कोई और कारण है कि वे वहाँ नहीं हैं?

वह तस्वीर लेरॉयज़ फ्रैंचाइज़ी में ली गई थी, जो एक छोटी और रूढ़िवादी स्पोर्ट्स बुक है। वे पहले स्प्रेड दिखाते हैं, और बाद में कुल और मनी लाइन।
काफी असंतुलित खेलों पर मनी लाइन देना भी असामान्य है, उदाहरण के लिए ईस्टर्न मिशिगन बनाम सेंट्रल मिशिगन, जिसमें 23-पॉइंट स्प्रेड है। ऐसे खेलों में सटीक मनी लाइन निर्धारित करना मुश्किल होता है, और असंतुलित कार्रवाई का जोखिम अधिक होता है। बड़े स्प्रेड वाले खेलों पर मनी लाइन पर दांव लगाने के लिए सबसे अच्छा कैसीनो हिल्टन है। अंत में, यदि पॉइंट स्प्रेड बहुत छोटा है, जैसे 1 या 1.5, तो अधिकांश स्पोर्ट्स बुक मनी लाइन पोस्ट करने की ज़हमत नहीं उठाते, क्योंकि स्प्रेड के विरुद्ध दांव लगाने पर भी वही परिणाम मिलने की संभावना होती है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
सुपर बाउल के सटीक स्कोर की भविष्यवाणी करके अपनी किताब की एक हस्ताक्षरित प्रति जीतने का अवसर देने के लिए धन्यवाद। लेकिन, क्या अपेक्षित मूल्य बहुत कम नहीं है? मेरे अनुमान से जीतने की संभावना लगभग 300 में से 1 है।
मुझे लगता है कि एक अच्छे और शिक्षित अनुमान के साथ संभावनाएँ इससे कहीं बेहतर हैं। किसी भी NFL खेल का सटीक परिणाम जानने के लिए मेरी यह बुनियादी रणनीति है।
- कुल और स्प्रेड का उपयोग करके, प्रत्येक टीम के कुल अंकों का अनुमान लगाएँ। उदाहरण के लिए, यदि हम सुपर बाउल के लिए कुल 57 और स्प्रेड -5 का उपयोग करते हैं, जिसमें c=कोल्ट्स अंक और s=सेंट्स अंक मान लिया गया है, तो...
(1) सी+एस=57
(2) सी-5=एस
समीकरण (1) में समीकरण (2) प्रतिस्थापित करने पर:
सी+(सी-5)=57
2सी-5=57
2सी=62
सी=31
एस=31-5=26
यहाँ रुकने की समस्या यह है कि कभी-कभी आपको ऐसे मान मिलते हैं जो किसी एक टीम द्वारा बनाए जाने की संभावना नहीं होती। उदाहरण के लिए, किसी एक टीम के 24 अंक होने की संभावना 6.5% है, लेकिन 25 अंक होने की संभावना केवल 0.9% है। नीचे दी गई तालिका 2000-2009 सीज़न के आधार पर, किसी एक टीम के कुल अंकों की संभावना दर्शाती है। इसलिए हम फ़ील्ड गोल और टचडाउन के वास्तविक संयोजनों के आधार पर प्रत्येक टीम के कुल अंकों का अनुमान लगा रहे हैं। - मान लीजिए कि पसंदीदा खिलाड़ी ने 2 फील्ड गोल किए।
- मान लीजिए कि अंडरडॉग ने 1 फील्ड गोल मारा।
- प्रत्येक से फ़ील्ड गोल पॉइंट घटाएँ। सुपर बाउल के उदाहरण में, इससे कोल्ट्स = 25 टचडाउन पॉइंट, सेंट्स = 23 टचडाउन पॉइंट बचेंगे।
- अनुमानित टचडाउन प्राप्त करने के लिए टचडाउन पॉइंट्स को 7 से विभाजित करें। c=3.57 TD, s=3.29 TD
- अनुमानित टचडाउन को निकटतम पूर्णांक तक पूर्णांकित करें। c=4, s=3.
- इस विधि का पालन करने पर, हमें कुल अंक c=(4×7)+(2×3)=34, s=(3×7)+(1×3)=24 प्राप्त होते हैं।
1983 से 2009 सीज़न तक के सभी 6,707 खेलों में इस पद्धति का उपयोग करने पर 69 सही चयन होते, और सफलता दर 1.03% होती। पिछली बार यह सही चयन 2009 के 13वें हफ़्ते में टाइटन्स/कोल्ट्स के खेल में हुआ था। उस खेल में कोल्ट्स -6.5 का स्प्रेड था, और कुल 46 थे। स्कोर था टाइटन्स 17, कोल्ट्स 27।
एक आलोचक का मानना था कि दोनों टीमों के लिए निकटतम महत्वपूर्ण एक-टीम योग चुनना एक बेहतर और सरल रणनीति होगी। इस पद्धति का उपयोग करने से केवल 51 जीतें मिलीं, और जीत दर 0.76% रही। मेरे विचार से, मज़बूत और कमज़ोर टीमों के बीच फ़ील्ड गोल 2 और 1 बाँटना महत्वपूर्ण है।एनएफएल2000-2009 सीज़न में एकल-टीम का कुल योग
| एक-टीम का कुल योग | नमूने में कुल | संभावना |
| 0 | 93 | 1.75% |
| 1 | 0 | 0.00% |
| 2 | 0 | 0.00% |
| 3 | 148 | 2.79% |
| 4 | 0 | 0.00% |
| 5 | 2 | 0.04% |
| 6 | 114 | 2.15% |
| 7 | 210 | 3.96% |
| 8 | 9 | 0.17% |
| 9 | 76 | 1.43% |
| 10 | 316 | 5.96% |
| 11 | 9 | 0.17% |
| 12 | 49 | 0.92% |
| 13 | 289 | 5.45% |
| 14 | 238 | 4.49% |
| 15 | 55 | 1.04% |
| 16 | 170 | 3.21% |
| 17 | 373 | 7.03% |
| 18 | 33 | 0.62% |
| 19 | 92 | 1.73% |
| 20 | 368 | 6.94% |
| 21 | 234 | 4.41% |
| 22 | 64 | 1.21% |
| 23 | 218 | 4.11% |
| 24 | 347 | 6.54% |
| 25 | 47 | 0.89% |
| 26 | 103 | 1.94% |
| 27 | 282 | 5.32% |
| 28 | 159 | 3.00% |
| 29 | 52 | 0.98% |
| 30 | 127 | 2.39% |
| 31 | 242 | 4.56% |
| 32 | 23 | 0.43% |
| 33 | 57 | 1.07% |
| 34 | 164 | 3.09% |
| 35 | 76 | 1.43% |
| 36 | 27 | 0.51% |
| 37 | 68 | 1.28% |
| 38 | 108 | 2.04% |
| 39 | 11 | 0.21% |
| 40 | 21 | 0.40% |
| 41 | 62 | 1.17% |
| 42 | 31 | 0.58% |
| 43 | 6 | 0.11% |
| 44 | 24 | 0.45% |
| 45 | 33 | 0.62% |
| 46 | 1 | 0.02% |
| 47 | 7 | 0.13% |
| 48 | 28 | 0.53% |
| 49 | 15 | 0.28% |
| 50 | 1 | 0.02% |
| 51 | 5 | 0.09% |
| 52 | 7 | 0.13% |
| 53 | 0 | 0.00% |
| 54 | 2 | 0.04% |
| 55 | 1 | 0.02% |
| 56 | 4 | 0.08% |
| 57 | 1 | 0.02% |
| 58 | 1 | 0.02% |
| 59 | 1 | 0.02% |
| कुल | 5304 | 100.00% |
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
एनएफएल में चौथे क्वार्टर से पहले ऑनसाइड किक के सफल होने की कितनी संभावना है? मेरा मतलब है, सुपर बाउल में किया गया यह कदम बिल्कुल शानदार था, लेकिन क्या सेंट्स कोच के पास अपने फैसले को पुष्ट करने के लिए आँकड़े थे, या वह बस एक अनुमान पर चल रहे थे?
advancedfootballanalytics.com पर प्रकाशित एक बेहतरीन लेख के अनुसार, सफलता की ऐतिहासिक संभावना 26% है। हालाँकि, ज़्यादातर ऑनसाइड किक में, दूसरी टीम इसकी उम्मीद कर रही होती है, जिससे सफलता की संभावना कम हो जाती है। सरप्राइज़ ऑनसाइड किक के लिए, सफलता की संभावना 60% है! लेख का मुख्य बिंदु यह है कि एक स्मार्ट रणनीति यह होगी कि सरप्राइज़ ऑनसाइड किक ज़्यादा बार की जाएँ। मैं सहमत हूँ; सेंट्स का यह एक शानदार कदम था।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
जैसे-जैसे सीज़न आगे बढ़ता है, मौसम खराब होता है, और टीमों के हालिया प्रदर्शन के बारे में ज़्यादा जानकारी मिलती है, फ़ुटबॉल के कुल योग पर सट्टेबाज़ी पर क्या प्रभाव पड़ता है? लाइन में गलतियाँ ढूँढ़ना कितना आसान (या मुश्किल) है?
इस प्रश्न का उत्तर देने में सहायता के लिए, मैंने 1983 से 2009 तक प्रत्येक सीज़न के आधार पर, एनएफएल में सप्ताह संख्या के आधार पर बनाए गए औसत अंकों का ग्राफ बनाया। निम्नलिखित ग्राफ परिणाम दर्शाता है।
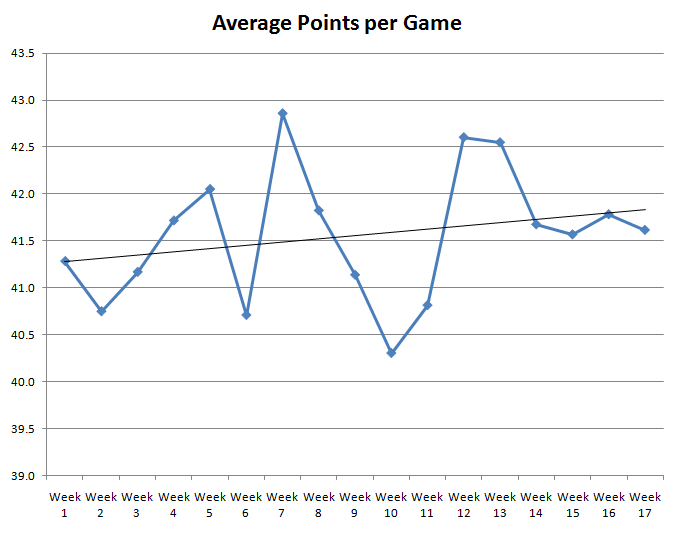
जैसा कि आप देख सकते हैं, रेखा बार-बार ऊपर-नीचे होती है। पतली काली रेखा एक न्यूनतम-वर्ग सर्वोत्तम फिट रेखा है, जो एक सामान्य ऊपर की ओर रुझान दर्शाती है। इसलिए जैसे-जैसे मौसम बदलता है और तापमान गिरता है, औसत अंक थोड़े बढ़ते हैं, लेकिन यह आसानी से एक यादृच्छिक बदलाव हो सकता है।
मैं बस इतना ही कह सकता हूँ। मौसम का खेल सट्टेबाजी पर क्या असर पड़ता है, इस बारे में सामान्य राय जानने के लिए मैंने अपने दोस्त जेसन बीन से बात की, जो इस विषय के विशेषज्ञ हैं। उन्होंने जो कहा, वह इस प्रकार है:
अधिकांश मामलों में, हवा मौसम का प्रमुख पहलू है जो खेल को सबसे अधिक प्रभावित करता है; लेकिन, यह एकमात्र नहीं है। बेसबॉल और अन्य आउटडोर खेलों में, छाया का समान प्रभाव हो सकता है, विशेष रूप से शुरुआती और बाद के सीज़न के बेसबॉल दोपहर के खेलों के दौरान। बारिश या बर्फ उतना बड़ा कारक नहीं है जितना कि ज्यादातर लोग फुटबॉल में सोचते हैं, क्योंकि यह आम तौर पर आक्रमण और रक्षा दोनों को समान रूप से प्रभावित करता है। एक उदाहरण एक विस्तृत रिसीवर के खिलाफ रक्षात्मक पीठ होगा। बारिश और बर्फ उन्हें समान रूप से धीमा कर देंगे, इस प्रकार किसी भी पक्ष को बढ़त नहीं मिलेगी। हवा किकिंग के साथ-साथ फुटबॉल में पासिंग गेम को भी खत्म कर सकती है। मैंने ऐसे खेल देखे हैं जहाँ एक पासिंग टीम को एक मजबूत क्रॉसविंड के कारण लगभग हर खेल में गेंद चलाने के लिए मजबूर होना पड़ा है।यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
एनएफएल में, औसतन, एक स्कोर के बाद दूसरी टीम द्वारा अगला स्कोर किये जाने की संभावना क्या होती है?
2000-2009 एनएफएल सीज़न के आधार पर, उत्तर 57% है।
अगर किसी NFL टीम को पिछले मैच में बुरी तरह से हार का सामना करना पड़ा है, तो क्या अगले मैच में उन पर दांव लगाना बेहतर होगा या उनके खिलाफ? बड़ी जीत के लिए भी यही सवाल है। मैं अक्सर सुनता रहता हूँ कि बड़ी हार के बाद टीम को "कुछ साबित करना होता है", जबकि बड़ी जीत वाली टीम अति-आत्मविश्वासी और आलसी हो सकती है। क्या इसमें कोई सच्चाई है?
मैं दिखाता हूँ कि 21 या उससे ज़्यादा अंकों की हार के बाद टीम 51.66% समय स्प्रेड को कवर कर लेगी। हालाँकि, यह त्रुटि सीमा के भीतर है। नीचे दी गई तालिका पिछले गेम के स्प्रेड के आधार पर, उसी टीम की पिछले गेम में जीत या हार के आधार पर, परिणाम दिखाती है। परिणाम कभी भी 50% से ज़्यादा नहीं होते और हमेशा इसके मानक विचलन के भीतर होते हैं। मूलतः, मुझे स्प्रेड के आधार पर जीत/हार और पिछले गेम तक टीम द्वारा जीते या हारे गए अंकों के बीच कोई सांख्यिकीय संबंध नहीं मिलता।
पिछले गेम में जीत या हार के अंतर के अनुसार स्प्रेड के विरुद्ध जीत, हार या टाई
| पिछले खेल के परिणाम | प्रसार के विरुद्ध जीत | प्रसार के विरुद्ध हानि | फैलाव के विरुद्ध टाई | जीतने की दर | मानक विचलन |
| 21 या अधिक अंकों से जीतें | 233 | 247 | 17 | 48.54% | 2.28% |
| 14 से 20 से जीत | 235 | 219 | 11 | 51.76% | 2.35% |
| 10 से 13 से जीत | 188 | 180 | 8 | 51.09% | 2.61% |
| 7 से 9 से जीत | 198 | 181 | 12 | 52.24% | 2.57% |
| 4 से 6 से जीत | 164 | 170 | 12 | 49.10% | 2.74% |
| 3 से जीत | 202 | 212 | 14 | 48.79% | 2.46% |
| 2 से हार से 2 से जीत | 184 | 188 | 14 | 49.46% | 2.59% |
| 3 से हार | 209 | 207 | 12 | 50.24% | 2.45% |
| 4 से 6 की हानि | 174 | 163 | 9 | 51.63% | 2.72% |
| 7 से 9 तक की हानि | 187 | 195 | 9 | 48.95% | 2.56% |
| 10 से 13 तक की हानि | 173 | 189 | 14 | 47.79% | 2.63% |
| 14 से 20 तक की हानि | 220 | 232 | 15 | 48.67% | 2.35% |
| 21 या अधिक से हार | 249 | 233 | 15 | 51.66% | 2.28% |
तालिका 2000 सीज़न के प्रथम सप्ताह से 2010 सीज़न के चौथे सप्ताह तक प्रत्येक एनएफएल खेल पर आधारित है।
पिनैकल स्पोर्ट्सबुक ने अभी-अभी अपने ऑड्स दशमलव प्रारूप में पोस्ट करना शुरू किया है। मैं स्पोर्ट्सबुक ऑड्स को दशमलव प्रारूप से अमेरिकी प्रारूप में कैसे बदलूँ?
आइए 25 अक्टूबर, 2010 के मंडे नाइट फुटबॉल मैच को एक उदाहरण के तौर पर देखें। यूरोपीय ऑड्स इस प्रकार हैं:
न्यूयॉर्क जायंट्स 2.750
डलास काउबॉयज़ 1.513
दोनों आंकड़े दर्शाते हैं कि जीतने पर आपको दांव पर लगाई गई एक इकाई के लिए कितना वापस मिलेगा, जिसमें आपका मूल दांव भी शामिल है। जब दशमलव ऑड्स 2 से अधिक या उसके बराबर हों, तो अनुवाद आसान है: बस एक घटाएँ, और फिर 100 से गुणा करें। यदि ऑड्स 2 से कम हैं, तो (1) 1 घटाएँ, (2) व्युत्क्रम लें, और (3) -100 से गुणा करें।
आप में से जो लोग सूत्र पसंद करते हैं, उनके लिए, यदि दशमलव ऑड्स x का भुगतान करते हैं, तो यहां समतुल्य अमेरिकी ऑड्स की गणना दी गई है:
यदि x>=2: 100*(x-1)
यदि x<2: -100/(x-1)
उपरोक्त उदाहरण में, अमेरिकी प्रारूप में पंक्तियाँ इस प्रकार हैं:
न्यूयॉर्क जायंट्स: 100*(2.750-1) = +175
डलास काउबॉयज़: -100/(1.513-1) = -195
आप पिनैकल की वेबसाइट के ऊपरी बाएँ भाग में, लोगो के ऊपर स्थित पुलडाउन मेनू में "अमेरिकन ऑड्स" का चयन करके सभी लाइनों को स्वचालित रूप से परिवर्तित कर सकते हैं।
मैंने अपने एक दोस्त, जो पहले बुकिंग करता था, से शर्त लगाई थी कि मैं इस आने वाले NFL सीज़न में हर नियमित सीज़न के खेल में 50% या उससे ज़्यादा का स्प्रेड जीत सकता हूँ। अगर मैं जीतता हूँ, तो मुझे $1000 मिलेंगे। अगर वह जीतता है, तो मुझे $500 देने होंगे। रविवार 31/10/10 तक मैं 19 गेम आगे हूँ और वह एक डील के बारे में बात कर रहा है। यहाँ कौन सा ऑफर अच्छा रहेगा?
एक बेहतरीन दांव, जैसे किसी बच्चे से कैंडी छीनना। यह सिक्के उछालने पर 2-1 मिलने जैसा है। और भी बेहतर, क्योंकि बराबरी पर भी आप जीत जाएँगे।
इस लेखन के समय, नियमित सीज़न में 256 में से 95 खेल खेले जा चुके हैं। द्विपद वितरण का उपयोग करके, मैं दिखाता हूँ कि आपकी जीत की संभावना 99.87% है। उचित निपटान मूल्य $998.02 होगा।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
लास वेगास में एक स्पोर्ट्स बुक ने कॉलेज फ़ुटबॉल का स्पष्ट रूप से गलत टोटल दिखाया। बाज़ार में 43 का आंकड़ा था, लेकिन उन्होंने उसे 53 पर दिखाया। इसलिए मैंने ध्यान आकर्षित न करने या लाइन को आगे न बढ़ाने के लिए, छोटी-छोटी रकमों पर लगभग 20 बार दांव लगाया। जैसी कि उम्मीद थी, मैं जीत गया। अब मैं भुगतान के लिए दांव पेश करने को लेकर घबरा रहा हूँ। क्या कैसीनो द्वारा भुगतान से इनकार करना उचित होगा?
मैं 10 से 1 का दांव लगाऊँगा, आपको भुगतान मिल जाएगा, हालाँकि वे पहले आपसे कुछ बातें कर सकते हैं। मुझे इसमें कुछ संदेह इसलिए है क्योंकि एक स्पोर्ट्स बुक, गेमिंग कंट्रोल बोर्ड की अनुमति से, स्पष्ट रूप से गलती से लगाए गए दांव को रद्द कर सकती है।
"कोई भी पुस्तक अध्यक्ष की पूर्व लिखित स्वीकृति के बिना किसी भी दांव को एकतरफा रद्द नहीं कर सकती।" - नेवादा विनियमन 22.115
हालाँकि यह अधिकार मौजूद है, लेकिन कुछ उदाहरणों के आधार पर, इसका इस्तेमाल बहुत कम होता है। मुझे बताइए क्या होता है।
पी.एस. मुझे बाद में प्रश्नकर्ता द्वारा सूचित किया गया कि उसे बिना किसी परेशानी के भुगतान कर दिया गया था।
टचडाउन स्कोर करने वाले पहले खिलाड़ी के अंतिम नाम में स्क्रैबल पॉइंट्स की संख्या पर एक सुपर बाउल शर्त लगाई जाती है। लाइन 10½ है और ओवर और अंडर दोनों पर -115 है। क्या दोनों में से कोई भी पक्ष अच्छा दांव है?
मुझे इस तरह के रचनात्मक दांव पसंद हैं। ये बॉयड कैसिनो के साथ-साथ पाम्स, एल कॉर्टेज़ और साउथ पॉइंट में भी मिल सकते हैं। इस सवाल का जवाब देने के लिए मैंने पहला टचडाउन बनाने वाले विशिष्ट खिलाड़ी पर दांवों के एक और सेट पर गौर किया। ये ऑड्स नीचे दी गई तालिका के दूसरे कॉलम में दिखाए गए हैं। सरलता के लिए, मैं 5-1 वाले क्षेत्र को नज़रअंदाज़ कर रहा हूँ, और 100-1 पर कोई टचडाउन नहीं बना। फिर मैंने उन जीतों को तीसरे कॉलम में "उचित संभावना" में बदल दिया, जिसका अर्थ है कि दांव के बिल्कुल निष्पक्ष होने के लिए आपको जीतने की कितनी संभावना चाहिए। प्रत्येक जीत के भुगतान को कम करने के कारण ये संभावनाएँ बढ़ जाती हैं, यही वजह है कि योग 166% है। चौथे कॉलम में "समायोजित संभावना" 1.660842 से विभाजित उचित बाधाओं को दर्शाती है, जिससे कुल संभावना 100% होती है। पाँचवाँ कॉलम प्रत्येक खिलाड़ी के नाम पर स्क्रैबल अंकों की संख्या दर्शाता है। छठे कॉलम में "अपेक्षित स्क्रैबल अंक" संभावना और स्क्रैबल अंकों का गुणनफल है। निचले दाएँ सेल में औसत स्क्रैबल अंक 14.18521 दिखाए गए हैं।
औसत के हिसाब से, ओवर सही लग रहा है। खिलाड़ी दर खिलाड़ी, 11 या उससे ज़्यादा स्क्रैबल पॉइंट्स की संभावना 0.641894 है, जो -179 की एक उचित रेखा में बदल जाती है। इसलिए -115 पर ओवर एक बेहतरीन दांव है। 115 पर दांव लगाने पर, खिलाड़ी को ओवर पर 20% का फायदा होता है।
दुर्भाग्यवश, जब तक मैं दांव लगाने गया, तब तक रेखा -180 पर पहुंच चुकी थी।
सुपर बाउल में टचडाउन स्कोर करने वाले पहले खिलाड़ी को स्क्रैबल अंक
| नाम | पोस्ट की गई बाधाएं | उचित संभावना | समायोजित संभावना | कुल स्क्रैबल अंक | अपेक्षित स्क्रैबल अंक |
|---|---|---|---|---|---|
| Mendenhall | 4 | 0.200000 | 0.120421 | 20 | 2.408416 |
| जेनिंग्स | 4.5 | 0.181818 | 0.109473 | 22 | 2.408416 |
| स्टार्क्स | 5 | 0.166667 | 0.100351 | 10 | 1.003507 |
| वालेस | 7 | 0.125000 | 0.075263 | 15 | 1.128945 |
| वार्ड | 8 | 0.111111 | 0.066900 | 8 | 0.535204 |
| रोजर्स | 8 | 0.111111 | 0.066900 | 10 | 0.669005 |
| नेल्सन | 8 | 0.111111 | 0.066900 | 9 | 0.602104 |
| चक्कीवाला | 10 | 0.090909 | 0.054737 | 11 | 0.602104 |
| ड्राइवर | 10 | 0.090909 | 0.054737 | 11 | 0.602104 |
| जोन्स | 12 | 0.076923 | 0.046316 | 15 | 0.694735 |
| रोथ्लिसबर्गर | 12 | 0.076923 | 0.046316 | 22 | 1.018945 |
| सैंडर्स | 15 | 0.062500 | 0.037632 | 9 | 0.338684 |
| भूरा | 18 | 0.052632 | 0.031690 | 12 | 0.380276 |
| रेड मैन | 18 | 0.052632 | 0.031690 | 11 | 0.348587 |
| क्वारलेस | 20 | 0.047619 | 0.028672 | 19 | 0.544761 |
| कुह्न | 25 | 0.038462 | 0.023158 | 12 | 0.277894 |
| जैक्सन | 30 | 0.032258 | 0.019423 | 24 | 0.466145 |
| मूर | 30 | 0.032258 | 0.019423 | 8 | 0.155382 |
| योग | 1.660842 | 1.000000 | 14.185214 | ||
दुर्भाग्यवश, जब तक मैं दांव लगाने के लिए कैसीनो में वापस गया, तब तक रेखा -180 पर पहुंच चुकी थी।
पुनश्च: खेल से कुछ घंटे पहले मैंने -170 पर एक शर्त लगाई थी। दुर्भाग्य से, वह हार गई। टचडाउन स्कोर करने वाला पहला खिलाड़ी जॉर्डी नेल्सन था। नेल्सन के 9 स्क्रैबल पॉइंट हैं।
2010-2011 के एनएफएल सत्र के दौरान अंडरडॉग्स ने स्प्रेड के विरुद्ध कैसा प्रदर्शन किया?
खेले गए 267 खेलों में, पसंदीदा टीम ने 128 बार स्प्रेड को हराया, कमज़ोर टीम ने 133 बार जीत हासिल की, और 6 खेलों में पुश पर दांव लगाया गया। तय किए गए दांवों में से, कमज़ोर टीम ने 51.0% जीते।
ज़्यादा दिलचस्प बात ओवर और अंडर की है। ओवर ने 148 जीते, अंडर ने 114, और 5 पुश पर पड़े। निपटाए गए दांवों में से, ओवर ने 56.5% बार जीत हासिल की। सुलझाए गए 262 दांवों में से अंडर के 114 या उससे कम जीतने की संभावना 2.1% है।
6 नवंबर, 2011 को रैम्स बनाम कार्डिनल्स के मैच में रैम्स ने तीसरे क्वार्टर में दो सेफ्टी स्कोर किए। इसकी संभावना क्या है?
ऐतिहासिक अनुभव के आधार पर, प्रति खेल कम से कम एक सुरक्षा की संभावना 5.77% है।
प्रति गेम अपेक्षित सेफ्टी की संख्या -ln(1-0.0577) = 0.0594 होगी।
प्रति टीम प्रति तिमाही अपेक्षित संख्या 0.0594/8 = 0.0074 होगी।
एक ही क्वार्टर में एक ही टीम द्वारा ठीक दो सेफ्टी की संभावना e -0.0074 ×0.0074 2 /fact(2) = 36,505 में 1 होगी।
एक एनएफएल सीज़न में 267 खेल होते हैं, और 267×8=2,136 टीम क्वार्टर होते हैं। तो, मेरे अनुमान के अनुसार, यह औसतन हर 36,505/2,136 = 17.1 वर्षों में एक बार होगा।
इसे सिर्फ़ एक मोटा अनुमान ही माना जाना चाहिए। खेल में कुछ ऐसे कारक भी हैं जिन पर मैं सरलता के लिए ध्यान नहीं दे रहा हूँ।
क्या आपने न्यू जर्सी के पॉपकॉर्न पार्क चिड़ियाघर की ऊँट प्रिंसेस की कहानी सुनी है, जिसका NFL में हैंडीकैपिंग के मामले में 88-51 का रिकॉर्ड है? इसकी संभावना कितनी है?
पुश को छोड़कर, 139 पिक्स में से कम से कम 88 जीत मिलने की संभावना 0.00107355 है, यानी 931 में से 1। यह काफी निराशाजनक है। मुझे यकीन है कि 930 और जानवर होंगे जिन्होंने इससे भी बुरा प्रदर्शन किया होगा, जिनके बारे में कोई नहीं लिखता। प्रिंसेस के बारे में अधिक जानकारी के लिए, ESPN.com पर "न्यू जर्सी के ऊँट ने पैट्रियट्स पर जायंट्स की जीत की भविष्यवाणी" लेख पढ़ें।
- बिल +3.5 (+3)
- चार्जर्स +7.5 (+7)
- कार्डिनल्स -2.5 (-3)
- डॉल्फ़िन -2.5 (-3)
- बियर्स +2.5 (0)
इस शर्त पर मेरा क्या लाभ है?
मैं यह मानकर चल रहा हूँ कि संभावना 1 के लिए 25 है, जो कि गोल्डन नगेट, साउथ प्वाइंट और विलियम हिल स्पोर्ट्स बुक परिवारों में आधे अंक वाले कार्ड पर उपलब्ध है।
नीचे दी गई तालिका आपको प्राप्त रेखा और बाजार मूल्य रेखा दर्शाती है।
सबसे पहले, किसी अंडरडॉग के स्प्रेड को मात देने की संभावना 51.6% है। यह अंडरडॉग के लिए -106.6 की उचित रेखा के बराबर है। तो, आपको अंडरडॉग पर 6.6 आधार अंक मिल रहे हैं, और पसंदीदा पर उन्हें खो रहे हैं।
दूसरा, एनएफएल में आधा पॉइंट खरीदने पर मेरी तालिका प्रत्येक अतिरिक्त आधे पॉइंट के लिए चुकाई जाने वाली उचित कीमत दर्शाती है। उदाहरण के लिए, 3 से अतिरिक्त आधा पॉइंट पाने के लिए -121.4, यानी 21.4 बेसिस पॉइंट्स लगाने पड़ते हैं।
तालिका बताती है कि आपको कितने आधार अंक मिल रहे हैं। बियर्स के लिए, मैंने 1 और 2 के आधार अंकों को दोगुना कर दिया है, क्योंकि अगर आप इन संख्याओं को पार कर जाते हैं तो आप हार को जीत में बदल रहे हैं।
फिर तालिका कुल आधार अंकों को जीतने की प्रायिकता में बदल देती है। सूत्र है p = (100+b)/(200+b), जहाँ p = जीतने की प्रायिकता और b = आधार अंकों की संख्या।
नीचे की पंक्ति प्रत्येक लेग की जीत का गुणनफल लेती है, जिससे पार्ले जीतने की प्रायिकता 0.046751 हो जाती है। 25 के लिए 1 के ऑड्स पर, उस दांव का अपेक्षित रिटर्न 0.046751*25-1=0.168783 है। दूसरे शब्दों में, 16.9% का लाभ। शाबाश!
रूडबॉयोई पार्ले कार्ड
| टीम | बाज़ी कार्ड | गोरा | कम क्षमता का व्यक्ती या समूह आधार अंक | कुल अतिरिक्त अंक | कुल | संभावना |
|---|---|---|---|---|---|---|
| विधेयकों | 3.5 | 3 | 6.6 | 20.8 | 27.4 | 0.560246 |
| चार्जर्स | 7.5 | 7 | 6.6 | 11.9 | 18.5 | 0.542334 |
| कार्डिनल्स | -2.5 | -3 | -6.6 | 20.8 | 14.2 | 0.533147 |
| डाल्फिन | -2.5 | -3 | -6.6 | 20.8 | 14.2 | 0.533147 |
| भालू | 2.5 | 0 | 0 | 18.0 | 18.0 | 0.541321 |
| उत्पाद | 0.046751 | |||||
क्या आपने सिएटल की उस कार डीलरशिप के बारे में सुना है जिसे सीहॉक्स द्वारा जायंट्स को हराने के कारण $420,000 का भुगतान करना पड़ा? मैंने पढ़ा है कि उन्हें इसके बदले बीमा पॉलिसी के लिए $7,000 का भुगतान करना पड़ा। उचित प्रीमियम क्या होता?
1983 से 2012 सीज़न तक के हर NFL गेम के आधार पर, किसी भी गेम की एक खास टीम को शटआउट कर दिया गया था। हालाँकि, सात अंकों से पिछड़ने वाली टीम होने के नाते, औसत ओवर/अंडर वाले गेम में, मैं कहूँगा कि जायंट्स के शटआउट होने की संभावना औसत से ज़्यादा थी। उस गेम में ओवर/अंडर 41 था। आइए जायंट्स के अपेक्षित अंकों की संख्या जानने के लिए थोड़ा बीजगणित करें।
होने देना:
s=सीहॉक्स अंक
g=दिग्गज अंक
हम जानते हैं कि s+g=41 और s=g+7, जो कि पॉइंट स्प्रेड और ओवर/अंडर टोटल पर आधारित है।
दूसरे समीकरण को पहले समीकरण में प्रतिस्थापित करने पर:
(जी+7) + जी = 41
2जी +7 = 41
2जी = 34
जी = 17
अब, आइए 1983 से 2012 के सीज़न के आधार पर, प्रत्येक टीम के अनुमानित अंकों के आधार पर शटआउट की संभावना पर नज़र डालें। मैंने उन पंक्तियों को छोड़ दिया है जहाँ नमूना आकार शून्य था।
शटआउट की संभावना
| अनुमानित अंक | नमूने का आकार | शटआउट | अनुपात |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11.00 | 13 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12.00 | 34 | 2 | 5.9% |
| 12.25 | 36 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 39 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16.00 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18.00 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21.00 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 48 | 0 | 0.0% |
| 29.25 | 34 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 25 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
अगले चरण इतने जटिल हैं कि उन्हें यहां समझाना संभव नहीं है, लेकिन मैंने अनुमानित अंकों की संख्या के आधार पर शटआउट की संभावना के लिए एक सूत्र विकसित किया है।
p = अनुमानित अंक.
x = 1.562545 -0.302485 * पी
शटआउट की संभावना = e x /(1+e x )
निम्नलिखित चार्ट 14 से 22 अंकों के लिए शटआउट की वास्तविक और अनुमानित संभावना को दर्शाता है।
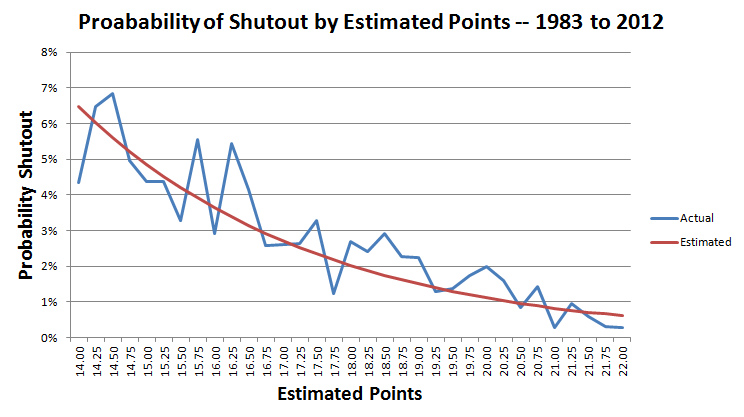
इस खेल में जायंट्स को 17 अंक बनाने की उम्मीद थी।
तालिका के ऊपर दिए गए सूत्र का उपयोग करें:
x = 1.562545 -0.302485 * 17 = -3.579706
शटआउट की संभावना = exp(-3.579706)/( exp(-3.579706)+1) = 2.71%. सटीक रूप से, 0.0271275.
यह देखते हुए कि जायंट्स के शटआउट की स्थिति में डीलरशिप को $420,000 का भुगतान करना पड़ता, पॉलिसी की उचित लागत $420,000 × 0.0271275 = $11,394 होती। आमतौर पर, इस तरह के असामान्य प्रचारों का बीमा करने वाली बीमा कंपनियाँ उचित लागत से दोगुनी होती हैं, इसलिए मुझे $22,788 का प्रीमियम मिलने की उम्मीद थी। इसलिए, डीलरशिप द्वारा चुकाया गया $7,000 का प्रीमियम एक चोरी था। यह मानते हुए कि बॉस ने गणना की है, मैं उस व्यक्ति की जगह नहीं लेना चाहूँगा जिसने $7,000 के प्रीमियम की गणना की थी।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।
वेगास में सबसे अच्छा वायदा ऑड्स कौन प्रदान करता है?
2015 सुपर बाउल पर वायदा दांव के अनुसार, विभिन्न वेगास खेल पुस्तक समूहों में औसत हाउस एज इस प्रकार है।
खेल वायदा में हाउस एज
| खेल पुस्तक | हाउस एज |
|---|---|
| सीजी प्रौद्योगिकी | 21.90% |
| विलियम हिल | 26.63% |
| व्यान | 27.96% |
| कैसर | 35.49% |
| स्टेशन/एल कॉर्टेज़ | 38.33% |
| सोने का टुकड़ा | 39.75% |
| एमजीएम | 40.88% |
| बॉयड/कोस्ट | 49.35% |
| ती | 57.93% |
किसी भी वायदा दांव पर औसत हाउस एज की गणना करने के लिए, कृपया मेरे स्पोर्ट्स फ्यूचर्स कैलकुलेटर का उपयोग करें।
मैंने सुना है कि जेरीज़ नगेट अब NFL टीज़र के लिए आकर्षक ऑड्स नहीं दे रहा है। क्या यह सच है?
दुर्भाग्य से, ऐसा ही है। जेरीज़ नगेट आखिरी जगह थी जहाँ दो लेग वाले 6-पॉइंट एनएफएल टीज़र पर -110, तीन लेग के लिए +180 और चार लेग के लिए +300 का उदार ऑड्स दिया गया था। वोंग टीज़र (जीत के 3- और 7-पॉइंट के अंतर को पार करके) करके, यह एक ठोस लाभप्रद खेल था।
आप विज़ार्ड ऑफ वेगास डॉट कॉम पर मेरे स्पोर्ट्स बुक सर्वेक्षण में वेगास के आसपास के सभी वर्तमान पार्ले और टीज़र ऑड्स पा सकते हैं।
सामान्य रूप से फुटबॉल टीज़र के बारे में अधिक जानकारी के लिए, कृपया एनएफएल में टीज़र बेट्स पर मेरा पेज देखें।
क्या एनएफएल में एक खेल पुस्तिका में 50 से अधिक और दूसरी में 52.5 से कम अंक लेना अच्छी शर्त है?
इस तरह के सवालों के लिए आप NFL में मेरे वैकल्पिक योगों का इस्तेमाल कर सकते हैं। इससे कुल दांव पर अतिरिक्त अंक मिलने की संभावना और उचित रेखा पता चल जाएगी।
मान लीजिए कि उचित ओवर/अंडर लाइन 51 है। पहली तालिका दर्शाती है कि 52.5 से कम पर दांव लगाने पर जीतने की संभावना 54.4% है, बशर्ते कि कोई बराबरी न हो। तीसरी तालिका दर्शाती है कि ओवर पर दांव लगाने पर जीतने की संभावना 53.5% है।
10% रस को मात देने के लिए, आपके जीतने की संभावना 11/21 = 52.38% होनी चाहिए। इन दोनों दांवों का औसत 53.95% है, तो हाँ, बीच का दांव लगाएँ। आपका लाभ 3.0% है।
जब मैं यह प्रश्न लिख रहा हूँ, नियमित एनएफएल सीज़न के ठीक बाद, बोवाडा कैरोलिना पैंथर्स के एनएफसी चैंपियनशिप जीतने पर 18 से 1 का ऑड्स दे रहा है। एरिज़ोना के खिलाफ पहला गेम जीतने के लिए वे पहले से ही छह अंकों के प्रबल दावेदार हैं। उसके बाद बस दो अंक और बाकी हैं।
क्या आपको नहीं लगता कि मैं कैरोलिना पर एनएफसी जीतने का दांव लगाकर जीत सुनिश्चित कर सकता हूं और साथ ही वे जिस किसी के साथ भी खेलें, उस पर पैसे का दांव लगा सकता हूं?
नहीं! फ़्यूचर्स और मनी लाइन पर पसंदीदा दांव लगाना, फ़ुटबॉल पर सट्टा लगाते समय आपके द्वारा लगाए जा सकने वाले दो सबसे खराब दांव हैं। यह एक सट्टेबाजी प्रणाली जैसा लगता है, जिसमें नकारात्मक दांवों का एक क्रम जोड़ा जाता है और योग के सकारात्मक होने की उम्मीद की जाती है। हालाँकि, आपको समझाने के लिए मुझे शायद इससे ज़्यादा की ज़रूरत होगी, तो आइए संख्याओं पर नज़र डालते हैं।
सबसे पहले, पैंथर्स प्लेऑफ़ में सिर्फ़ इसलिए हैं क्योंकि वे एक घटिया डिवीज़न (एनएफसी साउथ) में सबसे कमज़ोर टीम हैं। उनका रिकॉर्ड 7-8 है, और उन्होंने पूरे सीज़न में जितने अंक बनाए हैं, उससे 35 ज़्यादा अंक दिए हैं।
अगर वे इतने ही बुरे हैं, तो आप पूछ सकते हैं कि एरिज़ोना कार्डिनल्स के खिलाफ़ वे छह अंकों के प्रबल दावेदार क्यों हैं? एरिज़ोना ने पहले छह मैचों में कार्सन पामर के प्रयासों के दम पर प्लेऑफ़ में जगह बनाई। छठे मैच में वे चोटिल हो गए थे, लेकिन फिर भी वे प्लेऑफ़ में जगह बनाने में कामयाब रहे। इसके अलावा, कैरोलिना को घरेलू मैदान का फ़ायदा मिलता है।
यह देखते हुए कि कैरोलिना, एरिजोना के खिलाफ छह अंकों की पसंदीदा टीम है, मैं बताता हूं कि उस खेल को जीतने की उनकी संभावना 70.3% है।
मान लीजिए कि वे जीत जाते हैं, तो एनएफसी जीतने के लिए उन्हें ग्रीन बे और सिएटल दोनों को हराना होगा। इन दोनों टीमों को हराने की संभावना क्या है? ध्यान रखें, प्लेऑफ़ नियमों के अनुसार, वे दोनों बार मेहमान टीम ही होंगे।
किसी भी खेल में पॉइंट स्प्रेड का नज़दीकी अनुमान लगाने का एक आसान तरीका है। घरेलू टीम के पॉइंट स्प्रेड के लिए मेरा विज़ार्ड फ़ॉर्मूला यहाँ दिया गया है:
(बाहरी टीम के प्रति खेल नेट अंक) - (घरेलू टीम के प्रति खेल नेट अंक) - 2.67.
आइये एरिज़ोना और ग्रीन बे के बीच एक काल्पनिक मुकाबले पर नजर डालें।
2014 सीज़न के दौरान, कैरोलिना के नेट पॉइंट्स -35 रहे। ग्रीन बे के लिए, यह +138 है। दोनों संख्याओं को 16 से भाग दें, क्योंकि सीज़न में 16 मैच खेले गए हैं, जिससे प्रति मैच जीत का औसत अंतर होगा:
कैरोलिना: -2.1875
ग्रीन बे: +8.6250
मेरे सूत्र का उपयोग करते हुए, घरेलू टीम, ग्रीन बे, का प्रसार -2.1875 - 8.6250 - 2.67 = -13.4825 होना चाहिए।
तो, ग्रीन बे, कैरोलिना के खिलाफ लगभग 13.5 अंकों की पसंदीदा टीम होगी। मैं इस चरण में गणित को छोड़ दूँगा, लेकिन मैं दिखाता हूँ कि 13.5 अंकों से कमज़ोर कैरोलिना के जीतने की संभावना 14.3% है।
सिएटल का रिकॉर्ड ग्रीन बे जितना ही मज़बूत है, पूरे सीज़न में उसके 140 नेट पॉइंट्स हैं। इसलिए कैरोलिना के भी उस मैच को जीतने की संभावना लगभग 14.3% होगी।
कैरोलिना के तीनों गेम जीतने की संभावना 70.3% × 14.3% × 14.3% = 1.44% है। तो, इस संभावना पर एक उचित फ्यूचर्स दांव 68.6 से 1 है!
हाँ, आप तर्क दे सकते हैं कि डेट्रॉइट या डलास भाग्यशाली हो सकते हैं और कॉन्फ्रेंस चैंपियनशिप में जगह बना सकते हैं। आप यह भी तर्क दे सकते हैं कि कैरोलिना के ग्रीन बे और सिएटल को हराने की संभावनाएँ सकारात्मक रूप से सहसंबद्ध हैं। हालाँकि, ये इस तथ्य के सामने मामूली विचार हैं कि मेरी अनुमानित फ़ेयर लाइन 68.6 है और आपको केवल 18 मिल रहे हैं।
आपको मनी लाइन पर पसंदीदा टीमों पर दांव लगाने के खर्च पर भी विचार करना होगा। यह आम तौर पर एक बहुत ही खराब दांव होता है। स्क्वायर बेटर्स मनी लाइन पर बड़ी पसंदीदा टीमों पर दांव लगाना पसंद करते हैं, जिससे दूसरी दिशा में मूल्य बनता है। मनी लाइन पर सात या उससे अधिक अंक वाली अंडरडॉग टीमों पर दांव लगाना मोटे तौर पर एक उचित दांव है, जिसका अर्थ है कि पसंदीदा बेटर्स ही सारा पैसा खर्च कर रहे हैं।
मान लीजिए कि आपको एरिज़ोना पर +250 का दांव मिलता है और अगले दो मैचों में आप 5 से 1 का दांव लगाते हैं। मान लीजिए कि आप कैरोलिना पर 18 से 1 के अनुपात में $100 का दांव लगाते हैं।
सबसे पहले, आप +250 पर एरिजोना पर $40 का दांव लगाते हैं, एक बचाव के तौर पर। अगर वे जीत जाते हैं, तो आप उस दांव पर $100 जीतेंगे और फ्यूचर्स दांव पर $100 हारेंगे और बराबरी पर आ जाएँगे।
अगर कैरोलिना, एरिज़ोना को हरा देता है, तो आप सिएटल पर $140 जीतने के लिए $700 का दांव लगाएँगे। अगर सिएटल जीत जाता है, जो कि उसे जीतना चाहिए, तो आपको $140 का फायदा होगा, जो एरिज़ोना और फ्यूचर्स बेट पर आपके नुकसान की भरपाई कर देगा, यानी आप बराबरी पर होंगे।
अगर कैरोलिना कैरोलिना को हरा देती है, तो आपको एरिज़ोना, सिएटल और फ्यूचर्स बेट पर लगे $840 के नुकसान को जीतने के लिए $4,200 का दांव लगाना होगा। अगर कैरोलिना हार जाती है, तो आप बराबरी पर होंगे। अगर वे जीत जाते हैं, तो आप $40+$700+$4,200=$4,940 हार जाएँगे। फ्यूचर्स बेट पर जीते गए $1,800 उस नुकसान की भरपाई के लिए पर्याप्त नहीं होंगे।
अंत में, एनएफसी जीतने के लिए कैरोलिना को साथ ले जाने और रास्ते में हेजिंग करने का आपका विचार बहुत ही गलत है।
आत्महत्या पूल के लिए आपकी क्या सलाह है?
जो लोग नहीं जानते, उनके लिए बता दें कि सुसाइड पूल एक आखिरी व्यक्ति के लिए एक प्रतियोगिता है, जो आमतौर पर NFL पर आधारित होती है, हालाँकि कोई भी स्पोर्ट्स लीग चल सकती है। इसके कुछ बुनियादी नियम इस प्रकार हैं।
- प्रत्येक खिलाड़ी खेलने के लिए समान राशि का भुगतान करता है।
- हर हफ़्ते हर खिलाड़ी को उस हफ़्ते के एक खेल के विजेता की भविष्यवाणी करनी होती है। सभी खेलों का स्कोर सीधे ऊपर की ओर होता है, स्प्रेड के विपरीत नहीं।
- यदि कोई खिलाड़ी कभी गलत हो जाता है तो उसे तुरंत प्रतियोगिता से बाहर कर दिया जाता है।
- कोई भी खिलाड़ी एक ही टीम को एक से अधिक बार नहीं चुन सकता।
- जो व्यक्ति अंतिम स्थान पर खड़ा रहता है, वह पॉट जीतता है।
इसमें अतिरिक्त नियम भी हो सकते हैं, जैसे कि पूल चलाने वाले व्यक्ति को हिस्सा मिलेगा, तथा जब पूल कुछ लोगों में बंट जाएगा तो उसे आपस में बांट लिया जाएगा, बशर्ते कि यह आपसी सहमति से हो।
आगे बढ़ने से पहले, officefootballpool.com से पिछले सीज़न के परिणाम यहां दिए गए हैं।
ऑफिस फुटबॉल पूल — 2014 सीज़न
| सप्ताह | टीम | फैलाना | की पसंद |
|---|---|---|---|
| 1 | फिल | -10.5 | 54 |
| 1 | ठाठ | -7 | 29 |
| 1 | गड्ढा | -6.5 | 14 |
| 1 | डेट | -6 | 6 |
| 1 | केसी | -3 | 5 |
| 1 | एनवाईजे | -5.5 | 5 |
| 1 | पूर्वोत्तर | -4 | 1 |
| 1 | एस एफ | -4.5 | 1 |
| 1 | एसटीएल | -3.5 | 1 |
| 2 | मांद | -12.5 | 38 |
| 2 | जीबी | -8 | 23 |
| 2 | नहीं | -6.5 | 7 |
| 2 | एस एफ | -7 | 5 |
| 2 | टीबी | -5.5 | 3 |
| 2 | धोना | -6 | 2 |
| 2 | सिन | -5.5 | 1 |
| 2 | पूर्वोत्तर | -5.5 | 1 |
| 3 | पूर्वोत्तर | -14 | 44 |
| 3 | नहीं | -10 | 16 |
| 3 | एटल | -6.5 | 3 |
| 3 | सिन | -6.5 | 1 |
| 3 | इंडस्ट्रीज़ | -6 | 1 |
| 4 | एसडी | -13 | 34 |
| 4 | इंडस्ट्रीज़ | -7.5 | 20 |
| 4 | गड्ढा | -7.5 | 10 |
| 4 | बाल | -3 | 1 |
| 5 | नहीं | -10 | 21 |
| 5 | जीबी | -8 | 13 |
| 5 | मांद | -7.5 | 6 |
| 5 | डेट | -6.5 | 5 |
| 5 | फिल | -6.5 | 3 |
| 5 | दल | -6.5 | 2 |
| 5 | गड्ढा | -6 | 2 |
| 5 | एसडी | -6.5 | 1 |
| 5 | समुद्र | -7 | 1 |
| 5 | एस एफ | -5 | 1 |
| 6 | समुद्र | -8.5 | 21 |
| 6 | मांद | -9.5 | 13 |
| 6 | एसडी | -7 | 7 |
| 6 | सिन | -6.5 | 5 |
| 6 | दस | -4 | 2 |
| 6 | एटल | -3 | 1 |
| 6 | एस एफ | -3 | 1 |
| 7 | पूर्वोत्तर | -9.5 | 9 |
| 7 | समुद्र | -6.5 | 9 |
| 7 | जीबी | -6.5 | 3 |
| 7 | बाल | -6.5 | 2 |
| 7 | बुफ़ | -5.5 | 2 |
| 7 | धोना | -5 | 2 |
| 7 | दल | -6.5 | 1 |
| 8 | दल | -9.5 | 12 |
| 8 | केसी | -7 | 5 |
| 8 | क्लेव | -7 | 1 |
| 8 | एमआईए | -6 | 1 |
| 9 | एस एफ | -10 | 3 |
| 9 | सिन | -10.5 | 2 |
| 9 | होना | -14.5 | 2 |
| 10 | बाल | -9.5 | 2 |
| 10 | सिनेमा | -6 | 1 |
| 10 | होना | -9 | 1 |
| 11 | जीबी | -5.5 | 1 |
| 11 | मेरा | -6 | 1 |
| 11 | नहीं | -7 | 1 |
| 12 | औद्योगिक | -14 | 2 |
| 13 | बाल | -6.5 | 1 |
| 13 | डेट | -7 | 1 |
| 14 | नहीं | -10 | 1 |
"चयन" कॉलम उन खिलाड़ियों की संख्या को दर्शाता है जिन्होंने उस टीम को चुना।
ध्यान दें कि किसी ने भी एक बार भी किसी अंडरडॉग को नहीं चुना। 497 बार चुने गए खिलाड़ियों में, औसत पॉइंट स्प्रेड 9.3 था।
मुझे नहीं पता कि उन्होंने सप्ताह 14 में चयन क्यों दर्ज किया, क्योंकि उस समय केवल एक ही खिलाड़ी बचा था।
अन्य खिलाड़ियों के व्यवहार के इस अध्ययन के आधार पर, यहाँ सुसाइड पूल के लिए मेरी बुनियादी रणनीति दी गई है। ये सभी सामान्य दिशानिर्देश हैं, न कि कोई सख्त नियम जिनका आपको हर हफ्ते पालन करना होगा।
- याद रखें कि आपके दुश्मन दूसरे खिलाड़ी हैं। एनएफएल में बाधा डालने पर ज़्यादा ध्यान न दें, बल्कि अपने प्रतिद्वंद्वियों को हराने पर ध्यान दें।
- सबसे बड़े पसंदीदा को मत चुनिए। ज़्यादातर लोग यही करेंगे। उम्मीद है कि वह बड़ा पसंदीदा हार जाएगा और मैदान काफ़ी कम हो जाएगा। जब कोई बड़ा पसंदीदा हारता है, तो आप पीड़ित होने के बजाय, बचे रहना चाहेंगे।
- इस नियम को न भूलें कि आप एक ही टीम को दो बार नहीं चुन सकते। लेकिन, आप हमेशा बेहतरीन टीमें नहीं चुन सकते। कभी-कभी आपको बेहतरीन टीमों पर आसान जीत बरकरार रखने के लिए, खराब टीमों से खेलने वाली औसत टीमों को चुनना चाहिए।
- हैंडीकैपिंग की चिंता मत कीजिए। किसी भी पिक को जीतने की अपनी संभावनाओं के संकेतक के रूप में पॉइंट स्प्रेड का ही इस्तेमाल कीजिए।
- अगर किसी हफ़्ते में सिर्फ़ दो बड़े पसंदीदा मैच हों, तो मैं उन दोनों से बचूँगा। याद रखें कि आप जीतने की संभावना वाले मैच चुनने के साथ-साथ ज़्यादातर पसंदीदा मैचों को चुनने में संतुलन बनाने की कोशिश कर रहे हैं। एक सामान्य नियम के तौर पर, मुझे लगता है कि तीसरा सबसे ज़्यादा स्प्रेड चुनना एक अच्छा विचार है, खासकर अगर आप किसी बेहतरीन टीम को बर्बाद नहीं कर रहे हैं।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
टचडाउन के बाद अंक के लिए नए नियमों का आधे अंक वाले पार्ले कार्ड पर क्या प्रभाव पड़ेगा, इस पर आपकी क्या राय है?
अन्य पाठकों के लाभ के लिए, मेरी तरकीबों में एक चीज़ है, हाफ-पॉइंट पार्ले कार्ड्स पर 3 और 7 के पॉइंट स्प्रेड से अतिरिक्त हाफ पॉइंट्स का फ़ायदा उठाना। मैंने यह साबित कर दिया है कि यह एक विश्वसनीय, हालाँकि बहुत अस्थिर, फ़ायदे का खेल है।
नया नियम अतिरिक्त किक को 15-यार्ड लाइन पर वापस ले जाता है। इससे किक की सफलता की संभावना कम हो जाएगी और दो-पॉइंट रूपांतरण के ज़्यादा प्रयास होंगे। दो-पॉइंट रूपांतरण के ज़्यादा प्रयासों के साथ, चाहे वे सफल हों या नहीं, तीन या सात अंकों से ज़्यादा गेम नहीं तय होने चाहिए, जिससे आधे पॉइंट वाले पार्ले कार्ड पर इन महत्वपूर्ण अंकों से अतिरिक्त आधा पॉइंट पाने का महत्व कम हो जाएगा। क्या हमें चिंतित होना चाहिए? देखते हैं।
सबसे पहले, हमें चिंता करनी चाहिए, लेकिन ज़रूरी नहीं कि इसी वजह से। नियमों में हुए दूसरे बदलावों ने डिफेंस की आक्रामकता को कम किया है, जिससे ज़्यादा स्कोरिंग मैच हुए हैं। नीचे दिया गया ग्राफ़ 1994 से 2014 तक हर सीज़न में हर मैच में बनाए गए औसत अंकों को दर्शाता है।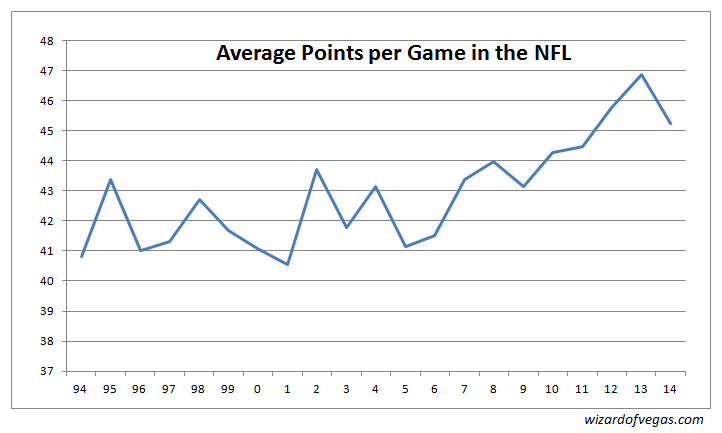
जैसा कि ग्राफ़ में दिखाया गया है, 2006 तक प्रत्येक खेल में औसत अंक लगभग 42 थे। हालाँकि, 2007 से, यह औसत हर साल लगभग आधा अंक बढ़ रहा है। इससे यह सवाल उठता है कि क्या औसत अंकों में यह वृद्धि जीत के अंतर के वितरण को, खासकर 3 और 7 के जादुई अंकों के लिए, समतल कर देती है। अगला ग्राफ़ वर्ष दर वर्ष जीत के अंतर के तीन और सात अंकों की संभावना दर्शाता है।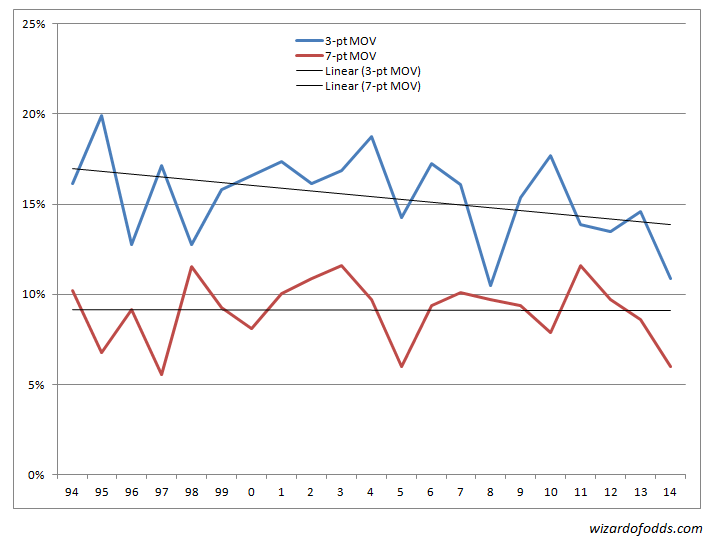
जैसा कि आप देख सकते हैं, सात अंकों के अंतर से जीत की संभावना 9.1% पर स्थिर बनी हुई है। हालाँकि, तीन अंकों के अंतर से जीत की संभावना लगातार कम होती जा रही है, खासकर 2004 के बाद से। यह बुरा है क्योंकि NFL में तीन अंकों का अंतर बहुत ज़्यादा है।
जीत के कम तीन-पॉइंट अंतर का कारण चाहे जो भी हो, आधे पॉइंट वाले पार्ले कार्डों का मूल्य घट रहा है। क्या नए अतिरिक्त पॉइंट नियम के साथ यह और भी बदतर हो जाएगा?
मेरा जवाब है कि इससे नुकसान तो होना चाहिए, लेकिन ज़्यादा नहीं। नियम बदलने से पहले, मेरा अनुमान है कि लगभग 4.8% टचडाउन के बाद दो-पॉइंट रूपांतरण का प्रयास किया गया था। जब मैं यह लिख रहा हूँ, नियम बदलने के बाद से केवल दो हफ़्ते ही खेल खेले गए हैं। 2015 सीज़न के पहले दो हफ़्तों में, 167 टचडाउन हुए और 15 टचडाउन के बाद दो-पॉइंट रूपांतरण का प्रयास किया गया, यानी प्रयास दर 9.0% रही।
गणितीय रूप से कहें तो, मुझे लगता है कि दो-पॉइंट रूपांतरण का इस्तेमाल ज़्यादा आम होना चाहिए, खासकर विचरण चाहने वाली कमज़ोर टीमों के लिए, और मुझे समझ नहीं आता कि ऐसा क्यों नहीं है। आपने यह नहीं पूछा था, लेकिन मुझे बस अपनी बात कहनी थी।
मान लीजिए, उदाहरण के लिए, मैं स्प्रेड के विरुद्ध लगातार 54% दांव लगा सकता हूँ। अपने बैंकरोल को जल्द से जल्द बढ़ाने के लिए, 6 से 1 का भुगतान करने वाली तीन-टीम पार्लेज़ में से कौन सा ज़्यादा मोटा, सपाट दांव होगा?
अच्छा सवाल है। 11 से 10 पर आपका लाभ 3.09% है और पार्ले पर 10.22%। यह पार्ले के लिए एक अच्छा मामला लगता है।
हालाँकि, याद रखें कि किसी भी लाभप्रद खेल में बैंकरोल वृद्धि के लिए सर्वोत्तम रणनीति केली मानदंड का उपयोग करना है। केली के अनुसार, सर्वोत्तम दांव का आकार वह है जो दांव के बाद बैंकरोल के अपेक्षित लॉग को अधिकतम करता है। केवल दो संभावित परिणामों वाले दांवों के लिए, सर्वोत्तम दांव का आकार, लाभ को दांव द्वारा प्राप्त राशि से "एक" के आधार पर विभाजित करने पर प्राप्त होने वाले लाभ के बराबर होता है।
स्ट्रेट बेट्स पर 10 से 11 का भुगतान होता है। इससे इष्टतम बेट का आकार 0.030909/(10/11) = 0.034000 होगा। 3.09% के खिलाड़ी लाभ पर, आप प्रति गेम स्ट्रेट बेटिंग पर अपने बैंकरोल का 0.001051 गुना जीतने की उम्मीद कर सकते हैं।
पार्ले पर इष्टतम दांव का आकार 0.102248/6 = 0.017041 है। 0.102248 के खिलाड़ी लाभ पर, आप प्रति गेम सीधे दांव पर अपने बैंकरोल का 0.001742 गुना जीतने की उम्मीद कर सकते हैं।
हालाँकि, सीधी सट्टेबाजी बेहतर है क्योंकि आप तीन बार दांव लगा सकते हैं। इसलिए, फ्लैट सट्टेबाजी के प्रति दांव पर अपेक्षित लाभ को तीन से गुणा करें, जिससे 3 × 0.001051 = 0.003153 प्राप्त होगा। यह पार्ले सट्टेबाजी के बैंकरोल वृद्धि से 81% अधिक है।
यदि आपका बैंकरोल इतना बड़ा है कि आप अधिकतम दांव सीमा से टकरा जाते हैं, तो आपको संभवतः पहले पार्ले दांव लगाना चाहिए, जो लाइनों को स्थानांतरित नहीं करता है, और फिर अपने सीधे दांव लगाएं।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
जैसा कि आप जानते हैं, एनएफएल में अब अतिरिक्त अंक के लिए 15-यार्ड लाइन से प्रयास करना होगा, जबकि दो-पॉइंट रूपांतरण का प्रयास दो-यार्ड लाइन पर ही रहता है। क्या आपको लगता है कि इससे निर्णय का गणित बदल जाएगा? दूसरे शब्दों में, अब सही खेल क्या है?
यह एक सीमांत निर्णय है, और मुझे लगता है कि NFL ने नियम बदलते समय यही सोचा था। निर्णय लेते समय जिन बातों पर विचार किया जाना चाहिए, वे हैं:
- किक मारने से सफलता की संभावना.
- दो-बिंदु रूपांतरण के लिए जाने पर सफलता की संभावना।
- प्रत्येक टीम की जीतने की समग्र संभावनाएँ।
खेल के अंतिम क्षणों में, महत्वपूर्ण संख्याओं पर विचार करना भी महत्वपूर्ण है। उदाहरण के लिए, अगर खेल का अंतिम समय हो चुका है और आपने अभी-अभी टचडाउन बनाकर अपनी टीम को तीन अंकों से आगे कर दिया है, तो आपको किक मारनी चाहिए। अगर आप टचडाउन बना लेते हैं, तो आप चार अंकों से आगे हो जाएँगे और दूसरी टीम को जीतने के लिए टचडाउन बनाने पर मजबूर कर देंगे। अगर आप दो अंक बनाने की कोशिश करते हैं और चूक जाते हैं, तो दूसरी टीम केवल एक फील्ड गोल से बराबरी कर सकती है। इसलिए, मैं अपनी चर्चा खेल के शुरुआती क्षणों तक ही सीमित रखूँगा, जब महत्वपूर्ण संख्याएँ कोई बड़ा कारक नहीं होतीं।
आपके प्रश्न का उत्तर देने के लिए, मैंने एक सिमुलेशन प्रोग्राम लिखा है। हालाँकि यह थोड़ा कच्चा है, मुझे लगता है कि यह फ़ील्ड गोल, टचडाउन और टर्नओवर के संदर्भ में NFL की प्रकृति को दर्शाने में काफी सटीक है।
केविन रूडी द्वारा लिखे गए लेख "15 यार्ड लाइन पर अतिरिक्त पॉइंट ले जाने से क्या प्रभाव पड़ेगा?" के अनुसार, 15 यार्ड लाइन से अतिरिक्त पॉइंट बनाने की संभावना 94.2% है। मैंने अपने प्रोग्राम में 94% की संभावना रखी है, ताकि संख्याएँ अच्छी और गोल रहें।
दो-बिंदु रूपांतरण की संभावना पर ज़्यादा मतभेद हैं। ज़ाहिर है, यह भी विशिष्ट रक्षा और आक्रमण के अनुसार काफ़ी भिन्न होगा। मैंने 1% के समूहों में, 46% से 50% की दो-बिंदु रूपांतरण सफलता पर सिमुलेशन चलाया।
हर सिमुलेशन में, मैंने एक टीम को हमेशा किक करने और विरोधी टीम को सफलता की हर संभावना पर कन्वर्ज़न के लिए प्रयास करने को कहा। मैंने ऐसे सिमुलेशन भी चलाए जहाँ दोनों टीमें हमेशा किक करती थीं, ताकि दो-पॉइंट कन्वर्ज़न के परिणामों की तुलना करने के लिए कुछ हो।
नीचे दी गई तालिका 1 दो समान रूप से कुशल टीमों के परिणाम दर्शाती है। टीम A हमेशा टचडाउन के बाद किक करती है। तालिका टीम B के जीतने की संभावना और प्रति गेम बनाए गए औसत अतिरिक्त अंकों को दर्शाती है, जो इस बात पर निर्भर करता है कि टीम B किक करती है या दो-पॉइंट रूपांतरण (2PC) अपनाती है और उसकी सफलता की संभावना क्या है।
तालिका 1 - समान टीमें
| टीम बी रणनीति | टीम बी सम्भवतः जीतना | औसत अतिरिक्त अंक |
|---|---|---|
| लात मारना | 50.00% | 0.0001 |
| 2पीसी -- 46% | 49.76% | 0.0491 |
| 2पीसी -- 47% | 49.90% | 0.0000 |
| 2पीसी -- 48% | 50.05% | 0.0492 |
| 2पीसी -- 49% | 50.19% | 0.0980 |
| 2पीसी -- 50% | 50.33% | 0.1461 |
ध्यान दें कि सफलता की 47% संभावना के साथ, किक करने या दो अंक प्राप्त करने की कोशिश करने पर अपेक्षित अतिरिक्त अंक 0.94 हैं। हालाँकि, दो अंक प्राप्त करने की कोशिश में जीतने की संभावना 0.1% कम है। मेरा अनुमान है कि ऐसा इसलिए है क्योंकि अगर आप चूक जाते हैं, तो दूसरी टीम के पास दो फील्ड गोल के साथ बराबरी करने का मौका होता है। यह ध्यान देने योग्य है कि यह महत्वपूर्ण संख्यात्मक प्रभाव काफी छोटा है, लेकिन अन्य सभी चीजें समान होने पर, रूढ़िवादी होने और किक करने के पक्ष में है। सार यह है कि दो बराबर टीमों के साथ, दो-पॉइंट रूपांतरण में सफलता की संभावना कम से कम 49% होनी चाहिए।
नीचे दी गई तालिका 2 दो असमान टीमों के परिणाम दिखाती है, जहाँ टीम A ज़्यादा मज़बूत है। टीम A हमेशा टचडाउन के बाद किक करती है। इसमें ऊपर दी गई तालिका 1 के समान आँकड़े दिखाई देते हैं।
तालिका 2 - टीम A अधिक मजबूत
| टीम बी रणनीति | टीम बी सम्भवतः जीतना | औसत अतिरिक्त अंक |
|---|---|---|
| लात मारना | 28.83% | -7.0039 |
| 2पीसी -- 46% | 29.01% | -7.0519 |
| 2पीसी -- 47% | 29.16% | -7.0039 |
| 2पीसी -- 48% | 29.30% | -6.9568 |
| 2पीसी -- 49% | 29.45% | -6.9083 |
| 2पीसी -- 50% | 29.60% | -6.8595 |
तालिका 2 दर्शाती है कि कमज़ोर टीम को सफलता की सभी सूचीबद्ध संभावनाओं पर दो-अंकीय रूपांतरण का विकल्प चुनना चाहिए। यहाँ तक कि 45% पर भी, जहाँ कुल अंकों की अपेक्षित संख्या कम है। आप पूछ सकते हैं कि ऐसा क्यों है? ऐसा इसलिए है क्योंकि किसी भी खेल में, कमज़ोर टीम को भिन्नता की तलाश करनी चाहिए और मज़बूत टीम को इससे घृणा करनी चाहिए।
नीचे दी गई तालिका 3 दो असमान टीमों के परिणाम दिखाती है, जहाँ टीम B ज़्यादा मज़बूत है। टीम A हमेशा टचडाउन के बाद किक करती है। इसमें ऊपर दी गई तालिका 1 और 2 के समान आँकड़े दिखाई देते हैं।तालिका 3 - टीम बी मजबूत
| टीम बी रणनीति | टीम बी सम्भवतः जीतना | औसत अतिरिक्त अंक |
|---|---|---|
| लात मारना | 71.17% | 7.0042 |
| 2पीसी -- 46% | 70.53% | 6.9349 |
| 2पीसी -- 47% | 70.67% | 7.0030 |
| 2पीसी -- 48% | 70.82% | 7.0725 |
| 2पीसी -- 49% | 70.97% | 7.1412 |
| 2पीसी -- 50% | 71.12% | 7.2109 |
ध्यान दें कि तालिका 3 में टीम B के किक मारकर जीतने की संभावना 71.17% के बराबर दिखाई गई है। यह दिखाई गई सफलता की सभी संभावनाओं के लिए इससे कम है, भले ही अपेक्षित अंकों की संख्या 49% या 50% की सफलता की संभावना पर अधिक हो। इसका कारण, फिर से, यह है कि कमज़ोर टीमों को भिन्नता की तलाश करनी चाहिए और मज़बूत टीमों को इससे बचना चाहिए। दो-बिंदु रूपांतरण का प्रयास खेल में अस्थिरता लाता है, यही कारण है कि कमज़ोर टीमों को, अन्य सभी चीज़ें समान होने पर, मज़बूत टीमों की तुलना में, इसे आज़माने के लिए अधिक इच्छुक होना चाहिए।
नियमित सीज़न में कैरोलिना पैंथर्स के 16-0 से जीतने की कितनी संभावना है? क्या इनमें से कोई भी दांव सही है?
हाँ +425?
नहीं -550?
मेरे पास किसी भी खेल के पॉइंट स्प्रेड का अनुमान लगाने का एक तरीका है जो वास्तविक स्प्रेड के काफ़ी क़रीब आता है, बशर्ते कोई बड़ी चोट, चोट से उबरना, निलंबन या ऐसी ही कोई समस्या न हो। किसी भी टीम द्वारा बनाए जाने वाले अपेक्षित पॉइंट्स का फ़ॉर्मूला इस प्रकार है:
[(औसत आक्रामक अंक) + (विरोधी टीम द्वारा दिए गए औसत अंक)]/2 + (घरेलू मैदान पर खेलने पर 1.5, अन्यथा -1.5)।
अंक प्रसार (अपेक्षित मेहमान टीम अंक) - (अपेक्षित घरेलू टीम अंक) होगा।
आइए सेंट्स के खिलाफ 13वें हफ्ते के मैच को एक उदाहरण के तौर पर देखें। पैंथर्स मेहमान टीम है। पैंथर्स ने इस सीज़न में औसतन प्रति गेम 32.3 आक्रामक अंक बनाए हैं। सेंट्स ने औसतन प्रति गेम 30.8 अंक गंवाए हैं। मेरे फॉर्मूले के हिसाब से, पैंथर्स (32.3+30.8)/2 - 1.5 = 30.05 अंक हासिल करने की उम्मीद कर सकते हैं।
फिर, सेंट्स के लिए भी यही करें। उन्होंने इस सीज़न में औसतन प्रति गेम 23.7 आक्रामक अंक बनाए हैं। पैंथर्स ने औसतन प्रति गेम 18.6 अंक गंवाए हैं। मेरे सूत्र से (23.7 + 18.6)/2 + 1.5 = सेंट्स द्वारा बनाए गए 22.65 अंक प्राप्त होते हैं।
इसलिए, पैंथर्स 30.05 - 22.65 = 7.4 अंकों से जीतने की उम्मीद कर सकते हैं। इसके बाद, प्रत्येक गेम जीतने की संभावना जानने के लिए मेरे प्रोप बेट कैलकुलेटर का उपयोग करें। मेरा कैलकुलेटर गेम में ओवर/अंडर पूछेगा, लेकिन मुझे लगता है कि सीधे तौर पर कौन जीतेगा, इसके लिए केवल स्प्रेड ही मायने रखता है। कुल योग के लिए, इस सीज़न का NFL औसत 46 डालें। आप देखेंगे कि 7.4 के पॉइंट स्प्रेड के लिए घरेलू टीम की जीत की फ़ेयर लाइन +271 है। इसका मतलब है कि पैंथर्स के लिए फ़ेयर लाइन -271 है। यह 271/371 = 73.05% जीतने की संभावना के बराबर है।
फिर बाकी चार खेलों के लिए भी ऐसा ही करें और गुणनफल निकालें। या आप नीचे दी गई तालिका का उपयोग कर सकते हैं।
पैंथर्स सप्ताह 13 से 17
| सप्ताह | विरोध टीम | जगह | अपेक्षित तेंदुआ अंक | अपेक्षित प्रतिद्वंद्वी अंक | पैंथर्स जीत अंतर | पैंथर्स गोरा रेखा | संभावना जीतना |
|---|---|---|---|---|---|---|---|
| 13 | संतों | दूर | 30.05 | 22.65 | 7.4 | -271 | 0.730458 |
| 14 | फाल्कन | घर | 28.3 | 19.6 | 8.7 | -323 | 0.763593 |
| 15 | दिग्गज | दूर | 27.05 | 23.85 | 3.2 | -154 | 0.606299 |
| 16 | फाल्कन | दूर | 25.3 | 22.6 | 2.7 | -144 | 0.590164 |
| 17 | बुक्कैनियर्स | घर | 30.35 | 19.05 | 11.3 | -458 | 0.820789 |
प्रायिकता स्तंभ का गुणनफल निकालने पर आपको पाँचों गेम जीतने की प्रायिकता मिलती है, जो 0.163813 है। यह +510 की एक उचित रेखा के अनुरूप है। इसलिए, आपके द्वारा उद्धृत दोनों रेखाएँ अच्छी नहीं हैं।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।
2015 सीज़न के 13वें सप्ताह में पैंथर्स/सेंट्स गेम के पहले हाफ में आखिरी खेल क्या था?
मेरा मानना है कि इसे "टचडाउन रिटर्न के बाद पॉइंट" कहा जाता है। इस सीज़न में लागू हुए नियम में बदलाव के अनुसार, अगर टचडाउन के बाद किक का प्रयास विफल हो जाता है और विरोधी टीम टचडाउन स्कोर कर लेती है, तो स्कोरिंग टीम के लिए दो पॉइंट गिने जाएँगे। 2015 सीज़न से पहले, यह डेड बॉल होता था। यह NFL में पहला और अब तक का एकमात्र ऐसा स्कोर था। आप इसका वीडियो YouTube पर देख सकते हैं।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।
जैसा कि आप शायद जानते होंगे, 16वीं वरीयता प्राप्त यूएमबीसी ने एनसीएए बास्केटबॉल चैंपियनशिप टूर्नामेंट में पहली वरीयता प्राप्त यूनिवर्सिटी ऑफ़ वर्जीनिया को हरा दिया। मार्च मैडनेस के 34 साल के इतिहास में, अपने वर्तमान स्वरूप में, ऐसा पहले कभी नहीं हुआ। इसका एक परफेक्ट ब्रैकेट भरने की संभावना पर क्या प्रभाव पड़ता है?
उस खेल और 2018 सीज़न के अन्य सभी खेलों के लिए अपने मॉडल को समायोजित करने के बाद, मुझे 42,743,890,552 में से 1 के परफेक्ट ब्रैकेट की प्रायिकता मिलती है। आप मेरी रणनीति और मैं उस आंकड़े तक कैसे पहुँचा, यह मेरे पेज "परफेक्ट ब्रैकेट की प्रायिकता" पर पढ़ सकते हैं।
मैं खेल सट्टेबाजी में बाधाओं को अमेरिकी और यूरोपीय तरीकों के बीच कैसे परिवर्तित कर सकता हूं?
आइए हम संभावनाओं को अमेरिकी तरीके से और संभावनाओं को यूरोपीय तरीके से व्यक्त करें।
अमेरिकी से यूरोपीय बनने के लिए:
यदि a>0, तो e=1+(a/100).
यदि a<0, तो e=(a-100)/a.
यूरोपीय से अमेरिकी बनने के लिए:
यदि e>=2, तो a=100×(e-1).
यदि e<2, तो a=100/(1-e).
मैंने विलियम हिल स्पोर्ट्स बुक्स पर इस बात पर प्रस्ताव दांव देखे हैं कि किसी मेजर लीग बेसबॉल खेल में किसी खास दिन ग्रैंड स्लैम होगा या नहीं। खेले गए खेलों की संख्या के आधार पर इसकी उचित संभावना और रेखा क्या है?
अन्य पाठकों की सुविधा के लिए, 11 मई, 2019 के ग्रैंड स्लैम के लिए यहाँ पंक्तियाँ दी गई हैं। कॉलम के शीर्षकों में "हाँ" और "नहीं" लिखा होना चाहिए, न कि "घर" और "बाहर"।

इस प्रश्न का उत्तर देने के लिए, मैंने 2011 से 2018 सीज़न तक के हर MLB गेम का अवलोकन किया। उन आठ सीज़न में, 19,440 खेलों में 858 ग्रैंड स्लैम हुए। इस प्रकार, प्रति गेम ग्रैंड स्लैम की औसत संख्या 0.0441 है। यह किसी भी दिए गए गेम में ग्रैंड स्लैम होने की संभावना के समान नहीं है, क्योंकि एक गेम में एक से अधिक ग्रैंड स्लैम हो सकते हैं। पॉइसन वितरण का उपयोग करते हुए, किसी भी दिए गए गेम में कम से कम एक ग्रैंड स्लैम होने की संभावना 4.3176% है।
इस संभावना के साथ, खेलों की संख्या के आधार पर कम से कम एक ग्रैंड स्लैम के लिए संभावना और उचित रेखा को दर्शाने वाली निम्नलिखित तालिका बनाना आसान है।
ग्रैंड स्लैम संभावना
| खेल | संभावना ग्रैंड स्लैम | फेयर लाइन |
|---|---|---|
| 1 | 4.32% | 2216 |
| 2 | 8.45% | 1084 |
| 3 | 12.40% | 706 |
| 4 | 16.18% | 518 |
| 5 | 19.80% | 405 |
| 6 | 23.27% | 330 |
| 7 | 26.58% | 276 |
| 8 | 29.75% | 236 |
| 9 | 32.78% | 205 |
| 10 | 35.68% | 180 |
| 11 | 38.46% | 160 |
| 12 | 41.12% | 143 |
| 13 | 43.66% | 129 |
| 14 | 46.09% | 117 |
| 15 | 48.42% | 107 |
| 16 | 50.65% | -103 |
मुझे एक चेतावनी ज़रूर जोड़नी चाहिए कि मेरा जवाब एमएलबी औसत पर आधारित है। किसी भी दिन, खिलाड़ी को खेले जा रहे विशिष्ट मैचों को ध्यान में रखना चाहिए। खासकर, ओवर/अंडर लाइन जितनी ज़्यादा होगी, ग्रैंड स्लैम जीतने की संभावना उतनी ही ज़्यादा होगी।
न्यू जर्सी स्थित MGM जैसी कई स्पोर्ट्स बुक, सचमुच मुफ़्त बेट की पेशकश कर रही हैं—अगर बेट हार जाती है, तो वे नकद में रिफंड कर देते हैं जिसे आप निकाल सकते हैं। स्लॉट्स के लिए 100% नुकसान की छूट की तरह, लेकिन स्पोर्ट्स बेटिंग पर भी लागू। इस प्रमोशन के तहत मुझे किस तरह का बेट लगाना चाहिए?
इस तरह के किसी भी फ्री-रोल के साथ, आपको चाँद पर निशाना लगाना चाहिए। अगर वे पार्ले की अनुमति देते हैं, तो इस प्रमोशन के तहत जितनी अनुमति हो, उतनी पार्ले बेट लगाएँ और अधिकतम भुगतान तक पहुँचने के लिए पर्याप्त इवेंट्स पार्ले करें, जो लास वेगास में आमतौर पर लगभग $100,000 होता है।
यदि आपको किसी एक घटना पर दांव लगाना है, तो सबसे बड़ा लॉन्ग-शॉट खोजें।
यह रणनीति सबसे अच्छी क्यों है, इसके एक उदाहरण के तौर पर, $100 के दांव वाले डबल-ज़ीरो रूलेट में इसी प्रमोशन पर विचार करें। अगर आप सम-राशि का दांव लगाते हैं, तो आपको मिलने वाली अपेक्षित राशि (18/38)×$200 + (20/38)×$100 = $147.37 होगी। हालाँकि, अगर आप एक ही संख्या पर दांव लगाते हैं, तो आपको (1/38)×$3600 + (37/38)×$100 = $192.11 मिलने की उम्मीद हो सकती है।
मैंने एक ऑनलाइन स्पोर्ट्स बुक पर एक प्रमोशन देखा, जहाँ NFL में मनी लाइन बेट को स्वतः ही विजेता घोषित कर दिया जाता था, अगर चुनी गई टीम 17 या उससे ज़्यादा अंकों से आगे होती। इसका मूल्य क्या है?
यह प्रमोशन उस हारी हुई शर्त को जीत में बदल देगा जो अन्यथा चुनी गई टीम के 17 या उससे ज़्यादा अंकों से आगे होने के बाद भी हार जाती है। ऐसी स्थिति का एक अच्छा उदाहरण सुपर बाउल 51 में अटलांटा फाल्कन्स पर लगाई गई शर्त है। तीसरे क्वार्टर में एक समय फाल्कन्स 28-3 से आगे थे, यानी 25 अंकों की बढ़त। हालाँकि, वे 28-34 से हार गए।
इस प्रश्न का उत्तर देने के लिए, मैंने 2000 से 2015 तक प्रत्येक NFL सीज़न में खेले गए 4,131 खेलों का अवलोकन किया। नीचे दी गई तालिका खेल के दौरान विजेता टीम के बीच हुए सबसे बड़े अंतर को दर्शाती है। प्रायिकता स्तंभ उन पाँच खेलों को छाँट देता है जो बराबरी पर समाप्त हुए।
सबसे बड़े घाटे पर काबू पाया गया
| घाटा | खेल | संभावना |
|---|---|---|
| बाँधना | 5 | 0.000000 |
| 0 | 1804 | 0.437227 |
| 1 | 100 | 0.024237 |
| 2 | 29 | 0.007029 |
| 3 | 560 | 0.135725 |
| 4 | 235 | 0.056956 |
| 5 | 23 | 0.005574 |
| 6 | 131 | 0.031750 |
| 7 | 622 | 0.150751 |
| 8 | 39 | 0.009452 |
| 9 | 34 | 0.008240 |
| 10 | 195 | 0.047261 |
| 11 | 84 | 0.020359 |
| 12 | 14 | 0.003393 |
| 13 | 49 | 0.011876 |
| 14 | 104 | 0.025206 |
| 15 | 10 | 0.002424 |
| 16 | 6 | 0.001454 |
| 17 | 36 | 0.008725 |
| 18 | 14 | 0.003393 |
| 19 | 2 | 0.000485 |
| 20 | 4 | 0.000969 |
| 21 | 22 | 0.005332 |
| 22 | 0 | 0.000000 |
| 23 | 2 | 0.000485 |
| 24 | 5 | 0.001212 |
| 25 | 1 | 0.000242 |
| 26 | 0 | 0.000000 |
| 27 | 0 | 0.000000 |
| 28 | 1 | 0.000242 |
| कुल | 4131 | 1.000000 |
"टाई" पंक्ति उन 16 सीज़न के पाँच मैचों को दर्शाती है जो बराबरी पर समाप्त हुए, इसलिए उन्हें गिनते नहीं हैं। "0" पंक्ति उन 43.7% मैचों को दर्शाती है जहाँ जीतने वाली टीम कभी पीछे नहीं रही।
तालिका दर्शाती है कि 87 खेलों में एक टीम 17 या उससे ज़्यादा अंकों से हारी और फिर जीत गई। 4126 खेलों में (अर्थात पाँच बराबरी वाले मैचों को छोड़कर) यह संभावना 2.11% है।
यह देखते हुए कि ये स्थितियाँ हार को जीत में बदल देंगी, हम इस संभावना को दोगुना करके 4.22% का मान प्राप्त करते हैं। मनी लाइन दांवों पर हाउस एज लगभग 4.76% पर स्प्रेड के विरुद्ध दांवों के बराबर है। 4.22% घटाने पर, हमें इस प्रमोशन के तहत 0.54% का बहुत कम हाउस एज मिलता है।
अब जबकि मार्च मैडनेस 2023 समाप्त हो चुका है, तो आपके परफेक्ट ब्रैकेट और सीड द्वारा अपेक्षित जीत की संभावना में क्या बदलाव आया है?
एक आदर्श ब्रैकेट के लिए मेरी रणनीति यह है कि हर मैच में उच्च वरीयता प्राप्त टीम (अर्थात कम वरीयता प्राप्त टीम) को चुना जाए। अंत में, जब 1 बनाम 1 वरीयता हो जाए, तो यादृच्छिक रूप से चुनें। 38 सीज़न के आँकड़ों के आधार पर। प्रत्येक संभावित मैच के लिए कुछ संभावनाएँ इस प्रकार हैं:
- 1 बनाम 16 बीज = 99.31%
- 2 बनाम 15 सीड = 93.06%
- 3 बनाम 14 सीड = 84.72%
- 4 बनाम 13 सीड = 78.47%
- 5 बनाम 12 सीड = 64.58%
- 6 बनाम 11 सीड = 62.50%
- 7 बनाम 10 बीज = 60.42%
- 8 बनाम 9 सीड = 51.39%
पहले राउंड में बने रहने के लिए, आपको ऊपर बताए गए सभी आठ गेम चार-चार बार जीतने होंगे। इसकी संभावना 1/4354 है।
यहां दूसरे राउंड में विभिन्न मुकाबले दिए गए हैं, बशर्ते आप इस रणनीति का उपयोग करके वहां तक पहुंच जाएं।
- 1 बनाम 8 बीज = 80.00%
- 2 बनाम 7 सीड = 69.51%
- 3 बनाम 6 बीज = 60.00%
- 4 बनाम 5 सीड = 56.00%
दूसरे राउंड में बने रहने के लिए, आपको ऊपर बताए गए चारों गेम में से प्रत्येक में चार-चार बार जीतना होगा। इसकी संभावना 1/811 है।
यहां तीसरे राउंड में विभिन्न मुकाबले दिए गए हैं, बशर्ते आप इस रणनीति का उपयोग करके वहां तक पहुंच जाएं।
- 1 बनाम 4 सीड = 73.44%
- 2 बनाम 3 सीड = 60.71%
दूसरे राउंड में बने रहने के लिए, आपको ऊपर बताए गए दोनों खेलों में से प्रत्येक में चार-चार बार जीत हासिल करनी होगी। इसकी संभावना 1/54 है।
चौथे राउंड में 1 बनाम 2 सीड गेम्स होंगे। 1 सीड के जीतने की संभावना 53.73% है। ऐसा चार बार होने की संभावना 0.5373 4 = 0.112355 है।
पाँचवें राउंड में, दो 1 बनाम 1 गेम होंगे। प्रत्येक जीतने की संभावना 1/2 है, इसलिए दो जीतने की संभावना 1/4 है।
छठे राउंड में, एक 1 बनाम 1 गेम होगा। जीतने की संभावना 1/2 है।
इन सभी संभावनाओं का गुणनफल निकालने पर 13,569,150,522 में 1 के पूर्ण ब्रैकेट की संभावना प्राप्त होती है।
आपके अन्य प्रश्नों के उत्तर देने के लिए, यहां प्रत्येक टीम की औसत जीत, सीड के अनुसार दी गई है।
- 1 सीड = 3.29 औसत जीत
- 2 सीड = 2.32 औसत जीत
- 3 सीड = 1.85 औसत जीत
- 4 सीड = 1.55 औसत जीत
- 5 सीड = 1.16 औसत जीत
- 6 सीड = 1.07 औसत जीत
- 7 सीड = 0.9 औसत जीत
- 8 सीड = 0.74 औसत जीत
- 9 सीड = 0.59 औसत जीत
- 10 सीड = 0.61 औसत जीत
- 11 सीड = 0.63 औसत जीत
- 12 सीड = 0.51 औसत जीत
- 13 सीड = 0.25 औसत जीत
- 14 सीड = 0.16 औसत जीत
- 15 सीड = 0.11 औसत जीत
- 16 सीड = 0.01 औसत जीत


