टीवी गेम शो - अक्सर पूछे जाने वाले प्रश्न
यह बिल्कुल जुआ नहीं है, लेकिन प्राइस इज़ राइट गेम शो में मैं हमेशा सोचता रहा हूँ कि जब आप आखिरी स्पिन नहीं कर रहे हों, तो बड़े पहिये को घुमाते समय सबसे अच्छी रणनीति क्या होनी चाहिए। मान लीजिए कि आप अपने स्पिन को नियंत्रित नहीं कर सकते (पूरी तरह से यादृच्छिक परिणाम), $.05 से $1.00 तक 5 सेंट की वृद्धि के साथ, आपको एक स्पिन या दो स्पिन एक साथ मिलते हैं, तो आप 1.00 से ऊपर नहीं जा सकते। आपको अपना दूसरा स्पिन किस राशि पर नहीं लेना चाहिए ताकि आपके पास अपने बाद स्पिन करने वाले खिलाड़ी को हराने का सबसे अच्छा मौका हो?
यदि पहले खिलाड़ी का पहला स्पिन 65 सेंट या उससे कम है तो उसे दोबारा स्पिन करना चाहिए।
यदि निम्नलिखित में से कोई भी शर्त सत्य हो तो दूसरे खिलाड़ी को पुनः स्पिन करना चाहिए।
- उसका स्कोर पहले खिलाड़ी के स्कोर से कम है।
- उसका स्कोर 50 सेंट या उससे कम है।
- उसका स्कोर 65 सेंट या उससे कम है और वह पहले खिलाड़ी के साथ बराबरी पर है।
प्राइस इज राइट पर प्लिंको गेम के लिए इष्टतम रणनीति क्या है?
बाएं से दाएं पुरस्कार $100, $500, $1000, $0, $10000, $0, $1000, $500, $100 हैं। मुझे सही विश्लेषण करने के लिए बोर्ड पर खूंटियों की सटीक संरचना जानने की आवश्यकता होगी, लेकिन बोर्ड को आंखों से देखने पर (ऊपर दिए गए लिंक को देखें) मुझे दृढ़ता से लगता है कि खिलाड़ी को पक को सीधे $10,000 के पुरस्कार के ऊपर गिराना चाहिए। हालांकि यह दो शून्य से घिरा हुआ है, लेकिन शीर्ष पुरस्कार की तुलना में अन्य सभी पुरस्कार फीके हैं। इसलिए खिलाड़ी की रणनीति शीर्ष पुरस्कार को सीधे ऊपर गिराकर इसकी संभावना को अधिकतम करने की होनी चाहिए। अपनी परिकल्पना की पुष्टि या खंडन करने के लिए मैंने खोज की और इस खेल के अध्ययन के लिए समर्पित कई लिंक हैं। यह ( www.amstat.org/publications/jse/v9n3/biesterfeld.html ) बेहतर लिंक में से एक है, इसमें आंशिक रूप से कहा गया है कि पक को बीच में गिराने पर अपेक्षित मूल्य $2557.91 है, बीच के दोनों ओर $2265.92 है, तथा जैसे-जैसे आप केंद्र से दूर जाते हैं, यह कम होता जाता है।
गेम शो "लेट्स मेक अ डील" में तीन दरवाज़े हैं। मान लीजिए कि दो दरवाज़ों से एक बकरी निकलती है और एक दरवाज़ा एक नई कार दिखाता है। होस्ट, मोंटी हॉल, दो प्रतियोगियों को एक दरवाज़ा चुनने के लिए चुनते हैं। हर बार मोंटी पहले एक दरवाज़ा खोलता है जिसमें एक बकरी निकलती है। मान लीजिए इस बार वह दरवाज़ा पहले प्रतियोगी का था। हालाँकि मोंटी ने वास्तव में ऐसा कभी नहीं किया, लेकिन अगर मोंटी दूसरे प्रतियोगी को इस समय दरवाज़ा बदलने का मौका दे, यानी दूसरे बंद दरवाज़े पर। क्या उसे दरवाज़ा बदलना चाहिए?
हाँ! इस समस्या की जड़ यह है कि मेज़बान को बकरी वाला दरवाज़ा खोलने के लिए पहले से ही तय कर दिया गया है। वह जानता है कि किस दरवाज़े में कार है, इसलिए खिलाड़ी चाहे कोई भी दरवाज़ा चुनें, वह हमेशा पहले बकरी ही दिखा सकता है। इस प्रश्न को "मोंटी हॉल विरोधाभास" के नाम से जाना जाता है। इसके बारे में ज़्यादातर भ्रम इसलिए है क्योंकि अक्सर जब प्रश्न पूछा जाता है, तो यह स्पष्ट नहीं किया जाता कि मेज़बान को कार कहाँ है, और वह हमेशा पहले बकरी ही दिखाता है। मुझे लगता है कि इसका कुछ दोष मर्लिन वोस सावंत पर भी है, जिन्होंने अपने कॉलम में प्रश्न को गलत तरीके से लिखा था। मान लीजिए कि इनाम दरवाज़ा 1 के पीछे है। अगर खिलाड़ी (दूसरा प्रतियोगी) ने बदलाव न करने की रणनीति बनाई होती, तो क्या होता, यहाँ बताया गया है।
- खिलाड़ी दरवाज़ा 1 चुनता है --> खिलाड़ी जीतता है
- खिलाड़ी दरवाज़ा 2 चुनता है --> खिलाड़ी हार जाता है
- खिलाड़ी दरवाज़ा 3 चुनता है --> खिलाड़ी हार जाता है
यदि खिलाड़ी के पास स्विचिंग की रणनीति होगी तो क्या होगा, नीचे बताया गया है।
- खिलाड़ी दरवाज़ा 1 चुनता है --> मेज़बान दरवाज़ा 2 या 3 के पीछे बकरी दिखाता है --> खिलाड़ी दूसरे दरवाज़े पर जाता है --> खिलाड़ी हार जाता है
- खिलाड़ी दरवाज़ा 2 चुनता है --> मेज़बान दरवाज़ा 3 के पीछे बकरी दिखाता है --> खिलाड़ी दरवाज़ा 1 पर जाता है --> खिलाड़ी जीतता है
- खिलाड़ी दरवाज़ा 3 चुनता है --> मेज़बान दरवाज़ा 2 के पीछे बकरी दिखाता है --> खिलाड़ी दरवाज़ा 1 पर जाता है --> खिलाड़ी जीतता है
इसलिए, स्विच न करने से खिलाड़ी के जीतने की संभावना 1/3 रह जाती है। स्विच करने से खिलाड़ी के जीतने की संभावना 2/3 रह जाती है। इसलिए खिलाड़ी को ज़रूर स्विच करना चाहिए।
मोंटी हॉल विरोधाभास पर आगे पढ़ने के लिए, मैं विकिपीडिया पर लेख की अनुशंसा करता हूं।
मेरा प्रश्न एक ऐसी समस्या के बारे में है जिसे "दो लिफाफों का विरोधाभास" कहा जाता है। आप एक गेम शो में हैं। आपके सामने दो लिफाफे हैं, जिनमें से प्रत्येक में अज्ञात राशि है। आपको बताया जाता है कि एक लिफाफे में दूसरे लिफाफे से दोगुनी राशि है। अब आपसे एक लिफाफा चुनने को कहा जाता है। आप एक लिफाफा चुनते हैं। उसमें $50,000 हैं। अब आपको बताया जाता है कि आप चुना हुआ लिफाफा रख सकते हैं या दूसरे लिफाफे से बदल सकते हैं। क्या आपको बदलना चाहिए? अगर आपको पहले से पता है कि आप बदल सकते हैं, तो इससे कोई फर्क नहीं पड़ता, क्योंकि आप वही लिफाफा चुनेंगे जो आपको अंततः चाहिए। लेकिन चूँकि आपको लिफाफा चुनने के बाद ही बदलने के बारे में पता चलता है, तो मूल चयन और बदलने का विकल्प दो स्वतंत्र घटनाएँ हैं, है ना? कहने का तात्पर्य यह है कि, बदलने या न बदलने का निर्णय लेते समय, दूसरे लिफाफे में या तो आपके पास मौजूद राशि का दोगुना या आधा होता है। तो उसमें या तो $100,000 होंगे या $25,000। चूँकि दोनों में से किसी एक के होने की 50% संभावना है, इसलिए दूसरे लिफाफे का अपेक्षित मूल्य $62,500 है। सामान्य तौर पर, अगर हम x = आपके द्वारा मूल रूप से चुनी गई राशि मान लें, तो दूसरे लिफ़ाफ़े का EV 1.25x होगा। इसलिए, अदला-बदली हमेशा सही होती है। क्या यह सही है? धन्यवाद।
मैं इस समस्या से अच्छी तरह वाकिफ़ हूँ। मैंने अपनी गणित की समस्याओं वाली वेबसाइट पर, समस्या संख्या 6 पर इसका समाधान किया है। वहाँ मैंने सामान्य स्थिति का समाधान किया है, जिसमें पहले लिफ़ाफ़े में बिल्कुल भी न देखने की बात भी शामिल है। हालाँकि, आपके प्रश्न का उत्तर देने के लिए, हम उस स्थान को नज़रअंदाज़ नहीं कर सकते जहाँ खेल हो रहा है। आपने कहा कि यह एक "गेम शो" था। ज़्यादातर गेम शो में $50,000 की जीत एक अच्छी जीत होती है। "प्राइस इज़ राइट" के बहुत कम प्रतियोगी कभी इतनी ऊँची रकम जीत पाते हैं। मेरा अनुमान है कि "हू वॉन्ट्स टू बी अ मिलियनेयर" के 50% से भी कम खिलाड़ी इतनी ऊँची रकम जीत पाते हैं। इस बीच, गेम शो में $25,000 की जीत कोई असामान्य बात नहीं है। "प्राइस इज़ राइट" में अक्सर कारें जीती जाती हैं, जिनका मूल्य लगभग $25,000 होता है। "हू वॉन्ट्स टू बी अ मिलियनेयर" में $32,000 का स्तर एक आम जीत है। "जेपर्डी" में प्रति शो औसत जीत लगभग $25,000 होती है। महान केन जेनिंग्स ने अपनी 74 जीतों में औसतन केवल $34,091 ही जीते थे। तो, मेरा कहना यह है कि किसी गेम शो के लिए $50,000 एक अच्छी जीत है, और $100,000 की जीत $25,000 की तुलना में बहुत कम देखी जाती है। इसलिए, एक गेम शो पारखी के रूप में, मेरा मानना है कि दूसरे लिफाफे में $100,000 की तुलना में $25,000 होने की संभावना ज़्यादा है। इसलिए, आपके उदाहरण में, मैं कह रहा हूँ कि $50,000 रखना बेहतर है। इससे यह भी पता चलता है कि आप यह कभी नहीं मान सकते कि दूसरे लिफाफे में आधी या दोगुनी राशि होने की संभावना बिल्कुल 50/50 है। एक बार जब आप राशि देख लेते हैं और उसे उस स्थान के संदर्भ में देखते हैं जहाँ यह खेला जा रहा है, तो आप बदलाव का एक समझदारी भरा फैसला ले सकते हैं, जिससे 1.25x का तर्क बेमानी हो जाता है।
मेरा सवाल गेम शो, "डील ऑर नो डील" के बारे में है, जो ऑस्ट्रेलिया में बहुत लोकप्रिय है और जल्द ही इंग्लैंड में भी आने वाला है। प्रतियोगी को छब्बीस गिने हुए ब्रीफ़केस दिखाए जाते हैं, जिनमें से प्रत्येक में 50 सेंट से लेकर 2,00,000 डॉलर तक की एक गुप्त राशि होती है, जैसा कि नीचे दिखाया गया है।
- $0.50
- $1
- $2
- $5
- $10
- $25
- $50
- $75
- $100
- $150
- $250
- $500
- $750
- $1,000
- $1,500
- $2,000
- $3,000
- $5,000
- $7,500
- $10,000
- $15,000
- $30,000
- $50,000
- $75,000
- $100,000
- $200,000
प्रतियोगी ब्रीफ़केस में से एक को अपना सूटकेस चुनता है। एलिमिनेशन प्रक्रिया के दौरान, दूसरे सूटकेस खोलकर, वे यह पता लगाने की कोशिश करते हैं कि उनके सूटकेस में कितने पैसे हैं, या "बैंक ऑफर" लेना ज़्यादा समझदारी होगी। बैंक ऑफर बचे हुए ब्रीफ़केस के अंकगणितीय माध्य पर आधारित होते हैं, लेकिन उसके बराबर नहीं। इसलिए, अगर ज़्यादातर बड़े मूल्य के ब्रीफ़केस बचे हैं, तो इस बात की ज़्यादा संभावना है कि प्रतियोगी का ब्रीफ़केस कीमती होगा, और इसलिए बैंक ऑफर ज़्यादा होगा। इसके विपरीत, अगर खिलाड़ी कम भाग्यशाली रहा है और उसने ज़्यादा मूल्यवान ब्रीफ़केस खोले हैं, तो बैंक ऑफर कम होगा। अगर आप इस खेल में एक प्रतियोगी होते, तो सबसे अच्छी रणनीति क्या होती? एक गैर-गणितीय सहज ज्ञान युक्त रणनीति यह होगी कि बैंक ऑफर को नज़रअंदाज़ कर दिया जाए और तब तक केस खोलते रहें जब तक कि या तो $200,000 के केस खुल न जाएँ और वे खत्म न हो जाएँ, या $100,000 और $75,000 दोनों खुल न जाएँ और वे खत्म न हो जाएँ। इस खेल के पीछे क्या गणित है, जादूगर?
डील या नो डील अभी अमेरिका में शुरू हुई है। नियम तो वही हैं, बस इनाम दस लाख डॉलर तक है, जो इस प्रकार है।
- 0.01
- 1
- 5
- 10
- 25
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 50000
- 75000
- 100000
- 200000
- 300000
- 400000
- 500000
- 750000
- 1000000
खेल का प्रवाह इस प्रकार है:
- खिलाड़ी अपने लिए एक केस चुनता है
- खिलाड़ी शेष 25 मामलों में से छह को खोलता है।
- बैंकर एक प्रस्ताव रखता है.
- यदि खिलाड़ी मना कर देता है तो वह शेष 19 मामलों में से पांच और खोल देता है।
- बैंकर एक प्रस्ताव रखता है.
- यदि खिलाड़ी मना कर देता है तो वह शेष 14 केसों में से चार और केस खोल देता है।
- बैंकर एक प्रस्ताव रखता है.
- यदि खिलाड़ी मना कर देता है तो वह शेष बचे 10 केसों में से तीन और केस खोल देता है।
- बैंकर एक प्रस्ताव रखता है.
- यदि खिलाड़ी मना कर देता है तो वह शेष 7 केसों में से दो और केस खोल लेता है।
- बैंकर एक प्रस्ताव रखता है.
- यदि खिलाड़ी मना कर देता है तो वह शेष बचे मामलों में से एक और खोल देता है।
- चरण 11 और 12 को तब तक दोहराते रहें जब तक खिलाड़ी प्रस्ताव स्वीकार नहीं कर लेता या खिलाड़ी के पास अंतिम बंद केस नहीं आ जाता।
निम्नलिखित चार्ट खिलाड़ी के अपेक्षित मूल्य और बैंकर के प्रस्ताव को दर्शाता है।
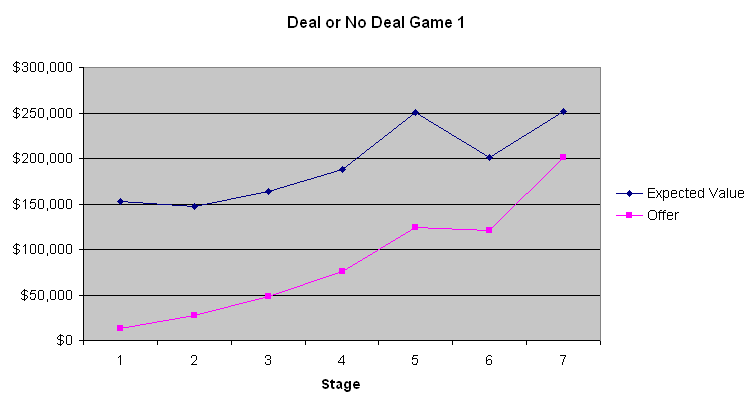
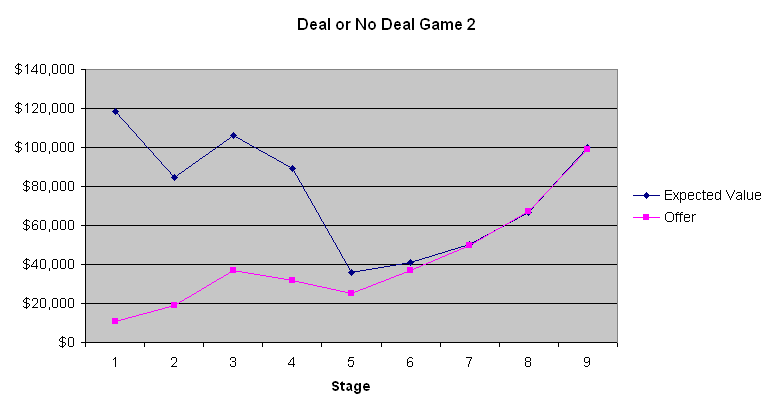
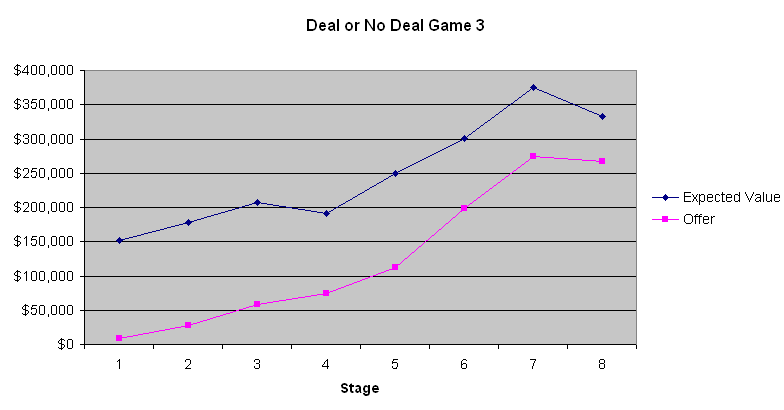
इन तीन चार्टों से सीखने वाली सबसे स्पष्ट बात यह है कि पहले चार से छह बैंक ऑफ़र बहुत ही खराब सौदे होते हैं। किसी भी सूटकेस के खुलने से पहले एक औसत सूटकेस में $131,477.54 होते हैं। पहले चरण में केवल $9000 से $13000 की पेशकश करना एक ऐसा सौदा है जो केवल एक मूर्ख ही कर सकता है। हालाँकि, धीरे-धीरे ऑफ़र बेहतर होते जाते हैं। गेम 2 हमें दिखाता है कि अपेक्षित मूल्य लगभग वही थे जो बैंकर ने खेल के अंत में पेश किए थे, जब खिलाड़ी का अपेक्षित मूल्य काफी कम था। हालाँकि, गेम 1 और 3 में, जब अपेक्षित मूल्य अधिक थे, तो बैंकर स्पष्ट रूप से बड़ी रकम शामिल होने पर अधिकांश लोगों के जोखिम से बचने वाले स्वभाव का फायदा उठाने की कोशिश कर रहा था। मुझे नहीं पता कि इससे कोई फर्क पड़ा या नहीं, लेकिन गेम 2 में प्रतियोगी एक जुआरी लग रहा था जो बड़ी जीत हासिल करना चाहता था। मेज़बान, जो बैंकर से फ़ोन पर संवाद करता है, की टिप्पणियों के आधार पर, ऐसा प्रतीत होता है कि बैंकर प्रतियोगियों के शब्दों और कार्यों को ध्यान में रखता है। अगर मैं बैंकर की जगह होता, तो मैं भी लगभग वैसा ही व्यवहार करता।
यदि खिलाड़ी न तो जोखिम से बचने वाला है और न ही जोखिम लेने को इच्छुक है, और कर संबंधी प्रभावों को भी अनदेखा कर रहा है, तो खिलाड़ी को बैंकरों के प्रस्तावों को तब तक अस्वीकार करते रहना चाहिए जब तक कि शेष सूटकेसों का औसत एक से अधिक न हो जाए। अधिकांश लोगों के लिए आयकर संहिता की प्रगतिशील प्रकृति सौदे को स्वीकार करने के पक्ष में है। जैसा कि मैंने पहले कहा है, मैं मोटे तौर पर कहूँगा कि धन का मूल्य राशि के लघुगणक के समानुपाती होता है। इसलिए खेल में जाने से पहले आपके पास जितनी अधिक संपत्ति होगी, उतना ही अधिक आपको जुआ खेलने और बैंकरों के प्रस्तावों को अस्वीकार करने के लिए इच्छुक होना चाहिए। इतनी बड़ी राशि शामिल होने के साथ, कोई भी रणनीति सभी के लिए उपयुक्त नहीं होगी। हालाँकि, मैं काफी विश्वास के साथ कह सकता हूँ कि खिलाड़ी को पहले चार से छह प्रस्तावों को अस्वीकार कर देना चाहिए और फिर मामले के आधार पर प्रस्तावों को स्वीकार करना चाहिए (शब्द-क्रीड़ा का इरादा)।
लिंक:
आप डील ऑर नो डील को NBC.com पर देख सकते हैं।
पिछले शो का संग्रह .
"डील या नो डील" देख रहा हूँ। मुझे समझ आ रहा है कि बैंकर का "ऑफ़र" बस केसों के बचे हुए मूल्य को केसों की संख्या से भाग देने पर मिलता है [लगभग बराबर या बराबर]। क्या इस खेल में कोई रणनीति है, या "डील" हमेशा ही एक ठीक-ठाक चीज़ होती है? क्या यह इस बात पर निर्भर करता है कि आपको कितने केस खोलने हैं या कुछ और?
जैसा कि मेरे 26 दिसंबर, 2005 के कॉलम में दिखाया गया है, बैंकर का प्रस्ताव आमतौर पर बाकी मामलों के औसत से बहुत कम होता है। हालाँकि, अगर ऐसा हमेशा होता, तो हर रणनीति का अपेक्षित मूल्य समान होता। खिलाड़ी हर प्रस्ताव पर उदासीन होता।
"डील या नो डील" की शुरुआत में 1,000,000 डॉलर वाले केस को चुनने की संभावना 26 में से 1 है। 1 को छोड़कर सभी मामलों को खत्म करने के बाद, क्या संभावना है कि मेरे केस में मिलियन डॉलर शामिल हों। क्या यह 50-50 है या अभी भी 26 में से 1 है?
50-50
अपने 5 अप्रैल, 2006 के कॉलम में आपने लिखा था कि अगर डील ऑर नो डील में सिर्फ़ दो मामले बचे हैं और मिलियन डॉलर अभी भी दांव पर है, तो मेरे मामले में मिलियन डॉलर मिलने की संभावना 50-50 है। मैं इससे सहमत नहीं हूँ। क्या यह मोंटी हॉल समस्या का ही एक रूपांतर नहीं है? यानी, उनके मामले की तुलना में स्टेज पर मिलियन डॉलर मिलने की संभावना ज़्यादा है?
नहीं। इस बारे में बहुत से लोग मुझसे बहस कर रहे हैं। कई लेखक दावा करते हैं कि अतिरिक्त जानकारी डालने पर प्रायिकताएँ नहीं बदल सकतीं। इसलिए अगर प्रायिकता 26 में 1 से शुरू होती है, तो उसे वहीं रहना चाहिए। सट्टेबाजी प्रणाली के विक्रेताओं के कहने के विपरीत, अतिरिक्त जानकारी डालने पर प्रायिकताएँ वास्तव में बदल सकती हैं। मैं यहाँ बुनियादी प्रायिकता सिखाने की कोशिश नहीं करना चाहता, लेकिन सशर्त प्रायिकता या बेयस प्रमेय पर किसी भी कॉलेज स्तर की गणित की किताब में इस विषय को अच्छी तरह से शामिल किया जाना चाहिए।
चलिए मैं आपको बताता हूँ कि 'लेट्स मेक अ डील' में क्या हुआ था। प्रतियोगी तीन पर्दों में से एक को चुनता था। एक में बहुत ही कीमती इनाम होता था और बाकी दो में छोटे इनाम। तर्क के लिए मान लेते हैं कि एक परदे के पीछे एक कार थी और बाकी दो के पीछे एक बकरी। तब मोंटी हमेशा, मैं दोहराता हूँ हमेशा, दो अनचुने पर्दों में से एक को खोलकर एक बकरी निकालता था। सैकड़ों शो के बाद इसका मतलब यह हुआ कि मोंटी हॉल (मेजबान) जानता था कि कार कहाँ है और उसने जानबूझकर एक पर्दा खोला जिससे एक बकरी निकल आई। ज़ाहिर है जब खिलाड़ी ने अपना पर्दा चुना तो कार को पकड़ने की प्रायिकता 1/3 थी और दो अनचुने पर्दों में से एक के कार को पकड़ने की प्रायिकता 2/3 थी। तब मोंटी को एक अनचुने परदे को खोलने के लिए पूर्वनिर्धारित किया जाता है जिसमें एक गोल होता है। यहाँ पूर्वनिर्धारित महत्वपूर्ण शब्द है। चूँकि मोंटी इस स्तर पर खिलाड़ी का पर्दा नहीं खोल सकता, इसलिए खिलाड़ी के पर्दे द्वारा कार को दिखाने की प्रायिकता 1/3 रहती है। एक बिना चुने हुए पर्दे पर कार दिखने की संभावना 2/3 रहती है, हालाँकि अब सब कुछ एक ही पर्दे पर है। इसलिए एक बकरी के दिखने के बाद, खिलाड़ी के पर्दे पर कार दिखने की संभावना 1/3 होती है और दूसरे बंद पर्दे पर कार दिखने की संभावना 2/3 होती है, जिससे बदलाव करना एक समझदारी भरा फैसला होता है।
नीचे दी गई तालिका सभी संभावित परिणामों को दर्शाती है। उस स्थिति में जहाँ खिलाड़ी ने कार वाला पर्दा चुना था, मैंने मोंटी को मनमाने ढंग से पर्दा खोलने को कहा था। आप देख सकते हैं कि स्विच न करने पर जीतने की संभावना 1/3 होती है, और स्विच करने पर जीतने की संभावना 2/3 होती है।
चलो एक सौदा करते हैं
| खिलाड़ी चुनता | कार | परदा खोला गया | संभावना | जीतें स्विचन |
| 1 | 1 | 1 | 0% | लागू नहीं |
| 1 | 1 | 2 | 5.56% | एन |
| 1 | 1 | 3 | 5.56% | एन |
| 1 | 2 | 1 | 0% | लागू नहीं |
| 1 | 2 | 2 | 0% | लागू नहीं |
| 1 | 2 | 3 | 11.11% | वाई |
| 1 | 3 | 1 | 0% | लागू नहीं |
| 1 | 3 | 2 | 11.11% | वाई |
| 1 | 3 | 3 | 0% | लागू नहीं |
| 2 | 1 | 1 | 0% | लागू नहीं |
| 2 | 1 | 2 | 0% | लागू नहीं |
| 2 | 1 | 3 | 11.11% | वाई |
| 2 | 2 | 1 | 5.56% | एन |
| 2 | 2 | 2 | 0% | लागू नहीं |
| 2 | 2 | 3 | 5.56% | एन |
| 2 | 3 | 1 | 11.11% | वाई |
| 2 | 3 | 2 | 0% | लागू नहीं |
| 2 | 3 | 3 | 0% | लागू नहीं |
| 3 | 1 | 1 | 0% | लागू नहीं |
| 3 | 1 | 2 | 11.11% | वाई |
| 3 | 1 | 3 | 0% | लागू नहीं |
| 3 | 2 | 1 | 11.11% | वाई |
| 3 | 2 | 2 | 0% | लागू नहीं |
| 3 | 2 | 3 | 0% | लागू नहीं |
| 3 | 3 | 1 | 5.56% | एन |
| 3 | 3 | 2 | 5.56% | एन |
| 3 | 3 | 3 | 0% | लागू नहीं |
इस बीच, डील ऑर नो डील में कुछ भी पूर्वनिर्धारित नहीं होता। मान लीजिए डील ऑर नो डील में शेष राशि $0.01, $1, और $1,000,000 थी। तीन केस बचे होने पर, यह संभव है कि खुले केस में मिलियन डॉलर हों। नीचे दी गई तालिका तीन केस बचे होने पर संभावित परिणाम दर्शाती है। याद रखें, खिलाड़ी अपना केस खुद नहीं खोल सकता।
सौदा या नहीं सौदा
| खिलाड़ी चुनता | मिलियन डॉलर | मामला खोला गया | संभावना | जीतें स्विचन |
| 1 | 1 | 1 | 0% | लागू नहीं |
| 1 | 1 | 2 | 5.56% | एन |
| 1 | 1 | 3 | 5.56% | एन |
| 1 | 2 | 1 | 0% | लागू नहीं |
| 1 | 2 | 2 | 5.56% | निराशाजनक |
| 1 | 2 | 3 | 5.56% | वाई |
| 1 | 3 | 1 | 0% | लागू नहीं |
| 1 | 3 | 2 | 5.56% | वाई |
| 1 | 3 | 3 | 5.56% | निराशाजनक |
| 2 | 1 | 1 | 5.56% | निराशाजनक |
| 2 | 1 | 2 | 0% | लागू नहीं |
| 2 | 1 | 3 | 5.56% | वाई |
| 2 | 2 | 1 | 5.56% | एन |
| 2 | 2 | 2 | 0% | लागू नहीं |
| 2 | 2 | 3 | 5.56% | एन |
| 2 | 3 | 1 | 5.56% | वाई |
| 2 | 3 | 2 | 0% | लागू नहीं |
| 2 | 3 | 3 | 5.56% | निराशाजनक |
| 3 | 1 | 1 | 5.56% | निराशाजनक |
| 3 | 1 | 2 | 5.56% | वाई |
| 3 | 1 | 3 | 0% | लागू नहीं |
| 3 | 2 | 1 | 5.56% | वाई |
| 3 | 2 | 2 | 5.56% | निराशाजनक |
| 3 | 2 | 3 | 0% | लागू नहीं |
| 3 | 3 | 1 | 5.56% | एन |
| 3 | 3 | 2 | 5.56% | एन |
| 3 | 3 | 3 | 0% | लागू नहीं |
डील या नो डील तालिका दर्शाती है कि तीन केस बचे होने पर खिलाड़ी द्वारा मिलियन डॉलर का केस खोलने की संभावना 1/3 (जीतने की कोई उम्मीद नहीं) है, स्विच करने वाले खिलाड़ी के जीतने की संभावना 1/3 है, और स्विच करने वाले खिलाड़ी के हारने की संभावना 1/3 है। इस प्रकार, केस बदलने की संभावनाएँ समान हैं। जब केवल दो केस बचे हों, तो प्रत्येक केस में बड़ा इनाम मिलने की संभावना 50/50 है।
अब एक और डील या नो डील वाले सवाल का समय आ गया है। मान लीजिए बैंकर के सारे सौदे और सेलीन डायोन की मेहमान भूमिका के बाद, आपके पास दो सूटकेस बचते हैं, $500,000 और $1,000,000 का। मुझे लगता है कि बैंकर का प्रस्ताव $750,000 से थोड़ा कम होगा। आप कौन सा चुनेंगे? अगर बचे हुए दो ब्रीफ़केस $0.01 और $1,000,000 वाले हों तो क्या होगा? मुझे लगता है कि यह सब इस बात पर निर्भर करता है कि आप जुआरी हैं या नहीं, और इसका ऑड्स से कोई लेना-देना नहीं है। मैं इसलिए पूछ रहा हूँ क्योंकि मुझे आश्चर्य है कि क्या कोई कभी $1,000,000 जीत पाएगा (भले ही उसने जादुई ब्रीफ़केस ही क्यों न चुना हो)।
जब इनाम जीवन बदल देने वाली रकम बन जाएँ, तो समझदार खिलाड़ी को अपेक्षित मूल्य को अधिकतम करने की कीमत पर संयम से खेलना चाहिए। एक अच्छी रणनीति अपेक्षित खुशी को अधिकतम करना होनी चाहिए। मुझे लगता है कि खुशी मापने का एक अच्छा फंक्शन आपकी कुल संपत्ति का लघुगणक है। मान लीजिए एक ऐसे व्यक्ति के पास $100,000 की मौजूदा संपत्ति है, जिसके सामने $0.01 और $1,000,000 के दो विकल्प हैं। "कोई सौदा नहीं" मानकर अपेक्षित खुशी 0.5*log($100,000.01) + 0.5*log($1,100,000) = 5.520696 है। मान लीजिए b वह बैंक ऑफर है जहाँ खिलाड़ी इसे लेने के लिए उदासीन है।
लॉग(बी) = 5.520696
बी = 10 5.520696
बी = $331,662.50.
तो इस काल्पनिक खिलाड़ी को $331,662.50 के बैंक ऑफर पर कोई आपत्ति नहीं होनी चाहिए। खेल में प्रवेश करते समय आपकी संपत्ति जितनी कम होगी, आपको उतना ही संयम से खेलना चाहिए। आमतौर पर खेल के अंतिम चरण में बैंक ऑफर अपेक्षित मूल्य के करीब होते हैं, कभी-कभी थोड़े ज़्यादा। एक खिलाड़ी के दस लाख जीतने का एकमात्र तर्कसंगत तरीका यह है कि उसके पास खेल में प्रवेश करते समय बहुत अधिक संपत्ति हो और/या बैंक ऑफर असामान्य रूप से कंजूस हों। ऐसा लगता है कि निर्माताओं को मेहनती मध्यम वर्ग के लोग पसंद हैं, इसलिए हमें कोई ऐसा व्यक्ति देखने की संभावना नहीं है जो बड़ी रकम की बात आने पर लापरवाही बरत सके। मैंने खेल के अंतिम चरण में बैंक को अपेक्षित मूल्य के 90% से कम का ऑफर देते भी कभी नहीं देखा। हम किसी को दस लाख जीतते तब देखेंगे जब कोई ऐसा घटिया जुआरी शो में आएगा जो रुक नहीं सकता। जब ऐसा होगा तो मैं बैंकर का समर्थन करूँगा।
यह "डील ऑर नो डील" का अनुवर्ती भाग है, जिसे मैंने हाल ही में पहली बार देखा था। आपके विश्लेषण में यह माना गया है कि घर को सूटकेस में रखे पैसों की कीमत का पता नहीं है। हालाँकि, मैंने जो शो देखा, उसमें अंतिम गेम में दोनों प्रतियोगियों ने एक मूल्यवान केस चुना था, और दोनों को अपेक्षित मूल्य (ईवी) से अधिक के सौदे की पेशकश की गई थी (या की गई होगी, क्योंकि एक पहले ही बाहर हो चुका था)। सबसे चरम स्थिति में, एक खिलाड़ी को $687,000 की पेशकश "की गई" होगी, जबकि शेष दो डॉलर की राशि $500,000 और $750,000 थी। इसका एकमात्र तर्कसंगत स्पष्टीकरण यह है कि बैंकर खिलाड़ी के सूटकेस का मूल्य जानता है और प्रस्तावित सौदे उसी के आधार पर होते हैं।
यह सिर्फ मेरी राय है, और किसी उत्तर की आवश्यकता नहीं है।
उत्तर की अपेक्षा न करने के लिए धन्यवाद, लेकिन मैं आमतौर पर गेम शो के सवालों का जवाब देता हूं। वे हर एपिसोड में दावा करते हैं कि मामलों में रकम बेतरतीब ढंग से रखी गई है, और यह कि न तो होवी, और न ही बैंकर, परिणाम जानते हैं। लेट्स मेक ए डील पर यह दावा कभी नहीं किया गया था, जहां मोंटी हॉल को स्पष्ट रूप से पता था। मैंने भी बैंकर को अंतिम प्रस्ताव के रूप में अपेक्षित मूल्य से अधिक की पेशकश करते देखा है, खासकर जब बड़ी रकम शामिल होती है। मेरी दृढ़ राय में, ऐसा इसलिए नहीं है क्योंकि बैंकर जानता है कि खिलाड़ी के मामले में क्या है। 1950 के दशक में एक बहुत बड़ा घोटाला हुआ था जब यह पता चला कि शो 21 , और साथ ही अन्य, तय किए गए थे। बैंक ऑफ़र के माध्यम से कुछ पुरस्कार राशि को कम करने के लिए एक सफल शो और सभी गेम शो की अखंडता को बर्बाद करने का कोई बाध्यकारी कारण नहीं है।
मैं तीन सिद्धांत प्रस्तुत कर सकता हूं कि क्यों बैंकर कभी-कभी शेष मामलों के औसत से अधिक की पेशकश करता है।
- शो में बैंकर को अपने दफ़्तर में पसीना बहाते हुए दिखाने की कोशिश की गई है। हॉवी मैंडल अक्सर बैंकर के मूड और आवाज़ के लहजे पर टिप्पणी करते हैं। शायद शो को और भी नाटकीय बनाने के लिए बैंकर को एक जोखिम-से-बचने वाला, बड़ा इनाम देने के बजाय अपने नुकसान को कम करना पसंद करने वाला दिखाना ज़रूरी है।
- असली बैंकर वाकई जोखिम से बचता है। यह मेरी विशेषज्ञता के दायरे से बाहर की बात है, लेकिन मेरी समझ से, गेम और रियलिटी शो आमतौर पर टेलीविज़न नेटवर्क से स्वतंत्र किसी कंपनी द्वारा बनाए जाते हैं। ये छोटी कंपनियाँ प्रतियोगियों के बड़े पुरस्कार जीतने के जोखिम को कम करने के लिए किसी बीमा कंपनी की मदद लेती हैं। ऐसे में, बीमा कंपनी ही असली बैंकर होगी, और शो में बैंकर के व्यवहार को प्रभावित कर सकती है। इस तरह की छोटी-मोटी चीज़ों का बीमा करने वाली बीमा कंपनियाँ बहुत बड़ी नहीं होतीं, और बड़ी रकम की बात होने पर वे सुरक्षित रहना पसंद करती हैं।
आपके उदाहरण में, बैंकर का प्रस्ताव अपेक्षित मूल्य से 9.92% अधिक था। अगर बैंकर केली मानदंड का पालन करता, तो ऐसा प्रस्ताव केवल $782,008 के कुल बैंकरोल के साथ दिया जाता, जो अधिकतम पुरस्कार से कम है। कोई भी स्वाभिमानी बीमा कंपनी इतनी रूढ़िवादी नहीं होगी। स्पष्ट रूप से, केवल यही कारण आपके उदाहरण में दिए गए प्रस्ताव को उचित नहीं ठहरा सकता।
- यह शो प्रतियोगियों को बेवकूफ़ और लालची दिखाने की कोशिश कर रहा है। "आर यू स्मार्टर दैन अ फिफ्थ ग्रेडर" और "टुनाइट शो" का "जे-वॉकिंग" जैसे शो सफल नहीं होते अगर हमें सामान्य ज्ञान की चुनौतियों पर हँसने में थोड़ी संतुष्टि न मिले। "फ्रेंड ऑर फ़ो" और "द वीकेस्ट लिंक" जैसे शो मानव स्वभाव के लालच को उजागर करने में बेजोड़ थे। मुझे स्वीकार करना होगा कि जब कोई प्रतियोगी उम्मीद से ज़्यादा कीमत का प्रस्ताव ठुकरा देता है और कम राशि लेकर चलता है, तो मुझे एक तरह का दुःख होता है ।
मैं सोचता हूं कि इसका कारण इन तीन कारणों का संयोजन है, लेकिन मुख्य रूप से तीसरा कारण है।
अगर मैं इस उत्तर को यहीं समाप्त कर दूँ, तो मुझे यकीन है कि मुझे टिप्पणियाँ मिलेंगी, जिनमें सवाल होगा कि क्या काल्पनिक बैंकर ऑफर वाकई दिए गए होंगे। इसका तात्पर्य यह है कि नाटकीय प्रभाव के लिए इन्हें बढ़ा-चढ़ाकर पेश किया गया है। मैंने 13 खेलों के विवरण दर्ज किए हैं। उनमें से एक में, जहाँ तीन मामले बचे थे ($1,000; $5,000; और $50,000), औसत $18,667 था, और प्रस्ताव $21,000 का था। यह अपेक्षित मूल्य से 12.5% अधिक है। एक अन्य शो में, जहाँ दो मामले बचे थे ($400 और $750,000), औसत $375,200 था, और प्रस्ताव $400,000 का था। यह अपेक्षित मूल्य से 6.6% अधिक है। इसलिए, मुझे काल्पनिक प्रस्तावों की सत्यता पर सवाल उठाने का कोई कारण नहीं दिखता।
लिंक:
डील या नो डील फार्मूला : यह पृष्ठ डील या नो डील वेबसाइट पर मुफ्त गेम के आधार पर बैंकर ऑफर की गणना के लिए पुराने और नए फार्मूले दिखाता है।
इन अंकों के साथ, फाइनल जेपर्डी में, प्रत्येक व्यक्ति के स्थान पर आप कितना दांव लगाएंगे:
खिलाड़ी A: $10,000
खिलाड़ी B: $8,000
खिलाड़ी C: $3,500
मैं कुछ धारणाएँ बनाकर शुरुआत करूँगा। पहला, मैं यह मान रहा हूँ कि तीनों खिलाड़ियों को फ़ाइनल जेपर्डी में सट्टेबाजी के व्यवहार की कोई पूर्व जानकारी नहीं है, सिवाय प्रस्तुत तालिका में सही होने की संभावनाओं के। दूसरा, मैं यह मान रहा हूँ कि श्रेणी जानने से कोई मदद नहीं मिलेगी। तीसरा, मैं यह भी मान रहा हूँ कि तीनों प्रतियोगी जीत के लिए प्रयास करना चाहते हैं, और बराबरी की स्थिति में किसी अन्य खिलाड़ी को अपने साथ नहीं ले जाना चाहते।
आइए खिलाड़ी C से शुरुआत करते हैं। उसे यह अनुमान लगाना चाहिए कि अगर B सही है, तो A, B से ऊपर रहने के लिए $6001 का दांव लगा सकता है। हालाँकि, अगर A गलत है, तो उसकी कीमत $3999 रह जाएगी। ऐसी स्थिति में, A को हराने के लिए C को कम से कम $500 का दांव लगाना होगा और सही होना होगा। हालाँकि, मेरी राय में, अगर आपको जीतना है, तो आपको बड़ा दांव लगाना चाहिए। इसलिए अगर मैं CI होता, तो मैं सब कुछ दांव पर लगा देता।
B बड़ा या छोटा दांव लगाने के बीच उलझा हुआ है। अगर C सही है, तो C से ऊपर रहने के लिए एक छोटा दांव $999 या उससे कम का होना चाहिए। छोटे दांव का फ़ायदा यह है कि चाहे कुछ भी हो, C से ऊपर बना रहे, इस उम्मीद में कि A बड़ा दांव लगाएगा, और ग़लत साबित होगा। एक बड़े दांव के लिए ज़रूरी नहीं कि वह पूरा दांव ही लगाए, लेकिन ऐसा हो भी सकता है। बड़े दांव का फ़ायदा यह उम्मीद करना है कि या तो A छोटा दांव लगाएगा, या बड़ा दांव लगाएगा और ग़लत साबित होगा, लेकिन दोनों के लिए B का सही होना ज़रूरी है।
A मूलतः B की तरह ही दांव लगाना चाहता है। A के लिए एक छोटा दांव $0 से $1000 तक कुछ भी हो सकता है, जो B से ऊपर रहेगा यदि B $999 का दांव लगाता है। एक बड़ा दांव $6001 का होना चाहिए, ताकि A के सही होने पर जीत की गारंटी हो, और अगर B बड़ा दांव लगाता है और तीनों खिलाड़ी गलत होते हैं, तब भी उम्मीद बनी रहे।
सही और गलत उत्तरों के आठ संभावित परिणामों की संभावनाओं को समझने में मदद के लिए, मैंने j-archive.com (जो अब उपलब्ध नहीं है) से सीज़न 20 से 24 तक के फ़ाइनल जेपर्डी परिणामों को देखा। परिणाम इस प्रकार हैं, जहाँ खिलाड़ी A अग्रणी है, उसके बाद खिलाड़ी B, और C अंत में है।
संभावित परिणाम अंतिम खतरे में
| खिलाड़ी A | खिलाड़ी बी | खिलाड़ी सी | संभावना |
| सही | सही | सही | 21.09% |
| सही | सही | गलत | 9.73% |
| सही | गलत | सही | 10.27% |
| गलत | सही | सही | 8.74% |
| सही | गलत | गलत | 13.33% |
| गलत | सही | गलत | 10.27% |
| गलत | गलत | सही | 8.63% |
| गलत | गलत | गलत | 17.92% |
अपनी साइट mathproblems.info पर समस्या 192 में मैंने जिस प्रकार के खेल सिद्धांत तर्क की व्याख्या की है, उसका उपयोग करते हुए, मैं पाता हूं कि A और B को अपनी रणनीति को निम्नानुसार यादृच्छिक बनाना चाहिए।
खिलाड़ी ए को 73.6% संभावना के साथ बड़ा दांव लगाना चाहिए और 26.4% संभावना के साथ छोटा दांव लगाना चाहिए।
खिलाड़ी बी को 67.3% संभावना के साथ बड़ा दांव लगाना चाहिए और 32.7% संभावना के साथ छोटा दांव लगाना चाहिए।
खिलाड़ी सी को 100.0% संभावना के साथ बड़ा दांव लगाना चाहिए।
यदि इस रणनीति का पालन किया जाए तो प्रत्येक खिलाड़ी की जीत की संभावना इस प्रकार होगी:
खिलाड़ी A: 66.48%
खिलाड़ी B: 27.27%
खिलाड़ी C: 6.25%
इसके अलावा, ऊपर दी गई तालिका के आधार पर, लीडर द्वारा फ़ाइनल जेपर्डी सही होने की संभावना 54.4%, दूसरे स्थान पर रहने वाले खिलाड़ी के लिए 49.8% और तीसरे स्थान पर रहने वाले खिलाड़ी के लिए 48.7% है। कुल संभावना 51.0% है।
व्यावहारिक रूप से, खिलाड़ियों को सट्टेबाजी के व्यवहार की जानकारी होती है। मेरे विचार से, खिलाड़ी गणितीय रूप से उचित से ज़्यादा बार बड़ा दांव लगाते हैं। दिलचस्प बात यह है कि मुझे डेली डबल में दांव लगाना गणितीय रूप से उचित से ज़्यादा रूढ़िवादी लगता है। केन जेनिंग्स के इतने अच्छे प्रदर्शन का एक कारण डबल डबल्स पर आक्रामक दांव लगाना था। खैर, अगर मैं वास्तव में शो में होता, तो मैं मानता कि बाकी दो खिलाड़ी आक्रामक दांव लगाएँगे। तो मेरा वास्तविक दांव A के लिए $6000 (B के प्रति दयालुता दिखाते हुए), B के लिए $0, और C के लिए $3495 (थोड़ा सा दांव छोड़कर, अगर A मूर्खतापूर्वक $1 के अलावा सब कुछ या सब कुछ दांव पर लगा दे, और गलत साबित हो जाए) होगा।
इससे पहले कि कोई मुझे चुनौती दे कि वास्तविक स्थल पर कोई यादृच्छिक संख्या कैसे निकाली जा सकती है, मैं स्टैनफोर्ड वोंग की रणनीति का सुझाव देना चाहता हूँ, जिसमें आप अपनी घड़ी की सेकेण्ड सुई का उपयोग करके 1 से 60 तक यादृच्छिक संख्या निकाल सकते हैं।
ब्रिटेन में " कलर ऑफ़ मनी " नाम से एक नया गेम शो शुरू हुआ है। एक अकेले प्रतियोगी को यादृच्छिक रूप से एक लक्ष्य राशि दी जाती है, जो £55,000 से £79,000 के बीच मानी जाती है। पैसे कमाने के लिए, वह 20 बैंक मशीनों में से 10 चुनता है, जिनमें से प्रत्येक में £1,000 से £20,000 तक, £1,000 के सम-विषम चरणों में, होते हैं। जब वह एक मशीन चुनता है, तो वह £1,000 से ऊपर की ओर, £1,000 के चरणों में गिनती शुरू कर देती है।
खिलाड़ी किसी भी समय "रुको!" चिल्ला सकता है, और वह स्क्रीन पर दिखाई देने वाली राशि बैंक में जमा कर देगा। अगर खिलाड़ी समय पर नहीं रुकता और मशीन के पैसे खत्म हो जाते हैं, तो वह कुछ भी बैंक में जमा नहीं कर पाएगा। एक होस्टेस आँकड़े उपलब्ध कराती है, जैसे कि चुनने के लिए बची हुई मशीनों की संख्या, जीतने के लिए बची हुई राशि, जीतने के लिए प्रत्येक मशीन की औसत राशि की आवश्यकता, और मशीनों में बची हुई राशि।
एक खिलाड़ी "गैप्स पर खेल" सकता है, यानी अगर मशीनों का एक क्रम चुना गया है, मान लीजिए, £4k, £5k, और £6k, तो एक मशीन के £3,000 के निशान को पार करने के बाद £7,000 तक पहुँचने की गारंटी होगी। मेरा सवाल यह है कि एक खिलाड़ी को किस तरह की रणनीति अपनानी चाहिए?
यह ऐसी चीज़ है जिसका विश्लेषण करने में मैं हफ़्तों लगा सकता हूँ। दुर्भाग्य से, "जादूगर से पूछो" जैसे सवालों का एक बड़ा बैकलॉग होने के कारण, मैंने आपका संदेश आपके लिखने के लगभग तीन महीने बाद पढ़ा। विकिपीडिया पेज पर ऐसा लगता है कि वह शो फ्लॉप रहा और उसे रद्द कर दिया गया। हालाँकि, यह अभी भी एक दिलचस्प समस्या है।
होस्टेस आपको आसानी से बता देती है कि आपको अपने गेम तक पहुँचने के लिए हर बची हुई मशीन पर कितनी औसत राशि की ज़रूरत है। घंटों लिखने-पढ़ने के बाद, मुझे इससे बेहतर कुछ नहीं सूझ रहा कि आप ज़रूरी औसत से लगभग 25% ज़्यादा स्टॉपिंग लक्ष्य निर्धारित करें। यह सिर्फ़ एक अनुमान है, इसलिए कृपया मुझसे यह साबित करने के लिए न कहें कि यह सबसे अच्छा है। जैसा कि आपने बताया, गैप्स पर भी चलते रहें, पहले से चुनी गई राशि से ठीक पहले कभी न रुकें।
जब केवल दो मशीनें बची हों, और कुल राशि £13,000 या उससे कम हो, तो मैं उसे दूसरी-से-आखिरी मशीन से प्राप्त करने की कोशिश करूँगा। अगर £14,000 या उससे ज़्यादा हो, तो मैं अगली मशीन से उसका आधा हिस्सा प्राप्त करने की कोशिश करूँगा।
अगर वे इस शो को वापस लाएँ, तो मुझे उम्मीद है कि मेरे यूके के पाठक मुझे ज़रूर बताएँगे। यह एक ऐसी पहेली है जिसका मैं दीवाना हो सकता हूँ, जैसे कि इटरनिटी पहेली , जो संयोग से (या नहीं) यूके से बाहर भी थी।
पुनश्च: आप यूके में "कलर" को au क्यों लिखते हैं? मुझे इसका कोई मतलब नहीं समझ आया।
द प्राइस इज राइट पर पंच ए बंच गेम के लिए प्रति पंच औसत पुरस्कार और इष्टतम रणनीति क्या है?
जो लोग नियमों से परिचित नहीं हैं, उनके लिए Price Is Right वेबसाइट पर नियम बताए गए हैं। अगर आप इस खेल से परिचित नहीं हैं, तो कृपया वहाँ ज़रूर जाएँ, क्योंकि मुझे लगता है कि आपको नियम पता होंगे। इस खेल के कई YouTube वीडियो भी हैं। यहाँ एक पुराना वीडियो है, जिसमें दूसरा मौका दिखाया गया है, लेकिन उस समय अधिकतम इनाम केवल $10,000 था। अब यह $25,000 है।
सबसे पहले, आइए उस पुरस्कार का अपेक्षित मूल्य ज्ञात करें जिसके साथ दूसरा मौका नहीं जुड़ा है। नीचे दी गई तालिका दर्शाती है कि औसत $1371.74 है।
बिना किसी दूसरे मौके के पंच ए बंच पुरस्कार वितरण
| पुरस्कार | संख्या | संभावना | अपेक्षित जीत |
| 25000 | 1 | 0.021739 | 543.478261 |
| 10000 | 1 | 0.021739 | 217.391304 |
| 5000 | 3 | 0.065217 | 326.086957 |
| 1000 | 5 | 0.108696 | 108.695652 |
| 500 | 9 | 0.195652 | 97.826087 |
| 250 | 9 | 0.195652 | 48.913043 |
| 100 | 9 | 0.195652 | 19.565217 |
| 50 | 9 | 0.195652 | 9.782609 |
| कुल | 46 | 1.000000 | 1371.739130 |
दूसरा, उस औसत पुरस्कार की गणना करें जिसके दूसरे मौके की संभावना है। नीचे दी गई तालिका दर्शाती है कि औसत $225 है।
दूसरे मौके के साथ पंच ए बंच पुरस्कार वितरण
| पुरस्कार | संख्या | संभावना | अपेक्षित जीत |
| 500 | 1 | 0.250000 | 125.000000 |
| 250 | 1 | 0.250000 | 62.500000 |
| 100 | 1 | 0.250000 | 25.000000 |
| 50 | 1 | 0.250000 | 12.500000 |
| कुल | 4 | 1.000000 | 225.000000 |
तीसरा, खिलाड़ी को मिलने वाले दूसरे मौकों की संख्या के आधार पर एक अपेक्षित मान तालिका बनाएँ। इसे सरल गणित से ज्ञात किया जा सकता है। उदाहरण के लिए, 2 दूसरे मौकों की प्रायिकता (4/50)×(3/49)×(46/48) है। 5 दूसरे मौकों पर अपेक्षित जीत $1371.74 + s×$225 है। निम्नलिखित तालिका 0 से 4 दूसरे मौकों के लिए प्रायिकता और औसत जीत दर्शाती है।
पंच ए बंच पुरस्कार वापसी तालिका
| दूसरी संभावना | संभावना | औसत जीत | अपेक्षित जीत |
| 4 | 0.000004 | 2271.739130 | 0.009864 |
| 3 | 0.000200 | 2046.739130 | 0.408815 |
| 2 | 0.004694 | 1821.739130 | 8.551020 |
| 1 | 0.075102 | 1596.739130 | 119.918367 |
| 0 | 0.920000 | 1371.739130 | 1262.000000 |
| कुल | 1.000000 | 1390.888067 |
अतः प्रति पंच औसत जीत (दूसरे मौके से प्राप्त अतिरिक्त धनराशि सहित) 1390.89 डॉलर है।
नीचे दी गई तालिका शेष मुक्कों की संख्या के अनुसार, न्यूनतम जीत की मेरी रणनीति दर्शाती है। ध्यान दें कि खिलाड़ी तीन दूसरे मौकों के ज़रिए $1,000 + $250, + $100 + $50 के पुरस्कारों के साथ $1,400 तक पहुँच सकता है।
पंच ए बंच रणनीति
| शेष पंच | खड़े होने के लिए न्यूनतम |
| 3 | $5,000 |
| 2 | $5,000 |
| 1 | $1,400 |
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
यदि आप उत्तर के बारे में निश्चित नहीं हैं, तो गेम शो मिलियन डॉलर मनी ड्रॉप पर अपने पैसे को विभाजित करने के लिए इष्टतम रणनीति क्या होगी?
अन्य पाठकों के लाभ के लिए, मैं पहले नियमों की समीक्षा कर लूँगा।
- खिलाड़ियों की एक टीम $1,000,000 से शुरू होती है।
- टीम को एक बहुविकल्पीय प्रश्न दिया जाता है।
- टीम को अपने पैसे संभावित उत्तरदाताओं में बाँटने हैं। सही उत्तर पर जो भी पैसा लगेगा, वह अगले प्रश्न पर जाएगा।
- टीम को कम से कम एक संभावित उत्तर पर कोई पैसा न लगाकर उसे पूरी तरह से खारिज करना होगा।
- यह प्रक्रिया कई राउंड तक दोहराई जाती है। खिलाड़ी को अपना मन बदलने का एक मौका भी दिया जाता है।
ज़ाहिर है, अगर टीम को जवाब पर पूरा यकीन है, तो उसे अपना सारा पैसा सही जवाब पर लगाना चाहिए। अगर टीम जवाब को दो तक सीमित कर पाती है, लेकिन हर एक के सही होने की 50% संभावना रखती है, तो उन्हें अपना पैसा दोनों विकल्पों में बराबर-बराबर बाँट देना चाहिए।
यह तब और मुश्किल हो जाता है जब टीम एक उत्तर की ओर झुकती है, लेकिन बाकी एक या ज़्यादा उत्तरों को पूरी तरह से खारिज नहीं करती। आइए एक उदाहरण देखें। मान लीजिए टीम प्रत्येक सही उत्तर की प्रायिकता इस प्रकार निर्धारित करती है: A 10%, B 20%, C 30%, D 40%। उन्हें उसका पैसा कैसे बाँटना चाहिए?
मेरा दावा है कि इसका उत्तर केली मानदंड का पालन करना है। संक्षेप में, टीम को हर प्रश्न के साथ अपनी संपत्ति का लॉग अधिकतम करना चाहिए। ऐसा करने के लिए, आपको यह विचार करना होगा कि आपके पास पहले से कितनी संपत्ति है।
मान लीजिए कि आपकी मौजूदा संपत्ति, जो आपने शो से स्वतंत्र रूप से जमा की है, $100,000 है। यह आपका पहला प्रश्न है, इसलिए आपके पास गेम शो की $1,000,000 की राशि है जिसे आपको बाँटना है। शो के नियमों के अनुसार, सबसे कम संभावना वाले विकल्प को पहले हटा दें। फिर आप 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000) को अधिकतम करना चाहते हैं, जहाँ छोटे अक्षर a, b, और c प्रत्येक उत्तर पर रखे गए भाग को दर्शाते हैं।
इसे कैलकुलस और त्रिपद समीकरण हल करके, परीक्षण और त्रुटि विधि से, या मेरी पसंद, एक्सेल में "लक्ष्य खोज" सुविधा से हल किया जा सकता है। आप जो भी तरीका अपनाएँ, सही उत्तर यह है कि B पर 18.9%, C पर 33.3% और D पर 47.8% लगाएँ।
बेशक, शो में कोई भी दिए गए समय में यह सारा गणित नहीं कर पाएगा, और यह भी नहीं कि आपको उस समय में ढेर सारा पैसा भी इधर-उधर करना होगा। मेरी ज़्यादा व्यावहारिक सलाह यही है कि आप उत्तर के सही होने की संभावना के अपने आकलन के अनुपात में पैसे बाँट लें, यह मानते हुए कि सबसे कम संभावना वाला विकल्प संभव नहीं है। इस उदाहरण में, इससे B पर 22.2%, C पर 33.3% और D पर 44.4% का बँटवारा होगा।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
मिशिगन लॉटरी में तीन खिलाड़ियों का खेल होता है जिसके नियम इस प्रकार हैं: क्या इस खेल में आखिरी में खेलने का कोई स्थानिक लाभ है? प्रत्येक खिलाड़ी के लिए सर्वोत्तम रणनीति क्या है? यहाँ एकYouTube वीडियो है जिसमें यह खेल दिखाया गया है।
सबसे पहले, आखिरी में खेलने का कोई स्थानिक लाभ नहीं होता। चूँकि पिछले खिलाड़ियों के खेलने के दौरान खिलाड़ियों को एक ध्वनिरोधी बूथ में रखा जाता है, इसलिए क्रम मायने नहीं रखता।
दूसरा, खेल में एक नैश संतुलन होना चाहिए जहाँ कम से कम x अंक के स्कोर के साथ खड़े होने की रणनीति किसी भी अन्य रणनीति से बेहतर होगी। सवाल x का पता लगाने का है।
मैंने खुद से पूछा कि अगर 1 से 100 तक के कार्ड के बजाय, हर खिलाड़ी को 0 और 1 के बीच समान रूप से वितरित एक यादृच्छिक संख्या मिले और वह उस बिंदु x की तलाश करे जहाँ एक आदर्श तर्कशास्त्री को खड़े होने और बदलने में कोई फ़र्क़ नहीं पड़ेगा, तो रणनीति क्या होगी। इस उत्तर के साथ, 1 से 100 तक के असतत वितरण पर उत्तर लागू करना आसान है।
मैं यहीं रुकता हूँ और अपने पाठकों को समस्या का आनंद लेने देता हूँ। उत्तर और समाधान के लिए नीचे दिए गए लिंक देखें।
0 से 1 तक सतत वितरण के लिए उत्तर दें ।
1 से 100 तक असतत वितरण के लिए उत्तर दें।
मेरे समाधान के लिए कृपया यहां क्लिक करें (पीडीएफ) ।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।
यह मानते हुए कि किसी भी चीज़ की कीमत के बारे में कोई जानकारी नहीं है, द प्राइस इज़ राइट पर रेस गेम के लिए इष्टतम रणनीति क्या है?
नियमों से अनजान लोगों के लिए, खिलाड़ी को चार मूल्य टैग दिए जाते हैं और उन्हें चार वस्तुओं पर लगाना होता है। जब वह ऐसा कर लेता है, तो वह एक लीवर खींचता है जो सही मिलानों की संख्या बताता है। अगर खिलाड़ी के पास चार से कम सही टैग हैं, तो वह टैग को फिर से व्यवस्थित कर सकता है और फिर से कोशिश कर सकता है। खिलाड़ी 45 सेकंड के भीतर जितनी बार चाहे कोशिश कर सकता है।
मेरी सलाह है कि हमेशा वही चयन सबमिट करें जिसके जीतने की संभावना हो, क्योंकि चयनों और अंकों का पिछला इतिहास ऐसा है। अगर पहला स्कोर 0 है, तो दो टैग के दो सेटों को उलटें नहीं, बल्कि हर चीज़ को किसी भी दिशा में एक स्थान आगे बढ़ाएँ।
अगर आप तुरंत तर्क नहीं कर पा रहे हैं, तो मैं नीचे आपको समझाता हूँ। इस रणनीति का इस्तेमाल करने के लिए, अलग-अलग टैग्स को A, B, C, और D अक्षर दें। फिर उन्हें स्टेज पर बाएँ से दाएँ, दिखाए गए क्रम में लगाएँ। हमेशा ABCD से शुरुआत करें। फिर नीचे दिए गए स्कोर इतिहास को देखें और उस स्कोर क्रम के लिए दिए गए टैग्स का क्रम चुनें।
यदि 0, तो BCDA
यदि 0-0, तो CDAB
यदि 0-0-0, तो DABC (जीतना आवश्यक है)
यदि 0-1, तो BDAC
यदि 0-1-0, तो CADB (जीतना आवश्यक है)
यदि 0-1-1, तो CDBA
यदि 0-1-1-0, तो DCAB (जीतना आवश्यक है)
यदि 0-2, तो BADC
यदि 0-2-0, तो DCBA (जीतना आवश्यक है)
यदि 1, तो ACDB
यदि 1-0, तो बी.डी.सी.ए.
यदि 1-0-0, तो CABD
यदि 1-0-0-1, तो CBAC (जीतना आवश्यक है)
यदि 1-1, तो BDCA
यदि 1-1-0, तो CABD
यदि 1-1-0-1, तो CBAC (जीतना आवश्यक है)
यदि 1-1-1, तो BCAD (जीतना आवश्यक)
यदि 2, तो ABDC
यदि 2-0, तो BACD (जीतना आवश्यक)
यदि 2-1, तो ACBD
यदि 2-1-0, तो DBCA
यदि 2-1-1, तो ADCB
यदि 2-1-1-0, तो CBAD (जीतना आवश्यक है)
निम्नलिखित तालिका कुल घुमावों की प्रत्येक संख्या की प्रायिकता दर्शाती है। नीचे दाएँ कक्ष में घुमावों की अपेक्षित संख्या 10/3 दर्शाई गई है।
रेस गेम
| मोड़ों | युग्म | संभावना | वापस करना |
|---|---|---|---|
| 1 | 1 | 0.041667 | 0.041667 |
| 2 | 4 | 0.166667 | 0.333333 |
| 3 | 8 | 0.333333 | 1.000000 |
| 4 | 8 | 0.333333 | 1.333333 |
| 5 | 3 | 0.125000 | 0.625000 |
| कुल | 24 | 1.000000 | 3.333333 |
इस प्रश्न पर मेरे फोरम विज़ार्ड ऑफ़ वेगास पर चर्चा की गई है।
किसी भी खिलाड़ी द्वारा प्राइस इज राइट पर शोकेस शोडाउन में $25,000 जीतने की क्या संभावना है?
अन्य पाठकों को समझाने के लिए, मैं आपको बता दूं कि आप किस बारे में बात कर रहे हैं। शोकेस शोडाउन, द प्राइस इज़ राइट नामक गेम शो में खेला जाने वाला एक खेल है। शोकेस शोडाउन में, प्रत्येक खिलाड़ी अपनी बारी में एक पहिया घुमाता है, जिसके .05 से 1.00 तक, .05 से समान रूप से विभाज्य प्रत्येक राशि पर रुकने की समान संभावना होती है। यदि खिलाड़ी को अपना पहला स्पिन पसंद नहीं आता है, तो वे दूसरे स्पिन को अपने पहले स्पिन में जोड़ते हुए, फिर से स्पिन कर सकते हैं, हालांकि, यदि वे 1.00 से अधिक स्पिन करते हैं, तो उन्हें तुरंत अयोग्य घोषित कर दिया जाएगा। बराबरी की स्थिति में, प्रत्येक खिलाड़ी को टाई-ब्रेकर राउंड में एक स्पिन मिलेगा, जिसमें सबसे अधिक स्पिन करने वाला खिलाड़ी जीतता है। एक और बराबरी की स्थिति में, यह प्रक्रिया तब तक दोहराई जाएगी जब तक कि टाई टूट न जाए।
शोकेस शोडाउन का मुख्य उद्देश्य शोकेस में आगे बढ़ना है। हालाँकि, इसमें तत्काल नकद पुरस्कार भी शामिल हैं, जो इस प्रकार हैं:
- पहले राउंड में, यदि कोई भी खिलाड़ी कुल $1.00 प्राप्त करता है, चाहे एक बार में या दो स्पिनों के योग में, तो वह $1,000 जीतेगा।
- पहले और एकमात्र टाई-ब्रेकर राउंड में, यदि पहिया $0.05 या $0.15 पर रुकता है, तो खिलाड़ी $10,000 जीतेगा।
- पहले और एकमात्र टाई-ब्रेकर राउंड में, यदि पहिया $1.00 पर रुकता है, तो खिलाड़ी $25,000 जीतेगा।
मैं कॉलम #101 में शोकेस शोडाउन के लिए सर्वोत्तम रणनीति समझाता हूँ। यह मानते हुए कि उस रणनीति का पालन किया जाता है, नीचे दी गई तालिका आपके और अन्य कई प्रश्नों के उत्तर देती है।
शोकेस शोडाउन आँकड़े
| सवाल | उत्तर |
|---|---|
| पहले दौर में अपेक्षित $1000 विजेता | 0.253790 |
| संभावना 2-खिलाड़ी टाई | 0.113854 |
| संभावना 3-खिलाड़ियों का टाई | 0.004787 |
| दूसरे दौर में $10000 के विजेताओं की उम्मीद | 0.024207 |
| दूसरे दौर में $25000 के विजेताओं की उम्मीद | 0.012104 |
| अपेक्षित कुल पुरस्कार राशि | $798.45 |
| किसी भी खिलाड़ी के $1000 जीतने की संभावना | 0.084597 |
| किसी भी खिलाड़ी के $10000 जीतने की संभावना | 0.008069 |
| किसी भी खिलाड़ी के $25000 जीतने की संभावना | 0.004035 |
तालिका की निचली पंक्ति से पता चलता है कि यदि आप स्पिन करने के अपने आदेश पर विचार किए बिना शोकेस शोडाउन बनाते हैं, तो आपके $25,000 जीतने की संभावना 0.004035, या 248 में 1 है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
गेम शो सर्वाइवर में दो टीमें थीं, एक में नौ खिलाड़ी और दूसरी में छह। फिर उन्हें बेतरतीब ढंग से पाँच-पाँच लोगों की तीन नई टीमों में बाँट दिया गया। हर नई टीम में पहले वाली नौ खिलाड़ियों वाली टीम के तीन सदस्य और पहले वाली छह खिलाड़ियों वाली टीम के दो सदस्य थे। ऐसा होने की संभावना क्या है?
मान लीजिए कि नौ खिलाड़ियों वाली पहली टीम को टीम 1 और छह खिलाड़ियों वाली टीम को टीम 2 कहते हैं। टीम 1 से तीन और टीम 2 से दो खिलाड़ियों को चुनने के तरीकों की संख्या combin(9,3)×combin(6,2) = 1,260 है। 15 खिलाड़ियों में से पाँच खिलाड़ियों को चुनने के कुल तरीकों की संख्या combin(15,5) = 3,003 है। इसलिए, पहली टीम के टीम 1 के पक्ष में 3/2 से विभाजित होने की संभावना 1,260/3,003 = 41.96% है।
अगर ऐसा हुआ, तो टीम 1 के पास छह और टीम 2 के पास चार खिलाड़ी बचेंगे। टीम 1 से तीन और टीम 2 से दो खिलाड़ियों को चुनने के तरीकों की संख्या combin(6,3)×combin(4,2) = 120 है। बचे हुए 10 खिलाड़ियों में से पाँच को चुनने के तरीकों की कुल संख्या combin(10,5) = 252 है। इसलिए, दूसरी टीम के टीम 1 के पक्ष में 3/2 से विभाजित होने की संभावना, यह देखते हुए कि पहली टीम पहले ही 3/2 से विभाजित हो चुकी है, 120/252 = 47.62% है।
यदि पहली दो नई टीमों को पूर्व टीम 1 के पक्ष में 3/2 से विभाजित किया जाता है, तो अंतिम टीम को शेष टीमों के बीच 3/2 से विभाजित किया जाएगा।
इस प्रकार, आपके प्रश्न का उत्तर 41.96% × 47.62% × 100% = 19.98% है।
सूत्र:
संयोजन(x,y)=x!/((y!*(xy)!)
x! = 1*2*3*...*x
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
मुझे लगता है कि जेम्स होल्ज़ाउर अपने आखिरी मैच में एम्मा से जानबूझकर हार गए थे। मेरे सबूत यह हैं कि वह तब तक हर मैच में बड़ा दांव लगा रहे थे और अचानक उन्होंने एम्मा के खिलाफ कम दांव लगा दिया। मुझे शक है कि निर्माता एलेक्स के जाने के बाद केन जेनिंग्स को शो होस्ट करना चाहते हैं। अगर होस्ट के पास दोनों शो के रिकॉर्ड और जीती हुई रकम होती, तो शो और भी नाटकीय होता। इसलिए, उन्होंने जेम्स को गेम हारने के लिए पैसे दिए।
चलिए, मैं मंच तैयार करता हूँ। 3 जून, 2019 को जेम्स नियमित खेलों में जीती गई कुल धनराशि का रिकॉर्ड तोड़ने के बेहद करीब थे, जो अभी भी $2,520,700 है। जेम्स की प्रति मैच औसत जीत, रिकॉर्ड तोड़ने के लिए ज़रूरी राशि से कहीं ज़्यादा थी। इसलिए सभी की निगाहें 3 जून को इस रिकॉर्ड को टूटते देखने पर टिकी थीं।
इसके बजाय, होता यह है कि जेम्स न सिर्फ़ रिकॉर्ड तोड़ पाता है, बल्कि हार भी जाता है। विजेता, एम्मा, ने बहुत मज़बूत रणनीतिक खेल दिखाया, साथ ही बजर पर अच्छी पकड़ बनाए रखी और सही जवाब भी दिए। उसने वैसा ही खेला जैसा जेम्स आमतौर पर खेलता था। फ़ाइनल जेपर्डी में जाने से पहले स्कोर इस प्रकार थे:
- एम्मा — $26,600
- जेम्स — $23,400
- जय - $11,000
ऐसी परिस्थितियों में, जहाँ दूसरे स्थान पर रहने वाले खिलाड़ी के पास पहले स्थान के आधे से ज़्यादा अंक होते हैं, और तीसरे स्थान पर रहने वाले खिलाड़ी के पास नहीं, आमतौर पर पहले और दूसरे स्थान पर रहने वाले खिलाड़ी अपने अंतिम दांव को ज़्यादा या कम करने का चुनाव करते हैं। अगर सही दांव लगाया जाए, तो पहले स्थान के लिए ज़्यादा दांव जीत पक्की करने के लिए काफ़ी है। विशेष रूप से, दूसरे स्थान के स्कोर का दोगुना, पहले स्थान के स्कोर से घटाकर एक डॉलर जोड़ने पर। एम्मा ने ठीक यही किया, 2×$23,400 - $26,600 + $1 = $20,201 के दांव के साथ। ज़्यादातर, पहले स्थान पर रहने वाला खिलाड़ी ऐसा ही करता है।
हालाँकि, जेम्स को नहीं पता था कि एम्मा उसकी बाजी तय करते समय क्या करेगी। नीचे दी गई तालिका दर्शाती है कि बाजी के किस संयोजन के अनुसार कौन जीतेगा।
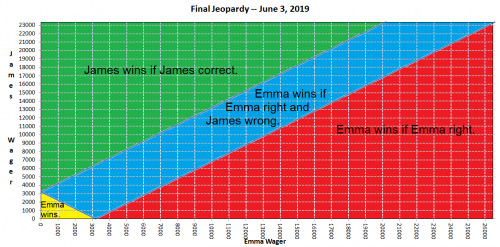
बड़े संस्करण के लिए छवि पर क्लिक करें।
यदि एम्मा कम से कम 20,201 डॉलर का दांव लगाती है तो सही होने पर वह जीत सुनिश्चित कर लेगी।
यदि एम्मा कम दांव लगाती है तो वह जीत जाएगी यदि (a) जेम्स कम दांव लगाता है या (b) जेम्स अधिक दांव लगाता है और गलत होता है।
यदि जेम्स अधिक दांव लगाता है तो वह जीत जाता है यदि (क) एम्मा अधिक दांव लगाती है, एम्मा गलत होती है, और जेम्स सही होता है, या (ख) एम्मा कम दांव लगाती है और जेम्स सही होता है।
यदि जेम्स कम दांव लगाता है तो वह जीत जाता है, जबकि एम्मा अधिक दांव लगाती है और गलत साबित होती है।
अगर कोई कुशल तर्कशास्त्री खेल रहा होता, तो दोनों अपने फैसले बेतरतीब ढंग से करते। हालाँकि, ऐसी परिस्थितियों में नेता शायद ही कभी नीचे जाता है जहाँ उसे पकड़ा जा सकता है। अगर जेम्स को एमा के ऊपर जाने का अनुमान है, तो उसे निश्चित रूप से नीचे जाना चाहिए। इस तरह उसे जीतने के लिए फ़ाइनल जेपर्डी को सही करने की ज़रूरत नहीं है, उसे बस उम्मीद करनी होगी कि एमा उसे गँवा दे।
जेम्स की वास्तविक बोली जे को कवर करने के लिए सही राशि थी यदि जे ने सब कुछ दांव पर लगा दिया और सही था: $23,400 - 2×$11,000 - $1 = $1,399, जो एम्मा को हराने के उद्देश्य से कम दांव के रूप में संतुष्ट था।
यदि यह सही है, तो जेम्स को तीसरे स्थान की तुलना में दूसरे स्थान पर आने के लिए अतिरिक्त 1,000 डॉलर मिलेंगे।
अंत में, मैं इस षड्यंत्र सिद्धांत को पूरी तरह से खारिज करता हूँ कि जेम्स ने गेम गँवा दिया। उसने सही तरीके से खेला और एक मज़बूत प्रतिद्वंद्वी के साथ खेलने और जिसे ज़्यादातर लोग "बुरी किस्मत" कहेंगे, उसके संयोजन के कारण हार गया।
बाहरी संबंध
- जेपार्डी हॉल ऑफ फ़ेम
- जेपार्डी पर जेम्स होल्ज़ाउर - विज़ार्ड ऑफ़ वेगास में मेरे मंच पर चर्चा।
फ़ाइनल जेपर्डी में, अगर दूसरे स्थान पर रहने वाले खिलाड़ी के पास पहले स्थान पर रहने वाले खिलाड़ी से 2/3 से ज़्यादा पैसा हो, तो सबसे अच्छी रणनीति क्या होगी? मान लीजिए कि तीसरे स्थान पर रहने वाला खिलाड़ी कोई फ़ैक्टर नहीं है।
पहले एक बात स्पष्ट कर दूँ। निम्नलिखित विश्लेषण सांख्यिकीय औसत पर आधारित है। एक वास्तविक खिलाड़ी को यह मानसिक रूप से समायोजित करना चाहिए कि वह फ़ाइनल जेपर्डी श्रेणी को कितनी अच्छी तरह जानता है और साथ ही प्रतिद्वंद्वी के सही अनुमान लगाने की संभावनाओं का भी अनुमान लगाना चाहिए।
आपके प्रश्न का उत्तर देने के लिए, मैंने सबसे पहले जेपर्डी आर्काइव से चार सत्रों के डेटा को देखा, ताकि पहले (अग्रणी) और दूसरे स्थान (पीछा करने वाले) खिलाड़ी के फाइनल जेपर्डी को सही और गलत करने के चार संभावित संयोजनों को देखा जा सके।
अंतिम जेपर्डी स्कोरकार्ड
| अग्रणी खिलाड़ी | पीछा करने वाला खिलाड़ी सही | पीछा करने वाला खिलाड़ी गलत | कुल |
|---|---|---|---|
| सही | 29.0% | 25.5% | 54.5% |
| ग़लत | 17.7% | 27.8% | 45.5% |
| कुल | 46.8% | 53.2% | 100.0% |
आगे बढ़ने से पहले, आइए कुछ चर परिभाषित करें:
x = सम्भावना अग्रणी खिलाड़ी उच्च जाता है।
y = संभावना है कि पीछा करने वाला खिलाड़ी ऊंचा हो।
f(x,y) = उच्च खिलाड़ी के जीतने की संभावना.
आइए ऊपर दी गई तालिका से f(x,y) को x और y के संदर्भ में व्यक्त करें:
f(x,y) = 0.823xy + 0.545x(1-y) + 0.468(1-x)y + (1-x)(1-y)
f(x,y) = 0.810 xy - 0.455x - 0.532y + 1
x और y के लिए इष्टतम मान ज्ञात करने के लिए, आइए x और y दोनों के संबंध में f(x,y) का व्युत्पन्न लें।
f(x,y) d/dx = -0.455 + 0.810y = 0
इस प्रकार y = 0.455/0.810 = 0.562
f(x,y) d/dy = -0.532 + 0.810x = 0
इस प्रकार x = 0.523/0.810 = 0.657
इसलिए, उच्च खिलाड़ी को 65.7% संभावना के साथ उच्च दांव लगाना चाहिए और निम्न खिलाड़ी को 56.2% संभावना के साथ उच्च दांव लगाना चाहिए।
देखने के आधार पर, मुझे लगता है कि उच्च खिलाड़ी 65.7% से अधिक समय में उच्च दांव लगाता है, इसलिए यदि मैं दूसरे स्थान पर होता, तो मैं कम दांव लगाता।
यदि दोनों खिलाड़ी इस यादृच्छिक रणनीति का पालन करते हैं, तो अग्रणी खिलाड़ी की जीत की संभावना 70.1% है।
सारे सिद्धांत एक तरफ़ रख दें, अगर आप आगे चल रहे हैं, तो भविष्यवाणी करें कि पीछा करने वाला खिलाड़ी क्या करेगा और वैसा ही करें। अगर आप पीछा कर रहे हैं, तो आगे चल रहे खिलाड़ी की कार्रवाई का अनुमान लगाएँ और उसके विपरीत करें। यह रणनीति ऐसे सभी टूर्नामेंटों के लिए लागू होती है।यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
जेपर्डी राउंड की शुरुआत में, जेम्स होल्ट्ज़हॉयर जैसे कुछ खिलाड़ी नीचे से चुनना क्यों शुरू करते हैं? क्या यह ज़्यादा समझदारी नहीं होगी कि ऊपर से आसान सवालों से अभ्यास किया जाए, ताकि उस श्रेणी की सही समझ सुनिश्चित हो सके, जो कभी-कभी मुश्किल होती है?
इसकी वजह यह है कि डेली डबल्स 91.5% बार निचली तीन पंक्तियों में रखे जाते हैं। नीचे दी गई तालिका 13,660 डेली डबल्स में से बोर्ड पर उनके स्थान दर्शाती है।
दैनिक डबल स्थान
| पंक्ति | स्तंभ 1 | कॉलम 2 | स्तंभ 3 | स्तंभ 4 | कॉलम 5 | स्तंभ 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1,147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3,712 |
| 4 | 1,095 | 659 | 982 | 907 | 895 | 627 | 5,165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3,620 |
| कुल | 2,987 | 1,641 | 2,548 | 2,406 | 2,360 | 1,718 | 13,660 |
स्रोत: जे! आर्काइव .
यहां बोर्ड के प्रत्येक सेल में डेली डबल कितनी बार पाया जाता है, इसका डेटा दिया गया है।
दैनिक दोहरी संभावना
| पंक्ति | स्तंभ 1 | कॉलम 2 | स्तंभ 3 | स्तंभ 4 | कॉलम 5 | स्तंभ 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.1% |
| 2 | 2.0% | 1.0% | 1.6% | 1.2% | 1.5% | 1.0% | 8.4% |
| 3 | 6.0% | 3.2% | 5.0% | 4.8% | 4.7% | 3.5% | 27.2% |
| 4 | 8.0% | 4.8% | 7.2% | 6.6% | 6.6% | 4.6% | 37.8% |
| 5 | 5.8% | 3.0% | 4.9% | 4.9% | 4.5% | 3.5% | 26.5% |
| कुल | 21.9% | 12.0% | 18.7% | 17.6% | 17.3% | 12.6% | 100.0% |
डेली डबल्स की खोज करने का कारण यह है कि ये आपके स्कोर को दोगुना करने का एक अच्छा तरीका है। ज़्यादातर प्रतियोगियों के किसी भी दिए गए सुराग के सही होने की संभावना लगभग 80% से 90% होती है। अगर आपके जीतने की संभावना 80% से 90% है, तो दांव पर बराबर राशि प्राप्त करना एक बेहतरीन विकल्प है। जेम्स होल्ट्ज़हॉयर की इतनी जीत का एक बड़ा कारण डेली डबल्स की आक्रामक खोज और फिर जब भी उन्हें कोई सुराग मिलता, तो ज़्यादातर बार "ऑल इन" करना था। इसी वजह से वह एम्मा से हार गए, जब एम्मा ने उनके खिलाफ भी यही रणनीति अपनाई थी।
यह मानते हुए कि खिलाड़ी को पुरस्कारों की कीमतों के बारे में कोई जानकारी नहीं है, प्राइस इज राइट पर रेस गेम खेलने के लिए सबसे अच्छी रणनीति क्या है?
जो पाठक इस खेल से परिचित नहीं हैं, उनके लाभ के लिए यहां इसका एक वीडियो है।
मेरा मानना है कि निम्नलिखित रणनीति से न्यूनतम औसत संख्या में फेरे प्राप्त होते हैं। ऐसी कई रणनीतियाँ हैं जो इसे बराबरी पर ला सकती हैं, लेकिन मुझे नहीं लगता कि कोई भी इसे हरा सकती है।
रणनीति का उपयोग करने के लिए, चार मूल्य टैगों को 1, 2, 3 और 4 के रूप में लेबल करें। उन्हें चार पुरस्कारों पर रखें, इतिहास के अनुसार कि आपने अतीत में कितने सही किए थे, बाईं ओर पहले मोड़ से शुरू करें।
रेस गेम रणनीति
| इतिहास | पुरस्कार 1 | पुरस्कार 2 | पुरस्कार 3 | पुरस्कार 4 |
|---|---|---|---|---|
| कोई नहीं | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
अगली तालिका चार मूल्य टैगों को व्यवस्थित करने के लिए 24 संभावित तरीकों में से 1 से 5 बार प्रयास करने की संभावना दर्शाती है।
आवश्यक मोड़
| मोड़ों | संख्या | संभावना |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| कुल | 24 | 100.00% |
डॉट उत्पाद को लेते हुए, इस रणनीति के तहत आवश्यक घुमावों की औसत संख्या 3.29167 है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
मैंने फ़ाइनल जेपर्डी के लिए दो-तिहाई दांव लगाने के नियम के बारे में सुना है। क्या आप इसके बारे में जानते हैं?
हाँ। यह दूसरे स्थान पर रहने वाले खिलाड़ी के लिए रणनीति में बदलाव को संदर्भित करता है यदि उसके पास पहले स्थान पर रहने वाले खिलाड़ी के स्कोर का 2/3 से अधिक स्कोर है।
आइये इस स्थिति को दो खिलाड़ियों वाले खेल के रूप में सरल करते हैं, जो इस प्रकार है:
- स्थिति A: दूसरे स्थान पर पहले स्थान के आधे से भी कम स्थान है।
- स्थिति B: दूसरे खिलाड़ी के पास पहले स्थान का 1/2 से 2/3 हिस्सा है।
- स्थिति C: दूसरे स्थान पर पहले स्थान का 2/3 से अधिक हिस्सा है।
आगे बढ़ने से पहले, मैं पाठकों को फ़ाइनल जेपर्डी के बाद टाई होने पर जेपर्डी नियम में हुए बदलाव की याद दिला दूँ। अब दोनों खिलाड़ी आगे नहीं बढ़ सकते, बल्कि सडन डेथ टाईब्रेकर का सवाल है। ऐसी ही एक स्थिति यहाँ है।
स्थिति A
मान लीजिए A=$10,000 और B=$4,000
खिलाड़ी A को A-2B-1 से ज़्यादा दांव लगाकर हारने का जोखिम नहीं उठाना चाहिए। अगर उसे इस श्रेणी में आत्मविश्वास नहीं है, तो वह $0 का दांव लगा सकता है। किसी भी तरह से, उसकी जीत पक्की है। ऐसे में, A को $0 से $1,999 के बीच दांव लगाना चाहिए।
खिलाड़ी B के पास कोई उम्मीद नहीं है, जब तक कि A बहुत ज़्यादा दांव लगाकर हार न जाए। यहाँ, B को तीसरे स्थान के स्कोर पर विचार करना चाहिए और अगर हो सके तो उससे ऊपर रहने की कोशिश करनी चाहिए, जिससे दूसरे स्थान के लिए $2,000 जीतना संभव हो, जबकि तीसरे स्थान के लिए $1,000।
स्थिति बी
मान लीजिए A=$10,000 और B=$6,000
A की रणनीति यह है कि B से पूरी बाजी लगाने की उम्मीद की जाए और अगर सही हो तो 2B को कवर करने लायक बाजी लगाई जाए। हालाँकि, सुरक्षा के लिए, उसे इतना ज़्यादा बाजी नहीं लगानी चाहिए कि गलत होने पर B से नीचे गिर जाए। इस स्थिति में, उसे कम से कम 2B-A+1 और AB-1 पर बाजी लगानी चाहिए। इस स्थिति में, रेंज $2,001 और $3,999 है।
B के लिए रणनीति यह है कि अगर सही हो, तो A को पास करने के लिए कम से कम इतना स्कोर हासिल करे और अपना पूरा स्कोर बढ़ाए। इस मामले में, $4,001 और $6,000।
अगर दोनों खिलाड़ी उम्मीद के मुताबिक़ प्रदर्शन करते हैं और इसी रणनीति पर चलते हैं, तो खिलाड़ी B के जीतने का एकमात्र तरीका यही है कि A गलत हो और B सही। इसकी संभावना लगभग 19% है।
स्थिति C
यहां चीजें अधिक जटिल हो जाती हैं और इसमें अधिक खेल सिद्धांत और यादृच्छिकीकरण शामिल होता है।
मान लीजिए A=$10,000 और B=$7,000.
आगे बढ़ने से पहले, फ़ाइनल जेपर्डी क्लू के सही उत्तर दिए जाने की संभावना का अनुमान लगाना ज़रूरी है। सीज़न 30 से 34 के आधार पर, पहले स्थान पर रहने वाला खिलाड़ी 52% बार और दूसरे स्थान पर रहने वाला खिलाड़ी 46% बार सही था। हालाँकि, ये संभावनाएँ सकारात्मक रूप से सहसंबद्ध हैं। यहाँ सभी चार संभावनाओं का विवरण दिया गया है:
- दोनों सही: 27%
- प्रथम स्थान सही, द्वितीय स्थान गलत: 25%
- प्रथम स्थान गलत, द्वितीय स्थान सही: 19%
- दोनों गलत 29%.
पहले दो खिलाड़ियों के लिए जेपर्डी औसत 49% होने के बावजूद, दोनों के सही होने या दोनों के गलत होने की संभावना 56% है।
बेशक, ये श्रेणी के आधार पर बदल सकते हैं, लेकिन आइए चीजों को सरल रखें और ऊपर दी गई संभावनाओं का उपयोग करें।
इस स्थिति में, खिलाड़ी B को A के गलत और B के सही होने पर निर्भर नहीं रहना पड़ता। वह कम, मान लीजिए $0, दांव लगा सकता है, जिससे A के गलत होने पर उसकी जीत सुनिश्चित हो जाती है। दूसरे शब्दों में, अगर A, B के सही होने पर उसे कवर करने के लिए पर्याप्त दांव लगाता है, तो गलत होने पर और B के $0 दांव लगाने पर उसे B से नीचे गिरने का जोखिम उठाना पड़ेगा।
हालाँकि, अगर A ने अनुमान लगाया कि B कम, मान लीजिए $0, पर दांव लगाएगा, तो A भी $0 का दांव लगाकर जीत पक्की कर सकता है। दोनों खिलाड़ियों के पास मूलतः एक विकल्प होता है, कम या ज़्यादा दांव लगाना। A को B की तरह ही दांव लगाना चाहिए और B को B के विपरीत दांव लगाना चाहिए। अगर दोनों खिलाड़ी पूर्ण तर्कशास्त्री होते, तो वे अपने निर्णय यादृच्छिक रूप से लेते।
इस स्थिति में, A का उच्च दांव 2B-A+1 से AB-1 होना चाहिए, जैसा कि स्थिति B में है। इस स्थिति में $2,999 और $4,001 हैं। A का निम्न दांव $0 होना चाहिए।
B द्वारा लगाया गया उच्च दांव, स्थिति B के समान ही होना चाहिए, और यदि सही हो तो A को पास करने के लिए पर्याप्त दांव होना चाहिए। इस स्थिति में, $3,001 और $7,000। B द्वारा लगाया गया निम्न दांव $0 होना चाहिए।
यदि मैं गणित को छोड़कर सीधे दोनों खिलाड़ियों के लिए यादृच्छिकरण रणनीतियों पर आ जाऊं तो मुझे क्षमा करें।
खिलाड़ी A को 62.3% संभावना के साथ उच्च और 37.7% संभावना के साथ निम्न पर जाना चाहिए।
खिलाड़ी बी की संभावना 61.2% के साथ उच्च और 38.8% के साथ निम्न होनी चाहिए।
यह मानते हुए कि दोनों खिलाड़ी इस यादृच्छिकरण रणनीति का पालन करते हैं और ऊपर बताई गई संभाव्यता जोड़ियों के सही होने की संभावना है, खिलाड़ी A के जीतने की संभावना 65.2% है।
यदि खिलाड़ी A का स्कोर खिलाड़ी B के स्कोर से 2/3 से अधिक होता, तो उसके जीतने की संभावना 81.0% तक बढ़ जाती।
डबल जेपर्डी पर दांव लगाते समय दोनों खिलाड़ियों को 2/3 नियम के महत्व को ध्यान में रखना चाहिए।