संभावना - पहेलियाँ
मुझे पासे फेंकने की संभावना के बारे में कुछ विशिष्ट जानकारी प्राप्त करने में रुचि है। यदि आपके पास 6 पासे हैं और आप उन्हें एक साथ फेंकते हैं, तो सभी पासों के एक होने की संभावना 46,656 में 1 है। मेरा प्रश्न यह है कि एक से पाँच पासे आने की संभावना क्या है। मुझे वास्तव में इस प्रकार की समस्या की गणना के लिए उपयोग किए जाने वाले सूत्र को जानने में रुचि है।
y पासों में से x इकाईयाँ आने की प्रायिकता combin(y,x)*(1/6) x *(5/6) yx है। combin(x,y) फ़ंक्शन की व्याख्या के लिए पोकर में प्रायिकताओं पर मेरा अनुभाग देखें। उदाहरण के लिए, 4 इकाईयाँ आने की प्रायिकता combin(6,4)*(1/6) 4 *(5/6) 2 = 0.803755% है।
छह पासों में इकाइयों की संख्या
| लोगों | संभावना |
|---|---|
| 0 | 0.3348980 |
| 1 | 0.4018776 |
| 2 | 0.2009388 |
| 3 | 0.0535837 |
| 4 | 0.0080376 |
| 5 | 0.0006430 |
| 6 | 0.0000214 |
| कुल | 1.0000000 |
आठ गोल्फ़र एक नए कोर्स पर गए। कैडी मास्टर ने चार कार्ट पर यादृच्छिक रूप से 8 बैग रखे। गोल्फ़रों ने 8 चिह्नित गोल्फ़ बॉल एक टोपी में रखीं। गेंदों को हवा में उछाला गया। एक-दूसरे के सबसे पास वाली दो गेंदें जोड़ीदार थीं। हर बार, जोड़ीदारों के गोल्फ़ बैग पहले से ही एक कार्ट पर थे। क्या संभावना है कि फेंकने से पहले गोल्फ़ बैग सही ढंग से जोड़े गए थे?
संयोजनों की संख्या का सूत्रीय उत्तर होगा संयोजन (8,2) * संयोजन (6,2) * संयोजन (4,2) / तथ्य (4) = 25 * 15 * 6/24 = 105। संयोजनों की संख्या को हल करने का एक और तरीका एक गोल्फ खिलाड़ी को यादृच्छिक रूप से लेना होगा। उसके साथ जोड़ी बनाने के लिए 7 संभावित लोग हैं। फिर बचे हुए छह में से यादृच्छिक रूप से एक और गोल्फ खिलाड़ी चुनें। उसके साथ जोड़ी बनाने के लिए 5 संभावित लोग हैं। फिर बचे हुए चार में से यादृच्छिक रूप से एक और गोल्फ खिलाड़ी चुनें। उसके साथ जोड़ी बनाने के लिए 3 संभावित लोग हैं। इसलिए संयोजनों की संख्या 7 * 5 * 3 = 105 है। इस प्रकार उत्तर 105 में 1 है।
एक मित्र ने मुझे यह भेजा था, मैं जानना चाहता था कि क्या इसका कोई सूत्र है कि यह कैसे काम करता है।
अक्सर ये दिमाग पढ़ने वाली संख्या पहेलियाँ एक दिलचस्प गणितीय विषमता के कारण कारगर होती हैं। यदि किसी संख्या के अंकों का योग 9 से विभाज्य है, तो वह संख्या स्वयं भी 9 से विभाज्य होगी। आइए इसे लास वेगास ट्रॉपिकाना (702-739-2222) के फ़ोन नंबर पर आज़माते हैं। अंकों का योग 7+0+2+7+3+9+2+2+2+2 = 36 है। 36, 9 से बराबर विभाजित होता है, इसलिए 702739222 भी 9 से विभाज्य होगा। इसका एक प्रमाण यहाँ दिया गया है।
- मान लीजिए n किसी पूर्णांक पर bet है। n को d 0 *1 + d 1 *10 + d 2 *100+ d 3 *1000+ ... + d n *10 n के रूप में व्यक्त करें, जहाँ d n पहला अंक है, d n-1 दूसरा अंक है, इत्यादि।
- n = [d 0 + d 1 + d 2 + ... + d n ] + [d 1 *9 + d 2 *99+ d 3 *999+ ...+ d n *999...9 ( n नाइन वाली एक संख्या)]
- n = [d 0 + d 1 + d 2 + ... + d n ] + 9*[d 1 *1 + d 2 *11+ d 3 *111+ ... d n *111...1 (n इकाइयों वाली एक संख्या)]
- 9*कोई भी पूर्णांक 9 से समान रूप से विभाज्य है। इसलिए यदि d 0 + d 2 + d 2 + ... + d n , या अंकों का योग, 9 से विभाज्य है, तो पूरी संख्या 9 से विभाज्य होनी चाहिए।
अब जब हमने यह प्रमाण दे दिया है, तो हम इस जादुई ट्रिक पर गौर कर सकते हैं। इस समस्या में आपको कोई भी संख्या चुननी है। फिर उसके अंकों को पुनर्व्यवस्थित करके दूसरी संख्या बनानी है। फिर छोटी संख्या को बड़ी संख्या से घटाना है।
उत्तर में हमेशा 9 से विभाज्य अंकों का योग होगा। क्यों? मूल संख्या के प्रत्येक अंक के लिए, वह दूसरी संख्या में कहीं और दिखाई देता है। एक बार में अंकों के एक समूह पर जाकर, बाकी सभी संख्याओं को शून्य में बदलकर, हम प्रत्येक समूह को इस प्रकार हल कर सकते हैं: +/- n*[10 x - 10 y ] (जहाँ x>=y और n अंक है) = +/-n *10 y * (10 xy - 1) = 10 y * (केवल नौ से बनी एक संख्या) = 9 से विभाज्य एक संख्या।
आइए एक उदाहरण देखें। मान लीजिए मूल संख्या 1965 है। इसे बदलकर 6951 प्राप्त करें। 6951 - 1965 = 6*(1000-10) + 9*(100-100) + 5*(10-1) + 1*(1-1000) = 6*990 + 9*0 + 5*9 + 6*-999। ध्यान दें कि प्रत्येक भाग 9 से विभाज्य है, इसलिए घटाने के बाद प्राप्त संख्या भी 9 से विभाज्य होनी चाहिए, और अंत में अंकों का योग भी 9 से विभाज्य होगा।
फिर यह ट्रिक आपको 0 को छोड़कर बाकी सभी अंकों का योग दर्ज करने के लिए कहती है। फिर प्रोग्राम को आपके द्वारा दर्ज की गई संख्या में केवल एक संख्या जोड़नी होती है ताकि योग 9 से विभाज्य हो। उदाहरण के लिए, अगर आपने कहा कि आपके अंकों का योग 13 है, तो आपको 5 पर गोला बनाना होगा, क्योंकि 13+5 = 9 से विभाज्य संख्या।
आप शून्य पर गोला नहीं लगा सकते, क्योंकि यदि आपने ऐसा किया और फिर 9 से विभाज्य कोई संख्या दर्ज की, तो प्रोग्राम को यह पता नहीं चलेगा कि आपने 0 पर गोला लगाया है या 9 पर।
शानदार साइट। मैं इसे अक्सर प्रायिकता और सांख्यिकी में रुचि रखने वाले जुआरी के रूप में संदर्भित करता हूँ, लेकिन यह प्रश्न वास्तव में मेरे काम से संबंधित है। मेरा मानव संसाधन विभाग इस बात पर ज़ोर देता है कि मैं अपने छोटे से स्टाफ (5 लोग) को एक बेल कर्व पर रेट करूँ—सभी कर्मचारियों में से शीर्ष 5% में एक, अगले 20% में एक, अगले 50% में एक, अगले 20% में एक, और सबसे निचले 5% में एक। कंपनी में लगभग 5000 कर्मचारी हैं। इतने छोटे नमूने के इस वितरण में फिट होने की क्या प्रायिकता है?
तारीफ़ के लिए शुक्रिया। यह एक अच्छी समस्या है। ठीक एक कर्मचारी के सबसे निचले 5% में होने की प्रायिकता 5*(.05)*(.95) 4 = 0.203627 है। यह मानते हुए कि एक कर्मचारी सबसे निचले 5% में है, अगले 20% में ठीक एक कर्मचारी के होने की प्रायिकता 4*(.2/.95)*(.75/.95) 3 = 0.414361 है। इन दो कम उपलब्धि वाले कर्मचारियों को देखते हुए, शेष 75% में से अगले 50% में ठीक एक कर्मचारी के होने की प्रायिकता 3*(.5/.75)*(.25/.75) 2 = 0.222222 है। शेष दो में से एक के 25% के निचले 20% में आने की प्रायिकता 2*(.2/.25)*(.05/.25) = 0.32 है। इन सभी संभावनाओं का गुणनफल लेने पर हमें 0.006, या 1% का 3/5 प्राप्त होता है।
ऑर्डर सांख्यिकी ( कॉलम #100 ) के बारे में प्रश्न पूछने वाले व्यक्ति से, मेरी दो आपत्तियाँ हैं: एक छोटी और एक बड़ी। आपकी विधि परिमित जनसंख्या सुधार करने में विफल रही, जो मैं मानता हूँ कि 5000 कर्मचारियों के साथ मामूली है, लेकिन अगर 20 कर्मचारी होते तो यह निश्चित रूप से संभव नहीं होता!
हालाँकि, इससे भी महत्वपूर्ण बात यह है कि आप यह मान लेते हैं कि प्रबंधकों का अपने कर्मचारियों पर कोई प्रभाव नहीं पड़ता। मान लीजिए कि अच्छे प्रबंधक, विवेकपूर्ण नियुक्ति और बर्खास्तगी के माध्यम से, या औसत से बेहतर प्रेरक कौशल के माध्यम से, अपने कर्मचारियों का औसत स्तर ऊँचा उठाते हैं। इस प्रभाव को ध्यान में रखे बिना, हम परिणामी संभावनाओं को या तो ऊपर की ओर या नीचे की ओर झुकाएँगे। मुझे यकीन है कि आप यह जानते होंगे, लेकिन मैं इसके प्रति संवेदनशील हूँ क्योंकि मैं भेदभाव के मामलों में इस तरह की कई गणनाएँ करता हूँ और जिन चीज़ों के लिए हम समायोजन कर सकते हैं (इस मामले में एक समूह-विशिष्ट प्रभाव) के लिए समायोजन न करने से अक्सर लोग भटक सकते हैं।
इन अच्छे बिंदुओं के लिए धन्यवाद। हालाँकि, नौकरी के प्रदर्शन की रेटिंग के वितरण पर नियंत्रण न होने का विकल्प रेटिंग में वृद्धि है। प्रबंधक को अपने कर्मचारियों को खुश रखने के लिए बढ़ा-चढ़ाकर रेटिंग देने की स्थिति में डाल दिया जाएगा। दस साल तक सरकारी कर्मचारी रहने के नाते, मैं इस बारे में कुछ अनुभव के साथ बात करता हूँ। जब मैं यूएनएलवी में पढ़ाता था, तब कक्षा का कोई औसत जीपीए मानक नहीं था, लेकिन सेमेस्टर के अंत में ग्रेडिंग कर्व कैसा होना चाहिए, इस बारे में कुछ अपेक्षाएँ थीं। कम से कम कॉलेज के माहौल में, मुझे लगा कि यह एक उचित नीति है। शायद व्यावसायिक माहौल में, किसी तरह का सामान्य ज्ञान वाला माध्यम भी सबसे अच्छा होगा।
क्या गेमिंग गणितज्ञों के सामने कोई प्रसिद्ध अनसुलझी समस्याएँ हैं? जैसे जुए की दुनिया में फ़र्मेट का अंतिम प्रमेय । अगर हाँ, तो कृपया कोई उदाहरण बताएँ।
अच्छा सवाल है। मुझे कोई भी याद नहीं आ रहा।
यह कैसे काम करता है: www.1800gotjunk.com/genie/ ?
आइए अपनी संख्या को 10t+u के रूप में व्यक्त करें। आपको प्रत्येक अंक घटाने के लिए कहा गया है, जिससे आपको 10t+utu = 9t प्राप्त होगा, जो 9 से विभाज्य एक संख्या है। ध्यान दें कि 9 से विभाज्य सभी संख्याओं में एक ही वस्तु है, और वह वही है जिसकी भविष्यवाणी जिन्न करता है।
मैं एक पेशेवर लाइसेंस परीक्षा देने वाला हूँ। नियमों के अनुसार:
- परीक्षा में 7 विषय होंगे।
- प्रत्येक विषय के लिए 60 बहुविकल्पीय प्रश्न पूछे जाएंगे।
- प्रत्येक बहुविकल्पीय प्रश्न के चार संभावित उत्तर होंगे, लेकिन सही उत्तर केवल एक होगा।
- उत्तीर्ण होने के लिए, परीक्षार्थी को कम से कम 75% का सामान्य औसत प्राप्त करना होगा तथा किसी भी विषय में उसका ग्रेड 65% से कम नहीं होना चाहिए।
मेरा सवाल यह है कि अगर कोई परीक्षार्थी अपने सभी उत्तरों का अनुमान लगा लेता है, तो उसके परीक्षा में पास होने की संभावना क्या है? दूसरे शब्दों में, सिर्फ़ भाग्य से परीक्षा में पास होने की संभावना क्या है?
75% अंक की आवश्यकता को पूरा करने के लिए, छात्र को 420 प्रश्नों में से कम से कम 315 सही उत्तर देने होंगे। अनुमान से सही उत्तरों की अपेक्षित संख्या 420*0.25=105 है। मानक विचलन (420*0.25*0.75)^0.5 = 8.87412 है। इसलिए, उम्मीदवार को 210 प्रश्नों के उत्तर, या 210/8.87412=23.66432 मानक विचलन, अपेक्षा से अधिक देने होंगे। ऐसा होने की संभावना चार्ट से बहुत दूर है। अगर पृथ्वी पर सभी जीवित प्राणी इस परीक्षा में यादृच्छिक उत्तर दें, तो मुझे संदेह है कि कोई भी या वस्तु पास होगी। मैं अन्य आवश्यकता पर तो बात ही नहीं करूँगा।
यदि किसी विश्वविद्यालय की फुटबॉल टीम के पास खेल 1 जीतने की 10% संभावना है और खेल 2 जीतने की 30% संभावना है, तथा दोनों खेल हारने की 65% संभावना है, तो उनके एक बार जीतने की संभावना क्या है?
अगर हम मान लें कि दोनों खेल स्वतंत्र हैं, तो दोनों में हारने की संभावना 90%*70%=63% होगी। लेकिन चूँकि आप कह रहे हैं कि दोनों में हारने की संभावना वास्तव में 65% है (जो कि 63% से ज़्यादा है), इसका मतलब है कि दोनों घटनाएँ परस्पर संबंधित हैं। अगर दोनों में हारने की संभावना 65% है और सिर्फ़ दूसरा खेल हारने की संभावना 70% है, तो पहला खेल जीतने और दूसरा खेल हारने की संभावना 5% होनी चाहिए। इसी तर्क से, पहला खेल हारने और दूसरा खेल जीतने की संभावना 25% होनी चाहिए। यानी दोनों खेल जीतने की संभावना केवल 5% बचती है। इसलिए ठीक एक बार जीतने की संभावना 25%+5% = 30% है।
गेम शो "लेट्स मेक अ डील" में तीन दरवाज़े हैं। मान लीजिए कि दो दरवाज़ों से एक बकरी निकलती है और एक दरवाज़ा एक नई कार दिखाता है। होस्ट, मोंटी हॉल, दो प्रतियोगियों को एक दरवाज़ा चुनने के लिए चुनते हैं। हर बार मोंटी पहले एक दरवाज़ा खोलता है जिसमें एक बकरी निकलती है। मान लीजिए इस बार वह दरवाज़ा पहले प्रतियोगी का था। हालाँकि मोंटी ने वास्तव में ऐसा कभी नहीं किया, लेकिन अगर मोंटी दूसरे प्रतियोगी को इस समय दरवाज़ा बदलने का मौका दे, यानी दूसरे बंद दरवाज़े पर। क्या उसे दरवाज़ा बदलना चाहिए?
हाँ! इस समस्या की जड़ यह है कि मेज़बान को बकरी वाला दरवाज़ा खोलने के लिए पहले से ही तय कर दिया गया है। वह जानता है कि किस दरवाज़े में कार है, इसलिए खिलाड़ी चाहे कोई भी दरवाज़ा चुनें, वह हमेशा पहले बकरी ही दिखा सकता है। इस प्रश्न को "मोंटी हॉल विरोधाभास" के नाम से जाना जाता है। इसके बारे में ज़्यादातर भ्रम इसलिए है क्योंकि अक्सर जब प्रश्न पूछा जाता है, तो यह स्पष्ट नहीं किया जाता कि मेज़बान को कार कहाँ है, और वह हमेशा पहले बकरी ही दिखाता है। मुझे लगता है कि इसका कुछ दोष मर्लिन वोस सावंत पर भी है, जिन्होंने अपने कॉलम में प्रश्न को गलत तरीके से लिखा था। मान लीजिए कि इनाम दरवाज़ा 1 के पीछे है। अगर खिलाड़ी (दूसरा प्रतियोगी) ने बदलाव न करने की रणनीति बनाई होती, तो क्या होता, यहाँ बताया गया है।
- खिलाड़ी दरवाज़ा 1 चुनता है --> खिलाड़ी जीतता है
- खिलाड़ी दरवाज़ा 2 चुनता है --> खिलाड़ी हार जाता है
- खिलाड़ी दरवाज़ा 3 चुनता है --> खिलाड़ी हार जाता है
यदि खिलाड़ी के पास स्विचिंग की रणनीति होगी तो क्या होगा, नीचे बताया गया है।
- खिलाड़ी दरवाज़ा 1 चुनता है --> मेज़बान दरवाज़ा 2 या 3 के पीछे बकरी दिखाता है --> खिलाड़ी दूसरे दरवाज़े पर जाता है --> खिलाड़ी हार जाता है
- खिलाड़ी दरवाज़ा 2 चुनता है --> मेज़बान दरवाज़ा 3 के पीछे बकरी दिखाता है --> खिलाड़ी दरवाज़ा 1 पर जाता है --> खिलाड़ी जीतता है
- खिलाड़ी दरवाज़ा 3 चुनता है --> मेज़बान दरवाज़ा 2 के पीछे बकरी दिखाता है --> खिलाड़ी दरवाज़ा 1 पर जाता है --> खिलाड़ी जीतता है
इसलिए, स्विच न करने से खिलाड़ी के जीतने की संभावना 1/3 रह जाती है। स्विच करने से खिलाड़ी के जीतने की संभावना 2/3 रह जाती है। इसलिए खिलाड़ी को ज़रूर स्विच करना चाहिए।
मोंटी हॉल विरोधाभास पर आगे पढ़ने के लिए, मैं विकिपीडिया पर लेख की अनुशंसा करता हूं।
मैं 19 नवंबर, 2004 के कॉलम में मोंटी हॉल के प्रश्न के आपके उत्तर से असहमत हूँ। यह मानते हुए कि कार दरवाज़े एक के पीछे है, वास्तव में चार संभावनाएँ इस प्रकार हैं, जहाँ पुरस्कार दरवाज़े एक के पीछे है।
- खिलाड़ी दरवाज़ा 1 चुनता है --> दिखाया गया 2 --> 3 पर स्विच करता है, हार जाता है
- खिलाड़ी दरवाज़ा 1 चुनता है --> दिखाया गया 3 --> 2 पर स्विच करता है, हार जाता है
- खिलाड़ी दरवाज़ा 2 चुनता है --> दिखाया गया 3 --> 1 पर स्विच करता है, जीतता है
- खिलाड़ी दरवाज़ा 3 चुनता है --> दिखाया गया 2 --> 1 पर स्विच करता है, जीतता है
जैसा कि आप देख सकते हैं, चाहे आप स्विच करें या नहीं, जीतने की संभावना 50% है। इसके अलावा, यह सामान्य समझ के बिल्कुल विपरीत है कि स्विच करना बेहतर होगा।
आपकी गलती यह मान लेना है कि इनमें से प्रत्येक घटना की संभावना 25% है। प्रत्येक घटना की सही संभावना नीचे दी गई है।
- खिलाड़ी दरवाज़ा 1 चुनता है (1/3) * दिखाया गया 2 (1/2) = खिलाड़ी हारता है (1/6)
- खिलाड़ी दरवाज़ा 1 चुनता है (1/3) * दिखाया गया 3 (1/2) = खिलाड़ी हारता है (1/6)
- खिलाड़ी दरवाज़ा 2 चुनता है (1/3) * दिखाया गया 3 (1/1) = खिलाड़ी जीतता है (1/3)
- खिलाड़ी दरवाज़ा 3 चुनता है (1/3) * दिखाया गया 2 (1/1) = खिलाड़ी जीतता है (1/3)
इसलिए हारने वाली घटनाओं की कुल संभावना 2*(1/6) = 1/3 है और जीतने वाली घटनाओं की कुल संभावना 2*(1/3)=2/3 है।
पांच अलग-अलग टॉपिंग में से चुनने के साथ, आप कितने अलग-अलग पिज्जा बना सकते हैं, किसी भी संख्या में टॉपिंग के साथ?
0 टॉपिंग वाला एक तरीका, 1 टॉपिंग वाला 5 तरीका, 2 टॉपिंग वाला 10 तरीका, 3 टॉपिंग वाला 10 तरीका, 4 टॉपिंग वाला 5 तरीका, और 5 टॉपिंग वाला 1 तरीका। तो जवाब है 1+5+10+10+5+1 = 32. हल करने का एक और तरीका यह है कि या तो टॉपिंग का इस्तेमाल किया जा सकता है या नहीं। तो कुल योग है 2 5 = 32.
मैंने पिछले हफ़्ते अख़बार में पढ़ा कि इंडोनेशिया में तबाही मचाने वाला ताज़ा भूकंप 26 दिसंबर को आया था। इसमें यह भी बताया गया था कि पिछले 100 सालों में आए आठ सबसे घातक भूकंपों में से तीन 26 दिसंबर को ही आए थे। मैं सोच रहा था कि इन तथ्यों को जानते हुए भी एक ही दिन तीन बड़े भूकंप आने की क्या संभावना है: इतनी तीव्रता (8.0 या उससे ज़्यादा) के भूकंप साल में सिर्फ़ एक बार आते हैं। आखिरी बड़ा भूकंप ठीक एक साल पहले, 26/12/03 को ईरान में आया था (क्या लगातार दो भूकंप आने की संभावना है?)। मैं आपसे सुनने के लिए उत्सुक हूँ।
यह पता चलने के बाद कि फ्लोरिडा के तूफ़ान सिर्फ़ बुश के वोट वाले काउंटियों में ही आए थे, यह दावा एक धोखा था ( 17 अक्टूबर, 2004 का कॉलम देखें), मैं ऐसे कथित संयोगों को लेकर और भी ज़्यादा संशयी हो जाऊँगा। राष्ट्रीय भूकंप सूचना केंद्र के अनुसार, 1990 के बाद से आए शीर्ष 11 भूकंपों में से सिर्फ़ 2004 का हालिया भूकंप ही 26 दिसंबर को आया था। आप जिस ईरानी भूकंप का ज़िक्र कर रहे हैं, उसकी तीव्रता सिर्फ़ 6.7 थी, जो शीर्ष आठ में शामिल होने से कोसों दूर है।
अगर आप हर दिन आधे अंडे और आधा अंडा बेचते हैं, तो शुरुआत में आपके पास कितने अंडे होंगे; और तीन दिन बाद आपके पास एक भी अंडा नहीं बचता? हर दिन के अंत में, अंडों की संख्या एक पूर्ण संख्या होती है।
मान लीजिए कि दिन के लिए d, दिन की शुरुआत में अंडों की संख्या है और रात के लिए n, दिन के अंत में अंडों की संख्या है। समस्या हमें बताती है कि d/2 - ? = n है। तो, आइए d को n के पदों में हल करें।
डी/2 = एन + ?
डी= 2एन + 1
तो तीसरे दिन n=0, तो d=1.
दूसरे दिन n=1, अतः d=3.
तीसरे दिन n=3, अतः d=7.
तो लीजिए, आपने 7 अण्डों से शुरुआत की।
एक ऐसे द्वीप की कल्पना कीजिए जहाँ 10 लोग रहते हैं, और वहाँ की राजनीति ऐसी है कि हर दिन एक द्वीपवासी को यादृच्छिक रूप से ठीक एक दिन के लिए मुखिया चुना जाता है; उस दिन के बीत जाने के बाद, एक और द्वीपवासी को यादृच्छिक रूप से चुना जाता है (इस प्रकार, वही द्वीपवासी जो अभी मुखिया था, उसके दोबारा मुखिया बनने की संभावना 1/10 है)। हल करने योग्य प्रश्न: औसतन, प्रत्येक द्वीपवासी को कम से कम एक बार मुखिया बनने में कितने दिन लगेंगे?
एक व्यक्ति के प्रमुख के रूप में कार्य करने में केवल 1 दिन लगेगा। दूसरे दिन नए प्रमुख की संभावना 0.9 है। यदि प्रत्येक दिन की संभावना 0.9 है, तो नए प्रमुख के आने में लगने वाले दिनों की अपेक्षित संख्या 1/0.9 = 1.11 है। यह किसी भी संभावना के लिए सत्य है: सफलता प्राप्त होने तक अपेक्षित प्रयासों की संख्या 1/p है। इसलिए 2 लोगों के कार्य करने के बाद अगले दिन नए प्रमुख की संभावना 0.8 है। इसलिए तीसरे प्रमुख के लिए प्रतीक्षा अवधि 1/0.8 = 1.25 दिन है। उत्तर प्रतीक्षा अवधियों का योग है, जो 1/1 + 1/.9 + 1/.8 + ... + 1/.1 = 29.28968 दिन है।
वृत्त की त्रिज्या 1 है। त्रिभुज समबाहु है। प्रत्येक रंगीन क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
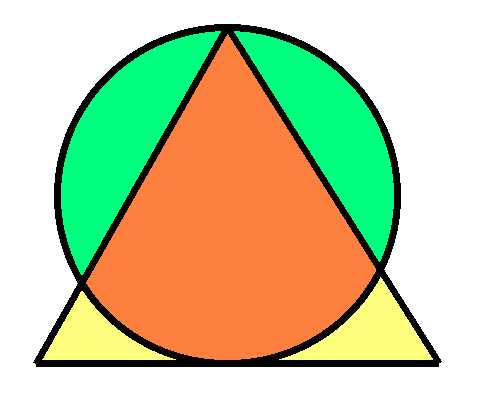
मैं उन लोगों के लिए उत्तर को उजागर नहीं करना चाहता जो इसे स्वयं हल करना चाहते हैं। उत्तर और समाधान के लिए मेरी दूसरी वेबसाइट mathproblems.info पर जाएँ, समस्या 189।
मान लीजिए आपने एक प्रतियोगिता जीती है जहाँ NBA गेम के हाफटाइम में आपको एक फ़्री थ्रो शूट करना है और अगर आप उसे पूरा कर लेते हैं तो आपको 1 मिलियन डॉलर मिलेंगे। इसके अलावा, आप तब तक फ़्री थ्रो शूट करते रह सकते हैं, डबल या बिल्कुल नहीं, जब तक आप चूक न जाएँ या रुकना न चाहें। अगर आप 75% फ़्री थ्रो शूट करते हैं, तो आप कब रुकेंगे? क्या आप कभी रुक सकते हैं? एक समय ऐसा आएगा जब पैसे का मतलब कम होता जाएगा। आप क्या करेंगे?
किसी बिंदु पर आपको एक अच्छा दांव अस्वीकार कर देना चाहिए क्योंकि दांव बहुत अधिक है। व्यक्तिगत रूप से मुझे लगता है कि धन से मिलने वाले आनंद का एक अच्छा उपाय राशि का लघुगणक है। लघुगणक का आधार मायने नहीं रखता इसलिए चलिए 10 का उपयोग करते हैं। हालांकि हम 10 से कम का लघुगणक नहीं ले सकते हैं, इसलिए मान लें कि दस से कम किसी भी राशि के लिए आनंद 0 है। इसलिए आपके उदाहरण में मान लें कि आपके पहले फेंक के साथ $1,000,000 जीतने से पहले आपके पास $0 है। अब आपके पास log(1,000,000) = खुशी की 6 इकाइयाँ हैं। एक और फ्री थ्रो लेने पर आपकी खुशी का अपेक्षित मूल्य 0.75*log(2,000,000) + 0.25*0 = 4.975772 है। यह 6 से कम है इसलिए इस मामले में आपको दस लाख लेकर चले जाना चाहिए। हालांकि तो वॉक करके आपकी खुशी log(1,200,000) = 6.07918 है। एक मिलियन का जोखिम उठाकर और एक और शॉट लेने पर आपकी खुशी 0.75*log(2,200,000) + 0.25*log(200,000) = 6.082075 है, इसलिए आप मामूली रूप से दूसरा शॉट लेते हैं। अगर आप वह जीत जाते हैं, तो आपका विकल्प log(2,200,000) = 6.34242 और 0.75*log(4,200,000)+0.25*log(200,000) = 6.29269 के बीच होगा। इस स्थिति में आपको तीसरा शॉट नहीं लेना चाहिए और $2,000,000 की जीत के साथ वॉक कर देना चाहिए। पहला डबल स्वीकार करने के लिए ब्रेक-ईवन पॉइंट $191,487 की मौजूदा संपत्ति है। दो डबल स्वीकार करने के लिए आपके पास अन्य धन के रूप में $382,975 होने चाहिए।
मुझे याद है कि अगर एक कमरे में 22 लोग हैं, तो संभावना बराबर है कि दो लोग एक ही जन्मदिन मनाएँगे [महीना और दिन, साल नहीं]। मैं इसे साबित करने का गणित भूल गया हूँ। क्या आप कृपया इसे बता सकते हैं।
मुझे लगता है कि मैंने इसका उत्तर पहले भी दिया है, लेकिन 50/50 अंक 23 के ज़्यादा करीब है। चीज़ों को आसान बनाने के लिए, लीप वर्ष को छोड़ दें। लंबा उत्तर यह है कि 23 लोगों को किसी तरह क्रम में रखा जाए। व्यक्ति #2 का जन्मदिन व्यक्ति #1 से अलग होने की प्रायिकता 364/365 है। व्यक्ति #3 का जन्मदिन व्यक्ति #1 और #2 से अलग होने की प्रायिकता, यह मानते हुए कि वे एक-दूसरे से अलग हैं, 363/365 है। व्यक्ति 23 तक दोहराते रहें। इस प्रकार प्रायिकता (364/365)*(363/365)*...*(343/365) = 49.2703% है। इसलिए, किसी भी मिलान की प्रायिकता 49.27% है और कम से कम एक मिलान की प्रायिकता 50.73% है। एक अन्य समाधान 23 विभिन्न जन्मदिनों के क्रमचयों की संख्या को 1 से 365 तक 23 यादृच्छिक संख्याएं चुनने के तरीकों की कुल संख्या से विभाजित करना है, जो कि क्रमचय (365,23)/365 23 = 42,200,819,302,092,400,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 / 85,651,679,353,150,300,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 = 49.27% है।
एक राज्य में शिक्षकों का साप्ताहिक वेतन सामान्य रूप से वितरित है, जिसका माध्य $490 और मानक विचलन $45 है। इसकी क्या प्रायिकता है कि एक यादृच्छिक रूप से चयनित शिक्षक प्रति सप्ताह $525 से अधिक कमाए? मुझे याद नहीं आ रहा कि बिना समष्टि के केवल माध्य और मानक विचलन (SD) से प्रायिकता की गणना कैसे की जाए।
यह औसत से $35 ज़्यादा होगा, यानी 7/9 मानक विचलन। उम्मीद से 7/9 मानक विचलन ज़्यादा होने की संभावना 1-Z(7/9) = 1- 0.78165 = 0.21835 होगी।
दो लोग पत्थर, कागज़ और कैंची खेल रहे हैं। यह माना जा रहा है कि इस खेल में कोई रणनीति शामिल नहीं है। अगर आप 'बेस्ट ऑफ़ थ्री' खेल रहे हैं और खिलाड़ी A पहला राउंड जीत जाता है, तो खिलाड़ी B के जीतने की क्या संभावना है?
खिलाड़ी बी को अगले दो मैच जीतने होंगे (टाई को छोड़कर) इसलिए संभावना (1/2)*(1/2) = 1/4 है।
नमस्ते, मैंने सोचा कि मैं आपसे यह पूछूँ क्योंकि मुझे यह वेब पर कहीं नहीं मिल रहा। मुझे उम्मीद है कि आप इसका जवाब देंगे: अस्तित्व में रहने की संभावनाएँ क्या हैं? चाहे वह पृथ्वी पर हो या ब्रह्मांड में कहीं और? यह कोई जुए का सवाल नहीं है, बल्कि एक ऐसा जवाब है जो हम सभी को पता होना चाहिए ताकि हम समझ सकें कि ज़िंदा रहकर हम कितनी संभावनाओं को मात दे सकते हैं!
मेरा मानना है कि आकाशगंगा में कहीं भी बुद्धिमान जीवन के अस्तित्व की संभावना बहुत ज़्यादा है। ड्रेक समीकरण आकाशगंगा में बुद्धिमान जीवन की घटनाओं की संख्या का अनुमान लगाने का प्रयास करता है, जो आपके द्वारा डाले गए आंकड़ों के आधार पर लगभग दस लाख तक पहुँचती है। हालाँकि, इस बात का भी कोई ठोस प्रमाण नहीं है कि इन सभ्यताओं ने कभी हमसे मुलाकात की हो या हमसे संपर्क किया हो। तो प्रसिद्ध फर्मी प्रश्न है, "सब लोग कहाँ हैं?" मुझे लगता है कि अन्य बुद्धिमान जीवन के प्रमाणों का अभाव ड्रेक समीकरण पर कुछ संदेह पैदा करता है, लेकिन मैं फिर भी हमारी आकाशगंगा में बुद्धिमान सभ्यताओं की संख्या लगभग 1000 मानूँगा। यह सिर्फ़ हमारी आकाशगंगा है, वहाँ अरबों आकाशगंगाएँ हैं। हालाँकि, आकाशगंगाओं के बीच की दूरी इतनी ज़्यादा है कि उनके बीच यात्रा या संचार पर चर्चा करने का कोई खास मतलब नहीं है। इसलिए आपके प्रश्न का उत्तर देने के लिए, मैं कहूँगा कि लगभग 99.9%।
मान लीजिए किसी होटल में 10,000,000 कमरे हैं और 10,000,000 इलेक्ट्रॉनिक चाबियाँ हैं। कंप्यूटर की एक गलती के कारण, प्रत्येक चाबी को एक यादृच्छिक कोड के साथ प्रोग्राम किया गया है, जिसके सही होने की संभावना 10,000,000 में से 1 है। होटल पूरी तरह से बिक चुका है। क्या संभावना है कि कम से कम एक ग्राहक के पास एक चालू चाबी हो?
सटीक उत्तर 1-(9,999,999/10,000,000) 10,000,000 = 0.632121 है। यह भी (e-1)/e के समान ही है, सात दशमलव स्थानों तक।
एक परीक्षा में 75 बहुविकल्पीय प्रश्न हैं। प्रत्येक प्रश्न के 4 संभावित उत्तर हैं, जिनमें से केवल 1 सही है। परीक्षा में उत्तीर्णता अंक 50% है। प्रत्येक उत्तर का अनुमान लगाकर परीक्षा में उत्तीर्ण होने की क्या संभावना है?
635,241 में 1.
इन-रनिंग सट्टेबाजी के लिए, यदि किसी टेनिस खिलाड़ी के पास गेम जीतने का मौका "p" है, तो उसके पास सेट जीतने का क्या मौका है?
जहाँ तक मैं टेनिस के नियमों को समझता हूँ, किसी सेट का विजेता वह होता है जो छह गेम सबसे पहले जीतता है, और कम से कम दो गेम के अंतर से, सिवाय इसके कि 6-6 से बराबरी पर एकल टाई-ब्रेकर गेम होगा। नीचे दी गई तालिका एक गेम जीतने की संभावना को देखते हुए, एक सेट जीतने की संभावना दर्शाती है।
टेनिस में संभावनाएँ
| संभावना खेल जीत | संभावना सेट जीत |
| 0.05 | 0.000003 |
| 0.1 | 0.000189 |
| 0.15 | 0.001899 |
| 0.2 | 0.009117 |
| 0.25 | 0.028853 |
| 0.3 | 0.06958 |
| 0.35 | 0.138203 |
| 0.4 | 0.23687 |
| 0.45 | 0.361085 |
| 0.5 | 0.5 |
| 0.55 | 0.638915 |
| 0.6 | 0.76313 |
| 0.65 | 0.861797 |
| 0.7 | 0.93042 |
| 0.75 | 0.971147 |
| 0.8 | 0.990883 |
| 0.85 | 0.998101 |
| 0.9 | 0.999811 |
| 0.95 | 0.999997 |
किसी खेल में जीतने की प्रायिकता p, और हारने की q, का सूत्र है 1*p 6 + 6*p 6 *q + 21*p 6 *q 2 + 56*p 6 *q 3 + 126*p 6 *q 4 + 252*p 7 *q 5 + 504*p 7 *q 6
आप एक नाव में हैं और एक पत्थर के साथ, एक मीठे पानी की झील पर हैं। आप पत्थर को झील में फेंकते हैं। ज़मीन (किनारे) के सापेक्ष, क्या जल स्तर बढ़ता है, घटता है, या वही रहता है? मेरे सहकर्मियों का मानना है कि जल स्तर वही रहेगा।
किनारे के सापेक्ष जल स्तर घटेगा। नाव के अंदर चट्टान डोंगी पर दबाव डाल रही है और इस प्रकार उसके आसपास के पानी को ऊपर धकेल रही है। विस्थापित पानी की मात्रा, डोंगी के भार के बराबर है। उदाहरण के लिए, 10 पाउंड का एक पत्थर, डोंगी के 10 पाउंड पानी को ऊपर की ओर विस्थापित करेगा। जब पत्थर को पानी में फेंका जाता है, तो भार का नहीं, बल्कि चट्टान के आयतन का महत्व होगा। इसलिए, चट्टान, डोंगी के आयतन के बराबर पानी को ऊपर की ओर धकेलेगी। चट्टान का द्रव्यमान पानी के द्रव्यमान से अधिक होता है, इसलिए चट्टान, डोंगी के अंदर के पानी की तुलना में नीचे की ओर धकेले जाने वाले पानी को अधिक विस्थापित करती है। इसलिए, डोंगी के अंदर के पत्थर के साथ झील का स्तर, झील के तल की तुलना में अधिक ऊँचा होगा।
कैसे यह काम करता है?
- एक कैलकुलेटर ले लो। (आप इसे अपने दिमाग से नहीं कर पाएंगे)
- अपने फ़ोन नंबर के पहले तीन अंक दर्ज करें (क्षेत्र कोड नहीं)
- 80 से गुणा करें
- 1 जोड़ें
- 250 से गुणा करें
- अपने फ़ोन नंबर के अंतिम 4 अंक जोड़ें
- अपने फ़ोन नंबर के अंतिम 4 अंक पुनः जोड़ें।
- 250 घटाएँ
- संख्या को 2 से विभाजित करें
क्या आप उत्तर पहचानते हैं?
चलिए आपके फ़ोन नंबर के पहले तीन अंकों को x और आखिरी चार को y कहते हैं। अब देखते हैं कि हर चरण में मेरे पास क्या है।
- तैयार!
- एक्स
- 80x
- 80x+1
- 250*(80x+1) = 20000x+250
- 20000x+250+y
- 20000x+250+2y
- 20000x+250+2y-250 = 20000x+2y
- (20000x+2y)/2 = 10000x+y
तो यह निश्चित रूप से आपके फ़ोन नंबर के बराबर होगा। हमें उपसर्ग को चार स्थान बाईं ओर ले जाने के लिए 10000x की आवश्यकता है, और फिर हम अंतिम चार अंक जोड़ते हैं।
$27,000 की एक कार के लिए ड्रॉ हो रहा है, जिसमें छह टिकट $500.00 में या एक टिकट $100.00 में बिक रहा है। 68 टिकट बिक चुके हैं, और कल टिकट खरीदने की आखिरी तारीख है। मुझे पता है कि जीतने की 50% संभावना के लिए, मुझे $5666.44 खर्च करने होंगे, और जीतने की 66.66% संभावना के लिए, मुझे $11,332.88 खर्च करने होंगे (ठीक है?)। कार "जीतने" की लगभग गारंटी के लिए मुझे कितना खर्च करना चाहिए (या मुझे कितने टिकट खरीदने चाहिए)? (90%? 95%?) क्या यह लॉटरी खेलने लायक है, या मुझे कार की कीमत खर्च करनी होगी?
1/2 और 2/3 संभावनाओं के बारे में आप सही हैं। अगर आप t टिकट खरीदते हैं, तो आपके जीतने की संभावना t/(68+t) है। इसलिए 90% संभावना के लिए, t का हल इस प्रकार निकालें।
0.9 = टी/(68+टी)
0.9*(68+टी) = टी
61.2 = 0.1 टन
t = 612, या $51,000
95% के लिए...
0.95= टी/(68+टी)
0.95(68+टी) = टी
64.6 = 0.05 टन
t = 1292, या $107,666.67
मान लें कि कार की कीमत आपके लिए 27,000 डॉलर है, तो आपको टिकट खरीदना बंद कर देना चाहिए, जैसे ही अगली बार बिकने वाली टिकट में आपके जीतने की संभावना इतनी नहीं बढ़ती कि वह कीमत वसूल सके।
किसी टिकट की कीमत के लायक होने के लिए, उसमें आपके जीतने की संभावना को p से बढ़ाना चाहिए, जहां...
27000*पी=(500/6)
पी=0.003086
मान लीजिए कि t आपके द्वारा खरीदी गई टिकटों की संख्या है, जहां आप एक और टिकट खरीदने के प्रति उदासीन हैं।
[(टी+1)/(टी+68+1)] − [टी/(टी+68)] = 0.003086
[(टी+1)/(टी+69)] − [टी/(टी+68)] = 0.003086
[((टी+1)*(टी+68))/((टी+69)*(टी+68))] − [(टी*(टी+69))/((टी+68)*(टी+69))] = 0.003086
[((टी 2 +69टी+68)/((टी+69)*(टी+68))] − [(टी 2 +69टी)/((टी+68)*(टी+69))] = 0.003086
68/((टी+68)*(टी+69)) = 0.003086
((टी+68)*(टी+69)) = 220.32
टी 2 +137टी+4692 = 22032
टी 2 +137टी - 17340=0
टी=(-137+/-(137 2 -4*1*-17340) 2 )/2
टी = 79.9326
आइए, खरीदे गए टिकटों के लिए कुछ मान डालकर इसका परीक्षण करें, यह मानते हुए कि खिलाड़ी हमेशा $500/6 = $83.33 प्रति टिकट खरीद सकता है।
79 टिकटों पर आपकी लागत 79*(500/6) = $6,583.33 है, आपकी जीतने की संभावना 79/(79+68) = 53.74% है, आपका अपेक्षित रिटर्न $27,000*0.5374 = $14,510.20 है, और आपका अपेक्षित लाभ $14,510.20 - $6,583.33 = $7,926.87 है।
80 टिकटों पर आपकी लागत 80*(500/6) = $6,666.67 है, आपके जीतने की संभावना 80/(80+68) = 54.04% है, आपका अपेक्षित रिटर्न $27,000*0.5405 = $14,594.59 है, और आपका अपेक्षित लाभ $14,594.59 - $6,666.67 = $7,927.92 है
81 टिकटों पर आपकी लागत 81*(500/6) = $6,750.00 है, आपकी जीतने की संभावना 81/(81+68) = 54.36% है, आपका अपेक्षित रिटर्न $27,000*0.5436 = $14,677.85 है, और आपका अपेक्षित लाभ $14,594.59 - $6,750.00 = $7,927.85 है।
अतः हम देख सकते हैं कि अधिकतम अपेक्षित जीत 80 टिकटों पर है।
मैं बिजली का खर्च बचाने के लिए पुराने फ्रिज को बदलने की लागत की तुलना अभी करने की कोशिश कर रहा हूँ, और उसके खराब होने तक इंतज़ार करने की तुलना में। मैं हिसाब लगा सकता हूँ कि नए फ्रिज को चलाना पुराने फ्रिज से कितना सस्ता है: $37/वर्ष, यह आसान है। लेकिन मैं नए फ्रिज की लागत को कैसे शामिल करूँ? मान लीजिए नए फ्रिज की कीमत $425 है। मैं यह नहीं कह सकता कि ये $425 नए खर्च हैं, क्योंकि मुझे पुराना फ्रिज *किसी दिन* बदलना ही होगा, अगर अभी नहीं, तो किसी न किसी समय तो नए फ्रिज का खर्च तो आएगा ही। मान लीजिए कि एक सामान्य फ्रिज 14 साल चलता है और मेरा पुराना फ्रिज 9 साल पुराना है, तो अगर मैं इसे अभी बदल दूँ तो मुझे इसे 5 साल में बदलना पड़ेगा। मैंने दो कॉलम वाली एक तालिका बनाने की कोशिश की, जिसमें मौजूदा फ्रिज को 9 साल तक रखने और फिर उसे बदलने की लागत और अभी बदलने की लागत की तुलना की गई थी, लेकिन मुझे समझ नहीं आ रहा था कि इसकी तुलना कैसे की जाए क्योंकि मुझे नहीं पता था कि लागत को भविष्य में कितने समय तक ध्यान में रखना है, और क्योंकि फ्रिज अलग-अलग वर्षों में बदले जाते हैं। मैं अभी बदलने और बाद में बदलने के आर्थिक लाभ की तुलना कैसे करूँ? वैसे, यह मेरे अपने मामले के लिए नहीं है, क्योंकि मेरा मौजूदा फ्रिज शायद 30 साल पुराना है। यह मेरे एक दोस्त के लिए है।
अगर आप मौजूदा फ्रिज रखते हैं, तो पाँच साल बाद आपको नए फ्रिज की तुलना में बिजली पर $37*5 = $185 अतिरिक्त खर्च करने होंगे। अगर आप इसे अभी बदल देते हैं, तो आपको $425 का नुकसान होगा, लेकिन पाँच साल बाद रैखिक मूल्यह्रास मानते हुए भी इसका मूल्य $425*(9/14) = $273.21 होगा। इसलिए मूल्यह्रास के कारण आपको $425*(5/14) = $151.79 का नुकसान होगा। इसलिए नए फ्रिज के मूल्यह्रास की लागत पुराने फ्रिज को रखने पर होने वाले अतिरिक्त बिजली खर्च से कम है, इसलिए मैं अभी नया फ्रिज खरीदने के पक्ष में हूँ।
यदि तीन व्यक्ति हैं, तो क्या संभावना है कि कम से कम दो व्यक्तियों का जन्मदिन एक ही तारीख को हो?
लीप डे को छोड़कर, तीनों अलग-अलग जन्मदिनों की प्रायिकता (364/365)*(363/365) = 0.99179583 है। इसलिए, कम से कम एक समान जन्मदिन की प्रायिकता 1 - 0.99179583 = 0.00820417 है।
एक कमरे में पाँच व्यक्ति हैं। क्या प्रायिकता है कि उनमें से कम से कम 2 का जन्म एक ही जन्म माह में हुआ हो?
सरलता के लिए, मान लीजिए कि प्रत्येक व्यक्ति के हर महीने में जन्म लेने की संभावना 1/12 है। सभी पाँच लोगों के अलग-अलग महीनों में जन्म लेने की संभावना (11/12)*(10/12)*(9/12)*(8/12) = 0.381944 है। इसलिए, एक समान महीने की संभावना 1 - 0.381944 = 0.618056 है।
काम पर हमें एक चुनौती दी गई है -- बस मज़े के लिए, और हममें से कोई भी इसे हल नहीं कर पा रहा है। एक किसान के पास भेड़ों से भरे पाँच ट्रेलर हैं। चार ट्रेलरों में 39 किलो वज़न की भेड़ें हैं और पाँचवें ट्रेलर में 40 किलो वज़न की भेड़ें हैं। सभी भेड़ें एक जैसी हैं। वह बाज़ार जाता है। वह जानना चाहता है कि किस ट्रेलर में 40 किलो वज़न की भेड़ है, और वह बड़े तराजू का इस्तेमाल सिर्फ़ एक बार ही कर सकता है!!! वह यह कैसे करता है? कृपया मदद करें, मेरे कार्यस्थल पर यह हम सभी को परेशान कर रहा है -- यह एक पशु चिकित्सक का क्लिनिक है!!
उत्तर कॉलम के अंत में है।
भेड़ के प्रश्न का उत्तर
ट्रेलर 1 से एक भेड़, ट्रेलर 2 से दो, ट्रेलर 3 से तीन, ट्रेलर 4 से चार और ट्रेलर 5 से शून्य लें। यदि सभी भेड़ों का वजन 39 किलोग्राम है तो कुल वजन 39 * 10 = 390 किलोग्राम होगा। हालांकि 0 से 4 भेड़ एक किलोग्राम भारी हैं। यदि कुल वजन 391 है, तो तराजू पर एक भारी भेड़ है; इस प्रकार यह ट्रेलर 1 से आई होगी। इसी तरह, यदि कुल वजन 392 है, तो तराजू पर दो भारी भेड़ें हैं, जो ट्रेलर 2 से आई होंगी। इसी तरह से 393 का वजन का मतलब है कि भारी भेड़ें ट्रेलर 3 में हैं, 394 का वजन का मतलब है कि भारी भेड़ें ट्रेलर 4 में हैं,
180 सीटों वाले हवाई जहाज में, क्या संभावना है कि मैं उस सुंदर लड़की के बगल में बैठूं जिसे मैं देख रहा हूं और जो उसी उड़ान पर होगी?
यह क्लस्टर में सीटों की संख्या पर निर्भर करता है। ज़्यादातर घरेलू उड़ानों में गलियारे के दोनों ओर तीन-तीन सीटें होती हैं। इस तरह 60 तीन-सीट वाले क्लस्टर बनेंगे। आप में से पहले व्यक्ति के बैठने के बाद, बाकी 179 सीटों में से उसी क्लस्टर में दो सीटें होंगी, इसलिए एक ही क्लस्टर में होने की संभावना 2/179 = 1.12% है। ऐसे में आप बीच वाली सीट पर किसी और को नहीं बिठा सकते। तीसरे व्यक्ति के बीच वाली सीट पर बैठने की संभावना 1/3 है। तो उत्तर है (2/179)*(2/3) = 0.74%, या 134.25 में 1।
तीन तर्कशास्त्री एक खेल खेल रहे हैं। प्रत्येक को गुप्त रूप से एक धनात्मक पूर्णांक लिखना होगा। सबसे कम अद्वितीय पूर्णांक वाला तर्कशास्त्री $3 जीतेगा। यदि तीनों के पास एक ही संख्या हो, तो प्रत्येक $1 जीतेगा। तर्कशास्त्री स्वार्थी हैं, और प्रत्येक अपनी जीत को अधिकतम करना चाहता है। बातचीत की अनुमति नहीं है। प्रत्येक तर्कशास्त्री क्या रणनीति अपनाएगा?
इसका उत्तर अगले कॉलम में दिया जाएगा।
मैंने पढ़ा कि वॉरेन बफेट (दुनिया के तीसरे सबसे अमीर आदमी) ने शिकायत की है कि उन्होंने केवल 17.7% संघीय कर दर का भुगतान किया, जबकि उनके सचिव ने 30% का भुगतान किया। यह मुझे अपमानजनक लगता है। क्या आप इस पर कोई टिप्पणी कर सकते हैं?
आम तौर पर मैं कहूँगा कि यह मेरे क्षेत्र से बाहर है। हालाँकि, आठ साल तक सरकारी एक्चुअरी के रूप में काम करने के नाते, मुझे टैक्स के बारे में कुछ-कुछ पता है। मैंने जो पढ़ा है, उसके अनुसार वॉरेन बफेट की ज़्यादातर आय पूंजीगत लाभ के रूप में परिभाषित है, जिस पर केवल 15% की दर से कर लगता है। चाहे आपको पसंद हो या न हो, कर कानून इसकी अनुमति देते हैं। मुझे इस बात पर हैरानी है कि उनके सचिव 30% तक का भुगतान क्यों कर रहे थे। इस वीडियो के अनुसार, वह "पेरोल और आयकर" की गणना कर रहे थे। "पेरोल कर" से उनका स्पष्ट रूप से सामाजिक सुरक्षा और मेडिकेयर करों का मतलब था। आइए देखें कि क्या उनके सचिव के लिए 30% एक उचित कुल संघीय कर दर है।
2007 में उच्चतम कर ब्रैकेट पर 35% कर लगाया गया था, लेकिन यह केवल $349,700 से अधिक की आय पर लागू होता है। उस बिंदु तक की आय पर बहुत कम कर लगता है। मान लीजिए कि उनकी सचिव अविवाहित हैं, उनके कोई आश्रित बच्चे नहीं हैं, और उनका वेतन $100,000 था। सबसे पहले, न्यूनतम कटौतियों को घटाते हैं। 2007 में एकल फाइलरों के लिए मानक कटौती $5,350 थी। व्यक्तिगत कटौती $3,400 थी। तो, हमारे पास $100,000 - $5,350 - $3,400 = $91,250 की आय बची है जो आयकर के अधीन है। 2007 में एकल फाइलरों के लिए, कर की दर पहले $7825 की आय पर 10% थी, फिर $31,850 तक 15%, फिर $77,100 तक 25% और $160,850 तक 28% थी। तो, उसका आयकर = 0.1×$7,825+0.15×($31,850-$7825)+0.25×($77,100-$31,850)+0.28×($91,250-$77,100) = $19,660.75 होता। यह उसकी आय का केवल 19.7% है। उसकी आय, दाखिल करने की स्थिति और मदवार विवरण न देने जैसी मेरी सभी धारणाएँ उसके विरुद्ध गईं, या उसके लिए कर की दर ऊँची कर दी गई।
अब सामाजिक सुरक्षा और मेडिकेयर की बात करते हैं। 2007 में, सामाजिक सुरक्षा कर 6.2% था, $97,500 तक की आय पर, जब इसे पूरी तरह से बंद कर दिया गया। 2007 में मेडिकेयर कर की दर 1.45% थी, जिसकी कोई सीमा नहीं थी। इसलिए, उसका संयुक्त सामाजिक सुरक्षा और मेडिकेयर कर 6.2%*97,500 + 1.45%*100000 = $7,495 होता। इन करों को मिलाकर, उसकी कुल कर दर ($19,660.75 + $7,495)/$100,000 = 27.2% होती। फिर भी हम 30% से 2.8% कम हैं।
मेरा सबसे अच्छा अनुमान यह है कि वह इस तथ्य पर भी विचार कर रही है कि अंततः वह नियोक्ता के सामाजिक सुरक्षा और मेडिकेयर कर का भुगतान करने वाली व्यक्ति है। जो लोग नहीं जानते हैं, उनके लिए सामाजिक सुरक्षा और मेडिकेयर कर वास्तव में आपके चेक से काटे गए कर का दोगुना है। नियोक्ता शेष आधा भुगतान करता है। हालांकि, कुछ लोग, जिनमें मैं भी शामिल हूं, तर्क देंगे कि अंततः यह कर्मचारी ही है जो दोनों का भुगतान करता है। यदि नियोक्ता को वह कर नहीं देना पड़ता, तो उसके पास अपने कर्मचारियों को भुगतान करने के लिए अधिक धन होता। ऐसा महसूस करना आसान है जब आप स्व-नियोजित हैं, जैसे मैं हूं, और दोनों का हिस्सा चुकाना है। यदि आप सामाजिक सुरक्षा/मेडिकेट कर को दोगुना करते हैं, तो अब दर ($19,660.75 + 2×$7,495)/$100,000 = 34.7% है।
सामाजिक सुरक्षा और मेडिकेयर कर वॉरेन बफेट पर ज़्यादा लागू नहीं होंगे। पहली बात, सामाजिक सुरक्षा की 97,500 डॉलर की सीमा उनके लिए महत्वहीन होगी। दूसरी बात, ये कर वेतन पर लागू होते हैं, पूंजीगत लाभ पर नहीं, जैसा कि वे अपनी अधिकांश आय को परिभाषित करते हैं।
तो, श्री बफेट के बयान के पीछे के गणित के बारे में मेरा सबसे अच्छा अनुमान यही है।
अपडेट: इस कॉलम के प्रकाशित होने के कुछ ही समय बाद मुझे यह प्रतिक्रिया मिली। निष्पक्षता के लिए, मैं यह तर्क प्रस्तुत करता हूँ कि श्री बफेट बहुत ज़्यादा कर चुका रहे हैं।
मैंने उस 'नाराज' व्यक्ति को दिए गए आपके जवाब को दिलचस्पी से पढ़ा, जो सोचता है कि यह बहुत अनुचित है कि वॉरेन बफेट अपनी सचिव से कम प्रतिशत कर चुकाते हैं। मुझे आपके जवाब से निराशा हुई, जिसमें उस गलत सूचना को सही नहीं किया गया है जिसका अर्थ है कि मिस्टर बफेट अपनी सचिव से कम कर चुकाते हैं।सबसे पहले, जैसा कि आपने बताया, निवेश आय पर वास्तव में 15% कर लगता है। यह वास्तव में दोहरा कराधान है क्योंकि श्री बफेट द्वारा निवेश की गई अर्जित आय पर उनकी 36% की सीमांत दर से कर लगाया गया था। सेब और संतरे की तुलना (कार्य आय बनाम निवेश आय)।
दूसरा, प्रतिशत पर ध्यान नहीं देना चाहिए। जुए की भाषा में कहें तो, 'भुगतान' पर ध्यान देना चाहिए। मुझे पूरा यकीन है कि मिस्टर बफेट ने उसी साल लाखों डॉलर का टैक्स चुकाया होगा जिस साल उनके सचिव ने हज़ारों डॉलर का टैक्स चुकाया था।क्या आपके पाठक को इस बात पर ज़्यादा नाराज़ नहीं होना चाहिए कि देश का एक नागरिक समान सरकारी सेवाओं के लिए दूसरे नागरिकों से हज़ारों गुना ज़्यादा टैक्स दे रहा है? कोई भी आसानी से कह सकता है, "मैंने सुना है कि वॉरेन बफ़ेट अपने सचिव से दस लाख गुना ज़्यादा टैक्स देते हैं, यह तो बेहद शर्मनाक है!"
बस सोचा कि बता दूँ कि सिर्फ़ "प्रतिशत" देखना, न कि "वास्तविक भुगतान" देखना एक भ्रांति है। आपके जुए से जुड़े कई भ्रांतियों की तरह।
साभार,
केविन ए. (डलास)
गणित की पहेलियों के आपके मनोरंजक संग्रह के लिए धन्यवाद। मेरी प्रेमिका और मैंने समुद्री डाकू पहेली का यह रूपांतर तैयार किया है। क्या होगा यदि सभी समुद्री डाकू समान रैंक के हों, और प्रत्येक दौर में विभाजन का प्रस्तावक लॉटरी द्वारा चुना जाए? इस रूपांतर में, मान लें कि प्रत्येक समुद्री डाकू की सर्वोच्च प्राथमिकता प्राप्त सिक्कों की अपेक्षित मात्रा को अधिकतम करना है। मेरे पास इसका समाधान है, लेकिन शायद आप पहले इसे आज़माना चाहेंगे। एक बार फिर धन्यवाद।
आपका स्वागत है। अगर सिर्फ़ दो समुद्री डाकू बचे हैं, तो सुझाव देने के लिए चुने गए समुद्री डाकू के पास कोई उम्मीद नहीं है, क्योंकि दूसरा समुद्री डाकू 'नहीं' वोट देगा। जो निकाला जाएगा उसे शून्य मिलेगा, और बाकी सभी को 1000। इसलिए, ड्रॉ से पहले, दो समुद्री डाकुओं के साथ अपेक्षित मूल्य 500 सिक्के हैं।
तीन समुद्री डाकुओं के चरण में, ड्रॉ किए गए समुद्री डाकू को दूसरे समुद्री डाकुओं में से एक को 501 और खुद को 499 देने का सुझाव देना चाहिए। 501 पाने वाला हाँ में वोट देगा, क्योंकि यह ना में वोट देने पर 500 के अपेक्षित मूल्य से अधिक है। ड्रॉ से पहले, जब तीन समुद्री डाकू बचे हों, तो आपके पास 0, 499 या 501 सिक्के पाने का 1/3 मौका होता है, जिसका औसत 333.33 होता है।
चार समुद्री डाकुओं के चरण में, ड्रॉ किए गए समुद्री डाकू को अन्य दो डाकुओं में से किसी एक को 334 और खुद को 332 देने का विकल्प चुनना चाहिए। इससे उसे 334 सिक्के पाने वाले डाकुओं से दो 'हाँ' वोट मिलेंगे, क्योंकि वे 333.33 की बजाय 334 लेना पसंद करेंगे। अपने वोट को मिलाकर, आपके पास 4 में से 3 वोट होंगे। ड्रॉ से पहले, प्रत्येक समुद्री डाकू के लिए अपेक्षित मान 0, 334, 334 और 332 का औसत है, या 1000/4=250।
इसी तर्क से, पाँच समुद्री डाकुओं वाले चरण में, चुने गए समुद्री डाकू को किन्हीं दो समुद्री डाकुओं को 251 और खुद को 498 देने का विकल्प चुनना चाहिए। मूल समस्या के विपरीत, इसमें उलटी गिनती करने की ज़रूरत नहीं है। बस सिक्कों की संख्या को समुद्री डाकुओं की संख्या से भाग दें, जिसमें खुद को शामिल न करें। फिर उनमें से आधे (नीचे की ओर पूर्णांकित करते हुए) उस औसत के साथ एक और सिक्का दें।
मुझे एटरनिटी II नामक एक पहेली में मदद चाहिए। इस पहेली को सुलझाने का इनाम $2,000,000 है, जो मेरे हिसाब से काफी बड़ी रकम है। यहाँ एक साक्षात्कार का लिंक दिया गया है, जिसमें गेम बनाने वाले क्रिस्टोफर मोंकटन (मार्गरेट थैचर के पूर्व सलाहकार, और कई अन्य) भी शामिल हैं। यह गेम स्पष्ट रूप से जुए से जुड़ा नहीं है, लेकिन इसके बावजूद, शायद आप अपने वेब पेज पर इसके बारे में एक-दो शब्द जोड़ सकें।
ऊपर दिए गए लिंक में, गेम बनाने वाला यह दावा कर रहा है कि पहेली हल नहीं हो सकती। मुझे लगने लगा है कि वह सही कह रहा है, और वह खुद ही वह व्यक्ति है जो अंततः उस (हास्यास्पद लेकिन दिलचस्प) गेम को बेचकर अमीर बनेगा। एक गणितज्ञ होने के नाते, आप इस तरह की पहेली को कैसे सुलझाएँगे?
मुझे उम्मीद है आप खुश होंगे; पिछले एक महीने से मैं इस पहेली में खोया हुआ हूँ। मैं खुशकिस्मत था (या शायद बदकिस्मत) कि मुझे स्थानीय बॉर्डर्स बुक स्टोर पर 256 टुकड़ों वाली पहेली मिल गई, लेकिन मुझे चार सुराग वाली पहेलियाँ eBay पर ऑस्ट्रेलिया के एक आदमी से खरीदनी पड़ीं।
मैंने एक ऐसा प्रोग्राम लिखा जो चार सुराग वाली पहेलियों को आसानी से हल कर सकता है। इसने 72 टुकड़ों वाली सुराग वाली पहेली #4 को एक सेकंड से भी कम समय में हल कर दिया। मैंने इसे एक साधारण ब्रूट-फोर्स रीकर्सिव प्रोग्राम की मदद से किया। मैंने बोर्ड पर बॉर्डर से शुरू करते हुए एक रास्ता बनाया। हर जगह, प्रोग्राम ने सभी बचे हुए टुकड़ों को एक-एक करके देखा और एक उपयुक्त टुकड़ा ढूँढ़ा। अगर कोई टुकड़ा मिल जाता, तो वह अगले वर्ग में चला जाता, और अगर नहीं मिलता, तो एक वर्ग पीछे चला जाता।
मैंने दो कंप्यूटरों से 256 टुकड़ों वाली 20 लाख डॉलर की पहेली को हफ़्तों तक हल किया है, और दोनों ही कहीं भी पास नहीं पहुँच पाए हैं। मैं उस वीडियो में निर्माता की कही बात से सहमत हूँ, कि अगर आप दुनिया के सबसे तेज़ कंप्यूटरों में से एक करोड़ को भी जोड़ दें, तो भी ब्रह्मांड के खत्म होने तक वे इसका हल नहीं ढूँढ पाएँगे। आप सोचेंगे कि मैंने शुरू करने से पहले उसकी चेतावनी पर ध्यान दिया होगा, लेकिन एक अच्छी पहेली के सामने, मेरे समय के व्यावहारिक उपयोग की सारी चिंताएँ खिड़की से बाहर चली जाती हैं।
मेरे पास शॉर्टकट के लिए ढेरों आइडियाज़ हैं, लेकिन अगर वे मेरे प्रोग्राम की गति एक अरब गुना भी बढ़ा दें, तब भी शायद कोई मदद नहीं मिलेगी। अगर कोई इसे हल कर ले, तो मैं बेहद प्रभावित हो जाऊँगा। मुझे जो बात सबसे ज़्यादा परेशान करती है, वह यह है कि मुझे लगता है कि गणित की कोई ऐसी शाखा है जिसकी अभी तक खोज नहीं हुई है और जो इस तरह की पहेलियों को आसानी से सुलझा सकती है। तब तक, मुझे लगता है कि इसे हल करने के लिए हम जो सबसे अच्छा कर सकते हैं, वह है परीक्षण और त्रुटि। आज के कंप्यूटर बहुत धीमे हैं, और संयोजनों की संख्या इतनी ज़्यादा है कि उनके सफल होने की संभावना बहुत कम है।

मान लीजिए दो शहरों के बीच की दूरी 1000 मील है। शून्य हवा में, एक विमान 500 मील प्रति घंटे की रफ़्तार से चल सकता है। क्या बिना हवा के, या एक दिशा में 100 मील प्रति घंटे की सीधी पछुआ हवा और दूसरी दिशा में बराबर विपरीत हवा के साथ, उसे पूरा चक्कर लगाने में ज़्यादा समय लगेगा?
शून्य-हवा में, विमान को प्रत्येक दिशा में 2 घंटे लगेंगे, यानी कुल 4 घंटे। पछुआ हवा के साथ, विमान 600 मील प्रति घंटे की गति से यात्रा करेगा, यानी यात्रा 1000/600 = 1.667 घंटे में पूरी होगी। अग्र-हवा के साथ, विमान 400 मील प्रति घंटे की गति से यात्रा करेगा, यानी यात्रा 1000/400 = 2.5 घंटे में पूरी होगी। इसलिए, हवा के साथ, कुल समय 4.167 घंटे, यानी 10 मिनट अधिक होगा।
इससे बस यही पता चलता है कि औसत निकालना खतरनाक है। आप यह नहीं कह सकते कि किसी यात्रा की औसत गति 500 मील प्रति घंटा है, अगर एक तरफ़ 400 मील प्रति घंटा और दूसरी तरफ़ 600 मील प्रति घंटा है, क्योंकि 400 मील प्रति घंटा वाला चरण लंबे समय तक चलता है।
अगर यह सहज नहीं है, तो 500 मील प्रति घंटे की रफ़्तार वाली हवा पर विचार करें। हवा के साथ तो विमान को सिर्फ़ एक घंटा लगेगा, लेकिन दूसरी तरफ़ से वह अपनी जगह पर स्थिर रहेगा, यानी हमेशा के लिए।
मैंने हाल ही में एक लॉटरी में हिस्सा लिया था जिसमें 7,033 इनाम थे और कहा जाता है कि इनाम जीतने की संभावना 13 में से 1 है। मैंने 5 टिकट खरीदे। मेरे जीतने की वास्तविक संभावना क्या है? इसके अलावा, 40 बड़े इनाम हैं। मेरे बड़ा इनाम जीतने की संभावना क्या है?
सरलता के लिए, आइए इस तथ्य को नज़रअंदाज़ कर दें कि आप जितने ज़्यादा टिकट खरीदेंगे, प्रत्येक टिकट का मूल्य उतना ही कम होता जाएगा क्योंकि आप खुद से प्रतिस्पर्धा कर रहे होंगे। जैसा कि कहा गया है, सभी पाँच टिकट खोने की संभावना (12/13) 5 = 67.02% है। इसलिए कम से कम एक पुरस्कार जीतने की संभावना 32.98% है। आपके द्वारा कोई भी टिकट खरीदने से पहले ड्रम में कुल 7033×13=91,429 टिकट हैं। 91,429-40=91,389 बड़े पुरस्कार नहीं हैं। पाँच टिकटों के साथ कोई भी बड़ा पुरस्कार न जीतने की संभावना (91,389/91429) 5 = 99.78% है। इसलिए कम से कम एक बड़ा पुरस्कार जीतने की संभावना 0.22%, या 458 में 1 है।
मेरे पास एक पहेली है जिसे मैं पिछले कुछ महीनों से सुलझाने की कोशिश कर रहा हूँ, लेकिन कोई प्रगति नहीं हुई है। अगर समय मिले, तो उम्मीद है कि आप मुझे इसमें शामिल कर पाएँगे, क्योंकि यह मुझे रातों को जगाए रखती है :-)। खैर, "बियॉन्ड काउंटिंग -- एक्ज़िबिट सीएए" की शब्दावली में, "मैजिक नंबर्स" के लिए तीन क्रमों में संख्याएँ और अक्षर दिए गए हैं। इनमें से एक संख्या तो किताब के कवर की शोभा भी बढ़ा रही है, इसलिए मुझे लगता है कि ये कुछ मायने रखती हैं। क्या आपके कोई विचार हैं?
मैं अक्सर ऐसा नहीं कहता, लेकिन मुझे इसकी कोई जानकारी नहीं है। जैसा कि आपने दूसरे ईमेल में बताया था, वे अमेरिकी मुद्रा के सीरियल नंबर का प्रारूप अपनाते हैं, दो अक्षर, जिनके बीच में दस अंकों की एक संख्या होती है। कॉपीराइट के सम्मान के कारण, मैं यहाँ संख्याओं का उल्लेख नहीं करूँगा।
मुझे जानने की उत्सुकता है कि उस इटरनिटी II पहेली चुनौती का क्या हुआ। क्या वह हल हो गई? क्या आप अभी भी उस पर काम कर रहे हैं?
पूछने के लिए शुक्रिया। नहीं, मैंने 17 नवंबर, 2008 के "आस्क द विज़ार्ड" कॉलम में लिखने के बाद से इस मामले को नहीं छुआ है। उनकी वेबसाइट के अनुसार, ज़रूरत पड़ने पर 31 दिसंबर, 2009 और 2010 को "जांच की तारीखें" होंगी। मेरी राय में, इसका कभी समाधान नहीं होगा।
अद्यतन: ऐसा प्रतीत होता है कि इटरनिटी II वेब आकार अब मौजूद नहीं है।
मैंने अर्नोल्ड श्वार्जनेगर के वीटो पत्र के बारे में विज़ार्ड के ब्लॉग को बड़े चाव से पढ़ा। मेरा सवाल गवर्नर के हास्यास्पद लेकिन अनुमानित जवाब से जुड़ा है। गवर्नर ने कहा कि यह सिर्फ़ एक 'अजीब संयोग' था। भारी परिस्थितिजन्य साक्ष्यों के बावजूद (बिल के प्रायोजक और पत्र के प्राप्तकर्ता वही व्यक्ति थे जिन्होंने एक हफ़्ते पहले गवर्नर को गालियाँ दी थीं), क्या आपके पास इस बात का कोई अनुमान है कि ठीक सात पंक्तियों वाले पत्र में संयोग से यह वाक्यांश लिखे जाने की कितनी संभावना है? मुझे लगता है कि इस्तेमाल किए गए अक्षरों को ध्यान में रखते हुए, यह हर एक के लिए 26 में से 1 संभावना बताने से भी ज़्यादा असंभव होगा। ऐसा नहीं लगता कि U, Y, और खासकर K शब्द के शुरुआती अक्षर आम हैं।
यदि आप आसानी से नाराज हो जाते हैं, तो कृपया अगले प्रश्न पर जाएं।
मेरे उन पाठकों के लाभ के लिए जिन्होंने वह ब्लॉग नहीं पढ़ा है, कैलिफोर्निया के गवर्नर अर्नोल्ड श्वार्जनेगर (पीडीएफ) द्वारा लिखे गए इस ज्ञापन में प्रत्येक पंक्ति के पहले अक्षर को देखें, जो अक्षर F से शुरू होने वाली पंक्ति से शुरू होता है।
इस पर मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास पर चर्चा हुई थी। इसका उत्तर जानने के लिए, मैंने विकिपीडिया पर अंग्रेज़ी भाषा के पहले शब्द के प्रत्येक अक्षर की आवृत्ति खोजी।
पहले अक्षर से शब्द आवृत्ति
| पत्र | आवृत्ति |
| ए | 11.60% |
| बी | 4.70% |
| सी | 3.51% |
| डी | 2.67% |
| ई | 2.00% |
| एफ | 3.78% |
| जी | 1.95% |
| एच | 7.23% |
| मैं | 6.29% |
| जे | 0.63% |
| कश्मीर | 0.69% |
| एल | 2.71% |
| एम | 4.37% |
| एन | 2.37% |
| हे | 6.26% |
| पी | 2.55% |
| क्यू | 0.17% |
| आर | 1.65% |
| एस | 7.76% |
| टी | 16.67% |
| यू | 1.49% |
| वी | 0.62% |
| डब्ल्यू | 6.66% |
| एक्स | 0.01% |
| वाई | 1.62% |
| जेड | 0.05% |
इस संभावना का अनुमान लगाने के लिए कि अर्नोल्ड का संदेश सचमुच एक संयोग था, Prob(F) × Prob(U) × ... × Prob(U) = 0.0378 × 0.0149 × 0.0351 × 0.0069 × 0.0162 × 0.0626 × 0.0149 = 486,804,391,348 में 1 होगा। इसमें यह तथ्य भी शामिल नहीं है कि दो शब्दों के बीच की जगह पर एक लाइन ब्रेक सुविधाजनक रूप से मौजूद था।
मैं इस समाधान में उनके योगदान के लिए एलियट जे. और जोनाथन एफ. को धन्यवाद देना चाहूंगा।
हवाई अड्डे पर लगेज कैरोसेल पर, मुझे जितने ज़्यादा बैग निकालने होंगे, मुझे सभी बैगों के बाहर आने का उतना ही ज़्यादा इंतज़ार करना पड़ेगा। अगर मेरे पास एक बैग है, तो मुझे लगभग आधे बैगों के बाहर आने तक इंतज़ार करना होगा। अगर मैं 2 बैग ले जाऊँ, तो मेरा इंतज़ार ज़्यादा लंबा होगा और 3 बैग के साथ, और भी ज़्यादा। मान लीजिए कि मेरे बैग बाकियों के साथ बेतरतीब ढंग से मिल गए हैं, तो मेरे बैगों की संख्या और कुल बैगों की संख्या के संदर्भ में, सभी बैग निकालने के लिए मुझे कितने बैगों का इंतज़ार करना होगा, इसका सामान्य सूत्र क्या है?
आइये पहले कुछ चरों को परिभाषित करें, इस प्रकार:
n = आपके बैगों की संख्या
b = बैगों की कुल संख्या
जैसे-जैसे कुल बैगों की संख्या बढ़ती जाएगी, उत्तर b×n/(n+1) के करीब होता जाएगा। एक बड़े विमान के लिए, इससे आपको एक अच्छा अनुमान मिल जाएगा। हालाँकि, यदि आप सटीक होना चाहते हैं, तो उत्तर है
[b× कॉम्बिन (b,n)-(कॉम्बिन(i,n) के i=n से b-1 तक का योग)]/कॉम्बिन(b,n)
उदाहरण के लिए, यदि कुल 10 बैग हैं, और उनमें से चार आपके हैं, तो अपेक्षित प्रतीक्षा समय =
[10×कॉम्बिन(10,4)-कॉम्बिन(4,4)-कॉम्बिन(5,4)-कॉम्बिन(6,4)-कॉम्बिन(7,4)-कॉम्बिन(8,4)-कॉम्बिन(9,4)]/कॉम्बिन(10,4) = 8.8 बैग।
समाधान:
b बैगों में से n बैग निकालने के तरीकों की संख्या combin(b,n) है। इसलिए, आपके सभी बैग पहले x बैगों में ही निकलने की प्रायिकता combin(x,n)/combin(b,n) है। x>=n+1 के लिए, आपके आखिरी बैग के निकलने वाले x वें बैग होने की प्रायिकता (combin(x,n)-combin(x-1,n))/combin(b,n) है। x=n के लिए यह 1/combin(b,n) है।
अतः अपेक्षित प्रतीक्षा समय और कुल प्रतीक्षा समय का अनुपात है:
n×कॉम्बिन(n,n)/कॉम्बिन(b,n) +
(n+1)×(combin(n+1,n)-combin(n,n))/combin(b,n) +
(n+2)×(combin(n+2,n)-combin(n+1,n))/combin(b,n) +
.
.
.
+
(बी-1)×(कॉम्बिन(बी-1,एन)-कॉम्बिन(बी-2,एन))/कॉम्बिन(बी,एन) +
b×(combin(b,n)-combin(b-1,n))/combin(b,n)
दूरबीनी योग लेते हुए, इसे सरलीकृत किया जा सकता है:
[बी×कॉम्बिन(बी,एन)-कॉम्बिन(बी-1,एन)-कॉम्बिन(बी-2,एन)-...-कॉम्बिन(एन,एन)]/कॉम्बिन(बी,एन)
बाद में एक पाठक ने लिखा कि उत्तर को n×(b+1)/(n+1) तक सरल किया जा सकता है। इसे आगमन द्वारा दर्शाया जा सकता है, जो एक वैध विधि है, लेकिन इससे मैं हमेशा भावनात्मक रूप से असंतुष्ट रहता हूँ।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
मैं मूर्तियाँ बेचता हूँ। औसतन, हर सात मूर्तियों की बिक्री में से एक कछुआ होगी, और बाकी अन्य प्रकार की मूर्तियाँ होंगी। अगर मैं चाहता हूँ कि अगली 100 मूर्तियों की बिक्री में 90% कछुए खत्म न हों, तो मुझे कितने कछुए स्टॉक में रखने होंगे?

मान लीजिए t बनाए गए कछुओं की संख्या है, और x बेचे गए कछुओं की संख्या है।
पीआर(x<=t)=0.9
pr(x-14.29<=t-14.29)=0.9
pr((x-14.29)/3.5)<=(t-14.29)/3.5))=0.9
असमानता का बायाँ भाग एक मानक सामान्य वितरण (माध्य 0, मानक विचलन 1) का अनुसरण करता है। इस अगले चरण को स्वीकार करने के लिए एक प्रारंभिक सांख्यिकी पाठ्यक्रम, या कुछ विश्वास की आवश्यकता होती है।
(t-14.29)/3.5 = normsinv(0.9) यह एक्सेल फ़ंक्शन है।
(टी-14.29)/3.5 = 1.282
टी-14.29 = 4.4870
टी = 18.77
कछुए की मूर्ति का 0.77 खरीदने की संभावना किसी में नहीं है, इसलिए मैं इसे 19 तक पूर्णांकित करूँगा। द्विपद वितरण के अनुसार, 18 या उससे कम बेचने की संभावना 88.35% है, और 19 या उससे कम बेचने की संभावना 92.74% है। यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फ़ोरम में उठाया गया था और इस पर चर्चा हुई थी।
पाँच नाविक एक जहाज़ दुर्घटना में बच जाते हैं। सबसे पहले वे नारियल इकट्ठा करते हैं और उन्हें एक बड़े सामुदायिक ढेर में जमा करते हैं। वे बाद में उन्हें बराबर-बराबर बाँटना चाहते थे, लेकिन नारियल इकट्ठा करने की कड़ी मेहनत के बाद वे बहुत थक जाते हैं। इसलिए वे रात को सो जाते हैं और सुबह ढेर को बाँटने का इरादा रखते हैं।
हालाँकि, नाविक एक-दूसरे पर भरोसा नहीं करते। आधी रात को उनमें से एक अपना हिस्सा लेने के लिए उठता है। वह ढेर को पाँच बराबर हिस्सों में बाँट देता है, एक नारियल बच जाता है। वह अपना हिस्सा ज़मीन में गाड़ देता है, बाकी चार ढेरों को मिलाकर एक नया सामूहिक ढेर बना देता है, और बचा हुआ नारियल एक बंदर को दे देता है।
1:00 बजे, 2:00 बजे, 3:00 बजे, तथा 4:00 बजे अन्य चार नाविक भी ठीक यही काम करते हैं।
सुबह कोई भी अपने किए की बात नहीं मानता, और वे मूल योजना के अनुसार ढेर को बराबर-बराबर बाँट लेते हैं। फिर एक नारियल बचता है, जो वे बंदर को दे देते हैं।
मूल ढेर में नारियलों की न्यूनतम संभावित संख्या क्या है?
"उत्तर के लिए 100 लाइन नीचे स्क्रॉल करें।
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
मूल ढेर में 15,621 नारियल थे। मेरे समाधान के लिए 100 पंक्तियाँ और नीचे स्क्रॉल करें।
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
मान लीजिए कि मूल ढेर में नारियलों की संख्या c है और अंतिम विभाजन के बाद प्रत्येक नाविक के लिए अंतिम हिस्सा f है।
नाविक 1 द्वारा अपना हिस्सा लेने और बंदर को अपना नारियल देने के बाद (4/5)×(c-1) = (4c-1)/5 शेष बचेगा।
नाविक 2 द्वारा अपना हिस्सा लेने और बंदर को अपना नारियल देने के बाद (4/5)×(((4c-1)/5)-1) = (16c-36)/25 शेष बचेगा।
नाविक 3 द्वारा अपना हिस्सा लेने और बंदर को अपना नारियल देने के बाद (4/5)×(((16c-36)/25)-1) = (64c-244)/125 शेष बचेगा।
नाविक 4 द्वारा अपना हिस्सा लेने और बंदर को अपना नारियल देने के बाद (4/5)×(((64c-244)/125)-1) = (256c-1476)/625 शेष बचेगा।
नाविक 5 द्वारा अपना हिस्सा लेने और बंदर को अपना नारियल देने के बाद (4/5)×(((256c-1476)/625)-1) = (1024c-8404)/3125 शेष बचेगा।
सुबह तक शेष ढेर में से प्रत्येक नाविक का हिस्सा f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625 शेष रह जाएगा।
तो, सवाल यह है कि c का सबसे छोटा मान क्या है जिससे f=(1024×c-11529)/15625 एक पूर्णांक हो। आइए c को f के पदों में व्यक्त करें।
(1024×सी-11529)/15625 = एफ
1024सी - 11529 = 15625×एफ
1024सी = 15625एफ+11529
सी = (15625एफ+11529)/1024
सी = 11+((15625×f+265)/1024)
सी = 11+15×f+(265×(f+1))/1024
तो, वह सबसे छोटा f क्या है जिसके लिए 265×(f+1)/1024 एक पूर्णांक हो? 265 और 1024 का कोई उभयनिष्ठ गुणनखंड नहीं है, इसलिए f+1 स्वयं 1024 से विभाज्य होगा। f+1 का सबसे छोटा संभावित मान 1024 है, इसलिए f=1023 है।
इस प्रकार, c = (15625×1023+11529)/1024 = 15,621.
प्रत्येक व्यक्ति और प्रत्येक बंदर को कितने नारियल मिले, यह इस प्रकार है:
नारियल की समस्या
| नाविक | नारियल |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| बंदर | 6 |
| कुल | 15621 |
डेविड फिल्मर, जिन्होंने मुझे यह प्रश्न चुनौती दी थी, पहले से ही इसका उत्तर जानते थे। दरअसल, उन्होंने मुझसे 5 नाविकों वाले सामान्य मामले का सूत्र पूछा था, लेकिन मुझे 5 नाविकों वाले विशिष्ट मामले में ही काफी परेशानी हुई। डेविड बताते हैं कि सामान्य मामले का उत्तर c = s s+1 - s + 1 है।
मैं इसका प्रमाण पाठक पर छोड़ता हूं।
समस्या के वैकल्पिक समाधान के लिए कुछ लिंक यहां दिए गए हैं:
एक आदमी को पैसों से भरे दो लिफाफे दिए जाते हैं। एक लिफाफे में दूसरे लिफाफे से दोगुनी रकम है। जब वह अपना लिफाफा चुन लेता है, उसे खोलकर गिन लेता है, तो उसे दूसरा लिफाफा बदलने का विकल्प दिया जाता है। सवाल यह है कि क्या लिफाफा बदलने से उस आदमी को कोई फायदा होगा?
ऐसा प्रतीत होता है कि लिफ़ाफ़े में बदलाव करने से, अगर शुरुआती लिफ़ाफ़े में कम राशि हो, तो उस व्यक्ति के पैसे दोगुने होने की संभावना 50% होगी और अगर शुरुआती लिफ़ाफ़े में ज़्यादा राशि हो, तो पैसे आधे होने की संभावना 50% होगी। इस प्रकार, मान लीजिए कि शुरुआती लिफ़ाफ़े में रखी राशि x है और लिफ़ाफ़े को बदलने का मान y है:
y = 0.5×(x/2) + 0.5×(2x) = 1.25x
मान लीजिए कि पहले लिफाफे में $100 थे। तो 50% संभावना है कि दूसरे लिफाफे में 2 × $100 = $200 हों और 50% संभावना है कि दूसरे लिफाफे में (1/2) × $100 = $50 हों। ऐसी स्थिति में, लिफाफे का मूल्य है:
0.5×($100/2) + 0.5×(2×$100) = $125
इसका मतलब यह है कि वह आदमी, सिर्फ़ लिफ़ाफ़े बदलकर, अपनी संपत्ति में औसतन 25% की बढ़ोतरी कर लेगा! ऐसा कैसे हो सकता है?
यह एक गणितीय विरोधाभास प्रतीत होता है, लेकिन वास्तव में यह अपेक्षित मूल्य सूत्र का दुरुपयोग मात्र है। जैसा कि आपने प्रश्न में उल्लेख किया है, ऐसा लगता है कि दूसरे लिफाफे में आपके द्वारा चुने गए लिफाफे से 25% अधिक होना चाहिए। हालाँकि, यदि आप उसे खरीदते हैं, तो आप शुरुआत में दूसरा लिफाफा चुन सकते हैं। इसके अलावा, यदि आपको बदलने का निर्णय लेने से पहले लिफाफे खोलने का मौका नहीं मिलता है, तो आप इस तर्क का उपयोग करके बार-बार बदलाव कर सकते हैं। स्पष्ट रूप से अपेक्षित मूल्य तर्क में कोई न कोई खामी अवश्य होगी। प्रश्न यह है कि खामी कहाँ है?
मैंने इस समस्या के बारे में पढ़ने और इस पर वर्षों से चर्चा करने में बहुत समय बिताया है। मैंने इस बारे में कई व्याख्याएँ सुनी और पढ़ी हैं कि y=.5x + .5*2x = 1.25x तर्क गलत क्यों है। कई लोगों ने इस व्याख्या में उन्नत गणित के कई पन्ने इस्तेमाल किए हैं, जो मुझे ज़रूरी नहीं लगता। यह एक साधारण प्रश्न है जिसका एक सरल उत्तर चाहिए। तो, यह मेरा इस पर प्रयास है।
आपको इस तथ्य के साथ बहुत सावधानी बरतनी चाहिए कि एक लिफ़ाफ़े में दूसरे लिफ़ाफ़े से दुगनी रकम है। मान लीजिए छोटे लिफ़ाफ़े में रखी रकम को S और बड़े लिफ़ाफ़े को L कहते हैं। तो हमारे पास है:
एल=2×एस
एस=0.5×एल
ध्यान दें कि 2 और 0.5 कारक अलग-अलग लिफाफों पर कैसे लागू होते हैं। आप दोनों कारकों को एक ही राशि पर लागू नहीं कर सकते। अगर पहले लिफाफे में $100 हैं, तो अगर वह छोटा लिफाफा था, तो दूसरे में $200 होंगे। अगर $100 बड़ा लिफाफा था, तो दूसरे में $50 होंगे। इस तरह दूसरे लिफाफे में $50 या $200 होंगे। हालाँकि, आप सीधे यह नहीं कह सकते कि दोनों में से किसी एक के जीतने की संभावना 50/50 है। ऐसा इसलिए है क्योंकि ऐसा करने पर 0.5 और 2 कारक एक ही राशि पर लागू होंगे, जो आप नहीं कर सकते। शुरुआत में पुरस्कार वितरण को जाने बिना, आप दूसरे लिफाफे के लिए संभावित राशि निर्धारित नहीं कर सकते।
यदि 0.5x/2x तर्क गलत है, तो दूसरे लिफाफे का अपेक्षित मान निर्धारित करने का सही तरीका क्या होगा? मैं यह कहूँगा कि दोनों लिफाफों के बीच का अंतर LS = 2S-S = S है। स्विच करने पर आपको S का या तो लाभ होगा या हानि, चाहे वह कुछ भी हो। यदि दोनों लिफाफों में $50 और $100 हैं, तो स्विच करने पर $50 का लाभ या हानि होगी। यदि दोनों लिफाफों में $100 और $200 हैं, तो स्विच करने पर $100 का लाभ या हानि होगी। किसी भी तरह से, स्विच करने पर अपेक्षित लाभ 0 है। मुझे लगता है कि मैं कह सकता हूँ कि यदि पहले लिफाफे में $100 हैं, तो 50% संभावना है कि दूसरे लिफाफे में अंतर $50 हो, और 50% संभावना है कि यह $100 हो। तो अपेक्षित अंतर $75 है। इस प्रकार, दूसरे लिफाफे का अपेक्षित मूल्य 0.5×($100+$75) + 0.5×($100-$75) = 0.5×($175+$25) = $100 है।
मुझे उम्मीद है कि इससे कुछ समझ में आया होगा। इस समस्या पर हमेशा ढेरों टिप्पणियाँ आती रहती हैं। अगर आपके पास कोई टिप्पणी है, तो कृपया मुझे सीधे न लिखें, बल्कि मेरे विज़ार्ड ऑफ़ वेगास फ़ोरम में पोस्ट करें। लिंक नीचे है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
लिंक
एक ट्रूएल (तीन-तरफ़ा द्वंद्वयुद्ध) पर विचार करें जिसमें प्रतिभागी A, B और C शामिल हैं। वे एक महिला के लिए मरते दम तक लड़ रहे हैं। वे सभी सज्जन हैं, और वे सभी निम्नलिखित नियमों पर सहमत हैं।
- तीन प्रतिभागी एक त्रिकोण बनाते हैं।
- प्रत्येक के पास केवल एक गोली है।
- पहले A जाता है, फिर B, और फिर C।
- A के द्वारा किसी इच्छित लक्ष्य को भेदने की संभावना 10% है।
- B के इच्छित लक्ष्य को भेदने की संभावना 60% है।
- C के इच्छित लक्ष्य को भेदने की संभावना 90% है।
- कोई आकस्मिक गोलीबारी नहीं हुई है।
- हवा में गोली चलाना (जानबूझकर चूक जाना) और खुद को गोली मारना स्वीकार्य है, और ये हमेशा सफल होते हैं।
- अगर किसी भी राउंड के बाद दो या तीन लोग बच जाते हैं, तो हर एक को एक नई गोली दी जाती है। फिर वे बारी-बारी से उसी क्रम में गोली चलाएँगे, और पहले से मरे हुए लोगों को छोड़कर।
- तीनों प्रतिभागी उत्तम तर्कशास्त्री हैं।
A को शुरुआत में किस पर निशाना साधना चाहिए? हर शुरुआती लक्ष्य पर उसके बचने की संभावना क्या है?
इस पहेली पर बीबीसी के शो क्वाइट इंट्रेस्टिंग में चर्चा की गई है। उत्तर और समाधान के लिए 100 पंक्तियों तक नीचे स्क्रॉल करें।
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
प्रत्येक प्रारंभिक लक्ष्य के अनुसार A के जीतने की मेरी संभावनाएँ यहाँ दी गई हैं। जैसा कि आप देख सकते हैं, जानबूझकर हवा में गोली चलाने से A के जीतने की संभावना अधिकतम हो जाती है।
ट्रूएल ऑड्स
| रणनीति | संभवतः जीत |
| वायु | 13.887% |
| ए | 0.000% |
| बी | 12.560% |
| सी | 13.094% |
समाधान के लिए, आइए Pr(X) संकेतन का उपयोग करके समूह X के एक राउंड के बाद केवल समूह X के बचे रहने की प्रायिकता को दर्शाते हैं। आइए Pr(X*) शब्दावली का उपयोग करके समूह X के अंततः राउंड जीतने की प्रायिकता को दर्शाते हैं, जब तक कि किसी के चोटिल होने से खेल की स्थिति बदल न जाए। मान लीजिए Pr(X**) वह प्रायिकता है कि खिलाड़ी X अकेला जीवित बचेगा। अंतिम प्रायिकताएँ ज्ञात करने के लिए, आइए पहले दो खिलाड़ियों की स्थितियों पर नज़र डालें। यह स्पष्ट है कि प्रत्येक खिलाड़ी दूसरे पर गोली चलाएगा।
A बनाम B
- पीआर(ए) = 0.1
- पीआर(बी) = 0.9×0.6 = 0.54
- पीआर(एबी) = 0.9×0.4 = 0.36
अगर दोनों बच जाते हैं, तो ये तब तक दोहराए जाएँगे जब तक कि केवल एक ही जीवित न बचे। तो, अंतिम जीवित बचे व्यक्ति के होने की संभावनाएँ हैं:
- पीआर(ए*) = पीआर(ए)/(1-पीआर(एबी)) = 0.1/0.64 = 0.15625
- पीआर(बी*) = पीआर(बी)/(1-पीआर(एबी)) = 0.54/0.64 = 0.84375
A बनाम C
- पीआर(ए) = 0.1
- पीआर(सी) = 0.9×0.9 = 0.81
- पीआर(एसी) = 0.9×0.1 = 0.09
अगर दोनों बच जाते हैं, तो ये तब तक दोहराए जाएँगे जब तक कि केवल एक ही जीवित न बचे। तो, अंतिम जीवित बचे व्यक्ति के होने की संभावनाएँ हैं:
- पीआर(ए*) = पीआर(ए)/(1-पीआर(एसी)) = 0.1/0.91 = 0.10989011
- पीआर(सी*) = पीआर(बी)/(1-पीआर(एसी)) = 0.81/0.91= 0.89010989
बी बनाम सी
- पीआर(बी) = 0.6
- पीआर(सी) = 0.4×0.9 = 0.36
- पीआर(बीसी) = 0.$×0.1 = 0.04
अगर दोनों बच जाते हैं, तो ये तब तक दोहराए जाएँगे जब तक कि केवल एक ही जीवित न बचे। तो, अंतिम जीवित बचे व्यक्ति के होने की संभावनाएँ हैं:
- पीआर(बी*) = पीआर(ए)/(1-पीआर(बीसी)) = 0.6/.96 = 0.625
- पीआर(सी*) = पीआर(बी)/(1-पीआर(बीसी)) = 0.36/.96= 0.375
अब हम तीन खिलाड़ियों वाले मामले का विश्लेषण करने के लिए तैयार हैं। आइए उस स्थिति पर विचार करें जहाँ A, B पर निशाना साधता है।
तीन खिलाड़ी - A, B पर निशाना साधता है
अगर A, B से टकराता है, तो C निश्चित रूप से बच जाएगा, और A से टकरा भी सकता है और नहीं भी। इसलिए B से टकराने के दो संभावित परिणाम AC और C हैं। अगर A, B से चूक जाता है, तो B, बड़े खतरे C पर निशाना साधेगा। अगर B, C से टकराता है, तो A और B बच जाएँगे। अगर B, C से चूक जाता है, तो C, बड़े खतरे B पर निशाना साधेगा। अगर C, B से चूक जाता है, तो तीनों बच जाएँगे। अगर C, B से टकराता है, तो A और C बच जाएँगे। इसलिए संभावित परिणाम C, AB, AC और ABC हैं।
- पीआर(ए) = 0.
- पीआर(बी) = 0.
- Pr(C) = 0.1 × 0.9 = 0.09. यह A द्वारा B को और फिर C द्वारा A को मारने पर प्राप्त होता है।
- Pr(AB) = 0.9 × 0.6 = 0.54. यह तब प्राप्त होता है जब A, B को चूक जाता है, और फिर B, C से टकराता है।
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334। इसे दो तरीकों से प्राप्त किया जा सकता है। पहला, A, B से टकराता है और फिर C, A से चूक जाता है। दूसरा, A, B से चूक जाता है, B, C से चूक जाता है और फिर C, B से टकराता है।
- पीआर(बीसी) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. यह तीनों लुप्त संख्याओं द्वारा प्राप्त होता है।
दो खिलाड़ियों वाले मामलों के समान तर्क से, हम प्रत्येक स्थिति की संभावनाओं को ज्ञात करने के लिए प्रत्येक परिणाम को (1-Pr(ABC))=0.964 से विभाजित कर सकते हैं, यह मानते हुए कि राउंड के बाद खेल की स्थिति बदल गई।
- पीआर(सी*) = 0.09/0.964 = 0.093361।
- पीआर(एबी*) = 0.54/0.964 = 0.560166।
- पीआर(एसी*) = 0.334/0.964 = 0.346473।
दो खिलाड़ियों वाले मामले से, हम जानते हैं कि अगर A और B की स्थिति आती है, तो A की जीत की संभावना 0.15625 और B की 0.84375 होगी। अगर A और C की स्थिति आती है, तो A की जीत की संभावना 0.109890 और C की 0.890110 होगी।
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. A दो तरीकों से विजेता हो सकता है: (1) AB अवस्था में पहुँचकर, और फिर जीत हासिल करके, या (2) AC अवस्था में पहुँचकर और फिर जीत हासिल करके।
- Pr(B**) = 0.560166 × 0.84375 = 0.472640. यदि B, AB अवस्था में पहुँच जाता है, तो वह विजेता होगा, और तब B जीत जाएगा।
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760. C जीत सकता है यदि A, B को मार दे, और फिर C पहले राउंड में A को मार दे, या फिर वह AC अवस्था में पहुँच जाए, और फिर C जीत जाए।
इसलिए, यदि A की रणनीति सबसे पहले B पर निशाना साधने की है, तो उसके अकेले जीवित बचे रहने की संभावना 12.56% है।
तीन खिलाड़ी - A, C पर निशाना साधता है
अगर A, C से टकराता है, तो B निश्चित रूप से बच जाएगा, और A से टकरा भी सकता है और नहीं भी। इसलिए C से टकराने के दो संभावित परिणाम AB और B हैं। अगर A, C से चूक जाता है, तो B, बड़े खतरे C पर निशाना लगाएगा। अगर B, C से टकराता है, तो A और B बच जाएँगे। अगर B, C से चूक जाता है, तो C, बड़े खतरे B पर निशाना लगाएगा। अगर C, B से चूक जाता है, तो तीनों बच जाएँगे। अगर C, B से टकराता है, तो A और C बच जाएँगे। इसलिए संभावित परिणाम B, AB, AC और ABC हैं।
- पीआर(ए) = 0.
- पीआर(बी) = 0.1 × 0.6 = 0.06.
- पीआर(सी) = 0.
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58. इसे दो तरीकों से प्राप्त किया जा सकता है।पहला है A, C को मारता है, और फिर B, A को चूक जाता है। दूसरा है A, B को चूक जाता है, और फिर B, C को मारता है।
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324. यह A द्वारा C को खो देने, B द्वारा C को खो देने और C द्वारा B को मार देने पर प्राप्त होता है।
- पीआर(बीसी) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. यह तीनों लुप्त संख्याओं द्वारा प्राप्त होता है।
दो खिलाड़ियों वाले मामलों के समान तर्क से, हम प्रत्येक स्थिति की संभावनाओं को ज्ञात करने के लिए प्रत्येक परिणाम को (1-Pr(ABC))=0.964 से विभाजित कर सकते हैं, यह मानते हुए कि राउंड के बाद खेल की स्थिति बदल गई।
- पीआर(बी*) = 0.06/0.964 = 0.062241।
- पीआर(एबी*) = 0.58/0.964 = 0.601660।
- पीआर(एसी*) = 0.324/0.964 = 0.336100।
ए मामले के समाधान के समान तर्क से बी मामले को लक्ष्य बनाया गया है:
- पीआर(ए**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943।
- पीआर(बी**) = 0.062241 + 0.601660 × 0.84375 = 0.569891।
- पीआर(सी**) = 0.336100 × 0.890110 = 0.299166।
इसलिए, यदि A की रणनीति पहले C पर निशाना साधने की है, तो उसके अकेले जीवित बचे रहने की संभावना 13.09% है।
तीन खिलाड़ी - A जानबूझकर चूक जाता है
A के जानबूझकर चूकने पर B, बड़े खतरे C पर निशाना लगाएगा। अगर B, C को मारता है, तो A और B बच जाएँगे। अगर B, C को चूक जाता है, तो C, बड़े खतरे B पर निशाना लगाएगा। अगर C, B को चूक जाता है, तो तीनों बच जाएँगे। अगर C, B को मारता है, तो A और C बच जाएँगे। इसलिए संभावित परिणाम AB, AC और ABC हैं।
- पीआर(ए) = 0.
- पीआर(बी) = 0.
- पीआर(सी) = 0.
- Pr(AB) = 0.6. यह B द्वारा C पर प्रहार करने पर प्राप्त होता है।
- Pr(AC) = 0.4 × 0.9 = 0.36. यह तब प्राप्त होता है जब B, C से चूक जाता है, और फिर C, B से टकराता है।
- पीआर(बीसी) = 0.
- Pr(ABC) = 0.4 × 0.1 = 0.04. यह तीनों लुप्त संख्याओं द्वारा प्राप्त होता है।
दो खिलाड़ियों वाले मामलों के समान तर्क से, हम प्रत्येक स्थिति की संभावनाओं को ज्ञात करने के लिए प्रत्येक परिणाम को (1-Pr(ABC))=0.96 से विभाजित कर सकते हैं, यह मानते हुए कि राउंड के बाद खेल की स्थिति बदल गई।
- पीआर(एबी*) = 0.6/0.96 = 0.625.
- पीआर(एसी*) = 0.36/0.96 = 0.375.
ए मामले के समाधान के समान तर्क से बी मामले को लक्ष्य बनाया गया है:
- पीआर(ए**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865।
- पीआर(बी**) = 0.625 × 0.84375 = 0.527344।
- पीआर(सी**) = 0.375 × 0.890110 = 0.333791।
इसलिए, यदि A की रणनीति पहले C पर निशाना साधने की है, तो उसके अकेले जीवित बचे रहने की संभावना 13.89% है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
एक समय में दो तत्वों की तुलना करते हुए, तुलना की अधिकतम संख्या को न्यूनतम करते हुए, सूची को क्रमबद्ध करने का सबसे तेज़ तरीका क्या है?
कई तरीके हैं जो लगभग समान रूप से अच्छे हैं। हालाँकि, मुझे जो सबसे आसान लगता है उसे मर्ज सॉर्ट कहते हैं। यह इस प्रकार काम करता है:
- सूची को दो भागों में विभाजित करें। प्रत्येक उपसमूह को दो भागों में विभाजित करते रहें, जब तक कि प्रत्येक उपसमूह का आकार 1 या 2 न हो जाए।
- 2 के प्रत्येक उपसमूह को छोटे सदस्य को पहले रखकर क्रमबद्ध करें।
- उपसमुच्चयों के जोड़ों को एक साथ मिलाएँ। तब तक दोहराते रहें जब तक कि केवल एक क्रमबद्ध सूची न बन जाए।
दो सूचियों को मर्ज करने का तरीका यह है कि प्रत्येक सूची के पहले सदस्य की तुलना करें और छोटे सदस्य को एक नई सूची में डालें। फिर दोहराएँ और छोटे सदस्य को पिछली तुलना के छोटे सदस्य के बाद रखें। तब तक दोहराते रहें जब तक कि दोनों समूह एक क्रमबद्ध समूह में मर्ज न हो जाएँ। यदि मूल दो सूचियों में से एक खाली है, तो आप दूसरी सूची को मर्ज की गई सूची के अंत में जोड़ सकते हैं।
निम्न तालिका सूची में तत्वों की संख्या के अनुसार आवश्यक तुलनाओं की अधिकतम संख्या दर्शाती है।
मर्ज सॉर्ट
| तत्वों | अधिकतम तुलना |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 32 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1,793 |
| 512 | 4,097 |
| 1,024 | 9,217 |
| 2,048 | 20,481 |
| 4,096 | 45,057 |
| 8,192 | 98,305 |
| 16,384 | 212,993 |
| 32,768 | 458,753 |
| 65,536 | 983,041 |
| 131,072 | 2,097,153 |
| 262,144 | 4,456,449 |
| 524,288 | 9,437,185 |
| 1,048,576 | 19,922,945 |
| 2,097,152 | 41,943,041 |
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
29 अक्टूबर, 2010 को, द लास वेगास रिव्यू जर्नल ने रीड-एंगल सीनेट चुनाव पर एक सर्वेक्षण प्रकाशित किया। इसमें कहा गया था कि 625 संभावित मतदाताओं के सर्वेक्षण में, एंगल को 49% और रीड को 45% वोट मिले। इसमें यह भी कहा गया था कि त्रुटि की संभावना 4% थी। मेरे प्रश्न ये हैं:
- एंगल की जीतने की संभावना क्या है?
- एंगल के वोट शेयर के लिए 95% विश्वास अंतराल क्या होगा?
- त्रुटि की सीमा का क्या अर्थ है?
इस पर दिए गए पुराने जवाब के लिए क्षमा चाहता हूँ। मैंने चुनाव से पहले यह लिखा था।
सबसे पहले, मैं उन बाकी 6% लोगों को हटा दूँगा, जो या तो अभी तक कोई निर्णय नहीं ले पाए हैं या किसी तीसरे पक्ष के उम्मीदवार या "इनमें से कोई नहीं" पर अपना वोट बर्बाद कर देंगे, जो नेवादा में एक विकल्प है। कुछ लोग इस धारणा से असहमत हो सकते हैं। सच कहूँ तो, उन्हें नज़रअंदाज़ करने का एक और कारण यह है कि दो से ज़्यादा उम्मीदवारों के साथ गणित और भी जटिल हो जाता है। इसलिए, पूर्णांकन के बाद, हमारे पास एंगल के लिए 306 और रीड के लिए 281 वोट बचेंगे, यानी नमूने में कुल 587।
मैं इस प्रश्न का उत्तर देने के लिए मानक सामान्य सन्निकटन का उपयोग करूँगा। अगर मैं पूर्णतावादी होता, तो मैं T वितरण का उपयोग करता, क्योंकि वास्तविक माध्य और प्रसरण ज्ञात नहीं हैं। हालाँकि, मेरी राय में, सामान्य वितरण के लिए 587 का नमूना आकार बिल्कुल ठीक है।
नमूना आकार = 306+281 = 587.
कोण नमूना माध्य 306/587 = 0.521295 है।
माध्य का अनुमानित मानक विचलन (0.521295 × 0.478705 / (587-1))^0.5 = 0.0206361 है।
50% से ऊपर एंगल का हिस्सा (0.521295-0.5)/0.0206361 = 1.031917 मानक विचलन है।
सामान्य वितरण के अनुसार, रीड के उम्मीद से 1.031917 मानक विचलन ऊपर समाप्त होने की संभावना 0.151055 है। इसे एक्सेल में NORMSDIST(-1.031917) फ़ंक्शन से पाया जा सकता है। इसलिए एंगल के जीतने की संभावना 1-0.151268 = 84.89% है।
95% विश्वास अंतराल बनाने के लिए, ध्यान दें कि गॉसियन वक्र के दोनों ओर 2.5% बिंदु माध्य से 1.959964 मानक विचलन पर है। इसे एक्सेल में NORMSINV(0.975) फ़ंक्शन से पाया जा सकता है। जैसा कि पहले ही उल्लेख किया गया है, नमूना माध्य का अनुमानित मानक विचलन 0.0206361 है। इसलिए 95% संभावना है कि कोई भी उम्मीदवार सर्वेक्षण परिणामों के 0.0206361×1.959964 = 0.040446 मानक विचलन के भीतर आएगा। इसलिए एंगल का 95% विश्वास अंतराल 0.521295 +/- 0.040446 = 48.08% से 56.17% है।
मुझे बताया गया है कि इसे इस तरह कहना गणितीय रूप से गलत होगा कि "एंगल/रीड के सभी वोटों में एंगल की हिस्सेदारी 48.08% और 56.17% के बीच होने की 95% संभावना है।" मैंने मूल रूप से अपने उत्तर को इसी तरह लिखा था, लेकिन दो सांख्यिकीविद् मेरे शब्दों से भयभीत हो गए। उनके उत्तर को संक्षेप में कहें तो, उन्होंने कहा कि मुझे कर्मवाच्य का प्रयोग करना होगा और कहना होगा कि "48.08% और 56.17%, 95% संभावना के साथ एंगल की हिस्सेदारी को घेर लेंगे।" सच कहूँ तो, मुझे भी यही लगता है। हालाँकि, उन्होंने इस बात पर ज़ोर दिया कि विश्वास अंतराल यादृच्छिक है और एंगल की हिस्सेदारी अपरिवर्तनीय है, और मेरे मूल शब्दों का अर्थ इसके विपरीत था। खैर, मुझे उम्मीद है कि फ़्रीक्वेंटिस्ट सांख्यिकीविद् दूसरे शब्द से संतुष्ट होंगे।
" त्रुटि का मार्जिन " 95% विश्वास अंतराल के दोनों सिरों के बीच के अंतर का आधा है। इस स्थिति में (56.17% - 48.08%)/2 = 4.04%।
अनुवर्ती कार्रवाई के रूप में, वास्तविक परिणाम इस प्रकार हैं:
रीड: 361,655
कोण: 320,996
अन्य: 21,979
तो, "अन्य" वोटों को छोड़कर, रीड को 53.0% और एंगल को 47.0% वोट मिले। यानी रीड के लिए 6% की आरामदायक जीत। सवाल उठता है कि पोल इतना अलग क्यों था। क्या यह संयोग था? क्या मतदाताओं ने अपना मन बदल लिया? या यह शुरू से ही एक खराब पोल था? मैं ये सवाल पाठकों पर छोड़ता हूँ (मुझे पाठ्यपुस्तकों में ऐसा लिखा जाना बिल्कुल पसंद नहीं)।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
मैंने आपका एक्चुरियल कैलकुलेटर आज़माया। ऐसा क्यों है कि मेरी मृत्यु की अपेक्षित आयु तक पहुँचने की संभावना 50% से कम है?
आप माध्य और माध्यिका को लेकर भ्रमित हो रहे हैं। आइए, मेरी स्थिति को एक उदाहरण के रूप में देखें। मैं 45 वर्षीय पुरुष हूँ। मेरी जीवन प्रत्याशा 78.11 वर्ष है, फिर भी मेरे 80 वर्ष तक जीवित रहने की संभावना 50.04% है।
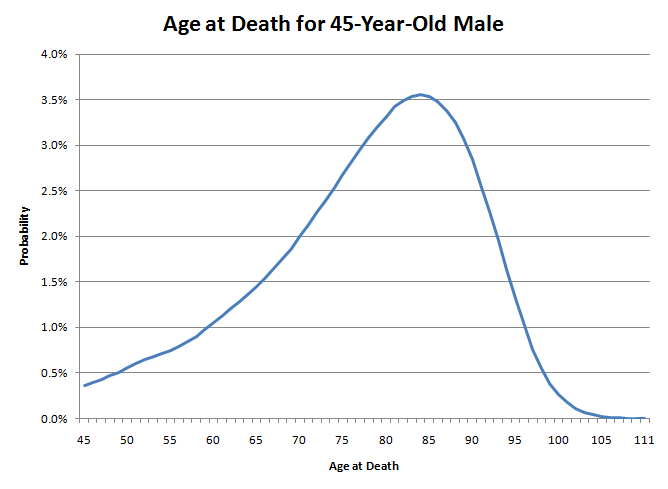
मेरी मृत्यु की आयु इस ग्राफ पर तीर चलाने जैसी होगी। ध्यान दें कि बायाँ भाग दाएँ भाग से कितना मोटा है। इसका मतलब है कि अभी मेरी मृत्यु की संभावना काफी कम है। हालाँकि, जैसे-जैसे मेरी उम्र बढ़ती जाएगी, अगले साल मृत्यु की संभावना और भी बढ़ती जाएगी। उदाहरण के लिए, एक 45 वर्षीय पुरुष के लिए 46 वर्ष तक जीवित रहने की संभावना 99.64% है, जो काफी अधिक है। हालाँकि, 85 वर्ष की आयु में 86 वर्ष तक जीवित रहने की संभावना केवल 89.21% है। यह ऐसा है जैसे प्रकृति धीरे-धीरे आपकी पीठ में छुरा घोंप रही हो। शुरुआत में शायद यह आपको नहीं मारेगी, लेकिन हर गुजरते साल के साथ, इसके होने की संभावना धीरे-धीरे बढ़ती जाती है। हालाँकि, जैसे-जैसे आप सत्तर के दशक के अंत में पहुँचते हैं, प्रकृति कहती है कि बहुत हो गया खेल और वास्तव में इसे अंदर धकेलना शुरू कर देती है।
इसलिए अगर 45 साल के बहुत से पुरुष इस ग्राफ़ पर तीर चलाएँ, तो 49.96% पुरुष 45 से 79 साल के बीच तीर चलाएँगे, और 50.04% पुरुष 80 से 111 साल के बीच तीर चलाएँगे। हालाँकि, ग्राफ़ के दाईं ओर आने वाले भाग्यशाली आधे पुरुष शायद 80 साल से ज़्यादा नहीं जी पाएँगे। एक बार जब कोई पुरुष 80 साल का हो जाता है, तो वह केवल 7.78 साल और जीने की उम्मीद कर सकता है। इस बीच, बदकिस्मत आधे पुरुषों में से कई, जो 80 साल तक नहीं पहुँच पाते, उससे भी कम उम्र में मर जाएँगे। इसलिए, कम उम्र में होने वाली मौतों की संख्या ही औसत जीवन प्रत्याशा को कम करती है।
इसी प्रकार की स्थिति के लिए, 10, 20, 30, 31, 32, 33 क्रमांक वाले पासे पर विचार करें। औसत 26 है, फिर भी इससे अधिक संख्या आने की 2/3 संभावना है।
माध्य और माध्यिका में अंतर को समझने के लिए, मान लीजिए कि हम नमूने में दो और मौतें जोड़ देते हैं। एक मौत 46 साल की उम्र में और एक 81 साल की उम्र में। 80 साल तक जीने की संभावना नहीं बदलती, लेकिन 45 साल की उम्र में औसत जीवन प्रत्याशा कम हो जाएगी।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
एक असीम रूप से प्रत्यास्थ रबर बैंड की कल्पना कीजिए जो बिना खींचे 1 किमी लंबा है। यह 1 किमी प्रति सेकंड की दर से फैलता है। अब, रबर बैंड के एक सिरे पर एक चींटी की कल्पना कीजिए। जिस क्षण रबर बैंड फैलना शुरू होता है, चींटी अपनी वर्तमान स्थिति के सापेक्ष 1 सेमी प्रति सेकंड की गति से दूसरे सिरे की ओर रेंगती है। क्या चींटी कभी दूसरे सिरे तक पहुँच पाएगी? यदि हाँ, तो कब?
हाँ, ऐसा होगा, e 100,000 -1 सेकंड के बाद। दो समाधानों के लिए मेरी mathproblems.info साइट, समस्या 206 देखें।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
क्या आपको लगता है कि बेहतर ईंधन दक्षता हाइब्रिड की अतिरिक्त लागत के लायक है? बराबरी पर आने के लिए आपको कितने मील गाड़ी चलानी होगी?
अच्छा सवाल। इसका जवाब देने के लिए मैंने टोयोटा हाईलैंडर पर विचार किया, जिसे मैं खरीदने की सोच रहा हूँ। इसके मानक हाइब्रिड मॉडल की खुदरा कीमत $37,490 है। उसी चार-पहिया ड्राइव वाली गैर-हाइब्रिड गाड़ी की कीमत $29,995 है। यानी हाइब्रिड इंजन की कीमत में $7,495 का इज़ाफ़ा होता है।
हाइब्रिड का माइलेज शहर और हाईवे दोनों पर 28 मील प्रति घंटा है। नॉन-हाइब्रिड का माइलेज शहर में 17 मील प्रति घंटा और हाईवे पर 22 मील प्रति घंटा है। औसत 19.5 मील प्रति घंटा है।
बराबरी पर पहुंचने के लिए मीलों की संख्या का सामान्य सूत्र h×m h ×m r /(g×(m h -m r )) है, जहाँ
h = हाइब्रिड की अतिरिक्त लागत.
g = एक गैलन गैस की लागत.
m r = गैर-हाइब्रिड के लिए माइलेज ('r' नियमित कार के लिए है)।
m h = हाइब्रिड के लिए माइलेज.
निम्नलिखित तालिका में इस सूत्र का उपयोग गैस की विभिन्न कीमतों के लिए 2 डॉलर से 5 डॉलर प्रति गैलन तक के लाभ-हानि बिंदु को ज्ञात करने के लिए किया गया है।
हाइब्रिड ब्रेक ईवन पॉइंट
| गैस की लागत | मीलों की संख्या |
| $2.00 | 240,722 |
| $2.25 | 213,975 |
| $2.50 | 192,577 |
| $2.75 | 175,070 |
| $3.00 | 160,481 |
| $3.25 | 148,136 |
| $3.50 | 137,555 |
| $3.75 | 128,385 |
| $4.00 | 120,361 | $4.25 | 113,281 |
| $4.50 | 106,987 |
| $4.75 | 101,357 |
| $5.00 | 96,289 |
तो, वेगास में $3.00 प्रति गैलन की मौजूदा कीमत पर, आपको आगे निकलने के लिए गाड़ी पर 160,481 मील से ज़्यादा चलना होगा। इसमें हाइब्रिड से जुड़े अन्य खर्च, जैसे बैटरियों की महंगी प्रतिस्थापन लागत, और कम जीवाश्म ईंधन की खपत के लिए किसी भी कथित ग्रीन पॉइंट्स को शामिल नहीं किया गया है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
समरूप जुड़वाँ के अलावा, मेरे किसी सगे भाई या बहन के साथ जीनों का कितना अनुपात समान होगा?
1/2.
अगर हम तुलना के लिए केनो का इस्तेमाल करें, तो हर व्यक्ति में 40 जीन होंगे, जिनमें से प्रत्येक एक केनो बॉल द्वारा दर्शाया जाएगा। हालाँकि, प्रत्येक बॉल का एक विशिष्ट नंबर होगा। जब दो लोग, जो आपस में संबंधित नहीं हैं, संभोग करते हैं, तो यह ऐसा है जैसे दोनों ने 80 गेंदों को एक हॉपर में मिला दिया हो, और संभोग से उत्पन्न संतानों के लिए यादृच्छिक रूप से 40 जीन चुन लिए हों।
तो जब आप गर्भवती हुईं, तो आपको हॉपर में आधी गेंदें मिलीं, और बाकी आधी बेकार हो गईं। जब आपके भाई या बहन का गर्भाधान हुआ, तो उन्हें आपके जन्म के समय निकाली गई गेंदों में से आधी मिलीं, और आधी जो नहीं निकाली गईं। तो आप आनुवंशिक रूप से 50% समान हैं। ठीक उसी तरह जैसे कि अगर केनो में 40 नंबर निकाले जाते हैं, तो दो लगातार निकाले गए नंबरों में औसतन 20 गेंदें समान होती हैं।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
मेज और कुर्सियाँ बनाने वाली एक फैक्ट्री में 10 आरी, 6 खराद और 18 सैंडिंग मशीनें लगी हैं। एक कुर्सी को आरी पर 10 मिनट, खराद पर 5 मिनट और सैंडिंग में 5 मिनट लगते हैं। एक मेज को आरी पर 5 मिनट, खराद पर 5 मिनट और सैंडिंग में 20 मिनट लगते हैं। एक कुर्सी 10 डॉलर में और एक मेज 20 डॉलर में बिकती है। फैक्ट्री को प्रति घंटे कितनी मेज और कुर्सियाँ बनानी चाहिए ताकि उसे सबसे ज़्यादा राजस्व मिले, और वह राजस्व कितना है?
मान लीजिए कि c प्रति घंटे बनाई गई कुर्सियों की संख्या है और t मेज़ों की संख्या। प्रति घंटे राजस्व 10×c + 20×t होगा।
10 आरी चलाने से प्रति घंटे 600 मिनट आरी चलती है। हमें बताया गया था कि एक कुर्सी को आरी चलाने में 10 मिनट और एक मेज को 5 मिनट लगते हैं। इस प्रकार, प्रति घंटे उत्पादन की सीमा इस प्रकार है:
(1) 10c + 5t <= 600
6 खराद मशीनों से प्रति घंटे 360 मिनट खराद का काम होता है। हमें बताया गया था कि एक कुर्सी को आरी चलाने में 5 मिनट और एक मेज को 5 मिनट लगते हैं। इस प्रकार, प्रति घंटे उत्पादन की सीमा इस प्रकार है:
(2) 5c + 5t <= 360
18 सैंडिंग मशीनों से प्रति घंटे 1080 मिनट सैंडिंग होती है। हमें बताया गया था कि एक कुर्सी को आरी चलाने में 5 मिनट और एक मेज को 20 मिनट लगते हैं। इस प्रकार, प्रति घंटे उत्पादन की सीमा इस प्रकार है:
(3) 5c + 20t <= 1080
निम्नलिखित ग्राफ़ मशीनों के तीन सेटों द्वारा लगाई गई तीन बाधाओं को दर्शाता है। कारखाना कुर्सियों और मेज़ों के किसी भी संयोजन का उत्पादन कर सकता है जो तीनों रेखाओं के अंतर्गत आता है। प्रश्न यह है कि तीनों रेखाओं के अंतर्गत सबसे अधिक राजस्व कहाँ से प्राप्त होता है।
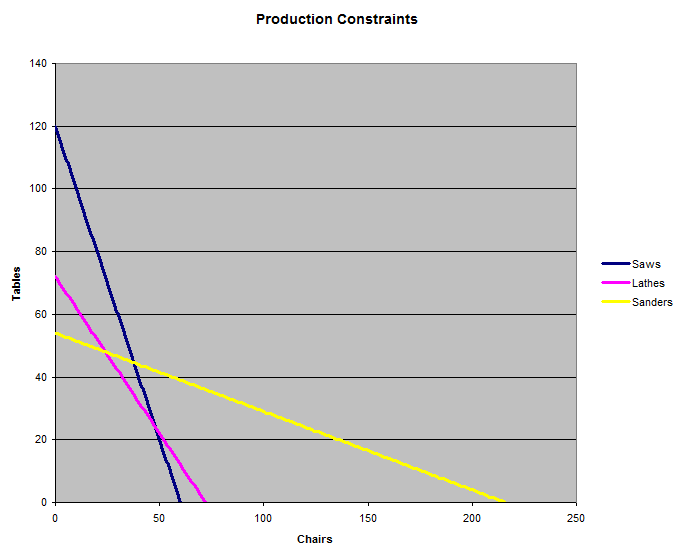
यह तर्कसंगत है कि उत्तर दो रेखाओं का प्रतिच्छेद बिंदु होगा, सभी कुर्सियाँ बनाएँ, या सभी मेज़ बनाएँ। तो आइए जानें कि रेखाएँ कहाँ प्रतिच्छेद करती हैं। सबसे पहले, आइए जानें कि समीकरण (1) और (2) कहाँ प्रतिच्छेद करते हैं। मशीनों का अधिकतम उपयोग करने के लिए हम <= व्यंजक को केवल = में बदल सकते हैं।
(1) 10c + 5t = 600
(2) 5c + 5t = 360
(1) में से (2) घटाएँ:
5सी = 240
सी = 48
समीकरण (1) में c के लिए 48 डालने पर:
10×48 + 5t = 600
5t = 120
टी = 24
अतः समीकरण (1) और (2) 48 कुर्सियों और 24 मेजों पर मिलते हैं।
अब, आइए जानें कि समीकरण (2) और (3) कहाँ मिलते हैं:
(2) 5c + 5t = 360
(3) 5c + 20t = 1080
(3) में से (2) घटाने पर:
15t = 720
टी = 48
इसे (2) या (3) में रखकर हम c का हल निकाल सकते हैं, जो 24 है।
अतः समीकरण (2) और (3) 24 कुर्सियों और 48 मेजों पर मिलते हैं।
हमें यह जानने की आवश्यकता नहीं है कि समीकरण (1) और (3) कहाँ मिलते हैं, क्योंकि हम ग्राफ से देख सकते हैं कि जहां आरी और सैंडर्स लाइनें मिलती हैं वह खराद बाधा के बाहर है।
यह भी संभव है कि केवल कुर्सियाँ बनाना ही सही उत्तर हो। ग्राफ़ दर्शाता है कि केवल कुर्सियाँ बनाने में आरी सबसे बड़ी बाधा है। समीकरण (1) से, यदि हम मेज़ों की संख्या के लिए 0 डालें, तो हमें c=60 प्राप्त होता है।
एक और संभावना केवल टेबल बनाने की है। ग्राफ़ दिखाता है कि सैंडर्स सबसे बड़ी सीमा होगी। समीकरण (3) में 0 कुर्सियाँ रखने पर, हम पाते हैं कि हम 54 से ज़्यादा टेबल नहीं बना सकते।
निम्नलिखित ग्राफ़ प्रत्येक व्यवहार्य उत्तर के लिए कुल राजस्व दर्शाता है। याद रखें, राजस्व प्रति कुर्सी $10 और प्रति मेज़ $20 है।
कुल प्रति घंटा राजस्व
| कुर्सियों | टेबल | आय |
| 0 | 54 | $1,080 |
| 24 | 48 | $1,200 |
| 48 | 24 | $960 |
| 60 | 0 | $600 |
राजा के पास शराब से भरा एक बैरल है।
सोमवार की रात को, एक नौकर बैरल से तीन कप चुरा लेता है और उनकी जगह तीन कप पानी रख देता है।
मंगलवार की रात को एक अन्य नौकर शराब के पतले हो चुके बैरल से तीन कप चुरा लेता है और उनकी जगह तीन कप पानी भर देता है।
बुधवार की रात को एक और नौकर शराब के अब अधिक पतले हो चुके बैरल से तीन कप चुरा लेता है और उनकी जगह तीन कप पानी भर देता है।
गुरुवार की सुबह बैरल में 50% शराब और 50% पानी होता है।
बैरल में शुरू में कितनी शराब थी?
यहां उत्तर और समाधान (पीडीएफ) दिया गया है।
इस समस्या पर चर्चा के लिए कृपया मेरे फोरम विज़ार्ड ऑफ़ वेगास पर जाएँ।
अगर मेरे पास 200 स्किटल्स का एक कटोरा है और उनमें से 3 मुझे मार देते हैं, तो क्या संभावना है कि अगर मैं मुट्ठी भर 12 स्किटल्स लेकर उन्हें खा लूँ तो मैं मर जाऊँगा? मान लीजिए कि मुझे मारने के लिए सिर्फ़ एक ज़हरीला स्किटल ही काफ़ी है।
इस प्रश्न पर अधिक चर्चा के लिए कृपया मेरे फोरम विज़ार्ड ऑफ़ वेगास पर जाएँ।
एक एलियन ने दस तर्कशास्त्रियों का अपहरण कर लिया है और उन्हें एक कमरे में रखा है। वह उन्हें समझाता है कि वह पहले उन्हें एक पंक्ति में, सबसे लंबे से सबसे छोटे तक, व्यवस्थित करेगा, और हर व्यक्ति का मुँह अगले सबसे छोटे व्यक्ति की दिशा में होगा, ताकि हर व्यक्ति सभी छोटे तर्कशास्त्रियों को देख सके, लेकिन उनसे लंबे तर्कशास्त्रियों को नहीं। फिर वह समझाता है कि वह हर व्यक्ति को एक काली या सफेद टोपी पहनाएगा, हालाँकि कोई भी अपनी टोपी का रंग नहीं देख पाएगा, केवल छोटे तर्कशास्त्रियों की टोपियाँ ही देख पाएगा। काली और सफेद टोपियों का वितरण कुछ भी हो सकता है, ज़रूरी नहीं कि पाँच-पाँच ही हों।
फिर एलियन समझाता है कि वह हर तर्कशास्त्री से, सबसे ऊँचे तर्कशास्त्री से शुरू करके, और पंक्ति में नीचे की ओर बढ़ते हुए, उसकी टोपी का रंग पूछेगा। तर्कशास्त्री अपने से पहले अभिनय करने वालों के जवाब सुन सकते हैं। काले/सफेद जवाबों के अलावा, खेल शुरू होने के बाद वे किसी भी तरह से संवाद नहीं कर सकते। अगर एक से ज़्यादा तर्कशास्त्री गलत होते हैं, तो उन सभी को खा लिया जाएगा। अगर कम से कम नौ जवाब सही होते हैं, तो उन्हें सुरक्षित धरती पर वापस भेज दिया जाएगा। फिर एलियन उन्हें रणनीति बनाने के लिए कुछ समय देता है। उनकी रणनीति क्या होनी चाहिए?
एक संभावित रणनीति यह है। पहले तर्कशास्त्री को, अगर वह सम संख्या में काली टोपियाँ देखता है, तो "काला" और बाकी नौ तर्कशास्त्रियों की विषम संख्या पर "सफ़ेद" कहने को कहें। उसकी अपनी टोपी के रंग से मेल खाने की 50% संभावना होगी, इसलिए उसे ही गलत होने की अनुमति होगी। वह जो भी कहे, उसे "चलता हुआ रंग" कहें।
इसके बाद, दूसरा तर्कशास्त्री, छोटे आठ तर्कशास्त्रियों की काली टोपियों की गिनती करेगा और पहले तर्कशास्त्री की तरह ही विषम और सम विधि से उनका मिलान किसी रंग से करेगा। अगर यह पहले तर्कशास्त्री द्वारा बताए गए रंग से मेल खाता है, तो उसके पास सफ़ेद टोपी होनी चाहिए, और उसे सफ़ेद बताना चाहिए। अगर यह असहमत है, तो उसके पास काली टोपी होनी चाहिए, और उसे काला बताना चाहिए। अगर वह "सफ़ेद" कहता है, तो चल रहा रंग वही रहेगा। अगर वह "काला" कहता है, तो चल रहा रंग विपरीत रंग में बदल जाएगा।
इसके बाद, तीसरा तर्कशास्त्री ठीक दूसरे तर्कशास्त्री की तरह ही कार्य करेगा, लेकिन सात छोटे तर्कशास्त्रियों की काली टोपियों की गिनती करेगा। इसी तरह, अगर वह चल रहे रंग से सहमत होता है, तो वह "सफ़ेद" कहेगा और चल रहा रंग वही रहेगा। अगर वह चल रहे रंग से असहमत होता है, तो वह "काला" कहेगा और चल रहा रंग पलट जाएगा।
अन्य सभी तर्कशास्त्री भी ठीक यही काम करेंगे।
बेशक, वे आसानी से काले को विषम योग से और सफेद को सम योग से जोड़ सकते हैं। महत्वपूर्ण बात यह है कि वे सभी इस बात पर सहमत हैं कि कौन सा रंग किस विषम/सम समता को दर्शाता है। किसी भी रणनीति का पालन करने पर दूसरे से दसवें तर्कशास्त्री तक सभी सही साबित होंगे और पहले तर्कशास्त्री के पास 50% संभावना होगी, इसलिए वे सभी जीवित रहेंगे। यह रणनीति किसी भी संख्या में तर्कशास्त्रियों के लिए काम करेगी।
एक्सल और बॉब, दोनों के पास 52 पत्तों का अपना डेक है। दोनों उन्हें बेतरतीब ढंग से फेंटते हैं। फिर वे हर डेक से एक-एक पत्ता एक साथ पलटते हैं। क्या संभावना है कि वे एक ही समय पर कम से कम एक बार एक ही पत्ता पलटें?
उत्तर का अनुमान लगाना आसान होगा: 1-(51/52) 52 = 0.63568648। हालाँकि, ये अनुमान बौद्धिक रूप से बहुत असंतोषजनक हैं। तो, आइए एक सटीक समाधान खोजें!
चरण 1: शुरू करने के लिए, दूसरे डेक को ऑर्डर करने के तरीकों की संख्या पर विचार करें जहां पहला कार्ड नंबर 1 है। उत्तर अन्य 51 कार्डों को ऑर्डर करने के तरीकों की संख्या है, जो 51 है! = 1551118753287382280224243016469303211063259720016986112000000000000.
कोई भी पत्ता पहले डेक से मेल खा सकता है, इसलिए हमें सभी 52 पत्तों के लिए ऐसा करना होगा। इससे हमें 52*51! = 52! संयोजन मिलते हैं जहाँ कम से कम एक पत्ता मेल खाता है।
चरण 2: हालांकि, चरण 1 हर उस स्थिति को दोगुना गिनता है जहां दो कार्ड मेल खाते हैं। उदाहरण के लिए, यदि पहले दो कार्ड 1 और 2 थे, तो हम अन्य कार्डों को व्यवस्थित करने के 50! तरीकों को दो बार गिनते, एक बार 1 को पहला कार्ड और दूसरी बार 2 को दूसरा कार्ड मानते हुए। 52 में से 2 कार्ड चुनने के तरीकों की संख्या combin(52,2) = 1326 है। दो कार्डों के प्रत्येक संयोजन के लिए, अन्य कार्डों को क्रम से लगाने के 50! = 304140932017133780436126081660647688443776415689605120000000000000
चरण 3: इसके बाद, उस स्थिति पर विचार करें जहां यादृच्छिक डेक में पहले तीन कार्ड क्रमशः 1, 2 और 3 हैं। अन्य 49 कार्डों को क्रमबद्ध करने के 49! तरीके हैं। कम से कम एक मिलान वाले कार्ड की गिनती के प्रारंभिक चरण में हमने उन्हें तीन बार गिना होगा। फिर हमने दूसरे चरण में इन तीन कार्डों में से 2 को चुनने के लिए सभी combin(3,2)=3 तरीकों को घटा दिया होगा। तो यह स्थिति 3-3=0 बार गिनी गई होगी, इसलिए हमें उन्हें वापस जोड़ना होगा। कम से कम 3 कार्ड चुनने के combin(52,3) ऐसे हालात हैं जो मेल खाते हैं। इसलिए हमें combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! संयोजनों को वापस जोड़ना होगा।
चरण 4: इसके बाद, उस स्थिति पर विचार करें जहां यादृच्छिक डेक में पहले चार कार्ड क्रमशः 1, 2, 3 और 4 हैं। अन्य 48 कार्डों को क्रमबद्ध करने के 48! तरीके हैं। कम से कम एक मिलान कार्ड की गिनती के प्रारंभिक चरण में हमने उन्हें चार बार गिना होगा। फिर हमने चरण 2 में इन चार कार्डों में से दो को चुनने के लिए सभी combin(4,2)=6 तरीकों को घटाया होगा। फिर हमने इन चार कार्डों में से 3 को चुनने के लिए सभी combin(4,3)=4 तरीकों को जोड़ा होगा। तो हम 4-6+4=2 तरीकों पर हैं, प्रत्येक ऐसी स्थिति को गिना गया होगा। इसलिए हमें उन तरीकों में से एक को घटाने की जरूरत है, ताकि प्रत्येक स्थिति को एक बार गिना जाए। ऐसी कई स्थितियाँ हैं combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4!
हम ऐसा करते रहेंगे, दोहरी गिनती को ठीक करने के लिए बारी-बारी से जोड़ और घटाव करेंगे।
अंत में, उन स्थितियों की संख्या जहां यादृच्छिक डेक में कम से कम एक कार्ड क्रमबद्ध डेक से मेल खाता है = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
52 कार्ड ऑर्डर करने के कुल तरीके 52 हैं! = y = 52717761549636521942261854154512265996921245386198220800000000000000 हैं।
इस प्रकार, उत्तर है x/y = 0.6321205588285576784044762298
कोई मिलान न होने की संभावना 1-(x/y) = 0.3678794411714423215955237702 है।
यदि यह संख्या परिचित लगती है, तो ऐसा होना चाहिए। 1/e = 0.3678794411714423215955237702.
अतः, उत्तर का अनुमान बहुत ही बारीकी से 1-(1/e) के रूप में लगाया जा सकता है।
स्वीकृतियाँ
गणितीय गणना Pari/GP में की गई
यह समस्या मेरे फोरम विजार्ड ऑफ वेगास में पूछी गई और इस पर चर्चा की गई।
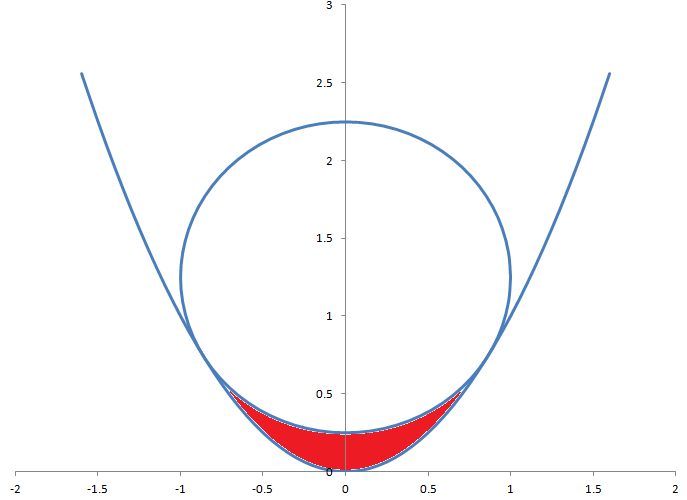
त्रिज्या 1 वाला एक वृत्त समीकरण y=x 2 वाले परवलय पर स्पर्शरेखा है। वृत्त और परवलय के बीच लाल रंग के क्षेत्र का क्षेत्रफल क्या है?
उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।
मेरा समाधान यहां है (पीडीएफ)
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
मुझे यह समस्या माइंड योर डिसीजन्स के प्रेश तलवाल्कर से मिली।
एक कैसीनो डीलर थ्री कार्ड पोकर के एक नए संस्करण पर काम कर रहा है। वह एक मानक डेक से सभी फेस कार्ड्स लेती है और उन्हें अच्छी तरह से फेंटती है। फिर वह खिलाड़ी #1 को 3 कार्ड, खिलाड़ी #2 को तीन कार्ड, खिलाड़ी #3 को तीन कार्ड और खिलाड़ी #4 को अंतिम तीन कार्ड देती है। क्या संभावना है कि सभी चार हाथों में एक स्ट्रेट (किसी भी सूट का JQK) होगा?

[स्पॉइलर=समाधान]
प्रथम हाथ AKQ होने की संभावना 1*(8/11)*(4/10) = 29.09% है।
दूसरा हाथ AKQ होने की संभावना, जबकि पहला हाथ पहले से ही AKQ है, 1*(6/8)*(3/7) = 32.14% के बराबर है।
तीसरा हाथ AKQ होने की संभावना, यह देखते हुए कि पहला और दूसरा हाथ पहले से ही AKQ है, 1*(4/5)*(2/4) = 40.00% के बराबर है
बचे हुए पत्ते AKQ होने चाहिए, क्योंकि पहले तीन हाथ AKQ हैं। इस प्रकार, प्रायिकता ऊपर दी गई तीन प्रायिकताओं का गुणनफल है, जो 216/5775 = लगभग 0.037402597 है।
[/spoiler]यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
त्रिज्या 1 के एक वृत्त में यादृच्छिक रूप से अंकित आयत का औसत क्षेत्रफल और परिमाप क्या है?
अच्छा सवाल है। मेरे जवाब ये हैं:
यहां दोनों के लिए मेरा समाधान है (पीडीएफ)।
एक दस-अंकीय संख्या ज्ञात कीजिए जैसे कि:
- संख्या का पहला अंक पूरी संख्या में 0 की संख्या है।
- संख्या का दूसरा अंक पूरी संख्या में 1 की संख्या है।
- संख्या का तीसरा अंक पूरी संख्या में 2 की संख्या है।
- संख्या का चौथा अंक पूरी संख्या में 3 की संख्या है।
- संख्या का 5वां अंक पूरी संख्या में 4 की संख्या है।
- संख्या का छठा अंक पूरी संख्या में 5 की संख्या है।
- संख्या का 7वां अंक पूरी संख्या में 6 की संख्या है।
- संख्या का 8वां अंक पूरी संख्या में 7 का अंक है।
- संख्या का 9वां अंक पूरी संख्या में 8 की संख्या है।
- संख्या का 10वाँ अंक पूरी संख्या में 9 का अंक है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
तीन बिंदु त्रिज्या 1 वाले एक वृत्त पर यादृच्छिक रूप से और समान रूप से वितरित हैं। तीन बिंदुओं के बीच अपेक्षित न्यूनतम दूरी क्या है, जहां दूरियां परिधि के साथ मापी जाती हैं?
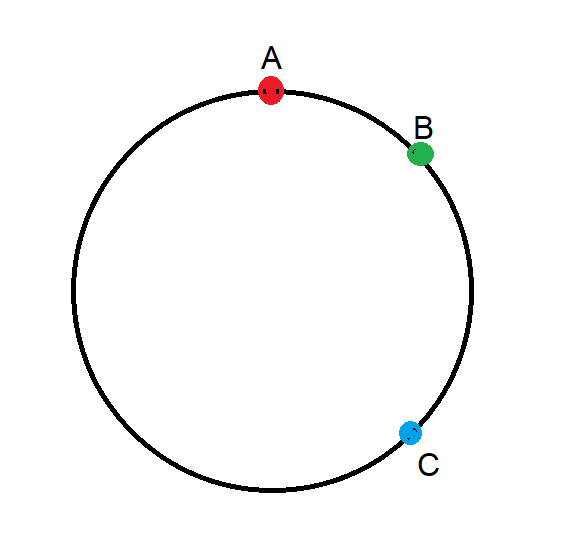
यहां मेरा समाधान (पीडीएफ) है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
ऐलिस और बिल को एक घर को पेंट करने में 3 घंटे लगते हैं।
ऐलिस और सिंडी को एक घर को पेंट करने में 4 घंटे लगते हैं।
बिल और सिंडी को एक घर को पेंट करने में 5 घंटे लगते हैं।
यदि वे सभी पेंटिंग करें तो कितना समय लगेगा?
यहां मेरा समाधान (पीडीएफ) है।


