इस पृष्ठ पर
सिक बो परिशिष्ट
इस पृष्ठ पर
परिचय

चित्र क्लेरिज होटल/कैसीनो नियम पुस्तिका से लिया गया है।
ऑनलाइन सिक बो बोनस सभी को देखें
- कम :
अगर ट्रिपल अपवाद न होता, तो इस दांव में हाउस एज नहीं होती। 1, 2, या 3 के ट्रिपल की प्रायिकता 3/216 है। 3 और 10 के बीच किसी भी योग की प्रायिकता 1/2, या 108/216 है। इसलिए, ट्रिपल जीतने की प्रायिकता 108/216 - 3/216 = 105/216 है। इस प्रकार, खिलाड़ी की एज (105/216)*(+1) + (111/216)*(-1) = -6/216 =~-2.78% है।
- उच्च : निम्न देखें.
- विशिष्ट संख्या :
किसी विशिष्ट संख्या के शून्य आने की संभावना (5/6) 3 =125/216 है।
किसी विशिष्ट संख्या के आने की संभावना 3*(1/6) 1 *(5/6) 2 = 75/216 है।
किसी विशिष्ट संख्या के दो आने की संभावना 3*(1/6) 2 *(5/6) 1 = 15/216 है।
किसी विशिष्ट संख्या के तीन आने की संभावना (1/6) 3 = 1/216 है।
इस प्रकार खिलाड़ी की बढ़त (125/216)*(-1) + (75/216)*(+1)+ (15/216)*(+2) + (1/216)*(+3) = -17/216 =~-7.780% है। - कुल 4 :
4 रोल करने के 3 तरीके हैं: (1+1+2, 1+2+1, 2+1+1)। इस प्रकार खिलाड़ी की बढ़त 3/216*(+60) + (213/216)*(-1) = -33/216 =-15.278% है।
- कुल 5 :
5 रोल करने के 6 तरीके हैं: (1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1)। इस प्रकार खिलाड़ी की बढ़त 6/216*(+30) + (210/216)*(-1) =-30/216 = -13.889% है।
- कुल 6 :
6 रोल करने के 10 तरीके हैं: (1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+1,3+1+2, 3+2+1, 2+2+2)। इस प्रकार खिलाड़ी की बढ़त 10/216*(+17) + (206/216)*(-1) = -36/216 =-16.667% है।
- कुल 7 :
7 को रोल करने के 15 तरीके हैं: (1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+1,4+1+2, 4+2+1, 1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2)। इस प्रकार खिलाड़ी की बढ़त 15/216*(+12) + (201/216)*(-1) =-21/216 = -9.722% है।
- कुल 8 :
8 रोल करने के 21 तरीके हैं: (1-6-6 * 3 तरीके, 1-2-5 * 6 तरीके, 1-3-4 * 6 तरीके, 2-2-4 * 3 तरीके, 2-3-3 * 3 तरीके)। इस प्रकार खिलाड़ी की बढ़त 21/216*(+8) + (195/216)*(-1) = -27/216 =-12.500% है।
- कुल 9 :
9 को रोल करने के 25 तरीके हैं: (1-2-6 * 6 तरीके, 1-3-5 * 6 तरीके, 1-4-4 * 3 तरीके, 2-2-5 * 3 तरीके, 2-3-4 * 6 तरीके, 3-3-3 * 1 तरीका)। इस प्रकार खिलाड़ी की बढ़त 25/216*(+6) + (191/216)*(-1) =-41/216 = -18.982% है।
- कुल 10 :
10 रोल करने के 27 तरीके हैं: (1-3-6 * 6 तरीके, 1-4-5 * 6 तरीके, 2-2-6 * 3 तरीके, 2-3-5 * 6 तरीके, 2-4-4 * 3 तरीके, 3-3-4 * 3 तरीके)। इस प्रकार खिलाड़ी की बढ़त 27/216*(+6) + (189/216)*(-1) =-27/216 = -12.500% है।
- कुल 11 : कुल 10 देखें
- कुल 12 : कुल 9 देखें
- कुल 13 : कुल 8 देखें
- कुल 14 : कुल 7 देखें
- कुल 15 : कुल 6 देखें
- कुल 16 : कुल 5 देखें
- कुल 17 : कुल 4 देखें
- दो संख्याएँ :
मान लीजिए चुनी गई दो संख्याएँ 1 और 2 हैं। 1 और 2 वाले 30 संयोजन हैं: 1-2-1 * 3 तरीके, 1-2-2 * 3 तरीके, 1-2-3 * 6 तरीके, 1-2-4 * 6 तरीके, 1-2-5 * 6 तरीके, 1-2-6 * 6 तरीके। इस प्रकार खिलाड़ी की बढ़त 30/216*(+5) +(186/216)*(-1) = -36/216 = -16.667% है।
- विशिष्ट त्रिक :
किसी विशिष्ट ट्रिपलेट को रोल करने का केवल एक ही तरीका है। इस प्रकार खिलाड़ी की बढ़त 1/216*(+180) + (215/216)*(-1) = -35/216 =-16.20% है।
- कोई भी त्रिक :
ट्रिपलेट रोल करने के 6 तरीके हैं। इस प्रकार खिलाड़ी की बढ़त 6/216*(+30) +(210/216)*(-1) = -30/216 = -13.889% है।
- विशिष्ट जोड़ी :
मान लीजिए कि चुना गया जोड़ा इकाई का है। उस संख्या के दो या तीन आने के 16 तरीके हैं: 1+1+1, 1+1+2 * 3 तरीके, 1+1+3 * 3 तरीके, 1+1+4 * 3 तरीके, 1+1+5 * 3 तरीके, 1+1+6 * 3 तरीके। इस प्रकार खिलाड़ी की बढ़त 16/216*(+10) + (200/216)*(-1) = -72/216 = -18.52% है।
निम्नलिखित n पासों पर s स्पॉट के लिए एक सूत्र है, जो रिचर्ड ए. एपस्टीन द्वारा द थ्योरी ऑफ गैंबलिंग एंड स्टैटिस्टिकल लॉजिक , सूत्र 5-14 से लिया गया है।
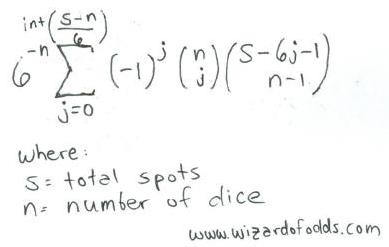
उदाहरण के लिए, आइए 3 पासों पर 11 स्थान प्राप्त करने के तरीकों की संख्या पर नजर डालें।
int[(sn)/6] = int[(11-3)/6] = int[1.33] = 1
कुल होगा 6 -3 * [-1 0 *कॉम्बिन(3,0)*कॉम्बिन(11-6*0-1,3-1) + -1 1 *कॉम्बिन(3,1)*कॉम्बिन(11-6*1-1,3-1) ] =
1/216 * [1*1*कॉम्बिन(10,2) + -1*3*कॉम्बिन(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12.5%
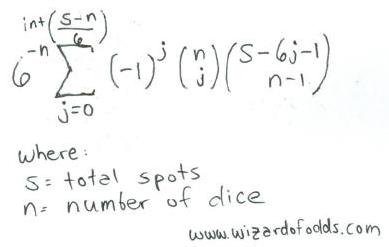













.png)










