इस पृष्ठ पर
आग शर्त
परिचय
फायर बेट क्रेप्स में एक लोकप्रिय साइड बेट है जो शूटर द्वारा अर्जित और जीते गए विशिष्ट अंकों की संख्या के आधार पर भुगतान करता है। मुझे तीन भुगतान तालिकाएँ ज्ञात हैं, जो इस प्रकार हैं। प्रत्येक का हाउस एज तालिका की निचली पंक्ति में है। भुगतान तालिका 1 सबसे आम है। भुगतान "एक" के आधार पर दर्शाए जाते हैं। ऋणात्मक होने पर नुकसान का संकेत मिलता है।
फायर बेट पे टेबल्स
| बनाए गए अंक | वेतन तालिका A | वेतन तालिका बी | वेतन तालिका C |
|---|---|---|---|
| 6 | 999 | 2000 | 299 |
| 5 | 249 | 200 | 149 |
| 4 | 24 | 10 | 29 |
| 3 | -1 | -1 | 6 |
| 2 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 |
| 0 | -1 | -1 | -1 |
| हाउस एज | 20.76% | 24.86% | 20.73% |
वेतन तालिका ए का मेरा विश्लेषण निम्नलिखित है। निचले दाएं सेल में 20.76% का हाउस एज दिखाया गया है।
फायर बेट — भुगतान तालिका A
| बनाए गए अंक | भुगतान करता है | संभावना | वापस करना |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 24 | 0.008798 | 0.211156 |
| 5 | 249 | 0.001640 | 0.408343 |
| 6 | 999 | 0.000162 | 0.162272 |
| कुल | 1 | -0.207628 |
वेतन तालिका बी का मेरा विश्लेषण निम्नलिखित है। निचले दाएं सेल में 24.86% का हाउस एज दिखाया गया है।
फायर बेट — भुगतान तालिका B
| बनाए गए अंक | भुगतान करता है | संभावना | वापस करना |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 10 | 0.008798 | 0.087982 |
| 5 | 200 | 0.001640 | 0.327987 |
| 6 | 2000 | 0.000162 | 0.324869 |
| कुल | 1 | -0.248562 |
वेतन तालिका सी का मेरा विश्लेषण निम्नलिखित है। निचले दाएं सेल में 20.73% का हाउस एज दिखाया गया है।
फायर बेट — भुगतान तालिका C
| बनाए गए अंक | भुगतान करता है | संभावना | वापस करना |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | 6 | 0.033434 | 0.200605 |
| 4 | 29 | 0.008798 | 0.255147 |
| 5 | 149 | 0.001640 | 0.244350 |
| 6 | 299 | 0.000162 | 0.048568 |
| कुल | 1 | -0.207295 |
निम्नलिखित तालिका 0 से 6 अंक बनाने की संभावनाओं को दर्शाती है, जिसमें एक्सेल जितने महत्वपूर्ण अंक संभाल सकता है, उतने शामिल हैं।
आग शर्त संभावनाओं
| बनाए गए अंक | संभावना |
|---|---|
| 0 | 0.593939393939394 |
| 1 | 0.260750492003903 |
| 2 | 0.101275355549231 |
| 3 | 0.0334342121788456 |
| 4 | 0.00879817844040312 |
| 5 | 0.00163993313895325 |
| 6 | 0.000162434749269826 |
मुझसे अक्सर पूछा जाता है कि ऊपर दी गई प्रायिकताओं की गणना कैसे की जाती है। यह एक चुनौतीपूर्ण गणित की समस्या है। नीचे, मैं 0 से 6 तक किसी भी संख्या में अंक प्राप्त करने की प्रायिकताओं को हल करने के तरीके बता रहा हूँ।
यादृच्छिक सिमुलेशन
फायर बेट का विश्लेषण करने का सबसे आसान तरीका एक यादृच्छिक सिमुलेशन है। आधुनिक कंप्यूटरों की गति के साथ, यह बेहद सटीक भी है। केवल गणित के सबसे शुद्धतावादी (मेरे जैसे) ही सटीक समाधान के लिए प्रयास करेंगे। निम्नलिखित तालिका भुगतान तालिका A के विरुद्ध हल किए गए लगभग 40 अरब फायर बेट्स के सिमुलेशन के परिणाम दिखाती है। निचले दाएँ सेल में 20.7531% का हाउस एज दिखाया गया है। वास्तविक हाउस एज 20.7628% है, इसलिए सिमुलेशन रिटर्न के 0.01% तक सटीक था।
फायर बेट सिमुलेशन
| बनाए गए अंक | भुगतान करता है | जीत | संभावना | वापस करना |
|---|---|---|---|---|
| 6 | 999 | 6,452,452 | 0.000162 | 0.162257 |
| 5 | 249 | 65,165,019 | 0.001640 | 0.408438 |
| 4 | 24 | 349,553,690 | 0.008799 | 0.211173 |
| 3 | -1 | 1,328,267,592 | 0.033435 | -0.033435 |
| 2 | -1 | 4,023,371,732 | 0.101275 | -0.101275 |
| 1 | -1 | 10,358,742,102 | 0.260747 | -0.260747 |
| 0 | -1 | 23,595,605,529 | 0.593941 | -0.593941 |
| कुल | 39,727,158,116 | 1.000000 | -0.207531 |
मार्कोव श्रृंखला
फायर बेट की ऑड्स की सटीक गणना करने का एक तरीका मार्कोव चेन है। इसका मतलब है कि पहले से पूरे किए गए 64 संभावित पॉइंट्स में से किसी भी स्थिति में, भविष्य में किसी भी पॉइंट्स की संख्या पूरी होने की संभावना की गणना करना। अंत में गणित काफी आसान है, सभी छह को पूरा करने के लिए बस एक और पॉइंट की आवश्यकता है। फिर पहले रोल की शुरुआती स्थिति पर वापस जाएँ।
यह पहली अवस्था तालिका में पहली पंक्ति के रूप में दर्शाई गई है, स्तंभ शीर्षकों को छोड़कर। यह 0 से 6 तक किसी भी संख्या में अंक पूरे करने की ऊपर दर्शाई गई संभावनाओं को दर्शाती है।
फायर बेट मार्कोव चेन
| अंक पहले से बनाया | संभावना 0 अंक | संभावना 1 अंक | संभावना 2 अंक | संभावना 3 अंक | संभावना 4 अंक | संभावना 5 अंक | संभावना 6 अंक |
|---|---|---|---|---|---|---|---|
| कोई नहीं | 0.593939 | 0.260750 | 0.101275 | 0.033434 | 0.008798 | 0.001640 | 0.000162 |
| 10 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 9 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0.022402 | 0.004153 | 0.000404 |
| 9,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 8 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 8,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 8,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 6,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 6,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6,8 | 0.000000 | 0.000000 | 0.732710 | 0.210728 | 0.048135 | 0.007762 | 0.000665 |
| 6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0.022402 | 0.004153 | 0.000404 |
| 5,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 5,9 | 0.000000 | 0.000000 | 0.685315 | 0.237358 | 0.064328 | 0.011875 | 0.001124 |
| 5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 5,8 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.876957 | 0.114977 | 0.008066 |
| 5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.934446 | 0.065554 |
| 4 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 4,10 | 0.000000 | 0.000000 | 0.647934 | 0.250930 | 0.079930 | 0.018752 | 0.002454 |
| 4,9 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,8 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,6 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 4,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.816667 | 0.164832 | 0.018502 |
| 4,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,5,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,5,9 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 4,5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.758221 | 0.208531 | 0.033248 |
| 4,5,8 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.934446 | 0.065554 |
| 4,5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
अगर आप मेरे काम को दोहराने की योजना बना रहे हैं, तो एक अवस्था से दूसरी अवस्था में जाने के बारे में यहाँ कुछ सलाह दी गई है। अंत के करीब वाली अवस्था से शुरुआत करें, जिसमें निशानेबाज़ ने पहले ही 5 अंक बना लिए हों। उदाहरण के लिए, अगर निशानेबाज़ को केवल 4 चाहिए, तो तीन चीज़ें हो सकती हैं: (1) वह 4 स्थापित करता है और बनाता है, (2) वह स्थापित करता है और वह अंक बनाता है जो उसने पहले ही बना लिया था, (3) वह सात अंक प्राप्त करता है। (1) की प्रायिकता (3/24)*(1/3) = 1/24 = 0.041667 है। (2) की प्रायिकता (4/24)*(2/5) + (5/24)*(5/11) + (5/24)*(5/11) + (4/24)*(2/5) + (3/24)*(1/3) = 0.364394 है। (3) की प्रायिकता 1-0.041667 - 0.364394 = 0.593939 है। अंततः घटना (1) या (3) घटित होगी। (1) के (3) से पहले घटित होने की प्रायिकता 0.041667/(0.041667+0.593939) = 0.065554 है। प्रारंभिक बिंदु पर वापस आते हुए पुनरावर्ती रूप से कार्य करें। यह या तो समय लेने वाला, निरर्थक और उबाऊ होगा, या आप इसे स्प्रेडशीट में स्वचालित तरीके से कर सकते हैं।
गणना
इस पद्धति का पहला चरण एक बिंदु स्थापित होने के बाद पास लाइन बेट के सभी 7 संभावित प्रासंगिक परिणामों की प्रायिकता की गणना करना है। हम कम आउट रोल पर खिलाड़ी के जीतने या हारने के 12 संयोजनों, या 1/3 संभावना को अनदेखा कर सकते हैं, क्योंकि ये घटनाएँ फ़ायर बेट के लिए महत्वपूर्ण नहीं हैं। इसलिए पहला रोल 36 के बजाय 24 संभावित संयोजनों पर आधारित होता है।
- 4 का अंक बनाया और जीता = (3/24) × (3/9) = 1/24 = लगभग 4.17%
- 5 का अंक बनाया और जीता = (4/24) × (4/10) = 1/15 = लगभग 6.67%
- 6 का अंक बना और जीता = (5/24) × (5/11) = 25/264 = लगभग 9.47%
- 8 का अंक बना और जीता = (5/24) × (5/11) = 25/264 = लगभग 9.47%
- 9 का अंक बना और जीता = (4/24) × (4/10) = 1/15 = लगभग 6.67%
- 10 का अंक बनाया और जीता = (3/24) × (3/9) = 1/24 = लगभग 4.17%
- कोई भी अंक बनाया गया और 7-आउट = 2×((3/24) × (6/9)) + 2× ((4/24) × (6/10)) + 2×((5/24) × (6/11)) = 98/165 = लगभग 59.39%
कृपया ध्यान दें, इन संभावनाओं का योग 1 के बराबर है।
इसके बाद, दो पासों के एक-एक करके लुढ़कने से फ़ायर बेट तय करने के बजाय, घटनाओं के बीच के समय को यादृच्छिक रूप से घटित होने पर विचार करें, जिसमें घटनाओं के बीच का समय एक घातांकीय वितरण का अनुसरण करता है जिसका माध्य घटनाओं के बीच समय की एक इकाई है। यदि कोई घटना घटती है, तो वह विशेष घटना हमारे द्वारा अभी-अभी गणना की गई क्रेप्स संभावनाओं का पालन करेगी।
उदाहरण के लिए, पॉइंट-4 की जीत की प्रायिकता 1/24 है। इस प्रकार, पॉइंट-4 की जीत के बीच का समय औसतन 24 इकाई होगा। पॉइंट-10 की जीत के बिना x इकाई समय तक जाने की प्रायिकता exp(-x/24) है। पूरक के रूप में, x इकाई समय में कम से कम एक पॉइंट-10 की जीत की प्रायिकता 1-exp(-x/24) है।
फायर बेट का फैसला करने के लिए, यह मायने नहीं रखता कि घटनाओं के बीच कितना समय बीतता है - बस यह मायने रखता है कि घटनाएँ क्या हैं। इसलिए हम बेट में विजेता के लिए कुल समय को इस प्रकार जोड़ सकते हैं:
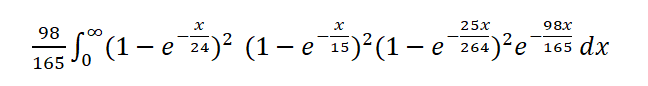
आइए मैं आपको समझाता हूँ कि इस समाकल का क्या अर्थ है। यह प्रायिकता है कि x इकाई समय के बाद प्रत्येक अंक की कम से कम एक जीत हुई हो, लेकिन 7 नहीं। चूँकि अंक-4 और अंक-10 की जीत की प्रायिकता समान है, इसलिए हम अंक-4 की जीत की प्रायिकता का वर्गमूल निकाल सकते हैं। 5 और 9 के साथ-साथ 6 और 8 के लिए भी यही बात लागू होती है। अंत में, हम इस पूरी संख्या को 98/165 से गुणा करते हैं, जो कि सात-आउट की प्रायिकता है, ताकि दांव बंद हो जाए। अगर हम ऐसा नहीं करते, तो खिलाड़ी को कई ओवरलैपिंग जीत के लिए भुगतान मिल सकता है।
इसे हाथ से एकीकृत करना बहुत थकाऊ और त्रुटिपूर्ण होगा। सौभाग्य से, समाकलन कैलकुलेटर उपलब्ध हैं। इस समस्या के लिए, लिंक पर क्लिक करें और ऊपर दिए गए टेक्स्ट बॉक्स में निम्नलिखित लिखें: (1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25x/264))^2*exp(-98x/165)/(165/98)। फिर विकल्पों पर क्लिक करें और निचली सीमा को 0 और ऊपरी सीमा को अनंत पर सेट करें। फिर "गो" पर क्लिक करें।
एकीकरण की सीमाओं पर विचार करने से पहले, उत्तर है (98*(-(165*e^(-(98*x)/165))/98+(2640*e^(-(839*x)/1320))/839+(330*e^(-(109*x)/165))/109-(220*e^(-(149*x)/220))/149+(880*e^(-(303*x)/440))/303-(1760*e^(-(309*x)/440))/309-(11* e^(-(8*x)/11))/8-(1320*e^(-(241*x)/330))/241+(1320*e^(-(491*x)/660))/491-(5280*e^(-(99) 7*x)/1320))/997+(528*e^(-(203*x)/264))/203+(2640*e^(-(1019*x)/1320))/1019-(60*e^(-(47*x) )/60))/47+(2640*e^(-(263*x)/330))/263-(132*e^(-(107*x)/132))/107+(528*e^(-(217*x)/264) )/217+(80*e^(-(33*x)/40))/33-(1760*e^(-(369*x)/440))/369+(40*e^(-(17*x)/20))/17-(88*e^( -(19*x)/22))/19-(15*e^(-(13*x)/15))/13-(480*e^(-(107*x)/120))/107+(528*e^(-(239*x)/264) )/239-(12*e^(-(11*x)/12))/11+(15*e^(-(14*x)/15))/7+(48*e^(-(23*x)/24))/23-e^(-x)))/165.
सौभाग्य से, वह कैलकुलेटर एकीकरण की सीमाओं की अनुमति देता है और समाधान 3700403899126040038831518494284887738125 / 22780863797678919004236184338193605974839452 देता है, जो लगभग 0.0001624347492698264 के बराबर है।
बेशक, यह सभी छह बिंदुओं के बनने की संभावना मात्र है, लेकिन इसी तर्क का इस्तेमाल किसी भी संख्या में बिंदुओं की संभावना ज्ञात करने के लिए किया जा सकता है। मैं इसे पाठक के लिए एक अभ्यास के रूप में छोड़ता हूँ ;-)।
बाहरी संबंध
- फायर बेट गणित पर मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास पर चर्चा की गई है
- मेरी अपनी स्प्रेडशीट देखें, जिसे मैंने गूगल डॉक्स पर पोस्ट किया है ताकि कोई भी इसे डाउनलोड कर सके।
- स्टुअर्ट एन. एथियर द्वारा लिखित पुस्तक 'द डॉक्ट्रिन ऑफ चांसेस: प्रोबेबिलिस्टिक आस्पेक्ट्स ऑफ गैंबलिंग' में फायर बेट गणित की चर्चा की गई है।
स्वीकृतियाँ
मैं विजार्ड ऑफ वेगास फोरम के सदस्य ऐस2 को धन्यवाद देना चाहूंगा, जिन्होंने एकीकरण का उपयोग करके फायर बेट की संभावना को हल करने के लिए अथक सलाह दी।



