इस पृष्ठ पर
अलग-अलग डबल्स
परिचय
डिफरेंट डबल्स एक क्रेप्स साइड बेट है जो बिलोक्सी के ब्यू रिवेज कैसीनो में देखा गया है। यह शूटर द्वारा कुल सात डबल्स रोल करने से पहले बनाए गए अद्वितीय डबल्स की संख्या के आधार पर भुगतान करता है। भुगतान तालिका इस प्रकार है:
- 6 डबल्स पर 100 से 1 का भुगतान
- 5 डबल्स पर 15 से 1 का भुगतान
- 4 डबल्स का भुगतान 8 से 1 होता है
- 3 डबल्स पर 4 से 1 का भुगतान
विश्लेषण
नीचे दी गई तालिका सभी संभावित परिणामों की संभावना और वापसी में योगदान को दर्शाती है। निचले दाएँ कक्ष में 27.92% (ओह!) का हाउस एज दिखाया गया है।
विभिन्न डबल्स रिटर्न तालिका
| डबल्स बनाए गए | भुगतान करता है | युग्म | संभावना | वापस करना |
|---|---|---|---|---|
| 6 | 100 | 1 | 0.001082 | 0.108225 |
| 5 | 15 | 6 | 0.006494 | 0.097403 |
| 4 | 8 | 21 | 0.022727 | 0.181818 |
| 3 | 4 | 56 | 0.060606 | 0.242424 |
| 2 | -1 | 126 | 0.136364 | -0.136364 |
| 1 | -1 | 252 | 0.272727 | -0.272727 |
| 0 | -1 | 462 | 0.500000 | -0.500000 |
| कुल | 924 | 1.000000 | -0.279221 |
बीजीय विश्लेषण
किसी भी दिए गए डबल की प्रायिकता 1/36 है। इस प्रकार, किसी भी डबल की प्रायिकता 6/36 = 1/6 है। किसी भी सात की प्रायिकता 1/6 है। हम डबल और सात के अलावा सभी रोल को अनदेखा कर सकते हैं। इसलिए, यह मानते हुए कि दांव से संबंधित एक रोल था, नीचे उस रोल की प्रायिकताएँ दी गई हैं:
- कोई भी डबल = 1/2
- कोई भी सात = 1/2
पहली महत्वपूर्ण संख्या के सात आने की प्रायिकता 1/2 है। इस प्रकार, शून्य डबल्स की प्रायिकता है।
अन्यथा, खिलाड़ी ने डबल रोल किया होता। अब हम उस डबल रोल को एक महत्वपूर्ण घटना मानकर नज़रअंदाज़ कर सकते हैं। दोनों प्रकार की महत्वपूर्ण घटनाओं की संभावनाएँ अब इस प्रकार हैं:
- कोई भी महत्वपूर्ण डबल = 5/11
- कोई भी सात = 6/11
इस बिंदु पर खिलाड़ी द्वारा एक डबल के लिए सात आने की संभावना 6/11 है। इस प्रकार, एक डबल की कुल संभावना (1/2)*(6/11) = 3/11 = लगभग 27.27% है।
अन्यथा, खिलाड़ी ने दूसरा डबल रोल किया होता। अब हम दो अलग-अलग डबल रोल को एक महत्वपूर्ण घटना मानकर अनदेखा कर सकते हैं। दोनों प्रकार की महत्वपूर्ण घटनाओं की संभावनाएँ अब इस प्रकार हैं:
- कोई भी महत्वपूर्ण डबल = 4/10
- कोई भी सात = 6/10
इस बिंदु पर खिलाड़ी द्वारा दो डबल के लिए सात आने की संभावना 6/10 है। इस प्रकार, एक डबल की कुल संभावना (1/2)*(5/11)*(6/10) = 3/22 = लगभग 13.6363636% है।
अन्यथा, खिलाड़ी ने तीसरा डबल रोल किया होता। अब हम तीन अलग-अलग डबल रोल को एक महत्वपूर्ण घटना मानकर अनदेखा कर सकते हैं। दोनों प्रकार की महत्वपूर्ण घटनाओं की संभावनाएँ अब इस प्रकार हैं:
- कोई भी महत्वपूर्ण डबल = 3/9
- कोई भी सात = 6/9
इस बिंदु पर खिलाड़ी द्वारा दो डबल के लिए सात आने की प्रायिकता 6/9 है। इस प्रकार, एक डबल की कुल प्रायिकता (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = लगभग 6.060606% है।
अन्यथा, खिलाड़ी ने चौथा डबल रोल किया होता। अब हम चार अलग-अलग डबल रोल को एक महत्वपूर्ण घटना मानकर अनदेखा कर सकते हैं। दोनों प्रकार की महत्वपूर्ण घटनाओं की संभावनाएँ अब इस प्रकार हैं:
- कोई भी महत्वपूर्ण डबल = 2/8
- कोई भी सात = 6/8
इस बिंदु पर खिलाड़ी द्वारा दो डबल के लिए सात आने की प्रायिकता 6/8 है। इस प्रकार, एक डबल की कुल प्रायिकता (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = लगभग 2.272727% है।
अन्यथा, खिलाड़ी पाँचवाँ डबल रोल करता। अब हम पाँच अलग-अलग डबल रोल को एक महत्वपूर्ण घटना मानकर अनदेखा कर सकते हैं। दोनों प्रकार की महत्वपूर्ण घटनाओं की संभावनाएँ अब इस प्रकार हैं:
- कोई भी महत्वपूर्ण डबल = 1/7
- कोई भी सात = 6/7
इस बिंदु पर खिलाड़ी द्वारा दो डबल के लिए सात आने की प्रायिकता 6/7 है। इस प्रकार, एक डबल की कुल प्रायिकता (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = लगभग 0.649351% है।
अन्यथा, खिलाड़ी आखिरी बचा हुआ डबल रोल करता। इसकी प्रायिकता (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = लगभग 0.108225% है।
अब हम इन सबको ऊपर दी गई रिटर्न तालिका में एक साथ रख सकते हैं। संयोजनों की संख्या 924 में से है।
समाकलन कलन विश्लेषण
कल्पना कीजिए कि महत्वपूर्ण घटनाओं को पासों के एक-एक करके लुढ़कने से निर्धारित करने के बजाय, उन्हें समय के एक क्षण के रूप में मानिए। मान लीजिए कि घटनाओं के बीच का समय स्मृति-रहित है, यानी घटनाओं के बीच का औसत समय समय की एक इकाई है। दूसरे शब्दों में, घटनाओं के बीच का समय एक घातांकीय वितरण का अनुसरण करता है जिसका माध्य 1 है। बाजी तय करने के लिए यह मायने नहीं रखेगा, क्योंकि घटनाएँ फिर भी एक-एक करके घटित होती हैं।
विशिष्ट डबल्स के बीच का समय एक घातांकीय वितरण का अनुसरण करेगा जिसका माध्य 12 होगा। 12 का कारण यह है कि यदि कोई महत्वपूर्ण घटना घटित होती है, तो 1/12 संभावना होती है कि वह विशिष्ट डबल ही था। इसलिए, x इकाई समय में किसी विशिष्ट डबल के घटित न होने की प्रायिकता exp(-x/12) है। इस प्रकार, उसके घटित होने की प्रायिकता 1-exp(-x/12) है।
मान लीजिए x, दांव शुरू होने के बाद से समय की इकाइयों की संख्या है। हर बार डबल होने और सात न होने की प्रायिकता (1-exp(-x/12)) 6 × exp(-x/2) है।
समय x पर 7 आने पर इसे बंद करने के लिए, इसे 1/2 से गुणा करें, जो कि 7 की संभावना है, जिससे कि समय x पर जीतने की संभावना प्राप्त हो सके (1/2) ×(1-exp(-x/12)) 6 × exp(-x/2)
सभी समय में जीतने वाली शर्त की संभावना का पता लगाने के लिए, 1 से अनंत तक एकीकृत करें:
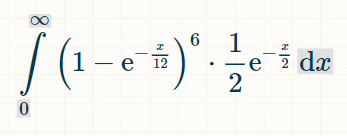
इसे एकीकृत करने के लिए, मैं इस इंटीग्रल कैलकुलेटर की सलाह देता/देती हूँ। इंटीग्रल फ़ील्ड में, "(1-exp(-x/12))^6*(1/2)*exp(-x/2)" लिखें। एकीकरण की सीमाओं के लिए, विकल्पों के अंतर्गत, 0 और ∞ लिखें। फिर "go" पर क्लिक करें।" यह आपको नीचे दिया गया समाकल देगा:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40 *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
हालाँकि, हमें इसमें 0 डालने की ज़रूरत नहीं है। कैलकुलेटर इसका उत्तर 1/924 = लगभग 0.001082251082251082 देता है।
यहाँ पाँच अलग-अलग द्विगुणों का समाकलन दिया गया है। 6 का कारण यह है कि 6 संभावित द्विगुण हैं जो नहीं बने:
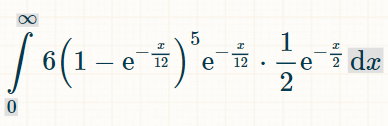
समय की x इकाइयों के भीतर जीतने की संभावना इस प्रकार है:
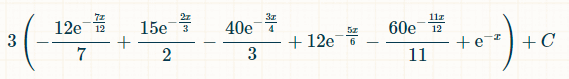
0 से अनन्त तक एकीकरण की सीमा में रखते हुए, ठीक पांच अलग-अलग डबल्स आने की संभावना 1/154 है।
यहाँ चार अलग-अलग डबल्स के लिए समाकलन दिया गया है। 15 का कारण यह है कि 6 में से 4 डबल्स के 6!/(4!*2!) = 15 संभावित संयोजन हैं:
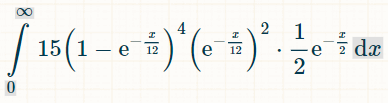
समय की x इकाइयों के भीतर जीतने की संभावना इस प्रकार है:
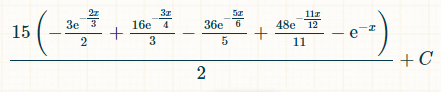
0 से अनन्त तक एकीकरण की सीमा में रखते हुए, ठीक चार अलग-अलग डबल्स आने की संभावना 1/44 है।
यहाँ तीन अलग-अलग डबल्स के लिए समाकल दिया गया है। 20 का कारण यह है कि 6 में से 3 डबल्स के 6!/(3!*3!) = 20 संभावित संयोजन हैं:
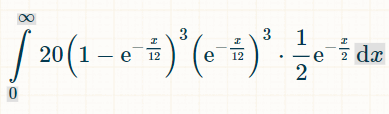
समय की x इकाइयों के भीतर जीतने की संभावना इस प्रकार है:
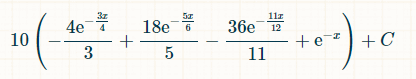
0 से अनन्त तक एकीकरण की सीमा में रखते हुए, ठीक तीन अलग-अलग डबल्स आने की संभावना 2/33 है।



