इस पृष्ठ पर
बोनस क्रेप्स
परिचय
बोनस क्रेप्स, क्रेप्स में पाए जाने वाले तीन साइड बेट्स का एक सेट है। ये इस प्रकार हैं:
- छोटा - यदि शूटर 2 से 6 तक प्रत्येक कुल को रोल करता है, तो कुल 7 रोल करने से पहले जीतता है। जीत आमतौर पर 30 से 1 का भुगतान करती है।
- लंबा - यदि शूटर 7 का कुल रोल करने से पहले 8 से 12 तक प्रत्येक कुल को रोल करता है तो जीतता है। जीत आमतौर पर 30 से 1 का भुगतान करती है।
- सभी - यदि शूटर 7 को छोड़कर 2 से 12 तक प्रत्येक कुल को रोल करता है, तो कुल 7 रोल करने से पहले जीतता है। जीत आमतौर पर 150 से 1 का भुगतान करती है।
2021 में, मैंने वेनिस में "डाइसियोलॉजी" नामक इन्हीं दांवों को देखना शुरू किया।
विश्लेषण
निम्नलिखित तालिका छोटे और बड़े दांवों के मेरे विश्लेषण को दर्शाती है, जब जीत 30 से 1 का भुगतान करती है। निचले दाएं सेल में 18.30% का हाउस एज दिखाया गया है।
छोटा और लंबा
| आयोजन | भुगतान करता है | संभावना | वापस करना |
|---|---|---|---|
| जीतना | 30 | 0.026354 | 0.790617 |
| नुकसान | -1 | 0.973646 | -0.973646 |
| कुल | 1.000000 | -0.183029 |
पहले, कुछ टेबलों पर छोटे और लंबे दांवों पर 34 से 1 का भुगतान किया जाता था। इन ज़्यादा उदार ऑड्स में हाउस एज 7.76% होता है।
निम्नलिखित तालिका में ऑल बेट का मेरा विश्लेषण दिखाया गया है, जिसमें जीत पर 150 से 1 का भुगतान होता है। निचले दाएं सेल में 20.61% का हाउस एज दिखाया गया है।
सभी
| आयोजन | भुगतान करता है | संभावना | वापस करना |
|---|---|---|---|
| जीतना | 150 | 0.005258 | 0.788655 |
| नुकसान | -1 | 0.994742 | -0.994742 |
| कुल | 1.000000 | -0.206087 |
मैंने ऑल बेट पर 155 और 175 से 1 सहित अन्य भुगतान देखे हैं। "एक के लिए" को "एक से एक" ऑड्स में बदलने के लिए भुगतान में से एक घटाना याद रखें। निम्नलिखित तालिका 150 से 175 तक 5 से समान रूप से विभाज्य सभी भुगतानों के लिए हाउस एज दर्शाती है।
सभी दांव पर हाउस एज सारांश
| भुगतान करता है | हाउस एज |
|---|---|
| 150 | 20.61% |
| 155 | 17.98% |
| 160 | 15.35% |
| 165 | 12.72% |
| 170 | 10.09% |
| 175 | 7.46% |
क्रियाविधि
मैंने बोनस क्रेप्स का विश्लेषण तीन तरीकों से किया है, जो इस प्रकार है:
- सिमुलेशन — यह शायद सबसे आसान तरीका है। हालाँकि, मेरे जैसे गणितीय शुद्धतावादियों के लिए, सिमुलेशन हमेशा बौद्धिक रूप से असंतोषजनक होते हैं।
- मार्कोव श्रृंखला — यह विधि जटिल और समय लेने वाली है। छोटे और बड़े के लिए 6x6 संक्रमण मैट्रिक्स और सभी के लिए 12x12 की आवश्यकता होगी।
- इंटीग्रल कैलकुलस — इंटीग्रल कैलकुलेटर की मदद से यह विधि आश्चर्यजनक रूप से आसान है। मैं इसे नीचे और विस्तार से समझाता हूँ।
कल्पना कीजिए कि महत्वपूर्ण घटनाओं को पासों के एक-एक करके लुढ़कने से निर्धारित करने के बजाय, उन्हें समय के एक क्षण के रूप में मानिए। मान लीजिए कि घटनाओं के बीच का समय स्मृति-रहित है, यानी घटनाओं के बीच का औसत समय समय की एक इकाई है। दूसरे शब्दों में, घटनाओं के बीच का समय एक घातांकीय वितरण का अनुसरण करता है जिसका माध्य 1 है। बाजी तय करने के लिए यह मायने नहीं रखेगा, क्योंकि घटनाएँ फिर भी एक-एक करके घटती हैं।
निम्नलिखित संभावना है कि किसी भी दिए गए कुल को समय की x इकाइयों के भीतर कम से कम एक बार रोल नहीं किया गया है:
- 2 या 12: exp(-x/36)
- 3 या 11: exp(-x/18)
- 4 या 10: exp(-x/12)
- 5 या 9: exp(-x/9)
- 6 या 8: exp(-5x/36)
- 7: एक्सप(-x/6)
आइए पहले छोटे दांव पर नज़र डालें। बड़े दांव के लिए भी ऑड्स बिल्कुल वही हैं।
समय की x इकाइयों में, 2, 3, 4, 5, और 6 के आने और 7 के न आने की संभावना है: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6) समय x पर, खिलाड़ी द्वारा 7 आने की संभावना, जबकि पहले उसने 2 से 6 तक प्रत्येक योग को रोल किया था, है:
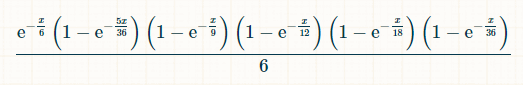
एकीकरण के लिए, मैंने इस इंटीग्रल कैलकुलेटर का उपयोग किया।
चूँकि विजयी 7 कभी भी आ सकता है, इसलिए जीतने की प्रायिकता 0 से अनंत तक x पर इस प्रायिकता का समाकलन है। ऐसा नहीं है कि हमें जानने की ज़रूरत है, लेकिन समाकलन की सीमाएँ निर्धारित करने से पहले समाकलन है। (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^ (-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(- (7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^ (-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6.
एकीकरण की सीमाएँ रखने पर, उत्तर 20049 / 760760 = लगभग 0.02635390924864609 है।
अब, आइये ऑल बेट पर नजर डालें।
समय की x इकाइयों में, 2, 3, 4, 5, 6, 8, 9, 10, 11, और 12 के आने और 7 के न आने की संभावना है: (1-exp(-x/36)) 2 *(1-exp(-x/16)) 2 *(1-exp(-x/12)) 2 *(1-exp(-x/9)) 2 *(1-exp(-5x/36)) 2 *exp(-x/6) संभावना है कि समय x पर, खिलाड़ी 7 लाता है, जबकि पहले उसने 2 से 6 तक प्रत्येक योग को रोल किया है:
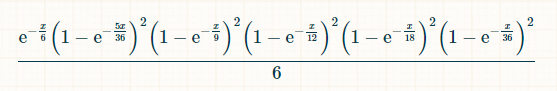
चूँकि विजयी 7 कभी भी आ सकता है, इसलिए जीतने की प्रायिकता 0 से अनंत तक x पर इस प्रायिकता का समाकलन है। ऐसा नहीं है कि हमें जानने की ज़रूरत है, लेकिन समाकलन की सीमाएँ निर्धारित करने से पहले समाकलन है (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6।
एकीकरण की सीमाएँ जोड़ने पर, उत्तर 126538525259 / 24067258815600 = 0.0052577040961964420049 है।



