इस पृष्ठ पर
प्रत्येक दांव के लिए हाउस एज कैसे प्राप्त किया जाता है
परिचय
क्रेप्स परिशिष्ट में आपका स्वागत है। यहीं से मैं क्रेप्स में सभी प्रमुख दांवों के लिए खिलाड़ी की बढ़त का आकलन करता हूँ। इस परिशिष्ट के अलावा, मैं आमतौर पर हाउस एज के बारे में बात करता हूँ, जो खिलाड़ी की बढ़त और -1 का गुणनफल होता है। हर दांव को -1 से गुणा करने से बचने के लिए, मैं हर चीज़ के बारे में खिलाड़ी की बढ़त के संदर्भ में बात करूँगा, जिसके नकारात्मक होने की उम्मीद की जा सकती है क्योंकि मुफ़्त ऑड्स को छोड़कर सभी दांवों पर अंततः हाउस की बढ़त होती है। कृपया थोड़ी देर रुकें और कुछ दांवों पर खुद काम करें। इससे न केवल आपको ऑड्स की गहरी समझ मिलेगी, बल्कि उम्मीद है कि यह आपको अपने गणित कौशल को ताज़ा करने या सुधारने के लिए प्रेरित करेगा।
आगे बढ़ने से पहले, आपको प्रत्येक योग को एक ही बार में फेंकने की प्रायिकता को समझना होगा। मेरे "पासा प्रायिकता मूल बातें" पृष्ठ पर इसकी विस्तार से व्याख्या की गई है। अगर आपको नहीं पता था या आप समझ नहीं पा रहे हैं कि 6 आने की प्रायिकता 5/36 है, तो इस पृष्ठ पर जाना अनिवार्य है।
किसी दांव पर अपेक्षित प्रतिफल का सामान्य सूत्र है:
∑ (घटना i की संभावना) × (घटना i की वापसी) सभी संभावित परिणामों पर।
खिलाड़ी की बढ़त, शुरुआती दांव से विभाजित अपेक्षित रिटर्न के बराबर होती है। उदाहरण के लिए, किसी खेल आयोजन में दांव लगाते समय, आपको $10 जीतने के लिए $11 का दांव लगाना होगा। जीतने की 50% संभावना मानते हुए, अपेक्षित रिटर्न 0.5×(10) + 0.5×(-11) = -0.5 होगा। खिलाड़ी की बढ़त -0.5/11 = -1/22 ≈ -4.545% होगी।
हाउस एज नियम का एक अपवाद तब होता है जब बराबरी संभव हो। आमतौर पर हाउस एज की गणना में बराबरी को नज़रअंदाज़ कर दिया जाता है। इसके लिए, जब बराबरी संभव हो, तो अपेक्षित रिटर्न को हल किए गए औसत दांव से भाग दें। "हल किया गया औसत दांव" प्रारंभिक दांव और दांव के हल होने की संभावना का गुणनफल होता है। क्रेप्स में, बराबरी वाली बाजी केवल "पास न करें" और "न करें" होती है।
क्रेप्स में कई दांव तब जीत जाते हैं जब एक विशेष घटना दूसरी घटना से पहले घटित होती है। इन दांवों को हल करने में कई या उससे ज़्यादा बार दांव लगाना पड़ सकता है। यदि कोई दांव p प्रायिकता से जीतता है, q प्रायिकता से हारता है, और 1-pq प्रायिकता के साथ सक्रिय रहता है, तो अंततः जीतने की प्रायिकता है:
∑ p×(1-pq) i (i=0 से अनंत तक) =
पी × (1/(1-(1-पीक्यू))) = पी × (1/(पी+क्यू)) = पी/(पी+क्यू)।
इस पूरे पृष्ठ पर आपको p/(p+q) के रूप के कई व्यंजक दिखाई देंगे। स्थान बचाने के लिए, मैं हर बार व्यंजक नहीं निकालता क्योंकि यह ऊपर बताया गया है।
पास/आओ
कम आउट रोल पर जीतने की संभावना pr(7)+pr(11) = 6/36 + 2/36 = 8/36 है।
एक बिंदु स्थापित करने और फिर जीतने की संभावना है pr(4)×pr(7 से पहले 4) + pr(5)×pr(7 से पहले 5) + pr(6)×pr(7 से पहले 6) + pr(8)×pr(7 से पहले 8) + pr(9)×pr(7 से पहले 9) + pr(10)×pr(7 से पहले 10) =
(3/36)×(3/9) + (4/36)×(4/10) + (5/36)×(5/11) + (5/36)×(5/11) + (4/36)×(4/10) + (3/36)×(3/9) =
(2/36) × (9/9 + 16/10 + 25/11) =
(2/36) × (990/990 + 1584/990 + 2250/990) =
(2/36) × (4824/990) = 9648/35640
जीतने की कुल संभावना 8/36 + 9648/35640 = 17568/35640 = 244/495 है
हारने की संभावना स्पष्ट रूप से 1-(244/495) = 251/495 है
इस प्रकार खिलाड़ी की बढ़त (244/495)×(+1) + (251/495)×(-1) = -7/495 ≈ -1.414% है।
पास मत करो/मत आओ
कम आउट रोल पर जीतने की संभावना pr(2)+pr(3) = 1/36 + 2/36 = 3/36 है।
बाहर आने वाले रोल पर धक्का देने की संभावना pr(12) = 1/36 है।
एक बिंदु स्थापित करने और फिर जीतने की संभावना है pr(4)×pr(4 से पहले 7) + pr(5)×pr(5 से पहले 7) + pr(6)×pr(6 से पहले 7) + pr(8)×pr(8 से पहले 7) + pr(9)×pr(9 से पहले 7) + pr(10)×pr(10 से पहले 7) =
(3/36)×(6/9) + (4/36)×(6/10) + (5/36)×(6/11) + (5/36)×(6/11) + (4/36)×(6/10) + (3/36)×(6/9) =
(2/36) × (18/9 + 24/10 + 30/11) =
(2/36) × (1980/990 + 2376/990 + 2700/990) =
(2/36) × (7056/990) = 14112/35640
जीतने की कुल संभावना 3/36 + 14112/35640 = 17082/35640 = 2847/5940 है
हारने की संभावना है 1-(2847/5940 + 1/36) = 1-(3012/5940) = 2928/5940
अपेक्षित रिटर्न 2847/5940×(+1) + 2928/5940×(-1) = -81/5940 = -3/220 ≈ 1.364% है
क्रेप्स के ज़्यादातर दूसरे स्रोत दावा करेंगे कि डोंट पास बेट पर हाउस एज 1.403% है। इस विसंगति का मूल कारण यह है कि टाई को गिना जाए या नहीं। मैं टाई को मनी बेट के रूप में गिनना पसंद करता हूँ और दूसरे नहीं। मैं यह नहीं कह रहा कि एक पक्ष सही है या गलत, बस मैं उन्हें गिनना पसंद करता हूँ।अगर आप बराबरी को मनी बेट नहीं मानते हैं, तो आपको ऊपर दिए गए आंकड़े को इस प्रायिकता से भाग देना चाहिए कि बेट जीत या हार में बदलेगी (35/36)। तो 1.364%/(35/36) ≈ -1.403%। यह हाउस एज है, यह मानते हुए कि खिलाड़ी कम आउट रोल पर कभी 12 नहीं रोल करता।
जीतने के लिए दांव लगाएँ
6 या 8 पर दांव लगाएं: [(5/11)×7 + (6/11)×(-6)]/6 = (-1/11)/6 = -1/66 ≈ -1.515%
5 या 9 पर दांव लगाएं: [(4/10)×7 + (6/10)×(-5)]/5 = (-2/10)/5 = -1/25 = -4.000%
4 या 10 पर दांव लगाएं: [(3/9)×9 + (6/9)×(-5)]/5 = (-3/9)/5 = -1/15 ≈ -6.667%
हारने के लिए दांव लगाएँ
6 या 8 पर हारने के लिए दांव लगाएं: [(6/11)×4 + (5/11)×(-5)]/5 = (-1/11)/5 = -1/55 ≈ -1.818%
5 या 9 पर हारने के लिए दांव लगाएं: [(6/10)×5 + (4/10)×(-8)]/8 = (-2/10)/8 = -1/40 = -2.500%
4 या 10 पर हारने के लिए दांव लगाएं: [(6/9)×5 + (3/9)×(-11)]/11 = (-3/9)/11 = -1/33 ≈ -3.030%
नोट: ज़मीनी कसीनो में इन दांवों की अनुमति नहीं है। ये केवल कुछ इंटरनेट कसीनो में ही उपलब्ध हैं।
खरीदना
6 या 8 पर खरीदें दांव: [(5/11)×23 + (6/11)×(-21)]/21 = (-11/11)/21 = -1/21 ≈ -4.762%
5 या 9 पर खरीदें दांव: [(4/10)×29 + (6/10)×(-21)]/21 = (-10/10)/21 = -1/21 = -4.762%
4 या 10 पर खरीदें दांव: [(3/9)×39 + (6/9)×(-21)]/21 = (-9/9)/21 = -1/21 ≈ -4.762%
बिछाना
6 या 8 पर हारने के लिए दांव लगाएं: [(6/11)×19 + (5/11)×(-25)]/25 = (-11/11)/25 = -1/25 ≈ -4.000%
5 या 9 पर हारने के लिए दांव लगाएं: [(6/10)×19 + (4/10)×(-31)]/31 = (-10/10)/31 = -1/31 = -3.226%
4 या 10 पर हारने के लिए दांव लगाएं: [(6/9)×19 + (3/9)×(-41)]/41 = (-9/9)/41 = -1/41 ≈ -2.439%
बिग 6/बिग 8
[(5/11)×1 + (6/11)×(-1)]/1 = -1/11 ≈ 9.091%
कठिन 4/कठिन 10
नोट: हार्ड 4 और हार्ड 10 में 7 से 1, या 8 के लिए 1 का भुगतान होता है। क्रेप्स में कपड़े पर बाधाओं को 1 के आधार पर सूचीबद्ध किया गया है, जिसमें ऊपर दिया गया ग्राफिक भी शामिल है।
किसी भी दिए गए रोल पर हार्ड 4 की संभावना 1/36 है।
किसी भी दिए गए रोल पर 7 आने की संभावना 6/36 है।
किसी भी दिए गए रोल पर सॉफ्ट 4 की संभावना 2/36 (1+3 और 3+1) है।
किसी भी दिए गए रोल पर जीतने की संभावना 1/36 है।
किसी भी दिए गए रोल पर हारने की संभावना 6/36 + 2/36 = 8/36 है।
शर्त जीतने की संभावना p/(p+q) (ऊपर देखें) = (1/36)/(9/36) = 1/9 है
अपेक्षित रिटर्न (1/9)×7 + (8/9)×(-1) = -1/9 ≈ 11.111% है।
खिलाड़ी की बढ़त भी -1/9 है क्योंकि दांव 1 इकाई का है।
हार्ड 10 के लिए भी संभावनाएं समान हैं।
कठिन 6/कठिन 8
नोट: हार्ड 4 और हार्ड 10 में 9 से 1, या 10 के लिए 1 का भुगतान होता है। क्रेप्स में कपड़े पर बाधाओं को 1 के आधार पर सूचीबद्ध किया गया है, जिसमें ऊपर दिया गया ग्राफिक भी शामिल है।
किसी भी दिए गए रोल पर हार्ड 6 आने की संभावना 1/36 है।
किसी भी दिए गए रोल पर 7 आने की संभावना 6/36 है।
किसी भी दिए गए रोल पर सॉफ्ट 6 की संभावना 4/36 (1+5, 2+3, 3+2, और 5+1) है।
किसी भी दिए गए रोल पर जीतने की संभावना 1/36 है।
किसी भी दिए गए रोल पर हारने की संभावना 6/36 + 4/36 = 10/36 है।
शर्त जीतने की संभावना p/(p+q) (ऊपर देखें) = (1/36)/(11/36) = 1/11 है
अपेक्षित रिटर्न (1/11)×9 + (10/11)×(-1) = -1/11 ≈ 9.091% है।
खिलाड़ी की बढ़त भी -1/11 है क्योंकि दांव 1 इकाई का है।
हार्ड 8 के लिए भी संभावनाएं समान हैं।
क्रेप्स 2/क्रेप्स 12
[(1/36)×30 + (35/36)×(-1)]/1 = -5/36 ≈ -13.889%
क्रेप्स 3/क्रेप्स 11
[(2/36)×15 + (34/36)×(-1)]/1 = -4/36 ≈ -11.111%
कोई भी क्रेप्स
[(4/36)×7 + (32/36)×(-1)]/1 = -4/36 ≈ -11.111%
कोई भी 7
[(6/36)×4 + (30/36)×(-1)]/1 = -6/36 ≈ -16.667%
सींग
2 या 12 आने की संभावना 1/36 + 1/36 = 2/36 है।
3 या 11 आने की संभावना 2/36 + 2/36 = 4/36 है।
किसी अन्य चीज के लुढ़कने की संभावना 1-2/36-4/36 = 30/36 है।
याद रखें कि हॉर्न बेट, क्रेप्स के चारों बेट्स को एक साथ मिलाने जैसा है। अगर एक जीत भी जाए, तो बाकी तीन फिर भी हार जाते हैं। हाउस एज है:
[(2/36)×27 + (4/36)×12 + (30/36)×(-4)]/4 = (-18/36)/4 = 12.500%
मैदान
जब 12 2:1 का भुगतान करता है तो अपेक्षित रिटर्न है:
2×(pr(2)+pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
2×(1/36 + 1/36) + 1×(2/36 + 3/36+ 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36+ 4/36) =
2×(2/36) + 1×(14/36) + -1×(20/36) = -2/36 = -1/18 ≈ 5.556%.
जब 12 3:1 का भुगतान करता है तो अपेक्षित रिटर्न है:
3×pr(2) + 2×pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
3×(1/36) + 2×(1/36) + 1×(2/36 + 3/36+ 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36+ 4/36) =
3×(1/36) + 2×(1/36) + 1×(14/36) + -1×(20/36) = -1/36 ≈ 2.778%.
खरीदने की संभावना
4 और 10: [(3/9)×2 + (6/9)×(-1)]/1 = 0.000%
5 और 9: [(4/10)×3 + (6/10)×(-2)]/2 = 0.000%
6 और 8: [(5/11)×6 + (6/11)×(-5)]/5 = 0.000%
बाधाएं लगाना
4 और 10: [(6/9)×1 + (3/9)×(-2)]/1 = 0.000%
5 और 9: [(6/10)×2 + (4/10)×(-3)]/2 = 0.000%
6 और 8: [(6/11)×5 + (5/11)×(-6)]/5 = 0.000%
संयुक्त पास और खरीद ऑड्स
संयुक्त पास और खरीद ऑड्स पर खिलाड़ी की बढ़त, औसत खिलाड़ी लाभ को औसत खिलाड़ी दांव से विभाजित करने पर प्राप्त होती है। पास लाइन पर लाभ हमेशा -7/495 होता है और ऑड्स पर लाभ हमेशा 0 होता है। अपेक्षित दांव इस बात पर निर्भर करता है कि आपको कितने ऑड्स की अनुमति है। मान लीजिए कि पूर्ण डबल ऑड्स हैं, या पास लाइन दांव $2 है, 4, 5, 9 और 10 पर ऑड्स दांव $4 है, और 6 या 8 पर ऑड्स $5 है।
औसत लाभ -2×(7/495) = -14/495 है।
औसत दांव 2 + (3/36)×4 + (4/36)×4 + (5/36)×5 + (5/36)×5 + (4/36)×4 + (3/36)×4] =
2 + 106/36 = 178/36
खिलाड़ी की बढ़त (-14/495)/(178/36) = -0.572% है।
यदि आप 6 और 8 पर x गुना, 5 और 9 पर y गुना, और 4 और 10 पर z गुना ऑड्स ले सकते हैं तो सामान्य सूत्र (-7 / 495) / [ 1 + ((5x + 4y + 3z) / 18) ] है
संयुक्त पास न करें और ऑड्स रखना
संयुक्त डोंट पास और लेइंग ऑड्स पर खिलाड़ी की बढ़त, खिलाड़ी के औसत लाभ को खिलाड़ी के औसत दांव से विभाजित करने पर प्राप्त होती है। डोंट पास पर लाभ हमेशा -3/220 होता है और ऑड्स पर लाभ हमेशा 0 होता है। अपेक्षित दांव इस बात पर निर्भर करता है कि आपको कितने ऑड्स की अनुमति है। मान लीजिए कि ऑड्स दोगुने हैं और डोंट पास बेट $10 है। तो खिलाड़ी 4 और 10 पर $20 की जीत के लिए $40, 5 और 9 पर $20 की जीत के लिए $30, और 6 और 8 पर $20 की जीत के लिए $24 का ऑड्स लगा सकता है। औसत लाभ -10×(3/220) = -30/220 है।
औसत दांव 10 + 2×[(3/36)×40 + (4/36)×30 + (5/36)×24] = 30 है।
खिलाड़ी की बढ़त (-30/220)/30 = -0.455% है।
सामान्य सूत्र यह है कि यदि आप x गुणा ऑड्स खरीद सकते हैं तो संयुक्त डोंट पास और लेइंग ऑड्स पर हाउस एज (3/220)/(1+x) है।
प्रति सत्र शुद्ध लाभ/हानि
नीचे दिया गया चार्ट 100 ट्रायल या कम आउट रोल्स में आपके द्वारा अपेक्षित शुद्ध लाभ या हानि को दर्शाता है। चार्ट बनाने के लिए, खिलाड़ी पास लाइन पर $1 का दांव लगाएगा और पूर्ण डबल ऑड्स लेगा।
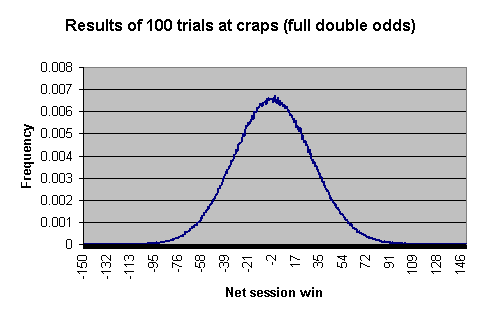
यहां कुछ वास्तविक संख्याएं दी गई हैं जो विभिन्न अंतरालों में गिरने की संभावना दर्शाती हैं।
सत्र जीत/हार
| अंतराल | संभावना |
|---|---|
| 100 डॉलर से अधिक का नुकसान | 0.0422% |
| $76-$100 का नुकसान | 0.6499% |
| $51-$75 का नुकसान | 4.6414% |
| $26-$50 का नुकसान | 16.3560% |
| $1-$25 का नुकसान | 30.0583% |
| ब्रेक - ईवन | 0.6743% |
| $1-$25 की जीत | 28.6368% |
| $26-$50 की जीत | 14.4257% |
| $51-$75 की जीत | 3.9097% |
| $76-$100 की जीत | 0.5639% |
| 100 डॉलर से अधिक की जीत | 0.0418% |
ग्राफ और तालिका 100 परीक्षणों के 1,000,000 सत्रों या कम आउट रोल्स का अनुकरण करके और प्रत्येक सत्र के परिणामों को सारणीबद्ध करके बनाई गई थी।
आंतरिक लिंक
- प्रत्येक दांव के लिए हाउस एज कैसे प्राप्त किया जाता है , संक्षेप में।
- प्रति-दांव और प्रति-रोल दोनों के आधार पर सभी प्रमुख दांवों का हाउस एज
- पासा नियंत्रण प्रयोग। कुशल पासा फेंकने पर दो प्रयोगों के परिणाम।
- पासा नियंत्रण लाभ। खिलाड़ी को लाभ, बशर्ते वह पासे को प्रभावित कर सके।
- क्रेप्स के प्रकार . वैकल्पिक नियम और दांव जैसे फायर बेट, क्रैपलेस क्रेप्स और कार्ड क्रेप्स।
- कैलिफोर्निया क्रेप्स . कैलिफोर्निया में ताश के पत्तों का उपयोग करके क्रेप्स कैसे खेला जाता है।
- क्रेप्स खेलें । सैन डिएगो में विएजस कैसीनो में कार्ड का उपयोग करके क्रेप्स गेम खेलें।
- रोल्स की संख्या तालिका . सात आउट से पहले एक शूटर के 1 से 200 रोल तक टिकने की संभावना।
- जादूगर से पूछो। देखिए मैंने किन बेकार सवालों के जवाब दिए हैं:
- सरल क्रेप्स खेल। मेरा सरल जावा क्रेप्स खेल।


