इस पृष्ठ पर
पासा संभावना
इस पृष्ठ पर
परिचय
कोई भी पासा खेलने से पहले, किसी भी दिए गए योग की प्रायिकता जानना ज़रूरी है। सबसे पहले, आइए दो पासों के योग की संभावनाओं पर नज़र डालें। नीचे दी गई तालिका बाएँ स्तंभ में पासा 1 की छह संभावनाएँ और ऊपर वाले स्तंभ में पासा 2 की छह संभावनाएँ दर्शाती है। तालिका का मुख्य भाग पासा 1 और पासा 2 का योग दर्शाता है।
दो पासों का योग
| मरो 1 | मरो 2 | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
तालिका के मुख्य भाग के रंग प्रत्येक योग को फेंकने के तरीकों की संख्या दर्शाते हैं। किसी भी दिए गए योग को फेंकने की प्रायिकता, उस योग को फेंकने के तरीकों की संख्या को संयोजनों की कुल संख्या (36) से विभाजित करके प्राप्त होती है। निम्नलिखित तालिका में प्रत्येक योग को फेंकने के विशिष्ट तरीकों की संख्या और उस योग को फेंकने की प्रायिकता दर्शाई गई है।
| कुल | की संख्या युग्म | संभावना |
|---|---|---|
| 2 | 1 | 2.78% |
| 3 | 2 | 5.56% |
| 4 | 3 | 8.33% |
| 5 | 4 | 11.11% |
| 6 | 5 | 13.89% |
| 7 | 6 | 16.67% |
| 8 | 5 | 13.89% |
| 9 | 4 | 11.11% |
| 10 | 3 | 8.33% |
| 11 | 2 | 5.56% |
| 12 | 1 | 2.78% |
| कुल | 36 | 100% |
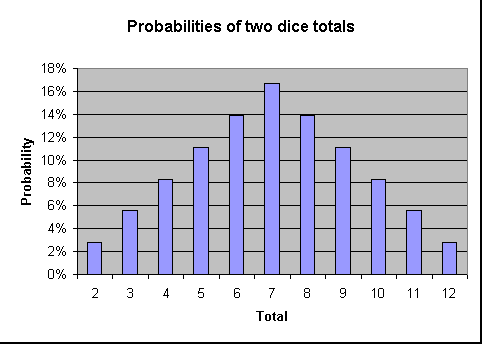
नीचे दिए गए चार्ट में प्रत्येक योग को फेंकने की संभावना दर्शाई गई है। जैसा कि चार्ट में दिखाया गया है, योग 7 के जितना करीब होगा, उसके फेंकने की संभावना उतनी ही अधिक होगी।
ऑनलाइन क्रेप्स कैसीनो बोनस सभी को देखें
फील्ड बेट उदाहरण
अब जब हम प्रत्येक योग को फेंकने की प्रायिकता समझ गए हैं, तो हम इस जानकारी को कैसिनो में पासों के खेल में हाउस एज की गणना के लिए लागू कर सकते हैं। उदाहरण के लिए, क्रेप्स में फ़ील्ड बेट पर विचार करें। यह बेट 1:1 (सम धन) के अनुपात में भुगतान करती है यदि अगली थ्रो 3, 4, 9, 10, या 11 हो, 2 पर 2:1 (बेट का दोगुना) और 12 पर 3:1 (बेट का तिगुना) हो। ध्यान दें कि 7 योग जीतते हैं और केवल 4 हारते हैं, जिससे कोई अनजान व्यक्ति यह सोच सकता है कि यह एक अच्छा जुआ था।
खिलाड़ी का रिटर्न प्रत्येक घटना की प्रायिकता और उस घटना के शुद्ध रिटर्न के गुणनफल के योग के रूप में परिभाषित किया जा सकता है। नीचे दी गई तालिका प्रत्येक संभावित योग, शुद्ध रिटर्न, उस कुल को फेंकने की प्रायिकता और औसत रिटर्न दर्शाती है। औसत रिटर्न, शुद्ध रिटर्न और प्रायिकता का गुणनफल होता है। खिलाड़ी का रिटर्न, औसत रिटर्न का योग होता है।
| कुल | शुद्ध रिटर्न | संभावना | औसत रिटर्न |
|---|---|---|---|
| 2 | 2 | 0.0278 | 0.0556 |
| 3 | 1 | 0.0556 | 0.0556 |
| 4 | 1 | 0.0833 | 0.0833 |
| 5 | -1 | 0.1111 | -0.1111 |
| 6 | -1 | 0.1389 | -0.1389 |
| 7 | -1 | 0.1667 | -0.1667 |
| 8 | -1 | 0.1389 | -0.1389 |
| 9 | 1 | 0.1111 | 0.1111 |
| 10 | 1 | 0.0833 | 0.0833 |
| 11 | 1 | 0.0556 | 0.0556 |
| 12 | 3 | 0.0278 | 0.0834 |
| कुल | 1 | -0.0278 |
आखिरी पंक्ति खिलाड़ी के रिटर्न को -.0278 दर्शाती है, दूसरे शब्दों में, हर $1 के दांव पर खिलाड़ी 2.78 सेंट के नुकसान की उम्मीद कर सकता है। खिलाड़ी का नुकसान घर के लाभ के बराबर है, इसलिए घर का लाभ -1 और खिलाड़ी के रिटर्न का गुणनफल है, इस मामले में 0.0278 या 2.78%।
दो से अधिक पासों के योग की संभावनाओं के लिए कृपया 1 से 25 पासों के लिए मेरी संभावनाओं वाले अनुभाग को देखें।
ओहियो अनुशंसित ऑनलाइन कैसीनो
सभी को देखें
$11,000 तक बोनस
सभी अमेरिकी खिलाड़ियों का स्वागत है
200 से अधिक कैसीनो खेल
पीसी या मोबाइल पर खेलें
$3000 तक बोनस
कैसीनो और स्पोर्ट्सबुक
केवल अमेरिकी खिलाड़ियों के लिए
डेस्कटॉप या मोबाइल पर चलाएँ
777$ तक बोनस
बड़ा स्वागत बोनस
दैनिक कैसीनो टूर्नामेंट
लोकप्रिय खेल
$7777 + 300 मुफ़्त स्पिन
लाइव डीलर गेम्स
दैनिक निःशुल्क टूर्नामेंट
मोबाइल और डेस्कटॉप के अनुकूल