रूले - सामान्य प्रश्न
अगर कोई रूलेट में दो कॉलम पर दांव लगाए, तो जीतने की संभावना 24/38, यानी 63% होगी। मुझे तो यह एक जीतने वाली रणनीति लगती है, आपकी क्या राय है?
रूलेट में किसी भी दांव या दांवों के संयोजन में उच्च हाउस एज होता है। आपके जीतने की संभावना जितनी अधिक होगी, आपको इनाम के सापेक्ष उतना ही अधिक जोखिम उठाना होगा। यदि आप ऐसा 10 बार करते हैं, तो लाभ दिखाने की संभावना 46.42% है। 100 बार करने पर यह संभावना घटकर 24.6% हो जाती है।
मुझे कैंसिलेशन बेटिंग सिस्टम पर आपका लेख पसंद आया। अगर आप काले या लाल पर दांव लगाने के बजाय, तीन में से दो ब्लॉकों पर दांव लगाते हैं, जिनमें 12 नंबर (जैसे: 1 से 12 और 25 से 36) होते हैं, तो आप किस तरह की कैंसिलेशन सिस्टम अपनाएँगे?
जैसा मैंने सम-धन वाले दांवों के साथ समझाया था, वैसे ही शुरुआत करें। प्रत्येक दांव बाएँ और दाएँ संख्याओं का योग होना चाहिए। हालाँकि, अपनी दो-स्तंभ वाली रणनीति का पालन करते हुए, हारने पर आपको दाएँ पक्ष में दोगुनी राशि जोड़नी चाहिए।
www.ccc-casino.com पर बिना शून्य वाला रूलेट है, जिसे वे सुपर चांस रूलेट कहते हैं। क्या कोई ऐसी प्रणाली है जो प्रभावी हो, क्योंकि शून्य है ही नहीं? शून्य के बिना क्या कोई एक ही समय में काला और लाल दोनों खेल सकता है, क्योंकि शून्य का कोई डर नहीं है?
मैंने इसे अभ्यास मोड में खेला और यह एक वैध नो-ज़ीरो रूलेट व्हील प्रतीत होता है। ऐसा कोई सिस्टम नहीं है जो लंबे समय में इस खेल को हरा सके या हरा सके। आप जितना ज़्यादा खेलेंगे, कुल दांव राशि और कुल जीत का अनुपात उतना ही शून्य के करीब होता जाएगा।
अद्यतन: यह कैसीनो अब बंद हो चुका है।
आपके लिए दो प्रश्न:
1) बुनियादी ब्लैकजैक रणनीतियों के बारे में, आपके पास अलग-अलग ऑनलाइन कैसीनो समूहों के लिए कुछ रणनीतियाँ हैं। खास तौर पर, दो अलग-अलग समूह जो दोनों सिंगल डेक का इस्तेमाल करते हैं: माइक्रोगेमिंग और यूनिफाइड गेमिंग। मुझे समझ नहीं आ रहा कि आपने माइक्रोगेमिंग के लिए 11 बनाम 10 को हिट क्यों बताया, जबकि यूनिफाइड के लिए डबल। चूँकि दोनों ही सिंगल डेक का इस्तेमाल करते हैं, इसलिए लगता है कि यहाँ भी यही रणनीति अपनाई जानी चाहिए। जब मैं इसे डबल करता हूँ, तो मैं जीतने की बजाय ज़्यादा बार हारता हूँ।
2) रूलेट में, मुझे लगता है कि लाल और तीसरे कॉलम, या काले और तीसरे कॉलम, दोनों पर बराबर दांव लगाने पर आपकी संभावनाएँ बेहतर होंगी। मेरा मानना है कि तीसरे कॉलम में 8 लाल और केवल 4 काले हैं। इसके विपरीत, पहले कॉलम में ज़्यादा काले हैं। क्या इस तरह दांव लगाने से हाउस एज कम होता है?
अगर आप माइक्रोगेमिंग कैसीनो में 11 पर डबल करते हैं और डीलर को ब्लैकजैक मिलता है, तो आप पूरी शर्त हार जाएँगे। यूनिफाइड गेमिंग में, अगर ऊपर वाला कार्ड दस का हो, तो ब्लैकजैक तुरंत पलट दिया जाता है, इसलिए ऐसी स्थिति में डबल करने पर ब्लैकजैक हारने का कोई जोखिम नहीं होता।
रूलेट में दांव के सभी संयोजन समान अपेक्षित रिटर्न देते हैं, यह मानते हुए कि खतरनाक पांच-संख्या संयोजन से बचा जाता है। आप सही हैं कि तीसरे कॉलम में आठ लाल और चार काले हैं। 3 इकाइयां जीतने की संभावना 8/38 है, 1 इकाई 4/38 है, यहां तक कि 10/38 है, और 2 इकाइयां खोना 16/38 है। प्रति इकाई दांव पर अपेक्षित संयुक्त रिटर्न (1/2) * (3 * 8 + 1 * 4 + 0 * 10 + 2 * 16) / 38 = -2/38 है। काले और तीसरे कॉलम पर दांव लगाने पर 3 इकाइयां जीतने की संभावना 4/38 है, 1 इकाई 8/38 है, यहां तक कि 14/38 है, और 2 इकाइयां खोना 12/38 है। अपेक्षित रिटर्न (1/2) * (3 * 4 + 1 * 8 + 0 * 14 + 2 * 12) / 38 = -2/38 है। दोनों संयोजन विभिन्न परिणामों को अलग-अलग महत्व देते हैं, लेकिन उनका औसत एक ही संख्या होता है।
हे विज़! मैं जानना चाहता हूँ कि अमेरिकन रूलेट व्हील में सभी 38 संख्याओं को कम से कम एक बार चुनने से पहले कितने घुमाव अपेक्षित हैं। क्या यह चयनों की संख्या (38) के समानुपाती है या यह इस संख्या से चरघातांकी रूप से संबंधित है? मैंने इसे 6-पक्षीय पासे के लिए समझने की कोशिश की, लेकिन जल्दी ही अटक गया।
एक बार जब आप n संख्याएँ प्राप्त कर लेते हैं, तो अगले स्पिन पर एक नई संख्या प्राप्त होने की प्रायिकता (38-n)/38 होती है। यदि किसी घटना की प्रायिकता p है, तो उसके घटित होने से पहले अपेक्षित प्रयासों की संख्या 1/p है। इस प्रकार, यदि आपके पास पहले से ही n संख्याएँ हैं, तो एक नई संख्या प्राप्त करने के लिए अपेक्षित स्पिनों की संख्या 38/(38-n) है। उदाहरण के लिए, एक बार जब आप 20 संख्याएँ प्राप्त कर लेते हैं, तो 21वीं संख्या प्राप्त करने के लिए अपेक्षित स्पिनों की संख्या 38/18=2.11 है। अतः उत्तर प्रत्येक चरण पर अपेक्षित स्पिनों की संख्या का योग है: (38/38)+(38/37)+(38/36)+...+(38/1)=160.66।
रूलेट में लगातार 18 बार लाल संख्या आने की संभावना क्या होगी?
(18/38) 18 =~ 693745 में 1.
छोटी स्टील की गेंदों की याददाश्त न होने के बारे में आपकी टिप्पणी पढ़कर मैं हैरान रह गया। मेरे घर पर एक रूलेट व्हील है और जब मैं अस्पताल से घर आता हूँ तो ये छोटी गेंदें खुशी से उछलती-कूदती हैं। ज़ाहिर है ऐसा इसलिए है क्योंकि वे मुझे याद रखती हैं, और मुझे लगता है कि आपकी बात से वे नाराज़ भी होंगी। मेरे ग्रह पर रूलेट खेलने की इजाज़त नहीं है क्योंकि इन छोटी गेंदों को आसानी से रिश्वत दी जा सकती है। मुझे लगता है कि आपके ग्रह से बदबू आ रही है और अब मैं घर वापस जाने के लिए अपने अंतरिक्ष यान की मरम्मत नहीं करवा सकता।
ओह, और मेरे पीछे सफ़ेद कोट वाला आदमी कहना चाहता है कि उसे आपकी वेबसाइट बहुत पसंद है और गणित दिखाने के लिए आपने जो मेहनत की है, उसके लिए वह आपका आभारी है। उसका कहना है कि इससे उसका बहुत समय और पैसा बचा है। अच्छा काम करते रहो।
मुझे खुशी है कि मैंने सफ़ेद कोट वाले मुख्य व्यक्ति की मदद की। मेरी रूलेट सलाह पृथ्वी पर खेलों तक सीमित है, आपके ग्रह पर रिश्वतखोरी की सलाह दी जाती है।
मैंने 0,00 व्हील पर लगातार 1000 बार एक ही नंबर खेला और 6 बार हिट हुआ। इस स्थिति में 6 या उससे कम बार हिट होने की क्या संभावना है?
आपके नंबर के ठीक x बार हिट होने की प्रायिकता combin(1000,x)*(1/38) x *(37/38) 1000-x है। निम्न तालिका 0 से 6 तक सभी हिट की संख्या और कुल की प्रायिकता दर्शाती है।
1000 रूलेट दांवों में जीत
| संख्या | संभावना |
| 0 | 0.00000000000262 |
| 1 | 0.00000000007078 |
| 2 | 0.00000000095556 |
| 3 | 0.00000000859146 |
| 4 | 0.00000005787627 |
| 5 | 0.00000031159330 |
| 6 | 0.00000139655555 |
| कुल | 0.00000177564555 |
तो जवाब है 0.00000177564555, या 563175 में 1। मुझे उम्मीद है कि यह किसी इंटरनेट कैसीनो में नहीं हुआ होगा।
आप सोच रहे होंगे कि मैंने ऊपर दिए गए सिक्के उछालने के सवाल में सामान्य सन्निकटन का इस्तेमाल क्यों नहीं किया। ऐसा इसलिए क्योंकि यह बहुत ज़्यादा और बहुत कम संभावनाओं के साथ ठीक से काम नहीं करता।
हाय माइक, माहौल को थोड़ा हल्का करने के लिए, मुझे याद है कि कुछ समय पहले मैंने आपको एक खास वेगास चैलेंज शो में रूलेट खेलते हुए देखा था। ज़ाहिर है आपको पता था कि आपकी रणनीति चाहे जो भी हो, आपका अपेक्षित मूल्य नहीं बदलेगा। मुझे याद है कि आप सिर्फ़ एक ही नंबर पर दांव लगाते थे, लेकिन मुझे याद नहीं कि जीतने के बाद आप बदलते थे या नहीं। मुझे नहीं पता कि आपकी स्थिति में मैं क्या करता, लेकिन जिज्ञासावश, क्या आपने विचरण को अधिकतम करने के लिए लाल/काले जैसे बाहरी दांव के बजाय एक ही नंबर पर दांव लगाया था? इस तरह अगर आप "भाग्यशाली" रहे तो आप सबसे ज़्यादा आगे रहेंगे? खैर, मुझे यह बात अच्छी लगी कि आपने वाकई एक रूढ़िवादी और उबाऊ रणनीति अपनाई।
आपने मेरी रणनीति को काफ़ी अच्छी तरह से समझा। मैंने ज़्यादातर समय न्यूनतम दांव लगाने का इरादा किया था ताकि हाउस एज मुझे परेशान न करे। निर्माता इस उबाऊ रणनीति से खुश नहीं था, इसलिए मैंने सामान्य से ज़्यादा उत्साहित होने का नाटक करने की कोशिश की। मैंने सम राशि के दांव के बजाय एक ही संख्या चुनी क्योंकि मैं अस्थिरता चाहता था। मुझे पता था कि अगर मैं $10,000 के अपने शुरुआती बिंदु के करीब पहुँच गया, तो शायद मैं हार जाऊँगा। इसलिए मैं आगे निकलने के लिए एक बड़ा मौका चाहता था। मैं पूरे समय 23 पर टिका रहा, हालाँकि अंत में मैंने 5 भी जोड़ दिए। मुझे खुशी है कि आपको शो पसंद आया।
मेरा सवाल ज़्यादातर आपके अवलोकनों और मेरे द्वारा सुनी गई अफवाहों पर आधारित है। अगर यह सच है कि लास वेगास के डीलर, जब उन्हें डीलर स्कूल में पढ़ाया जाता है, तो गेंद को उसी तरह घुमाना और रोल करना सीखते हैं, तो क्या यह सच है कि डीलर के घूमने के तरीके को देखकर, कोई यह तय कर सकता है कि गेंद पहिये के किस चतुर्थांश पर गिरेगी?
नहीं। डीलरों को सिर्फ़ बुनियादी बातें सिखाई जाती हैं, और उन्हें ज़्यादा कुशल नहीं बनाया जाता। दरअसल, अगर डीलर के पास इतना नियंत्रण होता, तो वह आसानी से अपने किसी साथी से गेंद को जहाँ भी गिराने की योजना बनाता, वहाँ दांव लगवा सकता था और आसानी से लाखों कमा सकता था।
यूरोपियन रूलेट पर 15 स्पिन खेलने, आठ नंबरों को कवर करने और उनमें से किसी को भी न पाने की संभावना क्या है?
किसी एक स्पिन के हारने की संभावना 1-(8/37) = 78.38% है। इसलिए 15 स्पिन हारने की संभावना .7838 15 = 2.59% है।
मैं जानना चाहता हूँ कि ऑनलाइन रूलेट गेम का परीक्षण कैसे किया जाता है, बाधाओं को कैसे जाना जाता है और क्या बाधाएं ईमानदार हैं?
सबसे पहले मैं आपको बता दूँ कि किसी भी खेल का परीक्षण कैसे नहीं करना चाहिए। आपको अपना पूरा खेल रिकॉर्ड नहीं करना चाहिए और जब आप खेल खत्म कर लें, तो किसी भी तरह की गड़बड़ी की जाँच करें, और फिर मुझे शिकायत लिखकर बताएं कि कैसीनो धोखाधड़ी कर रहा है। सही तरीका यह है कि पहले कैसीनो कैसे धोखाधड़ी कर रहा है, इसकी एक परिकल्पना बताएँ, फिर आँकड़े इकट्ठा करें, और अंत में देखें कि क्या आँकड़े आपकी परिकल्पना से मेल खाते हैं। अगर आपको समझ नहीं आ रहा है कि किस तरह की परिकल्पना बतानी है, तो मेरा सुझाव है कि आप बस जीत और हार की संख्या का परीक्षण करें, और फिर हर बार एक ही दांव लगाएँ। अगर आप पहले दो चरणों को ठीक से करते हैं और तीसरे चरण में मदद की ज़रूरत है, तो बेझिझक मुझे लिखें।
जब मैं $100 लेकर किसी कैसीनो में जाता हूँ और रूलेट खेलता हूँ, तो मैं 4% कम के साथ नहीं, बल्कि 25% कम के साथ बाहर निकलने की उम्मीद करता हूँ। क्या इस घटना का कोई औपचारिक नाम है? (मैं "रियल हाउस एज" गूगल कर रहा था) क्या इस "रियल हाउस एज" का अनुमान लगाने का कोई सूत्र/मॉडल है? इस पैरामीटर में कौन से खेल बेहतर हैं और कौन से खराब?
आपके उदाहरण में, कैसीनो का होल्ड 75% है। यह खिलाड़ियों द्वारा जीते गए चिप्स के मूल्य और डीलर द्वारा बॉक्स में डाली गई राशि का अनुपात है। हालाँकि ऐतिहासिक औसत मौजूद हैं, लेकिन हाउस एज से होल्ड तक जाने का कोई तरीका नहीं है। होल्ड आंशिक रूप से इस बात पर निर्भर करता है कि खिलाड़ी अपने चिप्स को कितनी देर तक घुमाता रहेगा, और यह जानने का कोई तरीका नहीं है।
अगर मेरे पास $200 का बैंकरोल है जिसे खोने से मुझे कोई फ़र्क़ नहीं पड़ता, और मैं यूरोपियन (सिंगल-ज़ीरो) रूलेट में एक ही नंबर पर $10 लगाता रहूँ, तो जीतने की क्या संभावना है, $200, $500 या $1000? मान लीजिए कि मैं लक्ष्य तक पहुँचने के बाद रुक जाऊँगा। शुक्रिया, बहुत बढ़िया साइट है, आप चाहते थे कि मैं इसे छोटा रखूँ :)
तारीफ़ के लिए शुक्रिया। इस तरह के सवालों के लिए एक सूत्र है, जिसे मैं अपनी साइट www.mathproblems.info पर समझाता हूँ, समस्या 116 देखें।
b इकाइयों के बैंकरोल, g इकाइयों के विजयी लक्ष्य, जीतने की प्रायिकता p, और हारने की प्रायिकता q के साथ, आपकी सफलता की प्रायिकता ((q/p) b -1)/((q/p) b+g -1) है। इस स्थिति में b=20, p=18/37, q=19/37, और g=20, 50, और 100 है। अतः $200 के बैंकरोल के लिए प्रायिकता ((19/18) 20 -1)/((19/18) 40 -1) = 0.253252 है।
500 डॉलर के विजयी लक्ष्य के लिए संभावना ((19/18) 20 -1)/((19/18) 70 -1) = 0.045293 है।
1,000 डॉलर के विजयी लक्ष्य के लिए संभावना ((19/18) 20 -1)/((19/18) 120 -1) = 0.002969 है।
38 नंबर वाले रूलेट व्हील पर....तीन लाल, एक हरा और फिर एक और लाल आने के बाद....क्या संभावना है कि अगले तीन घुमावों में लाल 23 आएगा?
इससे कोई फ़र्क़ नहीं पड़ता कि पिछली बार क्या स्पिन हुए थे। लगातार तीन बार लाल 23 आने की संभावना (1/38) 3 = 54,872 में 1 में 1 है।
मैंने बोडोग जाकर उनकी मुफ़्त साइट पर उनका रूलेट व्हील आज़माया। ऊपरी कोने में एक बॉक्स में पिछले दस नंबर दर्ज हैं जो आए थे। मुझे यकीन है कि मैंने इसे 20 से कम बार घुमाया होगा। वहाँ दर्ज नंबर इस प्रकार हैं: 9-9-29-21-11-11-20-28-32-1 दिलचस्प बात यह है कि इससे दो चक्कर पहले 32 पर एक और हिट हुआ था। यानी 9, 11 और 32, ये सभी नंबर 12 चक्करों के अंदर दो बार आए। जैसा कि मैंने कहा, मैं कोई सांख्यिकीविद् नहीं हूँ, लेकिन इन तीन नंबरों की आवृत्ति और मेरे द्वारा व्हील घुमाए जाने की न्यूनतम संख्या, यह दर्शाती है कि कुछ गड़बड़ है।
बारह स्पिनों में तीन युग्मों और छह एकलकों की प्रायिकता कॉम्बिन (38,3) × कॉम्बिन (35,6) × कॉम्बिन (12,2) × कॉम्बिन (10,2) × कॉम्बिन (8,2) × तथ्य (6)/38 12 = 9.04% है। कुल 20 स्पिनों में से किसी भी 12 स्पिन अवधि में ऐसा होने की प्रायिकता के बारे में पूछने पर गणित थोड़ा उलझ जाता है। इतना कहना ही काफी है कि यह 9% से कहीं ज़्यादा है, मेरे अनुमान से ज़्यादा संभावना है। इसलिए ये मुझे बहुत सामान्य परिणाम लगते हैं।
मेरे शहर का एक कसीनो, सिंगल-ज़ीरो रूलेट व्हील पर, उस दिन के लिए एक निश्चित संख्या पर, सीधे दांव लगाने पर 36 से 1 का भुगतान कर रहा है। उदाहरण के लिए, महीने की 8 तारीख को वह संख्या 8 है। इससे हाउस एज में क्या बदलाव आता है? आपकी मदद के लिए धन्यवाद।
निर्दिष्ट संख्या पर हाउस एज ठीक 0% होगी।
ऑरलियन्स में रूलेट में एक साइड बेट है जिसमें लगातार तीन लाल (या काले) कार्ड पर 8 से 1 का भुगतान होता है। यह डबल-ज़ीरो व्हील पर होता है। क्या आप मुझे ऑड्स बता सकते हैं?
जीतने की संभावना (18/38) 3 = 10.63% है। हाउस एज 8×0.1063 - 1×0.8937 = 4.34% है, जो बाकी सभी दांवों के 5.26% से कम है (खतरनाक 0,00,1,2,3 संयोजन को छोड़कर, जो 7.89% है)।
हॉलैंड में कुछ कैसीनो रूलेट में ट्रिपल प्रिज़नशिप की अनुमति देते हैं। उस नियम के तहत सम-धन दांव पर हाउस एज क्या है? मुझे जवाब से ज़्यादा समाधान में दिलचस्पी है।
अन्य पाठकों की सुविधा के लिए, यूरोप के कई कैसीनो में, अगर आप रूलेट में सम राशि का दांव लगाते हैं और गेंद शून्य पर गिरती है, तो दांव रद्द हो जाता है। अगर अगली बार दांव जीतने का कारण बनता है, तो दांव बिना जीत के वापस कर दिया जाता है। अगर गेंद विपरीत दिशा में गिरती है, तो दांव हार जाता है।
अगर गेंद शून्य पर गिरती है, तो एकल-कैद वाली बाजी का क्या होगा? अगर कैसीनो केवल एकल-कैद की अनुमति देता है, तो वह हार जाएगा। हालाँकि, कुछ कैसीनो दोहरे-कैद की अनुमति देते हैं, और यही होगा। अगर दोहरे-कैद वाली बाजी जीत जाती है, तो वह एकल-कैद वाली बाजी में बदल जाएगी। अगर कैसीनो केवल दोहरे-कैद तक की अनुमति देता है, तो दोहरे-कैद वाली बाजी एक और शून्य पर हार जाएगी। इसी तर्क से, अगर कैसीनो तिहरे-कैद की अनुमति देता है, तो दोहरे-कैद वाली बाजी एक और शून्य पर तिहरे-कैद वाली बाजी बन जाएगी।
ट्रिपल प्रिज़नेशन के तहत हाउस एज 1.370120% है। इससे पहले कि मैं बताऊँ कि मैं इस नतीजे पर कैसे पहुँचा, आइए पहले सिंगल और डबल प्रिज़नेशन पर गौर करें। मान लीजिए पहला दांव लाल पर है।
मान लीजिए Z = शून्य की संभावना = 1/37.
मान लीजिए R = लाल संख्या की प्रायिकता = 18/37.
एकल कारावास
पीआर(पुश) = ZR = 0.0131482834.
पीआर(जीत) = आर = 0.4864864865.
पीआर(नुकसान) = 1-पीआर(पुश)-पीआर(जीत) = 0.5003652301।
अपेक्षित मूल्य = pr(जीत)-pr(हानि) = -0.0138787436.
दोहरा कारावास
अगर पहला स्पिन शून्य आता है, तो खिलाड़ी पुश करेगा, फिर खिलाड़ी ZR को 0 से लेकर अनंत बार दोहरा सकता है, और फिर लाल कार्ड प्राप्त कर सकता है। दूसरे शब्दों में, पुश करने के ये तरीके हैं:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
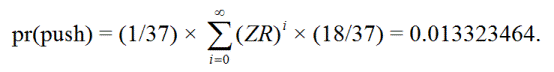
पीआर(पुश) = 0.013323464
पीआर(जीत) = 18/37 = 0.4864864865.
पीआर(नुकसान) = 1-पीआर(पुश)-पीआर(जीत) = 0.5001900494।
अपेक्षित मूल्य = pr(जीत)-pr(हानि) = -0.0137035629.
तिहरा कारावास
सबसे पहले, आइए प्रायिकता p 1 ज्ञात करें कि एक एकल कैद वाली शर्त दो और शून्यों के साथ तिगुनी कैद हो जाती है, और फिर अंततः वापस एकल कैद हो जाती है। यह इस प्रकार हो सकता है:
ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ...
दूसरे शब्दों में, शर्त तिगुनी और दोहरी कैद के बीच अनंत बार तक उछल सकती है।
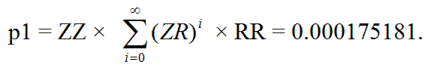
दूसरा, मान लें कि p 2 = संभावना है कि एक एकल कैद शर्त कारावास के पहले या दूसरे स्तर तक पहुंचती है और फिर एकल कारावास में वापस आती है।
मान लीजिए p 2 = ZR + p 1 = 0.013323464.
खिलाड़ी शून्य से लेकर अनंत बार तक पहले स्तर पर वापस आ सकता है। इसलिए, पुश की संभावना है:
जेडआर + जेड पी 2 आर + जेड पी 2 पी 2 आर + जेड पी 2 पी 2 पी 2 आर + ... =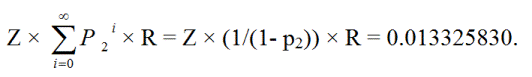
Z × (1/(1- p 2 )) × R = 0.013325830.
पीआर(पुश) = 0.013325830.
पीआर(जीत) = 18/37 = 0.4864864865.
पीआर(नुकसान) = 1-पीआर(पुश)-पीआर(जीत) = 0.5001876839।
अपेक्षित मूल्य = pr(जीत)-pr(हानि) = -0.0137011974.
अनंत कारावास
ऐसा नहीं है कि आपने पूछा, माफ़, लेकिन मैंने सुना है कि स्पेन में अनंत कारावास की अनुमति है। मान लीजिए p = धक्का लगने की संभावना। यह कारावास के स्तर x से शुरू होने, स्तरों में और नीचे गिरने, लेकिन अंततः x तक वापस चढ़ने की भी संभावना है।
पी = ZR + ZpR + ZppR + ZpppR + ...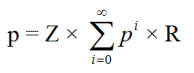
पी 2 - पी + जेडआर = 0
द्विघात सूत्र द्वारा p = (1-(1-4*RZ) 1/2 )/2 = 0.0133258620.
पीआर(पुश) = 0.0133258620.
पीआर(जीत) = 18/37 = 0.4864864865.
पीआर(नुकसान) = 1-पीआर(पुश)-पीआर(जीत) = 0.5001876515।
अपेक्षित मूल्य = pr(जीत)-pr(हानि) = -0.0137011650.
शून्यों ने कारावास की अनदेखी की
अंत में, कुछ कैसिनो में पहले शून्य के बाद शून्य को अनदेखा कर दिया जाता है, जिससे दांव बंध जाता है। वहाँ पुश की संभावना बस (1/37)×(1/2) = 0.0135135135 है।
निम्नलिखित तालिका में सभी चार प्रकार के नियमों का सारांश दिया गया है।
कारावास की संभावना
| कैद होना | जीतना | धकेलना | नुकसान | अपेक्षित कीमत |
| अकेला | 0.48648649 | 0.01314828 | 0.50036523 | -0.01387874 |
| दोहरा | 0.48648649 | 0.01332346 | 0.50019005 | -0.01370356 |
| ट्रिपल | 0.48648649 | 0.01332583 | 0.50018768 | -0.01370120 |
| अनंत | 0.48648649 | 0.01332586 | 0.50018765 | -0.01370117 |
| शून्यों की अनदेखी | 0.48648649 | 0.01351351 | 0.50000000 | -0.01351351 |
मैं चेस्टरडॉग और वीज़लमैन को उनकी गणितीय मदद के लिए धन्यवाद देना चाहता हूँ। मैं ऊपर दिए गए योग सूत्र के HTML के लिए प्रोफ़ेसर जी. आर्टिको और polarprof.it को भी धन्यवाद देना चाहता हूँ।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
क्या रूलेट व्हील पर संख्याओं के क्रम का कोई पैटर्न है?


विचार यह है कि पहिया संतुलित होना चाहिए। दूसरे शब्दों में, यदि आप पहिये पर क्रमागत संख्याओं के एक भाग का औसत निकालें, तो वे औसत संख्या 18.5 के करीब होंगे। मैंने दोहरे शून्य वाले पहिये पर संख्याओं के वितरण को समझाने का एक तरीका सोचा, जो इस प्रकार है।
- 00 को 12:00 बजे की स्थिति पर तथा 0 को 6:00 बजे की स्थिति पर रखें।
- पहिये के शीर्ष पर संख्याएं 13, 1, 00, 27, 10*, 25 हैं। इसे बस याद रखना होगा।
- सभी कम विषम संख्याएं (1 से 17 तक) बाईं ओर हैं और उच्च विषम संख्याएं (19 से 35 तक) दाईं ओर हैं।
- 1 और 13 से शुरू करते हुए, अगला विषम अंक प्राप्त करने के लिए चार स्थान वामावर्त आगे बढ़ें, लेकिन शून्य से आगे न बढ़ें।
- नियम 4 के अपवाद के रूप में, 19 को 17 से वामावर्त दिशा में न रखें, क्योंकि 19 एक उच्च विषम संख्या है और दाईं ओर स्थित है। इसके बजाय, 11 रखें, जो एकमात्र निम्न विषम संख्या है जो नियम 4 में शामिल नहीं है।
- सभी सम संख्याएं पहिये के ठीक सामने, पिछली विषम संख्या से 180 डिग्री पर होती हैं।
मैं एकल-शून्य पहिये पर क्रम समझाने में असमर्थ हूँ। फ़िलहाल, मैं इतना कह सकता हूँ कि अगर आप शून्य को 12:00 की स्थिति में रखें, तो:
- बायीं ओर सभी लाल निम्न संख्याएं और काली उच्च संख्याएं होंगी।
- दाहिनी ओर सभी लाल उच्च संख्याएं और काली निम्न संख्याएं होंगी।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
मैंने डबल-ज़ीरो रूलेट में 3,000 बार स्पिन किए क्योंकि पहले दर्जन नंबर दूसरे दो दर्जन के मुकाबले कम आए। 3,000 स्पिन में, 1 से 12 तक की संख्याएँ 742 बार आईं। इसकी संभावना क्या है?
आप उम्मीद करेंगे कि 1 से 12 तक गेंद कितनी बार गिरेगी, 3000*(12/38) = 947.37 होगी।
आपके परिणामों और अपेक्षाओं के बीच का अंतर 947.37 - 742 = 205.37 है।
विचरण 3000*(12/38)*(1-(12/38)) = 648.20 है।
मानक विचलन विचरण का वर्गमूल है = sqrt(648.20) = 25.46.
आपके परिणाम 205.37/25.46 = 11.75 मानक विचलन हैं जो अपेक्षाओं से कम हैं।
p मान, या 11.75 मानक विचलन या उससे अधिक से दूर होने की संभावना 28,542,806,257,940,300,000,000,000,000,000 में 1 है।
मुझे यह जानने में दिलचस्पी होगी कि पहिया कहां है।
इस वीडियो में बताई गई कॉम्प किलर रूलेट रणनीति के बारे में आपकी क्या राय है?
यह समझना आसान है कि इस प्रणाली का उद्देश्य ज़्यादातर संख्याओं को कवर करना है, इसलिए यह रूलेट खेलने का एक कम जोखिम वाला तरीका है। हर स्पिन पर क्या दांव लगाना है, यहाँ बताया गया है:
- 3, 16, 24, 28, और 33 पर 5 डॉलर प्रति व्यक्ति।
- संख्याओं के इन सेटों में से प्रत्येक पर एक कॉर्नर बेट लगाएं: 2/3/5/6, 7/8/10/11, 14/15/17/18, 19/20/22/23, 26/27/29/30, 31/32/34/35.
ध्यान दें कि इसमें निम्नलिखित नौ संख्याएँ शामिल नहीं हैं: 0, 00, 4, 9, 12, 13, 21, 25, और 36।
निम्नलिखित रिटर्न तालिका सभी संभावित परिणामों की वापसी में संभावना और योगदान को दर्शाती है।
कॉम्प किलर
| आयोजन | नेट जीत | युग्म | संभावना | वापस करना |
|---|---|---|---|---|
| सीधी जीत | 5 | 5 | 0.131579 | 0.657895 |
| कॉर्नर जीत | 50 | 24 | 0.631579 | 31.578947 |
| अन्य सभी | -175 | 9 | 0.236842 | -41.447368 |
| कुल | 38 | 1.000000 | -9.210526 |
निचले दाएँ सेल में प्रति स्पिन $9.21 का अपेक्षित नुकसान दर्शाया गया है। प्रति स्पिन कुल दांव राशि $175 है। इसके परिणामस्वरूप $9.21/$175 = 5.26% का हाउस एज बनता है, जो डबल-ज़ीरो रूलेट में हाउस एज होता है।
मैं यह भी जोड़ना चाहूँगा कि इस रणनीति या किसी भी रूलेट रणनीति के साथ, आप शायद मुकाबलों में जितना कमाएँगे, उससे ज़्यादा खो देंगे। सामान्य नियम यह है कि कैसीनो आपको मुकाबलों में आपके अपेक्षित नुकसान का लगभग 1/3 हिस्सा वापस देंगे। कैसीनो को यह झाँकने के कई तरीके हैं कि आपका अपेक्षित नुकसान वास्तविकता से ज़्यादा है, लेकिन इस रणनीति को अपनाना उनमें से एक नहीं है।
रूलेट में इस रणनीति के बारे में आप क्या सोचते हैं:
- काले पर दो इकाइयों का दांव लगाएँ
- तीसरे कॉलम पर एक इकाई का दांव लगाएँ
इस रणनीति की खूबसूरती यह है कि तीसरे कॉलम में 8 लाल संख्याएँ और 4 काली संख्याएँ हैं। 16 लाल संख्याओं में से आधी कॉलम 1 या 2 पर और आधी कॉलम 3 पर हैं। चलिए अभी के लिए 0 और 00 को नज़रअंदाज़ कर देते हैं। जब गेंद लाल रंग में गिरती है, तो 18 में से 8 लाल संख्याएँ तीसरे कॉलम में होती हैं। अगर जीतने की संभावना 8/18 है और जीतने पर 2 से 1 का भुगतान होता है, तो मेरे पास 33.3% का खिलाड़ी लाभ है। भले ही हम 0% हाउस एज के साथ काले पर दांव के साथ इसका औसत निकालें, फिर से अभी के लिए 0 और 00 को अनदेखा करते हुए, मेरे पास अभी भी 16.7% खिलाड़ी लाभ है। 0 और 00 को मिलाकर, क्या मेरा लाभ (2/38) * -100% + (36/38) * 16.7% = 10.53% नहीं है! आप क्या सोचते हैं?
मैं इस बात से सहमत हूँ कि तीसरे कॉलम के दांव का सशर्त लाभ 33.3% है, यह मानते हुए कि गेंद लाल रंग में गिरती है, और दोनों शून्यों को अनदेखा कर दिया जाता है। हालाँकि, इसी तर्क से, यदि गेंद काले रंग में गिरती है, तो तीसरे कॉलम के दांव के जीतने की संभावना 4/18 = 2/9 है। जीतने की 2/9 संभावना वाली एक शर्त जो 2 से 1 का भुगतान करती है, उसमें 33.33% का हाउस एडवांटेज होगा। तो, इसे अपने तरीके से देखें, तो तीसरे कॉलम के दांव में आधे समय खिलाड़ी का लाभ 33.33% और आधे समय 33.33% का हाउस एज होगा। एक दूसरे को रद्द करने पर, उस दांव में 0% हाउस एज होता है। अंत में, दो शून्यों को मिला दें और कुल खिलाड़ी का लाभ (2/38) * -100% + (36/38) * 0% = -5.26% है।
इसे दूसरे तरीके से देखें, तो निम्न तालिका सभी संभावित परिणामों के घटित होने के तरीकों की संख्या, संभावना, जीती गई इकाइयाँ और रिटर्न में योगदान दर्शाती है। निचले दाएँ कक्ष में -0.105263 इकाइयों का अपेक्षित नुकसान दर्शाया गया है। दांव पर लगाई गई दो इकाइयों से भाग देने पर, यह 5.26% का हाउस एज होता है।
बोहेमिया रणनीति
| आयोजन | भुगतान करता है | नंबर | संभावना | वापस करना |
|---|---|---|---|---|
| 0, 00 | -2 | 2 | 0.052632 | -0.105263 |
| लाल और स्तंभ 1 या 2 | -2 | 10 | 0.263158 | -0.526316 |
| लाल और स्तंभ 3 | 1 | 8 | 0.210526 | 0.210526 |
| काला और स्तंभ 1 या 2 | 0 | 14 | 0.368421 | 0.000000 |
| काला और स्तंभ 3 | 3 | 4 | 0.105263 | 0.315789 |
| कुल | 38 | 1.000000 | -0.105263 |
लगातार पांच लाल या पांच काले कार्ड प्राप्त करने के लिए अपेक्षित स्पिन की संख्या क्या है?
यहां मेरा समाधान (पीडीएफ) है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
सुना है अब चौगुना-शून्य रूलेट भी आ गया है। घर का फ़ायदा क्या है?

हाँ, ऐसा पहिया टीसीएस जॉन हक्सले द्वारा बेचा जाता है। मुझे अभी तक किसी प्लेसमेंट की जानकारी नहीं है।
मानक रूलेट में हाउस एज का सूत्र z/(36+z) है, जहाँ z = शून्यों की संख्या। इस स्थिति में, हाउस एज 4/(36+4) = 4/40 = 1/10 = 10% है।


