गैर-कैसीनो खेल - अक्सर पूछे जाने वाले प्रश्न
मुझे डॉलर के नोटों से "लायर्स पोकर" खेलना पसंद है। किसी नोट पर एक ही संख्या के 1,2,3,4, या 5 आने की प्रायिकता क्या है? धन्यवाद। अगर मैं 3 लोगों के साथ खेल रहा हूँ, तो किसी एक संख्या के आने की प्रायिकता क्या है?
सबसे पहले, मैं इस अनपूछे गए प्रश्न का उत्तर दूँगा कि किसी विशिष्ट संख्या के किसी यादृच्छिक बिल पर n बार आने की प्रायिकता क्या है। एक बिल में 8 अंक होते हैं, इसलिए किसी विशिष्ट संख्या के n की प्रायिकता combin(8,n)*0.1 n *0.9 8-n /10 8 है। यहाँ एक तालिका दी गई है जो किसी विशिष्ट संख्या के 0 से 8 तक की प्रायिकता दर्शाती है।
झूठे पोकर में विशिष्ट संख्या की संभावनाएँ
| संख्या | संभावना |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| कुल | 1.00000000 |
अगली तालिका हर संभावित प्रकार के बिल की प्रायिकता दर्शाती है, जिसे प्रत्येक n-of-a-kind की संख्या के आधार पर वर्गीकृत किया गया है। उदाहरण के लिए, सीरियल नंबर 66847680 में एक तीन एक तरह के, एक जोड़ा और तीन एकल होंगे, जिसकी प्रायिकता 0.1693440 है।
झूठे पोकर में सामान्य संभावनाएँ
| 8 ओक | 7 ओक | 6 ओक | 5 ओक | 4 ओक | 3 ओक | 2 ओक | 1 ओक | संभावना |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| कुल | 1.0000000 | |||||||
ओक = "एक प्रकार का"
अधिक जानकारी के लिए, झूठे पोकर पर मेरा पेज देखें।
बैंक ऑफ अमेरिका एटीएम में प्रतिदिन की गई चुनिंदा जमा राशि को तिगुना करने का ऑफर दे रहा है। यह प्रतियोगिता लगभग दो महीने तक चलेगी। क्या $300 जमा करने पर मेरे मौके बेहतर हैं... $100 के तीन जमा या $300 का एक जमा... या क्या मेरे कुल मौके इतने कम हैं कि अंतर प्रयास के लायक नहीं है?
आपकी अपेक्षित जीत वही रहेगी चाहे आप अपनी कुल जमा राशि को कितनी भी बार विभाजित करें। एक अच्छी रणनीति यह होगी कि आप एक ही राशि को जितनी बार हो सके उतनी बार जमा और निकालें। हालाँकि, आपकी संभावनाएँ इतनी कम हो सकती हैं कि यह परेशानी उठाने लायक नहीं है।
एक पूर्वी पासा खेल के बारे में बस एक प्रश्न, जहाँ खिलाड़ियों को यह अनुमान लगाना होता है कि पासे का कौन सा पक्ष दिखाई देता है। खिलाड़ी पहले 1, 2, 3, 4, 5, 6 (रूलेट की तरह) पर अपना दांव लगाएँगे और फिर "डीलर" एक साथ 3 पासे फेंकेगा। यदि चुनी गई संख्या एक बार (तीनों पासों में से किसी पर भी) दिखाई देती है, तो भुगतान 1:1 होगा, यदि चुनी गई संख्या दो बार दिखाई देती है, तो 2:1 होगा, और यदि चुनी गई संख्या तीनों पासों पर दिखाई देती है, तो 3:1 होगा। चूँकि खिलाड़ी बोर्ड पर कितने भी दांव लगा सकता है, तो दांव लगाने की इष्टतम संख्या क्या होगी? (यह मानते हुए कि मेरे सभी दांव बराबर आकार के हैं)
तीन मिलान की संभावना 1/216 है। दो मिलान की संभावना 3*5/216 है। एक मिलान की संभावना 25*5/216 है। 0 मिलान की संभावना 5*5*5/216 है। इसलिए अपेक्षित रिटर्न 3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7.87% है। दांव लगाने की कोई इष्टतम संख्या नहीं है, आप चाहे जो भी करें, कुल दांव पर लगाई गई राशि का अपेक्षित 7.87% ही हारेंगे।
ये दांव सिक बो और चक अ लक दोनों में लगाए जा सकते हैं।
विंडोज संस्करण में क्लोंडाइक सॉलिटेयर के मानक गेम को जीतने की संभावना क्या है?
यह शायद सबसे ज़्यादा पूछा जाने वाला सवाल है जिसका मेरे पास कोई जवाब नहीं है। क्लोंडाइक सॉलिटेयर जैसा विस्तृत खेल आज तक कभी नहीं बना है। हो सकता है, जब कंप्यूटर लाखों गुना तेज़ हो जाएँगे, तो कोई न कोई इसे ज़रूर बनाएगा। हालाँकि, ऐसी अफवाह है कि वेगास के कसीनो कम से कम पचास के दशक में यह खेल उपलब्ध कराते थे। मैंने वेगास के कई पुराने लोगों से इसकी पुष्टि करने के लिए कहा है, लेकिन अभी तक कोई भी इसकी पुष्टि नहीं कर पाया है।
हाल ही में, बैकगैमौन के एक खेल में, मैंने लगातार चार बार दोहरा छक्का मारा। क्या ऐसा दोबारा होने की संभावना है?
प्रत्येक नए रोल के साथ अगले चार रोल के सभी दोहरे छक्के होने की संभावना (1/36) 4 = 1679616 में 1 है।
नमस्ते, www.transience.com.au/pearl.html पर "स्वाइन के लिए मोती" नाम का एक खेल है। मोतियों को तीन पंक्तियों (5+4+3) में बाँटा जाता है, और अपनी बारी आने पर आप एक पंक्ति से जितने चाहें उतने मोती निकाल सकते हैं। खेल का उद्देश्य अपने प्रतिद्वंद्वी के लिए आखिरी मोती छोड़ना होता है। खिलाड़ी (मैं) हमेशा शुरुआत करता हूँ, (और हमेशा हारता हूँ)। मैं कभी क्यों नहीं जीतता? मेरे प्रतिद्वंद्वी के पास हमेशा जीतने का एक चालाक तरीका है, क्या आप उसका राज़ बता सकते हैं?
3 मोतियों वाली पंक्ति से 2 मोती हटाकर शुरुआत करें, जिससे 1+4+5 मोती बचेंगे। अगली बारी में आपका प्रतिद्वंद्वी चाहे जो भी करे, उसे निम्न में से कोई भी मोती दें: 1+1+1, 1+2+3, या 4+4। इनमें से किसी भी मोती से प्रतिद्वंद्वी को 2 या उससे अधिक की दो ढेरियों, या 1-1 की विषम संख्या वाली ढेरियों की स्थिति में लाएँ।
एकाधिकार में कौन सा सेट सबसे अच्छा है?
मुझे नारंगी रंग का सेट सबसे ज़्यादा पसंद है। यह निवेश पर सबसे अच्छा रिटर्न देता है। उदाहरण के लिए, नारंगी रंग के सेट पर एक होटल का किराया $500 है और औसत किराया $966.67 है, यानी किराया-व्यय अनुपात 1.93 है। इससे ज़्यादा अनुपात वाला एकमात्र सेट हल्का नीला सेट है, जिसका किराया-व्यय अनुपात 2.27 है। हालाँकि, हल्के नीले रंग का अधिकतम किराया केवल $600 है। नारंगी रंग के सेट पर तीन घरों के साथ किराया हल्के नीले रंग के सेट पर होटलों के समान ही है, लेकिन लागत 20% कम है, और निर्माण की गुंजाइश भी ज़्यादा है। इसके अलावा, नारंगी रंग के सेट जेल से छूटने के बाद ही खरीदे जा सकते हैं। इसलिए मेरी सलाह मानें और व्यापार करते समय नारंगी रंग का सेट खरीदने की कोशिश करें।
पत्थर/कागज़/कैंची खेलने के लिए आपकी क्या सलाह है?
इस साइट पर सबसे अच्छी सलाह शायद यही होगी: पहला राउंड, हमेशा कागज़ उठाएँ। ऐसा इसलिए क्योंकि शौकिया खिलाड़ी पहली बार में पत्थर उठाते हैं। बस हर स्थिति में एक-एक करके अपना हाथ बढ़ाएँ, और आप देखेंगे कि पत्थर सबसे आरामदायक और स्वाभाविक विकल्प है। अगर आप बार-बार राउंड खेलते हैं, तो आपको वह चुनना चाहिए जो आपके प्रतिद्वंदी को आखिरी राउंड में हरा दे, और संभावना एक-तिहाई से भी कम हो। ऐसा इसलिए क्योंकि मेरा मानना है कि शौकिया खिलाड़ी एक-तिहाई से भी कम बार दोहराते हैं। अगर आप किसी ऐसे पेशेवर खिलाड़ी के साथ खेल रहे हैं जिससे आपको डर है कि वह आपके दिमाग में घर कर सकता है, तो अपनी घड़ी की सेकंड सुई देखकर रैंडमाइज़ करें, सेकंड की संख्या को तीन से भाग दें और शेष निकालें, फिर शेष को इस तरह मैप करें: 0=पत्थर, 1=कैंची, 2=कागज़ (या पहले से तय की गई कोई भी अन्य मैपिंग)। तो अगली बार जब आप डच स्टाइल में किसी रेस्टोरेंट जाएँ, तो मेरा सुझाव है कि चेक के लिए एक राउंड खेलें और फिर कागज़ चुनें। आप मुझे बाद में धन्यवाद दे सकते हैं।
जब हमलावर तीन पासे फेंकता है और बचावकर्ता दो पासे फेंकता है तो जोखिम में किसे लाभ होता है?
जो लोग इस खेल से परिचित नहीं हैं, उनके लिए रिस्क अब तक का सबसे बेहतरीन बोर्ड गेम है। जिन्होंने इसे नहीं खेला है, उन्होंने अभी तक जीवन नहीं जिया है। आपके प्रश्न का उत्तर देने के लिए, इस आम 3 बनाम 2 लड़ाई में संभावित परिणाम निम्नलिखित हैं:
- डिफेंडर दोनों हारता है: 37.17%
- प्रत्येक को एक का नुकसान: 33.58%
- हमलावर दोनों हारता है: 29.26%
याहत्ज़ी के खेल में यदि कार्ड पर केवल याहत्ज़ी ही बचा हो तो उसके बनने की संभावना क्या है?
निम्नलिखित तालिका याहत्ज़ी बनाने के लिए आवश्यक अतिरिक्त पासों की संख्या के अनुसार अंतिम रोल पर सफलता की संभावना को दर्शाती है।
अंतिम रोल याहत्ज़ी संभावनाएँ
| आवश्यकता है | संभावना सफलता की |
| 0 | 1 |
| 1 | 0.166667 |
| 2 | 0.027778 |
| 3 | 0.00463 |
| 4 | 0.000772 |
अगली तालिका सुधार की संभावनाओं को दर्शाती है। बाएँ कॉलम में दिखाया गया है कि किसी भी दिए गए रोल से पहले आपको कितने पासों की आवश्यकता होगी और ऊपर वाले कॉलम में दिखाया गया है कि रोल के बाद आपको कितने पासों की आवश्यकता होगी। मुख्य भाग में सुधार की दी गई डिग्री की संभावना दर्शाई गई है।
सुधार की संभावनाएं
| रोल से पहले की जरूरत | 0 | 1 | 2 | 3 | 4 | कुल |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.833333 | 0 | 0 | 0 | 1 |
| 2 | 0.027778 | 0.277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0.00463 | 0.069444 | 0.37037 | 0.555556 | 0 | 1 |
| 4 | 0.000772 | 0.01929 | 0.192901 | 0.694444 | 0.092593 | 1 |
अगली तालिका में प्रारंभिक रोल पर याहत्ज़ी बनाने के लिए 0 से 4 अतिरिक्त पासों की आवश्यकता की संभावना को दर्शाया गया है।
प्रथम रोल याहत्ज़ी संभावनाएँ
| आवश्यकता है | संभावना |
| 0 | 0.000772 |
| 1 | 0.019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0.092593 |
अगली तालिका पहले पासे के बाद आवश्यक संख्या के अनुसार सुधार और फिर अंतिम सफलता की संभावना दर्शाती है। उदाहरण के लिए, यदि खिलाड़ी को याहत्ज़ी बनाने के लिए 3 और पासों की आवश्यकता है, तो दूसरे पासे के बाद 2 और पासों की आवश्यकता होने और तीसरे पासे पर याहत्ज़ी बनाने की संभावना 0.010288066 है।
दूसरे रोल से पहले और बाद में आवश्यक संख्या के अनुसार पहले रोल के बाद याहत्ज़ी की संभावनाएं
| रोल से पहले की जरूरत | 0 | 1 | 2 | 3 | 4 | कुल |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0.027778 | 0.046296 | 0.01929 | 0 | 0 | 0.093364 |
| 3 | 0.00463 | 0.011574 | 0.010288 | 0.002572 | 0 | 0.029064 |
| 4 | 0.000772 | 0.003215 | 0.005358 | 0.003215 | 0.000071 | 0.012631 |
अंतिम उत्तर पाने के लिए, पहले रोल के बाद दो टेबल ऊपर आवश्यक संख्या और अंतिम कॉलम में एक टेबल ऊपर अंतिम सफलता की प्रायिकता का डॉट गुणनफल लें। यह 0.092593*0.012631+ 0.694444*0.029064 + 0.192901*0.093364 + 0.019290*0.305556 + 0.000772*1 = 4.6028643% है। इसकी पुष्टि के लिए मैंने 100,000,000 गेम सिमुलेशन किया और सिम्युलेटेड प्रायिकता 4.60562% थी।
यदि पत्थर/कागज/कैंची के खेल में डायनामाइट को एक विकल्प के रूप में शामिल किया जाए, जहां डायनामाइट पत्थर और कागज को हरा देता है, लेकिन कैंची डायनामाइट को हरा देती है, तो दो कुशल तर्कशास्त्री खेलते समय इष्टतम रणनीति क्या होनी चाहिए?
सबसे पहले, हम कागज़ से खेलने की संभावना को ख़त्म कर सकते हैं। चाहे दूसरा व्यक्ति कुछ भी फेंके, आप कागज़ पर डायनामाइट फेंककर बराबर या उससे बेहतर प्रदर्शन करेंगे। एक बार कागज़ के हट जाने पर, डायनामाइट अनिवार्य रूप से नया कागज़ बन जाता है, पत्थर को हरा देता है और कैंची से हार जाता है। इसलिए सबसे अच्छी रणनीति यह है कि पत्थर, कैंची और डायनामाइट में से बेतरतीब ढंग से और समान संभावना के साथ, चुनें।
उन बूथों में से एक में सबसे अच्छी रणनीति क्या है, जहां पैसा इधर-उधर उड़ता रहता है, जबकि आपको सीमित समय में जितना संभव हो सके उतना पैसा इकट्ठा करना होता है?
मैंने यह सवाल फन इंडस्ट्रीज इंक . के रैंडी हिल से पूछा। उन्होंने बताया कि आपको अपनी बाहें सीधी फैलाकर, हथेलियाँ नीचे की ओर रखनी चाहिए, और पैसों को अपनी बाहों और बाजुओं के नीचे की ओर उछालना चाहिए। जब पर्याप्त पैसा जमा हो जाए, तो उसे स्लॉट में डाल दें।
मान लीजिए हम एक जुआ खेल रहे हैं। एक निष्पक्ष सिक्का बार-बार उछाला जाता है। हर बार उछालने पर हमें 1 रुपया देना होता है। इसके दो संभावित परिणाम हैं: H या T। अगर चित और पट के बीच का अंतर 3 हो जाता है, तो हमें जुआरी से 8 रुपये मिलेंगे। क्या हमें यह खेल खेलना चाहिए और क्यों? हमारे जीतने की संभावना कितनी है? जब हमें 7 या 9 रुपये मिल रहे हों, तो जीतने की संभावना पर क्या प्रभाव पड़ेगा?
आइए x को प्रारंभिक बिंदु से फ़्लिप की अपेक्षित संख्या कहें।
यदि एक पक्ष बहुमत में एक फ्लिप है, तो शेष फ्लिप की अपेक्षित संख्या को y कहें।
यदि एक पक्ष बहुमत में दो फ़्लिप है, तो शेष फ़्लिप की अपेक्षित संख्या को z कहें।
ई(एक्स) = 1 + ई(वाई)
ई(वाई) = 1 + 0.5*ई(एक्स) + 0.5*ई(जेड)
ई(जेड) = 1 + 0.5*ई(वाई)
मैट्रिक्स बीजगणित की मदद से यह देखना आसान है कि E(x) = 9, E(y) = 8, और E(z) = 5. तो औसतन चित और पट के बीच का अंतर 3 होने के लिए 9 उछाल लगेंगे। इसलिए 8 रुपये पर यह उस व्यक्ति के लिए एक अच्छा दांव है जो प्रति उछाल एक रुपया इकट्ठा करता है, क्योंकि उसे औसतन 9 रुपये मिलेंगे, लेकिन केवल 8 रुपये वापस मिलेंगे। जुआरी के लिए हाउस एज 11.11% है। 9 रुपये पर यह एक उचित दांव है, जबकि 7 रुपये पर हाउस एडवांटेज 22.22% है।
अपने 28 नवंबर 2002 के कॉलम में आपने पर्ल्स बिफोर स्वाइन गेम की उचित रणनीति के बारे में बताया था। इसका एक सीक्वल भी है जिसका नाम पर्ल्स बिफोर स्वाइन II है । मैं इस संस्करण को कैसे हरा सकता हूँ?
मैं 11/28/02 के कॉलम में बताता हूँ कि जब केवल तीन पंक्तियाँ बची हों, तो कैसे खेलें। चार पंक्तियों के लिए मेरी रणनीति यहाँ दी गई है। जब आपकी बारी आए, तो बाएँ कॉलम में दिए गए विन्यास को देखें और दाएँ कॉलम में जो है उसे खेलें। उदाहरण के लिए, 3456 की शुरुआती स्थिति सबसे आखिर में दी गई है और बताती है कि आपको 5 वाली पंक्ति से 4 मोती निकालने चाहिए, जिससे 1346 बचेंगे। अगर बाएँ कॉलम में "हार" लिखा है, तो अगर प्रतिद्वंद्वी सबसे अच्छी रणनीति अपनाता है, तो जीतने का कोई रास्ता नहीं है, जैसा कि ट्रांससाइंस के खेल में हमेशा होता है।
इस तालिका का एक पैटर्न यह प्रतीत होता है कि आपको प्रतिद्वंद्वी को ऐसी स्थिति में धकेलना चाहिए जहाँ सबसे छोटी और सबसे बड़ी पंक्तियों के मोतियों का योग बीच के दो मोतियों के योग के बराबर हो। इसमें सबसे कम मोतियों वाली पंक्ति में शून्य छोड़ना शामिल होगा।
सूअर के सामने मोती II रणनीति
| आपके पास | छुट्टी |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | खोना |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | खोना |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | खोना |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | खोना |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | खोना |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | खोना |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | खोना |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | खोना |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | खोना |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | खोना |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | खोना |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | खोना |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | खोना |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | खोना |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
ब्रैड एस. ने मोतियों और पंक्तियों की किसी भी संख्या के लिए एक सामान्य रणनीति जोड़ने के लिए लिखा है। सबसे पहले, आप प्रत्येक पंक्ति को उसके द्विआधारी घटकों में विभाजित करें। उदाहरण के लिए, ट्रांससाइंस गेम की शुरुआती स्थिति इस प्रकार होगी।
- 3 = 2+1
- 4 = 4
- 5 = 4+1
- 6 = 4+2
फिर आप 2 की प्रत्येक घात वाली एक सम संख्या छोड़ने का प्रयास करते हैं। उदाहरण के लिए, ऊपर दिए गए उदाहरण में दो 1, दो 2 और तीन 4 हैं। इस प्रकार एक अतिरिक्त 4 है। फिर आप 4 पदों वाली किसी भी पंक्ति से 4 हटा दें। ऐसा तब तक करते रहें जब तक कि आप अपने प्रतिद्वंद्वी को 2, 2 या 1 की विषम संख्या तक नहीं ले आते।
पर्ल 3 गेम में यह रणनीति आज़माएँ, आप हर बार जीतेंगे। अगर आप हारने की स्थिति से शुरुआत करते हैं, जैसा कि मैंने गेम 10 (4+7+8+11) में किया था, तो आप उसे पहले जाने के लिए "गो" पर क्लिक कर सकते हैं।
मैं आपके NIM गेम को समझ नहीं पाया! मैं हमेशा सोचता था कि जीतने की कुंजी अपने प्रतिद्वंद्वी (इस मामले में, कंप्यूटर) को ऐसे बिंदुओं के साथ छोड़ना है जिनका योग अगली सबसे छोटी संख्या तक हो जो बाइनरी संख्याओं में उसके सारांश के बराबर हो, यानी, अगर मेरे पास 17 बिंदु हैं, तो मैं 2 हटा देता हूँ और 15 छोड़ देता हूँ, जो बाइनरी संख्याओं 1,2,4,8 का सारांश है। लेकिन ऐसा लगता है कि यह काम नहीं करता। मैं सही हूँ या गलत?
बाइनरी संख्याओं के मामले में आप सही रास्ते पर हैं, लेकिन यह पूरी तरह से जीतने की रणनीति नहीं है। सबसे पहले, अगर आप अपने प्रतिद्वंद्वी को एक-एक पंक्ति की विषम संख्या में पंक्तियाँ दे सकते हैं, तो ऐसा करें। अन्यथा, प्रत्येक पंक्ति को उसके बाइनरी घटकों में विभाजित करें। उदाहरण के लिए, 99 = 64+32+2+1। फिर सभी पंक्तियों में प्रत्येक घटक की संख्या को जोड़ें। फिर एक ऐसा दांव लगाएँ जिससे आपके प्रतिद्वंद्वी को सभी पंक्तियों में सभी बाइनरी घटकों की सम संख्या मिले।
आइए एक उदाहरण देखें। मान लीजिए कि आपकी बारी है और निम्नलिखित परिदृश्य है।
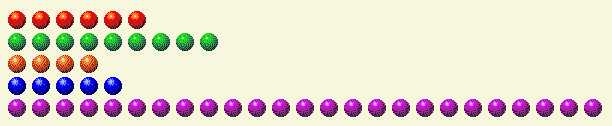
निम्नलिखित तालिका प्रत्येक पंक्ति को उसके बाइनरी घटकों में विभाजित करती है।
खिलाड़ी की बारी 1
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| कुल | 3 | 1 | 3 | 2 | 1 |
आप देख सकते हैं कि इकाई, दो, चार और सोलह की संख्या विषम है। स्पष्ट रूप से, हमें 16 इकाई को हटाने के लिए 25 की पंक्ति को 16 के नीचे लाना होगा। द्विआधारी घटकों का योग सम रखने के लिए, हमें 1 हटाना होगा, 2 जोड़ना होगा, 4 जोड़ना होगा, 8 रखना होगा और 16 हटाना होगा। इसका मतलब है कि सबसे अच्छा खेल आखिरी पंक्ति में 2+4+8=14 है। नीचे की पंक्ति में 14 छोड़ने पर हमें निम्नलिखित मिलता है।
कंप्यूटर की बारी 1
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| कुल | 2 | 2 | 4 | 2 | 0 |
कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।
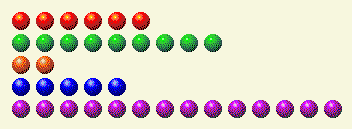
यहाँ इसका द्विआधारी विश्लेषण दिया गया है।
खिलाड़ी की बारी 2
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| कुल | 2 | 3 | 3 | 2 | 0 |
यहाँ हमें 2 और 4 को हटाना होगा, ताकि कुल योग बराबर हो जाए। केवल एक पंक्ति है, 14, जिसमें दोनों घटक हैं। इसलिए उसमें से 6 हटा दें, जिससे 8 बचेगा।
कंप्यूटर की बारी 2
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| कुल | 2 | 2 | 2 | 2 | 0 |
कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।
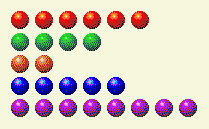
अब हमें 1, 4 और 8 कॉलम बदलने की जरूरत है।
खिलाड़ी की बारी 3
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| कुल | 1 | 2 | 3 | 1 | 0 |
ऐसा 8 की पंक्ति को 5 में बदलकर किया जा सकता है।
कंप्यूटर की बारी 3
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| कुल | 2 | 2 | 4 | 0 | 0 |
कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।
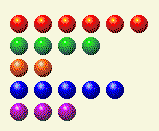
अब हमें 2 और 4 का योग बदलने की जरूरत है।
खिलाड़ी की बारी 4
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| कुल | 2 | 3 | 3 | 0 | 0 |
यह 6 को 0 में बदलकर किया जा सकता है।
कंप्यूटर की बारी 4
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| कुल | 2 | 2 | 2 | 0 | 0 |
कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।
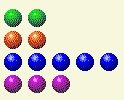
अब हमें 2 और 4 को बदलने की जरूरत है।
खिलाड़ी की बारी 5
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| कुल | 2 | 3 | 1 | 0 | 0 |
यह 5 की पंक्ति को 3 में बदलकर पूरा किया जा सकता है। यदि आप कभी भी अपने प्रतिद्वंद्वी को x,x,y,y स्थिति में ला सकते हैं, तो आप जीतने से खुद को नहीं रोक सकते, बशर्ते आप अंत तक उसी स्थिति को बनाए रख सकें।
कंप्यूटर की बारी 5
| पंक्ति | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| कुल | 2 | 4 | 0 | 0 | 0 |
अगली कुछ चालों में मैं कंप्यूटर को x,x,y,y पैटर्न पर रखता हूँ। यहाँ कंप्यूटर मुझे 2,2,3,2 पर छोड़ देता है; इसलिए मैं उसे 2,2,2,2 पर छोड़ देता हूँ।

कंप्यूटर मुझे 2,2,1,2 देता है। मैं उसे 2,2,1,1 पर छोड़ देता हूँ।
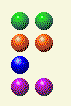
कंप्यूटर मुझे 2,2,1 देता है। मैं उसे 2,2 पर छोड़ देता हूँ। अगर आप कभी अपने प्रतिद्वंदी को दो बराबर पंक्तियों में ला पाए, तो आप जीत ही जाएँगे, बस पंक्तियाँ बराबर रखें।

इसके बाद कंप्यूटर मेरे पास 2 का एक ढेर छोड़ देता है, और मैं 1 हटा देता हूं।

खेल का अंत यहीं है।
मुझे हाल ही में एक कार्निवल व्हील मिला है जो मेरे परदादा का था। यह लगभग सौ साल पुराना है और मैं इस पर एक गेम बनाने की कोशिश कर रहा हूँ। इस पर 1 से 60 तक के नंबर बेतरतीब क्रम में हैं और यह हर पंद्रहवें निशान पर एक हरे तारे के साथ काले और लाल रंग में बदलता रहता है। क्या आप मुझे यह बताने में मदद कर सकते हैं कि हर स्पिन के लिए कितना भुगतान होना चाहिए?
तो कुल 30 काली, 30 लाल और 4 हरी संख्याएँ हैं। इससे काली संख्या की प्रायिकता 30/64, लाल संख्या की प्रायिकता 30/64 और हरी संख्या की प्रायिकता 4/64 होगी। यदि किसी घटना की प्रायिकता p है, तो उचित ऑड्स (1-p)/p से 1 हैं। इसलिए किसी भी लाल संख्या के लिए उचित ऑड्स (34/64)/(30/64) = 34 से 30 = 17 से 15 होंगे। काली संख्या के लिए भी यही बात लागू होती है। हरी संख्या के लिए उचित ऑड्स (60/64)/(4/64) = 60 से 4 = 15 से 1 हैं। किसी विशिष्ट संख्या के लिए उचित ऑड्स (63/64)/(1/64) से 63 से 1 हैं।
मेरा सुझाव है कि लाल और काले पर 1:1, हरे पर 14:1, और किसी भी एक संख्या पर 60:1 का दांव लगाएँ। हाउस एज का एक सूत्र (ta)/(t+1) है, जहाँ t वास्तविक ऑड्स है, और a वास्तविक ऑड्स है। इस स्थिति में, लाल या काले दांव पर हाउस एज (63-60)/(63+1) = 3/64 = 4.69% है। हरे दांव पर हाउस एज (15-14)/(15+1) = 1/16 = 6.25% है। अलग-अलग संख्याओं पर हाउस एज (63-60)/(63+1) = 3/64 = 4.69% है।
न्यूयॉर्क राज्य में ऑफ-ट्रैक सट्टेबाजी स्थलों पर वीडियो लॉटरी टर्मिनल (वीएलटी) हैं। आप सुनते होंगे कि जब कोई वीपी मशीन "हॉट" हो जाती है और लगातार जीतने वाले हाथ देती है, तो मशीन अपने "सेट पॉइंट" के करीब पहुँच जाती है। इससे यह समझ में आता है कि एक ही मशीन एक दिन भुगतान क्यों करती है और दूसरे दिन आपको जानना नहीं चाहती। इसके अलावा, इनमें से ज़्यादातर मशीनें आपको जीते हुए हाथ को हारने नहीं देतीं। उसे फेंक दें और यह बराबर या उससे बेहतर हाथ लौटा देगी। इस विषय पर आपके क्या विचार हैं?
वीएलटी (VLT) एक शानदार पुल-टैब गेम है। इसमें परिणामों का एक पूर्व-निर्धारित पूल होता है। जब आप खेलते हैं, तो गेम पूल से यादृच्छिक रूप से एक परिणाम चुनता है, और स्लॉट मशीन या वीडियो पोकर गेम के रूप में खिलाड़ी को जीत दिखाता है। चूँकि परिणाम पूर्वनिर्धारित होता है, इसलिए कौशल का कोई भी तत्व काल्पनिक होता है। उदाहरण के लिए, अगर आपको रॉयल फ्लश मिलता है और आप उसे फेंक देते हैं, तो ड्रॉ में आपको एक और मिलेगा। आमतौर पर मैं कहता हूँ कि जुए में अतीत मायने नहीं रखता, लेकिन इस मामले में निष्कासन का प्रभाव है। अगर आप एक बार खेलते हैं और हार जाते हैं, तो इससे बाकी खेल के परिणामों की संभावना थोड़ी बढ़ जाएगी, जब तक कि वर्चुअल पुल-टैब की आपूर्ति समाप्त नहीं हो जाती, और मुझे लगता है कि वर्चुअल ड्रम फिर से भर दिया गया है। मेरा मानना है कि आपके उतार-चढ़ाव सामान्य भाग्य हैं, और कोई भी पूर्वनियति काल्पनिक है।
बाद में एक पाठक ने इस विषय में निम्नलिखित बातें जोड़ीं।
आपके 14 फ़रवरी के "जादूगर से पूछो" कॉलम (संख्या 183) पर मेरी एक टिप्पणी है। इसका आपके द्वारा दिए गए उत्तर से कोई लेना-देना नहीं है। यह बस एक ऐसी बात है जो आपको दिलचस्प लग सकती है।
प्रस्ताव 1A के पारित होने से पहले, जिसने पूर्ण श्रेणी 3 गेमिंग की अनुमति दी थी, हमारे पास कुछ वर्षों तक VLT शैली का एक छोटा सा इंस्टॉलेशन था। हमारे सिस्टम में, जो SDG (अब बैली का हिस्सा) द्वारा संचालित था, पुरस्कार राशि 4 मिलियन ड्रॉ से शुरू होती थी। जब पूल कम हो गया और 2 मिलियन रह गए, तो 4 मिलियन का एक और पूल जोड़ा गया, जिससे कुल ड्रॉ की संख्या 6 मिलियन हो गई। जब पूल फिर से 2 मिलियन तक कम हो गया, तो प्रक्रिया दोहराई गई।
याहत्ज़ी प्राप्त करने के लिए अपेक्षित रोल की संख्या कितनी है?
यह मानते हुए कि खिलाड़ी के पास हमेशा सबसे ज़्यादा दर्शाई गई संख्या होती है, औसत 11.09 है। यहाँ एक तालिका दी गई है जो 82.6 मिलियन परीक्षणों के एक यादृच्छिक सिमुलेशन में रोल की संख्या के वितरण को दर्शाती है।
याहत्ज़ी प्रयोग
| रोल्स | पुनरावृत्तियां | संभावना |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0.00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0.00392347 |
| 29 | 271321 | 0.00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| कुल | 82600000 | 1 |
क्या आप किसी ऐसी वेबसाइट के बारे में जानते हैं जिसमें बैकगैमन ऑड्स/सांख्यिकी/संभावना का अच्छा विश्लेषण हो, और क्या कोई विशेष पुस्तक है जिसे आप खेल के किसी भी पहलू पर सुझा सकें?
बैकगैमौन मेरे पसंदीदा जुए के खेलों में से एक है। मैं इसके बारे में इसलिए नहीं लिखता क्योंकि खिलाड़ी बनाम खिलाड़ी खेलों का विश्लेषण करना बेहद मुश्किल होता है। मुझे इस खेल में कोई नया आयाम भी नहीं मिल रहा है। इसलिए, मैं यह सलाह दूसरों पर छोड़ता हूँ। मेरे सुझाए गए संसाधन ये हैं:
पॉल मैग्रील द्वारा लिखित बैकगैमौन : अगर बैकगैमौन की कोई बाइबल होती, तो वह यही होती। मुझे इसके पुराने हार्ड-कवर संस्करण का गर्व है। यह किताब शुरुआत करने के लिए एक बेहतरीन जगह होगी। हालाँकि यह 1976 में लिखी गई थी, फिर भी इसकी सलाह आज भी प्रासंगिक है।
बिल रॉबर्टी द्वारा लिखित 501 एसेंशियल बैकगैमौन प्रॉब्लम्स : मैं वर्षों से इस किताब को पढ़ने की कोशिश कर रहा हूँ, और अभी भी मैं आधी ही पहुँच पाया हूँ। आधी समस्याओं का गलत हल निकालना निराशाजनक है, इतना कि मुझे लगता है कि मैं बैकगैमौन में भी उतना ही बुरा हूँ जितना गोल्फ में। हालाँकि, हर समस्या के गलत होने पर एक मूल्यवान सबक सीखने को मिलता है। मध्यम से लेकर उन्नत स्तर के खिलाड़ियों के लिए, यह किताब एक मूल्यवान और विनम्र शिक्षण उपकरण है।
स्नोई बैकगैमौन सॉफ्टवेयर : मैं इस खेल के खिलाफ साल में लगभग 1000 गेम खेलता हूँ। स्नोई न केवल लगभग परफेक्ट गेम खेलता है, बल्कि आपको यह भी बताता है कि आपकी गलतियाँ कितनी भारी पड़ सकती हैं। इसके और भी कई फ़ीचर हैं जिनके बारे में मैंने कभी नहीं सोचा। अगर स्नोई से मैंने एक बात सीखी है, तो वह यह है कि मेरे खेल की सबसे बड़ी समस्या यह है कि मैं कभी-कभी बिल्कुल स्पष्ट चालें न देख पाने जैसी मूर्खतापूर्ण गलतियाँ कर बैठता हूँ। शतरंज की तरह, एक गलत चाल 100 अच्छी चालों को खत्म कर सकती है।
मोटिफ वेबसाइट : स्नोई खरीदने से पहले, मैंने मोटिफ के खिलाफ अनगिनत गेम खेले हैं। मेरी राय में, मोटिफ की रणनीति बहुत ही ठोस है। अपने खेल को बेहतर बनाने के लिए किसी मज़बूत प्रतिद्वंद्वी के खिलाफ खेलने से बेहतर कुछ नहीं है।
निम्नलिखित तालिका प्रत्येक खिलाड़ी की जीत की संभावना को दर्शाती है, जो पहले खिलाड़ी के पहले स्पिन के अनुसार है, जहाँ खिलाड़ी 1 पहले जाता है, उसके बाद खिलाड़ी 2 और खिलाड़ी 3 अंत में। निचली पंक्ति पहले स्पिन से पहले जीतने की समग्र संभावनाओं को दर्शाती है।
कीमत सही है शोकेस तसलीम में संभावनाएं
| स्पिन 1 | रणनीति | खिलाड़ी 1 | खिलाड़ी 2 | खिलाड़ी 3 |
| 0.05 | घुमाना | 20.59% | 37.55% | 41.85% |
| 0.10 | घुमाना | 20.59% | 37.55% | 41.86% |
| 0.15 | घुमाना | 20.57% | 37.55% | 41.87% |
| 0.20 | घुमाना | 20.55% | 37.55% | 41.9% |
| 0.25 | घुमाना | 20.5% | 37.56% | 41.94% |
| 0.30 | घुमाना | 20.43% | 37.56% | 42.01% |
| 0.35 | घुमाना | 20.33% | 37.58% | 42.10% |
| 0.40 | घुमाना | 20.18% | 37.60% | 42.22% |
| 0.45 | घुमाना | 19.97% | 37.64% | 42.39% |
| 0.50 | घुमाना | 19.68% | 37.71% | 42.61% |
| 0.55 | घुमाना | 19.26% | 37.81% | 42.93% |
| 0.60 | घुमाना | 18.67% | 37.96% | 43.36% |
| 0.65 | घुमाना | 17.86% | 38.21% | 43.93% |
| 0.70 | रहना | 21.56% | 38.28% | 40.16% |
| 0.75 | रहना | 28.42% | 35.21% | 36.38% |
| 0.80 | रहना | 36.82% | 31.26% | 31.92% |
| 0.85 | रहना | 46.99% | 26.35% | 26.66% |
| 0.90 | रहना | 59.17% | 20.36% | 20.47% |
| 0.95 | रहना | 73.61% | 13.19% | 13.21% |
| 1.00 | रहना | 90.57% | 4.72% | 4.72% |
| औसत | 30.82% | 32.96% | 36.22% |
यहां 6×20 6 संभावित संयोजनों में से विजेता संख्या दी गई है।
खिलाड़ी 1: 118,331,250खिलाड़ी 2: 126,566,457
खिलाड़ी 3: 139,102,293
घरेलू पोकर खेल में ऐसी ड्यूसी के लिए सही रणनीति क्या है? हमारे खेलने का तरीका यह है कि अगर तीसरा कार्ड पहले दो में से किसी एक से मेल खाता है, तो दांव पुश हो जाता है।
आप जिस तरह से खेलते हैं, जहाँ तीसरे पत्ते का मैच एक पुश होता है, वहाँ पहले दो पत्तों के बीच कम से कम छह रैंक होने पर ऑड्स आपके पक्ष में हो जाते हैं (छह पत्तों का स्प्रेड)। जिस तरह से मैंने ऑरेंज काउंटी में खेला, वहाँ तीसरे पत्ते के मैच में दोहरी हार हुई। उस नियम के तहत, आठ पत्तों के स्प्रेड पर ऑड्स बराबर हो जाते हैं। अगर तीसरे पत्ते के मैच में 1x हार होती है, तो ऑड्स आपके पक्ष में होने के लिए सात पत्तों का स्प्रेड ज़रूरी है।
वन-कार्ड पोकर के खेल में तीन पत्तों का डेक होता है, जिसमें एक इक्का, एक ड्यूस और एक ट्रे होता है। इक्का सबसे छोटा और एक ट्रे सबसे बड़ा होता है। दो खिलाड़ी पॉट में $1 डालते हैं। फिर, प्रत्येक खिलाड़ी को एक पत्ता मिलता है। दांव लगाने का क्रम पहले से तय होता है, जिसमें खिलाड़ी 1 पहले दांव लगाता है। खिलाड़ी 1 या तो $1 का दांव लगा सकता है या चेक लगा सकता है। यदि खिलाड़ी 1 दांव लगाता है, तो खिलाड़ी 2 या तो कॉल कर सकता है या फोल्ड कर सकता है। यदि खिलाड़ी 1 चेक करता है, तो खिलाड़ी 2 या तो $1 का दांव लगा सकता है या चेक लगा सकता है। यदि खिलाड़ी 1 चेक करता है, और खिलाड़ी 2 दांव लगाता है, तो खिलाड़ी 1 या तो कॉल कर सकता है या फोल्ड कर सकता है। यदि दोनों खिलाड़ी चेक करते हैं, या दोनों दांव लगाते हैं, तो बड़ा पत्ता पॉट जीत जाता है। यह मानते हुए कि दोनों खिलाड़ी पूर्ण तर्कशास्त्री हैं, प्रत्येक खिलाड़ी के लिए सर्वोत्तम रणनीति क्या है?
मुझे उम्मीद है आप खुश होंगे; मैंने इस पर पूरा दिन लगा दिया। इसका उत्तर और समाधान मेरी दूसरी साइट mathproblems.info , समस्या 203, या जेसन स्वानसन द्वारा लिखे गए अकादमिक पेपर "गेम थ्योरी एंड पोकर" पर मिल सकता है।
मैं एक मॉर्गेज के लिए खोज कर रहा हूँ। एक कंपनी 30 साल की फिक्स्ड लोन पर 5.75% ब्याज दर, एक पॉइंट प्लस, दे रही है। दूसरी कंपनी बिना पॉइंट के 5.875% ब्याज ले रही है। कौन सा ऑफर बेहतर है?
अन्य पाठकों की सुविधा के लिए, एक पॉइंट, ऋण के लिए लिया जाने वाला कमीशन होता है। उदाहरण के लिए, $250,000 के ऋण पर एक पॉइंट $2,500 के बराबर होगा। मैं यह मानकर चल रहा हूँ कि उधारकर्ता इस पॉइंट को मूलधन में जोड़ देगा, और मूलधन को कभी भी जल्दी नहीं चुकाएगा।
निम्नलिखित तालिका एक बिंदु और अवधि के साथ ब्याज दर के अनुसार, बिंदु के बिना समतुल्य ब्याज दर दर्शाती है।
बिना किसी अंक के समतुल्य ब्याज दर
| एक बिंदु के साथ ब्याज दर | 10 वर्ष | 15 वर्ष | 20 वर्ष | 30 वर्ष | 40 वर्ष |
| 4.00% | 4.212% | 4.147% | 4.115% | 4.083% | 4.067% |
| 4.25% | 4.463% | 4.398% | 4.366% | 4.334% | 4.318% |
| 4.50% | 4.714% | 4.649% | 4.617% | 4.585% | 4.570% |
| 4.75% | 4.965% | 4.900% | 4.868% | 4.836% | 4.821% |
| 5.00% | 5.216% | 5.151% | 5.119% | 5.088% | 5.073% |
| 5.25% | 5.467% | 5.402% | 5.370% | 5.339% | 5.324% |
| 5.50% | 5.718% | 5.654% | 5.621% | 5.590% | 5.576% |
| 5.75% | 5.969% | 5.905% | 5.873% | 5.842% | 5.827% |
| 6.00% | 6.220% | 6.156% | 6.124% | 6.093% | 6.079% |
| 6.25% | 6.471% | 6.407% | 6.375% | 6.344% | 6.330% |
| 6.50% | 6.723% | 6.658% | 6.626% | 6.596% | 6.582% |
| 6.75% | 6.974% | 6.909% | 6.878% | 6.847% | 6.834% |
| 7.00% | 7.225% | 7.160% | 7.129% | 7.099% | 7.085% |
| 7.25% | 7.476% | 7.412% | 7.380% | 7.350% | 7.337% |
| 7.50% | 7.727% | 7.663% | 7.631% | 7.602% | 7.589% |
| 7.75% | 7.978% | 7.914% | 7.883% | 7.853% | 7.841% |
| 8.00% | 8.229% | 8.165% | 8.134% | 8.105% | 8.093% |
| 8.25% | 8.480% | 8.416% | 8.385% | 8.357% | 8.344% |
| 8.50% | 8.731% | 8.668% | 8.637% | 8.608% | 8.596% |
| 8.75% | 8.982% | 8.919% | 8.888% | 8.860% | 8.848% |
| 9.00% | 9.233% | 9.170% | 9.140% | 9.112% | 9.100% |
| 9.25% | 9.485% | 9.421% | 9.391% | 9.363% | 9.352% |
| 9.50% | 9.736% | 9.673% | 9.642% | 9.615% | 9.604% |
| 9.75% | 9.987% | 9.924% | 9.894% | 9.867% | 9.856% |
| 10.00% | 10.238% | 10.175% | 10.145% | 10.119% | 10.108% |
इससे पता चलता है कि एक पॉइंट के साथ 5.75% ब्याज दर, बिना पॉइंट के 5.842% के बराबर है। दूसरे शब्दों में, यह मानते हुए कि लिया गया पॉइंट मूलधन में जोड़ा जाता है, भुगतान दोनों तरफ़ समान होगा। आपका दूसरा प्रस्ताव बिना पॉइंट के 5.875% था, जो 5.842% से ज़्यादा है, इसलिए मैं पॉइंट के साथ 5.75% ही लूँगा।
पी.एस. आप में से जो लोग सोच रहे हैं कि मैंने i का हल कैसे निकाला, तो बता दूं कि मैंने एक्सेल में रेट फंक्शन का उपयोग किया था।
मेरे बेटे ने दो हफ़्तों में एक ही होल में दो होल पूरे कर लिए। क्या संभावनाएँ हैं? मेरे बेटे का हैंडीकैप 1 है। पहला होल 151 गज और दूसरा होल 137 गज, दो अलग-अलग कोर्स पर।
ग्रेगरी बेयर द्वारा लिखित पुस्तक लाइफ: द ऑड्स (एण्ड हाउ टू इम्प्रूव देम) के अनुसार, पीजीए टूर में पार 3 होल पर एक होल इन वन की संभावना 2491 में 1 है। मेरा मानना है कि ये दूरियां पार 3 श्रेणी में आती हैं।
1 हैंडीकैप बहुत अच्छा है, इसलिए मैं पीजीए टूर खिलाड़ियों की तुलना में ज़्यादा छूट नहीं दूँगा। मान लीजिए आपके बेटे की प्रति पार 3 होल की संभावना 3,000 में 1 है। एक सामान्य गोल्ड कोर्स में लगभग चार पार 3 होल होंगे। मान लीजिए आपका बेटा रोज़ खेलता है। यानी हफ़्ते में 28 पार 3 होल। ठीक दो होल इन वन बनाने की संभावना (28,2)×(1/3000) 2 ×(2999/3000) 26 = 24,017 में 1 होगी।
मैंने हाल ही में एक लॉटरी में हिस्सा लिया था जिसमें 7,033 इनाम थे और कहा जाता है कि इनाम जीतने की संभावना 13 में से 1 है। मैंने 5 टिकट खरीदे। मेरे जीतने की वास्तविक संभावना क्या है? इसके अलावा, 40 बड़े इनाम हैं। मेरे बड़ा इनाम जीतने की संभावना क्या है?
सरलता के लिए, आइए इस तथ्य को नज़रअंदाज़ कर दें कि आप जितने ज़्यादा टिकट खरीदेंगे, प्रत्येक टिकट का मूल्य उतना ही कम होता जाएगा क्योंकि आप खुद से प्रतिस्पर्धा कर रहे होंगे। जैसा कि कहा गया है, सभी पाँच टिकट खोने की संभावना (12/13) 5 = 67.02% है। इसलिए कम से कम एक पुरस्कार जीतने की संभावना 32.98% है। आपके द्वारा कोई भी टिकट खरीदने से पहले ड्रम में कुल 7033×13=91,429 टिकट हैं। 91,429-40=91,389 बड़े पुरस्कार नहीं हैं। पाँच टिकटों के साथ कोई भी बड़ा पुरस्कार न जीतने की संभावना (91,389/91429) 5 = 99.78% है। इसलिए कम से कम एक बड़ा पुरस्कार जीतने की संभावना 0.22%, या 458 में 1 है।
हार्ट्स के खेल में, प्रत्येक खिलाड़ी को 13 पत्ते दिए जाते हैं। इन 13 पत्तों में से जिस सूट में सबसे ज़्यादा पत्ते होते हैं उसे "लॉन्ग सूट" कहा जाता है, जिसमें 4 से 13 पत्ते हो सकते हैं। इनमें से प्रत्येक के योग की प्रायिकता क्या है?
हार्ट्स में लॉन्ग सूट की संभावनाएं
| कार्ड | युग्म | संभावना |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 13 | 4 | 0.00000000000630 |
| कुल | 635013559600 | 1 |
72 का नियम कहता है कि आप वार्षिक रिटर्न दर को 72 से भाग दें, और इससे आपको अपने पैसे को दोगुना होने में लगने वाले वर्षों की संख्या पता चल जाएगी। उदाहरण के लिए, एक निवेश जो सालाना 10% रिटर्न देता है, उसका मूल्य दोगुना होने में 72/10 = 7.2 वर्ष लगेंगे। मेरा थोड़ा बेकार सा सवाल है, 72 क्यों?
सबसे पहले, "72 का नियम" आपके पैसे को दोगुना करने में लगने वाले समय का एक अनुमान है, न कि कोई सटीक उत्तर। नीचे दी गई तालिका विभिन्न वार्षिक ब्याज दरों के लिए "72 के नियम" के मान और वर्षों की सटीक संख्या दर्शाती है।
72 का नियम - पैसा दोगुना करने में लगने वाले वर्ष
| ब्याज दर | 72 का नियम | एकदम सही | अंतर |
|---|---|---|---|
| 0.01 | 72.00 | 69.66 | 2.34 |
| 0.02 | 36.00 | 35.00 | 1.00 |
| 0.03 | 24.00 | 23.45 | 0.55 |
| 0.04 | 18.00 | 17.67 | 0.33 |
| 0.05 | 14.40 | 14.21 | 0.19 |
| 0.06 | 12.00 | 11.90 | 0.10 |
| 0.07 | 10.29 | 10.24 | 0.04 |
| 0.08 | 9.00 | 9.01 | -0.01 |
| 0.09 | 8.00 | 8.04 | -0.04 |
| 0.10 | 7.20 | 7.27 | -0.07 |
| 0.11 | 6.55 | 6.64 | -0.10 |
| 0.12 | 6.00 | 6.12 | -0.12 |
| 0.13 | 5.54 | 5.67 | -0.13 |
| 0.14 | 5.14 | 5.29 | -0.15 |
| 0.15 | 4.80 | 4.96 | -0.16 |
| 0.16 | 4.50 | 4.67 | -0.17 |
| 0.17 | 4.24 | 4.41 | -0.18 |
| 0.18 | 4.00 | 4.19 | -0.19 |
| 0.19 | 3.79 | 3.98 | -0.20 |
| 0.20 | 3.60 | 3.80 | -0.20 |
72 क्यों? यह बिल्कुल 72 होना ज़रूरी नहीं है। यह बस वह संख्या है जो किसी निवेश पर मिलने वाली वास्तविक ब्याज दरों के लिए उपयुक्त है। यह लगभग 7.8469% की ब्याज दर के लिए सटीक है। 72 में कुछ खास नहीं है, जैसे π या e में है। कोई भी संख्या क्यों काम करती है? अगर ब्याज दर i है, तो आइए निवेश को दोगुना करने में लगने वाले वर्षों (y) की संख्या ज्ञात करें।
2 = (1+i) y
ln(2)= ln(1+i) y
ln(2)= y×ln(1+i)
y = ln(2)/ln(1+i)
यह शायद मेरा अब तक का सबसे अच्छा उत्तर नहीं है, लेकिन इस तर्क का पालन करने का प्रयास करें: मान लें y=ln(x).
dy/dx=1/x.
1/x =~ x, x के मान 1 के करीब होने पर।
अतः dy/dx = ~ 1, x के मान 1 के करीब होने पर।
अतः x के मान 1 के निकट होने पर ln(x) का ढलान 1 के निकट होगा।
अतः x के मान 0 के निकट होने पर ln(1+x) का ढलान 1 के निकट होगा।
"72 का नियम" कह रहा है कि .72/i =~ .6931/ln(1+i).
हमने यह स्थापित किया है कि i और ln(1+i) 0 के निकट i के मानों के लिए समान हैं।
अतः 0 के निकट i के मानों के लिए 1/i और 1/ln(1+i) समान हैं।
69.31 के स्थान पर 72 का उपयोग करने से i और ln(1+i) के बीच अंतर के लिए i के मान लगभग 8% समायोजित हो जाते हैं।
मुझे उम्मीद है कि आपको कुछ समझ में आया होगा। मेरी गणना थोड़ी ज़ंग खा गई है; मुझे खुद को यह समझाने में घंटों लग गए।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
हाल ही में एक स्ट्रीट मेले में, एक खेल चल रहा था जिसमें संख्याओं का एक क्षेत्र था, जिसमें उथले कप और गेंदों का एक कप था, और इसमें जोड़ भी शामिल था। मैंने खेल का नाम नहीं पूछा, और मैंने लगभग एक घंटे तक इंटरनेट पर खोज की, लेकिन इसके बारे में कुछ नहीं मिला। मुझे लगा कि शायद आपको इसके बारे में कुछ जानकारी हो, इसके ऑड्स, या कम से कम नाम तो पता ही होगा।
उस खेल के लिए उद्योग जगत का नाम है रैज़ल डैज़ल। मुझे याद है कि मैंने इसे बचपन में दक्षिणी कैलिफ़ोर्निया में और पिछले साल मेक्सिको के सैन फ़ेलिप में देखा था। इसे आमतौर पर फ़ुटबॉल खेल जैसा दिखाने के लिए डिज़ाइन किया जाता है। मेरी राय में, यह खेल कार्निवल गेम के सबसे बुरे घोटालों में से एक है। न्यूयॉर्क राज्य को इसे अनुमति देने के लिए शर्म आनी चाहिए। कुछ शोधों के आधार पर, नियम जगह-जगह अलग-अलग होते हैं, लेकिन धोखाधड़ी का सार हमेशा एक ही होता है।
यह क्रेप्स में फ़ील्ड बेट के समान ही भ्रम पर आधारित है। फ़ील्ड बेट से परिचित न होने वाले पाठकों के लिए, खिलाड़ी तभी जीतता है जब दो पासों के रोल का योग 2, 3, 4, 9, 10, 11, या 12 हो। हारने वाली संख्याएँ 5, 6, 7, और 8 हैं। जीतने पर सम राशि मिलती है, सिवाय इसके कि 2 पर 2 से 1 और 12 पर 3 से 1 का भुगतान होता है (कंजूस हैराह के कैसिनो को छोड़कर, जहाँ वे केवल 12 पर 2 से 1 का भुगतान करते हैं)। गणित में कमज़ोर जुआरी यह गलत तर्क दे सकता है कि यह एक अच्छा दांव है क्योंकि इसमें 7 योग जीतने वाले और केवल 4 हारने वाले होते हैं। ऑड्स घर के पक्ष में इसलिए होते हैं क्योंकि हारने वाले नंबरों के रोल होने की सबसे ज़्यादा संभावना होती है।
यहां रैज़ल डैज़ल के विशिष्ट नियम दिए गए हैं, जो डोनाल्ड ए. बेरी और रोनाल्ड आर. रीगल द्वारा लिखे गए लेख "एक निश्चित कार्निवल गेम जीतने की संभावनाएं " से लिए गए हैं, जो द अमेरिकन स्टेटिस्टिशियन के नवंबर 1978 के अंक में प्रकाशित हुआ था।
- इस खेल का उद्देश्य फ़ुटबॉल मैदान में 100 गज आगे बढ़ना है। ऐसा करने पर खिलाड़ी को कोई अच्छा इनाम दिया जाएगा।
- खिलाड़ी प्रति खेल एक निर्दिष्ट शुल्क का भुगतान करना शुरू करता है, जैसे कि $1.
- खिलाड़ी 11 गुणा 13 के ग्रिड पर 8 कंचे फेंकेगा। प्रत्येक कंचा 143 छेदों में से एक में गिरेगा।
- प्रत्येक छेद में 1 से 6 तक अंक होते हैं। निम्नलिखित तालिका प्रत्येक अंक की संख्या की आवृत्ति दर्शाती है।
रैज़ल डैज़ल पॉइंट्स वितरण
अंक संख्या
सवारसंभावना 1 11 0.076923 2 19 0.132867 3 39 0.272727 4 44 0.307692 5 19 0.132867 6 11 0.076923 कुल 143 1.000000 - कुल अंकों को जोड़ा जाएगा। कार्नी एक रूपांतरण चार्ट पर अंकों का योग देखेगा ताकि पता चल सके कि खिलाड़ी कितने गज आगे बढ़ता है। रूपांतरण चार्ट नीचे दिखाया गया है।
रैज़ल डैज़ल रूपांतरण चार्ट
अंक गज
प्राप्त की8 100 9 100 10 50 11 30 12 50 13 50 14 20 15 15 16 10 17 5 18 से 38 0 39 5 40 5 41 15 42 20 43 50 44 50 45 30 46 50 47 100 48 100 - यदि खिलाड़ी कुल 29 रोल करता है, तो उसके बाद के सभी रोल के लिए शुल्क दोगुना कर दिया जाएगा, और खिलाड़ी को फुटबॉल मैदान के दूसरे छोर पर पहुंचने पर एक अतिरिक्त पुरस्कार दिया जाएगा।
प्रत्येक कंचे पर औसत अंक 3.52 हैं, और मानक विचलन 1.31 है। ध्यान दें कि 3 और 4 अंकों की प्रायिकता सबसे ज़्यादा है। इससे मानक विचलन कम रहता है, और कई कंचों का योग अपेक्षा के करीब रहता है। तुलना करें तो, एक पासे के लुढ़कने का मानक विचलन 1.71 है।
इसके बाद, ध्यान दें कि यार्डेज रूपांतरण चार्ट पर 20 जीतने वाले योग और 21 हारने वाले योग कैसे हैं। कार्निवल खेलों पर दांव लगाने वाला कोई भी मूर्ख शायद गलत तर्क दे सकता है कि उसके आगे बढ़ने की संभावना 20/41 या 48.8% है। मुझे आश्चर्य नहीं होगा अगर कार्निवल वाले झूठा दावा करें कि ये आगे बढ़ने की संभावनाएँ हैं। हालाँकि, मैदानी दांव की तरह, सबसे संभावित परिणाम कुछ भी नहीं जीतते हैं।
अगली तालिका प्रत्येक बारी के अंकों की प्रायिकता, अर्जित गज और अपेक्षित अर्जित गज दर्शाती है। निचले दाएँ कक्ष में प्रति बारी औसत अर्जित गज 0.0196 है।
प्रति मोड़ अपेक्षित गज की प्राप्ति
| अंक | संभावना | गज प्राप्त की | अपेक्षित गज प्राप्त की |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 30 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 13 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 25 | 0.07566411880 | 0 | 0.00000000000 |
| 26 | 0.09221675088 | 0 | 0.00000000000 |
| 27 | 0.10431970222 | 0 | 0.00000000000 |
| 28 | 0.10958441738 | 0 | 0.00000000000 |
| 29 | 0.10689316272 | 0 | 0.00000000000 |
| 30 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 32 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 34 | 0.03009743061 | 0 | 0.00000000000 |
| 35 | 0.01833921711 | 0 | 0.00000000000 |
| 36 | 0.01023355162 | 0 | 0.00000000000 |
| 37 | 0.00520465303 | 0 | 0.00000000000 |
| 38 | 0.00239815734 | 0 | 0.00000000000 |
| 39 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 42 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 44 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 30 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 47 | 0.00000000176 | 100 | 0.00000017647 |
| 48 | 0.00000000005 | 100 | 0.00000000464 |
| योग | 1.00000000000 | 0 | 0.01961648451 |
यहां 17.5 मिलियन खेलों के यादृच्छिक सिमुलेशन के कुछ परिणाम दिए गए हैं।
रैज़ल डैज़ल सिमुलेशन परिणाम
| सवाल | उत्तर |
| प्रति बारी उन्नति की संभावना | 0.0028 |
| प्रति बारी अपेक्षित गज की प्राप्ति | 0.0196 |
| प्रति उन्नति अपेक्षित गज प्राप्ति | 6.9698 |
| प्रति खेल अपेक्षित बारी | 5238.7950 |
| प्रति गेम औसत डबल्स | 559.9874 |
| प्रति खेल औसत पुरस्कार | 560.9874 |
मैं प्रति गेम औसत कुल दांव बताना चाहता था, लेकिन मेरा कंप्यूटर इतनी बड़ी संख्याओं को संभाल नहीं सकता। औसत खेल में खिलाड़ी ने प्रति गेम 5,239 बार के औसत से 560 बार अपना दांव दोगुना किया। सिमुलेशन में एक खेल में खिलाड़ी ने अपना दांव 1,800 बार दोगुना किया। 560 बार के औसत पर भी, प्रति रोल दांव $3.77 × 10 168 होगा, यह मानते हुए कि शुरुआती दांव $1 है। यह ज्ञात ब्रह्मांड में परमाणुओं की संख्या से कई गुना अधिक परिमाण है ( स्रोत )।
अगर कोई खिलाड़ी हर 355 प्ले में सिर्फ़ एक बार ही आगे बढ़ रहा है, तो वह सबसे भोला-भाला खिलाड़ी भी ज़्यादा देर तक नहीं खेल पाएगा। कार्नीज़ शुरुआत में खिलाड़ी के पक्ष में धोखा देगा। वह खिलाड़ी के फ़्री रोल देख सकता है, या अंक जोड़ने में झूठ बोल सकता है, जिससे खिलाड़ी का आत्मविश्वास बढ़ाने के लिए उसे जीत का कुल योग मिल जाता है। मैंने यह खेल कभी नहीं खेला, लेकिन मुझे लगता है कि जब खिलाड़ी रेड ज़ोन (टचडाउन से 20 गज या उससे कम) के करीब पहुँच जाएगा, तो कार्नीज़ निष्पक्ष रूप से खेलना शुरू कर देगा। खिलाड़ी सोच सकता है कि वह अचानक कहाँ पहुँच रहा है, लेकिन पहले से ही निवेश किए गए पैसे और गोल लाइन के इतने करीब होने के कारण, वह उस यार्डेज को छोड़ने में झिझकेगा जिसके लिए उसने पहले ही भुगतान कर दिया है।
लिंक
- रैज़ल डैज़ल , ऑन द मिडवे पुस्तक से उद्धरण।
- कोलाहलपूर्ण चकाचौंध Carny बोर्ड खेल आर्केड घोटाला .
- डोनाल्ड ए. बेरी और रोनाल्ड आर. रीगल द्वारा एक निश्चित कार्निवल गेम जीतने की संभावनाएं
हाल ही में एक कार्निवल में टिक-टैक-टो जैसा खेल चल रहा था। £1 प्रति गेम के हिसाब से आपको तीन बेहद उछाल वाली गेंदें एक बड़े लकड़ी के डिब्बे की ओर फेंकनी होती हैं जिसके नीचे 9 पॉकेट हैं। मान लीजिए कि हर गेंद एक खास वर्ग में गिरती है, तो जीतने की संभावना क्या होगी?
जीतने के आठ तरीके हैं: तीन पंक्तियाँ, तीन स्तंभ और दो विकर्ण। कुल मिलाकर (9,3) = 84 तरीके हैं जिनसे 9 में से 3 वर्ग चुने जा सकते हैं। इसलिए जीतने की संभावना 8/84 = 9.52% है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
मोनोपोली खेलने के लिए आपकी क्या सलाह है?
मोनोपोली के लिए मेरे जादूगर की बुनियादी रणनीति यहां दी गई है:
- सब कुछ खरीद लो। अगर संपत्ति आपको एकाधिकार बनाने में मदद नहीं करती, किसी और को रोकने में मदद नहीं करती, और सौदेबाजी के लिए कम मूल्यवान है, तो उन्नत खिलाड़ी अपवाद कर सकते हैं। नकदी की कमी की स्थिति में उपयोगिताओं को भी अस्वीकार किया जा सकता है।
- जितना हो सके, उतना अच्छा व्यापार करें। यहीं पर कौशल की ज़रूरत पड़ती है। सबसे अच्छे सेट के लिए व्यापार करने की कोशिश करें। मैं उन्हें सामान्य तौर पर इस प्रकार क्रमबद्ध करता हूँ: नारंगी, पीला, हल्का नीला, गहरा नीला, हल्का बैंगनी, लाल, हरा, गहरा बैंगनी। यह परिस्थितियों के अनुसार अलग-अलग होगा। कम पैसे वाले खेल में, उन सेटों को प्राथमिकता दें जिन्हें विकसित करना सस्ता हो, जैसे हल्के नीले रंग। ज़्यादा पैसे वाले खेल में, उन सेटों को चुनें जिन पर पैसा खर्च करने की ज़्यादा संभावना हो, जैसे पीले या गहरे नीले रंग।
- एक बार जब आपको एक सेट मिल जाए, चाहे प्राकृतिक रूप से या व्यापार से, तो जल्दी से निर्माण शुरू कर दें। जितनी जल्दी हो सके, प्रत्येक संपत्ति पर तीन घर बनाने की कोशिश करें। तीन के बाद प्रति घर सीमांत रिटर्न कम हो जाता है। अपनी अधिकांश अन्य संपत्तियों को गिरवी रख दें और अपनी नकदी खर्च करें। आप छोटे-मोटे खर्चों के लिए थोड़ी इक्विटी छोड़ना चाहेंगे। अपना पैसा खर्च न करना युद्ध में एक सैनिक द्वारा अपनी गोलियों का इस्तेमाल न करने जैसा है।
- सभी बेतुके घरेलू नियमों का विरोध करें। यह ख़ास तौर पर मुफ़्त पार्किंग के पैसे वाले पॉट के लिए लागू होता है (मुझे वह बिल्कुल पसंद नहीं!)। अगर आप अपने विरोधियों से ज़्यादा कुशल हैं, तो आप खेल की अनियमितता को कम से कम रखना चाहेंगे।
यदि कोई बंदर रूबिक्स क्यूब के साथ खेल रहा हो, तो किसी भी समय हल किये गए पैटर्न में उसके होने की संभावना क्या होगी?
घन के छह केंद्रीय फलक स्थिर हैं। फलकों को घुमाकर आप केवल कोनों और किनारों को पुनर्व्यवस्थित कर सकते हैं। यदि आप घन को अलग कर दें, तो प्रत्येक टुकड़े की दिशा की परवाह किए बिना, आठ कोनों को व्यवस्थित करने के 8! = 40,320 तरीके होंगे। इसी प्रकार, दिशा की परवाह किए बिना, 12 किनारों को व्यवस्थित करने के 12! = 479,001,600 तरीके हैं।
प्रत्येक कोने को तीन तरीकों से उन्मुख किया जा सकता है, कुल मिलाकर 3 8 = 6,561 कोने अभिविन्यास। इसी प्रकार, प्रत्येक किनारे के टुकड़े को दो तरीकों से उन्मुख किया जा सकता है, कुल मिलाकर 2 12 = 4,096 किनारे अभिविन्यास।
इसलिए, अगर हम घन को अलग कर सकें, और किनारों और कोनों के समूहों को पुनर्व्यवस्थित कर सकें, तो 8! × 12! × 3 8 × 2 12 = 519,024,039,293,878,000,000 संभावित क्रमपरिवर्तन होंगे। हालाँकि, इन सभी क्रमपरिवर्तनों को फलकों को घुमाकर प्रारंभिक स्थिति से प्राप्त नहीं किया जा सकता है।
पहली बात, सिर्फ़ एक कोने को घुमाकर बाकी सब कुछ वैसा ही छोड़ना नामुमकिन है। घुमावों के किसी भी संयोजन से यह संभव नहीं होगा। मूलतः, हर क्रिया की एक प्रतिक्रिया होती है। अगर आप एक कोने को घुमाना चाहें, तो यह किसी न किसी तरह से बाकी मोहरों को बिगाड़ देगा। इसी तरह, सिर्फ़ एक किनारे वाले मोहरे को फ़्लॉप करना नामुमकिन है। इन कारणों से, हमें क्रमचयों की संख्या को 3 × 2 = 6 से भाग देना होगा।
दूसरा, क्यूब के बाकी हिस्सों को छेड़े बिना दो किनारे वाले टुकड़ों को बदलना असंभव है। यह इस उत्तर का सबसे कठिन हिस्सा है जिसे समझाना है। रुबिक क्यूब के साथ आप बस एक बार में एक चेहरा घुमा सकते हैं। प्रत्येक चाल चार किनारे वाले टुकड़ों और चार कोने वाले टुकड़ों को घुमाती है, कुल मिलाकर आठ टुकड़े घूमते हैं। घुमावों के अनुक्रम को 8 से विभाज्य टुकड़ों की संख्या के आंदोलनों द्वारा दर्शाया जा सकता है। अक्सर चालों के एक क्रम के परिणामस्वरूप दो चालें एक दूसरे को रद्द कर देती हैं। हालांकि, घुमावों के किसी भी क्रम के साथ हमेशा सम संख्या में टुकड़े घूमेंगे। दो किनारे वाले टुकड़ों की अदला-बदली करने के लिए एक चाल, एक विषम संख्या होगी, जो सम संख्याओं के किसी भी समूह के योग से प्राप्त नहीं की जा सकती। गणितज्ञ इसे समता समस्या कहेंगे।
तो रुबिक क्यूब के क्रमपरिवर्तनों के 3 × 2 × 2 = 12 संभावित समूह हैं। अगर आप रुबिक क्यूब को अलग-अलग करके बेतरतीब ढंग से वापस जोड़ दें, तो 12 में से 1 संभावना है कि वह हल हो जाएगा। तो रुबिक क्यूब में क्रमपरिवर्तनों की कुल संख्या 8! × 12! × 3 12 × 2 12 / 12 = 43,252,003,274,489,900,000 है। अगर आपके पास सात अरब बंदर हों, जो दुनिया की मानव आबादी के लगभग बराबर हों, और रुबिक क्यूब के साथ बेतरतीब ढंग से, प्रति सेकंड एक चक्कर की दर से खेल रहे हों, तो एक क्यूब औसतन हर 196 साल में एक बार हल की गई स्थिति से गुज़रेगा।
लिंक
मैं हार्ट्स खेल रहा था और मुझे 10 हार्ट्स मिले। इसकी संभावना क्या है?
जो लोग हार्ट्स के नियमों से परिचित नहीं हैं, उनके लिए बता दें कि खेल की शुरुआत चार खिलाड़ियों को 13-13 कार्ड बाँटने से होती है। हार्ट्स का रंग खेल के लिए महत्वपूर्ण होता है, इसलिए आपको कितने कार्ड मिलते हैं, यह भी महत्वपूर्ण है। नीचे दी गई तालिका 0 से 13 हार्ट्स मिलने की संभावना दर्शाती है।
13 कार्डों में से 0 से 13 पान की संभावना
| दिल | युग्म | संभावना | श्लोक में |
|---|---|---|---|
| 13 | 1 | 0.0000000000016 | 635,013,559,600.0 में 1 |
| 12 | 507 | 0.0000000007984 | 1,252,492,228.0 में 1 |
| 11 | 57,798 | 0.0000000910185 | 10,986,773.9 में 1 |
| 10 | 2,613,754 | 0.0000041160601 | 242,950.8 में 1 |
| 9 | 58,809,465 | 0.0000926113531 | 10,797.8 में 1 |
| 8 | 740,999,259 | 0.0011669030492 | 857.0 में 1 |
| 7 | 5,598,661,068 | 0.0088166008164 | 113.4 में 1 |
| 6 | 26,393,687,892 | 0.0415639752774 | 24.1 में 1 |
| 5 | 79,181,063,676 | 0.1246919258321 | 8.0 में 1 |
| 4 | 151,519,319,380 | 0.2386080062219 | 4.2 में 1 |
| 3 | 181,823,183,256 | 0.2863296074662 | 3.5 में 1 |
| 2 | 130,732,371,432 | 0.2058733541286 | 4.9 में 1 |
| 1 | 50,840,366,668 | 0.0800618599389 | 12.5 में 1 |
| 0 | 8,122,425,444 | 0.0127909480376 | 78.2 में 1 |
| कुल | 635,013,559,600 | 1.0000000000000 |
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
कैसीनो प्रमोशन में, जहाँ अभी भी असली ड्रम (इलेक्ट्रॉनिक नहीं) में नियमित टिकट इस्तेमाल होते हैं, जहाँ आप प्लेयर्स डेस्क पर अपने टिकट प्रिंट करके ड्रम में डालते हैं - क्या आप ड्रम में डालने से पहले अपने टिकटों को मोड़ते/सींचते हैं? क्या आपको लगता है कि मुड़े हुए टिकटों के चुने जाने की संभावना ज़्यादा होती है?
मुझे उम्मीद है आप खुश होंगे। इस सवाल का जवाब देने के लिए, मैंने ऑफिस डिपो से टिकटों का एक बड़ा रोल खरीदा। फिर मैंने उनमें से 500 टिकटों को एक कागज़ के थैले में रखा, आधा मोड़कर, लगभग 90 डिग्री के कोण पर, और बाकी आधा खोलकर। फिर मैंने छह स्वयंसेवकों से कहा कि वे एक-एक करके 40 से 60 टिकट निकालें, और साथ में एक और टिकट भी, और मैं नतीजे दर्ज करता रहा। ये रहे नतीजे।
ड्राइंग टिकट प्रयोग
| विषय | मुड़ा हुआ | सामने आया | कुल |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| कुल | 175 | 125 | 300 |
इस प्रकार, निकाले गए टिकटों में से 58.3% टिकटें मोड़ दी गईं!
अगर यह मान लिया जाए कि तह करने का कोई असर नहीं हुआ, तो ये नतीजे उम्मीदों से 2.89 मानक विचलन दूर होंगे। यह मानते हुए कि तह करने से ऑड्स पर कोई असर नहीं पड़ा, इतने या उससे ज़्यादा तह किए हुए टिकट मिलने की संभावना 0.19% या 514 में से 1 है।
मैं यह भी कहना चाहूँगा कि जिन लोगों ने जल्दी-जल्दी टिकट निकाले, उनके मुड़े हुए टिकट निकालने की संभावना ज़्यादा थी। जिन लोगों ने हर बार सावधानी से समय निकाला, उनके टिकट लगभग 50/50 के बराबर थे।
इसलिए, मेरा निष्कर्ष निश्चित रूप से उन्हें मोड़ना है।
इस प्रश्न पर चर्चा के लिए कृपया मेरे फोरम विज़ार्ड ऑफ़ वेगास पर जाएँ।