जादूगर से पूछो #284
क्या आपने सिएटल की उस कार डीलरशिप के बारे में सुना है जिसे सीहॉक्स द्वारा जायंट्स को हराने के कारण $420,000 का भुगतान करना पड़ा? मैंने पढ़ा है कि उन्हें इसके बदले बीमा पॉलिसी के लिए $7,000 का भुगतान करना पड़ा। उचित प्रीमियम क्या होता?
1983 से 2012 सीज़न तक के हर NFL गेम के आधार पर, किसी भी गेम की एक खास टीम को शटआउट कर दिया गया था। हालाँकि, सात अंकों से पिछड़ने वाली टीम होने के नाते, औसत ओवर/अंडर वाले गेम में, मैं कहूँगा कि जायंट्स के शटआउट होने की संभावना औसत से ज़्यादा थी। उस गेम में ओवर/अंडर 41 था। आइए जायंट्स के अपेक्षित अंकों की संख्या जानने के लिए थोड़ा बीजगणित करें।
होने देना:
s=सीहॉक्स अंक
g=दिग्गज अंक
हम जानते हैं कि s+g=41 और s=g+7, जो कि पॉइंट स्प्रेड और ओवर/अंडर टोटल पर आधारित है।
दूसरे समीकरण को पहले समीकरण में प्रतिस्थापित करने पर:
(जी+7) + जी = 41
2जी +7 = 41
2जी = 34
जी = 17
अब, आइए 1983 से 2012 के सीज़न के आधार पर, प्रत्येक टीम के अनुमानित अंकों के आधार पर शटआउट की संभावना पर नज़र डालें। मैंने उन पंक्तियों को छोड़ दिया है जहाँ नमूना आकार शून्य था।
शटआउट की संभावना
| अनुमानित अंक | नमूने का आकार | शटआउट | अनुपात |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11.00 | 13 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12.00 | 34 | 2 | 5.9% |
| 12.25 | 36 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 39 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16.00 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18.00 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21.00 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 48 | 0 | 0.0% |
| 29.25 | 34 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 25 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
अगले चरण इतने जटिल हैं कि उन्हें यहां समझाना संभव नहीं है, लेकिन मैंने अनुमानित अंकों की संख्या के आधार पर शटआउट की संभावना के लिए एक सूत्र विकसित किया है।
p = अनुमानित अंक.
x = 1.562545 -0.302485 * पी
शटआउट की संभावना = e x /(1+e x )
निम्नलिखित चार्ट 14 से 22 अंकों के लिए शटआउट की वास्तविक और अनुमानित संभावना को दर्शाता है।
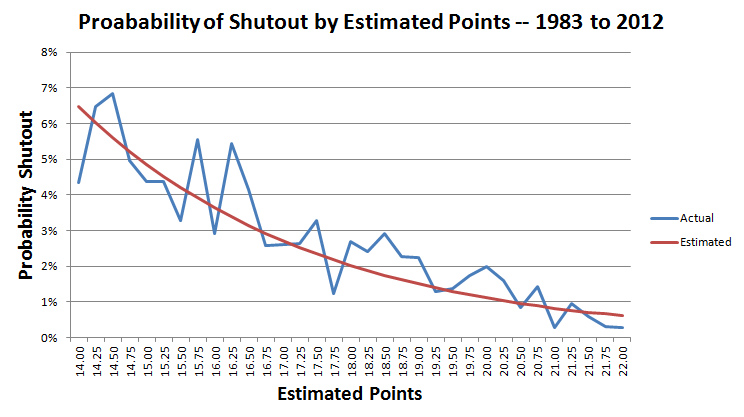
इस खेल में जायंट्स को 17 अंक बनाने की उम्मीद थी।
तालिका के ऊपर दिए गए सूत्र का उपयोग करें:
x = 1.562545 -0.302485 * 17 = -3.579706
शटआउट की संभावना = exp(-3.579706)/( exp(-3.579706)+1) = 2.71%. सटीक रूप से, 0.0271275.
यह देखते हुए कि जायंट्स के शटआउट की स्थिति में डीलरशिप को $420,000 का भुगतान करना पड़ता, पॉलिसी की उचित लागत $420,000 × 0.0271275 = $11,394 होती। आमतौर पर, इस तरह के असामान्य प्रचारों का बीमा करने वाली बीमा कंपनियाँ उचित लागत से दोगुनी होती हैं, इसलिए मुझे $22,788 का प्रीमियम मिलने की उम्मीद थी। इसलिए, डीलरशिप द्वारा चुकाया गया $7,000 का प्रीमियम एक चोरी था। यह मानते हुए कि बॉस ने गणना की है, मैं उस व्यक्ति की जगह नहीं लेना चाहूँगा जिसने $7,000 के प्रीमियम की गणना की थी।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।
इसका क्या प्रमाण है कि कोई सबसे बड़ा अभाज्य संख्या नहीं है?
मान लीजिए, एक मिनट के लिए, एक सबसे बड़ा अभाज्य संख्या है। हम अभाज्य संख्याओं को p1=2, p2=3, p3=5, p4=7, ... pL = सबसे बड़ा अभाज्य संख्या मान सकते हैं।
अब संख्या x = p1*p2*p3*p4*...*pL + 1 परिभाषित करें।
अभाज्य संख्या होने का अर्थ यह है कि कोई भी अन्य छोटा अभाज्य संख्या इसमें समान रूप से विभाजित नहीं होता।
यदि हम p1, p2, p3, ... pL को x से विभाजित करें तो हमें हर बार शेषफल 1 प्राप्त होता है।
आप तर्क दे सकते हैं कि शायद pL से बड़ा कोई अभाज्य संख्या x को समान रूप से विभाजित करती है। हाँ, लेकिन तब आपको तथाकथित सबसे बड़े अभाज्य संख्या से भी बड़ा अभाज्य संख्या मिल जाती। यदि ऐसा नहीं है, तो x एक नया सबसे बड़ा अभाज्य संख्या बन जाता है, जो विरोधाभास द्वारा सबसे बड़े अभाज्य संख्या के अस्तित्व के प्रारंभिक अनुमान को सिद्ध करता है।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर पूछा गया और इस पर चर्चा की गई।
क्या आप बिजनेस इनसाइडर पर प्रकाशित लेख'गणित कहता है कि आपको अभी मेगा मिलियन्स टिकट खरीदना चाहिए' से सहमत हैं?
नहीं, मैं इससे सहमत नहीं हूँ। यह पत्रकारिता का एक घटिया नमूना है और बिज़नेस इनसाइडर को इससे शर्मिंदा होना चाहिए।
शुरुआत में, यह लेख 17 दिसंबर, 2013 को, उस शाम 636 मिलियन डॉलर के ड्रॉ से पहले प्रकाशित हुआ था। आइए, 1 डॉलर के टिकट के मूल्य का आकलन करने के लिए गणित पर नज़र डालें। नीचे दी गई तालिका 636 मिलियन डॉलर के जैकपॉट के सभी संभावित परिणामों की संभावना और अपेक्षित रिटर्न को दर्शाती है, जिसमें एकमुश्त जुर्माना, कर और जैकपॉट शेयरिंग जैसी बातों पर विचार करने से पहले, यह दर्शाया गया है। शीर्ष तीन संभावनाएँ वैज्ञानिक संकेतन में हैं क्योंकि संख्याएँ बहुत छोटी हैं।
मेगा मिलियंस - 636 मिलियन डॉलर का जैकपॉट
| पकड़ना | मेगा बॉल | भुगतान करता है | युग्म | संभावना | वापस करना |
|---|---|---|---|---|---|
| 5 | हाँ | $636,000,000 | 1 | 3.86ई-09 | 2.456634 |
| 5 | नहीं | $1,000,000 | 14 | 5.41ई-08 | 0.054077 |
| 4 | हाँ | $5,000 | 350 | 1.35ई-06 | 0.006760 |
| 4 | नहीं | $500 | 4,900 | 0.000019 | 0.009463 |
| 3 | हाँ | $50 | 24,150 | 0.000093 | 0.004664 |
| 3 | नहीं | $5 | 338,100 | 0.001306 | 0.006530 |
| 2 | हाँ | $5 | 547,400 | 0.002114 | 0.010572 |
| 1 | हाँ | $2 | 4,584,475 | 0.017708 | 0.035416 |
| 0 | हाँ | $1 | 12,103,014 | 0.046749 | 0.046749 |
| परास्त | $0 | 241,288,446 | 0.932008 | 0.000000 | |
| कुल | 258,890,850 | 1.000000 | 2.630865 | ||
इससे पता चलता है कि एक डॉलर के टिकट पर 2.630864 डॉलर वापस मिलेंगे। टिकट की कीमत से एक डॉलर घटाने के बाद, अपेक्षित लाभ 1.630864 डॉलर होगा। बिज़नेस इनसाइडर को 1.632029 डॉलर मिलेंगे। 0.001164 का अंतर है, लेकिन कोई बड़ी बात नहीं है।
हालाँकि, तीन चीजें हैं जो मूल्य को काफी कम कर देती हैं:
- एकमुश्त जुर्माना.
- कर.
- जैकपॉट साझा करना.
आइये हम एक-एक करके उन पर नजर डालें।
बड़े लॉटरी प्रोग्रेसिव जैकपॉट आमतौर पर लगभग 30 साल की वार्षिकी के रूप में दिए जाते हैं, जिसमें मेगा मिलियन्स भी शामिल है। अगर विजेता पूरी रकम एक साथ चाहता है, जैसा कि ज़्यादातर लोग चाहते हैं, तो उसे एक बड़ी कटौती करनी होगी। यह उचित ही है क्योंकि आज का एक डॉलर भविष्य के एक डॉलर से ज़्यादा कीमती है। 17 दिसंबर, 2013 के ड्रॉ में, कुल पुरस्कार राशि घटाकर $347.6 मिलियन कर दी गई, यानी विज्ञापित जैकपॉट का 54.65%।
अब, आइए करों पर नज़र डालते हैं। उच्चतम संघीय सीमांत आयकर दर 39.6% है। राज्य कर 0% से 12.3% तक हैं, तो मान लीजिए कि औसतन 6% है। 45.6% करों को हटाने के बाद, हमारे पास $189.1 मिलियन बचते हैं।
अब सबसे मुश्किल हिस्सा आता है - जैकपॉट शेयरिंग। यह ध्यान देने योग्य है कि 22 अक्टूबर, 2013 के ड्रॉ से शुरू होकर मेगा मिलियंस ने नियमों को 75-15 प्रारूप में बदल दिया, जहां वे 1 से 75 तक पांच नंबर खींचते हैं, और फिर 1 से 15 के एक अलग पूल से एक नंबर निकालते हैं। इससे जीतने की संभावना 258,890,850 में 1 तक कम हो गई, जाहिर तौर पर बड़ा जैकपॉट पाने के प्रयास में। LottoReport.com से जैकपॉट और बिक्री डेटा का उपयोग करके, तब से केवल 17 ड्रॉ को देखते हुए, मुझे लगता है कि जैकपॉट के आकार और मांग के बीच एक घातीय संबंध है। वैसे, मुझे पावरबॉल लॉटरी के लिए भी यही बात मिली। घातीय प्रतिगमन का उपयोग करते हुए, कुल बेची गई टिकटों (मिलियन में) के लिए मेरा सूत्र 12.422 × exp(0.0052 × j) है, उदाहरण के लिए, $636 मिलियन के जैकपॉट के लिए, अपेक्षित बिक्री 12.422 * exp(0.0052*636) = 339.2 (मिलियन) होगी। वास्तविक बिक्री $337 मिलियन थी, यानी काफी करीब।
336,545,306 टिकटों की वास्तविक बिक्री के आधार पर, हम 336,545,306/258,890,850 = 1.300 विजेताओं की उम्मीद कर सकते हैं। प्रासंगिक प्रश्न यह है कि यदि आप जीतते हैं, तो आप कितने अन्य लोगों के साथ धनराशि साझा करने की अपेक्षा कर सकते हैं? पॉइसन वितरण को देखकर इसका उत्तर आसानी से मिल जाता है। 1.3 विजेताओं का माध्य दिया गया है, तो ठीक x विजेताओं की प्रायिकता exp(1.3)×1.3 x /fact(x) है। निम्न तालिका 0 से 10 अन्य विजेताओं की प्रायिकता, प्रत्येक स्थिति में जैकपॉट में आपका हिस्सा, और अपेक्षित हिस्सा, यह मानते हुए कि आप जीतते हैं, दर्शाती है।
अपेक्षित जैकपॉट शेयर औसतन 1.3 अन्य विजेताओं को दिया गया
| अन्य विजेता | संभावना | जैकपॉट शेयर | अपेक्षित शेयर |
|---|---|---|---|
| 10 | 0.000001 | 0.090909 | 0.000000 |
| 9 | 0.000008 | 0.100000 | 0.000001 |
| 8 | 0.000055 | 0.111111 | 0.000006 |
| 7 | 0.000339 | 0.125000 | 0.000042 |
| 6 | 0.001827 | 0.142857 | 0.000261 |
| 5 | 0.008431 | 0.166667 | 0.001405 |
| 4 | 0.032429 | 0.200000 | 0.006486 |
| 3 | 0.099786 | 0.250000 | 0.024946 |
| 2 | 0.230283 | 0.333333 | 0.076761 |
| 1 | 0.354295 | 0.500000 | 0.177148 |
| 0 | 0.272545 | 1.000000 | 0.272545 |
| कुल | 1.000000 | 0.559602 |
नीचे के दाहिने कक्ष से पता चलता है कि आप 55.96% धनराशि अपने पास रख सकते हैं, तथा शेष 44.04% धनराशि उन अन्य विजेताओं को मिलेगी, जिनके साथ आपको उसे साझा करना होगा।
अब हमारा $636 मिलियन का जैकपॉट घटकर $189.1 × 55.96% = $105.8 मिलियन रह गया है। आइए देखें कि इस आंकड़े को जैकपॉट मानकर रिटर्न टेबल कैसी दिखती है।
मेगा मिलियंस - $105.8 मिलियन का जैकपॉट
| पकड़ना | मेगा बॉल | भुगतान करता है | युग्म | संभावना | वापस करना |
|---|---|---|---|---|---|
| 5 | हाँ | $105,800,000 | 1 | 3.86ई-09 | 0.408666 |
| 5 | नहीं | $1,000,000 | 14 | 5.41ई-08 | 0.054077 |
| 4 | हाँ | $5,000 | 350 | 1.35ई-06 | 0.006760 |
| 4 | नहीं | $500 | 4,900 | 0.000019 | 0.009463 |
| 3 | हाँ | $50 | 24,150 | 0.000093 | 0.004664 |
| 3 | नहीं | $5 | 338,100 | 0.001306 | 0.006530 |
| 2 | हाँ | $5 | 547,400 | 0.002114 | 0.010572 |
| 1 | हाँ | $2 | 4,584,475 | 0.017708 | 0.035416 |
| 0 | हाँ | $1 | 12,103,014 | 0.046749 | 0.046749 |
| परास्त | $0 | 241,288,446 | 0.932008 | 0.000000 | |
| कुल | 258,890,850 | 1.000000 | 0.582898 | ||
नीचे दाएँ कोने में 58.29% का अपेक्षित रिटर्न दिखाया गया है। दूसरे शब्दों में, आपके $1 के निवेश से लगभग 58 सेंट की वापसी की उम्मीद की जा सकती है, जबकि अपेक्षित नुकसान या हाउस एज लगभग 42% है। क्या यह गणित आपको टिकट खरीदने के लिए प्रेरित कर रहा है?
लेख के अनुसार, "अतः, जब तक 730 मिलियन से कम टिकटें बिकती हैं, जो कि अभी काफी संभावित स्थिति है, टिकट का अपेक्षित मूल्य सकारात्मक होना चाहिए, और इसलिए आपको आज ही मेगा मिलियन्स टिकट खरीदने पर विचार करना चाहिए।"
बिक्री 730 मिलियन से भी कम थी और फिर भी यह एक बहुत ही खराब मूल्य था। हालाँकि, पूरी ईमानदारी से, लेख में आगे कहा गया:
"याद रखें कि इस विश्लेषण में कई चेतावनियाँ हैं। करों के कारण आपकी अपेक्षित जीत पर बहुत बुरा असर पड़ेगा - संघीय सरकार लगभग 40% ले लेगी, और आपका गृह राज्य 0% से लेकर लगभग 13% तक का दावा करेगा।
बहुत से लोग टिकट खरीद रहे हैं, और जैसा कि ऊपर चर्चा की गई है, इससे बराबरी की संभावना बहुत बढ़ जाएगी, और इसके साथ ही भुगतान भी कम हो जाएगा।" - बिजनेस इनसाइडर
ये कुछ बहुत बड़ी चेतावनियाँ हैं! इन्हें बस नीचे सरसरी तौर पर नहीं बताया जाना चाहिए, बल्कि विश्लेषण की शुरुआत में ही ध्यान में रखना चाहिए।
ऐसा नहीं है कि आपने पूछा था, लेकिन मुझे लगता है कि गणित कहता है कि आपको मेगा मिलियन्स कभी नहीं खेलना चाहिए। जैकपॉट के आकार के आधार पर टिकटों की बढ़ती माँग को देखते हुए, मुझे लगता है कि खेलने का सबसे अच्छा समय $545 मिलियन का जैकपॉट है। इससे बड़े जैकपॉट के लिए आपको इसे कई अन्य विजेताओं के साथ साझा करना होगा। इस जैकपॉट आकार पर, खिलाड़ी 60.2% रिटर्न या 39.8% नुकसान की उम्मीद कर सकता है। यह सबसे अच्छा है।
अंत में, नहीं, मैं बिजनेस इनसाइडर से सहमत नहीं हूं कि उसने सनसनीखेज शीर्षक से पाठकों को गुमराह किया है और करों तथा जैकपॉट बंटवारे का उचित विश्लेषण नहीं किया है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।


