जादूगर से पूछो #253
मुझे समझ में नहीं आता कि आपके टेक्सास होल्ड 'एम पावर टेबल में A-7 का स्थान KJ सूटेड से कम है, लेकिन आपके कैलकुलेटर पर A7 के जीतने की संभावना अधिक है।
अच्छा सवाल। अन्य पाठकों की सुविधा के लिए, दो खिलाड़ियों वाले खेल में इन दोनों शुरुआती हाथों में से प्रत्येक के साथ एक यादृच्छिक हाथ के विरुद्ध ऑड्स इस प्रकार हैं:
केजे सूटेड बनाम ए-7 ऑफ-सूट
| हाथ | जीतना | खोना | खींचना | अपेक्षित मूल्य |
कश्मीर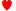 जे जे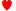 | 0.6148 | 0.3634 | 0.0218 | 0.2513 |
ए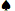 7 7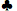 | 0.5717 | 0.3949 | 0.0334 | 0.1768 |
हालाँकि, मेरे टू-प्लेयर टेक्सास होल्ड 'एम कैलकुलेटर के अनुसार, इन दोनों हाथों के एक-दूसरे के सामने होने की संभावनाएं हैं:
A7 जीत = 53.52%
केजे जीत = 46.10%
टाई = 0.39%
तो KJ सूटेड मेरी तालिका में ऊपर है, लेकिन A7 अनसूटेड हेड-टू-हेड से कमतर है। क्यों?
इसका उत्तर समझाना मुश्किल है। जब दो हाथ एक-दूसरे के खिलाफ हों, तो आपको यह विचार करना होगा कि वे एक-दूसरे के साथ कैसे प्रतिक्रिया करते हैं। उदाहरण के लिए, शुरुआती हाथ की ताकत की तालिका में, AK ऑफ-सूट, AQ ऑफ-सूट से थोड़ा ही बेहतर है, जिसके अपेक्षित मान क्रमशः .3064 और .2886 हैं। हालाँकि, यदि आप उन्हें एक-दूसरे के खिलाफ खड़ा करते हैं, तो AK, AQ को इस प्रकार कुचल देता है:
AK जीत = 71.72%
AQ जीत = 23.69%
टाई = 4.58%
A7-ऑफसूट बनाम KJ-सूट में, इक्का, बादशाह और गुलाम से ऊँचा होता है। KJ खिलाड़ी के जीतने की सबसे ज़्यादा संभावना तब होती है जब वह K या J की जोड़ी बनाता है और कोई इक्का नहीं निकलता। मैं दिखाता हूँ कि इसकी संभावना केवल 37.73% है। KJ के जीतने की बाकी 46.10% संभावना उच्चतर हाथों से आती है।
जबकि A7, KJ के विरुद्ध मजबूत है, यह अक्सर यादृच्छिक हाथों द्वारा KJ की तुलना में अधिक हावी रहता है।
शायद यह एक गलत तुलना हो, लेकिन यह पत्थर, कागज़, कैंची जैसा खेल है। कुशल खिलाड़ियों के बीच, प्रत्येक थ्रो की शक्ति रेटिंग लगभग समान होनी चाहिए। हालाँकि, अगर एक खिलाड़ी कागज़ और दूसरा कैंची फेंकता है, तो शक्ति रेटिंग का कोई मतलब नहीं है, और कैंची जीत जाएगी।
लास वेगास के बिगहॉर्न और लॉन्गहॉर्न में, ब्लैकजैक में तीन कार्ड पर डबलिंग की अनुमति है। क्या इस नियम के तहत मुझे अपनी रणनीति में कोई बदलाव करना चाहिए?
मेरी विज़ार्ड ऑफ़ वेगास साइट के एक पाठक का कहना है कि मानक मल्टी-डेक रणनीति , जिसमें डीलर सॉफ्ट 17 हिट करता है, के सापेक्ष निम्नलिखित परिवर्तन किए जाने चाहिए:
- सॉफ्ट 13 बनाम 5 या 6 हिट करें
- हिट 2-कार्ड सॉफ्ट 15 बनाम 4
- हिट 3,3 बनाम 2
सॉफ्ट हैंड हिट करने का कारण यह है कि हिट के बाद आपको बेहतर सॉफ्ट डबल मिल सकता है। इस नियम के तहत थ्री हिट करने का मूल्य ज़्यादा होता है, क्योंकि इक्का मिलना एक अच्छा 3-कार्ड डबल होगा।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
यदि एक सिक्के को 100 बार उछाला जाए, तो कम से कम एक बार लगातार 7 बार सिर आने की संभावना क्या है?
अगर इस उत्तर के लिए कोई आसान, गैर-पुनरावर्ती व्यंजक है, तो मुझे उसकी जानकारी नहीं है। हालाँकि, एक आसान पुनरावर्ती उत्तर ज़रूर है।
f(n)= pr(पहले फ्लिप में पूंछ)×f(n-1) +
pr(पहली फ़्लिप में हेड, दूसरी फ़्लिप में टेल)×f(n-2) +
pr(पहले 2 फ़्लिप में हेड, तीसरे फ़्लिप में टेल)×f(n-3) +
pr(पहले 3 फ़्लिप में हेड, तीसरे फ़्लिप में टेल)×f(n-4) +
pr(पहले 4 फ़्लिप में हेड, चौथे फ़्लिप में टेल)×f(n-5) +
pr(पहले 5 फ़्लिप में हेड, पाँचवें फ़्लिप में टेल)×f(n-6) +
pr(पहले 6 फ़्लिप में हेड, छठे फ़्लिप में टेल)×f(n-7) +
pr(पहले 7 फ़्लिप में हेड) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
कहाँ:
f(n)=n फ़्लिप के भीतर सफलता की संभावना।
pr(x)=x घटित होने की संभावना.
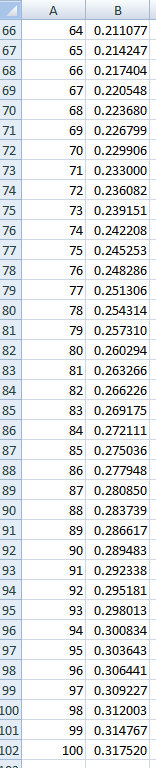
स्प्रेडशीट ऐसी समस्याओं के लिए एकदम सही हैं। नीचे दिए गए स्प्रेडशीट के स्क्रीनशॉट में, मैंने सेल B2 से B8 के लिए 0 की प्रायिकता दी है, क्योंकि 6 या उससे कम बार उछालने पर लगातार 7 चित नहीं आ सकते। सेल B9 के लिए, मैंने यह सूत्र दिया है:
=(1/2)*बी8+(1/2)^2*बी7+(1/2)^3*बी6+(1/2)^4*बी5+(1/2)^5*बी4+(1/2)^6*बी3+(1/2)^7*बी2+(1/2)^7
फिर मैंने इसे सेल B10 से सेल B102 में कॉपी और पेस्ट किया, जो 100 फ़्लिप के बराबर है। इसकी प्रायिकता 0.317520 है। एक यादृच्छिक सिमुलेशन इसकी पुष्टि करता है।
 |  |
इसके मूल प्रकाशन के बाद, रिक पर्सी ने अपना मैट्रिक्स अलजेब्रा का हल मेरे साथ साझा किया। यहाँ मेरे अपने शब्दों में है। मुझे लगता है कि पाठक मैट्रिक्स अलजेब्रा की मूल बातें पहले से ही जानते होंगे।
सबसे पहले, फ्लिपर किसी भी एक बिंदु पर आठ संभावित स्थितियों में हो सकता है:
p 1 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 7 और सिर की आवश्यकता हो।
p 2 = सफलता की संभावना, यह देखते हुए कि आपको वर्तमान बिंदु से 6 और सिर की आवश्यकता है।
p 3 = सफलता की संभावना, यह देखते हुए कि आपको वर्तमान बिंदु से 5 और सिर की आवश्यकता है।
p 4 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 4 और सिर की आवश्यकता हो।
p 5 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 3 और सिर की आवश्यकता हो।
p 6 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 2 और सिर की आवश्यकता हो।
p 7 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 1 और सिर की आवश्यकता हो।
p 8 = सफलता की संभावना, बशर्ते कि आपको और अधिक सिर की आवश्यकता न हो = 1.
आइए अधिकतम S n को n वें फ़्लिप के बाद प्रत्येक अवस्था में होने की प्रायिकता के रूप में परिभाषित करें। S 0 पहले फ़्लिप से पहले की प्रायिकताओं को दर्शाता है, जहाँ अवस्था 0 में होने की 100% संभावना होती है। अतः S 0 =
| 1 0 0 0 0 0 0 0 |
मान लीजिए T दो लगातार फ़्लिप से परिवर्तन मैट्रिक्स है, या S n से S n+1 तक, जहाँ S n+1 = T × S n
- यदि आप अवस्था 1 में हैं तो एक पलटी के बाद आपके पास अवस्था 2 (चित के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में पहुंचने की 0.5 संभावना है।
- यदि आप अवस्था 2 में हैं तो एक पलटी के बाद आपके पास अवस्था 3 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 3 में हैं तो एक पलटी के बाद आपके पास अवस्था 4 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 4 में हैं तो एक पलटी के बाद आपके पास अवस्था 5 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 5 में हैं तो एक पलटी के बाद आपके पास अवस्था 6 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 6 में हैं तो एक पलटी के बाद आपके पास अवस्था 7 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप स्थिति 7 में हैं तो एक पलटी के बाद आपके पास स्थिति 8 (सिर के साथ) में होने की 0.5 संभावना है, और स्थिति 1 (पूंछ के साथ) में वापस आने की 0.5 संभावना है।
- यदि आप अवस्था 8 में हैं तो आपने सफलता प्राप्त कर ली है, और 1.0 की संभावना के साथ आप अवस्था 8 में ही बने रहेंगे।
इन सबको संक्रमण मैट्रिक्स T = के रूप में रखने पर
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
एक फ्लिप के बाद प्रत्येक स्थिति की संभावना जानने के लिए...
(1) एस 1 = एस 0 × टी
दो फ़्लिप के बाद क्या होगा?
(2) एस 2 = एस 1 × टी
आइए समीकरण (1) को समीकरण (2) में प्रतिस्थापित करें...
(3) एस 2 = एस 0 × टी × टी = एस 0 × टी 2
तीन फ़्लिप के बाद क्या होगा?
(4) एस 3 = एस 2 × टी
समीकरण (3) को (4) में प्रतिस्थापित करने पर...
(5) एस 3 = एस 0 × टी 2 × टी = एस 0 × टी 3
हम 100वें फ्लिप के बाद भी राज्य तक ऐसा करते रह सकते हैं...
एस 100 = एस 0 × टी 100
तो, T 100 क्या है? कंप्यूटर से पहले ऐसी चीज़ों को समझना बहुत मुश्किल रहा होगा। हालाँकि, एक्सेल के MMULT फ़ंक्शन और काफ़ी कॉपी-पेस्ट करने पर हमें T 100 = मिलता है।
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
ऊपरी दाईं ओर दिया गया शब्द हमें 100 फ़्लिप के बाद स्थिति 8 में होने की संभावना दर्शाता है, जो 0.317520 है।
हाल ही में, टस्कनी कैसीनो ने एक प्रमोशन चलाया था जिसमें अगर आप 30 दिनों की अवधि में 30 ब्लैकजैक जीतते हैं, तो आपको $100 का बोनस मिलेगा। शुरुआत में, कार्ड पर स्टैम्प लगवाने के लिए न्यूनतम दांव $5 था। हालाँकि, बाद में मुझे पता चला कि स्टैम्प लगवाने की न्यूनतम राशि बढ़ाकर $15 कर दी गई है। मैंने कैसीनो मैनेजर को इस बारे में एक शिकायती पत्र लिखा, जिसमें कुछ अंश इस प्रकार थे:
मैं बस इस बदलाव पर अपनी निराशा व्यक्त करना चाहता था, अगर यह सच है। मुझे इस प्रमोशन का लाभ उठाने का कभी मौका नहीं मिला और मुझे शक है कि अब भी मैं ऐसा कर पाऊँगा। 30 ब्लैकजैक (मुझे बताया गया है कि लगभग 8 घंटे लगातार खेलना पड़ता है) प्राप्त करने के लिए आवश्यक समय $15 प्रति हाथ अनुचित लगता है, जबकि प्रमोशन अभी भी केवल $100 ही प्रदान करता है।
मुझे जो उत्तर मिला वह इस प्रकार है:
ब्लैकजैक ब्लैकआउट प्रमोशन पर आपके ईमेल के जवाब में, मुझे समझ नहीं आ रहा कि आपको ब्लैकआउट कार्ड पूरा करने में कितना समय लगता है, यह जानकारी कहाँ से मिली। हमने खिलाड़ियों को चार घंटे से भी कम समय में कार्ड पूरा करते देखा है। इसके अलावा, आपके पास कार्ड पूरा करने के लिए तीस दिन हैं। मुझे उम्मीद है कि आप समझ गए होंगे कि इतने समय में यह कोई असंभव काम नहीं है। आपके पत्र के लिए धन्यवाद। हमारे ग्राहकों की प्रतिक्रिया जानकर अच्छा लगा। उम्मीद है कि आप इसे आज़माएँगे और कुछ पैसे जीतेंगे!
चार घंटे में 30 ब्लैकजैक मिलने की संभावना क्या है?
मेरे खेल तुलना के अनुसार, ब्लैकजैक खिलाड़ी प्रति घंटे लगभग 70 हाथ खेलते हैं। छह-डेक वाले खेल में ब्लैकजैक की संभावना 24*96/combin(312,2)=4.75% है। मेरा मानना है कि ब्लैकजैक बराबर होने पर भी स्टैम्प मिलता है। इसलिए कार्ड भरने में लगभग 30/0.0475=632 हाथ, यानी 9.02 घंटे लगने चाहिए।
280 हाथ मानकर, 4 घंटे में कार्ड भरने की संभावना एक बार में एक हाथ खेलने पर 30,000 में से 1 है। मुझे शक है कि चार घंटे में यह लक्ष्य हासिल करने वाला कोई भी खिलाड़ी एक बार में कम से कम दो हाथ खेल रहा होगा।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।


