WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #171

मैं आपके NIM गेम को समझ नहीं पाया! मैं हमेशा सोचता था कि जीतने की कुंजी अपने प्रतिद्वंद्वी (इस मामले में, कंप्यूटर) को ऐसे बिंदुओं के साथ छोड़ना है जिनका योग अगली सबसे छोटी संख्या तक हो जो बाइनरी संख्याओं में उसके सारांश के बराबर हो, यानी, अगर मेरे पास 17 बिंदु हैं, तो मैं 2 हटा देता हूँ और 15 छोड़ देता हूँ, जो बाइनरी संख्याओं 1,2,4,8 का सारांश है। लेकिन ऐसा लगता है कि यह काम नहीं करता। मैं सही हूँ या गलत?

Jack से Troy

बाइनरी संख्याओं के मामले में आप सही रास्ते पर हैं, लेकिन यह पूरी तरह से जीतने की रणनीति नहीं है। सबसे पहले, अगर आप अपने प्रतिद्वंद्वी को एक-एक पंक्ति की विषम संख्या में पंक्तियाँ दे सकते हैं, तो ऐसा करें। अन्यथा, प्रत्येक पंक्ति को उसके बाइनरी घटकों में विभाजित करें। उदाहरण के लिए, 99 = 64+32+2+1। फिर सभी पंक्तियों में प्रत्येक घटक की संख्या को जोड़ें। फिर एक ऐसा दांव लगाएँ जिससे आपके प्रतिद्वंद्वी को सभी पंक्तियों में सभी बाइनरी घटकों की सम संख्या मिले।

आइए एक उदाहरण देखें। मान लीजिए कि आपकी बारी है और निम्नलिखित परिदृश्य है।

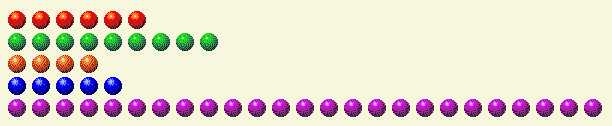
निम्नलिखित तालिका प्रत्येक पंक्ति को उसके बाइनरी घटकों में विभाजित करती है।

खिलाड़ी की बारी 1

पंक्ति 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
4 0 0 1 0 0
5 1 0 1 0 0
25 1 0 0 1 1
कुल 3 1 3 2 1

आप देख सकते हैं कि इकाई, दो, चार और सोलह की संख्या विषम है। स्पष्ट रूप से, हमें 16 इकाई को हटाने के लिए 25 की पंक्ति को 16 के नीचे लाना होगा। द्विआधारी घटकों का योग सम रखने के लिए, हमें 1 हटाना होगा, 2 जोड़ना होगा, 4 जोड़ना होगा, 8 रखना होगा और 16 हटाना होगा। इसका मतलब है कि सबसे अच्छा खेल आखिरी पंक्ति में 2+4+8=14 है। नीचे की पंक्ति में 14 छोड़ने पर हमें निम्नलिखित मिलता है।

कंप्यूटर की बारी 1

पंक्ति 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
4 0 0 1 0 0
5 1 0 1 0 0
14 0 1 1 1 0
कुल 2 2 4 2 0

कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।

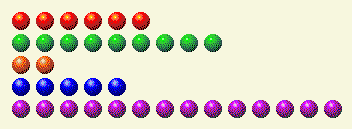
यहाँ इसका द्विआधारी विश्लेषण दिया गया है।

खिलाड़ी की बारी 2

पंक्ति 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
2 0 1 0 0 0
5 1 0 1 0 0
14 0 1 1 1 0
कुल 2 3 3 2 0

यहाँ हमें 2 और 4 को हटाना होगा, ताकि कुल योग बराबर हो जाए। केवल एक पंक्ति है, 14, जिसमें दोनों घटक हैं। इसलिए उसमें से 6 हटा दें, जिससे 8 बचेगा।

कंप्यूटर की बारी 2

पंक्ति 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
2 0 1 0 0 0
5 1 0 1 0 0
8 0 0 0 1 0
कुल 2 2 2 2 0

कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।

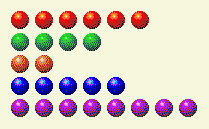
अब हमें 1, 4 और 8 कॉलम बदलने की जरूरत है।

खिलाड़ी की बारी 3

पंक्ति 1 2 4 8 16
6 0 1 1 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
8 0 0 0 1 0
कुल 1 2 3 1 0

ऐसा 8 की पंक्ति को 5 में बदलकर किया जा सकता है।

कंप्यूटर की बारी 3

पंक्ति 1 2 4 8 16
6 0 1 1 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
5 1 0 1 0 0
कुल 2 2 4 0 0

कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।

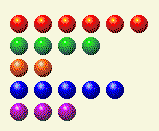
अब हमें 2 और 4 का योग बदलने की जरूरत है।

खिलाड़ी की बारी 4

पंक्ति 1 2 4 8 16
6 0 1 1 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
3 1 1 0 0 0
कुल 2 3 3 0 0

यह 6 को 0 में बदलकर किया जा सकता है।

कंप्यूटर की बारी 4

पंक्ति 1 2 4 8 16
0 0 0 0 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
3 1 1 0 0 0
कुल 2 2 2 0 0

कंप्यूटर अपनी बारी लेता है और हमें यहीं छोड़ देता है।

अब हमें 2 और 4 को बदलने की जरूरत है।

खिलाड़ी की बारी 5

पंक्ति 1 2 4 8 16
0 0 0 0 0 0
2 0 1 0 0 0
2 0 1 0 0 0
5 1 0 1 0 0
3 1 1 0 0 0
कुल 2 3 1 0 0

यह 5 की पंक्ति को 3 में बदलकर पूरा किया जा सकता है। यदि आप कभी भी अपने प्रतिद्वंद्वी को x,x,y,y स्थिति में ला सकते हैं, तो आप जीतने से खुद को नहीं रोक सकते, बशर्ते आप अंत तक उसी स्थिति को बनाए रख सकें।

कंप्यूटर की बारी 5

पंक्ति 1 2 4 8 16
0 0 0 0 0 0
2 0 1 0 0 0
2 0 1 0 0 0
3 1 1 0 0 0
3 1 1 0 0 0
कुल 2 4 0 0 0

अगली कुछ चालों में मैं कंप्यूटर को x,x,y,y पैटर्न पर रखता हूँ। यहाँ कंप्यूटर मुझे 2,2,3,2 पर छोड़ देता है; इसलिए मैं उसे 2,2,2,2 पर छोड़ देता हूँ।

कंप्यूटर मुझे 2,2,1,2 देता है। मैं उसे 2,2,1,1 पर छोड़ देता हूँ।

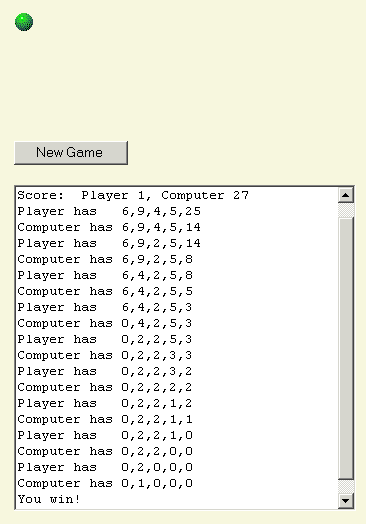
कंप्यूटर मुझे 2,2,1 देता है। मैं उसे 2,2 पर छोड़ देता हूँ। अगर आप कभी अपने प्रतिद्वंदी को दो बराबर पंक्तियों में ला पाए, तो आप जीत ही जाएँगे, बस पंक्तियाँ बराबर रखें।

इसके बाद कंप्यूटर मेरे पास 2 का एक ढेर छोड़ देता है, और मैं 1 हटा देता हूं।

खेल का अंत यहीं है।

मैं समझता हूँ कि जब ऑड्स 10x या उससे ज़्यादा हों, तो पुट बेट एक अच्छा बेट होता है। तो, अगर पॉइंट 6 या 8 है, तो $5 और $50 के मुफ़्त ऑड्स का बेट लगाएँ, उदाहरण के लिए। मेरा सवाल है, पॉइंट का इंतज़ार क्यों करें? पासलाइन पर बेट क्यों न लगाएँ, और फिर अगर पॉइंट 6 या 8 है, तो पूरे 10x ऑड्स पर बेट लगाएँ? इस तरह आपको ऑड्स का फ़ायदा तो मिलता ही है, साथ ही 7/11 रोल का फ़ायदा भी मिलता है। क्या मैं कुछ भूल रहा हूँ?

Jay से Whitestone

मैं सहमत हूँ। मैं पुट या प्लेस बेट लगाने की सलाह नहीं देता, क्योंकि जैसा आपने कहा, लाइन बेट और फिर मैक्सिमम ऑड्स लगाना बेहतर होता है। हालाँकि, कुछ लोगों को सीधे पॉइंट्स पर ही बेट लगाना ज़रूरी होता है। अगर यह तय है, तो मैं प्लेस, बाय और पुट के बीच सबसे अच्छा बेट लगाने की सलाह देता हूँ, जिसके बारे में मैंने अपने क्रेप्स सेक्शन में विस्तार से बताया है।
मेरे दोस्त, मैं LV खेल रहा था। हमारे बीच इस बात पर ज़ोरदार बहस हुई कि सांख्यिकीय रूप से किस चीज़ के ऑड्स बेहतर हैं, डबल डाउन में खिलाड़ी का कुल योग 10 हो और डीलर का 7 हो, या डबल डाउन में खिलाड़ी का कुल योग 11 हो और डीलर का 10 हो, दो डेक वाले खेल में। मुझे लगा कि यह पहले वाला ही होगा।

Brett से Alhambra

मेरा ब्लैकजैक परिशिष्ट 9 इसी तरह के सवालों के लिए बनाया गया था। 6 डेक मानते हुए, मेरी तालिका 8+2 बनाम 7 को दोगुना करने का अपेक्षित मान 0.396342 दिखाती है। 8+3 बनाम 10 को दोगुना करने का अपेक्षित मान 0.176919 है। तो आप सही कह रहे हैं, 10 बनाम 7 ज़्यादा बेहतर हाथ है।
आपकी साइट बहुत बढ़िया है, मैंने इससे बहुत कुछ सीखा है। होल्डम पोकर में फ्लॉप पर आपके पास 20 कार्ड होते हैं जो आपको जीत का हाथ देते हैं। रिवर तक आपके हाथ बनाने का प्रतिशत 67.5% क्यों है, 86% (20/47 + 20/46) क्यों नहीं? मैंने हर जगह ढूँढा है, लेकिन मुझे समझ नहीं आ रहा है, हालाँकि मुझे पता है कि यह शायद बहुत आसान है। मैं आपकी मदद के लिए आभारी रहूँगा, धन्यवाद!!

Kevin से Vernon, NJ

धन्यवाद! आपका तरीका डबल काउंटिंग है, यानी आपको ज़रूरी 20 पत्तों में से दो पत्ते मिल जाएँगे। टर्न पर आपको अपने ज़रूरी 20 पत्तों में से एक मिलने की संभावना 20/47 = 0.4255 है। टर्न पर न मिलने और फिर रिवर पर मिलने की संभावना (27/47)*(20/46) = 0.2498 है। तो कुल संभावना 0.4255 + 0.2498 = 0.6753 है।

हाल ही में मैंने स्थानीय आदिवासी कसीनो में क्रेप्स टेबल पर प्रोटोकॉल से जुड़ी एक ऐसी स्थिति देखी जिसने मुझे हैरान कर दिया, और मैं सोच रहा हूँ कि क्या आप इसे मेरे लिए स्पष्ट कर सकते हैं। अपने कम आउट रोल पर, खिलाड़ी 'ए' ने एक अंक फेंका और एक अंक स्थापित किया। अगले रोल के लिए, 'ए' के बगल वाले खिलाड़ी (खिलाड़ी 'बी') ने पासा उठाया और शॉट मारा। यह स्पष्ट नहीं है कि उसने ऐसा क्यों किया, या वह 'ए' को जानता भी था या नहीं। अन्य खिलाड़ियों में से एक ने आपत्ति जताई और बताया कि 'बी' मूल शूटर नहीं था। डीलरों और बॉक्समैन द्वारा काफी चर्चा और माथापच्ची के बाद, पासे अगले खिलाड़ी (खिलाड़ी 'सी') को दिए गए, जिसने हाथ पूरा किया (वह अंततः सेवन आउट हो गया)।

क्या इस स्थिति के लिए यही सही प्रोटोकॉल था, और अगर हाँ, तो इसके पीछे क्या तर्क है? अगर खिलाड़ी 'A' किसी वजह से और पासा नहीं चलाना चाहता, तो उसे पासा छोड़ने की इजाज़त क्यों नहीं दी जानी चाहिए? अगर खिलाड़ी 'B' ने पासा इसलिए उठाया क्योंकि उसे खेल समझ नहीं आया, या अगर स्टिकमैन ने गलती से उसे पासा उसके सामने रख दिया, तो क्या पासा 'A' के पास वापस नहीं जाना चाहिए ताकि हाथ पूरा हो सके?

DAVID से BAINBRIDGE ISLAND, WA

मैंने nextshooter.com के बोन मैन से यही पूछा। उन्होंने क्या कहा, यहाँ पढ़िए।

यदि सही शूटर के अलावा कोई अन्य खिलाड़ी पासा उठाता है और उसे घुमाता है, तो इसे नो-कॉल, नो-रोल माना जाना चाहिए और पासा सही शूटर को वापस कर दिया जाना चाहिए। हालाँकि यह वास्तव में उचित निर्णय है, बॉक्समैन कुछ मामलों में रोल की अनुमति दे सकता है यदि परिणाम सभी या अधिकांश खिलाड़ियों के पक्ष में हो। कुछ उदाहरणों में, रोल का परिणाम किसी भी खिलाड़ी के दांव को प्रभावित नहीं कर सकता है। इसके अलावा... कोई भी खिलाड़ी अनुरोध कर सकता है कि हाथ पूरा करने के लिए पासा अगले शूटर को भेजा जाए। ऐसे मामलों में वही पासा भेजा जा सकता है या नया शूटर नए पासे का अनुरोध कर सकता है। रोल पूरा होने पर, वही शूटर अपने हाथ से शूट कर सकता है, जिससे उसके पास एक से अधिक हाथ हो जाते हैं।

20 पासे फेंकने पर 100 से ज़्यादा का योग आने की क्या संभावना है? सादर प्रणाम

Terje से Stockholm

मैंने इसे हल करने के लिए सामान्य सन्निकटन का उपयोग करना शुरू किया, लेकिन 100 से ज़्यादा बिंदुओं की संभावना उस विधि के सटीक होने के लिए बहुत कम है। इसलिए मैंने 8.25 मिलियन परीक्षणों का एक यादृच्छिक सिमुलेशन किया और 101 या उससे ज़्यादा बिंदुओं वाले परीक्षणों की संख्या 127 थी। इसलिए संभावना लगभग 65,000 में से 1 है।
अब एक और डील या नो डील वाले सवाल का समय आ गया है। मान लीजिए बैंकर के सारे सौदे और सेलीन डायोन की मेहमान भूमिका के बाद, आपके पास दो सूटकेस बचते हैं, $500,000 और $1,000,000 का। मुझे लगता है कि बैंकर का प्रस्ताव $750,000 से थोड़ा कम होगा। आप कौन सा चुनेंगे? अगर बचे हुए दो ब्रीफ़केस $0.01 और $1,000,000 वाले हों तो क्या होगा? मुझे लगता है कि यह सब इस बात पर निर्भर करता है कि आप जुआरी हैं या नहीं, और इसका ऑड्स से कोई लेना-देना नहीं है। मैं इसलिए पूछ रहा हूँ क्योंकि मुझे आश्चर्य है कि क्या कोई कभी $1,000,000 जीत पाएगा (भले ही उसने जादुई ब्रीफ़केस ही क्यों न चुना हो)।

Jason से Vancouver

जब इनाम जीवन बदल देने वाली रकम बन जाएँ, तो समझदार खिलाड़ी को अपेक्षित मूल्य को अधिकतम करने की कीमत पर संयम से खेलना चाहिए। एक अच्छी रणनीति अपेक्षित खुशी को अधिकतम करना होनी चाहिए। मुझे लगता है कि खुशी मापने का एक अच्छा फंक्शन आपकी कुल संपत्ति का लघुगणक है। मान लीजिए एक ऐसे व्यक्ति के पास $100,000 की मौजूदा संपत्ति है, जिसके सामने $0.01 और $1,000,000 के दो विकल्प हैं। "कोई सौदा नहीं" मानकर अपेक्षित खुशी 0.5*log($100,000.01) + 0.5*log($1,100,000) = 5.520696 है। मान लीजिए b वह बैंक ऑफर है जहाँ खिलाड़ी इसे लेने के लिए उदासीन है।

लॉग(बी) = 5.520696
बी = 10 5.520696
बी = $331,662.50.

तो इस काल्पनिक खिलाड़ी को $331,662.50 के बैंक ऑफर पर कोई आपत्ति नहीं होनी चाहिए। खेल में प्रवेश करते समय आपकी संपत्ति जितनी कम होगी, आपको उतना ही संयम से खेलना चाहिए। आमतौर पर खेल के अंतिम चरण में बैंक ऑफर अपेक्षित मूल्य के करीब होते हैं, कभी-कभी थोड़े ज़्यादा। एक खिलाड़ी के दस लाख जीतने का एकमात्र तर्कसंगत तरीका यह है कि उसके पास खेल में प्रवेश करते समय बहुत अधिक संपत्ति हो और/या बैंक ऑफर असामान्य रूप से कंजूस हों। ऐसा लगता है कि निर्माताओं को मेहनती मध्यम वर्ग के लोग पसंद हैं, इसलिए हमें कोई ऐसा व्यक्ति देखने की संभावना नहीं है जो बड़ी रकम की बात आने पर लापरवाही बरत सके। मैंने खेल के अंतिम चरण में बैंक को अपेक्षित मूल्य के 90% से कम का ऑफर देते भी कभी नहीं देखा। हम किसी को दस लाख जीतते तब देखेंगे जब कोई ऐसा घटिया जुआरी शो में आएगा जो रुक नहीं सकता। जब ऐसा होगा तो मैं बैंकर का समर्थन करूँगा।

आपकी साइट बहुत अच्छी लगी! मैंने अभी-अभी लास वेगास ब्लैकजैक टेबल और उनके किनारों की आपकी विस्तृत सूची देखी, तो मैं सोच रहा था: मान लीजिए कि दो ब्लैकजैक टेबल हैं, जिनमें से एक में 0.2% का किनारा है और न्यूनतम $10 टेबल है, और 0.4% का किनारा है और न्यूनतम $5 टेबल है। दोनों टेबलों पर प्रति हाथ समान $0.02 का नुकसान होता है। क्या एक टेबल को दूसरे पर चुनने का कोई फ़ायदा है?

Milton से Santa Fe

धन्यवाद। इस सवाल का जवाब देने के लिए, आपको सबसे पहले खुद से पूछना होगा कि आप जुआ क्यों खेल रहे हैं। अगर आप कम से कम हारना चाहते हैं, तो आपको बिल्कुल नहीं खेलना चाहिए। हालाँकि, अगर आप जुआ खेलने के मज़े के लिए खेल रहे हैं, तो मैं 0.2% बढ़त वाले $10 वाले खेल को चुनूँगा। अपेक्षित नुकसान वही रहेगा, लेकिन बड़े दांव लगाने पर आपको ज़्यादा फ़ायदा होगा।
कैसीनो नियाग्रा में एक पै गौ पोकर साइडबेट है जो निश्चित ऑड्स के बजाय जैकपॉट से भुगतान करता है। मैं सोच रहा हूँ कि उस बेट को बराबर करने के लिए जैकपॉट की राशि कितनी होनी चाहिए (यह मानते हुए कि कोई जैकपॉट बेट पर अधिकतम रिटर्न पाने के लिए हाथ सेट करता है)।

William से Mississauga, Ontario

ब्रेक-ईवन पॉइंट $102,680.24 है। मैंने अभी-अभी इस दांव का विश्लेषण पै गौ पोकर साइड बेट्स वाले अपने सेक्शन में जोड़ा है।
मुझे पोकर के बारे में ज़्यादा जानकारी नहीं है, लेकिन मुझे यह मज़ेदार लगता है, तो शायद आप मुझे कुछ समझा सकें। हाल ही में अपनी पत्नी के साथ वेगास की यात्रा पर, हम एरिज़ोना चार्लीज़ डेकाटूर में रुके थे। हमारे यहाँ रुकने की वजह यह थी कि उन्होंने अपनी वेबसाइट पर $2-$4 होल्ड 'एम का विज्ञापन दिया था। पहली सुबह, हम पोकर रूम में गए और $2-$4 के लिए अपना नाम डाला। मैंने देखा कि पोकर वाला हमारे नाम $4-$8 वाले कॉलम में लिख रहा था। तो मैंने उससे कहा कि हमें $2-$4 चाहिए (उसी शीट पर "$2-$4" वाला एक कॉलम था)। उसने कहा कि यह $2-$4 है: फ्लॉप से पहले $2, फ्लॉप के बाद $4, और टर्न और रिवर के बाद $8। मैंने उसे समझाया कि $2-$4 से मेरा क्या मतलब है: फ्लॉप से पहले और बाद में $2, और टर्न और रिवर के बाद $4। वह हम पर ऐसे हँसा जैसे हमें समझ ही नहीं आ रहा हो कि हम क्या कह रहे हैं और कहा कि खेल ऐसे नहीं खेला जाता। हमने अपनी बाकी की यात्रा गोल्ड कोस्ट में पोकर खेलते हुए बिताई। क्या पोकर रूम में इस तरह की सट्टेबाजी आम बात है? (मैंने पोकर रूम के सुपरवाइजर से कहा कि अगर हम $4-$8 होल्ड 'एम का खर्च उठा सकते, तो हम एरिज़ोना चार्लीज़ में नहीं रुकते।)

Mike से Philadelphia, PA

मैं मानता हूँ कि "2/4" गेम का मतलब है कि टर्न से पहले दांव $2 यूनिट और टर्न के बाद $4 यूनिट के होते हैं। हालाँकि, स्मॉल ब्लाइंड संभवतः $1 ही होगा। ऐसा लगता है कि जब एरिज़ोना चार्लीज़ किसी गेम को "2/4" कहता है, तो वह ब्लाइंड्स की बात करता है, जिसका मतलब होगा $2 का स्मॉल ब्लाइंड और $4 का बिग ब्लाइंड, जिसका मतलब होगा टर्न के बाद $8 का दांव। मैंने यह प्रयोग पहले कभी नहीं सुना, इसलिए मैं आपको हैरान होने के लिए दोषी नहीं ठहराता।

बाद में मुझे पोकर रूम सुपरवाइजर एंथनी से निम्नलिखित जानकारी प्राप्त हुई।

मैं एक पोकर रूम सुपरवाइज़र हूँ। मैं आपको टेक्सास होल्ड 'एम में पोकर लिमिट के सही शब्दों के बारे में बताने के लिए लिख रहा था। अगर किसी गेम को $2/4 कहा जाता है, तो यह दांवों की बात करता है। (किसी गेम को ब्लाइंड्स तभी कहा जाता है जब वह नो-लिमिट हो।) फ्लॉप से पहले और बाद में $2, टर्न और रिवर पर $4। एक गेम जो $2/$4/$8 के रूप में सूचीबद्ध है (मुझे लगता है कि पिछले पत्र लेखक वास्तव में इसी का उल्लेख कर रहे थे), वह प्री-फ्लॉप में $2, फ्लॉप के बाद $4, टर्न और रिवर में $8 है। एक गेम को $2/$4/$6/$8 के रूप में सूचीबद्ध करना भी संभव है। बस जानकारी दे रहा हूँ, अच्छे पोकर सुपरवाइज़र चाहते हैं कि लोगों को ज़्यादा से ज़्यादा जानकारी हो।