सिक बो - बाधाओं की गणना करें और जीतें | वीडियो

हेलो दोस्तों, मैं माइक हूं।

आप सीखेंगे कि सिक बो खेल में ऑड्स की गणना कैसे की जाती है। संक्षेप में, सिक बो एक बहुत ही प्राचीन चीनी खेल है जो तीन पासे फेंकने पर आधारित है। इस खेल में चुनने के लिए कई तरह के दांव होते हैं।

मेरे द्वारा क्या होने वाला है :

इस विषय को दो वीडियो में विभाजित करना इसलिए ज़रूरी है क्योंकि मेरे फ़ोरम पर सभी लोग शिकायत कर रहे हैं कि मेरे वीडियो बहुत लंबे हैं। इस पहले भाग में , मैं तीन पासों से 3 से 18 तक किसी भी दिए गए योग के आने की प्रायिकता की गणना करने का तरीका बताने जा रहा हूँ, साथ ही किसी भी पासे के फलक पर 0, 1, 2 या 3 आने की प्रायिकता की भी गणना करूँगा।

एक बार जब हम उन प्रश्नों के उत्तर से लैस हो जाएंगे...

...हम भाग दो पर जा सकते हैं और विश्लेषण कर सकते हैं कि सिक बो में विभिन्न दांवों से आपको किस प्रकार का मूल्य मिल रहा है।

आइए इस प्रश्न का उत्तर दें : "तीन छह-पक्षीय पासों से किसी भी दिए गए योग को फेंकने की प्रायिकता क्या है?" यह तकनीक जो मैं आपको दिखाने जा रहा हूँ, किसी भी संख्या में पासों के लिए काम करेगी।

मैं इस छोटी सी मुश्किल तकनीक का श्रेय समरसेट, यूके के रॉबर्ट गुडहैंड को देना चाहूँगा। यह मेरे "आस्क द विज़ार्ड" कॉलम 264 में शामिल है। मैं इसे अभी आपके साथ साझा कर रहा हूँ।

सबसे पहले, हमें बस पाँच नकली वर्ग बनाने हैं। आपको थोड़ी देर में समझ आ जाएगा कि ऐसा क्यों होता है। अब, मैं 1 से 18 तक के हर योग को सूचीबद्ध करने जा रहा हूँ। एक पासे से, 1, 2 या 6 आने का एक ही तरीका है।

हर फलक का एक पहलू होता है, इसलिए यह बिल्कुल स्पष्ट है। दो पासों के साथ, आपको बाईं ओर वाले कॉलम का योग निकालना है, इस मामले में, B कॉलम, एक सेल से शुरू करके बाईं ओर ऊपर की ओर और फिर उसके ऊपर के पाँच सेल।

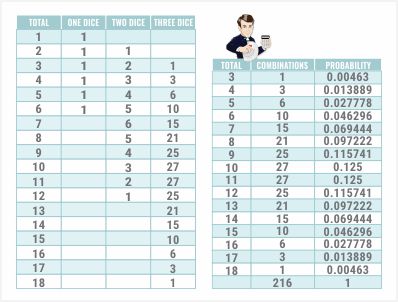
इस मामले में अभी...

...मैं सेल C8 पर काम कर रहा हूँ। यह दो पासों से कुल दो आने के तरीकों की संख्या दर्शाता है। मैं सेल B2 से B7 तक के मानों का योग ले रहा हूँ। अगर सेल खाली है, तो एक्सेल सही ढंग से मान लेता है कि वह शून्य है।

मैं बस इसे कॉपी करके 12 तक के सभी संभावित योगों में पेस्ट कर देता हूँ। आप देखेंगे कि कुल दो के लिए, इसे फेंकने का एक ही तरीका है। कुल तीन के लिए, दो तरीके हैं। कुल चार के लिए, तीन तरीके हैं।

खैर, यह काम क्यों करता है?

आइए दो का योग मान लें। कुल दो प्राप्त करने के लिए, पहले पासे का एक होना ज़रूरी है और फिर दूसरे पासे का भी एक होना ज़रूरी है। पहला पासा एक होने का सिर्फ़ एक ही तरीका है और ज़ाहिर है कि दूसरे पासे का भी एक होने का सिर्फ़ एक ही तरीका है। कुल तीन होने के लिए, दो तरीके हैं।

एक तरीका यह है कि पहला पासा एक और दूसरा पासा दो हो सकता है , और एक तरीका यह भी है कि पहला पासा दो और दूसरा पासा एक हो सकता है। कुल चार पासों के लिए, पहला पासा एक से तीन तक होना चाहिए।

कुल पांच...

पहले पासे का कुल योग एक से चार होना चाहिए। जब तक पहला पासा उस स्वीकार्य सीमा में है, तब तक एक तरीका है जिससे अगला पासा आपके बताए गए कुल योग को प्राप्त कर सकता है।

चलो तीन पासों पर चलते हैं

यह बिल्कुल वही तकनीक है। हम उसी सूत्र को कॉपी और पेस्ट कर सकते हैं। मैं इसे अभी-अभी की गई रेंज में कहीं से भी ले सकता हूँ। मैं बस यहाँ करूँगा, इसे दाईं ओर एक सेल में कॉपी और पेस्ट करूँगा और फिर नीचे कॉपी और पेस्ट करूँगा। यहाँ हमें तीन पासों से 3 से 18 तक के किसी भी योग के लिए संयोजनों की संख्या मिल जाएगी।

उदाहरण के लिए:

कुल तीन आने का एक तरीका है, कुल चार आने के तीन तरीके हैं, कुल पाँच आने के छह तरीके हैं, वगैरह। यह कैसे काम करता है? आप फिर पूछेंगे। खैर, उदाहरण के लिए, कुल सात पर ही गौर करते हैं। तीन पासों से कुल सात आने के लिए, ऐसा तब किया जा सकता है जब दो पासों का कुल योग दो हो और फिर आप उसमें पाँच जोड़ दें।

एक तरीका यह है कि पहले दो पासों का योग दो हो। दूसरा तरीका यह है कि पहले दो पासों का योग तीन हो और फिर तीसरे पासे का योग चार हो। जैसा कि हमने अभी देखा, पहले दो पासों का योग तीन होने के दो तरीके हैं, और पहले दो पासों का योग चार होने के तीन तरीके हैं।

कुल सात पाने के लिए ...

...आपके पहले दो पासों का कुल योग दो से छह तक होना चाहिए। हमने अभी देखा कि ऐसा होने के कुल तरीकों की संख्या यहाँ एक से पाँच तक का योगफल है, जो 15 है। आइए इसे एक अच्छी, उपयोगी तालिका में रखें। फिर से, यह रहा आपका कुल योग।

ये संयोजन इस प्रकार हैं :

आइए इसका कुल योग 216 लें। यह संख्या जानी-पहचानी लगती है। शायद, यह छः की घात हो सकती है।

अंत में, आइए प्रत्येक योग की संभावना ज्ञात करें:

हम संयोजनों की संख्या को कुल योग से भाग देते हैं। किसी भी दिए गए योग को 30 से 18 तक फेंकने की प्रायिकता होती है। अब, आइए किसी विशेष पासे को शून्य से तीन बार फेंकने की प्रायिकता पर नज़र डालें। सिक बो में छह अलग-अलग दांव होते हैं, प्रत्येक पासे के लिए एक।

अगर चुना हुआ फलक एक बार लुढ़का, तो खिलाड़ी एक-एक से जीतता है, अगर वह दो बार लुढ़का, तो दो-एक से जीतता है, और अगर वह तीन बार लुढ़का, तो तीन-एक से जीतता है। अब, बहुत से लोग कई घटनाओं की बात करते समय प्रायिकताएँ गलत तरीके से जोड़ देते हैं और हर पासा एक स्वतंत्र घटना की तरह होता है।

हम जोड़ते नहीं, गुणा करते हैं।

मुझे चीज़ों के संयोजनों के बारे में पहले सोचना अच्छा लगता है। मान लीजिए, आप बस छह चुनते हैं। तीन पासों पर तीन बार छह आने के संयोजनों की संख्या क्या है? खैर, यह बस एक ही है। ऐसा होने का सिर्फ़ एक ही तरीका है, 6-6-6। दो बार कैसा रहेगा?

उदाहरण के लिए:

6-6-4 या 2-6-6, 6-1-6। दो पासे छह हैं और एक कुछ और है। कुछ और पाँच अन्य फलकों में से कोई भी हो सकता है और ये कुछ और तीन पासों में से किसी एक पर दिखाई दे सकते हैं। आपके द्वारा चुना गया पासा फलक तीन पासों में से दो बार दिखाई देने के कुल तरीकों की संख्या 15 है।

एक बार में यह कितने तरीकों से प्रकट हो सकता है?

खैर, बाकी दो पासे जो आपके चुने हुए पासे के फलक नहीं हैं, वे पाँच में से कोई भी हो सकते हैं। हम 5 x 5 को गुणा करते हैं क्योंकि उनमें से एक छह या आपके द्वारा चुने गए किसी भी फलक के अलावा कुछ भी हो सकता है और दूसरा भी बाकी पाँच फलकों में से कोई भी हो सकता है।

अंत में…

...हम तीन से गुणा करते हैं क्योंकि आपके द्वारा चुना गया एक पासा तीनों पासों में से कोई भी हो सकता है। आप अपने चुने हुए फलक को एक बार जितने तरीकों से घुमा सकते हैं, वह 5 x 5 x 3 है, जो 75 के बराबर है। इसके उदाहरण हैं, मान लीजिए आपने फलक छह चुना है, तो यह 6-1-2, 1-4-6, 1-6-5, 2-6-2, 6-1-3, इत्यादि हो सकता है।

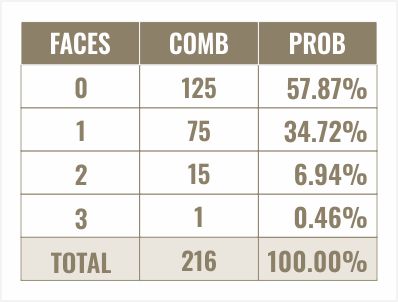
आपके द्वारा चुने गए पासे के किसी भी फलक के न लुढ़कने के संयोजनों की संख्या के बारे में आपका क्या विचार है?

खैर, तीनों पासों में से हर एक पाँच चीज़ों में से एक हो सकता है। पाँच पासे - मेरा मतलब है, तीन पासे, आपके चुने हुए फलक के अलावा हर एक के लिए पाँच अलग-अलग संयोजन, यानी 5 x 5 x 5 संयोजन या 125। आइए इन सभी संयोजनों का योग निकालें और हमें फिर से 216 मिलता है। फिर से, यह छः की तीसरी घात है, तो मैंने ज़रूर कुछ सही किया होगा।

अंत में, आइए संभावना पर नजर डालें

हम संयोजनों की संख्या को कुल संयोजनों से भाग देते हैं। इसे प्रतिशत में लिखते हैं। यहाँ हम देखते हैं कि आपके चुने हुए फलक के शून्य बार लुढ़कने की संभावना 57.87%, एक बार लुढ़कने की संभावना 34.72%, दो बार लुढ़कने की संभावना 6.94% और तीन बार लुढ़कने की संभावना 0.46% है।

मुझे उम्मीद है कि यह बात समझ में आ गई होगी। मुझे उम्मीद है कि दूसरे भाग में आपसे मुलाक़ात होगी जहाँ मैं कई अलग-अलग सिक बो दांवों की बाधाओं की गणना करूँगा।

देखने के लिए धन्यवाद।

यह दस्तावेज़ तत्काल HTML संपादक टूल का उपयोग करके तैयार किया गया है। यहाँ क्लिक करें और इसे निःशुल्क आज़माएँ।

भाग 2

द्वारा लिखित: Michael Shackleford