एक पूर्ण ब्रैकेट की संभावना पर वीडियो

नमस्कार, मैं माइक हूं, और यह वीडियो इस प्रश्न का उत्तर देने का प्रयास करेगा: एक आदर्श मार्च मैडनेस ब्रैकेट को भरने की संभावना क्या है?

मैं यह मानकर चल रहा हूँ कि आपको पहले से ही इसके काम करने के तरीके के बारे में कुछ बुनियादी जानकारी है, लेकिन संक्षेप में, एक एकल उन्मूलन टूर्नामेंट में 64 बास्केटबॉल टीमें प्रतिस्पर्धा कर रही हैं; इसका मतलब है कि कुल 63 खेल होंगे।

वे इसे चार डिवीजनों में बाँटते हैं , और हर डिवीजन में, पहले राउंड में, पहली वरीयता प्राप्त टीम 16वीं वरीयता प्राप्त टीम से, दूसरी वरीयता प्राप्त टीम 15वीं वरीयता प्राप्त टीम से, तीसरी वरीयता प्राप्त टीम 14वीं वरीयता प्राप्त टीम से, और इसी तरह आगे भी। फिर वे पहले राउंड के सभी मैचों के विजेताओं को चुनते हैं और फिर दूसरे राउंड में एक-दूसरे से खेलते हैं, और अंततः केवल एक ही विजेता बचता है।

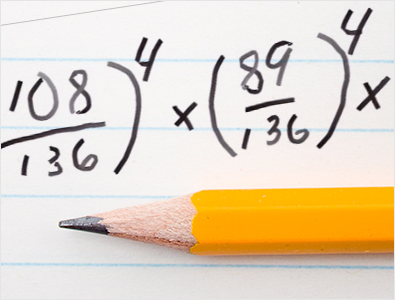
अब हर मार्च...

...मीडिया में हमेशा यह सवाल उठता है कि एक परफेक्ट ब्रैकेट भरने की संभावना क्या है और जब मैं यह आंकड़ा सुनता हूँ कि 9 क्विंटिलियन, 223 क्वाड्रिलियन, 372 ट्रिलियन, 36 बिलियन, 854 मिलियन, 781,000 में 1 होता है, तो मेरे रोंगटे खड़े हो जाते हैं; मुझे लगता है। यह बस लगातार 63 सिक्कों के उछाल की सही भविष्यवाणी करने की संभावना है। मुझे नहीं लगता कि कोई भी मार्च मैडनेस ब्रैकेट इस तरह भरता है क्योंकि कुछ टीमें स्पष्ट रूप से दूसरों से बेहतर होती हैं। उदाहरण के लिए, 1 सीड स्पष्ट रूप से 16 सीड से बेहतर है।

इससे पहले कि मैं आगे बढूं...

...मैं बता दूँ कि यह वीडियो अप्रैल 2018 में शूट किया गया था, इसलिए यह 1985 से 2018 तक खेले गए हर मार्च मैडनेस गेम पर आधारित है। ठीक है, मैं YouTube पर एक प्रोफ़ेसर, जेफ़ बर्गेन, के एक और वीडियो के बारे में भी बात करना चाहता था। वह कहते हैं कि किसी ऐसी रणनीति के साथ, जिसके बारे में वह ज़्यादा नहीं जानते, एक परफेक्ट ब्रैकेट की संभावना 128 बिलियन में 1 है। यह संख्या वास्तव में मेरे द्वारा प्राप्त संख्या के काफी करीब है।

मैं प्रोफ़ेसर बर्गेन को चुनौती देता हूँ कि वे विस्तार से बताएँ कि उन्हें यह आँकड़ा कैसे मिलता है, लेकिन मैं आपको विस्तार से बताऊँगा कि मुझे अपना आँकड़ा कैसे मिलता है। मेरी रणनीति बहुत सरल है। आप हर मैच में हमेशा ऊँची रैंक वाली टीम चुनते हैं और अंततः आपके पास सिर्फ़ चार नंबर 1 वरीयता प्राप्त टीमें बचती हैं, ऐसे में आप बेतरतीब ढंग से चुन सकते हैं।

इससे पहले कि कोई टिप्पणी पर कुछ लिखे

मैं यह कहना चाहता हूं कि आप खेलों पर वर्तमान बाधाओं को देखकर इसमें और भी सुधार कर सकते हैं, और उदाहरण के लिए, जब बात एक सीड बनाम एक सीड की आती है, तो आप मूल रूप से यह देखने के लिए कि किसके जीतने की संभावना बेहतर है, लास वेगास में चल रही बाधाओं को देख सकते हैं, लेकिन मैं इसमें नहीं जाऊंगा।

यह वीडियो बस हर बार बेहतर वरीयता प्राप्त टीम चुनने पर आधारित होगा, और फिर, जब चार नंबर 1 वरीयता प्राप्त टीमें नीचे आ जाएँगी, तो बस बेतरतीब ढंग से चुनेंगे। ठीक है, परिचय के लिए बस इतना ही कहना है।

पहले ही माफ़ी मांग लूँ कि इस वीडियो के अगले भाग में मैं टैबलेट का इस्तेमाल करने वाला हूँ। इसे ठीक से चलाने में मुझे पहले ही कई तकनीकी समस्याओं का सामना करना पड़ा है, इसलिए मैंने सोचा कि मैं इसका परिचय इसी तरह से शूट करूँगा। बिना किसी देरी के, यहाँ बताया गया है कि मैंने अभी जो रणनीति बताई है, उसके अनुसार एक आदर्श मार्च मैडनेस ब्रैकेट की प्रायिकता की गणना कैसे की जाती है।

ठीक है, तो चलिए शुरू करते हैं:

यह मेरा पहला वीडियो है जो क्रिएटिव पेन टैबलेट से बनाया गया है, अगर यही सही शब्द है। मैं हमेशा से खान अकादमी जैसे वीडियो बनाना चाहता था, लेकिन जुए और गणित के बारे में। परिचय के बाद, चलिए सीधे गणनाओं पर आते हैं।

मेरा अनुमान है कि एक वरीयता प्राप्त खिलाड़ी द्वारा 16 वरीयता प्राप्त खिलाड़ी को हराने की संभावना 136 में से 135 है क्योंकि अब तक ऐसे 136 मैच हुए हैं और एक वरीयता प्राप्त खिलाड़ी ने 135 बार जीत हासिल की है। यानी किसी भी एक मैच में एक वरीयता प्राप्त खिलाड़ी के जीतने की संभावना 99.26% है।

तथापि...

...इसमें चार अलग-अलग विभाजन हैं, इसलिए आपको इसे चार अलग-अलग बार हासिल करना होगा, इसलिए इसे चौथी घात तक ले जाएं।

अब, चार अलग-अलग खेल भी हैं जहाँ दूसरे नंबर की वरीयता प्राप्त टीम पंद्रहवीं वरीयता प्राप्त टीम से खेलती है। ऐसा 136 बार हुआ है। दूसरे नंबर की वरीयता प्राप्त टीम ने 127 बार जीत हासिल की है। ऐतिहासिक आंकड़ों के अनुसार, दूसरे नंबर की वरीयता प्राप्त टीम द्वारा पंद्रहवीं वरीयता प्राप्त टीम को हराने की संभावना 93.38% है, और आपको चार अलग-अलग डिवीजनों के लिए भी ऐसा चार बार करना होगा।

इसी तरह, तीसरे नंबर की टीम द्वारा 14 नंबर की टीम को हराने की प्रायिकता 115 को 136 से भाग देने पर मिलती है, और आपको इसे फिर से चार बार दोहराना होगा। फिर चौथे नंबर की टीम द्वारा 13 नंबर की टीम को हराने की प्रायिकता 108 को 136 से भाग देने पर मिलती है, और फिर से, आपको जिन चार गेमों में जीत हासिल करनी है, उनके लिए इसे चौथी घात पर ले जाएँ।

पाँचवीं वरीयता प्राप्त खिलाड़ी द्वारा बारहवीं वरीयता प्राप्त खिलाड़ी को हराने की प्रायिकता 136 में 89 है, जो लगभग 65.44% और चतुर्थ घात है। छठी वरीयता प्राप्त खिलाड़ी द्वारा ग्यारहवीं वरीयता प्राप्त खिलाड़ी को हराने की प्रायिकता 136 में 85 है, जो किसी भी खेल के लिए 62.5% है। सातवीं वरीयता प्राप्त खिलाड़ी द्वारा दसवीं वरीयता प्राप्त खिलाड़ी को हराने की प्रायिकता 136 में 83 है। प्रत्येक खेल में जीतने की प्रायिकता 61.03% है। अंत में, आठवीं वरीयता प्राप्त खिलाड़ी द्वारा नौवीं वरीयता प्राप्त खिलाड़ी को हराने की प्रायिकता 136 में 71 है, और आपको यह चार बार दोहराना होगा।

यदि आप ये सभी खेल जीत जाते हैं...

...आप पहले राउंड से आगे बढ़ेंगे। फिर, दूसरे राउंड में, आपको पहले सीड वाले और आठवें सीड वाले के बीच मुकाबला खेलना होगा। ऐसा अब तक 72 बार हो चुका है, और इन 72 बार में से पहले सीड वाले ने आठवें सीड वाले को 58 बार हराया है। पहले सीड वाले द्वारा आठवें सीड वाले को हराने की संभावना 80.56% है, और आपको ऐसा चार बार और करना होगा।

फिर, चार सीड पाँच सीड से खेलेंगे। ऐसा अब तक 73 बार हो चुका है, और 41 बार चौथी सीड जीती है, जिसकी संभावना हर गेम में 56.16% है, और हमारे पास अभी भी चार डिवीजन हैं, इसलिए इसे चौथी घात पर ले जाएँ।

फिर तीनों वरीयता प्राप्त टीमें, छठी वरीयता प्राप्त टीमों से खेलेंगी। तीनों वरीयता प्राप्त टीमें 70 में से 41 बार जीत चुकी हैं, यानी हर बार जीतने की संभावना 58.57% है। अंत में, दूसरे राउंड को पास करने के लिए, दोनों वरीयता प्राप्त टीमें, सातवीं वरीयता प्राप्त टीमों से खेलेंगी। दूसरी वरीयता प्राप्त टीमें 56 बार जीत चुकी हैं, और ऐसा 79 बार हुआ है, यानी हर बार जीतने की संभावना 70.89% है। ठीक है, तो मान लीजिए कि आप ये सभी गेम जीत जाते हैं, तो आप तीसरे राउंड में जाएँगे जहाँ पहली वरीयता प्राप्त टीम, चौथी वरीयता प्राप्त टीमों से खेलेगी।

टूर्नामेंट के इतिहास में अब तक ऐसा 61 बार हो चुका है और 44 बार पहली वरीयता प्राप्त टीम जीती है, और हर बार संभावना 72.13% है। इसके बाद, दूसरी वरीयता प्राप्त टीम तीसरी वरीयता प्राप्त टीम से खेलेगी। ऐसा अब तक 52 बार हो चुका है, और उनमें से 32 बार दूसरी वरीयता प्राप्त टीम जीती है। फिर, ऐसा अभी भी चार बार होना बाकी है।

यह मानते हुए कि आप वे सभी खेल जीत जाते हैं:

फिर आपके पास सिर्फ़ 1 सीड और 2 सीड बचेंगे। 1 सीड द्वारा 2 सीड को हराने की संभावना 64 में से 35 है, फिर से, ऐतिहासिक खेलों के आधार पर, और ऐसा चार डिवीजनों के लिए अभी भी चार बार होना है।

अब, अगर आप यहाँ तक पहुँच गए हैं... तो आप चारों डिवीज़न जीत चुके होंगे, और हर बार नंबर एक टीम शीर्ष पर होगी। यहीं से आप बेतरतीब ढंग से चुनना शुरू करते हैं। चार टीमों में से सर्वश्रेष्ठ टीम चुनने के लिए आपको तीन और मैचों की ज़रूरत है, और जैसा कि मैंने शुरुआत में कहा था, आपको बस बेतरतीब ढंग से चुनना है, इसलिए हर बार आपके जीतने की संभावना 2 में से 1 होगी, और तीन और मैच होंगे।

मेरी रणनीति का इस्तेमाल करके जीतने की आपकी संभावना यही है , और यह 42,743,890,552 में से 1 की संभावना के बराबर है। लीजिए, यह रहा। मेरा मानना है कि यह मार्च मैडनेस ब्रैकेट को पूरा करने का सबसे सटीक आँकड़ा है।

जैसा कि मैंने परिचय में कहा था, आप सट्टेबाज़ी बाज़ार में मौजूदा ऑड्स देखकर इसमें सुधार कर सकते हैं, और इस वीडियो को देखने के लिए शुक्रिया। मुझे पता है कि यह उतना अच्छा नहीं था।

इसे मेरे लिए एक सीखने का अनुभव मानिए, और फिर से, यह सब मेरी वेबसाइट wizardofodds.com के स्पोर्ट्स बेटिंग सेक्शन में लिखित रूप में है, और फिर एक परफेक्ट मार्च मैडनेस ब्रैकेट कैसे भरें, इस बारे में पेज देखिए। मुझे नहीं लगता कि इससे ज़्यादा कुछ कहने की ज़रूरत है।

तो देखने के लिए धन्यवाद.

द्वारा लिखित: Michael Shackleford