फाइव कार्ड स्टड पोकर में संभावनाएं

नमस्ते, मैं माइक हूँ, और इस वीडियो का उद्देश्य आपको यह दिखाना है कि पाँच-कार्ड स्टड पोकर में संभावनाओं की गणना कैसे की जाती है। दूसरे शब्दों में, 52 में से पाँच यादृच्छिक कार्ड दिए जाने पर किसी भी दिए गए पोकर हैंड के बनने की संभावना क्या है। प्रत्येक पोकर हैंड के संयोजनों की संख्या के प्रश्न का उत्तर देने से पहले, मैं आपसे एक सरल प्रश्न पूछता हूँ, और यदि आप जानते हैं कि इसका उत्तर कैसे प्राप्त किया जाता है, तो आप आगे बढ़ सकते हैं।

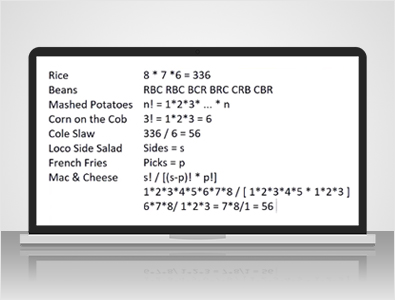
एल पोलो लोको में:

उनके पास आठ तथाकथित क्लासिक साइड्स हैं जिन्हें मैंने बाईं ओर सूचीबद्ध किया है। उनके पास कुछ डीलक्स साइड्स भी हैं, लेकिन मैं उनके बारे में ज़्यादा जानकारी नहीं दूँगा। अगर आप 12-पीस मील ऑर्डर करते हैं, तो आप इन आठ साइड्स में से कोई भी तीन चुन सकते हैं। मान लीजिए आपको तीन अलग-अलग चीज़ें चुननी हैं।

सवाल यह है की...

...आठ में से तीन अलग-अलग साइड्स कितने तरीकों से ऑर्डर कर सकते हैं? दूसरे शब्दों में, मान लीजिए कि आप रोज़ वहाँ जाते हैं, और हर दिन तीन अलग-अलग साइड्स ऑर्डर करते हैं। आप कितने दिन बिना वही तीन साइड्स दोहराए रह सकते हैं?

अगर आपके ऑर्डर का क्रम मायने रखता है, तो जवाब होगा 8 x 7 x 6 क्योंकि पहले वाले को चुनने के आठ तरीके हैं, दूसरे वाले को चुनने के सात तरीके हैं, और तीसरे वाले को चुनने के छह तरीके हैं, लेकिन कैशियर को इससे कोई फ़र्क़ नहीं पड़ता। आपने उन्हें जिस क्रम में ऑर्डर किया था।

अगर आप कहते हैं -

"मुझे चावल, बीन्स और मक्का चाहिए," आपको एक ही चीज़ मिलेगी चाहे आप "चावल, बीन्स और मक्का" कहें या "मक्का, बीन्स और चावल"। आप तीन अलग-अलग साइड डिश कितने अलग-अलग तरीकों से ऑर्डर कर सकते हैं? मान लीजिए आपको चावल, बीन्स और मक्का पसंद है। आप उन्हें इसी क्रम में ऑर्डर कर सकते हैं, आप चावल, मक्का, बीन्स ऑर्डर कर सकते हैं, आप बीन्स, मक्का, चावल ऑर्डर कर सकते हैं। आप बीन्स, चावल, मक्का या मक्का, चावल, बीन्स या मक्का, बीन्स, चावल ऑर्डर कर सकते हैं, यानी छह संभावित तरीके।

बिना लिखे मुझे कैसे पता चला कि ये छह हैं?

खैर, इसका एक बहुत ही सरल सूत्र है। यदि वहाँ N आइटम हैं, तो आप उन्हें 1 x 2 x 3 बार से लेकर N तक ऑर्डर कर सकते हैं।

इस मामले में, सवाल यह था कि आप तीन चीज़ें कितने तरीकों से ऑर्डर कर सकते हैं? तो, ये 3! हुआ, यानी 1 x 2 x 3, यानी 6। तीन चीज़ों को ऑर्डर करने के 336 तरीकों में से, क्रम के हिसाब से आठ में से, आपको छह से भाग देना होगा क्योंकि हर चीज़ को ऑर्डर करने के छह तरीके हैं, और आपके पास 56 बचे।

आप पूछेंगे कि सामान्य सूत्र क्या है?

अगर हैं, तो मान लीजिए कि भुजाओं की संख्या S के बराबर है, और आपको दी गई पिक्स की संख्या P है, तो S में से P चीज़ें चुनने के तरीकों की संख्या का सामान्य सूत्र s! / s - p! xp! है। मैं दिखाता हूँ कि यह उदाहरण प्रश्न के साथ कैसे काम करता है।

इस मामले में:

s = 8, अतः 8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8, और फिर हर है s - p, या 8 - 3, जो 5 या 5! है। तो, 1 x 2 x 3 x 4 x 5, साथ ही p! या 3!, जो 1 x 2 x 3 है। आप देख सकते हैं 1 x 2 x 3 x 4 x 5, जो 120 के बराबर है, और अंश और हर दोनों, तो चलिए इसे रद्द कर देते हैं, जिससे हमारे पास 6 x 7 x 8 / 1 x 2 x 3 बचता है। खैर, 2 x 3 = 6, और अंश और हर दोनों में एक छह दिखाई दे रहा है, तो चलिए इसे विभाजित करते हैं।

हमारे पास बस यही बचा है...

...7 x 8 / 1, जो कि 56 है। इस वीडियो के उद्देश्य के लिए, मैं एक फ़ंक्शन का परिचय देता हूँ। हम x और y के फ़ंक्शन C को x में से y आइटम चुनने के तरीकों की संख्या कहेंगे, या जैसा कि हम गणितीय रूप से कहेंगे, x, y चुनता है, और हम इसे x! / x - y! गुणा y! के रूप में परिभाषित करेंगे।

एल पोलो लोको उदाहरण के मामले में, यदि प्रश्न यह था:

"आप आठ में से तीन स्लाइड कितने तरीकों से चुन सकते हैं?"

हम इसे इस तरह व्यक्त करेंगे, जो बराबर होगा-- स्विच बराबर 56। मुझे लगता है कि हम पोकर के बारे में बात करने के लिए आखिरकार तैयार हैं। 52 में से पाँच पत्ते चुनने के कितने तरीके हैं? खैर, यह होगा 52 में से 5 चुनें, जो कि 52! / 47! है, 47 क्योंकि 52 - 5 x 5!, और यह 2,598,960 के बराबर है। चलिए रॉयल फ्लश से शुरुआत करते हैं।

खैर, यह बहुत आसान है। रॉयल फ्लश के चार सूट होते हैं: हार्ट्स, हुकुम, चिड़ी और ईंट।रैंक दस होनी चाहिए, गुलाम, बेगम, बादशाह, इक्का। हाँ, चार ही तरीके हैं। एक शाही और पान, ईंट, चिड़ी या हुकुम।

सीधे फ्लश के बारे में क्या ख्याल है?

खैर, फिर से, हमारे पास चार सूट हैं, लेकिन स्ट्रेट फ्लश की अवधि इक्का, यानी इक्का, दो, तीन, चार, पाँच, जिसे व्हील स्ट्रेट फ्लश भी कहते हैं, से शुरू होकर नौ, दस, गुलाम, रानी, राजा तक हो सकती है। अगर यह दस, गुलाम, रानी, राजा, इक्का होता, तो यह रॉयल फ्लश होता। सबसे छोटा पत्ता इक्का से लेकर नौ तक कहीं भी हो सकता है।

इस मामले में...

...इक्का एक के बराबर गिना जाता है। स्ट्रेट फ्लश के लिए नौ संभावित स्पैन हैं, इसलिए 4 सूट x 9 स्पैन = 36। एक तरह के चार के साथ, एक तरह के चार के लिए 13 संभावित रैंक हैं, उदाहरण के लिए, क्वींस, और फिर एक तरह के चार के लिए चार कार्ड निकालने के बाद सिंगलटन के लिए डेक में 48 कार्ड बचते हैं। यह 624 के बराबर है।

पूरे घर के लिए

तीन एक जैसे के लिए 13 संभावित रैंक हैं, और जोड़ी के लिए 12 रैंक बाकी हैं। तीन एक जैसे के लिए, जोड़ी के लिए चार विकल्प हैं, चार में से तीन सूट चुनने के तीन तरीके, चार में से दो सूट चुनने के दो तरीके। यह 13 x 12 x 4 x 6 के बराबर है, जो 3,744 के बराबर है। फ्लश के लिए, हमारे पास फ्लश के लिए चार सूट हैं।

दिए गए सूट में 13 में से पांच रैंक चुनने के कितने तरीके हैं?

खैर, यह 13 में से 5 चुनने का तरीका होगा, लेकिन इनमें से 10 तरीकों से स्ट्रेट फ्लश या रॉयल फ्लश बनेगा। उदाहरण के लिए, 5, 6, 7, 8, 9 से स्ट्रेट फ्लश बनेगा, इसलिए हमें उन 10 रैंकों को चुनना होगा जो क्रमागत हों। इससे हमारे पास 13 में से 5 चुनने का तरीका 1,287 बचता है, 10 को घटाकर 4 से गुणा करें, और हमें 5,108 मिलता है।

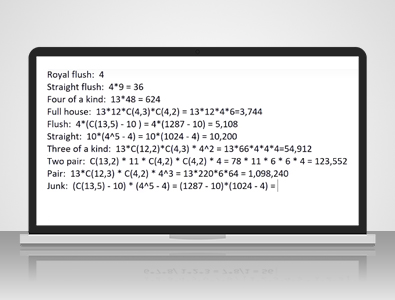
सीधे के बारे में क्या ख्याल है?

खैर, जैसा कि हमने अभी फ्लश में देखा, इक्का, दो, तीन, चार, पाँच से शुरू होकर दस तक, गुलाम, रानी, बादशाह, इक्का तक, स्ट्रेट के लिए 10 संभावित स्पैन हैं। उस स्ट्रेट में प्रत्येक कार्ड, प्रत्येक रैंक के लिए, चार संभावित सूट हैं। 4 x 4 x 4 x 4 x 4 = 4^5, पाँचों कार्डों में से प्रत्येक के लिए एक अलग सूट चुनने के तरीकों की संख्या। अगर हम पाँचों बार एक ही सूट चुनते हैं, तो हमारे पास स्ट्रेट फ्लश या रॉयल फ्लश भी बचेगा। हमें इन्हें घटाना होगा। 4^5 = 1,024 - 4 = स्ट्रेट बनाने के 10,200 तरीके।

एक तरह के तीन के बारे में क्या ख्याल है?

खैर, आप 13 तरीकों से तीन एक जैसे रंगों की रैंक चुन सकते हैं, और फिर आपको दो सिंगलटन के लिए बचे हुए 12 में से दो रैंक चुनने होंगे। ऐसा करने के बाद, आपको तीन एक जैसे रंगों के लिए तीन में से चार सूट चुनने होंगे, और फिर दोनों सिंगलटन के लिए चार में से एक सूट चुनना होगा।

हमारे पास एक तरह के तीन लोगों की रैंक चुनने के 13 तरीके बचे हैं। दो सिंगलटन के लिए बचे 12 में से दो रैंक चुनने के 66 तरीके हैं, गुणा तीन एक तरह के चार में से तीन सूट चुनने के चार तरीके, और दो सिंगलटन के लिए एक सूट चुनने के भी चार तरीके हैं। उत्तर 54,912 है।

दो जोड़ी के बारे में क्या ख्याल है?

खैर, आपके दो जोड़े के लिए 13 में से दो रैंक चुनने के लिए 13 चुनने के दो तरीके हैं, फिर आपके पास सिंगलटन के लिए एक रैंक बचेगी। प्रत्येक जोड़े के लिए, आपके जोड़े के लिए चार में से दो सूट चुनने के चार चुनने के दो तरीके हैं। आपके सिंगलटन के लिए चार सूट हैं। 13 चुनने के दो बराबर हैं 78 गुणा छह गुणा छह गुणा चार बराबर - मैं सिंगलटन के लिए अपनी 11 रैंक भूल गया। 78 x 11 x 6 x 6 x 4 = 123,552।

जोड़ी के लिए

जोड़ी की रैंक चुनने के 13 तरीके हैं, फिर आपको तीन सिंगलटन के लिए बची हुई बारह रैंक में से तीन रैंक चुननी होंगी। आपकी जोड़ी के लिए, चार में से दो सूट चुनने के चार विकल्प हैं, फिर तीन सिंगलटन में से प्रत्येक के लिए, चुनने के लिए चार संभावित सूट हैं। 4 x 4 x 4 उन तरीकों की संख्या है जिनसे आप अपने तीन सिंगलटन के लिए तीन सूट चुन सकते हैं, जो 13 x 12 के बराबर है - 12 में से तीन चुनें बराबर 220 x 6 x 4^3 = 64 = 1,098,240।

अंत में

आइए इक्का के बाएँ तरफ ऊपर या नीचे होने की प्रायिकता की गणना करें, जिसे मैं जंक कहूँगा। जंक पाने के लिए, आपके पास 13 में से पाँच अलग-अलग रैंक होनी चाहिए। दस में से पाँच रैंक चुनने के 13 तरीके हैं, लेकिन जैसा कि हमने फ्लश के साथ देखा, हमें दसवें स्पैन को ट्रैक करना होगा जो एक स्ट्रेट बनाते हैं। एक बार जब आप अपनी पाँच गैर-लगातार रैंक चुन लेते हैं, तो प्रत्येक रैंक के लिए चार संभावित सूट होते हैं।

आप चार की पांचवीं घात लें...

...और जैसा कि हमने स्ट्रेट्स के साथ देखा, हमें हर बार एक ही सूट चुनने के तरीकों की संख्या के लिए चार को घटाना होगा, जिसके परिणामस्वरूप फ्लश होगा। 13 चुनें पांच बराबर है 1,287 माइनस 10 स्ट्रेट्स के लिए चार से पांचवीं शक्ति के बराबर है 1,024 माइनस चार बराबर है 1,302,540।

अगला

आइए इसे एक स्प्रेडशीट में डालें। मैं आपको एक्सेल में यह सब कैसे करना है, यह जल्दी से दिखाता हूँ। हम पहले ही देख चुके हैं कि रॉयल फ्लश पाने के सिर्फ़ चार तरीके हैं, हर सूट के लिए एक, 36 स्ट्रेट फ्लश, चार सूट गुणा नौ संभावित स्पैन। आपके चार एक जैसे कार्डों के लिए, चुनने के लिए 13 रैंक हैं, चार एक जैसे कार्ड और सिंगलटन के लिए 48 कार्ड बचे हैं। फुल हाउस के लिए, तीन एक जैसे कार्डों के लिए 13 रैंक हैं, और जोड़ी के लिए 12।

चार लोग एक जैसे तीन लोगों के सूट चुनने के तीन तरीके चुनते हैं। चार लोग जोड़ी के लिए चार में से दो सूट चुनने के दो तरीके चुनते हैं। एक्सेल में इस फ़ॉर्मूले को इस सामान्य फ़ॉर्मूले से व्यक्त किया जाता है जिसमें बड़ी संख्या और छोटी संख्या के अल्पविराम को मिलाया जाता है, ठीक वैसे ही जैसे मैंने वहाँ लिखा था। इससे हमें पहले प्राप्त 3,744 प्राप्त होते हैं।

फ्लश के लिए

चुनने के लिए चार सूट हैं, 13 में से चुनने के पाँच तरीके हैं, उस सूट के 13 में से पाँच रैंक में से 10 स्पैन घटाएँ, जिससे स्ट्रेट फ्लश या रॉयल फ्लश बनेगा क्योंकि ये लगातार हैं। इससे हमारे पास 5,108 फ्लश बचते हैं। स्ट्रेट्स के लिए, 10 संभावित स्पैन हैं, स्पैन में प्रत्येक कार्ड के लिए चार सूट हैं, लेकिन चार सूट में से चार घटाएँ, जिससे आपको स्ट्रेट फ्लश या रॉयल फ्लश मिलेगा और हमें 10,200 मिलते हैं।

तीन प्रकार के लिए

तीन एक जैसे के लिए 13 रैंक हैं, 12 में से दो सिंगलटन के लिए दो रैंक चुनें। चार में से तीन सूट चुनने के लिए चार तरीके और दो सिंगलटन के लिए दो सूट चुनने के लिए चार गुना चार तरीके चुनें। 554,912, तीन एक जैसे। दो जोड़ों के लिए, 13 में से दो रैंक चुनने के लिए 13 तरीके हैं। सिंगलटन के लिए 11 बचे हैं, चार में से दो जोड़ों के लिए चार में से दो सूट चुनने के लिए दो तरीके और सिंगलटन के लिए चार सूट चुनने के लिए दो तरीके चुनें।

जोड़ी के लिए, हमारे पास 13 रैंक हैं, 12 तीन सिंगलटन के लिए 12 में से तीन रैंक चुनने के तीन तरीके चुनते हैं। चार जोड़ी के लिए चार में से दो सूट चुनने के दो तरीके चुनते हैं और तीन सिंगलटन के लिए तीन सूट चुनने के तरीकों के लिए चार की तीसरी घात।

अंत में, कबाड़ के लिए

13 में से पाँच रैंक चुनने के लिए पाँच तरीके हैं, जिनमें से 10 लगातार तरीके घटाएँ जिससे आपको एक स्ट्रेट मिलेगा और हर सूट चुनने के चार तरीके हैं। फ्लश पाने के लिए पाँचवीं घात के चार में से चार घटाएँ। जैसा कि आप देख सकते हैं, इन सबका योग 2,598,960 है, जो हमें इस वीडियो की शुरुआत में भी मिला था। ठीक है, आइए इन सबका व्यावहारिक अनुप्रयोग देखें।

मेरी वेबसाइट विज़ार्ड ऑफ़ ऑड्स पर जिन सैकड़ों कैसीनो खेलों को मैं कवर करता हूँ उनमें से एक का नाम है : लेट इट राइड ।

आइए उस पृष्ठ को खोलें और यह एक पोकर गेम है जो पांच-कार्ड पोकर हाथ पर आधारित है, इसमें कोई ड्रॉ नहीं है यह सब 52 में से सिर्फ पांच यादृच्छिक कार्डों पर आधारित है। मैं खेल के पूरे नियमों में नहीं जाऊंगा लेकिन एक साइड बेट है जो आपके पांच कार्डों के पोकर मूल्य के आधार पर भुगतान करता है।

आप देख सकते हैं...

...मैंने यहाँ नौ संभावित भुगतान तालिकाएँ सूचीबद्ध की हैं, लेकिन तालिका चार काफी सामान्य है। मैंने इसे पहले ही इस तालिका में लिख दिया है, दांव की कीमत $1 है। अगर आपको रॉयल फ्लश मिलता है तो आप $20,000 जीतते हैं, स्ट्रेट फ्लश पर 20,000 जीतते हैं, और फोर ऑफ अ काइंड पर 400 जीतते हैं। वैसे, ये भुगतान 4-1 के आधार पर होते हैं, जिसका अर्थ है कि अगर आप जीत जाते हैं तो आपको अपना मूल दांव नहीं रखना पड़ता।

यहां सभी संयोजन हैं जिनकी संभावनाओं पर मैंने पहले ही काम कर लिया है और यह रिटर्न कॉलम जीत और संभावना का गुणनफल है।

उदाहरण के लिए, यहाँ है:

जैसा कि हम पहले से जानते हैं, रॉयल फ्लश मिलने की संभावना लगभग चार करोड़ दो लाख साठ हज़ार है। अगर हम इस संभावना को 20,000 से गुणा करें, तो हमें 3.08 सेंट का अपेक्षित रिटर्न मिलेगा। अगर कोई खिलाड़ी एक डॉलर का दांव लगाता है, तो उसे रॉयल फ्लश जीत के रूप में इतनी ही रकम वापस मिलने की उम्मीद हो सकती है। उसे अपने स्ट्रेट फ्लश वगैरह के लिए 2.77 सेंट वापस मिलने की उम्मीद हो सकती है।

अगर आप सारा हिसाब लगाएँ तो नतीजा यह निकलता है कि खिलाड़ी $1 के दांव पर 74.4667 सेंट वापस पाने की उम्मीद कर सकता है। दूसरे शब्दों में, उस डॉलर के बदले खिलाड़ी लगभग 74 सेंट वापस पाने की उम्मीद कर सकता है।47% और कैसीनो 25.53% रखेगा।

मैं इसे जिस तरह से व्यक्त करूंगा...

...क्या हाउस एडवांटेज 25.53% है, तो इसे एक मिनट के लिए समझ लीजिए। कैसीनो उस दांव का 25% से ज़्यादा अपने पास रख रहा है, जो इस बात को दर्शाता है कि मैं 20 सालों से यही कहता आ रहा हूँ कि साइड बेट्स सभी बेकार दांव होते हैं। अगर आप इस वीडियो से बस एक बात सीखते हैं, तो मुझे उम्मीद है कि वो यही होगी। यह वीडियो पहले से ही काफी लंबा है, इसकी लंबाई के लिए क्षमा चाहता हूँ और मुझे उम्मीद है कि यह जानकारीपूर्ण रहा होगा और आपने कुछ सीखा होगा।

देखने के लिए धन्यवाद।

द्वारा लिखित: Michael Shackleford