प्रथम n पूर्णांकों के योग का प्रमाण

इस सप्ताह मैं अपने सबसे आसान प्रमाणों में से एक, यानी 1+2+3+…+n = n(n+1)/2 को सिद्ध करूँगा। मैं इसे दो बहुत ही सहज तरीकों से दिखाऊँगा। अब तक का मेरा सबसे आसान प्रमाण यही है। हालाँकि, इससे पहले कि हम उस पर पहुँचें, मैं अपनी हमेशा की तरह साप्ताहिक तर्क पहेली प्रस्तुत करूँगा।

तर्क पहेली

एलिस, बॉब और कोल निम्नलिखित कथन देते हैं:

1. • एलिस: बॉब झूठा है।
2. • बॉब: कोल झूठा है।
3. • कोल: एलिस और बॉब झूठे हैं।

ये तीनों या तो हमेशा सच बोलते हैं या हमेशा झूठ बोलते हैं। वे तीनों एक-दूसरे की सच्चाई जानते हैं। सच कौन बोल रहा है?

उत्तर और समाधान के लिए न्यूज़लेटर के अंत में देखें।

प्रथम n पूर्णांकों के योग का प्रमाण

सभी को यह ज्ञात होना चाहिए कि पहले n पूर्णांकों का योग n(n+1)/2 होता है। दूसरे शब्दों में, 1+2+3+…+n = n(n+1)/2। मैं इसके सत्य होने के दो सरल प्रमाण प्रस्तुत करता हूँ।

विधि 1

यह आसानी से देखा जा सकता है कि अनुक्रम में औसत संख्या (n+1)/2 है। श्रृंखला में पदों की संख्या n है। योग पदों की संख्या और औसत पद के गुणनफल के बराबर है = n × (n+1)/2 = n(n+1)/2।

इसी विधि का उपयोग किसी भी प्रारंभिक और अंतिम बिंदु के लिए योग ज्ञात करने हेतु किया जा सकता है। मान लीजिए प्रारंभिक संख्या a और अंतिम संख्या b है। औसत (a+b)/2 होगा। पदों की संख्या (a-b+1) होगी।अतः श्रृंखला में सभी संख्याओं का योग (a-b+1) × (a+b)/2 होगा।

विधि 2

अगली विधि को दृश्य रूप से समझाना आसान है। निम्नलिखित आरेख पर विचार करें, जहाँ नीले वर्ग 1 से 5 तक की पूर्णांक संख्याओं को दर्शाते हैं।

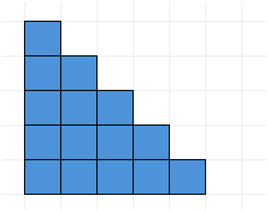
इसके बाद, इसकी प्रतिकृति बनाएं और इसे मूल टुकड़े के बगल में इस प्रकार रखें, जिससे एक आयत बन जाए।

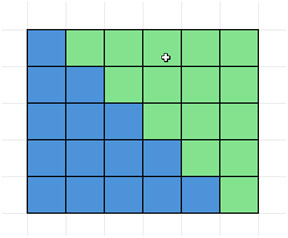
ध्यान दें कि ऊपर दिए गए आयत के आयाम 5 × 6 हैं। सामान्य स्थिति में, 1 से n तक पूर्णांकों को जोड़ने पर, आयाम n × (n+1) होते हैं। फिर उस क्षेत्रफल को 2 से भाग दें क्योंकि हमें केवल दो टुकड़ों में से एक का क्षेत्रफल ज्ञात करना है। इस प्रकार, एक टुकड़े का क्षेत्रफल n(n+1)/2 है।

तर्क पहेली का हल

तीनों व्यक्तियों के लिए दो संभावित स्थितियाँ हैं: सच बोलना या झूठ बोलना। इस प्रकार ^2³ = 8 संभावनाएँ बनती हैं। मैंने उन सभी को नीचे दी गई तालिका में सूचीबद्ध किया है।

परिदृश्य	1	2	3	4	5	6	7	8
एलिस	टी	टी	टी	टी	एफ	एफ	एफ	एफ
बीओबी	टी	टी	एफ	एफ	टी	टी	एफ	एफ
गोभी	टी	एफ	टी	एफ	टी	एफ	टी	एफ

ध्यान दें कि बॉब और कोल एक-दूसरे को झूठा कहते हैं। ऐसा तभी संभव है जब उनमें से एक सच बोलता हो और दूसरा झूठा। इसलिए, हम उन चार स्थितियों को हटा सकते हैं जहाँ बॉब और कोल दोनों एक ही सत्यवादी हैं। इससे परिदृश्य 2, 3, 6 और 7 बचते हैं। आइए हम इन पर एक-एक करके विचार करें।

दूसरे परिदृश्य में, यह माना गया है कि ऐलिस सच बोल रही है। उसके सच बोलने से बॉब झूठा साबित होता है। हालांकि, इस परिदृश्य में बॉब भी सच बोल रहा है, जिससे विरोधाभास उत्पन्न होता है। इसलिए दूसरा परिदृश्य गलत है।

परिदृश्य 3 में यह माना गया है कि ऐलिस सच बोलती है। वह कहती है कि बॉब झूठा है, जो परिदृश्य 3 की मान्यताओं के अनुसार सही है। हालांकि, कोल को सच बोलने वाला बताया गया है, जो कहता है कि ऐलिस झूठ बोल रही है। ऐलिस एक ही समय में सच बोलने वाली और झूठी नहीं हो सकती, इसलिए परिदृश्य 3 गलत है।

परिदृश्य 7 में यह माना गया है कि ऐलिस झूठ बोल रही है। वह कहती है कि बॉब झूठा है, जो कि सच है। हालाँकि, इससे ऐलिस भी सच बोलने लगेगी। ऐलिस एक ही समय में सच बोलने वाली और झूठी नहीं हो सकती, इसलिए परिदृश्य 7 गलत है।

अब केवल छठा परिदृश्य बचा है। चलिए देखते हैं कि यह सही बैठता है या नहीं। अगर एलिस झूठी होती, तो बॉब सच बोलता। अगर बॉब सच बोलता, तो एलिस या बॉब या दोनों सच बोलते। बॉब सच बोलता है, इसलिए कोल का कथन असत्य हो जाता है। अतः, यह कथन सही है। बॉब ही एकमात्र सच्चा व्यक्ति है।