त्रिभुज में कोणों का योग 180 डिग्री के बराबर होता है प्रमेय

यह सर्वविदित है कि किसी भी त्रिभुज के आंतरिक कोणों का योग 180 डिग्री होता है। इस न्यूज़लेटर में, मैं एक सरल प्रमाण प्रस्तुत करूँगा। हालाँकि, उससे पहले, मैं सामान्य साप्ताहिक तर्क पहेली प्रस्तुत करता हूँ।

तर्क पहेली

एक राजा के पास 49 सोने के सिक्के हैं। इन सिक्कों का वज़न 1, 2, 3, ... 49 ग्राम है। वह इन्हें अपने सात बेटों में कैसे बाँट सकता है ताकि हर बेटे को सात सिक्के मिलें और उनके वज़न का योग बराबर हो जाए?

प्रमाण कि किसी भी त्रिभुज के आंतरिक कोणों का योग 180 डिग्री होता है।

मैं एक मनमाना त्रिभुज बनाकर और उसके कोणों को चिह्नित करके शुरुआत करूँगा।

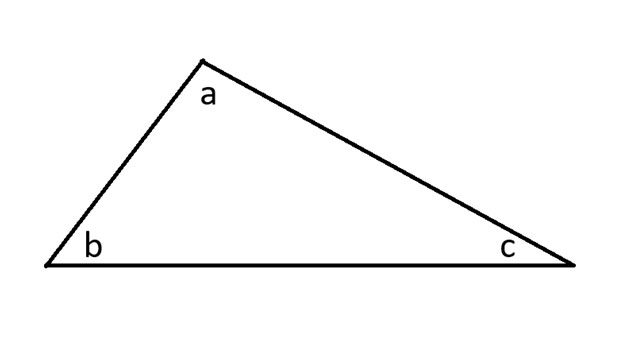
इसके बाद, मैं त्रिभुज की तीनों भुजाओं को बढ़ाऊंगा और साथ ही एक समान्तर रेखा खींचूंगा जो कोण a को स्पर्श करेगी।

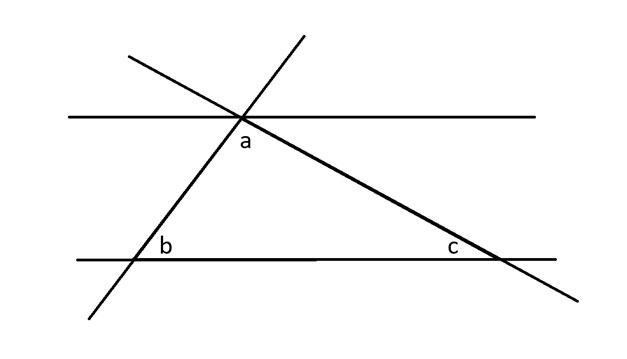
इसके बाद, मैं कोण b पर विपरीत कोण प्रमेय लागू करूंगा, जो कहता है कि दो प्रतिच्छेदित रेखाओं के विपरीत कोनों पर बने कोण बराबर होते हैं।

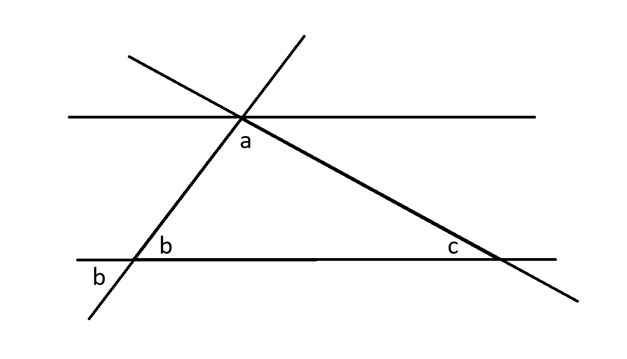
जब एक विकर्ण समांतर रेखाओं के समूह को काटता है, तो वह प्रत्येक रेखा को जहाँ वह काटता है, वहाँ समान कोण बनाता है। मैं इसे कोण a के बगल में b डिग्री का एक और कोण दिखाने के लिए लागू करता हूँ। फिर मैं कोण c के साथ भी यही करता हूँ।

6; फ़ॉन्ट-फ़ैमिली: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #313131 !महत्वपूर्ण; ">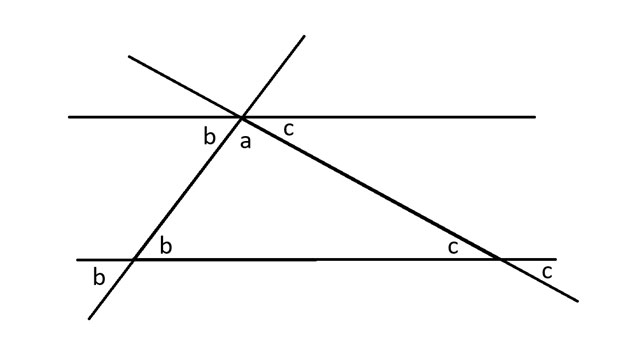

एक वृत्त में 360 डिग्री होती हैं। इस प्रकार, अर्धवृत्त में 180 डिग्री होती हैं। दूसरे शब्दों में, ऊपरी समांतर रेखा के नीचे के कोणों को देखते हुए, a + b + c = 180 डिग्री। ये मूल त्रिभुज के भी तीन कोण हैं। इस प्रकार, त्रिभुज के कोणों का योग 180 डिग्री के बराबर होता है।

तर्क पहेली समाधान

एक जादुई वर्ग बनाएँ और प्रत्येक बेटे को किसी एक कॉलम में सिक्के दें। आप सिक्कों को पंक्तियों में भी बाँट सकते हैं। आप पूछ सकते हैं, "आप 7x7 का जादुई वर्ग कैसे बनाते हैं?" इस विधि को स्यामी विधि के नाम से जाना जाता है और इसकी खोज भारत में बहुत पहले हुई थी।

आइए 7x7 बैटलशिप बोर्ड जैसे लेबल वाले ग्रिड से शुरुआत करें।

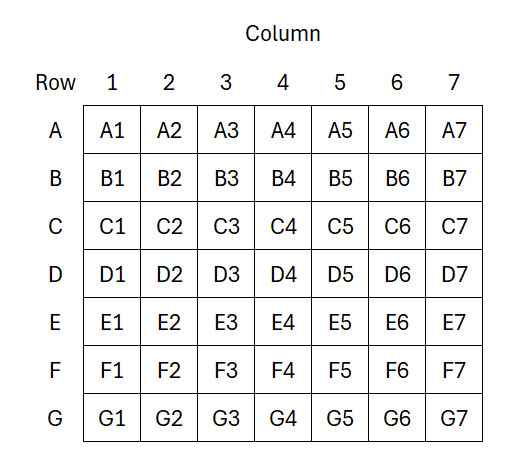
सेल A4 में 1 से शुरू करें। फिर इन नियमों का पालन करें:

1. अगली नियुक्ति के लिए हमेशा पिछली संख्या में 1 जोड़ें।
2. हमेशा उत्तर-पश्चिम दिशा में चलें, जब तक कि वह स्थान भरा हुआ न हो या आप पहले से ही पंक्ति A या स्तंभ 7 पर न हों।
3. यदि आप पंक्ति A पर हैं, तो अगले नंबर के लिए कॉलम G पर जाएँ।
4. यदि आप कॉलम 7 पर हैं, तो अगले नंबर के लिए कॉलम 1 पर जाएँ।
5. कॉल A7 दोनों तरफ से G1 तक जाएगी।
6. यदि अगला वर्ग, जहां आपको जाना है, व्यस्त है, तो अगले नंबर के लिए अगले वर्ग पर जाएं (यह खाली होना चाहिए)।

हम इस प्रकार शुरुआत करते हैं:

1. सेल A4 में 1.
2. हम पंक्ति A में हैं, इसलिए पंक्ति G पर जाएं, और सेल G5 में 2 डालें।
3. फिर हमने F6 में 3, E7 में 4 डाला।
4. हम स्तंभ 7 पर हैं, इसलिए हम D1 में 5 डालते हुए इसे लपेटते हैं।
5. C2 में 6, B3 में 7 रखें।
6. अब हम A4 पर आएंगे, लेकिन इसमें 1 लिखा है। इसलिए हम नीचे जाएंगे और अगली संख्या 8 को C3 में डालेंगे।
7. जब तक जादुई वर्ग पूरा न भर जाए तब तक दोहराते रहें।

पूरा होने पर यह कुछ इस प्रकार दिखेगा:

जेपीजी" />

यह विधि विषम संख्या वाले किसी भी जादुई वर्ग के लिए काम करेगी।

फिर, तय करें कि आप पंक्तियों में या स्तंभों में से किसमें भाग देंगे। प्रत्येक पुत्र को पंक्तियों/स्तंभों में से किसी एक में मिले सिक्के दें। उदाहरण के लिए, यदि आप स्तंभों के अनुसार भाग देते हैं, तो पुत्र 1 को 30, 38, 46, 5, 13, 21 और 22 सिक्के मिलेंगे।