राउंड रॉबिन शेड्यूलिंग

इस हफ़्ते का विषय होगा राउंड रॉबिन टूर्नामेंट का शेड्यूल कैसे बनाएँ। आगे बढ़ने से पहले, बता दूँ कि राउंड रॉबिन एक टूर्नामेंट फ़ॉर्मेट है जिसमें हर खिलाड़ी हर दूसरे खिलाड़ी से खेलता है। n खिलाड़ियों वाले टूर्नामेंट में, मैचों की संख्या n(n-1)/2 होगी।

n खिलाड़ियों के बीच सभी n(n-1)/2 संभावित जोड़ियों को सूचीबद्ध करना आसान होगा। हालाँकि, ऐसा राउंड में करना आदर्श है, जहाँ प्रत्येक खिलाड़ी प्रत्येक राउंड में एक बार खेलता है। सम संख्या में खिलाड़ियों के साथ ऐसा करने का तरीका यहाँ दिया गया है। आइए आठ खिलाड़ियों वाली स्थिति को एक उदाहरण के रूप में लेते हैं। निम्नलिखित चित्र में, हम खिलाड़ियों को A से H तक लेबल करते हैं और चार आयतों में एक मैच में भाग ले रहे दो खिलाड़ियों को दिखाते हैं। ये चार खेल पहले राउंड का निर्माण करेंगे। ध्यान दें कि हर कोई कैसे खेलता है।

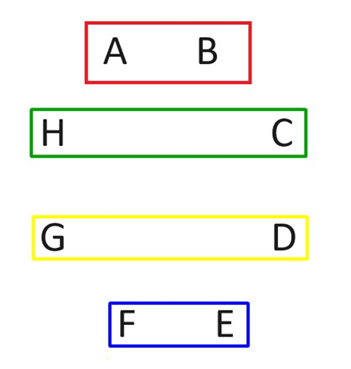
दूसरे राउंड में, खिलाड़ी A को उसी स्थिति में रखें। फिर बाकी सभी को दक्षिणावर्त घुमाएँ, जैसा कि नीचे दिए गए चित्र में दिखाया गया है।

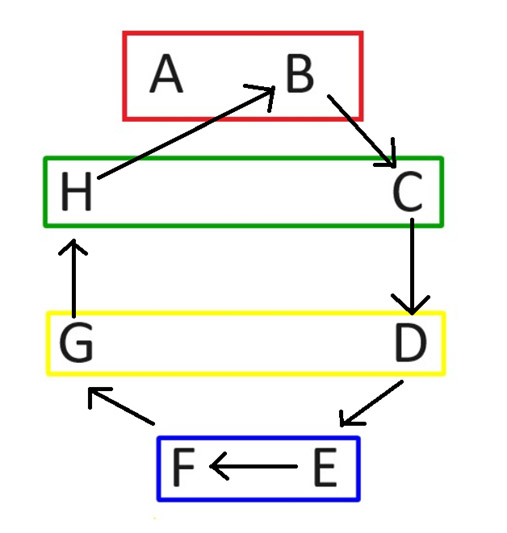
रोटेशन के बाद, मैचों का दूसरा दौर इस प्रकार होगा:

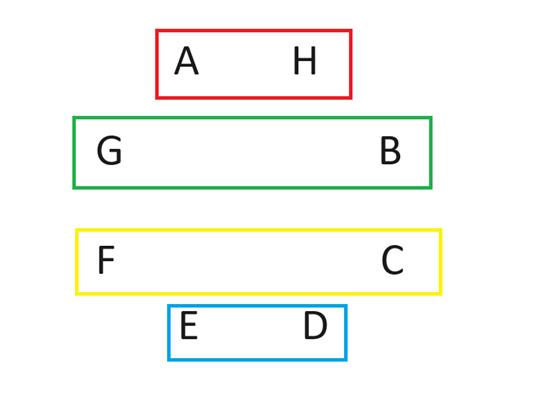
ऐसा तब तक करते रहें जब तक कि सभी खिलाड़ी A के खिलाफ न खेल लें। मैं यह नहीं समझा सकता कि यह कैसे काम करता है, लेकिन यह काम करता है। यह किसी भी सम संख्या के खिलाड़ियों के लिए काम करता है। इसके बारे में अधिक जानकारी के लिए, "सर्कल विधि" और "राउंड रॉबिन" पर खोजें।

नीचे दी गई तालिका आठ खिलाड़ियों के मामले में सभी मुकाबलों को दर्शाती है। ध्यान दें कि हर कोई एक-दूसरे के साथ ठीक एक बार खेलता है।

गोल	खिलाड़ी 1	खिलाड़ी 2
1	ए	बी
1	एच	सी
1	जी	डी
1	एफ	ई
1	ए	एच
2	जी	बी
2	एफ	सी
2	ई	डी
3	ए	जी
3	एफ	एच
3	ई	बी
3	डी	सी
4	ए	एफ
4	ई	जी
4	डी	एच
4	सी	बी
5	ए	ई
5	डी	एफ
5	सी	जी
5	बी	एच
6	ए	डी
6	सी	ई
6	बी	एफ
6	एच	जी
7	ए	सी
7	बी	डी
7	एच	ई
7	जी	एफ

विषम संख्या वाले खिलाड़ियों के लिए, सम संख्या पाने के लिए बस एक डमी खिलाड़ी को टूर्नामेंट में शामिल करें। जो भी डमी खिलाड़ी के खिलाफ खेलेगा उसे उस राउंड में बाई मिलेगी, यानी वह खेल से बाहर हो जाएगा। इसलिए, सभी खिलाड़ियों को एक राउंड में बाहर बैठना होगा। सात खिलाड़ियों वाले टूर्नामेंट में यह कैसा दिखेगा, यह इस प्रकार है।

गोल	खिलाड़ी 1	खिलाड़ी 2
1	ए	बी
1	अलविदा	सी
1	जी	डी
1	एफ	ई
2	ए	अलविदा
2	जी	बी
2	एफ	सी
2	ई	डी
3	ए	जी
3	एफ	अलविदा
3	ई	बी
3	डी	सी
4	ए	एफ
4	ई	जी
4	डी	अलविदा
4	सी	बी
5	ए	ई
5	डी	एफ
5	सी	जी
5	बी	अलविदा
6	ए	डी
6	सी	ई
6	बी	एफ
6	अलविदा	जी
7	ए	सी
7	बी	डी
7	अलविदा	ई
7	जी	एफ

अंत में, मान लीजिए कि यह एक टेनिस टूर्नामेंट है जहाँ हर कोर्ट का एक अच्छा और एक बुरा पक्ष होता है। बुरा पक्ष शायद सूर्य की ओर हो सकता है। यह सुनिश्चित करने का उचित तरीका क्या है कि हर खिलाड़ी को अच्छे और बुरे पक्ष बराबर संख्या में मिलें?

इस समस्या को हल करने के लिए, मैं बिग बैंग थ्योरी में बताए गए " लिज़र्ड स्पॉक एक्सपेंशन " का उपयोग करके प्रस्तुत करता हूँ। पत्थर-कागज़-कैंची खेलने का यह तरीका किसी भी विषम संख्या में प्रतीकों के साथ काम करता है। यह निर्धारित करने के लिए कि कौन सा खिलाड़ी अच्छा पक्ष प्राप्त करता है, सात खिलाड़ियों वाले मामले पर विचार करें। निम्नलिखित आरेख दर्शाता है कि कौन सा खिलाड़ी अच्छा पक्ष प्राप्त करता है, जैसा कि तीर द्वारा इंगित किया गया है जो खराब पक्ष प्राप्त करने वाले खिलाड़ी की ओर इशारा करता है।

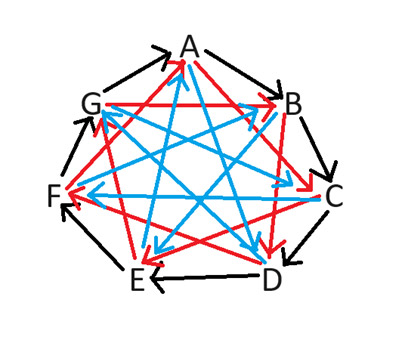
उदाहरण के लिए, अगर खिलाड़ी B और D खेलते हैं, तो B को अच्छा पक्ष मिलेगा, क्योंकि उनके बीच का तीर D की ओर इशारा करता है। यह समझना मुश्किल नहीं है कि मैंने चित्र कैसे बनाया। तीर हमेशा दक्षिणावर्त दिशा में इशारा करते हैं। आपको 1 से 3 तक हर संभव अंतराल के लिए तीर बनाने होंगे।

हालाँकि, ऐसा कोई आरेख बनाने की ज़रूरत नहीं है, बस अक्षरों का एक घेरा बनाना होगा। एक खिलाड़ी से दूसरे खिलाड़ी तक पहुँचने के लिए वृत्त के चारों ओर दक्षिणावर्त दिशा में घूमने के दोनों तरीकों पर विचार करें। कम कदमों वाला रास्ता अच्छा पक्ष देगा। B और F के बीच एक खेल पर विचार करें। दक्षिणावर्त दिशा में जाने पर, B से 4 तक चार कदम और F से B तक तीन कदम लगते हैं। चूँकि तीन, चार से कम है, इसलिए F को अच्छा पक्ष मिलेगा।

निम्नलिखित तालिका सात खिलाड़ियों के राउंड रोबिन में सभी संभावित मुकाबलों को दर्शाती है, जिसमें यह भी शामिल है कि कौन से खिलाड़ी अच्छे और कौन से बुरे पक्ष में हैं।

गोल	अच्छा पक्ष	बुरा पक्ष
1	ए	बी
1	सी	अलविदा
1	डी	जी
1	ई	एफ
2	ए	अलविदा
2	जी	बी
2	सी	एफ
2	डी	ई
3	जी	ए
3	एफ	अलविदा
3	बी	ई
3	सी	डी
4	एफ	ए
4	ई	जी
4	डी	अलविदा
4	बी	सी
5	ई	ए
5	डी	एफ
5	जी	सी
5	बी	अलविदा
6	ए	डी
6	सी	ई
6	एफ	बी
6	जी	अलविदा
7	ए	सी
7	बी	डी
7	ई	अलविदा
7	एफ	जी

दुर्भाग्य से, यह पक्ष संतुलन रणनीति सम संख्या में खिलाड़ियों के लिए काम नहीं करती। ऐसा इसलिए है क्योंकि जब दो खिलाड़ी बिल्कुल विपरीत दिशाओं में होते हैं, तो वृत्त के चारों ओर दोनों की दूरियाँ समान होती हैं। यदि मजबूर किया जाए, तो इस विधि का उपयोग अन्य सभी मुकाबलों के लिए किया जा सकता है, लेकिन खिलाड़ियों को वृत्त पर 180 डिग्री की दूरी पर यादृच्छिक रूप से खेलना होगा।

फिलहाल मैं इस विषय को यहीं तक ले जाऊँगा। मैं भविष्य में किसी न्यूज़लेटर में इस पर विस्तार से चर्चा करने का अधिकार सुरक्षित रखता हूँ। आगे की चर्चा के संभावित विषयों में तीन या अधिक खिलाड़ियों वाले मैच और कई कोर्ट का उपयोग शामिल हो सकता है, जहाँ यह संतुलन बनाना ज़रूरी है कि प्रत्येक खिलाड़ी प्रत्येक कोर्ट पर कितनी बार खेलता है।

अंत में, मैं आप सभी को हनुक्का की शुभकामनाएं देता हूँ!

द्वारा लिखित: Michael Shackleford