हार्मोनिक श्रृंखला के अपसारी होने का प्रमाण

इस सप्ताह का प्रमाण यह होगा कि हार्मोनिक श्रृंखला अभिसरित होती है। हालाँकि, इससे पहले, मैं हमेशा की तरह साप्ताहिक तर्क पहेली प्रस्तुत करता हूँ।

तर्क पहेली

सोमवार को अस्पताल की नर्सरी में दो बच्चे हैं, एक लड़का और एक लड़की।

मंगलवार को परिवार में एक नया बच्चा आया है।

बुधवार को एक बच्चे का चयन यादृच्छिक रूप से किया जाता है। वह एक लड़का है।

मंगलवार को पैदा हुए बच्चे के लड़का होने की संभावना क्या है?

हार्मोनिक श्रृंखला के अपसारी होने का प्रमाण

हार्मोनिक श्रृंखला सभी पूर्णांकों के व्युत्क्रमों का समुच्चय है। दूसरे शब्दों में, 1 1 , 1 2 , 1 3 , 1 4 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 5 ,…, 1 ∞ . एक श्रृंखला को अपसारी कहा जाता है यदि उसके सभी सदस्यों का योग अनंत हो। हार्मोनिक श्रृंखला के मामले में यह स्पष्ट नहीं है क्योंकि सदस्य अनंत रूप से छोटे होते जाते हैं। हालाँकि, मैं सिद्ध करता हूँ कि योग वास्तव में अनंत है।

विधि 1: तुलनात्मक परीक्षण

यदि मैं यह सिद्ध कर सकूँ कि समान या कम सदस्यों वाली कोई अन्य श्रृंखला अपसारी है, तो हार्मोनिक श्रृंखला भी अपसारी होनी चाहिए।

हार्मोनिक श्रृंखला: 1 1 , 1 2 , 1 3 , 1 4 , 1 5 , 1 6 ,6; फ़ॉन्ट-फ़ैमिली: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #313131 !महत्वपूर्ण;"> 1 7 , 1 8 , 1 9 , 1 10 , 1 11 , 1 12 , 1 13 ,…, 1 ∞ .

श्रृंखला 2: 1 1 , 1 2 ,6; फ़ॉन्ट-फ़ैमिली: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #313131 !महत्वपूर्ण;"> 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 ,6; फ़ॉन्ट-परिवार: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #313131 !महत्वपूर्ण;"> 1 16 , 1 16 , 1 16 , 1 32 ,…, 1 ∞ .

श्रृंखला 2 की शुरुआत हार्मोनिक श्रृंखला के समान दो सदस्यों से होती है। फिर, प्रत्येक n >= 2 के लिए, यह 1 / ²ⁿ x ^2n-1 बार दोहराई जाती है। ध्यान दें कि श्रृंखला 2 का प्रत्येक सदस्य हार्मोनिक श्रृंखला के सदस्य के बराबर या उससे कम है। श्रृंखला 2 को ऐसे समूहों में विभाजित किया जा सकता है जिनका योग 1 / ²ⁿ x ^2n-1 = 1/2 होता है। आइए प्रत्येक समूह को अलग-अलग रंग देकर इसे स्पष्ट करें:

श्रृंखला 2: 1 1 ,6; फ़ॉन्ट-फ़ैमिली: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #313131 !महत्वपूर्ण;"> 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6; फ़ॉन्ट-फ़ैमिली: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #00A0D1 !महत्वपूर्ण;"> 1 16 , 1 16 , 1 16 , 1 16 , 1 32 (16 बार), 1 64 (32 बार) …, 1 ∞

1 + ( 1 2 X ∞)= ∞

विधि 2: कैलकुलस

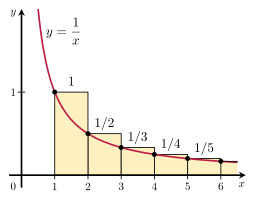
ध्यान दें कि पीले आयतों का क्षेत्रफल लाल वक्र के नीचे के क्षेत्रफल से अधिक है। लाल वक्र पर क्षेत्रफल है:

∫ ₁ ^∞ 1 x dx = ln(x) + c from 1 to ∞ = ln(∞) + c – ln(1) – c = ∞.

तर्क पहेली का हल

संक्षिप्त जवाब

जो कुछ हुआ उसके दो संभावित कारण हो सकते हैं। आइए उन्हें X और Y नाम दें।

X = मंगलवार को एक लड़का जोड़ा गया और बुधवार को एक लड़का देखा गया। इसकी प्रायिकता (1/2)*(2/3) = 2/6 = 1/3 है।

Y = मंगलवार को एक लड़की देखी गई और बुधवार को एक लड़का देखा गया। इसकी प्रायिकता (1/2)*(1/3) = 1/6 है।

X+Y = 1/3 + 1/6 = 1/2

प्रश्न में यह पूछा गया है कि दोनों में से किसकी प्रायिकता है, जहाँ X वह घटना है जो घटित हुई। प्रायिकता X/(X+Y) = (1/3)/(1/2) = 2/3 होगी।

लंबा उत्तर

बेयसियन सशर्त प्रायिकता सूत्र कहता है कि प्रायिकता (A, B दिए जाने पर) = प्रायिकता (A और B) / प्रायिकता (B), जहाँ प्रायिकता (x) किसी भी घटना x की प्रायिकता है। मान लीजिए:

ए = मंगलवार को जोड़ा गया लड़का

6; फ़ॉन्ट-फ़ैमिली: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #313131 !महत्वपूर्ण; ">B = बुधवार को देखा गया लड़का

इस मामले में:

प्रायिकता (A दिया गया है B) = प्रायिकता (मंगलवार को लड़का जोड़ा गया, बुधवार को लड़का देखा गया) = प्रायिकता (मंगलवार को लड़का जोड़ा गया और बुधवार को लड़का देखा गया) / प्रायिकता (बुधवार को लड़का देखा गया)।

मंगलवार के ड्रॉ के बारे में कोई जानकारी न होने के कारण, मंगलवार को लड़का होने की 50% संभावना है। यदि मंगलवार को लड़का हुआ था, तो बुधवार को लड़का होने की 2/3 संभावना है।

इसी प्रकार, मंगलवार के ड्रॉ के बारे में कोई जानकारी न होने पर, मंगलवार को लड़की होने की 50% संभावना है। यदि मंगलवार को लड़की का जन्म हुआ, तो बुधवार को लड़का होने की 1/3 संभावना होगी।

बुधवार को लड़का चुने जाने की प्रायिकता बराबर है (मंगलवार को जोड़ा गया लड़का) * (बुधवार को चुना गया लड़का) + (मंगलवार को जोड़ी गई लड़की) * (बुधवार को चुना गया लड़का) = (1/2) * (2/3) + (1/2) * (1/3) = 1/2।

मंगलवार को एक लड़के को जोड़े जाने और बुधवार को एक लड़के को निकाले जाने की प्रायिकता = (1/2)*(2/3) = 1/3.

अतः उत्तर (1/3)/(1/2) = 2/3 है।