मार्च पागलपन 2025

तर्क पहेली

इससे पहले कि हम इस सप्ताह के मार्च मैडनेस के आंकड़ों पर आएं, हमारी सामान्य साप्ताहिक तर्क पहेली का समय आ गया है। यह रही वह पहेली।

तीन खिलाड़ी एक खेल खेलते हैं। खिलाड़ियों की नज़रों से ओझल, तीन सिक्के उछाले जाते हैं, प्रत्येक खिलाड़ी के लिए एक। प्रत्येक सिक्के के उछाल के अनुसार, उस खिलाड़ी की आँखों पर पट्टी बाँध दी जाती है और उसे एक काली या सफेद टोपी दी जाती है। फिर आँखों से पट्टी हटा दी जाती है और प्रत्येक खिलाड़ी अन्य दो खिलाड़ियों की टोपियाँ देख सकता है, लेकिन अपनी टोपी नहीं।

फिर प्रत्येक खिलाड़ी को अपनी टोपी का रंग दर्ज करने के लिए एक गुप्त मतदान दिया जाता है। विकल्प हैं: काला, सफेद और पास। प्रयोग सफल होने के लिए, सफेद या काले रंग के लिए मतदान करने वाले सभी खिलाड़ियों का सही होना ज़रूरी है। हालाँकि, अगर तीनों खिलाड़ी "पास" के लिए मतदान करते हैं, तो प्रयोग विफल हो जाता है।

खिलाड़ियों को रणनीति बनाने के लिए कुछ समय दिया जाता है। वे कौन सी रणनीति अपना सकते हैं जिससे सफलता की संभावना 75% हो?

मार्च पागलपन अपडेट

मैं मार्च मैडनेस के प्रस्तावों पर खूब दांव लगाता था। इसका एक सामान्य उदाहरण पैसिफिक 12 कॉन्फ्रेंस में टीमों द्वारा जीते जाने वाले कुल खेलों की संख्या पर ओवर/अंडर हो सकता है। ऐसे दांवों को कम करने के लिए, यह जानना उपयोगी था कि किसी भी वरीयता प्राप्त टीम को कितने खेल जीतने की उम्मीद है।

कुछ दांव पहले ही राउंड में तय हो जाते हैं। खासकर, क्या 13 या उससे ज़्यादा की सीड कोई गेम जीतेगी? इस साल के कवर्स के कुछ उदाहरण यहां दिए गए हैं।

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">इस वर्ष, जीतने वाला सबसे कम रैंक वाला बीज (या उच्चतम बीज संख्या) 12 था। इसलिए, उपरोक्त में से कोई भी दांव नहीं जीता होगा।

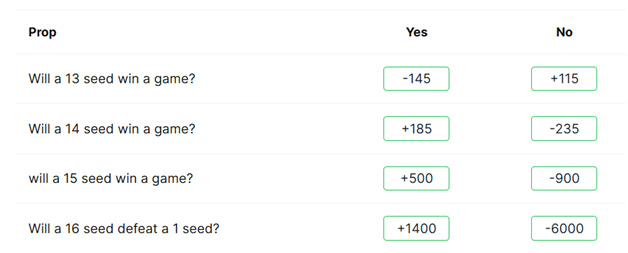
निम्नलिखित तालिका किसी भी विशिष्ट सीड के पहले दौर में एक गेम जीतने की संभावना दर्शाती है, साथ ही उस सीड की चार टीमों में से किसी एक के जीतने की भी। यह तालिका 1985-2025 तक के NCAA टूर्नामेंट के 40 वर्षों पर आधारित है।

बीज	विशिष्ट टीम की जीत	कोई भी टीम पहले राउंड में जीतती है
1	98.75%	100.00%
2	92.50%	100.00%
3	85.63%	99.96%
4	79.38%	99.82%
5	64.38%	98.39%
6	61.25%	97.75%
7	61.25%	97.75%
8	50.00%	93.75%
9	50.00%	93.75%
10	38.75%	85.93%
11	38.75%	85.93%
12	35.63%	82.83%
13	20.63%	60.31%
14	14.38%	46.25%
15	7.50%	26.79%
16	1.25%	4.91%

इस साल, पहले दौर में बचने वाले खिलाड़ियों की औसत वरीयता 5.34 थी। कुल मिलाकर टूर्नामेंट का औसत 5.84 है।

दूसरे राउंड में, स्वीट सिक्सटीन तक पहुँचने के लिए औसत सीड 3.44 था। टूर्नामेंट का औसत 4.52 है। दो गेम तक पहुँचने के लिए सबसे कम रैंक वाला सीड 10 था। दूसरे शब्दों में, इस साल पहले दो राउंड में अंडरडॉग्स का प्रदर्शन अच्छा नहीं रहा।

तीसरे राउंड में, एलीट आठ में पहुँचने के लिए औसत सीड 1.625 था। टूर्नामेंट का औसत 3.30 है। तीन गेम तक पहुँचने के लिए सबसे कम रैंक वाले सीड 3 थे, जिनमें से केवल एक ही था। यह टूर्नामेंट में सबसे कम रैंक वाले सीड के 3 गेम तक पहुँचने के रिकॉर्ड की बराबरी करता है। ऐसा पहले दो बार, 2007 और 2009 में हो चुका है। 1.625 का औसत सीड टूर्नामेंट के इतिहास में एक नया न्यूनतम रिकॉर्ड बनाता है।

फ़ाइनल फ़ोर में, चारों टीमें नंबर 1 थीं। टूर्नामेंट के इतिहास में ऐसा सिर्फ़ एक बार, 2008 में हुआ था। फ़ाइनल फ़ोर में जगह बनाने के लिए वन सीड्स की सटीक संख्या पर एक लोकप्रिय प्रस्ताव शर्त है। इस साल कवर्स की वह शर्त यहाँ दी गई है।

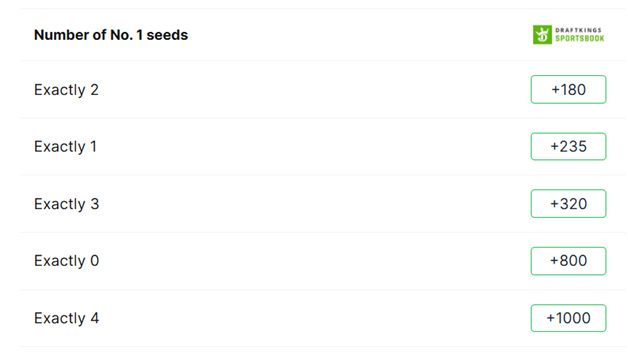
निम्नलिखित तालिका दर्शाती है कि टूर्नामेंट के 40 वर्षों के इतिहास में कितने नंबर वन सीड फाइनल फोर में पहुंचे हैं।

#1 बीज	गिनती करना	संभावना
4	2	5.00%
3	4	10.00%
2	15	37.50%
1	16	40.00%
0	3	7.50%
कुल	40	100.00%

किसी भी विशिष्ट नंबर वन सीड के फाइनल फोर में पहुंचने की संभावना 41.25% है।

यह कहने की आवश्यकता नहीं है कि फाइनल फोर में सभी चार टीमें नंबर वन सीड हैं, इसलिए दो वन सीड चैंपियनशिप गेम में पहुंचेंगे और उसे जीतेंगे भी।

एक और प्रस्तावित दांव चैंपियनशिप गेम जीतने के लिए सीड का है। इस साल कवर्स पर दांव इस प्रकार थे।

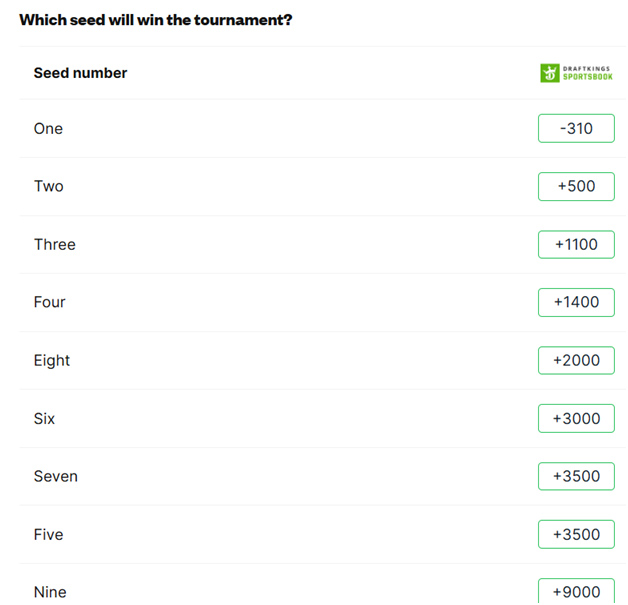
निम्नलिखित तालिका दर्शाती है कि प्रत्येक सीड ने कितनी बार चैम्पियनशिप गेम जीता है।

विजेता बीज	गिनती करना	संभावना
1	26	65.00%
2	5	12.50%
3	4	10.00%
4	2	5.00%
5	0	0.00%
6	1	2.50%
7	1	2.50%
8	1	2.50%
9 से 16	0	0.00%
कुल	40	100.00%

सीड द्वारा अपेक्षित जीतों पर वापस आते हुए, इस सीज़न के आंकड़ों सहित एक अद्यतन तालिका यहां दी गई है।

बीज	औसत जीत
1	3.34
2	2.33
3	1.84
4	1.56
5	1.14
6	1.06
7	0.89
8	0.73
9	0.59
10	0.61
11	0.64
12	0.51
13	0.24
14	0.16
15	0.11
16	0.01

एक सवाल जो मुझसे अक्सर पूछा जाता है, वह है परफेक्ट ब्रैकेट की प्रायिकता। 1 बनाम 1 वाली स्थिति में बेतरतीब ढंग से चुनने के अलावा, हर बार हमेशा उच्च वरीयता प्राप्त खेल (या कम संख्या) को चुनने की रणनीति मानते हुए, इस सीज़न के आंकड़ों सहित मेरी अद्यतन प्रायिकता 287,548,153 में 1 है।

तर्क पहेली का उत्तर

रणनीति इस प्रकार होनी चाहिए:

1. • यदि आपको विपरीत रंग की दो टोपियाँ दिखाई दें, तो आगे निकल जाएँ।
2. • यदि आपको एक ही रंग की दो टोपियाँ दिखें, तो विपरीत रंग की टोपियाँ चुनें।

तीन रंगों के अनुसार हम क्या होने की उम्मीद कर सकते हैं, वह इस प्रकार है:

1. • तीन काले: सभी खिलाड़ी दो काले देखेंगे और सफेद पर वोट देंगे। सभी गलत होंगे, इसलिए प्रयोग विफल हो जाएगा।
2. • दो काले, एक सफेद: सफेद खिलाड़ी दो काली टोपियाँ देखेगा और सही सफेद को वोट देगा। दो काले खिलाड़ी प्रत्येक रंग की एक टोपी देखेंगे और पास कर देंगे। प्रयोग सफल रहा।
3. • एक काला, दो सफ़ेद: काला खिलाड़ी दो सफ़ेद टोपियाँ देखेगा और सही काले रंग के लिए वोट देगा। दो सफ़ेद खिलाड़ी प्रत्येक रंग की एक टोपी देखेंगे और पास कर देंगे। प्रयोग सफल रहा।
4. • तीन सफ़ेद: सभी खिलाड़ी दो सफ़ेद देखेंगे और काले पर वोट देंगे। सभी गलत होंगे, इसलिए प्रयोग विफल हो जाएगा।

तीन सफेद या तीन काले होने की प्रायिकता 2*(1/2) ³ = 25% है। विकल्प यह है कि दोनों रंगों के बीच 2-1 का अनुपात हो, जिसकी प्रायिकता 75% है। जैसा कि ऊपर दिखाया गया है, 2-1 के अनुपात में विभाजन होने पर प्रयोग सफल होगा।