प्राइस इज राइट प्रतियोगी पंक्ति

मुख्य विषय पर आने से पहले, एक अपडेट। पिछले हफ़्ते मैंने बर्निंग मैन के टिकट पाने की प्रक्रिया के बारे में लिखा था। बुधवार को, मैंने मेन सेल में अपनी किस्मत आजमाई। जैसा कि आपको याद होगा, आखिरी काम 30 मार्च को ठीक दोपहर 12 बजे टिकट खरीदने के लिए तैयार रहना था। मैं तैयार था। दरअसल, मेरे पास सेल के लिंक वाले तीन ब्राउज़र तैयार थे। सच कहूँ तो, मुझे यकीन नहीं है कि इससे मेरी संभावनाएँ बढ़ीं या नहीं, लेकिन बर्निंग मैन से जुड़े दूसरे स्रोत ऐसा करने की सलाह देते हैं।

लंबी कहानी को संक्षेप में कहें तो, मुझे टिकट नहीं मिला। ऐसा होना ही था। कम से कम मैंने कोशिश तो की। 2019 के उलट, मेरी स्क्रीन पर नीचे जो तस्वीर आप देख रहे हैं, वह सेल शुरू होने के लगभग आधे घंटे बाद अपडेट की गई थी कि टिकट बिक चुके हैं। आप सोच रहे होंगे कि क्या मैंने "वापस" पर क्लिक किया था, जिसके बारे में स्क्रीन पर लिखा था कि इससे कोई मदद नहीं मिलेगी। मैंने ऐसा नहीं किया।

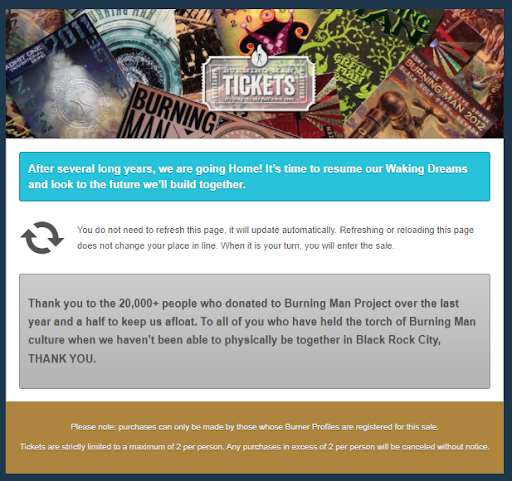
तो लगता नहीं कि मैं इस साल बर्निंग मैन देखने जा पाऊँगा। कोई बात नहीं। मेरे पास छुट्टियों के और भी कई आइडियाज़ हैं।

मुख्य विषय पर आते हैं, यानी "द प्राइस इज़ राइट" में प्रतियोगियों की लड़ाई। यह खेल हर शो में छह बार खेला जाता है। जो लोग नहीं जानते, उनके लिए ये हैं इसके नियम:

1. अगले मूल्य निर्धारण खेल में प्रतिस्पर्धा करने के लिए चार खिलाड़ियों को चुना जाता है।
2. एक वस्तु दिखाई जाती है, जिसकी कीमत आमतौर पर $1,000 से $2,000 के बीच होती है। उदाहरण के लिए, एक अच्छी साइकिल।
3. खिलाड़ी एक निर्दिष्ट क्रम में, वस्तु के मूल्य पर बोली लगाएंगे।
4. जिस खिलाड़ी की बोली वास्तविक मूल्य के सबसे करीब आती है, वह वस्तु जीत जाता है और उसे अगला मूल्य निर्धारण खेल खेलने का मौका मिलता है।
5. अगर चारों खिलाड़ी ज़्यादा बोली लगाते हैं, तो वे उसी क्रम में दोबारा बोली लगाते हैं, और उन्हें पिछले राउंड की सबसे कम बोली से ज़्यादा बोली न लगाने को कहा जाता है। यह तब तक जारी रहेगा जब तक कि कोई ऐसा राउंड न आ जाए जिसमें कम से कम एक खिलाड़ी ज़्यादा बोली न लगाए।

इस खेल में आपकी रणनीति क्या होनी चाहिए, यह मानते हुए कि आपको पुरस्कार के मूल्य के बारे में कुछ भी पता नहीं है?

शो के ज़्यादातर प्रतियोगियों की रणनीति बहुत खराब होती है। मान लीजिए कि आप बोली लगाने वाले आखिरी व्यक्ति हैं और पिछली बोलियाँ $1,500, $1,600 और $2,400 थीं। सबसे अच्छी बोलियाँ, जिन्हें वस्तु के मूल्य के बारे में कुछ भी पता नहीं है, ये होंगी:

• $1: इसमें $1499 की रेंज शामिल है - मूल्य $1 से $1499 तक, हालांकि पुरस्कार कभी भी $1 के करीब नहीं होते हैं।
• $1601: इसमें $800 की रेंज शामिल है - $1,600 से $2,399 तक के मूल्य।
• $2401: यह एक अनंत सीमा को कवर करता है - $2,400 से लेकर अनंत तक के मूल्य।

आप खिलाड़ियों को अक्सर ऐसी बोलियाँ लगाते हुए देखते हैं जो बेवजह सीमा छोड़ देती हैं। ऊपर दिए गए उदाहरण में, $2000। इससे $1600 से $1999 तक की सीमा मिल जाती है, जबकि $1600 की बोली बिना किसी कीमत के होती है।

कोई भी सामान्य नियम हर स्थिति को कवर नहीं करेगा। बस जितना हो सके, व्यापक दायरे को कवर करने की कोशिश करें, खासकर उस दायरे में जहाँ पुरस्कार मिलने की संभावना ज़्यादा होती है।

आप पूछेंगे कि अगर चार तर्कशास्त्री खेल रहे हों, तो क्या होगा? मान लीजिए कि तर्कशास्त्रियों को इनाम की कीमत के बारे में कुछ भी पता नहीं है। स्पष्टीकरण को आसान बनाने के लिए, मान लीजिए कि प्रतियोगी पैसे तक की बोली लगा सकते हैं।

6;font-family: 'Open Sans',sans-serif;color: #313131!important">आइए एक साधारण स्थिति से शुरुआत करें जहाँ पुरस्कार का मूल्य यादृच्छिक है और $0 से $1000 तक के एक समान वितरण से चुना गया है। ज़ाहिर है, आखिरी में जाने का एक स्थितिगत लाभ है। मैं गणित में नहीं जाऊँगा, लेकिन यहाँ बताया गया है कि चार तर्कशास्त्रियों को पहले से आखिरी तक कैसे बोली लगानी चाहिए:

• खिलाड़ी 1: $777.80
• खिलाड़ी 2: $555.57
• खिलाड़ी 3: $333.33
• खिलाड़ी 4: $0.01, $333.34, $555.57, या $777.79.

मुख्य बात यह है कि पहले तीन खिलाड़ी अपने बाद के सभी खिलाड़ियों को लगभग एक तटस्थ बिंदु पर लाना चाहते हैं। वे जितना हो सके उतनी जगह काटना चाहते हैं, बिना किसी बाद वाले खिलाड़ी को उनसे $0.01 ज़्यादा बोली लगाने के लिए प्रेरित किए।

अगर वे इस तरह बोली लगाते हैं, तो खिलाड़ी 4 के जीतने की संभावना 33.3% होगी, चाहे मैंने उसके लिए जो भी चार संभावित बोलियाँ सूचीबद्ध की हों। बाकी सभी खिलाड़ियों के जीतने की संभावना 22.2% होगी। मैंने खिलाड़ी 1 और 2 की बोलियों में एक या दो पैसे जोड़े, ताकि यह सुनिश्चित हो सके कि खिलाड़ी 3 और 4 उनसे $0.01 ज़्यादा बोली न लगाएँ।

हालाँकि, यह एक अवास्तविक उदाहरण है, क्योंकि पुरस्कारों का मूल्य एक घातांकीय वितरण का अनुसरण करता है। इसे और अधिक यथार्थवादी बनाने के लिए, मान लें कि पुरस्कार का मूल्य $1,000 के माध्य वाले घातांकीय वितरण से यादृच्छिक रूप से चुना गया है।

गणित में उलझे बिना, उपरोक्त धारणा के तहत इष्टतम बोलियां इस प्रकार हैं:

• खिलाड़ी 1: $1,504.08
• खिलाड़ी 2: $810.98
• खिलाड़ी 3: $405.47
• खिलाड़ी 4: $0.01, $405.48, $810.99, या $1,504.09

जीतने की संभावना पहले मामले के समान ही होगी, खिलाड़ी 4 के लिए 33.3% और अन्य सभी के लिए 22.22%।

इस हफ़्ते के लिए बस इतना ही। अगली बार तक, दुआ है कि हालात आपके पक्ष में रहें।

द्वारा लिखित: Michael Shackleford