PEMDAS नियम कैसे लागू करें?

अगर आप मेरी तरह हैं, तो आपके फ़ेसबुक लाइव फ़ीड में संक्रिया क्रम से जुड़े अनगिनत सवाल आते हैं। इन सबके बाद कमेंट्स में सैकड़ों जवाब आते हैं जिनमें ज़्यादातर लोग ग़लत होते हैं। ऐसे लोगों की संख्या हमेशा शून्य होती है जो कभी स्वीकार करते हैं कि वे ग़लत थे।

मेरी राय को सही क्या बनाता है? सबसे पहले, अगर मैं अपनी तारीफ़ करूँ, तो मैं यह मानना चाहूँगा कि मुझे कैसीनो गेम्स के गणित के एक प्रमुख स्रोत के रूप में मान्यता प्राप्त है। किसी भी कैसीनो गेम या शब्द को खोजें और आपको मेरा नाम हर जगह दिखाई देगा। इसके अलावा, मेरे पास सांता बारबरा स्थित कैलिफ़ोर्निया विश्वविद्यालय से गणित और अर्थशास्त्र में डिग्री है और मैं सोसाइटी ऑफ़ एक्चुअरीज़ का सेवानिवृत्त सहयोगी हूँ। कॉलेज से स्नातक होने के बाद से मैं जो कुछ भी कर रहा हूँ, वह कुछ हद तक गणितीय प्रकृति का रहा है।

ऐसे प्रश्न का एक उदाहरण है:

6 ÷ 2 (1 + 2) = ?

एक क्षण रुकें और इस पर काम करें।

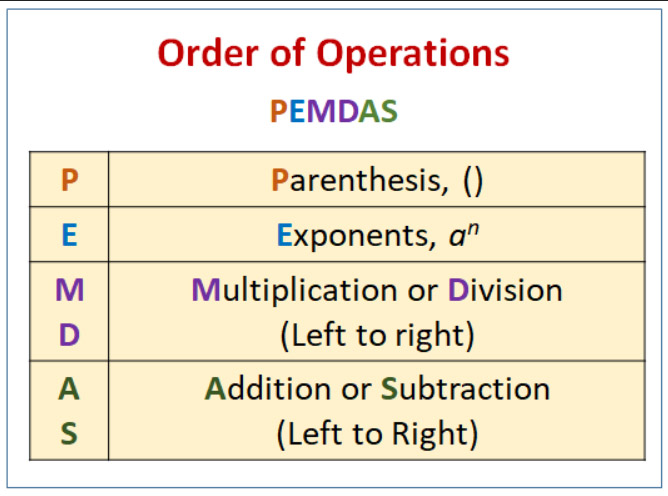
अगर आपको 1 मिला है, तो आप गलत हैं। मुझे शक है कि आप गलत हैं क्योंकि आप संक्रियाओं के क्रम के लिए PEMDAS के सामान्य नियम का पालन कर रहे हैं। यह एक स्मृति उपकरण है जो लगभग पाँचवीं कक्षा में पढ़ाया जाता है। मुझे इसे याद रखने का एक तरीका सिखाया गया था, "कृपया मेरी प्यारी चाची सैली को क्षमा करें।" इसका उद्देश्य बच्चों को किसी व्यंजक का मूल्यांकन निम्नलिखित क्रम में करना सिखाना है:

1. 1. कोष्ठक
2. 2. घातांक
3. 3. गुणन
4. 4. विभाजन
5. 5. अंकगणित
6. 6. घटाव

आपके व्याकरण-विद्यालय के शिक्षक को शायद सचमुच यही लगता होगा कि यह सही है। हालाँकि, ऐसा नहीं है। मुझे नहीं पता कि इसकी शुरुआत कहाँ से हुई, लेकिन मुझे लगता है कि यह एक सरलीकृत स्मृति उपकरण है जिसे 10 साल के बच्चे आसानी से समझ लेते हैं। किसी भी चीज़ को सरल बनाने में समस्या यह है कि हालाँकि इससे ज़्यादातर मामलों में सही उत्तर मिल सकता है, लेकिन अक्सर इस नियम के अपवाद भी होते हैं।PEMDAS के मामले में, यह किसी को पहले बताई गई 6 ÷ 2 (1 + 2) समस्या को इस प्रकार हल करने के लिए प्रेरित करेगा:

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) क्योंकि आप पहले कोष्ठक का मूल्यांकन करते हैं
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 क्योंकि कोष्ठक के बाहर कोई भी ऑपरेटर गुणन का संकेत नहीं देता है
3. 6 ÷ 2 × 3 = 6 ÷ 6 क्योंकि PEMDAS के अनुसार, गुणन भाग से पहले किया जाता है
4. 6 ÷ 6 = 1

उपरोक्त तर्क में त्रुटि तीसरे चरण में है। गुणा हमेशा भाग से पहले नहीं आता। दोनों की प्राथमिकता समान है। जब दोनों एक ही व्यंजक में हों, तो बाईं ओर वाला पहले करें।

मैं यह भी कहना चाहूँगा कि ज़रूरी नहीं कि जोड़ घटाव से पहले ही हो। दोनों की प्राथमिकता भी बराबर है। हालाँकि, जोड़ और घटाव के मामले में, जहाँ उच्चतर नियम लागू नहीं होते, इससे कोई फ़र्क़ नहीं पड़ता कि आप पहले क्या करते हैं।

6 ÷ 2 (1 + 2) का मूल्यांकन करने का सही तरीका यहां दिया गया है:

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) क्योंकि आप पहले कोष्ठक का मूल्यांकन करते हैं
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 क्योंकि कोष्ठक के बाहर कोई भी ऑपरेटर गुणन को नहीं दर्शाता है
3. 6 ÷ 2 × 3 = 3 × 3 क्योंकि गुणा और भाग दोनों में, आप पहले बाईं ओर से मूल्यांकन करते हैं
4. 3 × 3 = 9

आपके लिए एक और प्रश्न है:

7 + 7 ÷ 7 + 7 × 7 – 7 = ?

फ़ेसबुक पर आपको जवाब 56 दिखाई देगा। यह जवाब लोग PEMDAS की वजह से नहीं, बल्कि इसलिए गलत देते हैं क्योंकि "मेरे कैलकुलेटर ने जवाब 56 बताया।" यह उन लोगों द्वारा दिया गया एक आलसी और गलत जवाब है जो बस बाएँ से दाएँ जाते हैं।ग़लत तर्क यह है:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 14 ÷ 7 + 7 × 7 – 7 क्योंकि आप पहले बाईं ओर से मूल्यांकन करते हैं
2. 14 ÷ 7 + 7 × 7 – 7 = 2 + 7 × 7 – 7 क्योंकि आप पहले बाईं ओर से मूल्यांकन करते हैं
3. 2 + 7 × 7 – 7 = 9 × 7 – 7 क्योंकि आप पहले बाईं ओर से मूल्यांकन करते हैं
4. 9 × 7 – 7 = 63 – 7 क्योंकि आप पहले बाईं ओर से मूल्यांकन करते हैं
5. 63 – 7 = 56

इसका मूल्यांकन करने का सही तरीका यह है:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 7 + 1 + 7 × 7 – 7 क्योंकि भाग, जोड़ का स्थान लेता है और गुणन के बाईं ओर होता है
2. 7 + 1 + 7 × 7 – 7 = 7 + 1 + 49 – 7 क्योंकि गुणन, जोड़ और घटाव का स्थान लेता है
3. 7 + 1 + 49 – 7 = 8 + 49 – 7 क्योंकि जोड़ और घटाव के बीच सबसे बाईं ओर की क्रिया पहले करें
4. 8 + 49 – 7 = 57 – 7 क्योंकि जोड़ और घटाव के बीच सबसे बाईं ओर वाला ऑपरेशन पहले करें
5. 57 – 7 = 50

ध्यान दें कि PEMDAS यही काम सही करता है। लोग अपने कैलकुलेटर का सही इस्तेमाल न करके गलती कर बैठते हैं। संख्याओं और संक्रियाओं को सही क्रम में रखना बेहद ज़रूरी है। HP15C जैसे रिवर्स पोलिश नोटेशन वाले कैलकुलेटर के साथ ऐसा करना ज़्यादा आसान है। वैसे, जिस किसी के पास HP15C या 12C है, वह मेरा तुरंत दोस्त बन जाता है।

अंत में, मैं इन संक्रिया क्रम पहेलियों में एक नया मोड़ जोड़ना चाहूँगा, जिसे मैंने खुद बनाया है, पहेली का तर्क और लेआउट दोनों। मैं मानता हूँ कि मैंने चित्र गूगल से चुराए हैं। यह पहेली माइंड योर डिसीजन्स यूट्यूब चैनल पर मौजूद एक ऐसी ही, लेकिन उससे भी कठिन पहेली से प्रेरित है। कृपया इसे जहाँ चाहें पोस्ट करें; मुझे उम्मीद है कि यह वायरल हो जाएगी।

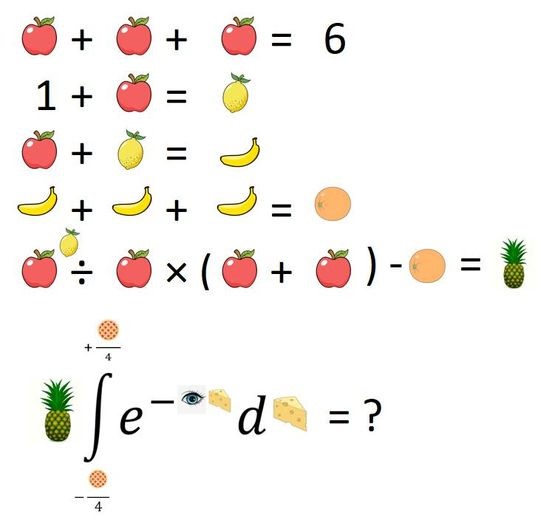
केवल अनानास को हल करने के लिए आंशिक क्रेडिट और समाकल को हल करने के लिए पूर्ण क्रेडिट।

मैं 29 जून के न्यूज़लेटर में जवाब पोस्ट करूँगा। तब तक, दुआ करता हूँ कि हालात हमेशा आपके पक्ष में रहें।

द्वारा लिखित: Michael Shackleford