बड़ी ज़ूम कॉल गणित पहेली
पिछले हफ़्ते मेरे न्यूज़लेटर में यह सवाल पूछा गया था। अगर आपको याद दिलाने की ज़रूरत हो, तो यह रहा सवाल।
सवाल
मान लीजिए कि अमेरिकी प्रतिनिधि सभा के सभी 435 मतदान सदस्य एक ही ज़ूम कॉल में शामिल होते हैं, जो सुबह 9 बजे से 10 बजे तक चलने वाली है। हालाँकि, पूरी कॉल में शामिल होना ज़रूरी नहीं है, बस उसके किसी एक हिस्से में शामिल होना ज़रूरी है। प्रत्येक सदस्य उस एक घंटे की अवधि के भीतर कॉल में शामिल होने और बाहर निकलने के लिए यादृच्छिक रूप से एक सटीक समय चुनता है।
इसकी क्या संभावना है कि कॉल पर कम से कम एक प्रतिनिधि हर दूसरे प्रतिनिधि को ओवरलैप करे? दूसरे शब्दों में, कॉल पर अपने समय के दौरान हर दूसरे सदस्य का चेहरा देखना, ज़रूरी नहीं कि सभी एक ही समय पर हों।
कृपया मेरा उत्तर और समाधान देखने के लिए इन चित्रों को स्क्रॉल करें।

उत्तर
2/3
समाधान
बड़े समूह से जुड़े सवालों के लिए मेरी सामान्य रणनीति दो लोगों से शुरुआत करना है। जवाब मिलने के बाद, मैं तीन लोगों से सवाल पूछता हूँ। फिर, अगर जवाब ज़्यादा मुश्किल न हो, तो मैं चार लोगों से सवाल पूछता हूँ। अगर मुझे कोई पैटर्न दिखता है, तो संभावना है कि वह पैटर्न किसी भी संख्या में लोगों पर लागू हो।
बुनियादी गणित की समीक्षा
आगे बढ़ने से पहले, मैं combin(x,y) फ़ंक्शन का बार-बार इस्तेमाल करूँगा। यह x के समूह में से y आइटम चुनने के तरीकों की संख्या है। उदाहरण के लिए, 52 में से पाँच कार्ड चुनने के तरीकों की संख्या, जहाँ क्रम मायने नहीं रखता, combin(52,5) = 2,598,960 है। उत्तर को x! / (y! * (xy)!) के रूप में व्यक्त किया जा सकता है।
इस स्थिति में, विस्मयादिबोधक चिह्न का अर्थ यह नहीं है कि मैं चिल्ला रहा हूँ, बल्कि यह फ़ैक्टोरियल फ़ंक्शन को दर्शाता है। यह किसी भी दी गई संख्या में वस्तुओं को क्रमबद्ध करने के तरीकों की संख्या है। उदाहरण के लिए, यदि आपको एक-एक करके छह किताबें पढ़नी हैं, तो किताबों के संभावित क्रमों की संख्या 6 है!। n के सामान्य मामले के लिए उत्तर 1*2*3*…*n है। छह किताबों के मामले में, उत्तर 1*2*3*4*5*6 = 720 है।
दो व्यक्तियों का मामला
तो चलिए, दो व्यक्तियों वाले मामले की समस्या हल करते हैं। लोगों के कॉल में आने और जाने का सटीक समय मायने नहीं रखता, बस घटनाओं का क्रम मायने रखता है। आइए कॉल में आने/जाने वाले किसी खास व्यक्ति को दर्शाने के लिए एक अक्षर का इस्तेमाल करें। बाईं ओर से शुरू करते हुए, दिए गए अक्षर का पहला प्रयोग कॉल में आने और दूसरा प्रयोग कॉल से बाहर आने को दर्शाएगा।
6;font-family: 'Open Sans',sans-serif;color: #313131!important">कॉल इतिहास में चार स्थानों में से, आप अक्षर A को 6 तरीकों से रख सकते हैं:1. एएबीबी
2. एबीएबी
3. एबीबीए
4. बाब
5. बाबा
6. बीबीएए
आइए देखें कि क्या प्रत्येक परिदृश्य में दोनों कॉलर एक ही समय पर थे:
1. AABB - नहीं, A आया और B के कॉल में शामिल होने से पहले ही चला गया।
2. ABAB - हाँ, B के आने और A के जाने के बीच ओवरलैप था।
3. एबीबीए - हां, बी के आने और बी के जाने के बीच ओवरलैप था।
4. बाब - हां, ए के आने और ए के जाने के बीच ओवरलैप था।
5. बाबा - हाँ, A के आने और B के जाने के बीच ओवरलैप था।
6. बीबीएए - नहीं, बी आया और ए के कॉल में शामिल होने से पहले ही चला गया।
प्रत्येक परिदृश्य समान रूप से संभावित है। छह में से चार में ओवरलैप था, इसलिए दो व्यक्तियों के मामले में ओवरलैप होने की संभावना 2/3 है।
तीन व्यक्तियों का मामला
तीन-व्यक्तियों वाले मामले में कॉल हिस्ट्री की संख्या, व्यक्ति A द्वारा हिस्ट्री में 6 में से दो स्पॉट चुनने के तरीकों की संख्या और व्यक्ति B द्वारा शेष 4 स्पॉट में से 2 चुनने के तरीकों की संख्या का गुणनफल है। यह कॉम्बिन(6,2)*कॉम्बिन(4,2) = 15*6 = 90 के बराबर है।
सभी 90 लोगों को सूचीबद्ध करना बहुत मुश्किल होगा। आइए इसे आसान बनाने के लिए मान लें कि व्यक्ति A पहले शामिल होता है। कोई न कोई तो पहले होगा ही, तो हो सकता है कि वह A ही हो।
सबसे पहले, आइए उस स्थिति पर विचार करें जहाँ कॉल इतिहास में अगली घटना A का कॉल छोड़ना है। इसे AA???? के रूप में दर्शाते हैं। B और C कॉल में कैसे भी आएँ और जाएँ, कोई भी A को ओवरलैप नहीं करेगा। इस प्रकार, AA परिदृश्य की सफलता की संभावना 0 है। AA परिदृश्य की संभावना स्वयं 1/5 है, क्योंकि A के पहले स्थान पर आने के बाद, आगे पाँच संभावित घटनाएँ घटित हो सकती थीं - A, B, B, C, और C।
दूसरा, आइए उस स्थिति पर विचार करें जहाँ A पहले जुड़ता है, B उसके बाद प्रवेश करता है, और फिर A चला जाता है। इस स्थिति में, B, A के अलावा किसी अन्य व्यक्ति (जो पहले ही कॉल समाप्त कर चुका है) को दर्शाता है। इसे ABA??? द्वारा दर्शाया जाता है। शेष रखे जाने वाले अक्षर B, C और C हैं। B को तीन तरीकों (BCC, CBC और CCB) में से, CBC और CCB के परिणामस्वरूप B, A और C दोनों को ओवरलैप करता है।इस प्रकार, ABA परिदृश्य में सफलता की संभावना 2/3 है। उस परिदृश्य की संभावना pr(A के अलावा कोई भी शामिल होता है)*pr(A छोड़ता है) = (4/5)*(1/4) = 1/5 है, जहाँ pr(x) घटना x की संभावना को दर्शाता है।
तीसरा, आइए उस स्थिति पर विचार करें जहाँ A पहले जुड़ता है, B उसके बाद प्रवेश करता है, और फिर B छोड़ देता है। इसे ABB??? से दर्शाया जाता है। शेष रखे जाने वाले अक्षर A, C और C हैं। A को तीन तरीकों (ACC, CAC और CCA) में से, CAC और CCA के परिणामस्वरूप A, B और C दोनों को ओवरलैप करता है। इस प्रकार, ABB परिदृश्य में सफलता की संभावना 2/3 है। उस परिदृश्य की संभावना स्वयं pr(A के अलावा कोई भी जुड़ता है)*pr(B छोड़ देता है) = (4/5)*(1/4) = 1/5 है।
चौथा, आइए उस स्थिति पर विचार करें जहाँ A पहले जुड़ता है, B उसके बाद आता है, और फिर C जुड़ता है। इसे ABC??? से दर्शाया जाता है। शेष अक्षर A, B और C हैं। यह देखना आसान है कि A जहाँ भी कॉल छोड़ता है, वह B और C को ओवरलैप करेगा। इसलिए, उस परिदृश्य में सफलता की संभावना 1 है। उस परिदृश्य की संभावना स्वयं pr(A के अलावा कोई भी जुड़ता है)*pr(तीसरा व्यक्ति जुड़ता है) = (4/5)*(2/4) = 2/5 है।
हमने हर संभावित परिदृश्य पर विचार किया, जैसा कि संभावनाओं (1/5 + 1/5 + 1/5 + 2/5) के योग से पता चलता है, जो 1 है। प्रत्येक परिदृश्य की संभावना और इसकी सफलता की संभावना के डॉट उत्पाद को लेते हुए, हम पाते हैं: (1/5) * 0 + (1/5) * (2/3) + (1/5) * (2/3) + (2/5) * 1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3।
चार व्यक्तियों का मामला
अगर मुझ पर समय का दबाव होता, तो मैं अनुमान लगा सकता था कि मूल प्रश्न का उत्तर 2/3 है, क्योंकि यह 2 और 3 व्यक्तियों वाले मामलों में भी सही है। हालाँकि, यह बहुत असंतोषजनक लगता है, इसलिए चलिए इसे चार व्यक्तियों वाले मामले पर ले चलते हैं।मैं इसे दस संभावित परिदृश्यों में विभाजित कर सकता हूँ, जो इस प्रकार हैं:
- एए??????
परिदृश्य की संभावना = 1/7
सफलता की संभावना = 0 (कोई भी A को ओवरलैप नहीं कर सकता)
- एबीए????
परिदृश्य की संभावना = 1/7
सफलता की संभावना = 16/30
- अब्बा????
परिदृश्य की संभावना = 1/35
सफलता की संभावना = 0 (कोई भी B को ओवरलैप नहीं कर सकता)
- एबीबीसी????
परिदृश्य की संभावना = 4/35
सफलता की संभावना = 2/3
- एबीसीए????
परिदृश्य की संभावना = 4/35
सफलता की संभावना = 5/6
- एबीसीबीए????
परिदृश्य की संभावना = 1/35
सफलता की संभावना = 2/3
- एबीसीबीसी????
परिदृश्य की संभावना = 1/35
सफलता की संभावना = 2/3
- एबीसीबीडी????
परिदृश्य की संभावना = 2/35
सफलता की संभावना = 1 (A, B, C और D को ओवरलैप करेगा)
- एबीसीसी????
परिदृश्य की संभावना = 4/35
सफलता की संभावना = 5/6
- ए बी सी डी????
परिदृश्य की संभावना = 8/35
सफलता की संभावना = 1 (A, B, C और D को ओवरलैप करेगा)
मैं प्रत्येक स्थिति के लिए सावधानीपूर्वक गणना न कर पाने के लिए क्षमा चाहता हूँ, लेकिन मैं नहीं चाहता था कि यह समाधान बहुत लंबा चले और मैं पाठक के लिए कुछ काम छोड़ना चाहता था।
निम्नलिखित तालिका चार व्यक्तियों के मामले के सभी दस परिदृश्यों का सारांश प्रस्तुत करती है।
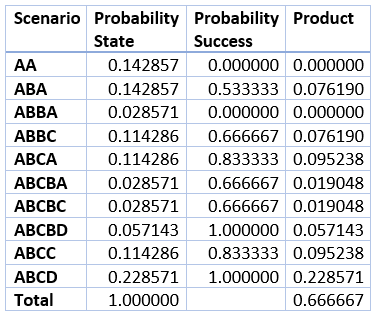
तालिका में निचले दाएं कक्ष में 2/3 की संभावना दर्शाई गई है।
सारांश
6;font-family: 'Open Sans',sans-serif;color: #313131!important">हमने दो, तीन और चार व्यक्तियों वाले मामलों के लिए 2/3 की प्रायिकता दर्शाई है। यह तर्कसंगत है कि यह प्रायिकता संभवतः किसी भी संख्या में लोगों के लिए बनी रहेगी। मुझसे ज़्यादा बुद्धिमान लोगों द्वारा किए गए सिमुलेशन और गणित ने इसकी सत्यता की पुष्टि की है।

