अंतर्निहित कोण प्रमेय का प्रमाण (भाग 2)

आपको याद होगा कि पिछले सप्ताह मैंने अंतर्निहित कोण प्रमेय के प्रमाण पर काम शुरू किया था। इस सप्ताह हम इसे पूरा करेंगे। लेकिन इससे पहले, मैं अपनी साप्ताहिक तर्क पहेली प्रस्तुत करता हूँ।

तर्क पहेली

निम्नलिखित बयानों में से कौन सा सही हैं?

1. इनमें से एक कथन असत्य है।
2. इनमें से दो कथन असत्य हैं।
3. इनमें से तीन कथन असत्य हैं।
4. इनमें से चार कथन असत्य हैं।
5. इनमें से पांच कथन असत्य हैं।
6. इनमें से छह कथन असत्य हैं।
7. इनमें से सात कथन असत्य हैं।
8. इनमें से आठ कथन असत्य हैं।
9. इनमें से नौ कथन असत्य हैं।
10. इनमें से दस कथन असत्य हैं।

इसका उत्तर न्यूजलेटर के अंत में दिया गया है।

अंतर्निहित कोण प्रमेय (भाग 2)

मैं आपको याद दिला दूं कि अंतर्निहित कोण प्रमेय क्या कहता है।

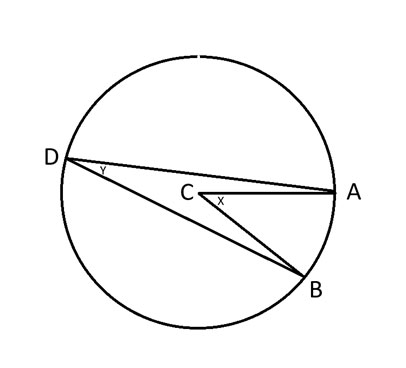
A, B और D = वृत्त पर स्थित कोई भी तीन बिंदु।

C = वृत्त का केंद्र।

x = कोण ACB.

y = कोण ADB.

अंतर्निहित कोण प्रमेय कहता है कि कोण 2y = x.

पिछले सप्ताह मैंने दिखाया था कि यह उस विशिष्ट स्थिति में सत्य है जहाँ AD या BD वृत्त का व्यास बनाते हैं। इस सप्ताह मैं इसका उपयोग यह दिखाने के लिए करूँगा कि यह प्रमेय D के सामान्य मामले के लिए सत्य है।

मैं D के लिए सभी संभावित स्थानों को इस प्रकार विभाजित करने जा रहा हूँ:

मामला 1 = AD या BD वृत्त का व्यास बनाते हैं (पिछले सप्ताह सिद्ध हो चुका है)

केस 2 = D, A और B के विपरीत दिशा में स्थित चाप के साथ स्थित है (या यह "स्थित है"?)।

केस 3 = अन्य सभी

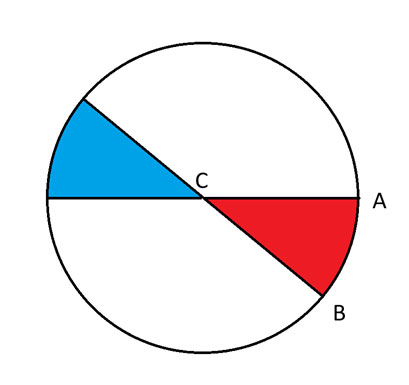
दूसरे शब्दों में, केस 2 में वे स्थितियाँ शामिल होंगी जहाँ D नीले क्षेत्र में वृत्त के किनारे पर स्थित है। केस 3 में नीले क्षेत्र के बाहर के अन्य स्थान शामिल होंगे।

आइए चर्चा के लिए निम्नलिखित आरेख का उपयोग करें।

होने देना:

x = x1 + x2

y = y1 + y2

z = z1 + z2

हम यह सिद्ध करने का प्रयास करते हैं कि x = 2y

मैंने सावधानीपूर्वक D से C तक एक रेखा खींची, जिससे वृत्त का व्यास बना। बिंदु E वह स्थान है जहाँ यह रेखा वृत्त की दूसरी भुजा को काटती है।

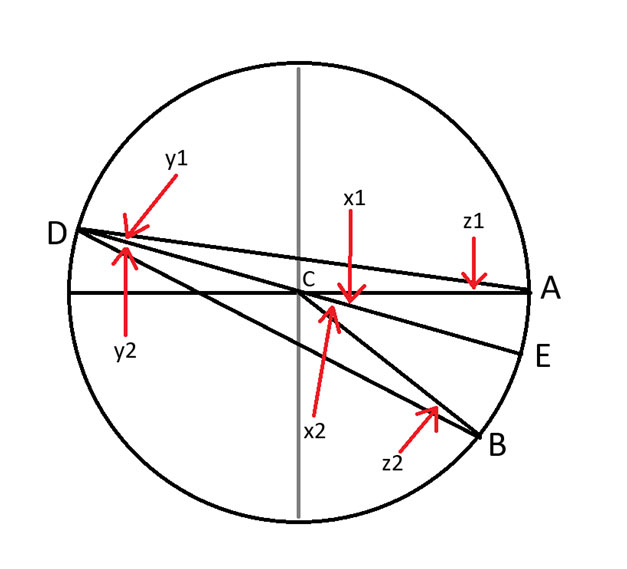
कोणों में लिखी संख्याओं को सबस्क्रिप्ट में लिखा जाना चाहिए था, लेकिन मेरे ड्राइंग सॉफ्टवेयर ने इसकी अनुमति नहीं दी।

त्रिभुज ADE पर विचार करें।

चूंकि DE एक व्यास बनाता है, इसलिए हम पिछले सप्ताह सिद्ध की गई बात का उपयोग करके यह दिखा सकते हैं कि 2x1 = 2y1।

अब त्रिभुज EDB पर विचार करें।

इसी तर्क के आधार पर, _2x² = _y² ।

इन समीकरणों को जोड़ने पर:

2x ₁ + 2x ₂ = y ₁ + y ₂

2(x ₁ + x ₂ ) = y ₁ + y ₂

2x = y

और हमने केस 2 पूरा कर लिया है।

आइए तीसरे मामले को देखें।

यहां हम यह दिखाने का प्रयास करते हैं कि 2x ₁ = y ₁ ।

पहले मामले से:

2x ₂ = y ₂

2(x ₁ + x ₂ ) = y< ₁ +y ₂

ऊपरी समीकरण को निचले समीकरण से घटाने पर:

2x ₁ = y ₁

और हमने केस 3 को साबित कर दिया है।

तर्क पहेली का उत्तर

केवल कथन 9 सत्य है।

तर्क पहेली का हल

हमारे पास दस ऐसे कथन हैं जो एक दूसरे के विरोधाभासी हैं। यदि दस लोग अलग-अलग बातें कह रहे हैं, तो या तो केवल एक व्यक्ति सही है या उनमें से कोई भी सही नहीं है।

मान लीजिए कि सभी दस कथन असत्य हैं। इससे कथन संख्या 10 सत्य हो जाएगा। इससे केवल नौ कथन असत्य रह जाएंगे। अतः विरोधाभास उत्पन्न होगा। कोई न कोई कथन सत्य अवश्य होगा। लेकिन कौन सा?

यदि एक कथन सत्य है, तो नौ कथन असत्य हैं। यह कथन संख्या नौ कहता है। अतः, केवल कथन नौ ही सत्य है।