WOO logo

विज़ार्ड अनुशंसा करता है

अंतर्निहित कोण प्रमेय का प्रमाण (भाग 1)

इस सप्ताह हम गणितीय प्रमेय को सिद्ध करने के अपने विषय पर लौट रहे हैं। इस सप्ताह का विषय है अंतर्निहित कोण प्रमेय। यह प्रमाण सामान्य से अधिक जटिल है, इसलिए मैं इसे दो भागों में विभाजित करूँगा, जिसका दूसरा भाग अगले सप्ताह आएगा। हालाँकि, उससे पहले, मैं अपनी सामान्य साप्ताहिक तर्क पहेली प्रस्तुत करता हूँ।

तर्क पहेली

नीचे दिए गए चित्र में, एक सिक्के को इस प्रकार खिसकाएं कि चार-चार सिक्कों की दो पंक्तियाँ बन जाएं।

आरेख

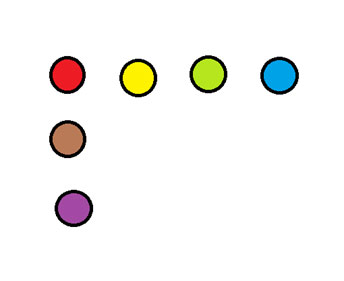
इसका उत्तर न्यूजलेटर के अंत में दिया गया है।

अंतर्निहित कोण प्रमेय का प्रमाण (भाग 1)

अंतर्निहित कोण प्रमेय को समझाने से पहले, आइए निम्नलिखित आरेख में वृत्त पर कुछ बिंदुओं को परिभाषित करें।

घेरा

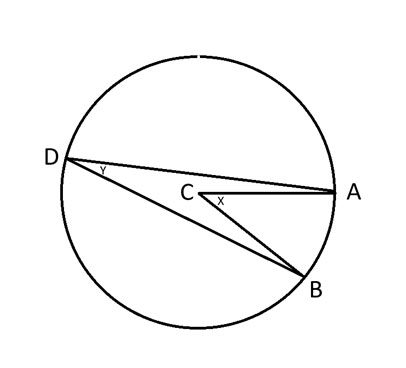
A, B और D = वृत्त पर स्थित कोई भी तीन बिंदु।

C = वृत्त का केंद्र।

x = कोण ACB.

y = कोण ADB.

अंतर्निहित कोण प्रमेय कहता है कि कोण 2y = x.

इस न्यूज़लेटर में, मैं उस विशिष्ट मामले के लिए इसे सिद्ध करने का प्रयास करूँगा जहाँ AD या BD वृत्त का व्यास बनाते हैं। अगले सप्ताह, मैं D की स्थिति के सामान्य मामले के लिए इस पर विस्तार से चर्चा करूँगा।

आइए उस विशिष्ट स्थिति को, जहाँ AD वृत्त का व्यास बनाता है, स्थिति 1 कहें। इस स्थिति के लिए एक नया आरेख यहाँ दिया गया है।

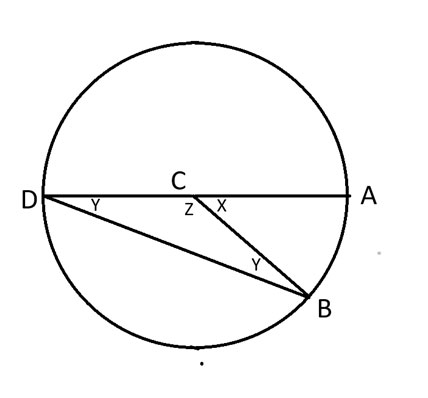
आरेख विज्ञापन

ऊपर दिए गए चित्र में, AD उस वृत्त का व्यास बनाता है जिसके केंद्र में C स्थित है।

हम कह सकते हैं कि x+z = 180 डिग्री, क्योंकि वे एक वृत्त के कुल 360 डिग्री का आधा हिस्सा बनाते हैं।

बीसीडी एक समद्विबाहु त्रिभुज बनाती है। अतः, कोण सीडीबी = सीबीडी = y।

जैसा कि मेरे 13 नवंबर, 2025 के न्यूज़लेटर में सिद्ध हो चुका है, त्रिभुज के आंतरिक कोणों का योग 180 डिग्री होता है। दूसरे शब्दों में, z + 2y = 180 डिग्री।

आइए दोनों समीकरणों को दोबारा लिखते हैं:

z = 180 – x

z = 180 – 2y

आइए इन दोनों को समीकरण के रूप में हल करें, क्योंकि ये दोनों z के बराबर हैं।

180 – x = 180 – 2y

-x = -2y

x = 2y.

तो, हमने अंतर्निहित कोण प्रमेय के उस विशिष्ट मामले को सिद्ध कर दिया है जहाँ वृत्त पर स्थित दो बिंदु व्यास बनाते हैं। अगले सप्ताह हम इसी आधार पर सामान्य मामले के लिए इसे सिद्ध करेंगे।

तर्क पहेली का हल

नीले सिक्के को लाल सिक्के के ऊपर रखें। नीचे दिए गए चित्र में संख्याएँ प्रत्येक ढेर में सिक्कों की संख्या दर्शाती हैं।

सिक्के

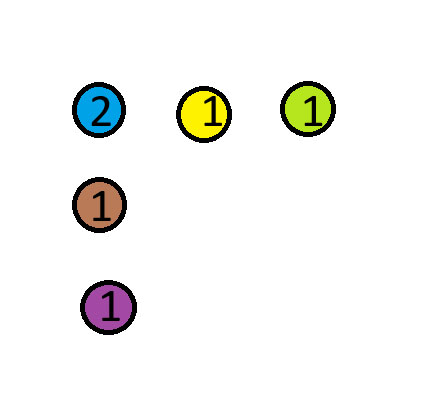
आभार: मुझे यह पहेली माइंड योर डिसीजन्स यूट्यूब चैनल से मिली है। लिंक किए गए वीडियो में यह पहेली संख्या 3 है।