शतरंज के रेटिंग नियमों का पालन कैसे करें

इस हफ़्ते हम शतरंज के खेल में ज़रा भी सुधार किए बिना, आपकी रेटिंग सुधारने के लिए गेम-टू-शतरंज रेटिंग फ़ॉर्मूले पर विचार करेंगे। यह एक छोटा सा फ़ायदा है और मुख्यतः अकादमिक रुचि का है। लेकिन, उससे पहले, हमेशा की तरह, मैं हमारी साप्ताहिक तर्क पहेली प्रस्तुत करता हूँ।

तर्क पहेली

एक पंक्ति में 50 लोग हैं, जिन्हें क्रम से 1 से 50 तक क्रमांकित किया गया है। पंक्ति में पहला व्यक्ति नंबर 1 है। हर व्यक्ति या तो हमेशा सच बोलता है या हमेशा झूठ। हर कोई एक-दूसरे की सच्चाई जानता है।

सभी सम संख्या वाले लोग कहते हैं, "मेरे सामने सभी लोग झूठे हैं।"

सभी विषम संख्या वाले लोग कहते हैं, "मेरे पीछे सभी लोग झूठे हैं।"

कौन सच बोल रहा है?

शतरंज के रेटिंग नियमों का पालन कैसे करें

जहाँ तक मुझे पता है, शतरंज की सबसे आम रेटिंग प्रणाली एलो रेटिंग प्रणाली है। इसका नाम अर्फ़द एलो के नाम पर रखा गया है। यही प्रणाली अन्य खेलों में भी इस्तेमाल की जाती है।

मूलतः, यह एक सूत्र के अनुसार काम करता है जो दोनों खिलाड़ियों की रेटिंग के आधार पर किसी भी खिलाड़ी के जीतने की संभावना निर्धारित करता है। जीतने वाले खिलाड़ी को उसकी हारने की संभावना के अनुपात में अंक मिलेंगे। इसी प्रकार, हारने वाले खिलाड़ी को उसकी जीतने की संभावना के अनुपात में अंक मिलेंगे। जीत के लिए एक अंक, ड्रॉ के लिए 0.5 अंक और बराबरी के लिए 0 अंक दिए जाएँगे।

यह प्रणाली इस धारणा पर आधारित है, जिससे मैं सहमत हूं, कि किसी खिलाड़ी के प्रदर्शन को बेल कर्व पर खींची गई यादृच्छिक संख्या के आधार पर मॉडल किया जा सकता है, जिसमें खिलाड़ी की रेटिंग को माध्य माना जाएगा।जो खिलाड़ी अधिक संख्या प्राप्त करता है वह जीत जाता है।

जीतने की संभावना निर्धारित करने का तरीका इस प्रकार है:

मान लें r1 = खिलाड़ी 1 की रेटिंग.

मान लें r2 = खिलाड़ी 2 की रेटिंग.

p = संभावना खिलाड़ी 1 जीतता है.

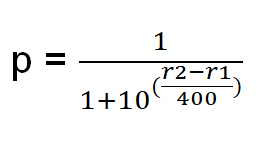
आइए एक उदाहरण देखें। मान लीजिए r1=1900 और r2=2000 है।

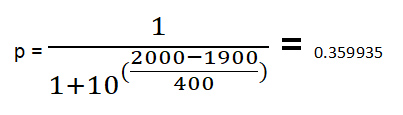
मान लें कि जीत के लिए 1 अंक और हार के लिए 0 अंक दिया जाता है, तो रेटिंग में वृद्धि 32*(वास्तविक अंक - जीतने की संभावना) होगी।

ऊपर दिए गए हमारे उदाहरण में, अगर खिलाड़ी 1 हार जाता है, जैसा कि उसके हारने की भविष्यवाणी की गई है, तो उसकी रेटिंग 11.52 अंक कम हो जाएगी और खिलाड़ी 2 की रेटिंग भी उतनी ही बढ़ जाएगी। अगर खिलाड़ी 1 जीत जाता है, तो उसकी रेटिंग 20.48 अंक बढ़ जाएगी और खिलाड़ी 2 की रेटिंग भी उतनी ही कम हो जाएगी।

एलो योजना प्रदर्शन में मानक विचलन पर आधारित है, जैसा कि ऊपर वर्णित यादृच्छिक संख्या पद्धति द्वारा प्रतिरूपित किया गया है, 200। मैं इसे सत्य मानता हूँ। हालाँकि, जीतने की संभावना का सूत्र, जिस पर एलो तालिकाएँ आधारित हैं, ऐसे मानक विचलन के अनुरूप नहीं है, सिवाय इसके कि रेटिंग में अंतर 0 या 189 हो।

r1 रेटिंग वाले खिलाड़ी के जीतने की सही संभावना है:

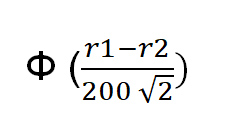
जहाँ फ़ंक्शन Φ(x) = किसी यादृच्छिक मानक प्रसामान्य चर के x से कम होने की प्रायिकता। Excel में, सही सूत्र norm.s.dist((r1-r2)/(200*sqrt(2)),1) है।

आइए एक ऐसे मामले पर विचार करें जहाँ रेटिंग में अंतर 100 है। आइए खिलाड़ी 1 को अंडरडॉग मान लें। एलो सूत्र के अनुसार, खिलाड़ी 1 के जीतने की संभावना 35.99% है। हालाँकि, 200 के प्रदर्शन में मानक विचलन के आधार पर, उसकी वास्तविक संभावना 36.18% है। दूसरे शब्दों में, खिलाड़ी 1 का खेल जीतना एक अच्छा दांव है और खिलाड़ी 2 के लिए एक बुरा दांव। मैं खिलाड़ी 1 की रेटिंग में अपेक्षित लाभ और खिलाड़ी 2 की अपेक्षित हानि 0.06 अंक दर्शाता हूँ।

अब आइए 300 की रेटिंग में अंतर देखें, जहाँ खिलाड़ी 1 कमज़ोर है। यहाँ एलो फ़ॉर्मूला खिलाड़ी 1 के जीतने की संभावना 15.10% देता है, जबकि मैं इसे 14.44% दिखाता हूँ। इससे खिलाड़ी 1 के लिए खेल में दांव लगाना एक बुरा दांव और खिलाड़ी 2 के लिए एक अच्छा दांव बन जाता है। खिलाड़ी 1 के लिए अपेक्षित नुकसान 0.21 अंक है और खिलाड़ी 2 के लिए अपेक्षित लाभ भी।

वास्तविक संभावनाओं के पीछे का गणित गौसियन वक्र पर आधारित है और इसमें इतना अधिक जटिल कुछ नहीं है जितना मैं इस न्यूज़लेटर के लिए बताना चाहता हूँ।

मूल बात यह है कि अगर रेटिंग्स में अंतर 189 से ज़्यादा है, तो पसंदीदा टीम के लिए गेम जीतना एक अच्छा दांव है। इसी तरह, अगर रेटिंग्स का अंतर 189 से कम है, तो कमज़ोर टीम के लिए गेम जीतना एक अच्छा दांव है।

हालाँकि, यह पक्षपात बहुत कम है। मैं इस जानकारी के आधार पर किसी खेल को स्वीकार या अस्वीकार नहीं करूँगा। बल्कि, मुझे लगता है कि आपको शतरंज के प्रति प्रेम के कारण कोई भी खेल अपना लेना चाहिए।

आगे पढ़ें: एलो रेटिंग प्रणाली पर विकिपीडिया लेख।

तर्क पहेली का उत्तर

केवल 2 और 49 लोग ही सच बोल रहे हैं।

तर्क पहेली समाधान

आइए पहले व्यक्ति से शुरू करते हैं। अगर वह सच बोल रहा है, तो बाकी सब झूठ बोल रहे हैं। लेकिन तीसरे व्यक्ति का कहना है कि 4 से 50 तक सभी झूठ बोल रहे हैं।अगर यह सच है, तो व्यक्ति 3 सच बोल रहा है। लेकिन व्यक्ति 1 कहता है कि वह झूठ बोल रहा है। इससे विरोधाभास पैदा होता है। इसलिए व्यक्ति 1 ज़रूर झूठ बोल रहा होगा।

व्यक्ति 2 केवल यही कहता है कि व्यक्ति 1 झूठ बोल रहा है। इससे व्यक्ति 2 सच्चा हो जाता है।

4 से 50 तक हर सम संख्या वाला व्यक्ति कहता है कि दूसरा व्यक्ति झूठ बोल रहा है। यानी वे सभी झूठे हैं।

व्यक्ति 49 कहता है कि व्यक्ति 50 झूठ बोल रहा है, जो सच है। इससे व्यक्ति 49 सच्चा साबित होता है।

3 से 47 तक हर विषम संख्या वाला व्यक्ति कहता है कि 49वाँ व्यक्ति झूठ बोल रहा है। यानी वे सभी झूठे हैं।

इस प्रकार, सच बोलने वाले एकमात्र व्यक्ति संख्या 2 और 49 हैं।