WOO logo

विज़ार्ड अनुशंसा करता है

यूलर की पहचान

इस सप्ताह हम एक बड़ी चुनौती का सामना करेंगे, यूलर की सर्वसमिका को सिद्ध करना। यदि आप भूल गए हों, तो यह शायद गणित की सबसे सुंदर सर्वसमिका है: e πi +1 = 0। मुझे यह सर्वसमिका इतनी पसंद है कि यह मेरे बिजनेस कार्ड पर भी है और मैं शायद इसका टैटू भी बनवा लूँ। लेकिन इससे पहले, मैं हमेशा की तरह साप्ताहिक तर्क पहेली प्रस्तुत करता हूँ।

तर्क पहेली

आपके पास तीन-तीन कड़ियों वाली चार श्रृंखलाएँ हैं। आप केवल तीन कड़ियों को काटे बिना उन सभी को आपस में जोड़कर 12 कड़ियों का एक वृत्ताकार लूप कैसे बना सकते हैं?

यूलर की सर्वसमिका को सिद्ध करना

गणित के सबसे प्रसिद्ध समीकरणों में से एक यूलर की सर्वसमिका है, जो कहती है e πi +1 = 0. इसकी सबसे आश्चर्यजनक बात यह है कि यह गणित की पांच सबसे महत्वपूर्ण संख्याओं को जोड़ती है: 0, 1, e, π और i.

मेरे हल के लिए टेलर विस्तार के सूत्र का ज्ञान आवश्यक है। याद दिलाने के लिए, सूत्र यह है:

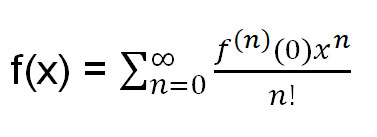
FORMULA

जहां f (n) (0) = f(x) का nवाँ व्युत्पन्न है जिसका मान 0 पर निकाला गया है।

मुझे व्यक्तिगत रूप से यह समीकरण गणित के सभी समीकरणों में सबसे अद्भुत और सुंदर लगता है। मेरे लिए, यह इस बात का प्रमाण है कि गणित में कुछ दिव्य तत्व मौजूद है।

इसके अलावा, यहां तीन टेलर विस्तार दिए गए हैं जो सामान्य कार्यों के लिए उपयोगी होंगे:

विस्तार
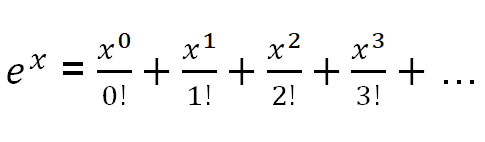
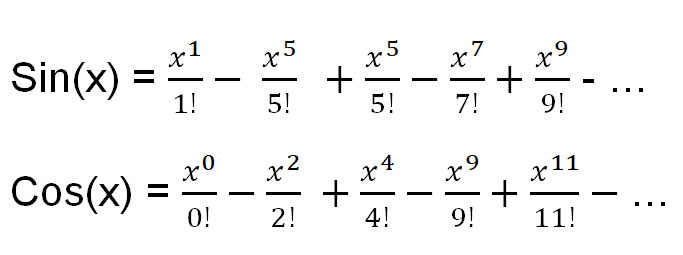
expansions

आइए e πi ज्ञात करने के लिए e x के टेलर विस्तार का उपयोग करें।

विस्तार

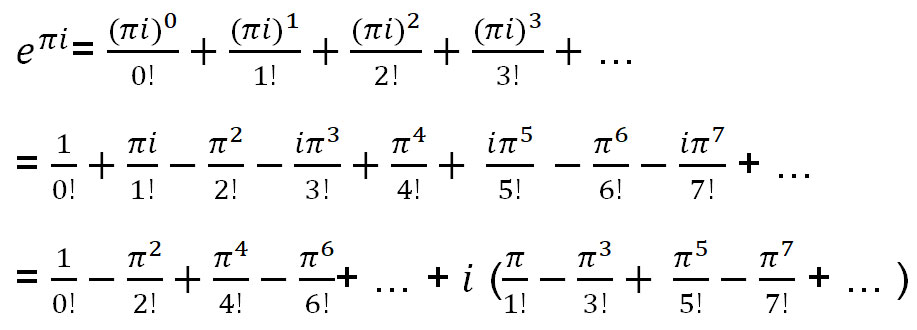
उपरोक्त समीकरण को sin(x) और cos(x) के फलनों के रूप में व्यक्त किया जा सकता है:

= cos(π)+i ×sin⁡(π)

= -1 + i ×0

= -1

अतः, हमारे पास e πi = -1 है। इसे सामान्य प्रारूप में पुनर्व्यवस्थित किया जा सकता है:

e πi +1 = 0

तर्क पहेली का हल

  1. चारों कड़ियों में से एक को लें और उसे खोलकर तीनों कड़ियों को अलग कर दें। बाकी तीन कड़ियों को 1, 2 और 3 नाम दें।
  2. एक कड़ी का उपयोग करके श्रृंखला 1 और 2 को मिलाएं, जिससे सात कड़ियों वाली श्रृंखला बन जाएगी।
  3. चरण 2 से सात-लिंक वाली श्रृंखला को श्रृंखला 3 में संयोजित करने के लिए एक और लिंक का उपयोग करें, जिससे 11-लिंक वाली श्रृंखला बन जाएगी।
  4. चरण 3 में बनाई गई 11 कड़ियों वाली श्रृंखला के दोनों सिरों को जोड़ने के लिए अंतिम कड़ी का उपयोग करें ताकि 12 कड़ियों वाला एक वृत्त बन जाए।