3 से विभाज्यता प्रमाण

इस हफ़्ते मैं राष्ट्रपति पद से जुड़ी सामान्य ज्ञान की बातों से थोड़ा ब्रेक लेकर कुछ नया करने की कोशिश करूँगा। मुझे हमेशा से ही अच्छे गणितीय प्रमाणों का आनंद मिलता रहा है। जब तक मेरे पास कोई विचार न रह जाए, मैं कुछ प्रसिद्ध गणितीय प्रमेयों पर चर्चा करूँगा और यथासंभव सरल भाषा में यह समझाने की कोशिश करूँगा कि वे क्यों सत्य हैं। शुरुआत में, इस हफ़्ते मैं यह बताऊँगा कि यदि किसी पूर्णांक के अंकों का योग 3 से विभाज्य है, तो पूर्ण संख्या भी 3 से विभाज्य होगी। हालाँकि, उस पर आने से पहले, मैं हमेशा की तरह साप्ताहिक तर्क पहेली प्रस्तुत करता हूँ।

तर्क पहेली

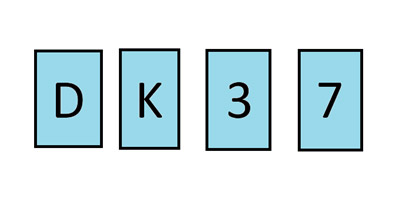
चार कार्ड मेज़ पर रखे हैं। आप देख सकते हैं कि खुले हुए कार्डों पर D, K, 3 और 7 अंकित हैं। आप जानते हैं कि हर कार्ड के एक तरफ एक अक्षर और दूसरी तरफ एक संख्या होती है। माना जाता है कि निर्माण का एक नियम यह है कि जिस कार्ड के एक तरफ D अंकित है, उसकी दूसरी तरफ 3 अंकित होना चाहिए। इस नियम का पालन किया गया है, यह सत्यापित करने के लिए आपको किन दो कार्डों को पलटना होगा?

इसका उत्तर समाचार-पत्र के अंत में दिया जाएगा।

3 से विभाज्यता प्रमाण

जैसा कि परिचय में बताया गया है, कोई पूर्णांक 3 से समान रूप से विभाज्य है या नहीं, इसका परीक्षण निम्न प्रकार से किया जा सकता है:

1. अंकों का योग लें.
2. यदि नियम 1 का योग 3 से समान रूप से विभाज्य है, तो मूल संख्या भी विभाज्य होगी। इसी प्रकार, यदि योग 3 से विभाज्य नहीं है, तो मूल संख्या भी विभाज्य नहीं होगी।

उदाहरण के लिए, आइए व्हाइट हाउस के फोन नंबर पर नजर डालें, जो 2024567041 है। अंकों का योग 2+0+2+4+5+6+7+0+4+1 = 31 है। 31, 3 से विभाज्य नहीं है, इसलिए मूल संख्या भी 3 से विभाज्य नहीं है।

यह सिद्ध करने के लिए कि यह कार्य करता है, मूल संख्या को निम्न प्रकार से विभाजित करें:

6; फ़ॉन्ट-फ़ैमिली: 'ओपन सैंस', सैंस-सेरिफ़; रंग: #313131 !important; ">2024567041 = (2*1000000000) + 0 + (2*10000000) + (4*1000000) + (5*100000) + (7*1000) + 0 + (4*10) + (1*1)

इसके बाद, 10 की घातों को दो भागों में विभाजित करें, एक 1 और शेष संख्या:

= (2*(999999999+1)) + 0 + (2*(9999999+1)) + (4*(999999+1)) + (5*(99999+1)) + (7*(9999+1)) + 0 + (4*(9+1)) + (1*(0+1))

यह स्पष्ट है कि सभी 9 वाली कोई भी संख्या 3 से समान रूप से विभाज्य होती है। उदाहरण के लिए, 99999 = 3 * 33333।

जैसा कि कहा गया है, आइए उपरोक्त संख्या में पदों को पुनः व्यवस्थित करें।

= (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) + (2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1)

पहले सात पदों में से प्रत्येक पद स्पष्ट रूप से 3 से समान रूप से विभाज्य है क्योंकि वे सभी 9 वाली संख्या से समान रूप से विभाजित होते हैं। दूसरे शब्दों में, (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) 9 से समान रूप से विभाज्य है, इसलिए हम उस भाग को हटा सकते हैं। हमें यह मिलता है:

(2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1) = 2+0+2+4+5+6+7+0+4+1 = 31

यह अंकों का योग है, जो 31 के बराबर है। चूंकि यह बचा हुआ भाग 3 से समान रूप से विभाजित नहीं होता है, इसलिए पूरी संख्या भी 3 से समान रूप से विभाजित नहीं हो सकती है।

इसी नियम से 9 से विभाज्यता की जाँच भी की जा सकती है। यदि मूल संख्या के अंकों का योग 9 से विभाज्य है, तो पूरी संख्या भी विभाज्य होगी। इसका विपरीत भी सत्य है, यदि अंकों का योग 9 से समान रूप से विभाज्य नहीं है, तो पूरी संख्या भी विभाज्य नहीं होगी।

तर्क पहेली समाधान

आइए उस नियम को "डी-3" नियम कहें, जिसके अनुसार 3 को डी नियम के विपरीत दिशा में होना चाहिए।

1. • यह स्पष्ट है कि हमें डी कार्ड को पलटना होगा ताकि यह सुनिश्चित हो सके कि दूसरी तरफ 3 है।
2. • K कार्ड के दूसरे तरफ एक नंबर होना चाहिए।चूंकि, दूसरे पक्ष के पास D नहीं हो सकता, इसलिए यह कार्ड हमें यह सिद्ध करने में मदद नहीं करता कि D-3 नियम का पालन किया गया था।
3. • 3 वाले कार्ड के दूसरी तरफ एक अक्षर होना चाहिए। अगर वह अक्षर D है, तो वह D-3 नियम का समर्थन करता है। अगर दूसरी तरफ कोई और अक्षर है, तो वह हमारी मदद नहीं करता। तो, या तो यह कार्ड D-3 नियम का पालन करेगा या प्रासंगिक नहीं होगा। किसी भी तरह, हम ऐसे कार्ड की तलाश में हैं जो D-3 नियम को अमान्य करने के लिए नियम का उल्लंघन करता हो। दूसरी तरफ जो भी अक्षर होगा, वह D-3 नियम को गलत साबित नहीं करेगा। इसलिए, इसकी जाँच करने की ज़रूरत नहीं है।
4. • 7 वाले कार्ड के दूसरी तरफ एक अक्षर होना चाहिए। अगर वह अक्षर D होता, तो वह कार्ड D-3 नियम को गलत साबित कर देता। इसलिए, यह सुनिश्चित करने के लिए इसकी जाँच की जानी चाहिए कि यह D-7 वाला कार्ड तो नहीं है, क्योंकि यह D-3 के दावे का खंडन होगा।

इस प्रकार, केवल D और 7 कार्ड ही ऐसे हैं जिन्हें जांचना आवश्यक है।