WOO logo

विज़ार्ड अनुशंसा करता है

मुड़ा हुआ आयत पहेली


इस समाचार-पत्र के लिए मैं मेन्सा बुलेटिन के नवंबर अंक से एक गणित पहेली प्रस्तुत कर रहा हूँ।

एक 1x4 आयत पर विचार करें। अब उस आयत को इस प्रकार मोड़ें कि विपरीत कोने एक-दूसरे पर आ जाएँ, जैसा कि इस चित्र में दिखाया गया है।

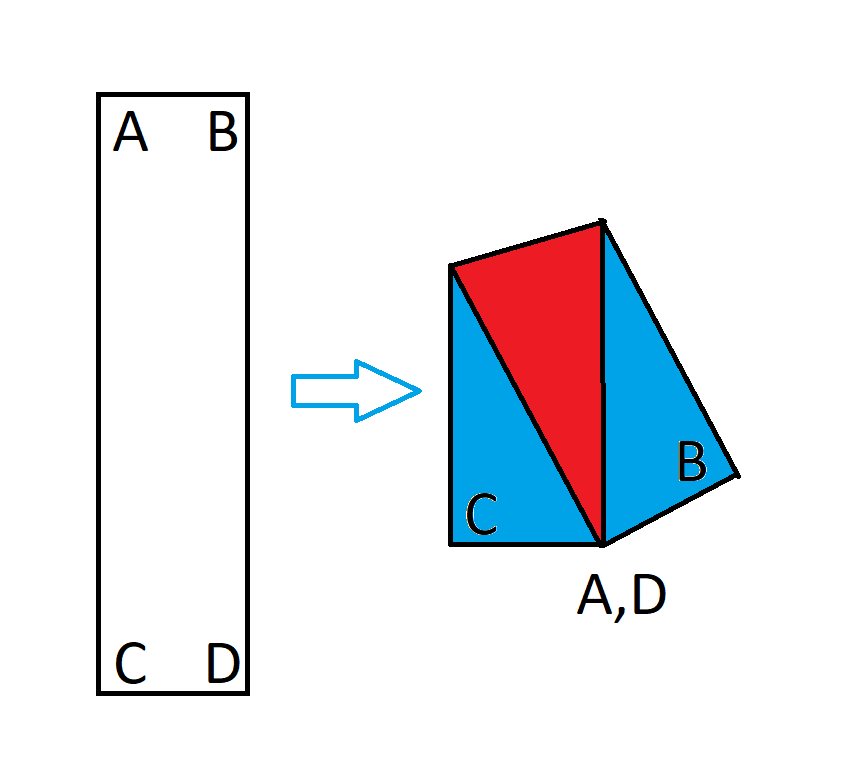
1x4 आयत

आयत को मोड़ने पर यह एक अनियमित पंचभुज बन जाता है। उस पंचभुज के उस भाग का, जहाँ कागज़ ओवरलैप होता है, कुल क्षेत्रफल से अनुपात क्या है? दूसरे शब्दों में, ऊपर दी गई छवि में लाल क्षेत्रफल का कुल क्षेत्रफल से अनुपात क्या है?

उत्तर और समाधान के लिए नीचे स्क्रॉल करें।

उत्तर

उत्तर है 17/47 = लगभग 0.3617

समाधान

हल समझाने के लिए, मैं कुछ और बिंदु परिभाषित करता हूँ, जैसा कि नीचे दी गई छवि में दिखाया गया है। F, E और G का मध्यबिंदु है।

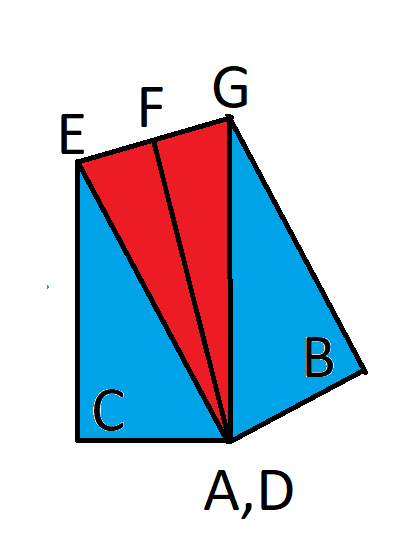
1x4 आयत, पंचकोण - समाधान

हम जानते हैं:

एसी = 1

सीई + एई = 4

आइए पाइथागोरस प्रमेय का उपयोग करके AE का हल निकालें:

1 2 + (सीई) 2 = (एई) 2

AE के स्थान पर 4 – CE प्रतिस्थापित करने पर हमें प्राप्त होता है:

1 2 + (सीई) 2 = (4 – सीई) 2

1 + (सीई) 2 = 16 - 8(सीई) + (सीई) 2

8(सीई) = 15

सीई = 15/8

1 2 + (CE) 2 = (AE) 2 पर वापस जाकर, हम (AE) का हल निकाल सकते हैं क्योंकि हम EC जानते हैं:

(एई) 2 = (सीई) 2 + 1 2

(एई) 2 = (15/8) 2 + 1 2

(एई) 2 = 225/64 + 64/64

(एई) 2 = 289/64

6;font-family: 'Open Sans',sans-serif;color: #313131!important">AE = 17/8

मोड़ने से पहले, A से D तक की लंबाई आयत का विकर्ण थी। पाइथागोरस विधि का पुनः प्रयोग करने पर, लंबाई sqrt(17) है।

(AF) उस लम्बाई का आधा है, या sqrt(17)/2 है।

AE और AF को जानते हुए, हम पुनः पाइथागोरस का उपयोग करके EF का हल निकाल सकते हैं:

(एई) 2 = (ईएफ) 2 + (एएफ) 2

(17/8) 2 = (ईएफ) 2 + (वर्ग(17)/2) 2

289/64 = (ईएफ) 2 + 17/4

289/64 = (ईएफ) 2 + 272/64

(ईएफ) 2 = 17/64

ईएफ = sqrt(17)/8

जैसा कि पहले बताया गया है, F, E और G का मध्यबिंदु है। यह EG = 2*sqrt(17)/8 = sqrt(17)/4 है।

लाल त्रिभुज, AEG = (1/2) × आधार × ऊँचाई =

= (1/2) × sqrt(17/4) × sqrt(17)/2

= (1/2) × (17/8) = 17/16

त्रिभुज ACE का क्षेत्रफल = (1/2)*आधार*ऊँचाई =

(1/2) × 1 × (15/8) = 15/16.

संपूर्ण पंचभुज का क्षेत्रफल = AEG + 2*ACE =

(17/16) + 2*(15/16) = 47/16

इस प्रकार, पूरे पंचभुज के लाल क्षेत्र का क्षेत्रफल =

(17/16) / (47/16) = 17/47 = लगभग 0.3617


द्वारा लिखित: Michael Shackleford