टेक्सास होल्डम - प्रायिकता - सामान्य
टेक्सास होल्ड एम खेल में 50 हाथों में दस खिलाड़ियों के साथ एक ही खिलाड़ी को दो चार प्रकार के कार्ड और एक स्ट्रेट फ्लश मिलने की संभावना क्या है?
सात पत्तों में एक ही तरह के चार आने की प्रायिकता 0.00168067 है, और स्ट्रेट फ्लश की प्रायिकता 0.00027851 है। यदि x एक ही तरह के चार आने की प्रायिकता है और y स्ट्रेट फ्लश की प्रायिकता है, तो आपके द्वारा पूछी गई प्रायिकता combin(50,2)*48*x 2 *y*(1-xy) 47 है। इसका उत्तर .0000421845, यानी 23,705 में 1 आता है।
टेक्सास होल्ड 'एम में फ्लश मिलने की सांख्यिकीय संभावनाएँ क्या हैं? एक खिलाड़ी के तौर पर 7-कार्ड स्टड या होल्डम में फ्लश पाना आसान है?
आप पोकर में संभावनाओं पर मेरे अनुभाग को देख सकते हैं और देख सकते हैं कि संभावना 3.03% है। टेक्सास होल्ड 'एम और 7-कार्ड स्टड, दोनों में ऑड्स समान हैं।
नदी पर टेक्सास होल्ड-एम में रॉयल फ्लश बनाने की संभावना क्या है?
जो पाठक नहीं जानते, उनके लिए बता दें कि रिवर टेक्सास होल्ड-एम में पाँचवाँ और आखिरी कम्युनिटी कार्ड होता है। खिलाड़ी को अपने दो कार्ड और पाँच कम्युनिटी कार्ड के बीच सबसे अच्छा पोकर हैंड बनाना होता है। तो आप पूछ रहे हैं कि सात कार्डों में एक खिलाड़ी के रॉयल फ्लश बनाने की क्या संभावना है, और यह कि बाँटा गया सातवाँ कार्ड रॉयल फ्लश का हिस्सा होगा। कार्ड पर विचार करने से पहले, 7 कार्डों में से 5-कार्ड रॉयल फ्लश बनाने की संभावना 4*कॉम्बिन(47,2)/कॉम्बिन(52,7) = 4324/133784560, या 30940 में 1 है। सातवें कार्ड के रॉयल फ्लश का हिस्सा होने की संभावना 5/7 है। तो अंतिम संभावना 21620/936491920, या 43316 में 1 है।
टेक्सास होल्ड एम में, फ्लॉप से शुरू होकर पांचवीं स्ट्रीट तक स्ट्रेट के अंदर एक या दो गैप बनाने की संभावना क्या है?
मेरे पाठकों के लाभ के लिए, यह प्रश्न पूछता है कि डेक में 47 कार्ड शेष रहते हुए, स्ट्रेट के अंदर एक या दो खाली स्थानों को दो और कार्डों से भरने की प्रायिकता क्या है। एक खाली स्थान होने पर प्रायिकता 1-combin(43,2)/combin(47,2) = 0.164662 है। दो खाली स्थानों पर प्रायिकता 4 2 /combin(47,2) = 0.0148 है।
टेक्सास होल्ड 'एम में यदि फ्लॉप कार्ड सभी एक ही सूट के हैं तो क्या संभावना है कि किसी भी खिलाड़ी के पास एक ही सूट के दो और कार्ड होंगे?
उसी सूट के 10 पत्ते बचे हैं, और डेक में 49 बचे हैं। तो संभावना है: combin(9,2)/combin(49,2) = 36/1176 = 0.0306।
क्या टेक्सास होल्ड 'एम में विभिन्न हाथों की संभावनाएँ सेवन-कार्ड स्टड की तरह ही होती हैं या सामुदायिक कार्डों के कारण वे किसी तरह अलग होती हैं? क्या आप कृपया बता सकते हैं कि ऐसा क्यों है या क्यों नहीं?
हाँ, संभावनाएँ एक जैसी ही हैं। 52 में से सात यादृच्छिक कार्डों के मिलने की संभावना एक जैसी ही होती है, चाहे उन्हें डेक से कैसे भी निकाला जाए या आप उन्हें किसके साथ बाँटें।
प्रारंभिक दो कार्डों में क्या आप मुझे बता सकते हैं कि 35 हाथों में होल्ड'एम में ऐस किंग के 7 हाथों या उससे बेहतर प्राप्त करने की क्या संभावना है?
इक्का/बादशाह मिलने की प्रायिकता (8/52)*(4/51) = 0.012066 है। किसी भी जोड़ी मिलने की प्रायिकता (3/51) = 0.058824 है। इसलिए एक जोड़ी या उससे बेहतर की प्रायिकता 0.07089 है। इक्का/बादशाह या उससे बेहतर के ठीक सात हाथ मिलने की प्रायिकता (35,7)*(.07089)^7*(1-.07089)^28 = 0.00772 है। 7 या उससे अधिक की प्रायिकता निकालने के लिए हमें एक-एक करके 7 से 35 तक के कुल योगों को देखना होगा। इसका योग 0.010366551 होता है।
यदि आपके होल कार्ड सूटेड हैं, तो आप होल्डम में फ्लॉप पर 4 कार्ड फ्लश या उससे बेहतर प्राप्त करने की संभावना का पता कैसे लगाएंगे।
एक ही सूट के 2 और जूते मिलने की प्रायिकता 39*combin(11,2)/combin(50,3) = 0.109439 है। एक ही सूट के 3 और जूते मिलने की प्रायिकता combin(11,3)/combin(50,3) = 0.008418 है। इसलिए, एक ही सूट के कम से कम 2 और जूते मिलने की प्रायिकता 0.117857 है।
मिस्टर विज़ार्ड, सबसे पहले, मैं कहना चाहूँगा कि आपकी साइट बहुत ही शानदार है! मैं इसे कुछ समय से पढ़ रहा हूँ। मैंने पोकर के सवाल देखे, और मुझे यह नहीं मिला। एक और साइट पर यह दावा किया गया है, "टेक्सास होल्डम में, प्री-फ्लॉप में AK मिलने और रिवर तक A या K मिलने की संभावना 2 में से 1 (सम) होती है।" यह सहज रूप से बहुत ज़्यादा लगता है। आपके क्या विचार हैं? फिर से धन्यवाद!
आपके अच्छे शब्दों के लिए आपका भी धन्यवाद। जो लोग होल्डम से परिचित नहीं हैं, उनके लिए यह प्रश्न पूछने जैसा है कि यदि किसी खिलाड़ी को एक इक्का और एक बादशाह दिया जाता है और शेष 50 कार्डों में से पाँच यादृच्छिक कार्ड दिए जाते हैं, तो क्या संभावना है कि खिलाड़ी बादशाह और/या इक्के की जोड़ी बनाएगा। अन्य 50 कार्डों में से 44 में से राजा या इक्के नहीं हैं। 44 में से कोई भी पाँच कार्ड निकालने के तरीकों की संख्या combin(44,5) = 1,086,088 है। सभी 50 में से कोई भी पाँच कार्ड निकालने के तरीकों की संख्या combin(50,5) = 2,118,760 है। इसलिए इक्का और/या बादशाह की जोड़ी न बनाने की संभावना 1086088/2118760 = 51.26% है।
टेक्सास होल्डम में दो खिलाड़ियों के पास अलग-अलग चार-एक-तरह के पत्ते होने की क्या संभावना है?
दो खिलाड़ियों के बीच कुल 9 पत्ते होते हैं। इनमें दो चार एक तरह के और एक सिंगलटन होना चाहिए। इसके लिए संयोजनों की संख्या combin(13,2)*44 = 3432 है। 52 में से 9 पत्ते चुनने के तरीकों की कुल संख्या combin(52,9) = 3,679,075,400 है। इसलिए, आपके पास सही पत्ते होने की संभावना, लेकिन ज़रूरी नहीं कि सही क्रम में, 3432/3,679,075,400 = 1,071,992 में 1 है।
हालाँकि, सिर्फ़ इसलिए कि पत्ते AAAABBBBC हैं, इसका मतलब यह नहीं है कि दोनों खिलाड़ियों के पास अलग-अलग चार-तरफ़ा पत्ते होंगे। उन्हें 5-पत्ते वाले हाथ और दो 2-पत्ते वाले हाथों में व्यवस्थित करने के तरीकों की संख्या 9!/(5!*2!*2!) = 756 है। ये 9 पत्ते नीचे दिए गए तरीकों से गिर सकते हैं।
चार तरह के बैड बीट संयोजन
खिलाड़ी 1 | खिलाड़ी 2 | फ्लॉप | दर्पण पैटर्न | प्रति पैटर्न संयोजन | कुल संयोजन |
आ | बी बी | एएबीबीसी | 2 | 72 | |
आ | अब | एबीबीबीसी | 4 | 48 | 192 |
आ | आ | बीबीबीबीसी | 2 | 6 | 12 |
आ | एसी | एबीबीबीबी | 4 | 12 | 48 |
आ | ईसा पूर्व | एएबीबीबी | 4 | 24 | 96 |
अब | अब | एएबीबीसी | 1 | 144 | 144 |
अब | एसी | एएबीबीबी | 4 | 48 | 192 |
इनमें से केवल पहले और पाँचवें समूह में ही दोनों खिलाड़ियों के पास एक ही तरह के अलग-अलग चार कार्ड होते हैं। इसलिए, AAAABBBBC कार्डों के सेट से दो अलग-अलग एक ही तरह के चार कार्ड आने की प्रायिकता 168/756 = 22.22% है।
तो आपके प्रश्न का उत्तर है (3432/3,679,075,400)*(168/756) = 4,823,963 में 1। व्यावहारिक रूप से, पार्टी पोकर में चार आठों के हारने वाले हाथ पर भी बैड बीट जैकपॉट होता है। चूँकि दो चार एक प्रकार के होते हैं, इसलिए दोनों के आठ या उससे अधिक होने की प्रायिकता कॉम्बिनेशन (7,2)/कॉम्बिनेशन (13,2) = 21/78 = 26.92% है। इसलिए, दो खिलाड़ियों में से किसी एक हाथ के इस बैड बीट जैकपॉट में आने की प्रायिकता 17,917,577 में 1 है।
कल रात एक खिलाड़ी ने मुझे टेक्सास होल्ड 'एम में एक अतिरिक्त दांव लगाने का प्रस्ताव दिया। उसने कहा कि फ्लॉप पर कम से कम एक फेस कार्ड (या कोई भी तीन रैंक) आएगा और बराबर राशि का दांव लगाने का प्रस्ताव दिया? क्या मुझे यह दांव स्वीकार कर लेना चाहिए था?
40 बिना-चेहरे वाले पत्तों में से 3 पत्ते चुनने के तरीकों की संख्या है: (40*39*38)/(1*2*3) = 9880। 52 पत्तों में से 3 पत्ते चुनने के तरीकों की संख्या है: (52*51*50)/(1*2*3) = 22100। इसलिए, चेहरे वाला पत्ता न मिलने की प्रायिकता 9880/22100 = 44.71% है। इस प्रकार, चेहरे वाला पत्ता मिलने की प्रायिकता 55.29% है। दांव पर उसके पक्ष को 10.58% का फायदा था।
52 पत्तों वाले एक मानक डेक का उपयोग करते हुए, 10 खिलाड़ियों के साथ टेक्सास होल्डम खेलते समय, प्रत्येक खिलाड़ी को पहले दो पत्ते बाँट दिए जाने के बाद, क्या संभावना है कि "फ्लॉप" (अगले तीन पत्ते) सभी एक ही सूट के होंगे? क्या इससे कोई फ़र्क पड़ता है कि मेरे हाथ में दोनों पत्ते एक ही सूट के हैं और/या हर एक अलग सूट का है?
अपने स्वयं के कार्ड पर विचार करने से पहले संभावना 4 × संयोजन (13,3) / संयोजन (52,3) = 5.1764706% है।
इसे देखने का एक और तरीका यह है कि फ्लॉप में दूसरे कार्ड के पहले सूट के कार्ड से मेल खाने की संभावना (12/51) है। फ्लॉप में तीसरे कार्ड के भी पहले सूट के कार्ड से मेल खाने की संभावना (11/50) है। (12/51)×(11/50)=5.1764706%.
अगर आप अपने कार्ड्स पर गौर करें तो ऑड्स थोड़े बदल जाते हैं। अगर आपके पास एक ही सूट के दो कार्ड हैं, तो एक सूट वाले फ्लॉप की प्रायिकता pr(एक ही सूट में फ्लश) + pr(दूसरे सूट में फ्लश) = कॉम्बिनेशन(11,3)/कॉम्बिनेशन(50,3) + 3×कॉम्बिनेशन(13,3)/कॉम्बिनेशन(50,3) = 5.2193878% है।
यदि आपके पास अलग-अलग सूट के दो कार्ड हैं, तो एक सूट वाले फ्लॉप की संभावना pr(सामान्य सूट में फ्लश) + pr(अलग सूट में फ्लश) = 2×combin(12,3)/combin(50,3) + 2×combin(13,3)/combin(50,3) = 5.1632653% है।
प्यारे जादूगर, काश मेरे पास भी तुम्हारा दिमाग होता। खैर, आँकड़ों के साथ मेरी जद्दोजहद जारी है। मैं फ्लॉप पर फ्लश मिलने की संभावना, टर्न तक और रिवर (टेक्सास होल्डम) तक पार करने की संभावना, इस बात पर निर्भर करती है कि मेरे होल कार्ड सूटेड हैं या नहीं, का पता लगाने के लिए एक सूत्र ढूँढ रहा हूँ। मैंने C(50,2) / C(47,5) की कोशिश की, लेकिन रिवर तक सूटेड पेयर के लिए यह कारगर नहीं हुआ... मुझे स्कूल में ज़्यादा ध्यान देना चाहिए था! शुक्रिया! आपका सबसे बड़ा प्रशंसक
आपके अच्छे शब्दों के लिए शुक्रिया, लेकिन मैं इतना समझदार नहीं हूँ। कुछ साल पहले मैंने मेन्सा प्रवेश परीक्षा दी थी, और ज़रूरी टॉप 2% में जगह नहीं बना पाया था। मुझे अब भी इस बात का दुख है कि उन्होंने मुझे यह बताने से इनकार कर दिया कि मैंने कितना अच्छा प्रदर्शन किया। 13 जनवरी को जेपर्डी के ट्रायल वेगास में होने वाले हैं, जिसके लिए मेरा अपॉइंटमेंट है, और मुझे यकीन है कि मैं उसे भी गँवा दूँगा। खैर, आपके सवाल का जवाब देने के लिए ये रहा:
उपयुक्त होल कार्ड के साथ:
फ्लॉप के बाद फ्लश: कॉम्बिन (11,3)/कॉम्बिन (50,3) = 165/19600 = 0.842%.
बारी के बाद फ्लश: (कॉम्बिन(11,2)*39/कॉम्बिन(50,3))*(9/47) = 2.096%.
नदी के बाद फ्लश: (कॉम्बिन(11,2)*कॉम्बिन(39,2)/कॉम्बिन(50,4))*(9/46) = 3.462%।
अनुपयुक्त होल कार्ड के साथ:
फ्लॉप के बाद फ्लश: 0%
बारी के बाद फ्लश: 2*कॉम्बिन(12,4)/कॉम्बिन(50,4) = 0.430%.
नदी के बाद फ्लश: (2*कॉम्बिन(12,3)*39/कॉम्बिन(50,4))*(9/46) = 1.458%.
यहाँ पर संचयी सम्भावनाएं दी गई हैं।
उपयुक्त होल कार्ड के साथ:
फ्लॉप द्वारा फ्लश: 0.842%.
बारी-बारी से फ्लश: 2.937%.
नदी द्वारा प्रवाहित: 6.400%.
अनुपयुक्त होल कार्ड के साथ:
फ्लॉप द्वारा फ्लश: 0.000%
बारी-बारी से फ्लश: 0.430%.
नदी द्वारा प्रवाहित: 1.888%.
नमस्ते जादूगर, सबसे पहले मैं यह कहना चाहूँगा कि मुझे आपके सटीक और बिना किसी झंझट के जवाब बहुत पसंद हैं। खैर, अगर होल्डम में पॉकेट कार्ड AA हैं और फ्लॉप कार्ड KQ9 हैं, तो फुल हाउस पूरा होने की संभावना क्या है? मैं इस पर बरसों से काम कर रहा हूँ :( और अभी भी मेरे पास ऐसा कोई जवाब नहीं है जिस पर मुझे भरोसा हो।
आप एक इक्का और एक K, Q, या 9 के साथ फुल हाउस पूरा कर सकते हैं। 2 इक्के बचे हैं और K, Q, और 9 के 3-3 इक्के बचे हैं। तो ऐसे 2*3*3=18 संयोजन हैं। K, Q, या 9 का जोड़ा ही एकमात्र दूसरा तरीका होगा। 3*combin(3,2)=9 ऐसे संयोजन हैं। सभी संयोजनों की संख्या 47*46/2 = 1081 है। तो संभावना (18+9)/1081 = 2.50% है।
मैं कई सालों से आपका बहुत बड़ा प्रशंसक रहा हूँ (पोकर और स्पोर्ट्स बेटिंग में आपकी रुचि होने से भी पहले) और हर Ask The Wizard कॉलम का बेसब्री से इंतज़ार करता था। यह देखकर बहुत अच्छा लगा कि आप उन्हें फिर से कर रहे हैं! मेरा सवाल यह है: मेरे स्थानीय कार्ड रूम में, कुछ घंटों के दौरान इक्के तोड़ो, एक रैक जीतो का ऑफर दिया जाता है। यानी, अगर आपके पास उनके 3-6 या 4-8 टेक्सास होल्ड 'एम गेम में पॉकेट इक्के हैं और आप पॉट हार जाते हैं, तो कैसीनो आपको चिप्स का एक रैक ($100) देगा। मैं यह जानने की कोशिश कर रहा हूँ कि कितनी बार (क) मुझे पॉकेट इक्के मिलते हैं (ख) अगर मैं उन्हें आक्रामक तरीके से खेलूँ जैसा कि मुझे करना चाहिए, तो वे कितनी बार हारेंगे और (ग) क्या यह बेहतर नहीं होगा कि मैं पूरी तरह से चेक कर लूँ और हारने की उम्मीद करूँ, क्योंकि $100 आमतौर पर पॉट से बेहतर होता है। आपके पास जो भी आँकड़े उपलब्ध हों, वे बहुत अच्छे होंगे और हमेशा के लिए सराहनीय होंगे! एक बार फिर धन्यवाद और लोगों को जागरूक करते रहिए!
आपके दयालु शब्दों के लिए धन्यवाद। किसी एक हाथ में पॉकेट इक्के मिलने की संभावना 6/1326 है, यानी हर 221 हाथ में एक बार। मेरे 10-खिलाड़ी टेक्सास होल्ड 'एम सेक्शन (/games/texas-hold-em/10players.html) के अनुसार, पॉकेट इक्कों से जीतने की संभावना 31.36% है, बशर्ते कि सभी खिलाड़ी अंत तक बने रहें। हालाँकि, यह एक बहुत बड़ी 'यदि' है। अगर मुझे अनुमान लगाने के लिए मजबूर किया जाए, तो मैं अनुमान लगाऊँगा कि 10 खिलाड़ियों वाले असली खेल में इक्कों से जीतने की संभावना लगभग 70% है। तो पॉकेट इक्के मिलने और फिर हारने की संभावना 0.3*(1/221) = 0.1357% है। तो, प्रति घटना $100 के हिसाब से यह प्रति हाथ 13.57 सेंट के बराबर है। दस से ज़्यादा लोगों पर पोकर रूम का औसतन प्रति हाथ $1.36 का खर्च आता है, जो रेक में काफ़ी कटौती करता है। मैं आपकी कॉल करने की रणनीति से सहमत हूं, जिससे आपके पास अधिक खिलाड़ी रहेंगे और आपके हारने की संभावना बढ़ जाएगी।
सबसे पहले, मैं आपको एक शानदार साइट के लिए धन्यवाद देना चाहता हूँ। अब मेरा प्रश्न यह है: हम टेक्सास होल्डम खेल रहे हैं और दो छोटे पत्तों के साथ फ्लश ड्रॉ फ्लॉप कर रहे हैं। हम सभी फ्लश हिट होने का प्रतिशत जानते हैं, लेकिन असल में हम हाथ जीतने का प्रतिशत जानना चाहते हैं। और मान लीजिए कि हमें यकीन है कि किसी के पास उस सूट का हमसे बड़ा पत्ता है। तो मेरा प्रश्न यह है कि उस सूट के केवल एक पत्ते के दिखने का प्रतिशत क्या है, दो का नहीं? सादर।
आपका स्वागत है। तो फ्लॉप के बाद बोर्ड पर दो के साथ आपके पास फ्लश के लिए चार हैं। ज़रूरी सूट का ठीक एक सूट मिलने की संभावना 9*38/ कॉम्बिनेशन (47,2) = 342/1081 = 31.64% है।
टेक्सास होल्ड 'एम में, मैं यह जानना चाहता हूँ कि क्या किसी दूसरे खिलाड़ी को दो सूट वाले पत्ते दिए गए होंगे जिससे मेरे मुकाबले ज़्यादा बड़ा फ्लश बन गया हो, जबकि रिवर पर ठीक 3 सूट वाले कम्युनिटी कार्ड हों। तो, उदाहरण के लिए, अगर मेरे पास हुकुम के 89 पत्ते हैं और कम्युनिटी कार्ड्स में हुकुम के 3, 7 और K पत्ते शामिल हैं, तो डेक में मेरे 9 पत्तों से 4 हुकुम बड़े हैं (TJQA)। क्या संभावना है कि किसी को दो हुकुम वाले पत्ते मिले हों जिनमें कम से कम एक बड़ा हुकुम भी शामिल हो (यह मानते हुए कि यह 9 पत्तों वाला खेल है)? क्या होगा अगर मेरे सबसे बड़े होल कार्ड से सिर्फ़ 2 (या 3 या x) हुकुम बड़े हों? आपकी मदद और बेहतरीन साइट के लिए धन्यवाद।
नीचे दी गई तालिका 1 से 8 उच्च रैंक और 2 से 10 खिलाड़ियों (जिनमें आप भी शामिल हैं) के लिए प्रायिकता दर्शाती है। आपके उदाहरण में, 4 उच्च रैंक और कुल 9 खिलाड़ियों के मामले में, प्रायिकता 16.45% है। मैंने इन प्रायिकताओं की गणना हाथों के बीच स्वतंत्रता मानकर की है, जो एक सही धारणा नहीं है, लेकिन परिणाम एक करीबी अनुमान होना चाहिए।
उच्च फ्लश की संभावनाउच्च रैंक (नीचे) कुल खिलाड़ियों द्वारा (सभी में)विज़ार्ड अनुमान
| उच्च रैंक | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.71% | 1.41% | 2.11% | 2.80% | 3.49% | 4.17% | 4.85% | 5.52% | 6.19% |
| 2 | 1.31% | 2.61% | 3.89% | 5.15% | 6.40% | 7.62% | 8.84% | 10.03% | 11.22% |
| 3 | 1.82% | 3.60% | 5.36% | 7.08% | 8.77% | 10.43% | 12.05% | 13.65% | 15.22% |
| 4 | 2.22% | 4.40% | 6.52% | 8.60% | 10.63% | 12.61% | 14.56% | 16.45% | 18.31% |
| 5 | 2.53% | 4.99% | 7.39% | 9.72% | 12.00% | 14.23% | 16.39% | 18.50% | 20.56% |
| 6 | 2.73% | 5.38% | 7.96% | 10.47% | 12.91% | 15.29% | 17.60% | 19.85% | 22.03% |
| 7 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
| 8 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
उच्च फ्लश की संभावना, कुल खिलाड़ियों (सभी में) द्वारा उच्च रैंक (नीचे) मिप्लेट सिमुलेशन
| उच्च रैंक | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.69% | 1.41% | 2.12% | 2.83% | 3.54% | 4.25% | 4.96% | 5.66% | 6.36% |
| 2 | 1.28% | 2.60% | 3.91% | 5.21% | 6.48% | 7.77% | 9.05% | 10.31% | 11.56% |
| 3 | 1.79% | 3.61% | 5.41% | 7.19% | 8.92% | 10.68% | 12.41% | 14.11% | 15.79% |
| 4 | 2.19% | 4.40% | 6.58% | 8.75% | 10.85% | 12.94% | 15.01% | 17.04% | 19.04% |
| 5 | 2.50% | 5.00% | 7.47% | 9.92% | 12.28% | 14.63% | 16.94% | 19.21% | 21.43% |
| 6 | 2.71% | 5.40% | 8.06% | 10.69% | 13.23% | 15.74% | 18.23% | 20.65% | 23.03% |
| 7 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
| 8 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
बहुत बढ़िया साइट। मैं अपनी निजी जानकारी के लिए यह पूछ रहा हूँ। मैं टेक्सास होल्डम का चार लोगों वाला गेम खेल रहा था। मुझे पॉकेट इक्के मिले। मुझे रिवर पर रॉयल फ्लश मिला। मैं सोच रहा था कि इक्के से शुरुआत करते हुए रिवर पर रॉयल फ्लश मिलने की क्या संभावना है?
धन्यवाद। मान लीजिए कि रॉयल आपके दो इक्कों में से एक है, तो रिवर तक रॉयल बनाने के तरीकों की संख्या 2*46=92 है। यह आपके पॉकेट इक्कों के दो सूट और अतिरिक्त पत्ते की 46 संभावनाएँ होंगी। 50 में से 5 पत्ते बाँटने के लिए (50,5) = 2,118,760 तरीके हैं। तो संभावना 92/2,118,760 = 23,030 में 1 है।
यदि फ्लॉप पर एक ही सूट के तीन कार्ड आते हैं और मेरे पास फ्लॉप से मेल खाने वाला कोई कार्ड नहीं है, तथा टेबल पर दस खिलाड़ी बचे हैं, तो किसी एक के पास फ्लश आने की संभावना क्या है?
किसी एक खिलाड़ी के फ्लश होने की प्रायिकता कॉम्बिन (11,2)/कॉम्बिन (49,2) = 55/1176 = 4.68% है। हाथों के बीच स्वतंत्रता मानते हुए, जो कि सच नहीं है, 9 खिलाड़ियों के फ्लश न होने की प्रायिकता (1 − 0.0468%) 9 = 64.98% है। इसलिए कम से कम एक खिलाड़ी के फ्लश होने की प्रायिकता 1-0.6498 = 35.02% है। यह केवल एक त्वरित अनुमान है। अगर मैं एक यादृच्छिक सिमुलेशन करता, तो मुझे लगता है कि हाथों के बीच निर्भरता के कारण, प्रायिकता थोड़ी अधिक होती।
प्रिय मिस्टर विज़ार्ड, मैं हाल ही में टेक्सास होल्ड 'एम में फ्लश मिलने की संभावना की गणना करने की कोशिश कर रहा हूँ, अगर मुझे दो सूट वाले होल कार्ड मिले हों? मेरा जवाब बार-बार 5.8% आ रहा है, लेकिन यह पूरी तरह से गलत लगता है। आपकी मदद के लिए बहुत-बहुत धन्यवाद।
आपके होल कार्ड्स के समान सूट के ठीक तीन कार्ड्स के साथ फ्लश बनाने की प्रायिकता कॉम्बिन (11,3) × कॉम्बिन (39,2) / कॉम्बिन (50,5) = 122265/2598960 = 0.057706 है। आपके होल कार्ड्स के समान सूट के चार और कार्ड्स के साथ फ्लश बनाने की प्रायिकता कॉम्बिन (11,4) × कॉम्बिन (39,1) / कॉम्बिन (50,5) = 2145/2118760 = 0.001012 है। आपके होल कार्ड्स के समान सूट के पाँच और कार्ड्स के साथ फ्लश बनाने की प्रायिकता कॉम्बिन (11,5) / कॉम्बिन (50,5) = 462/2118760 = 0.000218 है। बोर्ड पर किसी दूसरे सूट में फ्लश बनने की प्रायिकता 3×combin(13,5)/combin(50,5) = 3861/2118760 = 0.001822 है। इन सबको जोड़ने पर आपको 0.057706 + 0.001012 + 0.000218 + 0.001822 = 0.060759 प्राप्त होता है।
टेक्सास होल्ड'एम में "टूटे हुए बोर्ड" की संभावना क्या है? यानी, बोर्ड पर पाँच कार्ड ऐसे हों जहाँ कोई जोड़ी न हो, कोई फ्लश संभव न हो और कोई स्ट्रेट संभव न हो।
बोर्ड पर पांच अलग-अलग रैंकों के संयोजनों की संख्या संयोजन (13,5)*4 5 = 1287 × 1024 = 1,317,888 है।
इन पाँच रैंकों के तीन सूट, दो में से दो और एक में से एक, दर्शाने की प्रायिकता कॉम्बिन(4,2)*2*कॉम्बिन(5,2)*कॉम्बिन(3,2)=360 है। कॉम्बिन(4,2) दो बार दर्शाए गए सूट के लिए चार में से दो सूट चुनने के तरीकों की संख्या है। एक बार दर्शाए गए सूट को चुनने के दो तरीकों के लिए 2 है। कॉम्बिन(5,2) दो पत्तों के पहले सूट के लिए पाँच में से दो रैंक चुनने के तरीकों की संख्या है। 4 5 दो पत्तों के दूसरे सूट के लिए बचे तीन में से दो रैंक चुनने के तरीकों की संख्या है।
इन पाँच रैंकों के चार सूट, दो में से एक और एक में से तीन का प्रतिनिधित्व करने की प्रायिकता 4*कॉम्बिन(5,2)*3*2=240 है। 4, दो बार दर्शाए गए सूटों के लिए चार में से एक सूट चुनने के तरीकों की संख्या है। कॉम्बिन(5,2) दो पत्तों के उस सूट के लिए पाँच में से दो रैंक चुनने के तरीकों की संख्या है। 3, एक के पहले सूट के लिए बचे तीन में से एक रैंक चुनने के तरीकों की संख्या है। 2, एक के दूसरे सूट के लिए दो में से एक रैंक चुनने के तरीकों की संख्या है।
चार सूटों को पांच अलग-अलग रैंकों पर व्यवस्थित करने के 4 5 = 1024 तरीके हैं।
अतः एक ही सूट के दो से अधिक सिक्के मौजूद न होने की संभावना (360+240)/1024 = 600/1024 = 58.59% है।
13 में से 5 रैंकों को व्यवस्थित करने के लिए combin(13,5)=1287 तरीके हैं। ऐसे संयोजनों की संख्या जिनमें कोई भी तीन रैंक 5 के अंतराल में नहीं हैं, 79 है। इसके लिए कोई आसान सूत्र नहीं है। मुझे हर संयोजन को बार-बार दोहराना पड़ा। इसलिए रैंकों के बीच पर्याप्त दूरी होने की संभावना 79/1287 = 6.14% है।
तो, टूटे हुए बोर्ड की संभावना (1317888/2596960)*(600/1024)*(79/1287) = 1.825211% है।
मुझे मेरे टूटे हुए स्ट्रेट्स की संख्या पर चुनौती दी गई है। यहाँ सभी 79 संभावित स्ट्रेट्स की सूची दी गई है।
| 2378क्यू 2378के 2379क्यू 2379के 237टीक्यू 237टीके 237जेक्यू 237जेके 237क्यूके 2389के 238टीके 238जेके 238क्यूके 2479क्यू 2479के 247टीक्यू 247टीके 247जेक्यू 247जेके 247क्यूके | 2489के 248टीके 248जेके 248क्यूके 257टीक्यू 257टीके 257जेक्यू 257जेके 257क्यूके 258टीके 258जेके 258क्यूके 267जेक्यू 267जेके 267जेए 267क्यूके 267क्यूए 267केए 268जेके 268जेए | 268क्यूके 268क्यूए 268केए 269जेए 269क्यूए 269केए 278क्यूके 278क्यूए 278केए 279क्यूए 279केए 289केए 3489के 348टीके 348जेके 348क्यूके 358टीके 358जेके 358क्यूके 368जेके | 368जेए 368क्यूके 368क्यूए 368केए 369जेए 369क्यूए 369केए 378क्यूके 378क्यूए 378केए 379क्यूए 379केए 389केए 469जेए 469क्यूए 469केए 479क्यूए 479केए 489केए |
मैं सीज़र्स इंडियाना में टेक्सास होल्ड 'एम खेलता हूँ। उनके पास बैड बीट जैकपॉट है, यानी अब क्वाड या उससे बेहतर बीट। दोनों खिलाड़ियों को दोनों होल कार्ड खेलने होंगे, और चार खिलाड़ियों को कार्ड बाँटे जाने चाहिए। मेरा सवाल यह है कि किसी भी हाथ के बैड बीट होने की संभावना क्या है, यह मानते हुए कि सभी खिलाड़ी अंत तक बने रहते हैं?
मेरा नया बैड बीट जैकपॉट अनुभाग 10 खिलाड़ियों वाले खेल में इस प्रकार के बैड बीट की संभावना 0.0000108, या लगभग 93,000 में से 1 दर्शाता है।
आपके अल्टीमेट टेक्सास होल्ड 'एम रिटर्न टेबल में, उन दो-कार्ड वाले हाथों के लिए बड़ी रेज की सिफ़ारिश क्यों की जाती है जिनका अपेक्षित रिटर्न नकारात्मक है? उदाहरण के लिए, सूटेड K/2।
मेरे दो-खिलाड़ी टेक्सास होल्ड 'एम संभावनाओं के अनुसार, सूटेड K/2 के साथ संभावित परिणाम निम्नलिखित हैं:
51.24% जीत
44.82% की हानि
ड्रा 3.94%
अल्टीमेट टेक्सास होल्ड 'एम पर मेरी तालिका दर्शाती है कि खिलाड़ी को प्ले बेट पर बढ़त है, लेकिन एंटे और ब्लाइंड बेट पर नुकसान। इस स्थिति में, खिलाड़ी एंटे और ब्लाइंड बेट पर खराब ऑड्स के साथ फँसा हुआ है। हालाँकि, प्ले बेट पर उसके ऑड्स अनुकूल हैं। इसलिए, अधिकतम रेज लगाकर वह अपनी 50% से ज़्यादा की जीत की संभावना का अधिकतम मूल्य प्राप्त कर रहा है। अन्य दो बेट पर खराब ऑड्स कुल मूल्य को 50% से कम कर देते हैं। कम रेज के साथ यह मूल्य और भी कम होगा।
2008 की वर्ल्ड सीरीज़ ऑफ़ पोकर में, मोटोयुकी माबुची के क्वाड ऐस जस्टिन फिलिप के रॉयल फ्लश से हार गए थे। ऐसा होने की संभावना के बारे में मेरा एक साधारण सा सवाल है। ईएसपीएन और अन्य ने इसे लगभग 2.7 अरब में 1 बताया था। मुझे लगता है कि उन्होंने क्वाड होने की प्रकाशित संभावना को लिया और उसे रॉयल फ्लश होने की संभावना से गुणा कर दिया। क्या यह गणना का सही तरीका है?
मैं 2.7 अरब में 1 वाले आंकड़े से भी असहमत हूँ। जैसा कि आपने कहा, उन्होंने प्रत्येक खिलाड़ी के लिए अलग-अलग प्रायिकताएँ गणना कीं, ठीक उसी स्थिति में जब दोनों खिलाड़ी दोनों होल कार्ड इस्तेमाल करते हैं, और गुणा करते हैं। इस विधि का उपयोग करके मुझे 0.000000000341101, यानी लगभग 2.9 अरब में 1, की प्रायिकता प्राप्त होती है। हो सकता है कि 2.7 अरब में 1 में दोनों खिलाड़ियों की प्रायिकताओं पर पूर्णांकन त्रुटि का संयोजन भी शामिल हो। वे स्पष्ट रूप से प्रायिकता को 2 से गुणा करना भी भूल गए, जिसके कारण मैं बाद में बताऊँगा।
रॉयल फ्लश में चार इक्के हारने के तीन तरीके इस प्रकार हैं।
केस 1: एक खिलाड़ी के पास रॉयल फ्लश के दो कार्ड हैं, दूसरे के पास दो इक्के हैं, तथा बोर्ड पर अन्य दो इक्के, रॉयल फ्लश के अन्य दो कार्ड तथा कोई अन्य कार्ड है।
उदाहरण:
खिलाड़ी 1:

खिलाड़ी 2:

तख़्ता: 




ज़्यादातर पोकर रूम में, बैड-बीट जैकपॉट जीतने के लिए, जीतने वाले और हारने वाले दोनों खिलाड़ियों को दोनों होल कार्ड इस्तेमाल करने होते हैं। वीडियो में भी बैड बीट का यही प्रकार था; दरअसल, ये कार्ड बिल्कुल वही थे।
केस 2: एक खिलाड़ी के पास रॉयल फ्लश (टी.के.) के लिए दो कार्ड हैं, दूसरे के पास एक इक्का और एक "रिक्त" कार्ड है, तथा बोर्ड पर अन्य तीन इक्के और रॉयल के लिए अन्य दो कार्ड हैं।
उदाहरण:
खिलाड़ी 1:

खिलाड़ी 2:

तख़्ता: 




केस 3: एक खिलाड़ी के पास रॉयल फ्लश (टी.के.) का एक कार्ड और एक खाली कार्ड है, दूसरे के पास दो इक्के हैं, और बोर्ड पर अन्य दो इक्के और रॉयल फ्लश के अन्य तीन कार्ड हैं।
उदाहरण:
खिलाड़ी 1:

खिलाड़ी 2:

तख़्ता: 




निम्नलिखित तालिका खिलाड़ियों और बोर्ड दोनों के लिए प्रत्येक मामले में संयोजनों की संख्या दर्शाती है। निचले दाएँ कक्ष में कुल संयोजनों की संख्या 16,896 दिखाई गई है।
खराब बीट संयोजन
| मामला | खिलाड़ी 1 | खिलाड़ी 2 | तख़्ता | उत्पाद |
|---|---|---|---|---|
| 1 | 24 | 3 | 44 | 3,168 |
| 2 | 24 | 132 | 1 | 3,168 |
| 3 | 704 | 3 | 1 | 2,112 |
| कुल | 8,448 |
हालाँकि, हम दोनों खिलाड़ियों के पत्ते उलट सकते हैं, और फिर भी एक खराब बीट हो सकती है। इसलिए, हमें संयोजनों की संख्या को 2 से गुणा करना चाहिए। इसे समायोजित करने पर, कुल योग्य संयोजन 2 × 8,448 = 16,896 होंगे।
दो-खिलाड़ियों वाले टेक्सास होल्ड 'एम में सभी संयोजनों की कुल संख्या संयोजन (52,2) × संयोजन (50,2) × संयोजन (48,5) = 2,781,381,002,400 है। इसलिए, चार इक्कों के रॉयल फ्लश से हारने की संभावना 8,448/2,781,381,002,400 = 0.0000000060747 है, यानी लगभग 165 मिलियन में 1। सिर्फ़ एक केस में खराब हार की संभावना 439 मिलियन में 1 है। ऑड्स उस वीडियो में बताए गए लंबे समय तक नहीं हैं, इसका सीधा कारण यह है कि दोनों हाथ ओवरलैप होते हैं, जिसमें साझा इक्का होता है। दूसरे शब्दों में, दोनों घटनाएँ सकारात्मक रूप से सहसंबद्ध हैं।
"न्यू यॉर्क वीडियो पोकर के बारे में सच बताना" नामक पत्रिका के अनुसार, आप बिल्कुल सही हैं। खिलाड़ी का परिणाम वास्तव में पूर्वनिर्धारित होता है। खिलाड़ी चाहे जितने भी पत्ते रखे, वह अपने भाग्य से बच नहीं सकता। यदि खिलाड़ी जानबूझकर अपने भाग्य से बचने की कोशिश करता है, तो खेल खिलाड़ी की गलती सुधारने के लिए एक संरक्षक देवदूत सुविधा का उपयोग करेगा। मैं लेखक से पूरी तरह सहमत हूँ कि ऐसे खेलों में खिलाड़ी को चेतावनी दी जानी चाहिए कि वे असली वीडियो पोकर नहीं खेल रहे हैं, और भुगतान तालिका खिलाड़ी की वास्तविक बाधाओं का एक अर्थहीन माप है। यह भी ध्यान देने योग्य है कि इस प्रकार की नकली वीडियो पोकर मशीनें केवल न्यूयॉर्क तक ही सीमित नहीं हैं।
नमस्ते, मैं हवाई में सातवीं कक्षा का छात्र हूँ। मैं पोकर और शफलिंग पर एक विज्ञान मेले का प्रोजेक्ट कर रहा हूँ। मैं खेल में खिलाड़ियों की संख्या के अनुसार पॉकेट टेक्सास होल्ड 'एम हैंड के जीत प्रतिशत के बारे में आपके चार्ट का उपयोग कर रहा हूँ। मुझे उम्मीद थी कि आप कुछ सवालों के जवाब दे पाएँगे जो मेरे प्रोजेक्ट में मेरी मदद करेंगे:
- आपने चार्ट में प्रतिशत कैसे प्राप्त किया?
- यदि आपने कंप्यूटर प्रोग्राम का उपयोग किया, तो आपने इसे कैसे विकसित किया और इसमें कितना समय लगा?
- आपने बताया कि आपने Wizard of Odds एक शौक़ के तौर पर शुरू किया था। क्या आपकी साइट के ज़्यादा मशहूर होने के साथ-साथ प्रयोग करने के तरीके में कोई बदलाव आया? क्यों या क्यों नहीं?
- दो-खिलाड़ियों वाली टेबल एक ब्रूट-फोर्स लूपिंग प्रोग्राम द्वारा बनाई गई थी, जिसमें सभी 1225 संभावित प्रतिद्वंद्वी कार्डों और 1,712,304 संभावित सामुदायिक कार्डों का चक्र चलाया गया था। तीन से आठ खिलाड़ियों के लिए, लूपिंग में बहुत अधिक समय लगता, इसलिए मैंने एक यादृच्छिक सिमुलेशन किया।
- मैं अपने लगभग सभी प्रोग्राम C++ में लिखता हूँ, जिनमें अभी बताए गए दोनों प्रोग्राम भी शामिल हैं। बाकी जावा या PERL में हैं। मैंने ज़्यादातर कोड दूसरे पोकर-आधारित प्रोग्रामों से कॉपी और पेस्ट किया है। नया कोड लिखने में बस एक दिन लगता है।
- हाँ, मैंने जून 1997 में एक शौक़ के तौर पर अपनी साइट शुरू की थी। जनवरी 2000 तक मैंने विज्ञापन स्वीकार नहीं किए थे, और इसे व्यवसाय बनाने की कोशिश की। यह वर्षों में तीन अलग-अलग डोमेन से गुज़री है। मई 1999 में यह कुछ इस तरह दिखती थी। साइट का उद्देश्य हमेशा एक ही रहा है, गणितीय रूप से आधारित जुए की रणनीति के लिए एक संसाधन। वर्षों से, मैं बस और खेल और सामग्री जोड़ता रहा हूँ। एक प्रयोग 2005 सीज़न के लिए मेरी NFL पसंद प्रदान करना था, जो पूरी तरह से विफल रहा।
नमस्ते जादूगर। मैंने आपके टेक्सास होल्ड 'एम प्रश्न पढ़े, और मैंने देखा कि आपने पॉकेट क्वीन रखते हुए बोर्ड पर इक्का या बादशाह आने की 59.85% संभावना का अनुमान लगाया था। आपने यह आँकड़ा कैसे निकाला?
डेक में बचे हुए 50 पत्तों में से पाँच पत्तों के संयोजन (50,5) = 2,118,760 हैं। उनमें से 42 पत्ते 2-Q हैं। 42 पत्तों में से 5 पत्तों के संयोजनों की संख्या (42,5) = 850,668 है। इसलिए, बादशाह या इक्का न मिलने की प्रायिकता 850,668/2,118,760 = 40.15% है। इस प्रकार, कम से कम एक इक्का या बादशाह मिलने की प्रायिकता 1-40.15% = 59.85% है।
एक वैकल्पिक गणना है 1 - pr (फ्लॉप में पहला कार्ड इक्का या बादशाह नहीं है) × pr (फ्लॉप में दूसरा कार्ड इक्का या बादशाह नहीं है) × pr (फ्लॉप में तीसरा कार्ड इक्का या बादशाह नहीं है) × pr (फ्लॉप में चौथा कार्ड इक्का या बादशाह नहीं है) × pr (फ्लॉप में पांचवां कार्ड इक्का या बादशाह नहीं है) = 1 - (42/50) × (41/49) × (40/48) × (39/47) × (38/46) = 59.85%.
टेक्सास होल्ड 'एम में दो सूट वाले कार्ड रखने पर, फ्लॉप पर उसी सूट के दो और कार्ड मिलने की मेरी क्या संभावना है?
एक ही सूट के दो और कार्ड पाने के लिए कॉम्बिन (11,2) = 55 तरीके हैं, और अनसूट कार्ड के लिए 39। फ्लॉप पर कार्डों के कुल संभावित संयोजन कॉम्बिन (50,3) = 19,600 हैं। इसलिए, फ्लॉप के बाद फ्लश के लिए ठीक चार कार्ड मिलने की संभावना 55×39/19,600 = 10.94% है।
मैं ऑनलाइन पोकर के एक खेल में शामिल था और ऐसा होने की संभावना जानना चाहता हूँ, कृपया:
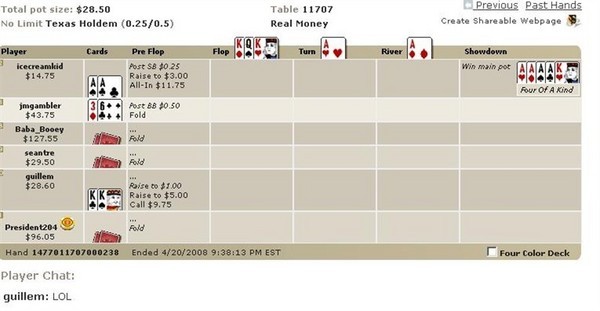
आम तौर पर मैं खराब बीट वाले सवालों से तंग आ जाता हूँ, लेकिन इस सवाल को नज़रअंदाज़ करना बहुत मुश्किल था। पहला पत्ता बंटने से पहले, दो खिलाड़ियों वाले खेल में, जिसमें दोनों खिलाड़ियों के पास पॉकेट पेयर हों, चार बादशाहों के चार इक्कों से हारने की प्रायिकता 2* कॉम्बिन (4,2)*कॉम्बिन(4,2)*44/(कॉम्बिन(52,2)*कॉम्बिन(50,2)*कॉम्बिन(48,5)) = 2*6*6*44/(1326*1225*1712304) = 877,961,175 में 1 है। यह छह खिलाड़ियों वाला खेल था, इसलिए कॉम्बिन(6,2) = 15 अलग-अलग खिलाड़ियों के जोड़े हैं। छह खिलाड़ियों वाले खेल में, यह प्रायिकता 15 गुना ज़्यादा है, यानी 58,530,745 में 1। संकेतित होल कार्ड बांटे जाने के बाद, तथा फ्लॉप से पहले, संभावना 38,916 में 1 है कि हाथ वैसे ही समाप्त होगा जैसा हुआ था।
लास वेगास के एक कार्ड रूम में एक प्रमोशन चल रहा है: चारों सूट में फ्लश बनाने पर आपको $400 मिलेंगे। आपको अपने दोनों होल कार्ड इस्तेमाल करने होंगे, और इसके लिए पाँच घंटे की समय सीमा है। मान लीजिए कि प्रति घंटे 35 सुइयाँ हैं, और घड़ी पहले फ्लश से शुरू होती है, तो पाँच घंटे के भीतर बाकी तीन फ्लश बनाने की संभावना क्या है? धन्यवाद।
मान लीजिए कि आपका पहला फ्लश हुकुम में है। 35 हाथ प्रति घंटे के हिसाब से, पाँच घंटों में 175 हाथ खेले जा सकते हैं। फिर आपके पास पान, ईंट और चिड़ी में फ्लश बनाने के लिए 175 हाथ होंगे। मैं यह मानकर चल रहा हूँ कि खिलाड़ी कभी भी ऐसा हाथ नहीं मोड़ेगा जिसमें उसके लिए ज़रूरी सूट में से किसी एक में फ्लश मिलने की संभावना हो।
किसी विशिष्ट सूट, मान लीजिए हार्ट, के फ्लश की संभावना, दोनों होल कार्ड्स का उपयोग करके, कॉम्बिनेशन (13,2) × [कॉम्बिनेशन (11,3) × कॉम्बिनेशन (39,2) + कॉम्बिनेशन (11,4) × 39 + कॉम्बिनेशन (11,5)]/(कॉम्बिनेशन (52,2) × कॉम्बिनेशन (50,5)) = 10576566/2809475760=0.003764605 है। अगले 175 हाथों में हार्ट फ्लश छूटने की संभावना (1-0.003764605) 175 =0.51682599 होगी।
यह कहना गलत होगा कि बाकी तीन सूट न बनने की प्रायिकता pr(हार्ट फ्लश नहीं) + pr(डायमंड सूट नहीं) + pr(क्लब फ्लश नहीं) होगी, क्योंकि आप उनमें से दो न बनने की प्रायिकता को दोगुना कर देंगे। इसलिए आपको pr(हार्ट या डायमंड फ्लश नहीं) + pr(हार्ट या क्लब फ्लश नहीं) + pr(क्लब या डायमंड फ्लश नहीं) को वापस जोड़ना चाहिए। हालाँकि, यह तीनों फ्लश न बनने की प्रायिकता को गलत तरीके से घटा देगा। इसलिए आपको pr(क्लब, डायमंड या हार्ट फ्लश नहीं) को वापस जोड़ना चाहिए।
175 बार हाथ खेलने के बाद भी दो विशिष्ट सूटों में से कोई भी न मिलने की संभावना (1-2×0.003764605) 175 =0.266442448 है।
175 हाथ चलने पर भी तीनों सूट में से कोई भी सूट न मिलने की संभावना (1-3×0.003764605) 175 =0.137015266 है।
तो उत्तर है 1-3×0.51682599 + 3×0.266442448 - 0.137015266 = 0.111834108.
मैं इस समस्या में मदद के लिए ड्वेटली का शुक्रिया अदा करना चाहता हूँ। विज़ार्ड ऑफ़ वेगास में मेरे बुलेटिन बोर्ड पर इस पर चर्चा की गई है।
डॉयल ब्रूनसन ने 1976 और 1977, दोनों बार वर्ल्ड सीरीज़ ऑफ़ पोकर में मेन इवेंट जीता था। हर बार उनके पास होल कार्ड के रूप में 10-2 थे, और दोनों बार उन्होंने रिवर पर फुल हाउस बनाया। इसकी संभावना क्या है?
अलग-अलग रैंक के दो कार्ड दिए जाने पर, फुल हाउस बनने की संभावना 121.6 में 1 है। रिवर पर फुल हाउस बनने की संभावना 207 में 1 है।
नदी पर दो में से दो बार ऐसा हाथ बनने की संभावना 43,006 में से 1 है।
केवल रैंक में समान दो प्रारंभिक कार्डों के साथ ऐसा होने की संभावना 3,564,161 में 1 है।
दोनों बार ठीक 10-2 के साथ ऐसा होने की संभावना 295,379,826 में 1 है।
अभी-अभी VFW में पोकर नाइट से लौटा हूँ। लगातार तीन बार 6-6 होल में मिला! ऐसा पहले कभी नहीं हुआ था। एक ही शाम में लगातार तीन बार एक ही रैंक का पॉकेट पेयर मिलने की संभावना क्या है? आप मान सकते हैं कि एक शाम में कुल 120 राउंड होते हैं।
उत्तर और समाधान निम्नलिखित स्पॉयलर टैग में दिखाई देते हैं।
[बिगाड़ने वाला]किसी भी समय आप चार संभावित स्थितियों में हो सकते हैं:
- स्थिति 1: पहला हाथ या कोई भी हाथ जहां अंतिम हाथ पॉकेट जोड़ी नहीं था।
- स्थिति 2: अंतिम हाथ पॉकेट पेयर था।
- स्थिति 3: अंतिम दो हाथ एक ही पॉकेट जोड़ी थे।
- स्थिति 4: एक पंक्ति में तीन समान पॉकेट जोड़े पहले ही प्राप्त किए जा चुके हैं।
यदि आप अवस्था 1 में हैं, तो आप 3/51 की संभावना के साथ अवस्था 2 में पहुँच सकते हैं। अन्यथा, आप अवस्था 1 में ही रहेंगे।
यदि आप अवस्था 2 में हैं, तो आप (4/52)×(3/51) की प्रायिकता के साथ अवस्था 3 में आगे बढ़ सकते हैं। अन्यथा, आप अवस्था 1 में वापस चले जाएँगे।
यदि आप अवस्था 3 में हैं, तो आप (4/52)×(3/51) की प्रायिकता के साथ अवस्था 4 में आगे बढ़ सकते हैं। अन्यथा, आप अवस्था 1 में वापस चले जाएँगे।
यदि आप राज्य 4 में हैं, तो आप वहीं रहें।
जैसा कि कहा गया है, आप अपना संक्रमण मैट्रिक्स, T, इस प्रकार बना सकते हैं:
| 0.941176 | 0.058824 | 0.000000 | 0.000000 |
| 0.941176 | 0.054299 | 0.004525 | 0.000000 |
| 0.941176 | 0.054299 | 0.000000 | 0.004525 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
कुल 120 हाथ खेले गए हैं, इसलिए T^120 ज्ञात कीजिए।
| 0.941044 | 0.058549 | 0.000265 | 0.000141 |
| 0.941025 | 0.058548 | 0.000265 | 0.000162 |
| 0.936786 | 0.058284 | 0.000264 | 0.004666 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
ऊपरी दाहिना कोष्ठ हमें यह संभावना दिखाता है कि स्थिति 1 से शुरू करने पर हम तीन-हाथ अनुक्रम में 120 प्रारंभिक हाथों के बाद स्थिति 4 में पहुंच जाएंगे, जो कि 0.000141471 है।
उस संख्या का व्युत्क्रम लें, तो संभावना 7068.605131 में 1 है।
[/spoiler]यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
कैसीनो रोयाल फिल्म में, एक पोकर टूर्नामेंट के अंतिम हाथ में, चार खिलाड़ियों के पास निम्नलिखित हाथ होते हैं:
- लालिमा
- पूरा घर
- फुल हाउस (पहले वाले से भिन्न मूल्य का)
- स्ट्रेट फ्लश
इसकी संभावना क्या है?
मुझे इसके लिए एक सिमुलेशन चलाना पड़ा। मेरे सिमुलेशन में, मैं मानता हूँ कि कोई भी कभी भी झुकता नहीं है। लगभग 2.2 अरब चक्कर लगाने के बाद, ऐसा 312 बार हुआ। यानी लगभग सात लाख में से एक की संभावना।


