विज़ार्ड अनुशंसा करता है

$11000 स्वागत बोनस

खेल
समीक्षा पढ़ें
$3000 स्वागत बोनस

खेल
समीक्षा पढ़ें
$777 तक बोनस

खेल
समीक्षा पढ़ें

घर ›
जादूगर से पूछो ›
संभावना - सामान्य प्रश्न

संभावना - सामान्य प्रश्न

क्या आप यह कह रहे हैं कि अंततः आप हर कैसीनो गेम में हारेंगे, चाहे आप कुछ भी करें?

Joe से Harrisburg, US

ब्लैकजैक और वीडियो पोकर में दुर्लभ सकारात्मक उम्मीद के अवसरों को छोड़कर, हां, मैं यही कह रहा हूं।

मैं आपकी संभावनाओं को x से y प्रारूप में कैसे परिवर्तित कर सकता हूँ?

Ralph Harpster से Turlock, USA

किसी घटना के घटित होने की संभावना x से y होने का अर्थ है कि वह घटना हर y बार न घटने पर x बार घटित होगी। रूपांतरण के लिए, मान लीजिए p किसी घटना की प्रायिकता है। प्रायिकता को (1/p)-1 से 1 के रूप में भी व्यक्त किया जा सकता है। आइए एक उदाहरण देखें। पाँच पत्तों वाले स्टड में फुल हाउस निकलने की प्रायिकता 0.00144058 है। इसे 693.165 से 1 के रूप में भी दर्शाया जा सकता है।

मैं हाल ही में एक फुटबॉल पूल देख रहा था जो चल रहा था। यह उनमें से एक था जहाँ 100 बॉक्सों का एक ग्रिड था और 0-9 तक के अंक X और Y अक्षों पर चलते थे और स्कोर के अंतिम अंक के अनुरूप थे। मैं फुटबॉल का प्रशंसक नहीं हूँ और मैंने इस पूल पर दांव नहीं लगाया था, लेकिन मैं एक जुआरी हूँ और मुझे नहीं लगता कि यह कोई बहुत अच्छा दांव है।

मैं यह मानकर चल रहा हूँ कि आप उस पूल के प्रकार को जानते हैं जिसकी मैं बात कर रहा हूँ। प्रत्येक बॉक्स की कीमत $5 है और भुगतान प्रत्येक तिमाही में होता है। अगर आपका बॉक्स जीतता है, तो आप $125 जीतेंगे और अगर आखिरी संख्याएँ समान रहती हैं, तो सभी 4 तिमाहियाँ जीतना संभव है, यानी $500 जीतना, यानी 100 से 1 का भुगतान।

शर्त लगाने वाला व्यक्ति मुझे यह बताने की कोशिश कर रहा था कि 500 डॉलर जीतने की संभावना 100 से 1 है। मैं इससे सहमत नहीं हूँ। सबसे पहले, जिस बॉक्स में 0 + 7 है, उसके जीतने की संभावना 2 + 9 वाले बॉक्स से कहीं ज़्यादा है। हालाँकि, पूरे खेल में आखिरी 2 नंबर 0 + 7 रहने की संभावना ज़्यादा होनी चाहिए। अगर आपके लिए बॉक्स यादृच्छिक प्रक्रिया से चुने जाते हैं, तो क्या आप मुझे 500 डॉलर का इनाम जीतने की अनुमानित संभावना बता सकते हैं?

Sam से Phillipsburg, USA

यह मानते हुए कि ग्रिड में सेल यादृच्छिक रूप से चुने गए हैं, किसी एक तिमाही में जीतने की संभावना 1/100 होगी। यह मानते हुए कि प्रत्येक तिमाही एक स्वतंत्र घटना थी, जो कि नहीं है, सभी चार तिमाहियों में जीतने की संभावना (1/100) ⁴ = 100 मिलियन में 1 होगी।

मैं सचमुच जानना चाहता हूँ कि 12 से 1 या 3 से 2 जैसे ऑड्स को कैसे पढ़ा जाता है। इनमें से कौन जीतने की सबसे अच्छी संभावना दर्शाता है? 12 से 1 या 3 से 2?

Louis से Montreal, Canada

मुझे प्रायिकताओं का इस रूप में प्रयोग करना पसंद नहीं है, लेकिन आमतौर पर इनका प्रयोग इस प्रकार के वाक्यविन्यास में किया जाता है, "रॉयल फ्लश न मिलने की संभावना 649,739 से 1 है।" इसका मतलब है कि 649,739 ऐसे तरीके हैं जिनसे आप रॉयल फ्लश नहीं निकाल सकते और 1 तरीका है जिससे आप निकाल सकते हैं। आपके उदाहरणों में 12 से 1 की प्रायिकता 1/13, या 7.69% है, और 3 से 2 की प्रायिकता 2/5, या 40.00% है, इसलिए 3 से 2 जीतने की बेहतर संभावना है।

सेंट लुइस पोस्ट-डिस्पैच के एक लेख में, रिपोर्टर कहता है, "500 साल में आने वाली बाढ़ किसी भी साल में आने की 500 में से 1 संभावना होती है। दूसरे शब्दों में, 50 सालों में आने की 10 में से 1 संभावना होगी, या एक सदी में आने की 5 में से 1 संभावना होगी।" आपके जुए वाले सारे पन्ने पढ़ने के बाद, मुझे लगता है कि यह कहने का सही तरीका नहीं है, है ना? उनके दावे का विस्तार से मतलब होगा कि हर 500 साल में बाढ़ आने की 1 में से 1 संभावना होती है, और यह बात सच नहीं हो सकती।

गुमनाम

आप सही हैं, वह लेख गलत है। x वर्षों की अवधि में 500 वर्षों की बाढ़ की संभावना 1-e ^-x/500 है। इसलिए 50 वर्षों में कम से कम एक 500-वर्षीय बाढ़ की संभावना 9.52% और 100 वर्षों में 18.13% है।

अगर मैं किसी खेल की फ़ेयर लाइन -160/+160 निर्धारित करता हूँ और मुझे -145 की रॉग लाइन मिलती है, तो मेरा EV क्या होगा? आप कोई भी फ़ॉर्मूला बताएँ जिससे मैं फ़ेयर लाइन निर्धारित होने के बाद अपना EV +/- निकाल सकूँ, तो मैं बहुत आभारी रहूँगा।

गुमनाम

मान लीजिए p पसंदीदा के जीतने की प्रायिकता है। यदि -160 एक निष्पक्ष रेखा है, तो:

100*पी - 160*(1-पी) = 0
260पी = 160
पी = 160/260 = 8/13 = 61.54%.

तो -145 लाइन पर $145 के दांव पर अपेक्षित रिटर्न (8/13)*100 + (5/13)*-145 = 75/13 = $5.77 होगा। तो खिलाड़ी का लाभ $5.77/$145 = 3.98% होगा।

आइए t को बिना किसी हाउस एज वाली सच्ची मनी लाइन और a को वास्तविक मनी लाइन के रूप में परिभाषित करें। खिलाड़ी के अपेक्षित रिटर्न के सूत्र निम्नलिखित हैं:

A ऋणात्मक है, t ऋणात्मक है: (100*(ta) / (a*(100-t))
A धनात्मक है, t धनात्मक है: (at)/(100+t)
A धनात्मक है, t ऋणात्मक है: (a*t + 10000)/((t-100)*100)

तो आपके मामले में आपका अपेक्षित रिटर्न 100*(-160 -(-145))/(-145*(100-(-160))) = 3.98% है।

नीचे दिए गए इस दावे के बारे में आप क्या सोचते हैं कि ईश्वर एक डेमोक्रेट है, जैसा कि इस तथ्य से प्रमाणित होता है कि 2000 में गोर के लिए मतदान करने वाले सभी काउंटी हाल ही में फ्लोरिडा में आए तीन तूफानों से बच गए थे?

गुमनाम

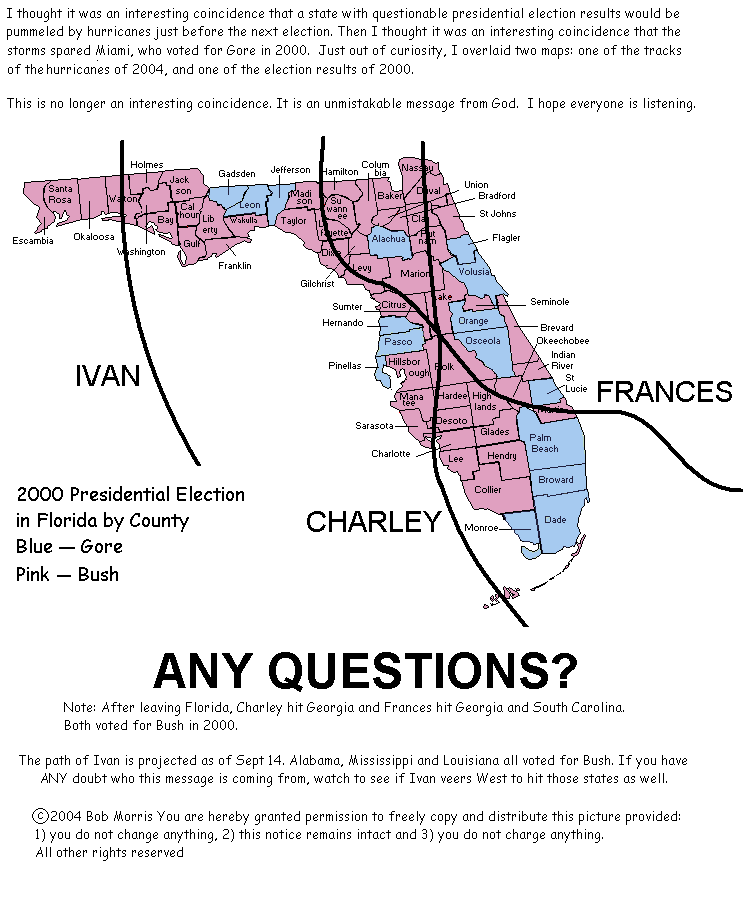
सबसे पहले, मैं इसे इसलिए प्रकाशित कर रहा हूँ क्योंकि लेखक ने नीचे इसकी अनुमति दी है। यह एक अच्छा उदाहरण है कि सहसंबंध का मतलब ज़रूरी नहीं कि कार्य-कारण हो। समय में पीछे मुड़कर देखना और ढेर सारे संयोग ढूँढ़ना आसान है। किसी भी बात को पुष्ट करने के लिए, कोई भी प्रमाण इकट्ठा करने से पहले एक परिकल्पना प्रस्तुत की जानी चाहिए।

अनुवर्ती (13 नवंबर, 2004): एक अन्य पाठक ने बताया कि यह नक्शा शुरू में एक मज़ाक के तौर पर लिखा गया था, लेकिन बाद में एक शहरी किंवदंती बन गया। जैसा कि इस लिंक से पता चलता है, ग्राफ़िक में तूफ़ान के रास्ते बिल्कुल सटीक नहीं थे और असल तूफ़ान गोर के कई ज़िलों में आए थे। इससे यह पता चलता है कि आपको हर उस बात पर विश्वास नहीं करना चाहिए जो आप पढ़ते हैं, खासकर इंटरनेट पर।

बस सोचा कि शायद आपको यह दिलचस्प लगे। बोडोग पर वे यह शर्त लगाते हैं, "ब्रिटनी स्पीयर्स और केविन फेडरलाइन का दूसरा बच्चा लड़का होगा या लड़की?" लड़के की संभावना +105 है, और लड़की की -145। पिछली बार जब मैंने देखा था, तो मानवजाति की शुरुआत से ही यह अनुपात 1:1 रहा है। मैं जानना चाहता हूँ कि इस बार -145 वाला पक्ष कौन ले रहा है। साइट पसंद है, अक्सर आते रहें, और अपने प्रायोजकों की सराहना में क्लिक करें।

गुमनाम

आपके दयालु शब्दों के लिए धन्यवाद। सच कहूँ तो अब क्लिक-थ्रू दरों की कोई ज़्यादा परवाह नहीं करता। इसलिए अगर यह सिर्फ़ दिखावे के लिए हो, तो बैनर पर क्लिक करने के लिए बाध्य न महसूस करें। आपके प्रश्न का उत्तर देने के लिए, संयुक्त राज्य अमेरिका में संभावनाएँ लगभग 50.5% लड़का और 49.5% लड़की होने के आसपास हैं। यह मानते हुए कि सट्टेबाज़ समुदाय को और कोई जानकारी नहीं है, लड़के पर दांव लगाने वाले खिलाड़ी का लाभ .505*1.05 - .495 = 3.53% होगा। हो सकता है कि कोई अंदरूनी जानकारी रखने वाला व्यक्ति लड़की पर दांव लगा रहा हो। एक और सिद्धांत यह है कि कुछ लोग ग़लतफ़हमी में माँ के पेट के आकार से लिंग का पता लगा सकते हैं, और ये लोग लड़की पर दांव लगा रहे हैं। व्यक्तिगत रूप से, मैं इस पर विचार नहीं करूँगा।

इस यूट्यूब वीडियो में, मैट डेमन कहते हैं कि जॉन मैक्केन के अपने पहले कार्यकाल में बच न पाने की संभावना तीन में से एक है। क्या वह सही हैं?

Lisa से San Antonio, TX

नहीं। सीडीसी (रोग नियंत्रण केंद्र) की इस बीमांकिक तालिका के अनुसार, एक 72 वर्षीय श्वेत पुरुष के 76 वर्ष की आयु तक जीवित रहने की संभावना 85.63% है। यानी मृत्यु की संभावना लगभग 7 में से 1 है। उत्तरजीविता दर का पता लगाने के लिए, पृष्ठ 14 पर दी गई श्वेत पुरुषों की तालिका से 76 वर्ष की आयु में जन्म लेने वाले समूह (57,985) को 72 वर्ष की आयु में जन्म लेने वाले समूह (67,719) से भाग दिया जा सकता है। इस तालिका को "अवधि जीवन तालिका" कहा जाता है, जो यह मानती है कि 2003 की मृत्यु दर भविष्य में नहीं बदलेगी, और यह सबसे अधिक इस्तेमाल की जाने वाली बीमांकिक तालिका है। एक पूर्णतावादी शायद 1936 की जीवन तालिका का उपयोग करना चाहे, लेकिन मुझे नहीं लगता कि इससे कोई खास फर्क पड़ेगा।

ps इस उत्तर को पोस्ट करने के बाद मुझे कई टिप्पणियाँ मिलीं कि मेरे जवाब में जॉन मैक्केन की व्यक्तिगत स्वास्थ्य स्थिति पर विचार नहीं किया गया। उनके ख़िलाफ़ काम करना कैंसर से बचे रहना है। उनके पक्ष में काम करना पैसे से खरीदी जा सकने वाली सर्वोत्तम चिकित्सा सेवा तक उनकी पहुँच है, एक 72 वर्षीय व्यक्ति के लिए वे स्पष्ट रूप से मानसिक और शारीरिक रूप से अभी भी अच्छी स्थिति में हैं, और उनकी दीर्घायु भी, जैसा कि इस तथ्य से प्रमाणित होता है कि उनकी माँ अभी भी जीवित हैं। हालाँकि, मेरा इस जानकारी को ध्यान में रखने का कभी इरादा नहीं था। मैट डेमन ने बीमांकिक तालिकाओं का हवाला दिया था, जिसका मैं ज़िक्र कर रहा था। मैं बस इतना कह रहा हूँ कि एक औसत 72 वर्षीय श्वेत पुरुष के लिए, चार और साल जीवित रहने की संभावना 86% है। अगर मजबूर किया जाए, तो मैं अनुमान लगाऊँगा कि जॉन मैक्केन की संभावना इससे भी बेहतर है।

बराबर मात्रा में कागज़ होने पर, कौन सा कागज़ का कप ज़्यादा पानी रखेगा, बेलनाकार या शंकु आकार का? मान लीजिए कि बेलनाकार एक सिरे से खुला है और दोनों ही स्थितियों में इसके आयाम इष्टतम हैं।

गुमनाम

कृपया उत्तर और समाधान के लिए मेरी सहयोगी साइट MathProblems.info , समस्या संख्या 210 देखें।

क्या आपने न्यू जर्सी के पॉपकॉर्न पार्क चिड़ियाघर की ऊँट प्रिंसेस की कहानी सुनी है, जिसका NFL में हैंडीकैपिंग के मामले में 88-51 का रिकॉर्ड है? इसकी संभावना कितनी है?

गुमनाम

पुश को छोड़कर, 139 पिक्स में से कम से कम 88 जीत मिलने की संभावना 0.00107355 है, यानी 931 में से 1। यह काफी निराशाजनक है। मुझे यकीन है कि 930 और जानवर होंगे जिन्होंने इससे भी बुरा प्रदर्शन किया होगा, जिनके बारे में कोई नहीं लिखता। प्रिंसेस के बारे में अधिक जानकारी के लिए, ESPN.com पर "न्यू जर्सी के ऊँट ने पैट्रियट्स पर जायंट्स की जीत की भविष्यवाणी" लेख पढ़ें।

8 मई, 2012 को चेल्सी लेटली शो में, चेल्सी ने कहा कि रेडहेड्स इसलिए खत्म हो रहे हैं क्योंकि वे एक-दूसरे के साथ संभोग नहीं करते। क्या यह सच है?

गुमनाम

मुझे आशा है कि आप खुश होंगे; मैंने इस पर घंटों काम किया है।

इस प्रश्न का उत्तर देने के लिए, चेल्सी हैंडलर रेड हेड परिकल्पना के अंतर्गत व्यवहार का परिमाणन करना महत्वपूर्ण है। यहाँ मेरी धारणाएँ हैं।

एक लाल सिर वाला कभी भी दूसरे लाल सिर वाले के साथ संभोग नहीं करेगा।
मादा हमेशा संभोग के लिए नर को ही चुनेगी।
सभी लोग संभोग करेंगे और प्रत्येक संभोग से समान संख्या में बच्चे पैदा होंगे।
लाल बालों वाली महिलाओं को गैर-लाल बालों वाली महिलाओं में से यादृच्छिक रूप से साथी चुनने का पहला अधिकार मिलेगा।
मादा वाहक (एक लाल बालों वाले जीन के साथ) लाल बालों वाले पुरुषों द्वारा छोड़े गए पुरुषों में से यादृच्छिक रूप से एक साथी का चयन करेगी।
नकारात्मक मादाएं (जिनमें लाल बालों वाला जीन नहीं है) लाल बालों वाले और वाहकों द्वारा छोड़े गए पुरुषों में से यादृच्छिक रूप से चयन करेंगी।

मैं टुडे आई फाउंड इट के अनुसार, लाल बालों वाली महिलाओं की संभावना 4% से शुरू करता हूँ। फिर मैं यह मान लेता हूँ कि अब से पहले लाल बालों वालों के प्रति कोई पूर्वाग्रह नहीं था।

यह मानते हुए कि लाल बालों वाले लोगों के प्रति पूर्वाग्रह अगली पीढ़ी से शुरू होकर जारी रहेगा, तो कुल आबादी में लाल बाल रखने का रुझान क्या होगा? एक स्प्रेडशीट में काफ़ी काम करने के बाद, जिसके बारे में मैं विस्तार से नहीं बताऊँगा, यहाँ इस पीढ़ी से शुरू करते हुए पहली आठ पीढ़ियाँ दी गई हैं।

लाल बालों का अनुपात

पीढ़ी	अनुपात
1	4.000000%
2	3.888889%
3	3.895219%
4	3.894863%
5	3.894883%
6	3.894882%
7	3.894882%
8	3.894882%

हम देख रहे हैं कि तीसरी पीढ़ी तक लाल बालों वाली आबादी का अनुपात 3.90% हो जाएगा। इसलिए, चेल्सी चाहे जो भी कहे, मुझे लगता है कि लाल बालों वालों को चिंता करने की कोई बात नहीं है।

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।

CardPlayer.com के अनुसार, अमीर लेहावोट, जो 2013 में वर्ल्ड सीरीज़ ऑफ़ पोकर की फ़ाइनल टेबल में जगह बनाने वाले नौ खिलाड़ियों में से एक हैं, नौवें स्थान के लिए न्यूनतम $733,224 से ऊपर की अपनी जीत की राशि को प्रत्येक 1% शेयर के लिए $29,248 की कीमत पर बेच रहे हैं। क्या यह उचित मूल्य है?

गुमनाम

सबसे पहले, आइए चिप स्टैक की समीक्षा करें।

2013 WSOP फाइनल टेबल चिप स्टैक

खिलाड़ी	चिप्स
जेसी ट्रान	38,000,000
अमीर लेहावोत	29,700,000
मार्क मैकलॉघलिन	26,525,000
जे फ़ार्बर	25,975,000
रयान रीस	25,875,000
सिल्वेन लूस्ली	19,600,000
मिशेल ब्रुमेलहुइस	11,275,000
मार्क न्यूहाउस	7,350,000
डेविड बेनेफील्ड	6,375,000

अगली तालिका टूर्नामेंट में प्रत्येक अंतिम परिणाम के लिए जीत को दर्शाती है।

2013 WSOP फाइनल टेबल पुरस्कार राशि

जगह	जीतना
1	$8,359,531
2	$5,173,170
3	$3,727,023
4	$2,791,983
5 वीं	$2,106,526
6	$1,600,792
7	$1,225,224
8	$944,593
9	$733,224

यह मानते हुए कि प्रत्येक खिलाड़ी समान कौशल का है, जीतने की संभावना का अनुमान कुल चिप स्टैक के हिस्से के रूप में लगाया जा सकता है। हालाँकि, इसके बाद प्रत्येक स्थिति के लिए यह अधिक जटिल हो जाता है। इस प्रश्न का उत्तर देने में मदद के लिए, मैंने अपना पोकर टूर्नामेंट कैलकुलेटर विकसित किया है।

ऊपर दी गई जानकारी डालने के बाद, आप देखेंगे कि आमिर की अपेक्षित जीत $3,658,046 है। फिर 9वें स्थान के लिए न्यूनतम पुरस्कार $733,224 घटाएँ और आपको अपेक्षित गैर-गारंटीकृत जीत $2,924,822 मिलेगी। प्रत्येक 1% शेयर का मूल्य $29,248.22 है। यह cardplayer.com लेख में बताई गई कीमत है।

वैसे, लेहावोट तीसरे स्थान पर रहे, उन्हें $3,727,023 की पुरस्कार राशि मिली। नौवें स्थान के लिए $733,224 की गारंटीकृत राशि को घटाकर और 100 से भाग देने पर, प्रत्येक 1% शेयर पर $29,938 का लाभ हुआ। प्रति शेयर मूल लागत $29,248 थी, इसलिए प्रत्येक शेयर पर 2.36% का लाभ होता।

इस प्रश्न पर विज़ार्ड ऑफ़ वेगास में मेरे मंच पर चर्चा की गई है।

कैसीनो प्रमोशन में, जहाँ अभी भी असली ड्रम (इलेक्ट्रॉनिक नहीं) में नियमित टिकट इस्तेमाल होते हैं, जहाँ आप प्लेयर्स डेस्क पर अपने टिकट प्रिंट करके ड्रम में डालते हैं - क्या आप ड्रम में डालने से पहले अपने टिकटों को मोड़ते/सींचते हैं? क्या आपको लगता है कि मुड़े हुए टिकटों के चुने जाने की संभावना ज़्यादा होती है?

AxiomOfChoice

मुझे उम्मीद है आप खुश होंगे। इस सवाल का जवाब देने के लिए, मैंने ऑफिस डिपो से टिकटों का एक बड़ा रोल खरीदा। फिर मैंने उनमें से 500 टिकटों को एक कागज़ के थैले में रखा, आधा मोड़कर, लगभग 90 डिग्री के कोण पर, और बाकी आधा खोलकर। फिर मैंने छह स्वयंसेवकों से कहा कि वे एक-एक करके 40 से 60 टिकट निकालें, और साथ में एक और टिकट भी, और मैं नतीजे दर्ज करता रहा। ये रहे नतीजे।

ड्राइंग टिकट प्रयोग

विषय	मुड़ा हुआ	सामने आया	कुल
1	25	25	50
2	38	22	60
3	25	15	40
4	34	16	50
5	27	23	50
6	26	24	50
कुल	175	125	300

इस प्रकार, निकाले गए टिकटों में से 58.3% टिकटें मोड़ दी गईं!

अगर यह मान लिया जाए कि तह करने का कोई असर नहीं हुआ, तो ये नतीजे उम्मीदों से 2.89 मानक विचलन दूर होंगे। यह मानते हुए कि तह करने से ऑड्स पर कोई असर नहीं पड़ा, इतने या उससे ज़्यादा तह किए हुए टिकट मिलने की संभावना 0.19% या 514 में से 1 है।

मैं यह भी कहना चाहूँगा कि जिन लोगों ने जल्दी-जल्दी टिकट निकाले, उनके मुड़े हुए टिकट निकालने की संभावना ज़्यादा थी। जिन लोगों ने हर बार सावधानी से समय निकाला, उनके टिकट लगभग 50/50 के बराबर थे।

इसलिए, मेरा निष्कर्ष निश्चित रूप से उन्हें मोड़ना है।

इस प्रश्न पर चर्चा के लिए कृपया मेरे फोरम विज़ार्ड ऑफ़ वेगास पर जाएँ।

दो खिलाड़ियों को (0,1) में से प्रत्येक को एक यादृच्छिक संख्या दी जाती है। पहला खिलाड़ी या तो स्थिर रहने का फैसला करता है या त्यागकर एक नई संख्या निकालता है। फिर दूसरा खिलाड़ी भी यही करता है। सबसे ज़्यादा संख्या जीतने वाला खिलाड़ी जीतता है। प्रत्येक खिलाड़ी के लिए इष्टतम रणनीति क्या है? इष्टतम रणनीति मानते हुए, प्रत्येक खिलाड़ी के जीतने की क्या संभावना है?

Joe Shipman से New Jersey

अच्छा सवाल! ये रहा मेरा जवाब और सरसरी तौर पर समाधान । मेरा समाधान PDF फॉर्मेट में भी देखें।

मान लीजिए आपको सिक्का उछालने का खेल खेलने का मौका दिया जाता है। अगर पहली बार चित आता है, तो आपको $2 वापस मिलते हैं और खेल खत्म हो जाता है। नहीं तो, आपको फिर से उछालना होगा। अगर दूसरी बार चित आता है, तो आपको $4 वापस मिलेंगे। अगर दूसरी बार भी पट आता है, तो आप तब तक उछालते रहेंगे जब तक चित न आ जाए। हर बार उछालने पर इनाम दोगुना हो जाता है। दूसरे शब्दों में, आपको 2^n वापस मिलते हैं, जहाँ n उछालों की संख्या है (चित आने पर आखिरी उछाल सहित)। इस खेल को खेलने के लिए आप कितना भुगतान करेंगे? मैंने सुना है कि गणितीय उत्तर अनंत धनराशि है, लेकिन यह समझ में नहीं आता, क्योंकि आपको किसी न किसी बिंदु पर एक निश्चित धनराशि जीतनी ही होगी।

Omaha

इसे सेंट पीटर्सबर्ग विरोधाभास के नाम से जाना जाता है।

यह सच है कि खेल में अपेक्षित जीत ∞ है, जबकि साथ ही संभावना यह भी है कि सिक्का अंततः पट पर गिरेगा, जिससे एक निश्चित धनराशि प्राप्त होगी। अपेक्षित जीत की गणना इस प्रकार है:

अपेक्षित जीत = pr(1 फ़्लिप)×2 + pr(2 फ़्लिप)×4 + pr(3 फ़्लिप)×8 + pr(4 फ़्लिप)×16 + pr(5 फ़्लिप)×32 + pr(6 फ़्लिप)×64 + ... =

(1/2) ¹ × 2 ¹ + (1/2) ² × 2 ² + (1/2) ³ × 2 ³ + (1/2) ⁴ × 2 ⁴ + (1/2) ⁵ × 2 ⁵ + (1/2) ⁶ × 2 ⁶ + ...

= ((1/2)*(2/1)) ¹ + ((1/2)*(2/1)) ² + ((1/2)*(2/1)) ³ + ((1/2)*(2/1)) ⁴ + ((1/2)*(2/1)) ⁵ + ((1/2)*(2/1)) ⁶ + ...

= 1 ¹ + 1 ² + 1 ³ + 1 ⁴ + 1 ⁵ + 1 ⁶ + ...

= 1 + 1 + 1 + 1 + 1 + 1 + ... = ∞

यहाँ विरोधाभास यह है कि खिलाड़ी को एक निश्चित राशि जीतनी होती है, लेकिन अपेक्षित जीत अनंत होती है। ऐसा कैसे हो सकता है?

यह शायद कोई बहुत संतोषजनक उत्तर न हो, लेकिन ∞ की बात करें तो इसमें कई विरोधाभास हैं। इस वजह से मुझे कुछ गुस्से भरे ईमेल मिल सकते हैं, लेकिन अनंत के इतने विरोधाभासों के बावजूद, जो बात मुझे रातों को सोने देती है, वह यह है कि मेरा मानना है कि ∞ एक गणितीय या दार्शनिक अवधारणा है जिसका वास्तविक भौतिक ब्रह्मांड में अस्तित्व सिद्ध नहीं हुआ है। अनंत की यह अवधारणा या सिद्धांत अपने साथ अंतर्निहित विरोधाभास लेकर चलता है।

जो लोग इससे असहमत हैं, कृपया मुझे ऐसी कोई भी चीज़ बताएँ जिसकी मात्रा या माप अनंत सिद्ध हो। कृपया यह न कहें कि ब्लैक होल का घनत्व अनंत होता है, जब तक कि आपके पास उसके आकार का प्रमाण न हो।

इस खेल को खेलने के लिए कितना भुगतान करना चाहिए, इस शुरुआती सवाल का जवाब देने के लिए, हमें यह ध्यान रखना चाहिए कि खुशी पैसे की मात्रा के अनुपात में नहीं होती। निजी तौर पर, मुझे अर्थशास्त्र की कक्षाओं में पढ़ाया गया था, और मेरा मानना है कि पैसे से मिलने वाली उपयोगिता, या खुशी, पैसे की मात्रा के लघुगणक के समानुपाती होती है। इस धारणा के तहत, यदि आप शून्य प्रारंभिक संपत्ति के अलावा, किन्हीं दो लोगों की संपत्ति में समान प्रतिशत की वृद्धि या कमी करते हैं, तो उन दोनों की खुशी में समान परिवर्तन होगा। उदाहरण के लिए, यदि जिम की संपत्ति अचानक $1,000 से बढ़कर $1,100 हो जाती है और जॉन की संपत्ति अचानक $10,000,000 से बढ़कर $11,000,000 हो जाती है, तो दोनों की खुशी में समान वृद्धि होगी, क्योंकि दोनों ही मामलों में उनकी संपत्ति में 10% की वृद्धि हुई है। यह मानते हुए कि पैसे से मिलने वाली खुशी वास्तव में राशि के लघुगणक के समानुपाती है, तो निम्न तालिका दर्शाती है कि खेलने के लिए भुगतान करने से पहले किसी व्यक्ति को अपनी संपत्ति के अनुसार अधिकतम कितना भुगतान करने को तैयार होना चाहिए।

उदासीनता खेलने की राशि

संपत्ति	उदासीनता मात्रा
$ 10	$ 4.97
$ 100	$ 7.79
$ 1,000	$ 10.96
$ 10,000	$ 14.26
$ 100,000	$ 17.78
$ 1,000,000	$ 20.88
$ 10,000,000	$ 24.19
$ 100,000,000	$ 27.51
$ 1,000,000,000	$ 30.84

जैसा कि आप देख सकते हैं, व्यावहारिक परिस्थितियों में, आपको जो राशि चुकानी चाहिए वह $∞ से बहुत कम है। उदाहरण के लिए, अगर आपकी संपत्ति एक मिलियन डॉलर है, तो आपको $20.88 की लागत पर खेलने में कोई आपत्ति नहीं होनी चाहिए।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास पर उठाया गया है और इस पर चर्चा की गई है।

मिशिगन लॉटरी में तीन खिलाड़ियों का खेल होता है जिसके नियम इस प्रकार हैं:

खिलाड़ी एक-एक करके खेलते हैं, जबकि अभी खेलने वाले खिलाड़ियों को मंच से बाहर रखा जाता है और उन्हें पिछले खिलाड़ियों के प्रदर्शन के बारे में कोई जानकारी नहीं दी जाती।

1 से 100 तक क्रमांकित 100 कार्ड होते हैं।

खिलाड़ी कोई भी कार्ड चुनकर शुरुआत करता है।

उसे देखने के बाद, खिलाड़ी उसे रख सकता है या नया कार्ड ले सकता है।

सभी कार्ड बदले में बाँटे जाते हैं। दूसरे शब्दों में, पुराने कार्डों को, फेंकने के बाद भी, डेक में वापस रख दिया जाता है।

जो खिलाड़ी सबसे बड़ा कार्ड खींचता है, वह जीत जाता है।

क्या इस खेल में आखिरी में खेलने का कोई स्थानिक लाभ है? प्रत्येक खिलाड़ी के लिए सर्वोत्तम रणनीति क्या है?

यहाँ एकYouTube वीडियो है जिसमें यह खेल दिखाया गया है।

Dween

सबसे पहले, आखिरी में खेलने का कोई स्थानिक लाभ नहीं होता। चूँकि पिछले खिलाड़ियों के खेलने के दौरान खिलाड़ियों को एक ध्वनिरोधी बूथ में रखा जाता है, इसलिए क्रम मायने नहीं रखता।

दूसरा, खेल में एक नैश संतुलन होना चाहिए जहाँ कम से कम x अंक के स्कोर के साथ खड़े होने की रणनीति किसी भी अन्य रणनीति से बेहतर होगी। सवाल x का पता लगाने का है।

मैंने खुद से पूछा कि अगर 1 से 100 तक के कार्ड के बजाय, हर खिलाड़ी को 0 और 1 के बीच समान रूप से वितरित एक यादृच्छिक संख्या मिले और वह उस बिंदु x की तलाश करे जहाँ एक आदर्श तर्कशास्त्री को खड़े होने और बदलने में कोई फ़र्क़ नहीं पड़ेगा, तो रणनीति क्या होगी। इस उत्तर के साथ, 1 से 100 तक के असतत वितरण पर उत्तर लागू करना आसान है।

मैं यहीं रुकता हूँ और अपने पाठकों को समस्या का आनंद लेने देता हूँ। उत्तर और समाधान के लिए नीचे दिए गए लिंक देखें।

0 से 1 तक सतत वितरण के लिए उत्तर दें ।

1 से 100 तक असतत वितरण के लिए उत्तर दें।

मेरे समाधान के लिए कृपया यहां क्लिक करें (पीडीएफ) ।

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।

मान लीजिए आपके पास दस लाल और दस काले पत्तों का एक डेक है। यादृच्छिक रूप से फेरबदल करने के बाद, आप बिना प्रतिस्थापन के पत्ते निकालते हैं। पाँच लाल पत्तों से पहले सभी दस काले पत्तों के निकलने की प्रायिकता क्या है?

Don

यह पूछने जैसा है कि 14 यादृच्छिक कार्डों में सभी 10 काले कार्ड होने की क्या प्रायिकता है। डेक में 10 में से 4 लाल कार्ड चुनने के लिए संयोजन (10,4) = 210 तरीके हैं। बेशक, सभी दस काले कार्ड चुनने का केवल एक ही तरीका है। 20 में से 14 कार्ड चुनने के लिए संयोजन (20,14) = 38,760 तरीके हैं। तो उत्तर है 210/38,760 = 0.005418, या 184.57 में 1।

मैं एक ऐसे प्रमोशन के बारे में जानता हूँ जिसमें सभी 13 रैंक में एक जैसे चार कार्ड मिलने पर बोनस मिलता है। औसतन इसमें कितने हाथ लगेंगे?

AxelWolf

आइये आपके प्रश्न का उत्तर देने के लिए वीडियो पोकर के स्वर्ण मानक, 9-6 जैक या बेहतर पर नजर डालें।

पहला कदम मेरे कैलकुलेटर को संशोधित करना है ताकि उसमें सभी 13 प्रकार के चार के लिए एक लाइन आइटम शामिल हो। यहाँ वह संशोधित रिटर्न तालिका दी गई है:

संशोधित जैक या बेहतर रिटर्न तालिका

आयोजन	भुगतान करता है	युग्म	संभावना	वापस करना
रॉयल फ़्लश	800	493,512,264	0.000025	0.019807
स्ट्रेट फ्लश	50	2,178,883,296	0.000109	0.005465
चार ए	25	3,900,253,596	0.000196	0.004892
चार के	25	3,904,533,816	0.000196	0.004897
चार क्यू	25	3,898,370,196	0.000196	0.004889
चार जे	25	3,886,872,684	0.000195	0.004875
चार 10	25	3,471,687,732	0.000174	0.004354
चार 9	25	3,503,226,684	0.000176	0.004394
चार 8	25	3,504,128,652	0.000176	0.004395
चार 7	25	3,504,825,252	0.000176	0.004396
चार 6	25	3,504,861,888	0.000176	0.004396
चार 5	25	3,504,895,944	0.000176	0.004396
चार 4	25	3,504,032,676	0.000176	0.004395
चार 3	25	3,503,177,148	0.000176	0.004394
चार 2	25	3,502,301,496	0.000176	0.004393
पूरा घर	9	229,475,482,596	0.011512	0.103610
लालिमा	6	219,554,786,160	0.011015	0.066087
सीधा	4	223,837,565,784	0.011229	0.044917
तीन हास्य अभिनेता	3	1,484,003,070,324	0.074449	0.223346
दो जोड़ी	2	2,576,946,164,148	0.129279	0.258558
जैक या बेहतर	1	4,277,372,890,968	0.214585	0.214585
कुछ नहीं	0	10,872,274,993,896	0.545435	0.000000
कुल		19,933,230,517,200	1.000000	0.995439

एक ही प्रकार के चार फल प्राप्त होने की संभावना 0.002363 है।

अगला प्रश्न यह है कि सभी 13 प्रकार प्राप्त करने के लिए औसतन कितने चार एक प्रकार के लगेंगे? इस प्रश्न का उत्तर देने के लिए, मैंने अपना अपेक्षित परीक्षण कैलकुलेटर बनाया है। इसका उपयोग करने के लिए, पहले 13 कक्षों में प्रत्येक चार एक प्रकार के संयोजनों की संख्या दर्ज करें। कैलकुलेटर आपको बताएगा कि सभी 13 प्रकार प्राप्त करने के लिए अपेक्षित 41.532646 चार एक प्रकार के लगेंगे।

अतः, सभी 13 चार एक प्रकार के कार्ड प्राप्त करने के लिए खेले जाने वाले हाथों की अपेक्षित संख्या 41.341739/0.002363 = 17,580 है।

घास का एक मैदान ठीक से भोजन दे सकता है:

एक गाय और एक लामा 21 दिनों के लिए।
एक लामा और एक भेड़ 42 दिनों के लिए।
एक भेड़ और एक गाय 28 दिनों के लिए।
गाय उतनी ही घास खाती है जितनी लामा और भेड़ मिलकर खाते हैं।
घास एक स्थिर दर से बढ़ती है।

तीनों जानवरों को मिलकर घास के मैदान को पूरी तरह से खा जाने में कितना समय लगेगा?

MatiX

[स्पॉइलर] आइए:
c = गाय द्वारा घास खाने की दर
l = दर लामा घास खाता है
s = भेड़ द्वारा घास खाने की दर
g = घास बढ़ने की दर

एक निश्चित समयावधि के अंत में, खाई गई घास की मात्रा, शुरू में उगाई गई घास की मात्रा और उस समयावधि में उगाई गई घास की मात्रा के बराबर होनी चाहिए। तो...

(1) 21*(सी+एल) = 1 + 21 ग्राम
(2) 42*(l+s) = 1+42g
(3) 28*(एस+सी) = 1+28 ग्राम

जहाँ 1 घास के एक मैदान को दर्शाता है।

हमें यह भी दिया गया है:

(4) सी=एस+एल

सबसे पहले, समीकरण (4) को (2) में प्रतिस्थापित करें:

(5) 42c = 1 + 42g

इसे g के संदर्भ में व्यक्त करें:

(6) जी = (42सी-1)/42

इसके बाद, समीकरण (6) को (1) में प्रतिस्थापित करें...

(7) 21(सी+एल) = 1 + 21*(42सी-1)/42

थोड़ा सा बीजगणित के बाद हम पाते हैं...

(8) एल = 1/42.

इसके बाद, समीकरण (4) को (3) में प्रतिस्थापित करें...

(9) 28*(2s + l) = 1+28g

हम जानते हैं l=1/42, अतः...

28*(2s + 1/42) = 1+28 ग्राम
56s + 28/42 = 1 + 28g
2352s + 28 = 42 + 1176g
(10) जी = (2352s - 14)/1176

इसके बाद, समीकरण (8) और (10) को (2) में प्रतिस्थापित करें...

42*(1/42 + एस) = 1 + 42*(2352 एस - 14)/1176

कुछ आसान बीजगणित के बाद हम पाते हैं:

(11) एस = 14/1176 = 1/84

समीकरण (4) से

(12) सी = (1/84) + (1/42) = 3/84 = 1/28

इसलिए, यदि घास नहीं उगती, तो गाय को खेत को खाने में 28 दिन लगेंगे, लामा को 42 दिन, और भेड़ को 84 दिन।

अब, g का हल निकालते हैं। (11) को (10) में प्रतिस्थापित करें:

जी = [2352*(1/84)- 14]/1176
(13) जी = 14/1176 = 1/84.

संयोगवश यह वही दर है जिस दर पर भेड़ घास खाती है।

मान लीजिए t अंतिम उत्तर है। हम जानते हैं कि t दिनों में खाई गई घास की मात्रा खेत में मौजूद घास (1) की मात्रा और उस समय में उगाई गई घास के योग के बराबर होनी चाहिए। तो...

(13) टी*(एस+एल+सी) = 1 + टीजी

टी के लिए हल करना ...

टी*[(1/84) + (1/42) + (1/28)] = 1 + टी/84
टी = 1/[(1/84) + (1/42) + (1/28) - (1/84)]
(14) t = 84/5 = 16.8 दिन = 16 दिन, 19 घंटे, 12 मिनट

[/spoiler]

यह प्रश्न विज़ार्ड ऑफ वेगास के मेरे फोरम में उठाया गया और इस पर चर्चा की गई।

एक इकाई वर्ग में दो यादृच्छिक बिंदुओं के बीच औसत दूरी क्या है?

गुमनाम

इतने आसान सवाल का हल भी जटिल है। मैंने जिस तरह से किया, आपको इस समाकलन को जानना होगा।

यहाँ उत्तर और मेरा समाधान (पीडीएफ) है।

फिल्म गुड विल हंटिंग में चॉकबोर्ड पर गणित की समस्या क्या थी?

गुमनाम

यह वास्तव में काफी आसान था, खासकर एमआईटी में संयोजन गणित के पाठ्यक्रम के लिए। समस्या का शब्दांकन इस प्रकार है:

"आकार n=10 के सभी समरूपी अपरिवर्तनीय वृक्ष बनाएं।"

मैं इसे सरल एवं सादी अंग्रेजी में कहने का प्रयास कर रहा हूँ।

केवल सीधी रेखाओं का उपयोग करके, वे सभी आकृतियाँ बनाएँ जहाँ प्रतिच्छेदों और मृत सिरों का योग 10 के बराबर हो। आपके पास कोई बंद लूप नहीं होना चाहिए। आपके पास दो समतुल्य आकृतियाँ भी नहीं होनी चाहिए। किसी भी प्रतिच्छेदन से कम से कम तीन रास्ते निकलने चाहिए।

आप पूछेंगे, "समतुल्य" से मेरा क्या मतलब है? इसका मतलब है कि आप टुकड़ों को, उनके प्रतिच्छेदन को छोड़कर, अपनी इच्छानुसार किसी भी तरह हिला सकते हैं और इससे कोई नई आकृतियाँ नहीं बनेंगी।

यहाँ एक उदाहरण है: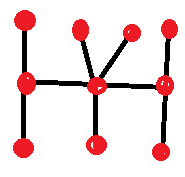

मैं तुम्हें एक इशारा देता हूँ। फिल्म में दिए गए जवाब के उलट, यहाँ दस हैं। विल को सिर्फ़ आठ मिले। देखो, क्या तुम विल हंटिंग की बराबरी कर सकते हो या उसे हरा सकते हो।

[बिगाड़ने वाला]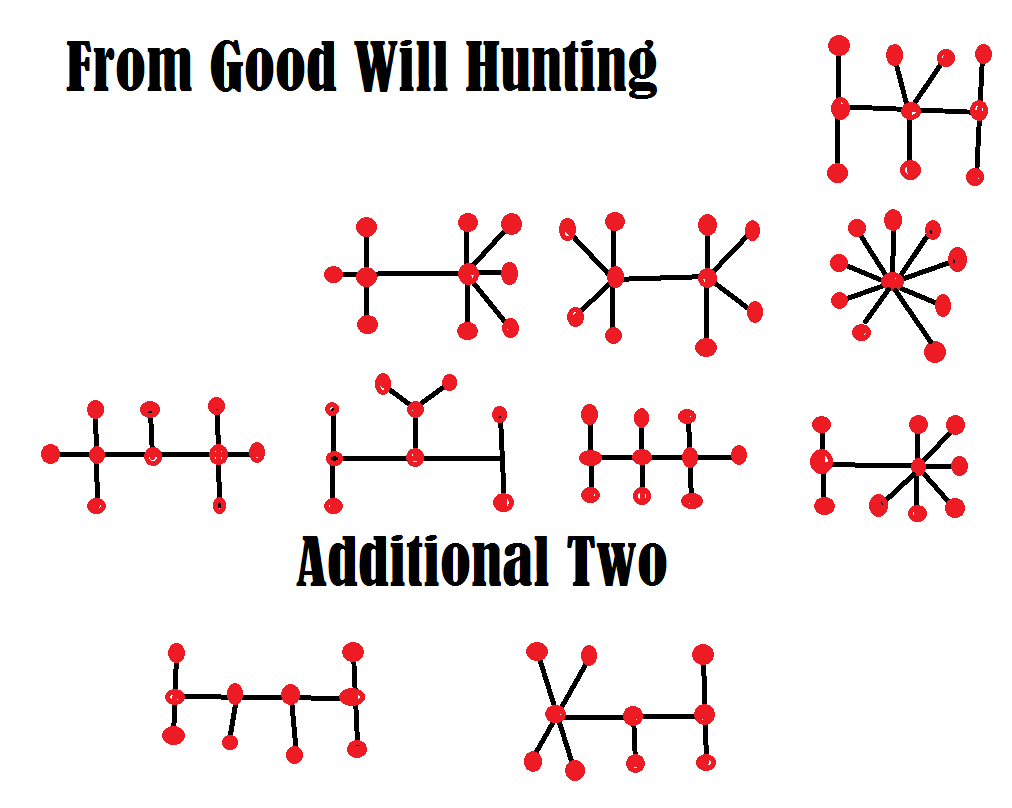

मैं अपनी MathProblems.info साइट पर समस्या 220 पर सभी दस प्रश्नों को हल करने के लिए अपना तर्क प्रस्तुत करता हूँ।

[/spoiler] आगे पढ़ें:

गुड विल हंटिंग में गणित II: छात्रों के परिप्रेक्ष्य से समस्याएं - समस्या पर अकादमिक पेपर।
गुड विल हंटिंग गणित समस्या - मेरे मंच पर इस समस्या के बारे में चर्चा।

निम्नलिखित नियमों वाले एक खेल पर विचार करें:

यादृच्छिक संख्या जनरेटर 0 और 1 के बीच समान रूप से वितरित यादृच्छिक संख्याएं प्रदान करता है।
दो खिलाड़ियों को एक अलग नंबर मिलता है। प्रत्येक खिलाड़ी केवल अपना ही नंबर देख सकता है।
खिलाड़ी 1 अपना प्रारंभिक नंबर रख सकता है या किसी नए यादृच्छिक नंबर से बदल सकता है।
खिलाड़ी 2, खिलाड़ी 1 की कार्रवाई को जानते हुए, अपना मूल नंबर रखने या नया नंबर लेने का विकल्प रखता है।
अधिक संख्या वाला खिलाड़ी जीतता है।

खेल के बारे में मेरे चार प्रश्न हैं:

खेल के बारे में निम्नलिखित प्रश्नों के उत्तर दें:
किस नंबर पर खिलाड़ी 1 खड़े होने और स्विच करने के प्रति उदासीन है?
यह मानते हुए कि खिलाड़ी 1 स्विच करता है, खिलाड़ी 2 को किस नंबर पर खड़े होकर स्विच करने में कोई आपत्ति नहीं होनी चाहिए?
मान लें कि खिलाड़ी 1 खड़ा है, तो खिलाड़ी 2 को किस नंबर पर खड़े होने और स्विच करने में कोई आपत्ति नहीं होनी चाहिए?
यह मानते हुए कि दोनों खिलाड़ियों द्वारा इष्टतम रणनीति अपनाई गई है, खिलाड़ी 1 के जीतने की क्या संभावना है?

गुमनाम

इसका उत्तर और समाधान मेरे गणित समस्याओं के पृष्ठ, समस्या 225 में पाया जा सकता है।

मैं 2018 के "डेड पूल" में भाग ले रहा हूँ। नियम ये हैं:

प्रत्येक खिलाड़ी को 100 वर्ष से कम आयु के दस जीवित हस्तियों की सूची प्रस्तुत करनी होगी।
यदि किसी सेलिब्रिटी की मृत्यु हो जाती है, जैसा कि एसोसिएटेड प्रेस द्वारा उल्लेख किया गया है, 2018 में, तो उस सेलिब्रिटी का नाम अपनी सूची में रखने वाले किसी भी व्यक्ति को 100-x अंक प्राप्त होंगे, जहां x मृत्यु की आयु है।
1/1/2019 को सबसे अधिक अंक वाला खिलाड़ी जीतता है।

औसत के आधार पर, इस खेल के लिए इष्टतम रणनीति क्या है?

गुमनाम

एक पूर्व एक्चुअरी होने के नाते, आपने बिल्कुल सही सवाल पूछा है। उम्मीद है कि एक्चुअरी सोसाइटी मेरे जवाब को पेशे का दुरुपयोग नहीं मानेगी। बहरहाल, आपके सवाल का जवाब देने के लिए मैंने अपने पूर्व कार्यस्थल, सामाजिक सुरक्षा प्रशासन के मुख्य एक्चुअरी कार्यालय, की 2014 की जीवन-अवधि तालिका देखी।

एक अवधि जीवन तालिका, अन्य बातों के अलावा, 2014 में किसी भी आयु और लिंग के व्यक्ति की मृत्यु की संभावना को दर्शाती है। उस जानकारी का उपयोग करके मैंने निम्नलिखित तालिका बनाई है, जो 0 से 100 तक की सभी आयु और दोनों लिंगों के लिए मृत्यु की संभावना और अपेक्षित अंक दोनों को दर्शाती है।

2014 अवधि जीवन तालिका मृत्यु पूल

आयु	की संभावना मृत्यु — पुरुष	की संभावना मृत्यु — महिला	अपेक्षित अंक — पुरुष	अपेक्षित अंक — महिला
0	0.006320	0.005310	0.632000	0.531000
1	0.000403	0.000352	0.039852	0.034835
2	0.000282	0.000221	0.027626	0.021683
3	0.000211	0.000161	0.020514	0.015612
4	0.000181	0.000131	0.017405	0.012556
5	0.000161	0.000111	0.015313	0.010515
6	0.000141	0.000111	0.013260	0.010405
7	0.000131	0.000101	0.012184	0.009360
8	0.000121	0.000091	0.011127	0.008334
9	0.000091	0.000081	0.008256	0.007328
10	0.000101	0.000091	0.009073	0.008154
11	0.000101	0.000081	0.008973	0.007168
12	0.000131	0.000101	0.011535	0.008861
13	0.000202	0.000131	0.017547	0.011389
14	0.000303	0.000151	0.026023	0.012992
15	0.000404	0.000191	0.034304	0.016267
16	0.000505	0.000232	0.042393	0.019464
17	0.000616	0.000272	0.051129	0.022582
18	0.000748	0.000302	0.061316	0.024796
19	0.000880	0.000343	0.071262	0.027768
20	0.001022	0.000373	0.081780	0.029855
21	0.001145	0.000404	0.090445	0.031884
22	0.001258	0.000444	0.098105	0.034643
23	0.001310	0.000475	0.100880	0.036546
24	0.001332	0.000495	0.101246	0.037625
25	0.001344	0.000526	0.100811	0.039422
26	0.001377	0.000556	0.101864	0.041162
27	0.001389	0.000577	0.101371	0.042106
28	0.001421	0.000608	0.102330	0.043740
29	0.001454	0.000648	0.103234	0.046036
30	0.001507	0.000669	0.105517	0.046837
31	0.001530	0.000710	0.105584	0.048998
32	0.001574	0.000751	0.107011	0.051084
33	0.001617	0.000813	0.108364	0.054454
34	0.001661	0.000864	0.109644	0.057041
35	0.001716	0.000926	0.111521	0.060194
36	0.001781	0.001008	0.113970	0.064538
37	0.001857	0.001081	0.116963	0.068090
38	0.001933	0.001164	0.119830	0.072145
39	0.002020	0.001237	0.123207	0.075427
40	0.002118	0.001340	0.127066	0.080422
41	0.002258	0.001445	0.133232	0.085232
42	0.002410	0.001560	0.139778	0.090455
43	0.002615	0.001696	0.149075	0.096649
44	0.002843	0.001853	0.159228	0.103761
45	0.003105	0.002011	0.170771	0.110606
46	0.003401	0.002191	0.183635	0.118300
47	0.003742	0.002403	0.198314	0.127342
48	0.004108	0.002647	0.213613	0.137656
49	0.004532	0.002894	0.231133	0.147577
50	0.004994	0.003194	0.249696	0.159718
51	0.005473	0.003487	0.268191	0.170880
52	0.005993	0.003794	0.287656	0.182103
53	0.006565	0.004104	0.308561	0.192871
54	0.007159	0.004428	0.329324	0.203676
55	0.007799	0.004767	0.350946	0.214498
56	0.008475	0.005153	0.372902	0.226729
57	0.009179	0.005534	0.394696	0.237972
58	0.009856	0.005889	0.413944	0.247347
59	0.010575	0.006272	0.433558	0.257150
60	0.011350	0.006683	0.453991	0.267338
61	0.012209	0.007180	0.476135	0.280016
62	0.013061	0.007720	0.496330	0.293355
63	0.013921	0.008339	0.515084	0.308537
64	0.014814	0.009029	0.533320	0.325041
65	0.015831	0.009839	0.554094	0.344371
66	0.016981	0.010741	0.577354	0.365197
67	0.018300	0.011752	0.603909	0.387812
68	0.019778	0.012879	0.632894	0.412117
69	0.021443	0.014142	0.664734	0.438397
70	0.023384	0.015613	0.701513	0.468376
71	0.025547	0.017271	0.740873	0.500852
72	0.027877	0.019047	0.780560	0.533320
73	0.030384	0.020918	0.820374	0.564797
74	0.033098	0.022938	0.860535	0.596385
75	0.036256	0.025299	0.906400	0.632465
76	0.039868	0.028043	0.956841	0.673035
77	0.043883	0.031127	1.009299	0.715914
78	0.048257	0.034590	1.061657	0.760984
79	0.053128	0.038456	1.115692	0.807583
80	0.058709	0.043007	1.174177	0.860145
81	0.065070	0.048186	1.236322	0.915536
82	0.072149	0.053762	1.298691	0.967712
83	0.079906	0.059769	1.358409	1.016065
84	0.088524	0.066380	1.416378	1.062085
85	0.098157	0.073823	1.472348	1.107351
86	0.108904	0.082381	1.524651	1.153334
87	0.120889	0.092180	1.571556	1.198344
88	0.134134	0.103305	1.609607	1.239664
89	0.148707	0.115744	1.635778	1.273180
90	0.164522	0.129477	1.645220	1.294772
91	0.181584	0.144435	1.634254	1.299911
92	0.199903	0.160621	1.599225	1.284970
93	0.219362	0.177816	1.535534	1.244713
94	0.239881	0.196194	1.439286	1.177165
95	0.260293	0.214694	1.301463	1.073469
96	0.280129	0.233056	1.120515	0.932225
97	0.299042	0.251152	0.897125	0.753456
98	0.316317	0.268235	0.632634	0.536471
99	0.332667	0.284442	0.332667	0.284442
100	0.348651	0.301417	0.000000	0.000000

तालिका से पता चलता है कि 90 वर्षीय व्यक्ति के लिए अधिकतम अपेक्षित अंक 1.645220 है।

यह प्रश्न मेरे गैर-जुआ मंच, डाइवर्सिटी टुमॉरो में उठाया गया है और इस पर चर्चा की गई है।

यदि आप एक कैन में 355 मिलीलीटर रखना चाहते हैं, तो सतह क्षेत्र को न्यूनतम करने के लिए आयाम क्या होने चाहिए?

गुमनाम

अच्छा सवाल! मैं बस यही सोच रहा था जब मैंने एक गेमिंग शो में कुछ पतले सोडा कैन देखे, जिनमें मानक आकार के अनुसार 355 मिलीलीटर की मात्रा थी। दोनों ही बातें सही नहीं हो सकतीं (और मुझे शर्ली मत कहिएगा)। [स्पॉइलर] आइए:
r = कैन की त्रिज्या
h = कैन की ऊँचाई
v = कैन का आयतन
s= कैन का सतही क्षेत्रफल

हम सरल ज्यामिति से जानते हैं कि सतह क्षेत्र = 2*pi*r^2 + 2*pi*r*h.

इसी प्रकार, हम यह भी जानते हैं कि आयतन pi*r^2*h है, जो हमें 355 के बराबर दिया गया है।

तो, 355=pi*r^2*h.

आइये इसे पुनः व्यवस्थित करें:

(1) h = 355/(pi*r^2)

हम जानते हैं:

(2) एस = 2*pi*r^2 + 2*pi*r*h.

आइए समीकरण (1) में h के लिए हमारे व्यंजक को (2) में प्रतिस्थापित करके इसे केवल एक चर के फ़ंक्शन पर ले जाएं:

s = 2*pi*r^2 + + 2*pi*r*(355/(pi*r^2))) = 2*pi*r^2 + 710/r.

आइए, s का व्युत्पन्न लें और इसे शून्य के बराबर रखें, ताकि इष्टतम r का हल निकाला जा सके।

डीएस/डीआर = 4*पीआई*आर - 710/(आर^2 ) = 0

4*π*r = 710/(r^2)

दोनों पक्षों को r^2 से गुणा करने पर:

4*π*r^3 = 710

आर^3 = 177.5/π.

आर = (177.5/पीआई)^(1/3) = 3.837215248।

उस मान को समीकरण (1) में डालें और h = 7.674430496 प्राप्त करें।[/spoiler]

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।

मुझे लगता है कि मेरे जानने वाले ज़्यादातर जुआ विशेषज्ञ किसी खेल की अस्थिरता को मानक विचलन के बजाय विचरण के रूप में जानना पसंद करते हैं। बेशक, पहला विचलन दूसरे विचलन का वर्ग मात्र है। हालाँकि, मैं मानक विचलन को प्राथमिकता देता हूँ क्योंकि यह दांव और जीत/हार के समान इकाइयों में होता है। शायद वे बड़ी अस्थिरता को उजागर करने के लिए एक बड़ी संख्या पसंद करते हैं? आपका क्या विचार है - क्या जुआरी "विचरण" का उपयोग करना पसंद करते हैं और यदि हाँ, तो क्यों?

Gary J. Koehler

मैं मानता हूँ कि आप किसी खेल के मानक विचलन से ज़्यादा उसके विचरण के बारे में सुनते हैं, जो मुझे हमेशा थोड़ा परेशान करता है। मुझे लगता है कि जुआरियों को खेल की अस्थिरता की परवाह इसलिए करनी चाहिए क्योंकि वे जीत या हार को खेल के एक सत्र की संभावना से जोड़ते हैं। उदाहरण के लिए, ब्लैकजैक के 200 हाथों के बाद 1% की बुरी हार क्या होगी? इसका उत्तर देने के लिए, आप ब्लैकजैक के मानक विचलन का उपयोग करेंगे, जो नियमों के आधार पर लगभग 1.15 होता है।

इस प्रश्न का विशिष्ट उत्तर है 1.15 × 200^0.5 × -2.32635 (जो गॉसियन वक्र पर 1% बिंदु है) = अपेक्षा से -37.83 इकाई कम। यह न भूलें कि हाउस एज के कारण आप कुछ नुकसान की उम्मीद कर सकते हैं। अगर हम हाउस एज 0.3% मानते हैं, तो 200 हाथों के बाद आप 0.003*200 = 0.6 हाथ खोने की उम्मीद कर सकते हैं। इसलिए 1% खराब नुकसान 0.6 + 37.83 = 38.43 हाथ होगा।

मैंने सुना है कि संयुक्त राज्य अमेरिका में आमतौर पर 50% बताई गई एक शादी के तलाक में खत्म होने की संभावना, उसी समयावधि में हुई शादियों की संख्या के मुकाबले तलाक की संख्या के आधार पर निकाली जाती है। क्या यह सच है? क्या आपको लगता है कि यह आँकड़ा निकालने का उचित तरीका है? मैं इस पर सवाल उठा रहा हूँ क्योंकि आप लंबे समय में हुई शादियों की तुलना में कम समय में हुए तलाक को देख रहे हैं।

Gialmere

यदि जनसंख्या और आयु वितरण स्थिर थे, और तलाक की संभावना वास्तव में 50% थी, तो हम बड़े नमूने के आकार को देखते हुए, किसी भी समयावधि में दो विवाहों के मुकाबले एक तलाक का अनुपात देखने की उम्मीद करेंगे।

हालाँकि, जनसंख्या स्थिर नहीं है। इस ग्राफ़ से ऐसा लगता है कि अमेरिका की जनसंख्या प्रति दशक 10.71% की दर से बढ़ रही है। यानी प्रति वर्ष 1.02%। इसे सरल रखने के लिए हम इसे केवल 1% ही मानेंगे।

मानचित्र स्रोत: अमेरिकी जनगणना

फादरली डॉट कॉम के अनुसार, असफल विवाह की औसत अवधि 8 वर्ष होती है।

यदि आप वर्तमान में विवाहों की तुलना में तलाक का अनुपात 1:2 पर देख रहे हों, तो किसी भी विवाह के तलाक में समाप्त होने की औसत संभावना क्या होगी?

अभी हम जो तलाक देख रहे हैं, वे 8 साल पहले हुई शादियों से हैं, जब जनसंख्या आज की तुलना में 92.35% थी। सरल गणित बताता है कि तलाक की वास्तविक संभावना 54.14% है।

आइये इसकी जांच करें।

सबसे पहले, सीडीसी के अनुसार, प्रति वर्ष प्रति 1000 जनसंख्या पर 6.9 विवाह होते हैं। यह आँकड़ा इस प्रश्न से संबंधित नहीं है, लेकिन मुझे लगता है कि इससे संबंधित संख्याओं को समझने में मदद मिलती है।

मान लीजिए 8 साल पहले जनसंख्या 300,000,000 थी। तो उस साल 0.69% * 300 मिलियन = 2,070,000 शादियाँ हुईं।

यदि आठ वर्ष बाद उनमें से 54.14% तलाक में परिणत होते हैं, तो वर्तमान में हम 2,070,000 * 54.14% = 1,120,698 तलाक देख रहे होंगे।

1,120,698 / 2,070,000 = वर्तमान में विवाह की तुलना में तलाक का 50% अनुपात देखा गया।

कहीं कोई यह न कह दे, हाँ, मुझे पता है कि सभी तलाक ठीक आठ साल में खत्म नहीं होते। फिर भी, सभी बातों को ध्यान में रखते हुए, मैं कहता हूँ कि अंतिम परिणाम मेरे 54.14% वास्तविक तलाक दर से ज़्यादा दूर नहीं होगा।

आपके 100 कर्मचारियों का कार्यालय एक सीक्रेट सांता उपहार विनिमय करता है। इसमें आप कागज़ के अलग-अलग टुकड़ों पर सबके नाम लिखते हैं, उन्हें एक टोपी में डालते हैं, और हर कोई उपहार देने के लिए यादृच्छिक रूप से एक नाम चुनता है।

सवाल यह है कि औसतन कितने बंद लूप होंगे? उदाहरण के लिए, बंद लूप में गॉर्डन डॉन को देता है, जो जॉन को देता है, जो नाथन को देता है, जो गॉर्डन को देता है। या फिर अपना नाम खुद बनाना।

गुमनाम

मान लीजिए कि हर कोई एक-एक करके एक ही चीज़ चुनता है। जैसे-जैसे हर व्यक्ति चुनता जाएगा, दो तरह की स्थितियाँ पैदा होंगी:

चुनने वाले का नाम पहले ही चुन लिया गया है।
चुनने वाले का नाम अभी भी नामों की टोकरी में है।

किसी भी चयनकर्ता के लिए, मान लीजिए कि चुनने के लिए n लोग बचे हैं।

अगर चुनने वाले का नाम पहले ही चुन लिया गया है, तो 1/n संभावना है कि चुनने वाला अपने नाम से जुड़े लूप को बंद कर देगा। उदाहरण के लिए, मान लीजिए एमी चुन रही है। एमी का नाम पहले से ही बॉब के पास है, बॉब का नाम पहले से ही चार्ली के पास है, और चार्ली का नाम अभी भी बिन में है। बिन में अभी भी n नाम होने पर, एमी द्वारा चार्ली का नाम चुनने की 1/n संभावना है, जिससे लूप बंद हो जाता है।

यदि चुनने वाले का नाम पहले से नहीं चुना गया है, तो 1/n संभावना है कि एमी अपना नाम चुन ले, जिससे लूप बंद हो जाएगा।

किसी भी तरह, अगर पिकर लूप बंद नहीं करता, तो वह एक और चेन का हिस्सा जोड़ रहा होता है, जिसे अंततः कोई और बंद कर देगा। हर चेन को सिर्फ़ एक बार ही गिना जाना चाहिए, जब वह बंद हो जाए।

इस प्रकार उत्तर है 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518.

खिलाड़ियों की किसी भी पर्याप्त बड़ी संख्या, n, के लिए अनुमान ln(n) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

विज़ार्ड से पूछें कॉलम #314 के सम्मान में, आपकी पसंदीदा अनंत श्रृंखलाएं कौन सी हैं जिनका योग पाई के किसी फलन के बराबर होता है?

Heather

इन दोनों को चुनना आसान है, क्योंकि संभवतः ये दो सबसे प्रसिद्ध हैं:

1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 + ... = π^2/6

मैंने सुना है कि 23 यादृच्छिक लोगों में से, दो या उससे ज़्यादा लोगों का कम से कम एक जन्मदिन एक जैसा होने की संभावना 50% से ज़्यादा होती है? क्या यह सच है? दूसरे समूह के लोगों के लिए एक ही जन्मदिन होने की संभावना क्या है? यही सवाल 3, 4 और 5 लोगों के लिए भी एक ही जन्मदिन होने की संभावना है।

गुमनाम

यह सच है, 23 यादृच्छिक लोगों के साथ, कम से कम एक जोड़ी लोगों का जन्मदिन एक ही दिन होने की संभावना 50.73% है। इसमें लीप डे को नज़रअंदाज़ कर दिया जाता है और यह मान लिया जाता है कि सभी के बाकी 365 दिनों में पैदा होने की संभावना बराबर है (जो कि वास्तव में सच नहीं है, बसंत और पतझड़ में जन्मदिन थोड़े ज़्यादा आम हैं)।

आपके प्रश्न के उत्तर में दी गई तालिकाएँ उद्धरण चिह्नों से लंबी हैं, इसलिए मैं उन्हें स्पॉइलर टैग में डाल दूँगा। उत्तरों के लिए बटन पर क्लिक करें।

2+ लोगों के लिए सामान्य जन्मदिन

समूह का आकार	संभावना
2	0.002740
3	0.008204
4	0.016356
5	0.027136
6	0.040462
7	0.056236
8	0.074335
9	0.094624
10	0.116948
11	0.141141
12	0.167025
13	0.194410
14	0.223103
15	0.252901
16	0.283604
17	0.315008
18	0.346911
19	0.379119
20	0.411438
21	0.443688
22	0.475695
23	0.507297
24	0.538344
25	0.568700
26	0.598241
27	0.626859
28	0.654461
29	0.680969
30	0.706316
31	0.730455
32	0.753348
33	0.774972
34	0.795317
35	0.814383
36	0.832182
37	0.848734
38	0.864068
39	0.878220
40	0.891232
41	0.903152
42	0.914030
43	0.923923
44	0.932885
45	0.940976
46	0.948253
47	0.954774
48	0.960598
49	0.965780
50	0.970374
51	0.974432
52	0.978005
53	0.981138
54	0.983877
55	0.986262
56	0.988332
57	0.990122
58	0.991665
59	0.992989
60	0.994123
61	0.995089
62	0.995910
63	0.996604
64	0.997190
65	0.997683
66	0.998096
67	0.998440
68	0.998726
69	0.998964
70	0.999160
71	0.999321
72	0.999453
73	0.999561
74	0.999649
75	0.999720
76	0.999777
77	0.999824
78	0.999861
79	0.999891
80	0.999914
81	0.999933
82	0.999948
83	0.999960
84	0.999969

3+ लोगों के लिए सामान्य जन्मदिन

समूह का आकार	संभावना
3	0.000008
4	0.000030
5	0.000075
6	0.000149
7	0.000261
8	0.000416
9	0.000623
10	0.000888
11	0.001218
12	0.001621
13	0.002102
14	0.002670
15	0.003329
16	0.004088
17	0.004953
18	0.005929
19	0.007024
20	0.008243
21	0.009592
22	0.011078
23	0.012705
24	0.014481
25	0.016409
26	0.018497
27	0.020747
28	0.023167
29	0.025760
30	0.028531
31	0.031484
32	0.034624
33	0.037954
34	0.041479
35	0.045202
36	0.049126
37	0.053254
38	0.057589
39	0.062133
40	0.066889
41	0.071859
42	0.077044
43	0.082446
44	0.088065
45	0.093903
46	0.099960
47	0.106236
48	0.112731
49	0.119444
50	0.126375
51	0.133522
52	0.140885
53	0.148460
54	0.156246
55	0.164241
56	0.172441
57	0.180844
58	0.189445
59	0.198242
60	0.207230
61	0.216405
62	0.225761
63	0.235294
64	0.244999
65	0.254869
66	0.264899
67	0.275082
68	0.285413
69	0.295883
70	0.306487
71	0.317217
72	0.328066
73	0.339026
74	0.350088
75	0.361246
76	0.372491
77	0.383814
78	0.395207
79	0.406662
80	0.418169
81	0.429720
82	0.441307
83	0.452920
84	0.464550
85	0.476188
86	0.487826
87	0.499455
88	0.511065
89	0.522648
90	0.534196
91	0.545698
92	0.557148
93	0.568537
94	0.579855
95	0.591096
96	0.602252
97	0.613314
98	0.624275
99	0.635127
100	0.645865
101	0.656480
102	0.666967
103	0.677318
104	0.687529
105	0.697593
106	0.707505
107	0.717260
108	0.726853
109	0.736279
110	0.745536
111	0.754619
112	0.763525
113	0.772251
114	0.780795
115	0.789155
116	0.797330
117	0.805319
118	0.813121
119	0.820580
120	0.827964
121	0.835152
122	0.842144
123	0.848940
124	0.855540
125	0.861945
126	0.868155
127	0.874172
128	0.879996
129	0.885631
130	0.891076
131	0.896335
132	0.901409
133	0.906302
134	0.911015
135	0.915552
136	0.919915
137	0.924108
138	0.928135
139	0.931997
140	0.935700
141	0.939246
142	0.942640
143	0.945885
144	0.948985
145	0.951944
146	0.954766
147	0.957456
148	0.960016
149	0.962452
150	0.964767
151	0.966965
152	0.969050
153	0.971028
154	0.972900
155	0.974672
156	0.976347
157	0.977930
158	0.979423
159	0.980831
160	0.982158
161	0.983407
162	0.984581
163	0.985684
164	0.986719
165	0.987690
166	0.988600
167	0.989452
168	0.990248
169	0.990992
170	0.991687
171	0.992335
172	0.992938
173	0.993500
174	0.994022
175	0.994508
176	0.994958
177	0.995376
178	0.995763
179	0.996121
180	0.996452
181	0.996758
182	0.997040
183	0.997300
184	0.997540
185	0.997760
186	0.997963
187	0.998149
188	0.998319
189	0.998476
190	0.998619
191	0.998750
192	0.998869
193	0.998979
194	0.999078
195	0.999169
196	0.999251
197	0.999326
198	0.999394
199	0.999456
200	0.999512
201	0.999562
202	0.999608
203	0.999650
204	0.999687
205	0.999720
206	0.999751
207	0.999778
208	0.999802
209	0.999824
210	0.999844
211	0.999862
212	0.999877
213	0.999891
214	0.999904
215	0.999915
216	0.999925
217	0.999934
218	0.999942
219	0.999949
220	0.999955
221	0.999961
222	0.999966
223	0.999970
224	0.999974
225	0.999977
226	0.999980
227	0.999982
228	0.999985
229	0.999987
230	0.999988
231	0.999990
232	0.999991
233	0.999992
234	0.999994
235	0.999994
236	0.999995
237	0.999996
238	0.999996
239	0.999997
240	0.999997
241	0.999998
242	0.999998
243	0.999998
244	0.999999

4+ लोगों के सामान्य जन्मदिन

समूह का आकार	संभावना
4	0.000000
5	0.000000
6	0.000000
7	0.000001
8	0.000001
9	0.000003
10	0.000004
11	0.000007
12	0.000010
13	0.000014
14	0.000020
15	0.000027
16	0.000036
17	0.000048
18	0.000061
19	0.000077
20	0.000096
21	0.000119
22	0.000145
23	0.000175
24	0.000209
25	0.000248
26	0.000293
27	0.000343
28	0.000399
29	0.000462
30	0.000532
31	0.000610
32	0.000695
33	0.000790
34	0.000893
35	0.001006
36	0.001129
37	0.001263
38	0.001408
39	0.001566
40	0.001736
41	0.001919
42	0.002116
43	0.002328
44	0.002555
45	0.002798
46	0.003058
47	0.003334
48	0.003629
49	0.003943
50	0.004276
51	0.004629
52	0.005003
53	0.005399
54	0.005817
55	0.006258
56	0.006724
57	0.007214
58	0.007730
59	0.008272
60	0.008841
61	0.009439
62	0.010065
63	0.010721
64	0.011408
65	0.012126
66	0.012876
67	0.013659
68	0.014476
69	0.015327
70	0.016215
71	0.017139
72	0.018100
73	0.019099
74	0.020137
75	0.021215
76	0.022334
77	0.023495
78	0.024698
79	0.025944
80	0.027235
81	0.028570
82	0.029951
83	0.031379
84	0.032855
85	0.034379
86	0.035952
87	0.037575
88	0.039249
89	0.040974
90	0.042752
91	0.044583
92	0.046467
93	0.048407
94	0.050402
95	0.052453
96	0.054561
97	0.056726
98	0.058950
99	0.061233
100	0.063576
101	0.065978
102	0.068442
103	0.070967
104	0.073554
105	0.076204
106	0.078917
107	0.081694
108	0.084535
109	0.087441
110	0.090412
111	0.093449
112	0.096552
113	0.099722
114	0.102958
115	0.106262
116	0.109633
117	0.113072
118	0.116579
119	0.120154
120	0.123798
121	0.127510
122	0.131292
123	0.135142
124	0.139061
125	0.143050
126	0.147107
127	0.151234
128	0.155429
129	0.159694
130	0.164027
131	0.168429
132	0.172899
133	0.177438
134	0.182044
135	0.186719
136	0.191460
137	0.196269
138	0.201144
139	0.206085
140	0.211091
141	0.216163
142	0.221299
143	0.226499
144	0.231763
145	0.237089
146	0.242476
147	0.247925
148	0.253434
149	0.259002
150	0.264629
151	0.270314
152	0.276055
153	0.281852
154	0.287703
155	0.293608
156	0.299566
157	0.305575
158	0.311634
159	0.317741
160	0.323897
161	0.330099
162	0.336346
163	0.342637
164	0.348970
165	0.355343
166	0.361757
167	0.368208
168	0.374696
169	0.381218
170	0.387774
171	0.394362
172	0.400980
173	0.407626
174	0.414299
175	0.420997
176	0.427718
177	0.434462
178	0.441224
179	0.448005
180	0.454803
181	0.461615
182	0.468439
183	0.475274
184	0.482118
185	0.488969
186	0.495826
187	0.502685
188	0.509546
189	0.516407
190	0.523265
191	0.530119
192	0.536967
193	0.543807
194	0.550636
195	0.557454
196	0.564258
197	0.571046
198	0.577817
199	0.584568
200	0.591298
201	0.598005
202	0.604687
203	0.611342
204	0.617969
205	0.624565
206	0.631129
207	0.637659
208	0.644154
209	0.650611
210	0.657030
211	0.663407
212	0.669743
213	0.676035
214	0.682281
215	0.688481
216	0.694632
217	0.700734
218	0.706784
219	0.712782
220	0.718726
221	0.724614
222	0.730446
223	0.736220
224	0.741936
225	0.747591
226	0.753185
227	0.758717
228	0.764185
229	0.769590
230	0.774929
231	0.780202
232	0.785409
233	0.790547
234	0.795618
235	0.800619
236	0.805551
237	0.810412
238	0.815202
239	0.819921
240	0.824569
241	0.829144
242	0.833646
243	0.838076
244	0.842432
245	0.846716
246	0.850925
247	0.855061
248	0.859123
249	0.863112
250	0.867027
251	0.870868
252	0.874635
253	0.878329
254	0.881950
255	0.885498
256	0.888973
257	0.892375
258	0.895705
259	0.898964
260	0.902151
261	0.905268
262	0.908314
263	0.911290
264	0.914197
265	0.917036
266	0.919806
267	0.922509
268	0.925145
269	0.927715
270	0.930220
271	0.932661
272	0.935037
273	0.937351
274	0.939603
275	0.941793
276	0.943923
277	0.945993
278	0.948005
279	0.949960
280	0.951857
281	0.953699
282	0.955486
283	0.957218
284	0.958898
285	0.960527
286	0.962104
287	0.963631
288	0.965109
289	0.966540
290	0.967923
291	0.969260
292	0.970553
293	0.971802
294	0.973007
295	0.974171
296	0.975294
297	0.976377
298	0.977421
299	0.978427
300	0.979397
301	0.980330
302	0.981228
303	0.982092
304	0.982923
305	0.983722
306	0.984490
307	0.985227
308	0.985935
309	0.986614
310	0.987266
311	0.987890
312	0.988489
313	0.989063
314	0.989612
315	0.990138
316	0.990641
317	0.991122
318	0.991581
319	0.992021
320	0.992440
321	0.992841
322	0.993223
323	0.993587
324	0.993935
325	0.994266
326	0.994581
327	0.994882
328	0.995167
329	0.995439
330	0.995698
331	0.995943
332	0.996176
333	0.996398
334	0.996608
335	0.996807
336	0.996996
337	0.997175
338	0.997344
339	0.997505
340	0.997657
341	0.997801
342	0.997936
343	0.998065
344	0.998186
345	0.998300
346	0.998408
347	0.998510
348	0.998606
349	0.998696
350	0.998781
351	0.998861
352	0.998937
353	0.999008
354	0.999074
355	0.999137
356	0.999195
357	0.999250
358	0.999302
359	0.999350
360	0.999396
361	0.999438
362	0.999478
363	0.999515
364	0.999550
365	0.999582
366	0.999613
367	0.999641
368	0.999668
369	0.999692
370	0.999715
371	0.999736
372	0.999756
373	0.999775
374	0.999792
375	0.999808
376	0.999823
377	0.999837
378	0.999850
379	0.999861
380	0.999872
381	0.999883
382	0.999892
383	0.999901
384	0.999909
385	0.999916
386	0.999923
387	0.999930
388	0.999935
389	0.999941
390	0.999946
391	0.999950
392	0.999955
393	0.999959
394	0.999962
395	0.999965
396	0.999969
397	0.999971
398	0.999974
399	0.999976
400	0.999978
401	0.999980
402	0.999982
403	0.999984
404	0.999985
405	0.999987
406	0.999988
407	0.999989
408	0.999990
409	0.999991
410	0.999992
411	0.999993
412	0.999993
413	0.999994
414	0.999995
415	0.999995
416	0.999996
417	0.999996
418	0.999996
419	0.999997
420	0.999997
421	0.999997
422	0.999998
423	0.999998
424	0.999998
425	0.999998
426	0.999998
427	0.999999
428	0.999999
429	0.999999

5+ लोगों के सामान्य जन्मदिन

समूह का आकार	संभावना
5	0.000000
6	0.000000
7	0.000000
8	0.000000
9	0.000000
10	0.000000
11	0.000000
12	0.000000
13	0.000000
14	0.000000
15	0.000000
16	0.000000
17	0.000000
18	0.000001
19	0.000001
20	0.000001
21	0.000001
22	0.000002
23	0.000002
24	0.000003
25	0.000004
26	0.000004
27	0.000005
28	0.000006
29	0.000008
30	0.000009
31	0.000011
32	0.000013
33	0.000015
34	0.000017
35	0.000020
36	0.000023
37	0.000026
38	0.000030
39	0.000034
40	0.000039
41	0.000044
42	0.000050
43	0.000056
44	0.000063
45	0.000070
46	0.000079
47	0.000087
48	0.000097
49	0.000108
50	0.000119
51	0.000132
52	0.000145
53	0.000159
54	0.000175
55	0.000192
56	0.000209
57	0.000229
58	0.000249
59	0.000271
60	0.000295
61	0.000320
62	0.000347
63	0.000375
64	0.000406
65	0.000438
66	0.000472
67	0.000509
68	0.000547
69	0.000588
70	0.000631
71	0.000676
72	0.000725
73	0.000775
74	0.000829
75	0.000885
76	0.000944
77	0.001007
78	0.001072
79	0.001141
80	0.001213
81	0.001289
82	0.001369
83	0.001452
84	0.001539
85	0.001630
86	0.001726
87	0.001825
88	0.001930
89	0.002038
90	0.002152
91	0.002270
92	0.002394
93	0.002522
94	0.002656
95	0.002796
96	0.002941
97	0.003092
98	0.003249
99	0.003412
100	0.003581
101	0.003757
102	0.003939
103	0.004128
104	0.004325
105	0.004528
106	0.004739
107	0.004957
108	0.005183
109	0.005417
110	0.005659
111	0.005909
112	0.006168
113	0.006436
114	0.006712
115	0.006998
116	0.007293
117	0.007597
118	0.007912
119	0.008236
120	0.008570
121	0.008915
122	0.009270
123	0.009636
124	0.010013
125	0.010402
126	0.010801
127	0.011213
128	0.011637
129	0.012072
130	0.012521
131	0.012981
132	0.013455
133	0.013942
134	0.014442
135	0.014956
136	0.015484
137	0.016026
138	0.016582
139	0.017153
140	0.017739
141	0.018340
142	0.018956
143	0.019588
144	0.020235
145	0.020899
146	0.021580
147	0.022277
148	0.022991
149	0.023722
150	0.024470
151	0.025237
152	0.026021
153	0.026824
154	0.027645
155	0.028485
156	0.029344
157	0.030222
158	0.031120
159	0.032037
160	0.032975
161	0.033934
162	0.034913
163	0.035912
164	0.036934
165	0.037976
166	0.039040
167	0.040127
168	0.041235
169	0.042367
170	0.043521
171	0.044698
172	0.045898
173	0.047122
174	0.048370
175	0.049642
176	0.050939
177	0.052260
178	0.053606
179	0.054977
180	0.056374
181	0.057796
182	0.059245
183	0.060719
184	0.062220
185	0.063748
186	0.065302
187	0.066884
188	0.068493
189	0.070130
190	0.071795
191	0.073487
192	0.075209
193	0.076958
194	0.078737
195	0.080544
196	0.082381
197	0.084247
198	0.086143
199	0.088068
200	0.090024
201	0.092009
202	0.094026
203	0.096072
204	0.098150
205	0.100259
206	0.102398
207	0.104569
208	0.106772
209	0.109006
210	0.111272
211	0.113570
212	0.115899
213	0.118262
214	0.120656
215	0.123083
216	0.125542
217	0.128035
218	0.130559
219	0.133117
220	0.135708
221	0.138332
222	0.140989
223	0.143679
224	0.146403
225	0.149160
226	0.151950
227	0.154774
228	0.157632
229	0.160522
230	0.163447
231	0.166405
232	0.169396
233	0.172421
234	0.175480
235	0.178572
236	0.181698
237	0.184857
238	0.188049
239	0.191275
240	0.194534
241	0.197827
242	0.201152
243	0.204511
244	0.207902
245	0.211327
246	0.214784
247	0.218274
248	0.221796
249	0.225351
250	0.228937
251	0.232556
252	0.236207
253	0.239889
254	0.243603
255	0.247348
256	0.251124
257	0.254931
258	0.258768
259	0.262636
260	0.266534
261	0.270462
262	0.274419
263	0.278406
264	0.282422
265	0.286466
266	0.290539
267	0.294639
268	0.298768
269	0.302924
270	0.307106
271	0.311316
272	0.315551
273	0.319813
274	0.324100
275	0.328412
276	0.332749
277	0.337110
278	0.341495
279	0.345903
280	0.350334
281	0.354788
282	0.359264
283	0.363761
284	0.368279
285	0.372818
286	0.377376
287	0.381955
288	0.386552
289	0.391167
290	0.395801
291	0.400452
292	0.405119
293	0.409803
294	0.414503
295	0.419217
296	0.423946
297	0.428689
298	0.433445
299	0.438214
300	0.442995
301	0.447787
302	0.452590
303	0.457403
304	0.462226
305	0.467057
306	0.471897
307	0.476744
308	0.481599
309	0.486459
310	0.491325
311	0.496196
312	0.501070
313	0.505949
314	0.510830
315	0.515713
316	0.520598
317	0.525483
318	0.530369
319	0.535253
320	0.540137
321	0.545018
322	0.549896
323	0.554771
324	0.559642
325	0.564507
326	0.569367
327	0.574221
328	0.579067
329	0.583906
330	0.588736
331	0.593557
332	0.598368
333	0.603169
334	0.607958
335	0.612735
336	0.617500
337	0.622251
338	0.626988
339	0.631710
340	0.636417
341	0.641107
342	0.645781
343	0.650437
344	0.655075
345	0.659695
346	0.664295
347	0.668875
348	0.673434
349	0.677972
350	0.682488
351	0.686981
352	0.691451
353	0.695897
354	0.700319
355	0.704716
356	0.709088
357	0.713433
358	0.717752
359	0.722043
360	0.726307
361	0.730543
362	0.734750
363	0.738927
364	0.743075
365	0.747193
366	0.751279
367	0.755335
368	0.759359
369	0.763351
370	0.767310
371	0.771237
372	0.775130
373	0.778990
374	0.782815
375	0.786606
376	0.790363
377	0.794084
378	0.797770
379	0.801420
380	0.805034
381	0.808611
382	0.812152
383	0.815656
384	0.819123
385	0.822553
386	0.825945
387	0.829300
388	0.832616
389	0.835895
390	0.839135
391	0.842336
392	0.845499
393	0.848624
394	0.851709
395	0.854756
396	0.857764
397	0.860733
398	0.863663
399	0.866553
400	0.869405
401	0.872217
402	0.874990
403	0.877724
404	0.880419
405	0.883075
406	0.885692
407	0.888269
408	0.890808
409	0.893309
410	0.895770
411	0.898193
412	0.900578
413	0.902924
414	0.905232
415	0.907502
416	0.909734
417	0.911929
418	0.914086
419	0.916205
420	0.918288
421	0.920334
422	0.922344
423	0.924317
424	0.926254
425	0.928155
426	0.930020
427	0.931851
428	0.933646
429	0.935406
430	0.937133
431	0.938825
432	0.940483
433	0.942108
434	0.943699
435	0.945258
436	0.946785
437	0.948279
438	0.949741
439	0.951173
440	0.952573
441	0.953942
442	0.955281
443	0.956590
444	0.957870
445	0.959120
446	0.960342
447	0.961535
448	0.962701
449	0.963838
450	0.964949
451	0.966032
452	0.967090
453	0.968121
454	0.969127
455	0.970107
456	0.971063
457	0.971994
458	0.972902
459	0.973785
460	0.974646
461	0.975484
462	0.976299
463	0.977093
464	0.977865
465	0.978616
466	0.979346
467	0.980056
468	0.980746
469	0.981416
470	0.982067
471	0.982699
472	0.983313
473	0.983909
474	0.984488
475	0.985049
476	0.985593
477	0.986121
478	0.986633
479	0.987128
480	0.987609
481	0.988074
482	0.988525
483	0.988962
484	0.989384
485	0.989793
486	0.990189
487	0.990571
488	0.990941
489	0.991299
490	0.991644
491	0.991978
492	0.992301
493	0.992612
494	0.992913
495	0.993203
496	0.993483
497	0.993753
498	0.994013
499	0.994264
500	0.994506
501	0.994740
502	0.994964
503	0.995180
504	0.995389
505	0.995589
506	0.995782
507	0.995967
508	0.996146
509	0.996317
510	0.996482
511	0.996640
512	0.996793
513	0.996939
514	0.997079
515	0.997213
516	0.997343
517	0.997466
518	0.997585
519	0.997699
520	0.997808
521	0.997913
522	0.998013
523	0.998109
524	0.998200
525	0.998288
526	0.998372
527	0.998452
528	0.998529
529	0.998602
530	0.998673
531	0.998739
532	0.998803
533	0.998864
534	0.998923
535	0.998978
536	0.999031
537	0.999082
538	0.999130
539	0.999176
540	0.999219
541	0.999261
542	0.999301
543	0.999338
544	0.999374
545	0.999408
546	0.999441
547	0.999471
548	0.999501
549	0.999528
550	0.999555
551	0.999580
552	0.999604
553	0.999626
554	0.999648
555	0.999668
556	0.999687
557	0.999705
558	0.999722
559	0.999739
560	0.999754
561	0.999769
562	0.999782
563	0.999795
564	0.999808
565	0.999819
566	0.999830
567	0.999841
568	0.999851
569	0.999860
570	0.999868
571	0.999877
572	0.999884
573	0.999892
574	0.999899
575	0.999905
576	0.999911
577	0.999917
578	0.999922
579	0.999927
580	0.999932
581	0.999936
582	0.999941
583	0.999945
584	0.999948
585	0.999952
586	0.999955
587	0.999958
588	0.999961
589	0.999964
590	0.999966
591	0.999968
592	0.999971
593	0.999973
594	0.999975
595	0.999976
596	0.999978
597	0.999980
598	0.999981
599	0.999982
600	0.999984
601	0.999985
602	0.999986
603	0.999987
604	0.999988
605	0.999989
606	0.999990
607	0.999990
608	0.999991
609	0.999992
610	0.999992
611	0.999993
612	0.999994
613	0.999994
614	0.999994
615	0.999995
616	0.999995
617	0.999996
618	0.999996
619	0.999996
620	0.999997
621	0.999997
622	0.999997
623	0.999997
624	0.999998
625	0.999998
626	0.999998
627	0.999998
628	0.999998
629	0.999998
630	0.999999
631	0.999999
632	0.999999
633	0.999999
634	0.999999

मान लीजिए एक डीलर के पास हर मूल्य के चिप्स हैं जो $1 से बराबर विभाजित होते हैं। आप टेबल पर $10 में खरीदते हैं। डीलर $10 के बदले कितने अलग-अलग तरीकों से छुट्टे दे सकता है? बाकी ख़रीदी गई राशियों के बारे में क्या?

गुमनाम

डीलर $10 को 42 तरीकों से तोड़ सकता है। ये रहे:

10
9,1
8,2
8,1,1
7,3
7,2,1
7,1,1,1
6,4
6,3,1
6,2,2
6,2,1,1
6,1,1,1,1
5,5
5,4,1
5,3,2
5,3,1,1
5,2,2,1
5,2,1,1,1
5,1,1,1,1,1
4,4,2
4,4,1,1
4,3,3
4,3,2,1
4,3,1,1,1
4,2,2,2
4,2,2,1,1
4,2,1,1,1,1
4,1,1,1,1,1,1
3,3,3,1
3,3,2,2
3,3,2,1,1
3,3,1,1,1,1
3,2,2,2,1
3,2,2,1,1,1
3,2,1,1,1,1,1
3,1,1,1,1,1,1,1
2,2,2,2,2
2,2,2,2,1,1
2,2,2,1,1,1,1
2,2,1,1,1,1,1,1
2,1,1,1,1,1,1,1,1
1,1,1,1,1,1,1,1,1,1,1

गणितज्ञ इन्हें विभाजन कहते हैं। यहाँ 405 तक की प्रारंभिक मात्राओं के लिए विभाजनों की संख्या दी गई है, जो मेरे कंप्यूटर द्वारा गणना की जा सकने वाली अधिकतम संख्या (2^64) है।

2+ लोगों के सामान्य जन्मदिन

>241

प्रारंभिक मात्रा	कुल विभाजन
1	1
2	2
3	3
4	5
5	7
6	11
7	15
8	22
9	30
10	42
11	56
12	77
13	101
14	135
15	176
16	231
17	297
18	385
19	490
20	627
21	792
22	1002
23	1255
24	1575
25	1958
26	2436
27	3010
28	3718
29	4565
30	5604
31	6842
32	8349
33	10143
34	12310
35	14883
36	17977
37	21637
38	26015
39	31185
40	37338
41	44583
42	53174
43	63261
44	75175
45	89134
46	105558
47	124754
48	147273
49	173525
50	204226
51	239943
52	281589
53	329931
54	386155
55	451276
56	526823
57	614154
58	715220
59	831820
60	966467
61	1121505
62	1300156
63	1505499
64	1741630
65	2012558
66	2323520
67	2679689
68	3087735
69	3554345
70	4087968
71	4697205
72	5392783
73	6185689
74	7089500
75	8118264
76	9289091
77	10619863
78	12132164
79	13848650
80	15796476
81	18004327
82	20506255
83	23338469
84	26543660
85	30167357
86	34262962
87	38887673
88	44108109
89	49995925
90	56634173
91	64112359
92	72533807
93	82010177
94	92669720
95	104651419
96	118114304
97	133230930
98	150198136
99	169229875
100	190569292
101	214481126
102	241265379
103	271248950
104	304801365
105	342325709
106	384276336
107	431149389
108	483502844
109	541946240
110	607163746
111	679903203
112	761002156
113	851376628
114	952050665
115	1064144451
116	1188908248
117	1327710076
118	1482074143
119	1653668665
120	1844349560
121	2056148051
122	2291320912
123	2552338241
124	2841940500
125	3163127352
126	3519222692
127	3913864295
128	4351078600
129	4835271870
130	5371315400
131	5964539504
132	6620830889
133	7346629512
134	8149040695
135	9035836076
136	10015581680
137	11097645016
138	12292341831
139	13610949895
140	15065878135
141	16670689208
142	18440293320
143	20390982757
144	22540654445
145	24908858009
146	27517052599
147	30388671978
148	33549419497
149	37027355200
150	40853235313
151	45060624582
152	49686288421
153	54770336324
154	60356673280
155	66493182097
156	73232243759
157	80630964769
158	88751778802
159	97662728555
160	107438159466
161	118159068427
162	129913904637
163	142798995930
164	156919475295
165	172389800255
166	189334822579
167	207890420102
168	228204732751
169	250438925115
170	274768617130
171	301384802048
172	330495499613
173	362326859895
174	397125074750
175	435157697830
176	476715857290
177	522115831195
178	571701605655
179	625846753120
180	684957390936
181	749474411781
182	819876908323
183	896684817527
184	980462880430
185	1071823774337
186	1171432692373
187	1280011042268
188	1398341745571
189	1527273599625
190	1667727404093
191	1820701100652
192	1987276856363
193	2168627105469
194	2366022741845
195	2580840212973
196	2814570987591
197	3068829878530
198	3345365983698
199	3646072432125
200	3972999029388
201	4328363658647
202	4714566886083
203	5134205287973
204	5590088317495
205	6085253859260
206	6622987708040
207	7206841706490
208	7840656226137
209	8528581302375
210	9275102575355
211	10085065885767
212	10963707205259
213	11916681236278
214	12950095925895
215	14070545699287
216	15285151248481
217	16601598107914
218	18028182516671
219	19573856161145
220	21248279009367
221	23061871173849
222	25025873760111
223	27152408925615
224	29454549941750
225	31946390696157
226	34643126322519
227	37561133582570
228	40718063627362
229	44132934884255
230	47826239745920
231	51820051838712
232	56138148670947
233	60806135438329
234	65851585970275
235	71304185514919
236	77195892663512
237	83561103925871
238	90436839668817
239	97862933703585
240	105882246722733
114540884553038
242	123888443077259
243	133978259344888
244	144867692496445
245	156618412527946
246	169296722391554
247	182973889854026
248	197726516681672
249	213636919820625
250	230793554364681
251	249291451168559
252	269232701252579
253	290726957916112
254	313891991306665
255	338854264248680
256	365749566870782
257	394723676655357
258	425933084409356
259	459545750448675
260	495741934760846
261	534715062908609
262	576672674947168
263	621837416509615
264	670448123060170
265	722760953690372
266	779050629562167
267	839611730366814
268	904760108316360
269	974834369944625
270	1050197489931117
271	1131238503938606
272	1218374349844333
273	1312051800816215
274	1412749565173450
275	1520980492851175
276	1637293969337171
277	1762278433057269
278	1896564103591584
279	2040825852575075
280	2195786311682516
281	2362219145337711
282	2540952590045698
283	2732873183547535
284	2938929793929555
285	3160137867148997
286	3397584011986773
287	3652430836071053
288	3925922161489422
289	4219388528587095
290	4534253126900886
291	4872038056472084
292	5234371069753672
293	5622992691950605
294	6039763882095515
295	6486674127079088
296	6965850144195831
297	7479565078510584
298	8030248384943040
299	8620496275465025
300	9253082936723602
301	9930972392403501
302	10657331232548839
303	11435542077822104
304	12269218019229465
305	13162217895057704
306	14118662665280005
307	15142952738857194
308	16239786535829663
309	17414180133147295
310	18671488299600364
311	20017426762576945
312	21458096037352891
313	23000006655487337
314	24650106150830490
315	26415807633566326
316	28305020340996003
317	30326181989842964
318	32488293351466654
319	34800954869440830
320	37274405776748077
321	39919565526999991
322	42748078035954696
323	45772358543578028
324	49005643635237875
325	52462044228828641
326	56156602112874289
327	60105349839666544
328	64325374609114550
329	68834885946073850
330	73653287861850339
331	78801255302666615
332	84300815636225119
333	90175434980549623
334	96450110192202760
335	103151466321735325
336	110307860425292772
337	117949491546113972
338	126108517833796355
339	134819180623301520
340	144117936527873832
341	154043597379576030
342	164637479165761044डी>
343	175943559810422753
344	188008647052292980
345	200882556287683159
346	214618299743286299
347	229272286871217150
348	244904537455382406
349	261578907351144125
350	279363328483702152
351	298330063062758076
352	318555973788329084
353	340122810048577428
354	363117512048110005
355	387632532919029223
356	413766180933342362
357	441622981929358437
358	471314064268398780
359	502957566506000020
360	536679070310691121
361	572612058898037559
362	610898403751884101
363	651688879997206959
364	695143713458946040
365	741433159884081684
366	790738119649411319
367	843250788562528427
368	899175348396088349
369	958728697912338045
370	1022141228367345362
371	1089657644424399782
372	1161537834849962850
373	1238057794119125085
374	1319510599727473500
375	1406207446561484054
376	1498478743590581081
377	1596675274490756791
378	1701169427975813525
379	1812356499739472950
380	1930656072350465812
381	2056513475336633805
382	2190401332423765131
383	2332821198543892336
384	2484305294265418180
385	2645418340688763701
386	2816759503217942792
387	2998964447736452194
388	3192707518433532826
389	3398704041358160275
390	3617712763867604423
391	3850538434667429186
392	4098034535626594791
393	4361106170762284114
394	4640713124699623515
395	4937873096788191655
396	5253665124416975163
397	5589233202595404488
398	5945790114707874597
399	6324621482504294325
400	6727090051741041926
401	7154640222653942321
402	7608802843339879269
403	8091200276484465581
404	8603551759348655060
405	9147679068859117602

जैसा कि फिल्म मीन गर्ल्स में पूछा गया है, क्या है:

गुमनाम

आइए n (x-अक्ष) तथा f(n) (y-अक्ष) के ग्राफ को देखकर शुरुआत करें।

जैसा कि आप देख सकते हैं, सीमा बाईं ओर से ∞ और दाईं ओर से -∞ की ओर बढ़ रही है। चूँकि यह दोनों ओर से एक ही स्थान पर नहीं घूमती, इसलिए कोई सीमा नहीं है।

हालाँकि, आइए इस प्रश्न का उत्तर बिना ग्राफ़ के दें। एल'हॉस्पिटल का नियम कहता है कि यदि f(x)/g(x) की सीमा = 0/0, तो lim f(x)/g(x) = lim f'(x)/g'(x) होगा। तो, आइए f'(x) और g'(x) का हल निकालें।

f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos ² (n)) d/dn = sin ² (n) d/dn

आइए sin ² (n) d/dn को हल करने के लिए गुणन नियम का उपयोग करें

पाप ² (एन) डी/डीएन = पाप(एन) × पाप(एन) डी/डीएन =
पाप (एन) × कॉस (एन) + कॉस (एन) × पाप (एन) =
2sin(n)cos(n).

अब, आइए n = 0 पर f'(n) और g'(n) का हल निकालें।

f'(0) = -1/(1-0) - cos(0) = -2.
जी'(0) = 2sin(0)cos(0) = 0

तो, f'(0)/g'(0) = -2/0 = -∞. इस प्रकार, मूल फलन की सीमा मौजूद नहीं है।

मैं "मीन गर्ल्स" के लेखकों को इस फिल्म में गणित को बेहतरीन ढंग से पेश करने के लिए बधाई देना चाहूँगा। यहाँ तक कि "गुड विल हंटिंग" जैसी गंभीर गणितीय फिल्में भी अक्सर गणित को पूरी तरह से ध्वस्त कर देती हैं।

यंग शेल्डन के सीज़न 3 के एपिसोड 4, " हॉबिट्स, फ़िज़िक्सेस एंड अ बॉल विद ज़िप" में, शेल्डन खुद से बिंगो कार्ड पर संभावित संयोजनों की संख्या पूछता है। इसका उत्तर क्या है और क्या शो में दिखाए गए सूत्र सही हैं?

गुमनाम

सबसे पहले, मैं क्रमपरिवर्तनों की संख्या पर चर्चा करूँगा। इसका मतलब है कि न केवल संख्याएँ मायने रखती हैं, बल्कि कार्ड पर उनका क्रम भी मायने रखता है। B, I, G, और O स्तंभों के लिए क्रमपरिवर्तन (15,5) = 15!/(15-5)! = 15*14*13*12*11 = 360,360 संभावित क्रमपरिवर्तन हैं। N स्तंभ के लिए, क्रमपरिवर्तनों की संख्या क्रमपरिवर्तन (14,4) = 15!/(15-4)! = 15*14*13*12 = 32,760 है। इस प्रकार, बिंगो कार्डों के क्रमपरिवर्तनों की कुल संख्या 360,360 ⁴ × 32,760 = 552446474061128648601600000 है।

दूसरा, मैं संयोजनों की संख्या पर चर्चा करूँगा। इसका मतलब है कि संख्याएँ मायने रखती हैं, लेकिन कार्ड पर उनका क्रम मायने नहीं रखता। B, I, G, और O स्तंभों के लिए संयोजन(15,5) = 15!/(5!*(15-5)!) = (15*14*13*12*11)/(1*2*3*4*5) = 3,003 संभावित संयोजन हैं। N स्तंभ के लिए, क्रमपरिवर्तनों की संख्या संयोजन(14,4) = 15!/(4!*(15-4)!) = (15*14*13*12)/(1*2*3*4) = 1,365 है। इस प्रकार, बिंगो कार्डों के क्रमपरिवर्तनों की कुल संख्या 3,003 ⁴ × 1,365 = 111007923832370565 है।

शो में, शेल्डन खुद से पूछता है कि इतने अनोखे बिंगो कार्ड कैसे होते हैं। बाद में दिए गए गलत सूत्रों के आधार पर, मुझे लगता है कि उसका मतलब क्रमपरिवर्तन से है। दूसरे शब्दों में, एक ही संख्या वाले लेकिन अलग-अलग स्थानों पर स्थित दो कार्ड, दोनों ही अनोखे होंगे।

ऊपर दी गई छवि B, I, G, और O स्तंभों के लिए शेल्डन के सूत्र को दर्शाती है। शुरुआत में वह सूत्र 5! × combin(15,5) पर सही है। हालाँकि, वह इसे गलत तरीके से सरल करके 15!/(15!-5)! कर देता है। दूसरा विस्मयादिबोधक चिह्न वहाँ नहीं होना चाहिए। इसे 15!/(15-10)! पढ़ना चाहिए। हालाँकि, वह फिर 360,360 पर सही उत्तर पर पहुँच जाता है।

N कॉलम के साथ भी हमें बिल्कुल यही समस्या है। सूत्र 15!/(15-4)! होना चाहिए, न कि 15!/(15!-4)!। दूसरा विस्मयादिबोधक चिह्न इसे बिगाड़ देता है।

विडंबना यह है कि एपिसोड में आगे चलकर शेल्डन को लॉर्ड ऑफ द रिंग्स के कालक्रम में त्रुटियों का जुनून सवार हो जाता है, ठीक उसी तरह जैसे मुझे इस पर जुनून सवार है।

एक 100 लीटर की टंकी में पानी और 10 किलो नमक है। अगर हम प्रति मिनट 10 लीटर शुद्ध पानी डालें और साथ ही प्रति मिनट 10 लीटर घोल भी निकाल दें, तो 30 मिनट बाद टंकी में कितना नमक बचेगा?

Ace2

आइये कुछ चरों को परिभाषित करके शुरुआत करें:

s = टैंक में नमक की मात्रा किलोग्राम
t = नमक को टैंक में डाले जाने के बाद से बीते मिनट

हमें बताया गया है कि प्रति मिनट 10% नमक बह जाता है। इसे गणितीय भाषा में कहें तो:

डीएस/डीटी = (-10/100) × एस

इसे पुनः व्यवस्थित करें:

डीएस = (-10/100) × एस डीटी

-10/s डीएस = डीटी

दोनों पक्षों को एकीकृत करना:

(1) -10×ln(s) = t + c

अब, आइए समाकलन के खतरनाक स्थिरांक का पता लगाएँ। ऐसा करने के लिए, हमें दिया गया है कि t = 0 होने पर s = 10। इसे ऊपर दिए गए सूत्र (1) में डालने पर हमें यह मिलता है:

-10 × ln(10) = 0 + सी

तो c = -10×ln(10)

इसे समीकरण (1) में रखने पर हमें मिलता है:

(2) -10×ln(s) = t -10×ln(10)

प्रश्न यह है कि t=30 पर टैंक में कितना नमक होगा। t=30 पर s का हल:

-10×ln(s) = 30 -10×ln(10). अब दोनों पक्षों को -10 से भाग दें...

ln(s) = -3 + ln(10)

एस = एक्सप(-3 + एलएन(10))

एस = एक्सप(-3) × एक्सप(ln(10))

एस = एक्सप(-3) × 10

s =~ 0.4979 किलोग्राम नमक.

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

दिया गया है कि बड़ी आकृति एक वर्ग है, x का क्षेत्रफल क्या है?

Dyana से Las Vegas

इस तरह की समस्याओं की कुंजी उन्हें व्यवस्थित करने में है। मेरा सुझाव है कि समस्या को यथासंभव कम अज्ञात मानों तक सीमित रखने का प्रयास करें। इस स्थिति में, हम वर्ग पर अज्ञात दूरियों को केवल तीन में व्यक्त कर सकते हैं, इस प्रकार:

त्रिभुजों की तुलना में आयतों से निपटना आसान होता है। चूँकि हमें तीन त्रिभुजों का क्षेत्रफल पता है, इसलिए हम उनका आकार और क्षेत्रफल दोगुना कर सकते हैं। इससे हमें मिलता है:

अब=10
एसी=16
(एबी)(एसी)=14

आइए (ab)(ac) का गुणनखंड करें:

a ² - ab- ac + bc = 14

a ² - 10 - 16 + bc = 14

(1) a ² + bc = 40

आइए b और c को a के रूप में व्यक्त करें, ताकि इसे एकल चर में लाया जा सके:

बी = 10/ए

सी = 16/ए

समीकरण (1) में b और c के लिए उन मानों को प्रतिस्थापित करने पर:

ए ² + (10/ए)*(16/ए) = 40

a ² + 160/a ² = 18

अब, आइए सभी चीजों को ² से गुणा करके हर में से ² को हटा दें।

ए ⁴ + 160 = 40*ए ²

ए ⁴ - 40*ए ² + 160 = 0

आइए एक नया चर y = a ² परिभाषित करें

y ² - 18y + 32 = 0

अब, आइए द्विघात सूत्र का उपयोग करके y का हल निकालें:

y = (40 +/- sqrt(1600-640))/2

y = (40 +/- sqrt(960))/2

y = (40 +/- 8*sqrt(15))/2

y = 20 +/- 4*sqrt(15)

पूरे वर्ग का क्षेत्रफल a ² है, जो सुविधाजनक रूप से y के बराबर है। उपरोक्त समीकरण से, यदि +/- ऋणात्मक है, तो y = लगभग 4.5081 है, जो स्पष्ट रूप से गलत है, क्योंकि हम जानते हैं कि क्षेत्रफल कम से कम 20 है, जिसमें x भी शामिल नहीं है। इसलिए वर्ग का क्षेत्रफल 20 + 4*sqrt(15) होना चाहिए।

हमें दिए गए तीन त्रिभुजों का क्षेत्रफल 5+7+8=20 है। इसे वर्ग के कुल क्षेत्रफल से घटाने पर हमें x का क्षेत्रफल प्राप्त होता है: 20 + 4*sqrt(15) - 20 = 4*sqrt(15) = लगभग 15.4919।

इस तस्वीर में मेरी टी-शर्ट देखिये। जब मैं "अनकट जेम्स" देखने गया था, तो सिनेमाघर के कैशियर ने इसकी तारीफ़ की थी। मैंने उसे इस समस्या से परेशान करके धन्यवाद दिया, सिर्फ़ क्षेत्रफल 2, 3 और 4 के त्रिभुजों से। फिल्म के बाद, मैंने उससे पूछा कि उसने अभी तक इसे हल नहीं किया था, लेकिन ऐसा लग रहा था कि वह कोशिश कर रही है। इसलिए मैंने सनकोस्ट बार में उसके लिए यह हल लिखा। उसे वाकई यह पसंद आया। मुझे लगता है कि वह युवती ज़िंदगी में बहुत आगे जाएगी।

1 गुणा 1 विमाओं वाला एक वर्गाकार डार्टबोर्ड है। इस पर एक डार्ट इस प्रकार फेंका जाता है कि वह समान संभावना के साथ कहीं भी गिरे। मान लीजिए कि जहाँ वह गिरेगा उसके निर्देशांक (x,y) हैं, जहाँ x और y दोनों 0 से 1 तक समान रूप से और स्वतंत्र रूप से वितरित हैं।

मान लीजिए z = round(x/y)। दूसरे शब्दों में, z = x/y, निकटतम पूर्णांक तक पूर्णांकित। इसकी क्या प्रायिकता है कि z सम हो?

गुमनाम

निम्नलिखित संकेत में अनंत श्रृंखला को जानना बहुत उपयोगी होगा।

[स्पॉइलर=संकेत]

π के लिए लाइबनिज़ सूत्र कहता है:

1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4

[/spoiler]

केवल उत्तर के लिए, निम्नलिखित बटन पर क्लिक करें।

(5 - π)/4 = लगभग। 0.464601836602552।

समाधान के लिए नीचे दिए गए बटन पर क्लिक करें।

[स्पॉइलर=समाधान]

यदि x/y < 0.5 है, तो अनुपात n को 0 तक पूर्णांकित करेगा, और सम संख्या भी। डार्टबोर्ड पर (0,0) और (0.5) से बनी रेखा के बाईं ओर स्थित कोई भी बिंदु 0 तक पूर्णांकित होगा। वह क्षेत्र 1 और 1/2 भुजाओं वाला एक समकोण त्रिभुज है। याद रखें कि त्रिभुज का क्षेत्रफल (1/2)*आधार*ऊँचाई होता है। इस प्रकार, 0 तक पूर्णांकित करने पर उन बिंदुओं का क्षेत्रफल (1/2)*(1/2) = 1/4 होगा।

ग्राफ़ पर अगला क्षेत्र जो अगली सम संख्या, 2, तक पूर्णांकित होगा, वह तब होगा जब 1.5 < x/y < 2.5 हो। यह क्षेत्र एक त्रिभुज होगा जिसका आधार 2/3 - 2/5 और ऊँचाई 1 होगी। ध्यान दें कि ये x/y की सीमाओं के व्युत्क्रम हैं, क्योंकि x बराबर 1 है, इसलिए हमें y को उलटना होगा। इसलिए, 2 तक पूर्णांकित होने वाला क्षेत्र (1/2)*(2/3 - 2/5) होगा।

ग्राफ़ पर अगला क्षेत्र जो अगली सम संख्या, 4, तक पूर्णांकित होगा, वह तब होगा जब 3.5 < x/y < 4.5 हो। यह क्षेत्र एक त्रिभुज होगा जिसका आधार 2/7 - 2/9 और ऊँचाई 1 होगी। इसलिए, 2 तक पूर्णांकित होने वाला क्षेत्र (1/2)*(2/7 - 2/9) होगा।

ग्राफ़ पर अगला क्षेत्र जो अगली सम संख्या, 6, तक पूर्णांकित होगा, वह तब होगा जब 5.5 < x/y < 6.5 होगा। यह क्षेत्र एक त्रिभुज होगा जिसका आधार 2/11 - 2/13 और ऊँचाई 1 होगी। इसलिए, 2 तक पूर्णांकित होने वाला क्षेत्र (1/2)*(2/11 - 2/13) होगा।

क्या आपको कोई पैटर्न नज़र आने लगा है? यह इस प्रकार है:

1/4 + 1/2*(2/3 - 2/5 + 2/7 - 2/9 + 2/11 - 2/13 + ... ) =

1/4 + (1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =

आइए उन कोष्ठकों के अंदर -1 ले जाएं।

5/4 + (-1 + 1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =

5/4 - (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 + ... ) =

अब, ऊपर दिए गए हमारे संकेत को याद करें:

1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11

अब हम अपने प्रश्न पर वापस आते हैं...

5/4 - π/4 =

(5 - π) / 4 = लगभग. 0.464601836602552.

यह दिलचस्प है कि कैसे π और e गणित में हर जगह दिखाई देते हैं।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मान लीजिए 9 ^x + 12 ^x = 16 ^x

X क्या है?

गुमनाम

उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

x = [ln(1 + sqrt(5)) - ln(2)] / [ln(4) - ln(3) ] = लगभग 1.67272093446233.

समाधान के लिए नीचे दिए गए बटन पर क्लिक करें।

[स्पॉइलर=समाधान]

9 ^x + 12 ^x = 16 ^x =

दोनों पक्षों को 9 ^x से विभाजित करें

1 + (12/9) ^x = (16/9) ^x

1 + (4/3) ^x = ((4/3) ^x ) ²

(1) मान लीजिए u = (4/3) ^x

1 + यू = यू ²

द्विघात सूत्र द्वारा...

u = (1+sqrt(5)) / 2 (स्वर्ण अनुपात)

इसे समीकरण (1) में वापस रखते हुए:

(4/3) ^x = (1+sqrt(5)) / 2

दोनों पक्षों का लघुगणक लें:

x ln(4/3) = ln[(1+sqrt(5)) / 2]

x = ln[(1+sqrt(5)) / 2] / ln(4/3)

x = [ln(1+sqrt(5) - ln(2)] / [ln(4) - ln(3)] = लगभग 1.67272093446233. [/spoiler]

आभार: मुझे इस समस्या का एक भिन्न रूप माइंड योर डिसीजन्स के प्रेश तलवलकर से मिला।

एक किसान सेब के 5 बीज बोता है। हर दिन, प्रत्येक बीज के अंकुरित होने की संभावना 1/3 होती है। सभी पाँच पेड़ों के अंकुरित होने में औसतन कितना समय लगता है?

गुमनाम

उत्तर लगभग 6.131415853 दिन है।

[स्पॉइलर=समाधान]

आइए पीछे की ओर से गणना करें। अगर एक बीज बचा है जो अंकुरित नहीं हुआ है, तो उसे अंकुरित होने में औसतन 1/p दिन लगेंगे, जहाँ p किसी भी दिन अंकुरित होने की संभावना है। चूँकि p = 1/3 है, इसलिए अंकुरित होने में औसतन 3 दिन लगेंगे। इसे t ₁ = 3 मान लेते हैं।

अगर दो बीज बचे हों तो क्या होगा? अगले दिन दोनों के अंकुरित होने की संभावना ap ² = 1/9 है और हमारा काम हो गया। अगले दिन एक बीज के अंकुरित होने की संभावना 2×p×q है, जहाँ q अंकुरित न होने की संभावना है। इस प्रकार, एक बीज के अंकुरित होने की संभावना 2×(1/3)(2/3) = 4/9 है। किसी भी बीज के अंकुरित न होने की संभावना q ² = (2/3) ² = 4/9 है। आइए दो बीजों के साथ अपेक्षित दिनों की संख्या को t ₂ कहें।

टी ₂ = 1 + (4/9)×टी ₁ + (4/9)टी ₂

टी ₂ = (1 - (4/9)) = 1 + (4/9)×टी ₁

टी ₂ = (1 + (4/9)×3) / (1 - (4/9))

टी ₂ = (21/9) / (5/9)

टी ₂ = (21/9) × (9/5) = 21/5 = 4.2

अगर तीन बीज बचे रहें तो क्या होगा? अगले दिन सभी के अंकुरित होने की ap ³ = 1/27 संभावना है और हमारा काम पूरा हो जाएगा। अगले दिन एक बीज के अंकुरित होने की संभावना 3×p ×q ² = 3×(1/3)(2/3) ² = 12/27 है। अगले दिन दो बीजों के अंकुरित होने की संभावना 3×p ² ×q = 3×(1/3) ² ×(2/3) = 6/27 है। किसी भी बीज के अंकुरित न होने की संभावना q ³ = (2/3) ³ = 8/27 है। आइए तीन बीजों वाले दिनों की अपेक्षित संख्या को t ₃ कहें।

टी ₃ = 1 + (6/27)टी ₁ + (12/27)×टी ₂ + (8/27)×टी ₃

टी ₃ = 1 + (6/27)×3 + (12/27)×4.2 + (8/27)×टी ₃

टी ₃ × (1 - 8/27) = (1 + 18/27 + 28/15)

टी ₃ = (1 + 18/27 + 28/15) / (1 - 8/27) = 477/95 = लगभग 5.02105263

अगर चार बीज बचे रहें तो क्या होगा? अगले दिन चारों के अंकुरित होने की ap ⁴ = 1/81 संभावना है और हमारा काम पूरा हो जाएगा। अगले दिन एक के अंकुरित होने की संभावना 4×p×q ³ = 4×(1/3)(2/3) ³ = 32/81 है। अगले दिन दो के अंकुरित होने की संभावना combin(4,2)×p ² ×q ² = 6×(1/3) ² ×(2/3) ² = 24/81 है। अगले दिन तीन के अंकुरित होने की संभावना combin(4,3)×p ³ ×q = 4×(1/3) ³ ×(2/3) = 8/81 है। कोई भी बीज अंकुरित न होने की संभावना q ⁴ = (2/3) ⁴ = 16/81 है। आइए तीन बीजों के साथ अपेक्षित दिनों की संख्या को t ₄ कहें।

टी ₄ = 1 + (8/81)×टी ₁ + (24/81)×टी ₂ + (32/81)×टी ₃ + (16/81)×टी ₄

टी ₄ = 1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263 + (16/81)×टी ₄

टी ₄ = (1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263) / (1 - (16/81))

टी ₄ = लगभग 5.638056680161943319838056680.

अगर सभी पाँच बीज बचे रहें तो क्या होगा? अगले दिन सभी पाँचों के अंकुरित होने की संभावना ap ⁵ = 1/243 है और हमारा काम पूरा हो जाएगा। अगले दिन एक के अंकुरित होने की संभावना 5×p×q ⁴ = 5×(1/3)(2/3) ⁴ = 80/243 है। अगले दिन दो के अंकुरित होने की संभावना combin(5,2)×p ² ×q ³ = 10×(1/3) ² ×(2/3) ³ = 80/243 है। अगले दिन तीन के अंकुरित होने की संभावना combin(5,3)×p ³ ×q = 10×(1/3) ³ ×(2/3) ² = 40/243 है। अगले दिन चार बीजों के अंकुरित होने की संभावना है: (5,4)×p ⁴ ×q = 5×(1/3) ⁴ ×(2/3) = 10/243। किसी भी बीज के अंकुरित न होने की संभावना है: q ⁵ = (2/3) ⁵ = 32/243। आइए तीन बीजों वाले दिनों की अपेक्षित संख्या को t ₅ कहें।

टी ₅ = 1 + (10/243)×टी ₁ + (40/243)×टी ₂ + (80/81)×टी ₃ + (80/243)×टी ₄ + (32/243)×टी ₅

टी ₅ = (1 + (10/243)×टी ₁ + (40/243)×टी ₂ + (80/81)×टी ₃ + (80/243)×टी ₄ ) / (1 - (32/243))

टी ₅ = (1 + (10/243)×3 + (40/243)×4.2 + (80/243)×(477/95) + (80/243)×5.63805668) / (1 - (32/243))

टी ₅ = लगभग 6.131415853.

[/spoiler]

यह समस्या माइंड योर डिसीजन्स के प्रेश तलवलकर द्वारा दी गई इसी प्रकार की समस्या से अनुकूलित है।

मेरा प्रश्न दो भागों में है।

भाग 1 के लिए, दिया गया:

x + y + z = 1
x^2 + y^2 + z^2 = 4
x^3 + y^3 + z^3 = 9

x^4 + y^4 + z^4 क्या है?

दूसरे भाग के लिए, सामान्य स्थिति का उत्तर क्या है जब:

x + y + z = ए
x^2 + y^2 + z^2 = बी
x^3 + y^3 + z^3 = सी

गुमनाम

प्रश्न 1: 97/6 = लगभग 16.166666

प्रश्न 2: a ⁴ /6 + (4/3)ac - a ² b + b ² /2

[स्पॉइलर=समाधान]

मेरा समाधान देखने के लिए (पीडीएफ)

[/spoiler]

एक सूक्ष्म जीव, मान लीजिए इसे कोविड-20 कहते हैं, किसी भी समय एक नया सूक्ष्म जीव पैदा कर सकता है। किसी विशिष्ट जनक सूक्ष्म जीव से किसी भी समय किसी विशेष सूक्ष्म जीव के पैदा होने की संभावना हमेशा एक समान होती है, चाहे पिछले बार पैदा होने के बाद कितना भी समय क्यों न बीत गया हो। एक ही सूक्ष्म जीव से पैदा होने के बीच का औसत समय एक दिन होता है। गणितीय रूप से, एक ही सूक्ष्म जीव से पैदा होने के बीच का अपेक्षित समय एक घातांकीय वितरण का अनुसरण करता है जिसका माध्य एक दिन होता है।

एक बार जब कोई सूक्ष्म जीव आपके फेफड़ों में प्रवेश कर जाता है, तो सात दिनों के बाद आपके फेफड़ों में सूक्ष्म जीवों की अपेक्षित संख्या कितनी होगी?

गुमनाम

उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

उत्तर है e ⁷ = लगभग 1,096.6332.

समाधान के लिए नीचे दिए गए बटन पर क्लिक करें।

[स्पॉइलर=समाधान]

इस हल के लिए एक साधारण अवकल समीकरण की आवश्यकता होगी। अगर आप अभी गणित की शिक्षा में उस स्तर पर नहीं पहुँचे हैं, तो आपको यह समझ नहीं आएगा।

होने देना:
m = कोविड-20 रोगाणुओं की संख्या
t = समय, दिनों में

चूँकि प्रत्येक सूक्ष्मजीव प्रतिदिन औसतन एक बार एक नया सूक्ष्मजीव उत्पन्न करता है, इसलिए m सूक्ष्मजीव प्रतिदिन औसतन m नए सूक्ष्मजीव उत्पन्न करेंगे। दूसरे शब्दों में, किसी भी समय t पर सूक्ष्मजीवों की वृद्धि दर (m) को इस प्रकार लिखा जा सकता है:

डीएम/डीटी = एम.

मुझे इसे व्यक्त करने का उचित तरीका नहीं पता, लेकिन dt को दाईं ओर अलग करें:

डीएम = एम डीटी.

दोनों पक्षों को m से विभाजित करें:

1/एम डीएम = 1 डीटी.

दोनों पक्षों को एकीकृत करें:

ln(m) = t + C, जहाँ C एकीकरण का स्थिरांक है।

हमें दिया गया है कि समय 0 पर एक सूक्ष्म जीव है। दूसरे शब्दों में, जब t = 0, m = 1। हम C का मान हल करने के लिए इन मानों को ऊपर दिए गए समीकरण में रख सकते हैं:

ln(1) = 0 + सी

0 = 0 + सी

सी = 0.

अब हमारे पास ln(m) = t है।

दोनों पक्षों का exp() लें:

m = e ^t

तो, समय t=7 पर, e ⁷ = लगभग 1096.6332 सूक्ष्मजीव होंगे।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

एक पुराने पश्चिमी सैलून में, ताश के खेल को लेकर हुई बहस इतनी बढ़ गई कि आस-पास के सभी काउबॉय अपनी बंदूकें निकालकर एक-दूसरे पर गोलियां चलाने लगे।

जब धुआँ छँटा, तो 90% काउबॉयज़ के पैर में, 85% के हाथ में, 80% के पेट में और 75% के सिर में गोली लगी थी। हैरानी की बात यह थी कि इस भीषण गोलीबारी में सिर्फ़ वही काउबॉयज़ मारे गए जिन्हें चारों तरह के ज़ख्म लगे थे।

उन काउबॉय का सबसे छोटा संभावित प्रतिशत क्या है जिन्हें दफनाया गया?

Gialmere

30%

सबसे पहले, 90% काउबॉय के पैर में गोली मारो।

इसके बाद, बाँह में बचे हुए 10% हिस्से पर गोली चलाएँ। आपके पास बाँह में गोली मारने के लिए 75% और हैं, इसलिए उन्हें पहले से पैर में लगी गोली से निकाल लें।

तो, अब हम यहां हैं:

पैर केवल 15% (90% - 75%)
केवल 10% आर्म
दोनों 75%
न तो 0%

कुल पैर: 90%
कुल भुजा: 85%

अब, आइए पेट की चोटों (80%) पर आते हैं। 25% लोगों को सिर्फ़ एक बार पेट में चोट लगने पर गोली मारें। हमारे पास 80%-25% = 55% ज़्यादा लोग हैं जिन्हें गोली मारनी है। हम उन 55% लोगों को गोली मारेंगे जिन्हें दोनों चोटें लगी हैं। तो अब हम यहाँ हैं:

पैर और आंत 15%
बांह और आंत 10%
पैर और हाथ 20% (75% - 55%)
तीनों 55%
एक चोट 0%
शून्य चोटें 0%

अंत में, सिर में चोट लगने वाले 75% लोगों पर विचार करें। सबसे पहले, केवल दो चोटों वाले 45% लोगों को हटाएँ। हमारे पास 30% और हैं, इसलिए उन्हें तीनों चोटों वाले 55% लोगों से हटाएँ। इससे बचता है:

सिर, पैर और आंत 15%
सिर, बांह और आंत 10%
सिर, पैर और हाथ 20%
पैर, हाथ और आंत: 25% (55% - 30%)
सभी चार 30%
शून्य चोटें 0%
एक चोट 0%
दो चोटें 0%

[स्पॉइलर=चार्लीपैट्रिक समाधान]

मान लीजिए 20 काउबॉय हैं। हमने यह संख्या इसलिए चुनी है क्योंकि इसमें शामिल सभी संभावनाएँ 5% से समान रूप से विभाज्य हैं और 20 का 5% 1 है।

उन्हें एक पंक्ति में लगाएँ। फिर, बाएँ से शुरू करते हुए, उनमें से 90%, यानी 18, पैर में गोली मारें। फिर ऊपर वाली पंक्ति में काउबॉय संख्या और बाएँ कॉलम में प्रत्येक को हुई कुल चोटों का एक आरेख बनाएँ, जैसा कि नीचे दिया गया है।

चोट	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल
2
3
4
कुल	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0

इसके बाद, आपको 85%, यानी 17 शॉट हाथ में लगाने होंगे। शुरुआत उन दो काउबॉय से करें जिनके पैर में गोली नहीं लगी है। आपके पास 15 शॉट और बचे हैं। बाईं ओर वाले काउबॉय के पास वापस जाएँ और पंक्ति में नीचे की ओर बढ़ते हुए, कुल 15 शॉट पैर में लगाएँ। आपका चोट कार्ड इस तरह दिखना चाहिए:

चोट	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	ए	ए
2	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए
3
4
कुल	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	1	1	1	1	1

इसके बाद, आपको 80%, यानी 16 काउबॉयज़ को पेट में गोली मारनी होगी। शुरुआत उन पाँच काउबॉयज़ से करें जिन्हें सिर्फ़ एक चोट लगी है। आपके पास 11 और बचे हैं। बाईं ओर वाले काउबॉय के पास वापस जाएँ और पंक्ति में नीचे की ओर बढ़ते हुए, कुल 11 काउबॉयज़ को दो बार गोली मारें। आपका चोट कार्ड इस तरह दिखना चाहिए:

चोट	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	ए	ए
2	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	जी	जी	जी	जी	जी
3	जी	जी	जी	जी	जी	जी	जी	जी	जी	जी	जी
4
कुल	3	3	3	3	3	3	3	3	3	3	3	2	2	2	2	2	2	2	2	2

इसके बाद, आपको 75%, यानी 15, सिर पर गोली चलानी होगी। शुरुआत उन नौ काउबॉय से करें जिन्हें सिर्फ़ दो बार गोली मारी गई है। आपके पास 6 और बचे हैं। बाईं ओर वाले काउबॉय के पास वापस जाएँ और पंक्ति में नीचे जाएँ, कुल 6 काउबॉय को तीन बार गोली मारते हुए। आपका इंजरी कार्ड इस तरह दिखना चाहिए:

चोट	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	एल	ए	ए
2	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	ए	जी	जी	जी	जी	जी
3	जी	जी	जी	जी	जी	जी	जी	जी	जी	जी	जी	एच	एच	एच	एच	एच	एच	एच	एच	एच
4	एच	एच	एच	एच	एच	एच
कुल	4	4	4	4	4	4	3	3	3	3	3	3	3	3	3	3	3	3	3	3

जैसा कि आप देख सकते हैं, 6 काउबॉय को चार बार और 14 को तीन बार गोली मारी गई है। इस प्रकार, केवल तीन बार घायल होने वाले का अधिकतम प्रतिशत 14/20 = 70% है।

सामान्य स्थिति के लिए, यदि चार संभावनाएँ a, b, c, और d हैं, तो अधिकतम अनुपात जो जीवित रह सकता है वह 1-(a+b+c+d) है, जब तक कि a+b+c+d >=3 और a+b+c+d <=4 हो।

मैं इस समाधान के लिए विज़ार्ड ऑफ वेगास फोरम के सदस्य चार्लीपैट्रिक को धन्यवाद देना चाहता हूँ।

[/spoiler]

यह प्रश्न मेरे मंच पर पूछा गया है और इस पर चर्चा की गई है, जिसकी शुरुआत इस पोस्ट से हुई है।

एक मेंढक एक फुट या दो फुट तक कूद सकता है। मेंढक कई बार छलांग लगाकर कुल दस फुट की छलांग लगाता है, हमेशा आगे की ओर। छलांग की दूरी और क्रम को ध्यान में रखते हुए, ऐसा कितने अलग-अलग तरीकों से किया जा सकता है?

गुमनाम

[स्पॉइलर=समाधान]

अगर मेंढक को सिर्फ़ एक फ़ुट ही कूदना है, तो ज़ाहिर है कि उसके पास सिर्फ़ एक ही रास्ता है। याद रखें, मेंढक अपने लक्ष्य से आगे नहीं बढ़ सकता।
यदि मेंढक को दो फीट कूदने की जरूरत है, तो ऐसा करने के दो तरीके हैं - (1) 1 फीट और 1 फीट, या (2) 2 फीट।

अगर मेंढक को तीन फ़ीट कूदना है, तो वह अंतिम छलांग से पहले एक फ़ीट या दो फ़ीट दूर हो सकता है। दो फ़ीट दूर होने का एक तरीका है, जैसा कि चरण 1 में दिखाया गया है, और एक फ़ीट दूर होने के दो तरीके हैं, जैसा कि चरण 2 में दिखाया गया है। इस प्रकार, तीन फ़ीट दूर कूदने के तीन तरीके हैं। इसे (1) 1+1+1, (2) 1+2, (3) 2+1 से भी आसानी से सत्यापित किया जा सकता है।

अगर मेंढक को चार फ़ीट कूदना है, तो वह अंतिम छलांग से पहले दो फ़ीट या तीन फ़ीट दूर हो सकता है। 2 फ़ीट दूर होने के दो तरीके हैं, जैसा कि चरण 2 में दिखाया गया है, और 1 फ़ीट दूर होने के तीन तरीके हैं, जैसा कि चरण 3 में दिखाया गया है। इस प्रकार, चार फ़ीट दूर कूदने के पाँच तरीके हैं। इसे भी आसानी से सत्यापित किया जा सकता है: (1) 1+1+1+1, (2) 1+1+2, (3) 1+2+1, (4) 2+1+1, (5) 2+2।

अगर मेंढक को 5 फ़ीट कूदना है, तो वह अंतिम छलांग से पहले 3 फ़ीट या 4 फ़ीट दूर हो सकता है। 2 फ़ीट दूर होने के 3 तरीके हैं, जैसा कि चरण 3 में दिखाया गया है, और 1 फ़ीट दूर होने के 5 तरीके हैं, जैसा कि चरण 4 में दिखाया गया है। इस प्रकार, पाँच फ़ीट दूर कूदने के 3+5=8 तरीके हैं। इसे इस प्रकार भी आसानी से सत्यापित किया जा सकता है: (1) 1+1+1+1+1, (2) 1+1+1+2, (3) 1+1+2+1, (4) 1+2+1+1, (5) 2+1+1+1, (6) 2+2+1, (7) 2+1+2, (8) 1+2+2।

1, 5, 10, 25, 50 सेंट और $1 के मानक अमेरिकी सिक्कों का उपयोग करके, $1 के लिए कितने तरीकों से बदलाव किया जा सकता है?

Gialmere

उत्तर 293 है।

[स्पॉइलर=समाधान]

मान लें कि a(x) = केवल पेनी और निकल का उपयोग करके x सेंट बनाने के तरीकों की संख्या, जहां x, 5 से विभाज्य है।

ए(एक्स) = 1+(एक्स/5)

दूसरे शब्दों में, तरीकों की संख्या परिवर्तन में संभावित निकल्स की संख्या है, जो 0 से x/5 तक होगी।

मान लें कि b(x) = केवल पेनी, निकल और डाइम का उपयोग करके x सेंट बनाने के तरीकों की संख्या, जहां x, 5 से विभाज्य है।

बी(0)=1
बी(5)=2
b(x) = a(x) + b(x-10), जहाँ x>=10.

सरल अंग्रेजी में, x सेंट बनाने के तरीकों की संख्या, (1) b(x-10) = प्रत्येक तरीके में एक डाइम जोड़कर x-10 सेंट के लिए तरीकों की संख्या और (2) a(x) = बिना डाइम का उपयोग किए तरीकों की संख्या का योग है।

मान लें कि c(x) = x सेंट बनाने के तरीकों की संख्या, केवल पेनी, निकल, डाइम और क्वार्टर का उपयोग करके, जहां x, 25 से विभाज्य है।

सी(0) = 1
c(x) = b(x) + c(x-25), जहाँ x>=25.

सरल अंग्रेजी में, x सेंट बनाने के तरीकों की संख्या, (1) c(x-25) = प्रत्येक तरीके में एक चौथाई जोड़कर x-25 सेंट के लिए तरीकों की संख्या और (2) b(x) = बिना किसी चौथाई का उपयोग किए तरीकों की संख्या का योग है।

मान लें कि d(x) = x सेंट बनाने के तरीकों की संख्या, केवल पेनी, निकल, डाइम, क्वार्टर और आधे डॉलर का उपयोग करके, जहां x 50 से विभाज्य है।

डी(0) = 1
d(x) = c(x) + d(x-50), जहाँ x>=50.

सरल अंग्रेजी में, x सेंट बनाने के तरीकों की संख्या, (1) d(x-50) = प्रत्येक तरीके में आधा डॉलर जोड़कर x-50 सेंट के तरीकों की संख्या और (2) c(x) = बिना आधे डॉलर का उपयोग किए तरीकों की संख्या का योग है।

नीचे दी गई तालिका x = 5 से 100 तक के लिए इन मानों को दर्शाती है।

बदलाव लाने के तरीके

एक्स	ए(एक्स)	बी(एक्स)	सी(एक्स)	डी(एक्स)
0	1	1	1
5	2	2	0
10	3	4	0
15	4	6	0
20	5	9	0
25	6	12	13
30	7	16	0
35	8	20	0
40	9	25	0
45	10	30	0
50	11	36	49	50
55	12	42	0
60	13	49	0
65	14	56	0
70	15	64	0
75	16	72	121
80	17	81	0
85	18	90	0
90	19	100	0
95	20	110	0
100	21	121	242	292

अंत में, $1 के सिक्के के लिए एक जोड़ें और उत्तर 292+1 = 293 होगा।

[/spoiler]

अनगिनत बल्ब हैं, सभी बंद। बल्बों के जलने के बीच का समय एक घातांकीय वितरण* का होता है जिसका माध्य एक दिन होता है। एक बार बल्ब जलने के बाद, उसकी जीवन प्रत्याशा भी एक घातांकीय वितरण का अनुसरण करती है जिसका माध्य एक दिन होता है।

पहला प्रकाश बल्ब जलने तक का औसत समय क्या है?

*: घातांकीय वितरण का पालन करने वाली यादृच्छिक घटनाओं में स्मृति-रहित गुण होता है, अर्थात अतीत का कोई महत्व नहीं होता। दूसरे शब्दों में, कोई भी घटना कभी भी अतिदेय नहीं होती और उसके घटित होने की संभावना हमेशा समान रहती है।

Ace2

उत्तर है e - 1 = लगभग 1.7182818...

[स्पॉइलर=समाधान]

औसतन, पहला प्रकाश बल्ब जलने में एक दिन लगेगा।

उसके बाद, अगली महत्वपूर्ण घटना, या तो नया बल्ब जलेगा या पहला बल्ब जल जाएगा, तक औसतन आधा दिन लगेगा। हम उस घटना तक प्रतीक्षा समय में आधा दिन जोड़ देते हैं। तो, अब हमारे पास 1 + (1/2) = 1.5 दिन हैं।

दूसरी घटना में दूसरा बल्ब जलने की आधी संभावना है। उस स्थिति में, अगली महत्वपूर्ण घटना (या तो पहले दो बल्बों में से एक का जलना या एक नया बल्ब जलना) होने तक 1/3 दिन का प्रतीक्षा समय है। इसलिए, प्रतीक्षा समय में 1/2 (इतनी दूर तक पहुँचने की संभावना) और 1/3 का गुणनफल, जो 1/6 के बराबर है, जोड़ें। तो, हम 1.5 + 1/6 = 5/3 = 1.66667 दिन पर नहीं हैं।

तीसरी महत्वपूर्ण घटना के तीसरे बल्ब के जलने की (1/2)*(1/3) = 1/6 संभावना है। उस स्थिति में, अगली महत्वपूर्ण घटना (या तो पहले तीन बल्बों में से एक का जलना या एक नया बल्ब जलना) होने तक 1/4 दिन का प्रतीक्षा समय है। इसलिए, प्रतीक्षा समय में 1/6 (इतनी दूर तक पहुँचने की संभावना) और 1/4 का गुणनफल, जो 1/24 के बराबर है, जोड़ें। तो, हम 5/3 + 1/24 = 41/24 = 1.7083 दिन पर नहीं हैं।

इस पैटर्न का अनुसरण करते हुए, उत्तर है (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...

यह सामान्य ज्ञान होना चाहिए कि e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...

अंतर सिर्फ़ इतना है कि हमारे उत्तर में 1/0! कारक नहीं है। इसलिए, उत्तर है e - 1/0! = e - 1 = लगभग 1.7182818...

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

A, B, C, और D सभी भिन्न धनात्मक पूर्णांक हैं।

ए < बी < सी < डी

सबसे बड़ा D ज्ञात कीजिए ताकि

1/ए + 1/बी + 1/सी + 1/डी = 1

Gialmere

उत्तर 42 है। A, B और C क्रमशः 2, 3 और 7 हैं।

1/2 + 1/3 + 1/7 + 1/42 = 1.

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

द क्वीन्स गैम्बिट देखने के बाद, मैंने देखा कि शो में कोई भी गेम ड्रॉ पर समाप्त नहीं हुआ। मुझे लगा कि उच्च स्तर पर शतरंज में बहुत सारे ड्रॉ होते हैं। ग्रैंडमास्टर स्तर के शतरंज में, कितने प्रतिशत गेम ड्रॉ पर समाप्त होते हैं?

गुमनाम

ChessBase.com पर प्रकाशित लेख "क्या शतरंज में ड्रॉ की संख्या बढ़ गई है?" के अनुसार, लेखक कियु झोउ ने बताया है कि 2600 या उससे अधिक (ग्रैंडमास्टर बनने के लिए 2500 अंक चाहिए) के खिलाड़ियों के बीच 78,468 रेटेड खेलों में, निम्नलिखित परिणाम सामने आए:

काला जीतता है: 18.0%
सफेद जीत: 28.9%
ड्रा: 53.1%

एक 5x5 पेगबोर्ड और 3 खूंटियाँ हैं। क्या संभावना है कि तीन बेतरतीब ढंग से रखी खूंटियाँ मिलकर एक त्रिभुज बनाएँ?

गुमनाम

93.39%

[स्पॉइलर=समाधान]

सबसे पहले, खूंटियों के लिए combin(25,3) = 2,300 संभावित संयोजन हैं।

इनमें से कितने संयोजन मिलकर त्रिभुज बनाते हैं? आइए इस बोर्ड की मदद लें:

खूंटी बोर्ड

सबसे पहले, पाँच पंक्तियाँ, पाँच स्तंभ और दो विकर्ण हैं। इनमें से किसी एक के लिए, खूँटियों को एक पंक्ति में रखने के लिए संयोजन (5,3) = 10 तरीके हैं। इस प्रकार, 12*10 = 120 संयोजन हैं।

दूसरा, किसी पंक्ति/स्तंभ के मध्य वर्ग को आसन्न पंक्ति/स्तंभ के मध्य वर्ग से जोड़ने के चार तरीके हैं। दूसरे शब्दों में, ये तीन स्थान हैं:

ए3, बी4, सी5
सी5, डी4, ई3
ई3, डी2, सी1
सी1, बी2, ए3

तो, अब हम 120 + 4 = 124 पर हैं

तीसरा, चार अलग-अलग विकर्ण रेखाएँ हैं जो चार स्थान हैं:

ए2, बी3, सी4, डी5
बी5, सी4, डी3, ई2
ई4, डी3, सी2, बी1
डी1, सी2, बी3, ए4

उनमें से प्रत्येक के लिए तीन खूंटियाँ लगाने के combin(4,3)=4 तरीके हैं। तो इसमें 4*4 = 16 और जुड़ जाते हैं।

अब हम 124+16 = 140 पर हैं

चौथा, शतरंज में घोड़ों के 2x1 L आकार में चलने के तरीके पर विचार करें। प्रत्येक कोने के लिए घोड़ा दो तरह से चल सकता है। इन सभी में घोड़ा उसी पंक्ति में दोबारा चल सकता है जहाँ पहली चाल चली थी। यानी 4*2 = 8 और:

ए1, सी2, ई3 ए1, बी3, सी5
ए5, बी3, सी1
ए5, सी4, ई3
ई5, सी4, ए3
ई5, डी3, सी1
ई1, डी3, सी5
ई1, सी2, ए3

चार ऐसी नाइट लाइनें भी हैं जो केंद्र से होकर जाती हैं:

ए2, सी3, ई4
ए4, सी3, ई2
बी5, सी3, डी1
डी5, सी3, बी1

12 नाइट लाइनों को जोड़ने पर, हम 140+12= 152 पर हैं

यदि कुल 2,300 संयोजन हैं और 152 रेखाएँ बनाते हैं, तो 2300-152 = 2,148 रेखाएँ नहीं बनाते हैं और इस प्रकार त्रिभुज बनाते हैं।

इस प्रकार, हमारा उत्तर 2,148/2,300 = 93.39% है।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

आपको दिया गया है:

उस समय सतह से हवा में मार करने वाली मिसाइल के ठीक ऊपर आठ मील की दूरी पर एक हवाई जहाज खड़ा था, जिसे दागा गया था।
हर समय, हवाई जहाज सीधी दिशा में चलता है।
हवाई जहाज 600 मील प्रति घंटे की गति से चलता है।
यह मिसाइल 2000 मील प्रति घंटे की गति से चलती है।
मिसाइल हमेशा ऐसे कोण पर चलती है जो सीधे हवाई जहाज के सामने होता है।

प्रश्न:

मिसाइल से टकराने से पहले विमान कितनी दूरी तय करेगा?
मिसाइल को विमान पर हमला करने में कितना समय लगेगा?
मिसाइल का उड़ान पथ कितना लम्बा है?

गुमनाम

मिसाइल से टकराने से पहले विमान कितनी दूरी तय करेगा? = 240/91 मील
मिसाइल को विमान पर हमला करने में कितना समय लगेगा? = 2/455 घंटे
मिसाइल कितनी दूरी तय करेगी? = 800/91 मील

यहाँ मेरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मान लीजिए:

90% जनता मास्क पहनती है।
मास्क पहनने वालों में कोरोना वायरस होने की संभावना 1% है, जबकि मास्क न पहनने वालों में 3% है।

किसी व्यक्ति को यादृच्छिक रूप से कोरोनावायरस के साथ चुना जाता है। क्या संभावना है कि वह मास्क पहनता हो?

गुमनाम

यह एक क्लासिक बायेसियन सशर्त संभाव्यता प्रश्न है।

उत्तर है संभावना (कोई व्यक्ति मास्क पहनता है और उसे कोरोनावायरस है)/संभावना (किसी को कोरोनावायरस है) =

(0.9*0.01) / (0.9*0.01 + 0.1*0.03) = 75%.

एक वर्ग के बीच में एक चींटी है। वह ऊपरी बाएँ कोने से 17 इंच, ऊपरी दाएँ कोने से 20 इंच और निचले दाएँ कोने से 13 इंच की दूरी पर है।

वर्ग कितना बड़ा है?

गुमनाम

c^2 = a^2 + b^2 -2ab*cos(c)
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)

369 वर्ग इंच.

[स्पॉइलर=समाधान]

सबसे पहले, त्रिभुज ABE को 90 डिग्री घुमाकर एक नया त्रिभुज BDF बनाएं।

चूँकि त्रिभुज को 90 डिग्री घुमाया गया था, इसलिए परिभाषा के अनुसार कोण EBF = 90 है। पाइथागोरस सूत्र के अनुसार, EF = 20*sqrt(2)।

कोसाइन के नियम से: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).

289 = 169 + 800 - 520*sqrt(2)*cos(DEF)

520*sqrt(2)*cos(DEF) = 680.

cos(DEF) = 17*sqrt(2)/26.

याद करें, sin^2(x) + cos^2(x) = 1. आइए इसका उपयोग sin(DEF) को हल करने के लिए करें।

sin^2(DEF) + cos^2(DEF) = 1

sin^2(DEF) + (17*sqrt(2)/26)^2 = 1

sin^2(DEF) + 289/338 = 1

sin^2(DEF) = 49/338

sin(DEF) = 7*sqrt(2)/26

अब कोण BED पर विचार करें।

कोण BED = कोण BEF + कोण FED.

हम जानते हैं कि EBF 90 डिग्री का होता है और एक समद्विबाहु त्रिभुज है। इससे कोण BEF 45 डिग्री का हो जाएगा।

तो, कोण BED = 45 डिग्री + कोण FED.

याद करें, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).

cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - पाप(BEF)*sin(FED)

= (1/वर्ग(2))*17*वर्ग(2)/26 - (1/वर्ग(2))*7*वर्ग(2)/26

= (17/26) - (7/26) = 10/26 = 5/13

आइये कोसाइन के नियम को पुनः लागू करें, इस बार त्रिभुज BED पर।

बीडी^2 = 20^2 + 13^2 - 2*20*13*(5/13)

= 400 + 169 - 200 = 369

BD प्रश्नगत वर्ग की भुजा है, अतः BD^2 उस वर्ग का क्षेत्रफल है, जिसे हमने 369 दर्शाया है।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

आप एक मनोरंजन पार्क में रात्रिकालीन आतिशबाजी प्रदर्शन के प्रभारी एक आतिशबाज़ी विशेषज्ञ हैं। आपको यूरोप से कुछ नए स्टाइल के रॉकेट मिले हैं और आप उनमें से एक का परीक्षण कर रहे हैं ताकि उसे अपने शो के संगीत साउंडट्रैक के साथ समयबद्ध किया जा सके।

आतिशबाजी रॉकेट को 4 ms^-2 के निरंतर त्वरण के साथ ऊर्ध्वाधर रूप से ऊपर की ओर तब तक दागा जाता है जब तक कि रासायनिक ईंधन समाप्त न हो जाए। फिर गुरुत्वाकर्षण द्वारा इसकी चढ़ाई धीमी हो जाती है जब तक कि यह 138 मीटर की अधिकतम ऊँचाई तक नहीं पहुँच जाता, जहाँ यह विस्फोटित हो जाता है।

यह मानते हुए कि कोई वायु प्रतिरोध नहीं है तथा गुरुत्वाकर्षण के कारण त्वरण 9.8 मीटर प्रति सेकंड है, रॉकेट को अपनी अधिकतम ऊंचाई तक पहुंचने में कितना समय लगेगा?

Gialmere

उत्तर है 483/49 = लगभग 9.8571 सेकंड.

[स्पॉइलर=समाधान]

होने देना:
t = रॉकेट ईंधन समाप्त होने के बाद का समय।
r = रॉकेट ईंधन का समय।

मैं त्वरण को ऊपर की दिशा में व्यक्त करूँगा। तो, रॉकेट ईंधन के जलने के बाद त्वरण -9.8 है।

याद दिला दें कि त्वरण का समाकल वेग है और वेग का समाकल स्थान है। आइए स्थान को ज़मीन के सापेक्ष बनाएँ।

जब रॉकेट को पहली बार प्रक्षेपित किया गया तो हमें बताया गया कि त्वरण 4 है।

समाकलन लेते हुए, r सेकण्ड के बाद रॉकेट का वेग 4r के बराबर होता है।

वेग का समाकल लेने पर हमें 2r ² के r सेकंड के बाद रॉकेट का स्थान मिलता है।

अब आइए देखें कि रॉकेट ईंधन के जलने के बाद क्या होता है।

हमें दिया गया है कि गुरुत्वाकर्षण के कारण त्वरण -9.8 है।

समय t पर गुरुत्वाकर्षण के कारण वेग -9.8t है। हालाँकि, रॉकेट से ऊपर की ओर इसका वेग भी 4r है।

मान लीजिए v(t) = समय t पर वेग

वी(टी) = -9.8टी + 4आर

रॉकेट अधिकतम ऊंचाई तब प्राप्त करेगा जब v(t) = 0 होगा। आइये इसका हल निकालें।

v(t) = 0 = -9.8t + 4r
4आर = 9.8टी
टी = 40/98 आर = 20आर/49.

दूसरे शब्दों में, रॉकेट ईंधन जितना भी समय तक चला, रॉकेट उस समय के 20/49 भाग तक ऊपर की ओर यात्रा करता रहेगा।

हमें यह भी बताया गया है कि अधिकतम ऊंचाई पर तय की गई दूरी 138 है।

आइए, तय की गई दूरी का सूत्र प्राप्त करने के लिए v(t) का समाकल लें, जिसे हम d(t) कहेंगे।

d(t) = -4.9t ² + 4rt + c, जहाँ c एकीकरण का स्थिरांक है।

जैसा कि हम पहले ही दिखा चुके हैं, ईंधन के जलने तक रॉकेट 2r ² की दूरी तय कर चुका था, इसलिए यह समाकलन का स्थिरांक होना चाहिए। इससे हमें यह मिलता है:

डी(टी) = -4.9 ^{टी 2} + 4आरटी + 2आर ²

हम जानते हैं कि 138 की अधिकतम ऊंचाई 20r/49 समय पर पहुंची थी, तो आइए r को हल करने के लिए समीकरण में t=20r/49 डालें:

d((20r/49) = -4.9((20r/49) ² + 4r(20r/49) + 2r ² = 138

आर ² *(-1960/2401 + 80/49 + 2) = 138

आर ² = 49

आर = 7

इस प्रकार, रॉकेट ईंधन सात सेकंड तक चला।

हम पहले से ही जानते हैं कि रॉकेट उस समय के 20/49 भाग तक ऊपर जाता रहा, जो कि 140/49 = लगभग 2.8571 सेकंड है।

इस प्रकार, प्रक्षेपण से अधिकतम वेग तक का समय 7 + 140/49 = 483/49 = लगभग 9.8571 सेकंड है

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

2 से 12 तक का योग प्राप्त करने के लिए दो पासों को कितनी बार उछालना चाहिए? कृपया अपने उत्तर के लिए कैलकुलस का प्रयोग करें।

BruceZ

लगभग 61.2173847639572 रोल.

[स्पॉइलर=समाधान]

याद रखें कि कुल 2 रोल आने की प्रायिकता 1/36 है। t रोल में, कुल 2 रोल आने की अपेक्षित प्रायिकता t/36 है। मान लें कि रोल के बीच का समय t/36 के माध्य के साथ चरघातांकी रूप से वितरित है। पॉइसन वितरण हमें बताता है कि कुल 2 रोल आने पर शून्य रोल आने की प्रायिकता exp(-t/36) है।

याद कीजिए कि कुल 3 आने की प्रायिकता 2/36 = 1/18 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 3 आने पर शून्य आने की प्रायिकता exp(-t/18) है।

याद कीजिए कि कुल 4 आने की प्रायिकता 3/36 = 1/12 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 4 आने पर शून्य आने की प्रायिकता exp(-t/12) है।

याद कीजिए कि कुल 5 आने की प्रायिकता 4/36 = 1/9 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 5 आने पर शून्य आने की प्रायिकता exp(-t/9) है।

याद कीजिए कि कुल 6 आने की प्रायिकता 5/36 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 6 आने पर शून्य आने की प्रायिकता exp(-5t/36) है।

याद कीजिए कि कुल 7 आने की प्रायिकता 6/36 = 1/6 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 7 आने पर शून्य आने की प्रायिकता exp(-t/6) है।

8 से 12 के लिए संभावनाएं 2 से 6 के लिए समान हैं।

इस प्रकार, संभावना है कि प्रत्येक कुल की t इकाइयों में कम से कम एक बार रोल किया गया है:

(1-एक्सप(-t/36))^2 * (1-एक्सप(-t/18))^2 * (1-एक्सप(-t/12))^2 * (1-एक्सप(-t/9))^2 * (1-एक्सप(-5t/36))^2 * (1-एक्सप(-t/6))

कम से कम कुल समय की t इकाइयों में रोल न किए जाने की संभावना 1 है - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))

कम से कम एक कुल के बिना अपेक्षित समय प्राप्त करने के लिए हम उपरोक्त फ़ंक्शन को 0 से अनंत तक एकीकृत करते हैं।

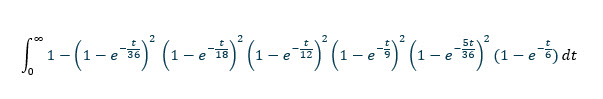
एक इंटीग्रल कैलकुलेटर (मैं इसकी अनुशंसा करता हूं) इसे आसानी से हल कर देगा क्योंकि 769767316159/12574325400 = लगभग 61.2173847639572 रोल्स।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

घनाभ एक त्रि-आयामी ब्लॉक है, जो इकाई-वर्गों से बना होता है।

घनाभ

एक a × b × c घनाभ, समान इकाई घनों abc से बना है, जैसे 3x3x3 रूबिक घन। घनों को दो परस्पर अनन्य प्रकारों में विभाजित करें। बाह्य घन वे होते हैं जो घनाभ के फलकों का निर्माण करते हैं; आंतरिक घन पूरी तरह से घिरे होते हैं। उदाहरण के लिए, चित्रित घनाभ में 74 बाह्य और 10 आंतरिक घन हैं।

सभी घनाभों की विमाएँ इस प्रकार बताइए कि बाह्य घनों की संख्या आंतरिक घनों की संख्या के बराबर हो।

Gialmere

ऐसे 20 संभावित घनाभ हैं।

[स्पॉइलर=सटीक आयाम]

5 x 13 x 132
5 x 14 x 72
5 x 15 x 52
5 x 16 x 42
5 x 17 x 36
5 x 18 x 32
5 x 20 x 27
5 x 22 x 24
6 x 9 x 56
6 x 10 x 32
6 x 11 x 24
6 x 12 x 20
6 x 14 x 16
7 x 7 x 100
7 x 8 x 30
7 x 9 x 20
7 x 10 x 16
8 x 8 x 18
8 x 9 x 14
8 x 10 x 12

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मान लीजिए 0 < a < b. कौन सा अधिक है a^b या b^a?

गुमनाम

इसका उत्तर विशेष रूप से a और b पर निर्भर करता है, लेकिन दो सामान्य नियम अधिकांश स्थितियों को संबोधित करेंगे।

यदि a > e, तो a^b > b^a

यदि b < e, तो a^b < b^a

यदि a < e तथा b > e, तो निर्धारण के लिए पर्याप्त जानकारी नहीं है।

समाधान यहां है (पीडीएफ).

एक ग्रेनेड को एक अथाह गड्ढे में फेंका जाता है। औसतन, ग्रेनेड छह सेकंड में फट जाता है। इसके फटने तक का समय स्मृतिहीन होता है, यानी किसी भी क्षण विस्फोट की संभावना हमेशा एक समान होती है और पिन खींचने के बाद से कितना भी समय बीत गया हो, इससे स्वतंत्र होती है। दूसरे शब्दों में, इसका जीवनकाल घातांकीय वितरण का अनुसरण करता है। मान लीजिए त्वरण 32 फीट प्रति सेकंड है।

Ace2

1,152 फीट

यहां मेरा पूरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

एक गेम शो के बारे में सोचिए जिसमें दो प्रतियोगी स्वार्थी और बेहतरीन तर्कशास्त्री दोनों हैं। ये रहे नियम।

मेजबान दो प्रतियोगियों के बीच एक मेज पर 1,000,000 डॉलर रखता है।
प्रतियोगी 'ए' से यह सुझाव देने को कहा गया कि धनराशि को दोनों प्रतियोगियों के बीच किस प्रकार बांटा जाए।
प्रतियोगी बी को सुझाव को स्वीकार या अस्वीकार करने के लिए कहा जाएगा।
यदि प्रतियोगी बी सुझाव स्वीकार कर लेता है, तो वे पैसे को इस प्रकार बांट लेते हैं और खेल समाप्त हो जाता है।
यदि प्रतियोगी बी सुझाव को अस्वीकार कर देता है, तो मेजबान मेज पर मौजूद राशि का 10% हटा देगा।
इसके बाद मेजबान प्रतियोगी बी से सुझाव मांगेगा और प्रतियोगी ए को उसे स्वीकार या अस्वीकार करने का समान अवसर मिलेगा।
अगर प्रतियोगी A सुझाव स्वीकार कर लेता है, तो वे उसे उसी तरह बाँट लेते हैं और खेल खत्म हो जाता है। अगर वह उसे अस्वीकार कर देता है, तो मेज़बान मेज पर बची हुई राशि का 10% और ले लेता है। फिर चरण 2 पर वापस जाएँ और सुझाव स्वीकार होने तक यही दोहराते रहें।

प्रश्न यह है कि प्रतियोगी 'ए' को अपनी प्रारंभिक बारी में धन को किस प्रकार विभाजित करने का सुझाव देना चाहिए?

गुमनाम

उसे सुझाव देना चाहिए कि वह अपने लिए 10/19 हिस्सा रखे, जिसमें से एक पैसा कम हो, और बी को 9/19 हिस्सा, जिसमें एक पैसा और हो, दे। दूसरे शब्दों में:

ए: $526,315.78
बी: $473,684.22

[स्पॉइलर=समाधान]

मुख्य बात यह है कि A को B को यथासंभव उदासीनता बिंदु के करीब रखना चाहिए।

आइए दूसरे खिलाड़ी के साथ पॉट के अनुपात को r कहें। अगर B प्रस्ताव स्वीकार कर लेता है, तो उसे r×$1,000,000 मिलता है।

अगर B प्रस्ताव को अस्वीकार कर देता है, तो मेज़बान 10% हिस्सा ले लेगा। इसके बाद, B को स्थिति का लाभ मिल जाएगा और वह प्रतियोगी A को r का एक हिस्सा दे देगा और 1-r अपने पास रख लेगा।

r के लिए हल करना...

आर×$1,000,000 = (1-आर)×$900,000.
आर×$1,900,000 = $900,000.
आर = $900,000/$1,900,000 = 9/19.

A नहीं चाहता कि B पूरी तरह से उदासीन रहे, कहीं ऐसा न हो कि वह बेतरतीब ढंग से चुनाव कर ले और मेज़बान के जीतने की संभावना बढ़ जाए। इसलिए, A को B को अतिरिक्त पैसा देना चाहिए और उसे (9/19) × $1,000,000 + $0.01 = $473,684.22 की पेशकश करनी चाहिए।

ए: $526,315.78
बी: $473,684.22

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

दो शहर, फॉन्टलरॉय और साउथवर्थ, एक नहर के ठीक सामने स्थित हैं। दो फ़ेयर दिन भर इन दोनों शहरों के बीच आते-जाते रहते हैं। दोनों फ़ेयर अलग-अलग गति से चलते हैं। एक ही समय पर, दोनों फ़ेयर, हर शहर से एक, निकलते हैं।

पहली बार वे साउथवर्थ से 5 मील दूर से पार करते हैं। दूसरी बार वे फॉन्टलरॉय से 3 मील दूर से पार करते हैं। मान लीजिए कि सामान चढ़ाने और उतारने में कोई समय नहीं लगता, लेकिन दोनों तुरंत यू-टर्न ले लेते हैं। यह भी मान लीजिए कि वे सीधी रेखा में चलते हैं।

दोनों शहर एक दूसरे से कितनी दूरी पर हैं?

गुमनाम

12 मील

मान लीजिए t ₁ = पहली क्रॉसिंग तक का समय
मान लें t ₂ = दूसरी क्रॉसिंग तक का समय
r = फॉन्टलरॉय से आरंभ में रवाना होने वाली नौका की गति का साउथवर्थ से आरंभ में रवाना होने वाली नौका की गति से अनुपात।
c = दो शहरों के बीच चैनल की दूरी.

हमें दिया गया है कि वे पहली बार साउथवर्थ से 5 मील की दूरी पर पार करते हैं। इसे सूत्रों में व्यक्त करने के लिए:

सी-5 = आर*टी ₁
5 = टी ₁

t ₁ को समान करने पर, हमें प्राप्त होता है:

c-5 = 5r, या r = (c-5)/5

हमें यह भी बताया गया है कि दूसरी बार वे फॉन्टलरॉय से 3 मील की दूरी पर पार करते हैं। इसे सूत्रों में व्यक्त करने के लिए:

3c - 3 = r*t ₂
सी+3 = टी ₂

t ₂ को समान करने पर, हमें प्राप्त होता है:

2c - 3 = r*(c+3)

प्रतिस्थापित करें r=(c-5)/5

2c-3 = [(c-5)/5] * (c+3)
10c - 15 = c^2 - 2c - 15
सी^2 - 12सी = 0 सी - 12 = 0 सी = 12

तो, चैनल 12 मील लंबा है।

निम्नलिखित आरेख में, नीले क्षेत्र का क्षेत्रफल क्या है?

गुमनाम

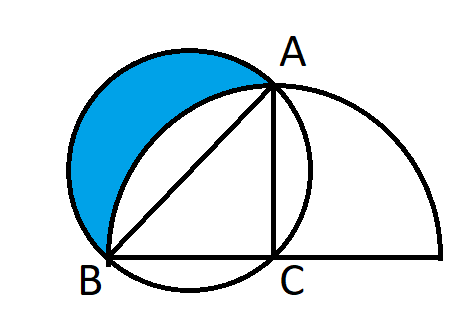
उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

1/2

यहाँ मेरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

शतरंज प्रतियोगिता में, प्रत्येक प्रतियोगी दूसरे प्रतियोगी के विरुद्ध एक मैच खेलता है। प्रत्येक प्रतियोगी को प्रत्येक जीत पर 1 अंक, प्रत्येक बराबरी पर 0.5 अंक और प्रत्येक हार पर 0 अंक मिलते हैं।

टूर्नामेंट के अंत में यह देखा गया कि सभी प्रतियोगियों को अलग-अलग अंक मिले तथा स्कोर रैंकिंग में अंतिम प्रतियोगी ने शीर्ष तीन प्रतियोगियों में से प्रत्येक को हराया।

तदनुसार, टूर्नामेंट में भाग लेने वाले प्रतियोगियों की न्यूनतम संख्या क्या है?

Gialmere

[स्पॉइलर=समाधान]

आइए खिलाड़ियों की संख्या को n कहें।

मेरा अनुमान है कि आखिरी स्थान पर रहने वाले खिलाड़ी ने शीर्ष 3 खिलाड़ियों के खिलाफ केवल तीन जीत हासिल की हैं, और बाकी सभी मैच हारे हैं। इससे उसे 3 अंक मिलते हैं।

फिर मैं हर अगले खिलाड़ी को अंकों के क्रम में पिछले खिलाड़ी से 0.5 अंक ज़्यादा अंक के रूप में गिनता हूँ। इससे सबसे ऊँची रैंकिंग वाले खिलाड़ी को 3+(n-1)/2 अंक मिलेंगे।

3 से 3+(n-1)/2 का योग, प्रति चरण 1/2 अंक लेने पर हमें (((n+5)*(n+6)/2)-15)/2 प्राप्त होता है।

n खिलाड़ियों के साथ खेले गए कुल खेल n*(n-1)/2 होते हैं, जहाँ हर कोई एक-दूसरे के साथ एक-एक बार खेलता है। प्रत्येक खेल में कुल एक अंक मिलता है, जो सभी खिलाड़ियों द्वारा अर्जित कुल अंकों के बराबर होता है।

फिर n के लिए हल करें:

(((एन+5)*(एन+6)/2)-15)/2 = एन*(एन-1)/2
((एन+5)*(एन+6)/2)-15 = एन*(एन-1)
(एन+5)*(एन+6)/2 = एन*(एन-1) + 15
(एन+5)*(एन+6) = 2*एन*(एन-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
एन^2 + 11एन = 2एन^2 - 2एन
एन + 11 = 2एन-2
एन=13

नीचे दी गई तालिका में यह कैसे हो सकता है, इसका एक तरीका दिया गया है। तालिका का मुख्य भाग सभी 78 खेलों के विजेता को दर्शाता है।

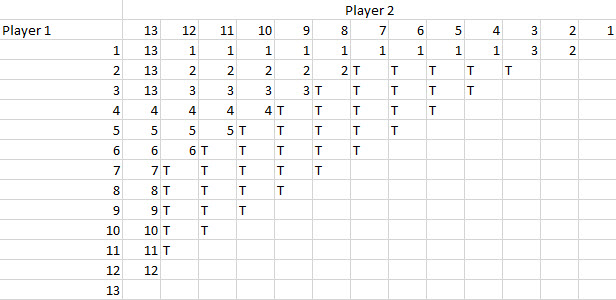
निम्नलिखित तालिका प्रत्येक खिलाड़ी के अंकों की संख्या दर्शाती है।

खिलाड़ी द्वारा कुल अंक

खिलाड़ी	अंक
13	3
12	3.5
11	4
10	4.5
9	5
8	5.5
7	6
6	6.5
5	7
4	7.5
3	8
2	8.5
1	9

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

तोप के गोलों को ढेर करने का कौन सा तरीका अधिक कुशल है - वर्गाकार आधार वाले पिरामिड में, जैसे मिस्र के पिरामिड में, या त्रिभुजाकार आधार वाले पिरामिड में, जैसे चतुष्फलक का निर्माण करते हुए?

गुमनाम

यहां कुछ सूत्र दिए गए हैं जो पाठक के लिए उपयोगी हो सकते हैं:

[स्पॉइलर=पहली n वर्ग संख्याओं का योग] 1 ² + 2 ² + 3 ² + 4 ² + 5 ² + 6 ² + ... + n ² = n*(n+1)*(2n+1)/6 [/स्पॉइलर]

1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6

मेरे उत्तर और समाधान के लिए नीचे स्क्रॉल करें।

"कुशल" से मेरा तात्पर्य यह है कि आपका मतलब है कि जिसमें तोप के गोलों के बीच सबसे कम जगह बर्बाद होती है।

चीजों को सरल रखने के लिए, किसी भी पिरामिड का आयतन निर्धारित करने के लिए, आइए पिरामिड के कोनों पर स्थित गेंदों के केंद्र का उपयोग करें। मान लीजिए कि n, किसी भी पिरामिड के आधार के एक तरफ तोप के गोलों की संख्या है।

आइये सबसे पहले वर्गाकार आधार वाले पिरामिड को देखें।

पूरे पिरामिड में तोप के गोलों की संख्या 1 ² + 2 ² + 3 ² + 4 ² + 5 ² + 6 ² + ... + n ² = n*(n+1)*(2n+1)/6 है।

अब, आइए इस वर्गाकार पिरामिड की ऊँचाई ज्ञात करें जहाँ आधार की एक भुजा n है। जैसा कि चित्र में देखा जा सकता है, भुजाएँ (वर्गाकार आधार के अलावा) समबाहु त्रिभुज हैं। इस प्रकार, तिर्यक ऊँचाई भी n है। आधार के एक कोने से विपरीत कोने की दूरी n*sqrt(2) है। इस प्रकार आधार के एक कोने से आधार के केंद्र की दूरी n*sqrt(2)/2 है। मान लीजिए ऊँचाई h है। ऊँचाई, आधार के एक कोने से आधार के केंद्र की दूरी और तिर्यक ऊँचाई से बने समकोण त्रिभुज पर विचार करें।

h ² + (n*sqrt(2)/2) ² = n ²
h = n*sqrt(2)/2.

याद कीजिए कि पिरामिड का आयतन आधार*ऊँचाई/3 होता है। इससे पिरामिड का आयतन बनता है:

n ² * n* sqrt(2)/2 * (1/3) = n ³ *sqrt(2)/6.

गेंदों का आयतन से अनुपात इस प्रकार है [n*(n+1)*(2n+1)/6] / [n ³ *sqrt(2)/6] = sqrt(2)*n*(n+1)*(2n+1)/(2*n ³ ) = sqrt(2)*(n+1)*(2n+1)/(2*n ² )

अब, आइए त्रिकोणीय आधार वाले पिरामिड को देखें।

पूरे पिरामिड में तोप के गोलों की संख्या 1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6 है।

अब, आधार का क्षेत्रफल ज्ञात करते हैं। याद कीजिए, 30-60-90 के त्रिभुज की भुजाएँ 1/2, sqrt(3)/2 और 1 के समानुपाती होती हैं। इससे, n भुजा वाले समबाहु त्रिभुज की ऊँचाई ज्ञात करना कठिन नहीं है, जो n*sqrt(3)/2 है। इससे आधार का क्षेत्रफल n ² *sqrt(3)/4 हो जाता है।

आधार के एक कोने से आधार के केंद्र तक की दूरी sqrt(3)/3 है। यह देखते हुए कि पिरामिड की तिरछी ऊँचाई 1 है, हम पिरामिड की ऊँचाई sqrt(6)/3 ज्ञात करने के लिए पाइथागोरस का उपयोग कर सकते हैं।

अब हम पिरामिड का आयतन इस प्रकार ज्ञात कर सकते हैं: आधार*ऊंचाई/3 = (n ² *sqrt(3)/4) * (n*sqrt(6)/3) * (1/3) = n ³ *sqrt(18)/36 = n ³ *sqrt(2)/12.

गेंदों का आयतन से अनुपात इस प्रकार है [n*(n+1)*(n+2)/6] / [n ³ *sqrt(2)/12] = sqrt(2)*n*(n+1)*(2n+1)/(2*n ³ ) = sqrt(2)*(n+1)*(n+2)/n ²

यहां गेंदों के आयतन अनुपात की तुलना दी गई है:

वर्गाकार आधार: sqrt(2)*(n+1)*(2n+1)/(2*n ² )
त्रिभुज आधार: sqrt(2)*(n+1)*(n+2)/n ²

आइए दोनों अनुपातों को sqrt(2)*(n+1)/n ² से विभाजित करें:

वर्गाकार आधार: (2n+1)/2 = n + 0.5
त्रिभुज आधार: n+2

जैसे-जैसे n बड़ा होता जाएगा, दोनों पिरामिडों के लिए गेंदों का आयतन अनुपात n के करीब पहुँच जाएगा। दूसरे शब्दों में, तोप के गोले जितने ज़्यादा होंगे, उनकी दक्षता उतनी ही ज़्यादा होगी।

एक तोप के गोले का आयतन दिए जाने पर, दोनों पिरामिडों में दक्षता, जिसे तोप के गोले के आयतन और कुल आयतन के अनुपात के रूप में परिभाषित किया जाता है, pi*sqrt(2)/6 =~ लगभग 74.05% तक पहुँचती है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

किसी भी बड़ी संख्या के लिए, उस संख्या के निकट अभाज्य संख्याओं के बीच औसत दूरी क्या है? साथ ही, उस संख्या से छोटी कितनी अभाज्य संख्याएँ हैं?

गुमनाम

किसी भी बड़ी संख्या n के निकट अभाज्य संख्याओं के बीच औसत दूरी का एक बहुत अच्छा अनुमान ln(n) है। यह उल्लेखनीय है कि यह अनुमानक कितना अच्छा है।

प्रमाण के तौर पर, निम्न तालिका दस लाख के समूहों में पहले 15 मिलियन अभाज्य संख्याओं का परिसर दर्शाती है। यह तालिका अभाज्य संख्याओं के बीच परिसर में औसत दूरी और औसत दूरी के अनुमान को दर्शाती है। यह अनुमान परिसर में सबसे बड़े और सबसे छोटे अभाज्य संख्याओं के औसत का प्राकृतिक लघुगणक है। उदाहरण के लिए, दस लाख अभाज्य संख्याओं के 15वें समूह के लिए, यह ln((256,203,221+275,604,541)/2) है।

अभाज्य संख्याओं के बीच औसत दूरी

प्रथम प्रधान सीमा में	अंतिम प्राइम सीमा में	अभाज्य सीमा में	औसत दूरी	अनुमान लगाना
2	15,485,863	1,000,000	15.485861	15.86229105
15,485,867	32,452,843	1,000,000	16.966976	16.9922867
32,452,867	49,979,687	1,000,000	17.52682	17.53434381
49,979,693	67,867,967	1,000,000	17.888274	17.89175615
67,867,979	86,028,121	1,000,000	18.160142	18.15864108
86,028,157	104,395,301	1,000,000	18.367144	18.3716137
104,395,303	122,949,823	1,000,000	18.55452	18.54883262
122,949,829	141,650,939	1,000,000	18.70111	18.70058553
141,650,963	160,481,183	1,000,000	18.83022	18.83322787
160,481,219	179,424,673	1,000,000	18.943454	18.95103217
179,424,691	198,491,317	1,000,000	19.066626	19.05703535
198,491,329	217,645,177	1,000,000	19.153848	19.15337672
217,645,199	236,887,691	1,000,000	19.242492	19.24163365
236,887,699	256,203,161	1,000,000	19.315462	19.32305683
256,203,221	275,604,541	1,000,000	19.40132	19.39864545

स्रोत: प्राइम पेज पर प्राइम्स के बीच का अंतराल ।

किसी भी दी गई संख्या के अंतर्गत अभाज्य संख्याओं की संख्या ज्ञात करने के लिए, हम ln(n) के औसत दूरी अनुमान को एकीकृत करके शुरुआत कर सकते हैं। इससे हमें किसी भी संख्या n तक के अभाज्य संख्याओं के बीच की औसत दूरियों का योग प्राप्त होगा।

f(n)=ln(n) का समाकल क्या है? याद कीजिए कि भागों द्वारा एकीकरण हमें बताता है:

f(n)*g'(n) dn का समाकल = f(n)*g(n) - (f'(n)*g(n)) dn का समाकल

मान लीजिए f(n)=ln(n) और g'(n)=1. तो f'(n)=1/n और g(n)=n. इस प्रकार ln(n) का समाकल ln(n)*n - ((1/n)*n) का समाकल = ln(n)*n - n = n*(ln(n)-1) होगा।

यदि हम n*(ln(n)-1) को n से भाग दें, तो हमें 2 से n तक की संख्याओं के परिसर के लिए अभाज्य संख्याओं के बीच की औसत दूरी प्राप्त होती है। यह ln(n)-1 है।

यदि हम n को अभाज्य संख्याओं के बीच की इस औसत दूरी से विभाजित करते हैं, तो हमें n के अंतर्गत अभाज्य संख्याओं की औसत संख्या प्राप्त होती है, जो n/(ln(n)-1) के बराबर होती है।

प्रमाण के तौर पर, नीचे दी गई तालिका विभिन्न बड़ी संख्याओं के अंतर्गत अभाज्य संख्याओं की संख्या और अनुमानित मान दर्शाती है। कृपया 15 सार्थक अंकों की सटीकता को क्षमा करें, जो कि एक्सेल में संभव नहीं है। कृपया कोई ऐसी स्प्रेडशीट बनाएँ जो इससे ज़्यादा अंकों को संभाल सके।

अभाज्य संख्याओं के बीच औसत दूरी

एन	n से कम अभाज्य संख्याएँ	एन/(एलएन(एन)-1)
10	4	8
100	25	28
1,000	168	169
10,000	1,229	1,218
100,000	9,592	9,512
1,000,000	78,498	78,030
10,000,000	664,579	661,459
100,000,000	5,761,455	5,740,304
1,000,000,000	50,847,534	50,701,542
10,000,000,000	455,052,511	454,011,971
100,000,000,000	4,118,054,813	4,110,416,301
1,000,000,000,000	37,607,912,018	37,550,193,650
10,000,000,000,000	346,065,536,839	345,618,860,221
100,000,000,000,000	3,204,941,750,802	3,201,414,635,781
1,000,000,000,000,000	29,844,570,422,669	29,816,233,849,001
10,000,000,000,000,000	279,238,341,033,925	279,007,258,230,820
100,000,000,000,000,000	2,623,557,157,654,230	2,621,647,966,812,030
1,000,000,000,000,000,000	24,739,954,287,740,800	24,723,998,785,920,000
10,000,000,000,000,000,000	234,057,667,276,344,000	233,922,961,602,470,000
100,000,000,000,000,000,000	2,220,819,602,560,910,000	2,219,671,974,013,730,000
1,000,000,000,000,000,000,000	21,127,269,486,018,700,000	21,117,412,262,910,000,000
10,000,000,000,000,000,000,000	201,467,286,689,315,000,000	201,381,995,844,660,000,000
100,000,000,000,000,000,000,000	1,925,320,391,606,800,000,000	1,924,577,459,166,810,000,000
1,000,000,000,000,000,000,000,000	18,435,599,767,349,200,000,000	18,429,088,896,563,900,000,000
10,000,000,000,000,000,000,000,000	176,846,309,399,143,000,000,000	176,788,931,049,964,000,000,000

स्रोत: प्राइम पेज पर कितने प्राइम हैं?

नॉनगोन

उपरोक्त आकृति एक भुजा की लम्बाई वाली एक नौभुज है।

कौन अधिक है, AB+AC या AE?

यह समस्या मेन्सा बुलेटिन के मार्च 2021 अंक से ली गई है।

गुमनाम

दोनों बराबर हैं।

इस समस्या का मेरा समाधान यहां है। (पीडीएफ)

मैं किसी भी तीन या चार अंकों वाली संख्या का वर्गमूल आसानी से कैसे ज्ञात कर सकता हूँ, यह मानते हुए कि उत्तर एक पूर्णांक है?

गुमनाम

निम्नलिखित तालिका में 0 से 9 तक की संख्याएं, प्रत्येक का वर्ग तथा उस वर्ग का अंतिम अंक दर्शाया गया है।

वर्ग संख्याओं का अंतिम अंक

मूल संख्या	वर्ग	अंतिम अंक वर्ग का
0	0	0
1	1	1
2	4	4
3	9	9
4	16	6
5	25	5
6	36	6
7	49	9
8	64	4
9	81	1

ध्यान दें कि सम वर्ग वाली संख्याएँ हमेशा 0, 1, 4, 5, 6, या 9 पर समाप्त होती हैं। यह सभी वर्गों के लिए सत्य है। ऐसा इसलिए है क्योंकि मूल संख्या का अंतिम अंक वर्ग के अंतिम अंक को निर्धारित करता है।

चरण 1: वर्ग के अंतिम अंक के आधार पर, हम वर्गमूल के अंतिम अंक को कम करने के लिए निम्न तालिका का उपयोग कर सकते हैं। उदाहरण के लिए, यदि 2809 वर्ग है, तो वर्गमूल का अंतिम अंक 3 या 7 होगा।

मूल संख्या का अंतिम अंक

अंतिम अंक वर्गमूल का	अंतिम अंक वर्ग का
0	0
1	1 या 9
4	2 या 8
5	5
6	4 या 6
9	3 या 7

चरण 2: अब, मूल संख्या लें और उसके दाएँ दो अंक हटा दें। उदाहरण के लिए, यदि मूल संख्या 2809 थी, तो 28 का प्रयोग करें।

चरण 3: चरण 2 के परिणाम से छोटी या बराबर सबसे छोटी वर्ग संख्या ज्ञात कीजिए। फिर, उस वर्ग संख्या का वर्गमूल निकालें। उदाहरण के लिए, 28 से छोटा सबसे छोटा वर्ग 25 है। 25 का वर्गमूल निकालें और आपको 5 प्राप्त होगा।

यदि आपने 100 तक के वर्ग याद नहीं किए हैं, तो आप निम्न तालिका का उपयोग कर सकते हैं।

वर्गमूल का पहला भाग

चरण दो	चरण 3
1 से 3	1
4 से 8	2
9 से 15	3
16 से 24	4
25 से 35	5
36 से 48	6
49 से 63	7
64 से 80	8
81 से 99	9

चरण 4: यदि चरण 1 का परिणाम 0 या 5 है, तो उसे चरण 3 के परिणाम के बाद रखें और आपका काम पूरा हो गया।

अन्यथा, मान लीजिए कि चरण 3 का परिणाम a = है। मान लीजिए b=a×(a+1)। उदाहरण के लिए, यदि चरण 3 का परिणाम 5 है, तो b=5×6=30 है।

चरण 5: यदि b < a, तो वर्गमूल का अंतिम अंक चरण 1 की संभावनाओं में से छोटा होगा। अन्यथा, यदि b >= a, तो यह दो संभावनाओं में से बड़ा होगा।

चरण 6: वर्गमूल निकालने के लिए, चरण 3 से परिणाम लें और फिर चरण 5 से परिणाम प्राप्त करें। दूसरे शब्दों में 10×(चरण 3)+चरण 5।

आइये कुछ उदाहरण देखें:

256 का वर्गमूल ज्ञात करें।

चरण 1: वर्गमूल का अंतिम अंक 4 या 6 है।
चरण 2: अंतिम दो अंक हटाने पर हमें 2 प्राप्त होता है।
चरण 3: 2 से छोटा या उसके बराबर सबसे छोटा वर्ग 1 है। 1 का वर्गमूल 1 है।
चरण 4: 1*(1+1) = 2.
चरण 5: चरण 4 का परिणाम चरण 2 के परिणाम के बराबर है, इसलिए हम चरण 1 के विकल्पों में से बड़े अंक को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 6 है।
चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया जाता है, जो 1 & 6 = 16 आता है।

1369 का वर्गमूल ज्ञात करें।

चरण 1: वर्गमूल का अंतिम अंक 3 या 7 है।
चरण 2: अंतिम दो अंक हटाने पर हमें 13 प्राप्त होता है।
चरण 3: 13 से छोटा या उसके बराबर सबसे छोटा वर्ग 9 है। 9 का वर्गमूल 3 है।
चरण 4: 3*(1+3) = 12.
चरण 5: चरण 2 का परिणाम चरण 4 के परिणाम से बड़ा है, इसलिए हम चरण 1 के विकल्पों में से बड़े अंक को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 7 है।
चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया जाता है, जो 3 & 7 = 37 आता है।

2704 का वर्गमूल ज्ञात कीजिए।

चरण 1: वर्गमूल का अंतिम अंक 2 या 8 है।
चरण 2: अंतिम दो अंक हटाने पर हमें 27 प्राप्त होता है।
चरण 3: 27 से कम या उसके बराबर सबसे छोटा वर्ग 25 है। 25 का वर्गमूल 5 है।
चरण 4: 5*(1+5) = 60.
चरण 5: चरण 2 का परिणाम चरण 4 के परिणाम से छोटा है, इसलिए हम चरण 1 के विकल्पों में से छोटे अंक को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 2 है।
चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया गया परिणाम है, जो 5 & 2 = 52 आता है।

5625 का वर्गमूल ज्ञात कीजिए।

चरण 1: वर्गमूल का अंतिम अंक 5 है।
चरण 2: अंतिम दो अंक हटाने पर हमें 56 प्राप्त होता है।
चरण 3: 56 से छोटा या उसके बराबर सबसे छोटा वर्ग 49 है। 49 का वर्गमूल 7 है।
चरण 4: चरण 1 का परिणाम 0 या 5 है, इसलिए उत्तर चरण 3 का परिणाम है जिसमें चरण 1 का परिणाम जोड़ा गया है: 7 और 5 = 75

6561 का वर्गमूल ज्ञात कीजिए।

चरण 1: अंतिम अंक 1 या 9 है।
चरण 2: अंतिम दो अंक हटाने पर हमें 65 प्राप्त होता है।
चरण 3: 65 से कम या उसके बराबर सबसे छोटा वर्ग 64 है। 64 का वर्गमूल 8 है।
चरण 4: 8*(1+8) = 72.
चरण 5: चरण 2 का परिणाम चरण 4 के परिणाम से कम है, इसलिए हम चरण 1 के विकल्पों में से कम वाले विकल्प को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 1 है।
चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया गया परिणाम है, जो 8 और 1 = 81 आता है।

आप इस विधि का प्रदर्शन यूट्यूब पर देख सकते हैं।

एक भुजा की लंबाई 1 वाले नियमित पंचभुज का क्षेत्रफल क्या है?

गुमनाम

उत्तर के लिए नीचे दिए गए बॉक्स पर क्लिक करें।

(sqrt(5)/4)*sqrt(5+2*sqrt(5)) = लगभग 1.72047740058897.

संकेत के लिए नीचे दिए गए बॉक्स पर क्लिक करें।

[स्पॉइलर=संकेत]

पेंटागन संकेत

उपरोक्त चित्र पर विचार करें. AC = CD.

[/spoiler]

मेरा समाधान यहां है (पीडीएफ)

एक शांत दिन में, चार्ली अपनी डोंगी लेकर नदी पर जाता है और धारा के विपरीत दिशा में चप्पू चलाता है। वह हमेशा एक ही गति से चप्पू चलाता है (दूसरे शब्दों में, अगर हम धारा की उपेक्षा करें, तो वह हमेशा एक ही गति से जाएगा)। नाव छोड़ने के एक मील बाद, उसकी टोपी नदी में गिर जाती है। दस मिनट बाद, उसे एहसास होता है कि उसकी टोपी गायब है और वह तुरंत उसे पकड़ने के लिए यू-टर्न लेता है। चार्ली अपनी टोपी उसी जगह पर पाता है जहाँ से उसने नाव छोड़ी थी।

धारा कितनी तेज़ है?

गुमनाम

उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

3 मील प्रति घंटा.

यहाँ मेरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

निम्नलिखित प्रश्न एक बार बेट से संबंधित है। किसी भी बिल के लिए एक यादृच्छिक अमेरिकी सीरियल नंबर का उपयोग किया जाता है। खिलाड़ी 0 से 9 तक कोई भी तीन अंक चुनता है। उसे तीन अलग-अलग संख्याएँ चुननी होंगी। जीत इस बात पर निर्भर करती है कि इन तीन चुने हुए अंकों में से कितने सीरियल नंबर पर कम से कम एक बार दिखाई देते हैं।

उदाहरण के लिए, अगर खिलाड़ी 7-0-2 चुनता है और सीरियल नंबर 22227755 है, तो दो मैच होंगे। इससे कोई फ़र्क़ नहीं पड़ता कि 2 और 7 कई बार मेल खाते हैं।

यहां प्रस्तावित संभावनाएं इस प्रकार हैं:

3 मैच: 5 से 1
2 मैच: 1 से 1
1 मैच: 9 से 5
0 मैच: 15 से 1

प्रत्येक दांव पर जीतने की संभावना और हाउस एज क्या है?

गुमनाम

निम्नलिखित तालिका में विजेता संयोजनों की संख्या, जीतने की संभावना और प्रत्येक दांव के लिए हाउस एज दर्शाया गया है। दाएँ कॉलम में हाउस एज 7.4% से 8.5% तक है।

सीरियल नंबर दांव

माचिस	भुगतान करता है	युग्म	संभावना	हाउस एज
3	5	15,426,684	0.154267	0.074399
2	1	45,771,270	0.457713	0.084575
1	1.8	33,037,245	0.330372	0.074957
0	15	5,764,801	0.057648	0.077632

1 से 9 तक प्रत्येक अंक का ठीक एक बार प्रयोग करते हुए, तीन भिन्न बनाएं, जिनमें से प्रत्येक के अंश में एक अंक और हर में दो अंक हों, तथा तीनों भिन्नों का योग एक हो।

उदाहरण के लिए, 8/16 + 9/27 + 3/24 सभी शर्तों को पूरा करता है, सिवाय इसके कि योग 23/24 के बराबर है, 1 नहीं।

Gialmere

5/34 + 7/68 + 9/12

[स्पॉइलर=समाधान]

उत्तर खोजने के लिए permut(9,3)*permut(6,3)*permut(3,3)/fact(3) = 60,480 संभावित क्रमपरिवर्तनों को छाँटना होगा। मुझे स्वीकार करना होगा कि मैंने कम से कम एक घंटे तक कोशिश की और कोई हल नहीं मिला।

इसलिए, मैंने नौ अंकों को क्रमबद्ध करने के सभी 362,880 तरीकों से एक प्रोग्राम बनाया और उन सभी का परीक्षण किया। सबसे मुश्किल काम नौ संख्याओं को क्रमबद्ध करने के हर संभव तरीके से क्रमबद्ध करना था। लेक्सोग्राफ़िक सॉर्टिंग का उपयोग करके इसे कैसे किया जाता है, यहाँ बताया गया है।

सभी नौ तत्वों को एक सारणी में रखें, निम्नतम से उच्चतम तक व्यवस्थित करें।
सारणी में वह अंतिम तत्व ढूँढें जिससे अगला तत्व बड़ा हो। यदि कोई तत्व न मिले, तो प्रोग्राम से बाहर निकलें।
चरण 2 के बाद वाले तत्व से शुरू करते हुए, सरणी में वह अंतिम तत्व ढूंढें जो चरण 2 से बड़ा हो।
चरण 2 और 3 से सरणी में तत्वों को बदलें।
चरण 2 से अंत तक सरणी में तत्वों को उलट दें।
चरण 2 पर वापस जाएँ

इस प्रक्रिया का पालन करने पर, आपको छह बार सही उत्तर मिलेगा, तीनों भिन्नों को क्रमबद्ध करने के सभी छह तरीकों के लिए एक बार। [/spoiler]

[स्पॉइलर=कोड]

मैंने निम्नलिखित कोड लिखा, 1 से 9 तक प्रत्येक अंक को लेक्सोग्राफिक क्रम में क्रमबद्ध करने के लिए तथा प्रत्येक का परीक्षण करने के लिए कि क्या यह एक हल है।


शून्य तीन_अंश(शून्य)
{
 int i, x_max, y_max, temp_array[100], होल्ड, pt;
 int lex_array[] = { 1,2,3,4,5,6,7,8,9 };
 int num_elements = sizeof(lex_array) / sizeof(lex_array[0]);
 int गिनती = 0;
 बूल स्टॉप = झूठ;
 डबल टोट3;
 cerr << "तत्वों की संख्या =\t" << num_elements << "\n";
 करना
 {
  गिनती++;
  tot3 = (डबल)lex_array[0] / (डबल)(10 * lex_array[1] + lex_array[2]);
  tot3 += (डबल)lex_array[3] / (डबल)(10 * lex_array[4] + lex_array[5]);
  tot3 += (डबल)lex_array[6] / (डबल)(10 * lex_array[7] + lex_array[8]); 
  यदि (tot3 == 1.0)
  {
   cerr << गिनती << "\t";
   cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
   cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
   cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
  } 
  x_मैक्स = -1;
  के लिए (i = 0; i < (num_elements - 1); i++)
  {
   यदि (lex_array[i] < lex_array[i + 1])
    x_मैक्स = i;
  }
  यदि (x_max >= 0)
  {
   y_मैक्स = 0;
   (i = x_max + 1; i < num_elements; i++) के लिए
   {
    यदि (lex_array[x_max] < lex_array[i])
     y_मैक्स = i;
   }
   होल्ड = lex_array[x_max];
   लेक्स_एरे[x_मैक्स] = लेक्स_एरे[y_मैक्स];
   lex_array[y_max] = होल्ड;
   यदि (x_max + 1 < num_elements - 1) // उलटा
   {
    (i = x_max + 1; i < num_elements; i++) के लिए
    {
     अस्थायी_सरणी[i] = लेक्स_सरणी[i];
    }
    पीटी = 0;
    (i = x_max + 1; i < num_elements; i++) के लिए
    {
     lex_array[i] = temp_array[num_elements - 1 - pt];
     पीटी++;
    }
   }
  }
  अन्य
   रोक = सच;
 } जबकि (रोक == गलत);
}

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

एक आदमी के पास दस गैलन की शराब का एक केग और एक जग था। एक दिन, उसने एक जग शराब से भरा और फिर उसमें पानी भर दिया। बाद में, जब शराब और पानी अच्छी तरह मिल गए, तो उसने एक और जग भरा और फिर से केग में पानी भर दिया। अब केग में शराब और पानी बराबर मात्रा में थे।

जग की क्षमता क्या थी?

Gialmere

10-5*sqrt(2) =~ 2.9289 गैलन

[स्पॉइलर=समाधान]

माना j = जग का आयतन.

पहली बार जग भरने के बाद, जग में 10-j गैलन वाइन बची थी। वाइन की जगह पानी डालने के बाद, पूरे केग में वाइन का अनुपात (10-j)/10 था।

जग से तनुकृत शराब निकालने के बाद, केग में 10 गैलन तनुकृत शराब बची थी। तनुकृत शराब में शुद्ध शराब की मात्रा इस प्रकार व्यक्त की जा सकती है:

(10-जे)*((10-जे)/10) = 5

(10-j)^2 = 50

j^2 - 20j + 100 = 50

जे^2 - 20जे + 50 = 0

j = (20 +/- sqrt(400-200))/2

j = (20 +/- 10*sqrt(2))/2

j = 10 +/- 5*sqrt(2)

जग, केग से बड़ा नहीं हो सकता, इसलिए हमें ऋणात्मक चिह्न का प्रयोग करना चाहिए:

j = 10 - 5*sqrt(2) =~ लगभग 2.92893218813452 गैलन.

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

थैंक्सगिविंग मनाने के लिए, आप और 19 गणितज्ञ एक गोलाकार मेज़ पर बैठे हैं। मेज़ पर बैठे सभी लोग क्रैनबेरी सॉस खाना चाहेंगे, जो इस समय आपके सामने है।

सबसे पहले, आप खुद को परोसें। फिर, सॉस को गोल-गोल घुमाने के बजाय, आप इसे अपने बाएँ या दाएँ बैठे व्यक्ति को बेतरतीब ढंग से देते हैं। फिर वे भी ऐसा ही करते हैं, इसे बेतरतीब ढंग से अपने बाएँ या दाएँ बैठे व्यक्ति को देते हैं। यह तब तक चलता रहता है जब तक कि सभी को किसी न किसी समय क्रैनबेरी सॉस नहीं मिल जाता।

घेरे में मौजूद 20 लोगों में से, क्रैनबेरी सॉस सबसे आखिर में पाने की सबसे अधिक संभावना किसकी है?

Gialmere

बाकी सभी के पास क्रैनबेरी सॉस को अंतिम रूप से प्राप्त करने का समान मौका है।

[स्पॉइलर=समाधान]

आइए एक गणितज्ञ का नाम G लें। G को अंतिम स्थान पर रखने के लिए दो चीजें घटित होनी चाहिए:

क्रैनबेरी को सबसे पहले G के किसी पड़ोसी तक पहुंचना होगा।
क्रैनबेरी को कभी भी G तक पहुंचे बिना विपरीत दिशा में 19 स्थान चलना चाहिए।

आखिरी में पहुँचने के लिए, क्रैनबेरी को अंततः किसी एक पड़ोसी तक पहुँचना होगा। तो इसकी संभावना 100% है।

तो, दूसरे भाग के लिए जो भी संभावना है, वह हर व्यक्ति के लिए समान है। इस प्रकार, प्रत्येक व्यक्ति के अंतिम भाग में आने की संभावना समान है।

अगर यह स्पष्टीकरण स्पष्ट नहीं था, तो जियाल्मेरे को यह समस्या fivethirtyeight.com से मिली। यहाँ वे इसका समाधान बताते हैं । नीचे स्क्रॉल करके उस भाग पर जाएँ जहाँ लिखा है "पिछले हफ़्ते के रिडलर क्लासिक का समाधान।"

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

यहाँ द रिडलर से एक और पहेली है।

एक थैले में 100 कंचे हैं। हर कंचा लाल, नीला या हरा है। अगर थैले से तीन कंचे निकाले जाएँ, तो हर रंग का एक कंचा मिलने की संभावना 20% होगी। थैले में हर रंग के कितने कंचे हैं? कृपया ध्यान दें, मैंने यह नहीं बताया कि कंचे बदले में निकाले जाएँगे या बदले में।

Gialmere

लाल, नीले और हरे कंचों की संख्या क्रमशः 21, 35 और 44 है। इन्हें थैले से बिना बदले निकाला जाता है।

[स्पॉइलर=समाधान]

आइए इसे "प्रतिस्थापन के साथ" मानकर हल करने का प्रयास करें। मान लीजिए कि r, b, और g क्रमशः लाल, नीले और हरे कंचों की संख्या हैं। तब, प्रत्येक रंग का एक कंचा निकालने की प्रायिकता 6*(r/100)*(b/100)*(g/100) होगी। इसे 0.2 के बराबर रखते हुए, हम कह सकते हैं:

6*(आर/100)*(बी/100)*(जी/100) = 0.2
6*आर*बी*जी = 200000

6, 200,000 में समान रूप से विभाजित नहीं होता है। इस प्रकार, r*b*g = 33333.333... के लिए कोई पूर्णांक हल संभव नहीं है। इसलिए, हम प्रतिस्थापन के साथ आरेखण की स्थिति को समाप्त कर सकते हैं।

अब, आइए "बिना प्रतिस्थापन" वाली धारणा को आज़माएँ। इस स्थिति में, प्रत्येक रंग का एक-एक चित्र बनाने की प्रायिकता r*b*g/combin(100,3) = 0.2 है। इसका हल निकालने का प्रयास कर रहे हैं...

आर*बी*जी/161700 = 0.2
आर*बी*जी = 32340

32340 का अभाज्य गुणनखंड 2*2*3*5*7*7*11 है।

हमें इन कारकों को r, b और g के बीच बाँटना होगा, जबकि r+b+g=100 रखना होगा। उदाहरण के लिए, हम यह कोशिश कर सकते हैं:

आर = 2*3*5 = 30
बी = 2*11 = 22
जी = 7*7 = 49

यद्यपि ये सभी अभाज्य गुणनखंडों का सही उपयोग करते हैं, r+b+g = 101, अतः यह वैध समाधान नहीं है।

मुझे डर है कि मुझे किसी भी क्रम में 21, 35, और 44 के मान वाले r, b, और g का हल प्राप्त करने के लिए एक क्रूर बल लूपिंग प्रोग्राम लिखना पड़ा।

[/spoiler]

निम्नलिखित प्रश्न हमें रिडलर एक्सप्रेस के सौजन्य से प्राप्त हुआ है।

मान लीजिए NFL के नियम लागू होते हैं। इस स्थिति पर विचार करें:

खेल के अंत में रेड टीम 14 अंक पीछे है
रेड टीम के पास दो और कब्जे होंगे
ब्लू टीम के पास अब कोई भी कब्ज़ा नहीं रहेगा
आइए फील्ड गोल और सेफ्टी को नजरअंदाज करें, क्योंकि रेड टीम को जीतने का मौका पाने के लिए दो टचडाउन स्कोर करने होंगे।
यदि खेल अतिरिक्त समय तक खिंचता है, तो प्रत्येक टीम के जीतने की संभावना 50% होगी। खेल बराबरी पर समाप्त नहीं हो सकता।
टचडाउन के बाद एक-पॉइंट किक बनाने की संभावना 100% है।
दो-बिंदु रूपांतरण की संभावना p है।

p के किस मान पर लाल टीम को पहले टचडाउन (अब 8 से नीचे) के बाद दो-बिंदु रूपांतरण के लिए किक करने और जाने के प्रति उदासीन होना चाहिए?

गुमनाम

(3-sqrt(2))/2 = लगभग 0.381966011250105

[स्पॉइलर=समाधान]

मान लें कि p = दो-बिंदु रूपांतरण और किक के बीच उदासीनता बिंदु है।

यदि पहला दो-बिंदु रूपांतरण प्रयास सफल होता है, तो लाल टीम दूसरी बार गेंद को किक कर सकती है और जीत सकती है।

यदि पहला दो-बिंदु रूपांतरण प्रयास असफल हो जाता है, तो लाल टीम को दूसरे टचडाउन के बाद फिर से प्रयास करना होगा और फिर ओवरटाइम में खेल जीतना होगा।

पहले टचडाउन के बाद दो-पॉइंट रूपांतरण के लिए जीतने की संभावना p + (1-p)*p/2 है। हम इसे पहले टचडाउन के बाद किक मारकर जीतने की 50% संभावना के बराबर मानते हैं और p के लिए हल करते हैं।

पी + (1-पी)*पी/2 = 1/2
2पी + (1-पी)*पी = 1
3p - p^2 = 1
पी^2 - 3पी + 1 = 0

द्विघात सूत्र का उपयोग करके, p का हल निकालें:

पी = (3 +/- sqrt(5))/2

हम नकारात्मक विकल्प लेते हैं, p को 0 और 1 के बीच रखते हुए, p = (3-sqrt(2))/2 = लगभग 0.381966011250105 प्राप्त करते हैं

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

पिछले "आस्क द विज़ार्ड" कॉलम में, आपसे दो पासों से लगातार दो बार कुल 12 प्राप्त करने के लिए अपेक्षित रोल की संख्या के बारे में पूछा गया था। इसी से संबंधित एक बात यह है कि मैंने आपके फ़ोरम पर किसी को क्रेप्स टेबल पर लगातार 18 पासों (कुल 11) के होने का दावा करते हुए देखा है। ऐसा होने के लिए अपेक्षित रोल क्या हैं?

गुमनाम

41660902667961039785742

यहाँ मेरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

WizCalc की सहायता से सटीक उत्तर मिला।

एक घास का मैदान 100 मीटर त्रिज्या के एक वृत्त के आकार का है और एक गोलाकार बाड़ से घिरा हुआ है। बाड़ के एक निश्चित बिंदु पर एक बकरी को एक जंजीर से हुक से बाँधा गया है। बकरी को ज़्यादा मोटा होने से बचाने के लिए, किसान यह सुनिश्चित करना चाहता है कि वह खेत की आधी घास तक ही पहुँच सके। जंजीर कितनी लंबी होनी चाहिए?

उदाहरण के लिए, वृत्त घास के मैदान को दर्शाता है। S उस जगह को दर्शाता है जहाँ मैदान के किनारे पर ज़ंजीर लगी है। वृत्त का पीला भाग वह है जहाँ बकरी पहुँच सकती है। हरा भाग ज़ंजीर की पहुँच से बाहर है। लक्ष्य ज़ंजीर को सही दूरी पर रखना है ताकि हरा और पीला भाग बराबर हो जाएँ।

बकरी का सवाल

Gialmere

115.87286 मीटर.

[स्पॉइलर=समाधान]

कृपया इस समस्या को हल करने के लिए निम्नलिखित आरेख का संदर्भ लें।

बकरी पहेली

बिंदु Q घास वाले वृत्त का केंद्र है। बकरी की जंजीर बिंदु R पर लगी है। बकरी सभी रंगीन क्षेत्रों तक पहुँच सकती है, जिसमें रेखा PR के नीचे उनका दर्पण प्रतिबिंब भी शामिल है।

आपको दिया गया है कि घास वाले वृत्त की त्रिज्या 100 है, इसलिए b+c = d = 100.

मैं इसे इस तरह हल करूँगा कि हर चीज़ को b के संदर्भ में परिभाषित करूँ। फिर मैं b के साथ तब तक खेलूँगा जब तक मुझे मनचाहा परिणाम न मिल जाए, जहाँ बकरी आधी घास खा सके।

आइए b के पद में e का हल निकालने से शुरुआत करें। b, d, और e भुजाओं वाले त्रिभुज को देखते हुए और पाइथागोरस सूत्र का उपयोग करते हुए:

बी^2 + ई^2 = डी^2
बी^2 + ई^2 = 10000
ई = sqrt(10000 - बी^2)

अब, f को b के पदों में हल करते हैं। याद रखें, हम पहले से ही जानते हैं कि b+c=100, इसलिए c=100-b। पाइथागोरस का प्रयोग करते हुए:

सी^2 + ई^2 = एफ^2
(100-बी)^2 + (10000 - बी^2) = एफ^2
f^2 = 10000 - 200b + b^2 + 10000 - b^2
f^2 = 20000 - 200b
f^2 = 100*(200 - 2b)
f = 10*sqrt(200-2b)

अब, आइए त्रिभुज QRS का क्षेत्रफल ज्ञात करें:

क्यूआरएस = (1/2)*100*e = 50*sqrt(10000 - b^2)

अब, आइए कोण SQR द्वारा काटे गए घास के टुकड़े का क्षेत्रफल ज्ञात करें:

टैन(एसक्यूआर) = ई/बी = sqrt(10000-बी^2)/बी.

स्लाइस SQR = atan(sqrt(10000-b^2)/b)

लाल क्षेत्र स्लाइस SQR माइनस त्रिकोण QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2) के बराबर है।

अब, नीला + हरा + पीला + बैंगनी क्षेत्र ज्ञात करते हैं। ऐसा करने के लिए, हमें कोण QRS ज्ञात करना होगा।

टैन(क्यूआरएस) = ई/सी = sqrt(10000-बी^2)/(100-बी)

कोण QRS = atan(sqrt(10000-b^2)/(100-b)).

इसमें लाल क्षेत्र को जोड़ दें तो हमारे पास बकरी द्वारा खाए जाने वाले कुल क्षेत्रफल का आधा हिस्सा होगा:

atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2)।

कुल क्षेत्रफल प्राप्त करने के लिए, रेखा PR के नीचे वाले भाग के लिए इसे दोगुना करें:

2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2).

घास क्षेत्र का कुल क्षेत्रफल 10,000*pi है।

अब, b के साथ तब तक खेलते रहो जब तक आपको बकरी द्वारा खाए जा सकने वाला क्षेत्रफल 5,000*π के बराबर न मिल जाए। एक्सेल में गोलसीक फ़ंक्शन इस तरह की समस्याओं के लिए बहुत अच्छा है। स्प्रेडशीट से पहले कोई कुछ कैसे कर पाता था, मुझे नहीं पता।

इस विधि का उपयोग करने पर आप पाएंगे कि b = 32.867402.

वहां से हम f = श्रृंखला की लंबाई = 115.8728598 मीटर प्राप्त कर सकते हैं।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

वर्डले में आपका अनुशंसित प्रारंभिक शब्द क्या है?

गुमनाम

इसका उत्तर देने के लिए, मैंने सबसे पहले अनुमत वर्डले समाधानों की सूची के आधार पर प्रत्येक स्थिति में प्रत्येक अक्षर की आवृत्ति को देखा।

वर्डले में अक्षरों की आवृत्ति

पत्र	स्थिति 1	स्थिति 2	स्थिति 3	स्थिति 4	स्थिति 5	कुल
ए	141	304	307	163	64	979
बी	173	16	57	24	11	281
सी	198	40	56	152	31	477
डी	111	20	75	69	118	393
ई	72	242	177	318	424	1233
एफ	136	8	25	35	26	230
जी	115	12	67	76	41	311
एच	69	144	9	28	139	389
मैं	34	202	266	158	11	671
जे	20	2	3	2	0	27
कश्मीर	20	10	12	55	113	210
एल	88	201	112	162	156	719
एम	107	38	61	68	42	316
एन	37	87	139	182	130	575
हे	41	279	244	132	58	754
पी	142	61	58	50	56	367
क्यू	23	5	1	0	0	29
आर	105	267	163	152	212	899
एस	366	16	80	171	36	669
टी	149	77	111	139	253	729
यू	33	186	165	82	1	467
वी	43	15	49	46	0	153
डब्ल्यू	83	44	26	25	17	195
एक्स	0	14	12	3	8	37
वाई	6	23	29	3	364	425
जेड	3	2	11	20	4	40

फिर मैंने वर्डले समाधान सूची में पाँच अलग-अलग अक्षरों वाले सभी शब्दों को देखा और ऊपर दी गई अक्षर आवृत्ति तालिका के अनुसार उन्हें अंक दिए। मैंने सही स्थान पर मिलान के लिए दो अंक और गलत स्थान पर मिलान के लिए एक अंक दिया। फिर मैंने सूची को क्रमबद्ध किया, जो आप नीचे देख सकते हैं।

वर्डले में सर्वश्रेष्ठ शुरुआती शब्द

केंद्रित">बिंदु

रैंक	शब्द
1	घूरना	5835
2	पड़ी	5781
3	स्लेट	5766
4	उठाना	5721
5	उठना	5720
6	सानेर	5694
7	जाल	5691
8	क्रुद्ध	5682
9	बासी	5665
10	टोकरा	5652
11	पता लगाना	5616
12	बाद में	5592
13	शेयर करना	5562
14	इकट्ठा करना	5547
15	डराना	5546
16	ऑल्टर	5542
17	क्रेन	5541
18	चेतावनी	5483
19	आंसू भरी	5479
20	तलें	5475
21	पूरा	5460
22	अतिरिक्त	5457
23	अकेला	5452
24	व्यापार	5449
25	सोते सोते चूकना	5403
26	जाली	5403
27	एक प्रकार की शीस्ट	5392
28	कम से कम	5390
29	चुराई	5377
30	पैमाना	5376
31	प्रतिक्रिया	5376
32	तुरही बजाना	5368
33	पार्स	5351
34	चमक	5340
35	मेल करना	5338
36	सीखना	5324
37	जल्दी	5320
38	लीनट	5307
39	पीला	5285
40	चमक	5280
41	गलियारा	5280
42	किनारा	5274
43	चुराना	5268
44	क्षण	5267
45	अंक	5258
46	स्पष्ट	5258
47	बुढ़ीया	5253
48	पत्थर	5253
49	दिल	5252
50	परास्त	5251
51	शंकु	5248
52	नफरत	5243
53	रिले	5241
54	थाली	5240
55	पूजा	5239
56	सॉस	5236
57	सुरक्षित	5235
58	विदेशी	5233
59	जाति	5232
60	कतरनी	5231
61	बेलर	5230
62	भोंपू	5226
63	डोंगी	5215
64	प्रांत	5213
65	गुर्दे	5210
66	परत	5206
67	जानवरों का शिक्षक	5200
68	बड़ा	5196
69	मोती	5196
70	मार्ग	5194
71	ब्रेस	5192
72	टुकड़ा	5178
73	अवस्था	5171
74	गद्य	5170
75	बीजाणु	5169
76	जगाना	5166
77	अनुग्रह	5164
78	सौर	5152
79	सुइट	5150
80	भूनना	5145
81	बीर	5130
82	विमान	5129
83	क्लीट	5129
84	निपटा	5128
85	भाला	5126
86	महान	5126
87	एडर	5123
88	खीस्तयाग	5116
89	शिखर	5108
90	चाल	5107
91	गुलाम	5097
92	बंद करना	5090
93	बरछा	5090
94	कुल्ला	5088
95	कारण	5087
96	प्रवृत्त	5087
97	मुफ़्तक़ोर	5082
98	शोर	5079
99	क्रेस्ट	5073
100	गंभीर	5068

तो, यह लीजिए, मेरा अनुशंसित प्रारंभिक शब्द, जिसका मैं उपयोग करता हूँ, वह है घूरना।

i^i क्या है?

Aidan

e^(-pi/2) =~ 0.20788.

यहाँ मेरा समाधान (पीडीएफ) है।

आप एक ऐसा खेल खेलना चाहते हैं जिसमें दो साधारण छह-तरफा पासों की ज़रूरत होती है। दुर्भाग्य से, आप पासे खो बैठे हैं। हालाँकि, आपके पास नौ इंडेक्स कार्ड हैं, जिन पर आप अपनी इच्छानुसार निशान लगा सकते हैं। खिलाड़ी को नौ में से दो इंडेक्स कार्ड बिना बदले, यादृच्छिक रूप से चुनने होंगे और उन दोनों कार्डों का योग निकालना होगा।

Gialmere

कार्ड का मान पूर्णांक होना आवश्यक नहीं है।

कार्डों को इस प्रकार चिह्नित करें:

1 @ 0.5
1 @ 1.5
2 @ 2.5
1 @ 3.5
2 @ 4.5
1 @ 5.5
1 @ 6.5

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

क्या यह सच है कि एक निष्पक्ष सिक्के के उछाले जाने पर, उस तरफ गिरने की अधिक संभावना होती है, जिस तरफ से वह उछलकर शुरू हुआ था?

गुमनाम

सबूत बताते हैं कि यह सच है!

स्टैनफोर्ड विश्वविद्यालय के पर्सी डायकोनिस और सुसान होम्स ने 10,000 सिक्कों की उछाल दर्ज की। 50.8% बार सिक्का उसी तरफ़ गिरा जिस तरफ़ से वह शुरू हुआ था (स्रोत: अमेरिकन मैथमेटिकल सोसाइटी के न्यूज़लेटर "व्हाट्स हैपनिंग इन द मैथमेटिकल साइंसेज" से लिया गया इक्यावन परसेंट सॉल्यूशन )। इतने ज़्यादा या उससे ज़्यादा अनुपात की संभावना 5.48% है।

इसे गणितीय रूप से सिद्ध करने के लिए, मैंने मान लिया कि एक सिक्के के वास्तविक चक्करों की संख्या पॉइसन वितरण का पालन करती है। अधिक विशिष्ट रूप से, यदि चक्करों की माध्य संख्या m थी, तो ठीक n चक्करों की प्रायिकता exp(-m)*m^n/n! है। पॉइसन वितरण को स्पष्ट करने के लिए, निम्नलिखित ग्राफ़ 0 से 25 चक्करों की प्रायिकता दर्शाता है, जिसका माध्य 10 है।

मैंने पॉइसन धारणा को इसलिए चुना क्योंकि यह पर्याप्त रूप से बड़े माध्य के लिए लगभग घंटी वक्र आकार का अनुसरण करती है और वास्तविक परिणाम कभी भी शून्य से नीचे नहीं जा सकता।

फिर मैंने अर्ध-चक्रों के विभिन्न माध्यों के लिए अर्ध-चक्रों की सम संख्या (जिसके परिणामस्वरूप प्रारंभिक स्थिति के समान ही भुजा ऊपर की ओर उतरती है) की प्रायिकता की गणना की। निम्न तालिका 0.5 से 5.0 माध्यों के परिणाम दर्शाती है।

सम और विषम संख्या में चक्करों की संभावना

औसत क्रांतियाँ	सम कुल	विषम कुल
0.5	0.567667642	0.432332358
1	0.509157819	0.490842181
1.5	0.501239376	0.498760624
2	0.500167731	0.499832269
2.5	0.500022700	0.499977300
3	0.500003072	0.499996928
3.5	0.500000416	0.499999584
4	0.500000056	0.499999944
4.5	0.500000008	0.499999992
5	0.500000001	0.499999999

फिर मैं सोचने लगा कि सम संख्या की प्रायिकता हमेशा 50% से ज़्यादा क्यों होती है। पता चला कि सम संख्या की प्रायिकता, जिसका माध्य m दिया गया हो, 0.5 + e^(-2m)/2 के रूप में व्यक्त की जा सकती है। e की घात किसी भी चीज़ की धनात्मक होनी चाहिए, इसलिए सम संख्या में चक्करों की प्रायिकता भी धनात्मक होती है।

आप इस सूत्र का मेरा प्रमाण यहां देख सकते हैं।

x के लिए हल करें:

9 ^x + 12 ^x = 16 ^x

गुमनाम

[spoiler=उत्तर]=(लॉग(1+SQRT(5))-लॉग(2))/(लॉग(4)-लॉग(3)) =~ 1.67272093446233. [/स्पॉइलर]

यहां मेरा समाधान (पीडीएफ) है।

यह समस्या मेरे फोरम Wizard of Odds में पूछी गई और इस पर चर्चा की गई।

यह समस्या एक कठिन घातांकीय प्रश्न वीडियो से प्रेरित थी।

प्रश्न यह है कि औसतन कितने बंद लूप होंगे?

आकार 4 के बंद लूप का उदाहरण: गॉर्डन डॉन को देता है, डॉन जॉन को देता है, जॉन नाथन को देता है, और नाथन गॉर्डन को देता है।

अपना स्वयं का नाम बनाना आकार 1 का एक बंद लूप होगा।

गुमनाम

(1/1) + (1/2) + (1/3) + ... + (1/100) =~ 5.187377518.

[स्पॉइलर=समाधान]

मान लीजिए कि सीक्रेट सांता पार्टी में सिर्फ़ एक कर्मचारी आता है। ज़ाहिर है, वह खुद ही पार्टी चुनेगा, तो यह एक बंद लूप है।

फिर एक दूसरा कर्मचारी देर से आता है और शामिल होने के लिए कहता है। वे उसे अब दो कर्मचारियों की सूची देते हैं। 1/2 संभावना है कि वह कर्मचारी 1 को चुनेगी और 1/2 संभावना है कि वह खुद भी चुनेगी। अगर वह कर्मचारी 1 को चुनती है, तो उसे कर्मचारी 1 के लिए खरीदारी करने वाले के साथ जोड़ा जा सकता है, जहाँ वह कर्मचारी 1 के लिए खरीदारी करती है और कर्मचारी 1 उसके लिए खरीदारी करता है। तो, अब हम 1 + 0.5*1 = 1.5 पर हैं।

फिर एक तीसरा कर्मचारी देर से आता है और शामिल होने के लिए कहता है। वे उसे अब तीन कर्मचारियों की सूची देते हैं। 2/3 संभावना है कि वह कर्मचारी 1 या 2 को चुनेगी और 1/3 संभावना है कि वह खुद भी चुनेगी। अगर वह कर्मचारी 1 या 2 को चुनती है, तो उसे उनके चक्र में शामिल किया जा सकता है, जहाँ वह अपने चुने हुए कर्मचारी के लिए खरीदारी करती है और जो व्यक्ति पहले उस कर्मचारी के लिए खरीदारी करने वाला था, वह अब तीन कर्मचारियों के लिए खरीदारी करता है। तो, अब हम 1.5 + (1/3) = 11/6 पर हैं।

फिर एक चौथा कर्मचारी देर से आता है और शामिल होने के लिए कहता है। वे उसे अब चार कर्मचारियों की सूची देते हैं। 3/4 संभावना है कि वह कर्मचारी 1 से 3 को चुनेगी और 1/4 संभावना है कि वह खुद भी चुनेगी। अगर वह कर्मचारी 1 से 3 को चुनती है, तो उसे उनके साथ जोड़ा जा सकता है, जहाँ वह अपने चुने हुए कर्मचारी के लिए खरीदारी करती है और जो व्यक्ति पहले उस कर्मचारी के लिए खरीदारी करने वाला था, वह अब चार के लिए खरीदारी करता है। तो, अब हम 11/6 + (1/4) = 25/12 पर पहुँच गए हैं।

ऐसा करते रहें और अंतिम उत्तर 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5.187377518 होगा।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

1 त्रिज्या वाले एक अर्धवृत्त पर विचार करें जिसके अंदर दो आयत एक के ऊपर एक रखे हुए हैं। दोनों आयतों का अधिकतम संयुक्त क्षेत्रफल क्या है?

अर्धवृत्त में दो आयत

गुमनाम

sqrt(5)-1 =~ 1.236067977499790.

यहां मेरा पूरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

कृपया समान जुड़वाँ बच्चों को नज़रअंदाज़ करें और मान लें कि हर बच्चे के लड़का या लड़की पैदा होने की 50/50 संभावना है। अगर 2 से 5 के निर्दिष्ट आकार वाले परिवारों में से बच्चों का यादृच्छिक रूप से सर्वेक्षण किया जाए, तो लड़के या लड़की की बहन होने की क्या संभावना है?

गुमनाम

दिलचस्प बात यह है कि परिवार के आकार की परवाह किए बिना, यह संभावना दोनों लिंगों के लिए समान है।

उदाहरण के लिए, आइए तीन लोगों के परिवार पर नज़र डालें। लड़के और लड़कियों को क्रम के अनुसार व्यवस्थित करने के आठ संभावित तरीके इस प्रकार हैं:

बीबीबी
बीबीजी
बी जी बी
बीजीजी
जीबीबी
जीबीजी
जीजीबी
जीजीजी

अगर आप ऊपर दी गई सूची में से किसी भी लड़की को यादृच्छिक रूप से चुनें, तो आप देखेंगे कि 12 लड़कियों में से 9 की बहनें हैं। यही बात 12 लड़कों के लिए भी लागू होती है, जिनमें से 9 की बहनें हैं। इसलिए, संभावना 9/12 = 3/4 है।

किसी भी बच्चे की बहन होने की संभावना का सामान्य सूत्र, जहाँ बच्चों की संख्या n है, 1-(1/2) ^n-1 है।

परिवार में कुल बच्चों की संख्या के आधार पर बहन होने की संभावना इस प्रकार है:

1: 0
2: 1/2
3: 3/4
4: 7/8
5: 15/16
6: 31/32

वैकल्पिक रूप से, यह समझ में आता है कि लड़के और लड़कियों के लिए संभावना समान होगी। आपके भाई-बहनों का लिंग आपके लिंग से संबंधित नहीं है। इसलिए, केवल परिवार का आकार मायने रखता है, आपका अपना लिंग नहीं।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

सर्वाइवर के सीज़न 37 के एपिसोड 4 में, एक चुनौती थी जिसमें पहेली के चार टुकड़ों को एक वर्ग और एक समबाहु त्रिभुज दोनों में व्यवस्थित करना था। इसके लिए टुकड़ों का सटीक माप क्या होना चाहिए?

गुमनाम

सबसे पहले, आइए एक उचित आरेख बनाएं और उसे लेबल करें।

बिसाती समाधान वर्ग

निम्नलिखित हल किये गए त्रिभुज का आरेख मात्र है।

[स्पॉइलर=हल किया गया त्रिभुज] बिसाती समाधान त्रिकोण

[/spoiler]

इसके बाद, यह मानते हुए कि वर्ग की भुजाओं की लंबाई 1 है, यहां ऊपर दिए गए चित्र में प्रत्येक अक्षर की लंबाई दी गई है।

[बिगाड़ने वाला]

ए = डी = ई = एच = 1/2

बी = जी = एसक्यूआरटी((4-एसक्यूआरटी(3))/(4*एसक्यूआरटी(3))) =~ 0.572145321740575

सी = एफ = 1-एसक्यूआरटी((4-एसक्यूआरटी(3))/(4*एसक्यूआरटी(3))) =~ 0.427854678259425

k = m = 1/SQRT(SQRT(3)) =~ 0.759835685651592

n = (3-SQRT(4*SQRT(3)-3))/(2*SQRT(SQRT(3))) =~ 0.386767938902275

पी = (एसक्यूआरटी(4*एसक्यूआरटी(3)-3)-1)/(2*एसक्यूआरटी(एसक्यूआरटी(3))) =~ 0.373067746749317

[/spoiler]

अंत में, यहां मेरा पूरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मुझे यकीन है कि आप बिग बैंग थ्योरी के प्रशंसक हैं। मेरे पसंदीदा दृश्यों में से एक रॉक पेपर सिज़र्स लिज़र्ड स्पॉक का खेल है। यह रॉक पेपर सिज़र्स के पाँच-चिन्हों वाले खेल जैसा है, जिसके नियम इस प्रकार हैं:

कागज़ के कवर कमाल के हैं
चट्टान ने छिपकली को कुचल दिया
छिपकली ने स्पॉक को जहर दिया
स्पॉक ने कैंची तोड़ दी
कैंची कागज काटती है
छिपकली कागज खाती है
कैंची से छिपकली का सिर काटा
पेपर ने स्पॉक को गलत साबित किया
चट्टान ने कैंची को कुचल दिया

मेरा प्रश्न यह है कि क्या अधिक प्रतीकों को जोड़ा जा सकता है, जिससे प्रत्येक पक्ष को किसी यादृच्छिक खिलाड़ी के विरुद्ध समान अवसर प्राप्त हो सकें?

गुमनाम

हाँ, मुझे भी वो सीन बहुत पसंद है! उसका यूट्यूब वीडियो यहाँ है।

आपको विषम संख्या में चिह्नों की आवश्यकता है। सिद्धांततः, आप सम संख्या भी रख सकते हैं, लेकिन फिर आपको ऐसे नियम बनाने होंगे जहाँ अलग-अलग चिह्नों के कुछ जोड़े बराबरी पर आएँ। नहीं, हम एक निर्णायक खेल चाहते हैं जहाँ केवल तभी बराबरी हो जब दोनों खिलाड़ी एक ही चिह्न खेलें।

अभाज्य संख्या के प्रतीकों के साथ एक हल विशेष रूप से सुंदर और समझाने में आसान होता है। उदाहरण के तौर पर, मुझे सात प्रतीकों के साथ समझाने की अनुमति दें। आइए, प्रतीकों A से G तक को लेबल करें और उन्हें नीचे दिए गए चित्र में एक वृत्त पर दर्शाएँ।

आरपीएस1

इसके बाद, A से शुरू करें और फिर दक्षिणावर्त दिशा में अगले चिह्न तक एक तीर बनाएँ। तीर इन दोनों के बीच वाले चिह्न की ओर इंगित करेगा। इसे ऐसे समझें जैसे उस चिह्न पर एक तीर से निशाना लगाया जा रहा हो। जब तक आप A पर वापस न आ जाएँ, तब तक दक्षिणावर्त दिशा में चलते रहें। चित्र ऐसा नहीं दिखेगा:

आरपीएस2

अब, यही प्रक्रिया दोहराएँ, लेकिन A से शुरू करते हुए, दो चिह्नों को दक्षिणावर्त घुमाएँ। दरअसल, आप अपनी इच्छानुसार कहीं से भी शुरू कर सकते हैं। अब आरेख इस तरह दिखता है:

अंत में, यही प्रक्रिया दोहराएँ, लेकिन तीन चिह्नों को दक्षिणावर्त दिशा में छोड़ दें। अब आरेख इस प्रकार दिखाई देगा:

आरपीएस4

ध्यान दें कि इस बिंदु पर प्रत्येक प्रतीक तीन अन्य प्रतीकों को हराता है तथा तीन अन्य भिन्न प्रतीकों द्वारा पराजित होता है।

यह विधि किसी भी अभाज्य संख्या के प्रतीकों के लिए काम करेगी क्योंकि जब तक आप मूल प्रतीक पर वापस लौटेंगे, तब तक आप हर प्रतीक से गुज़र चुके होंगे। n प्रतीकों के लिए, आपको इस प्रक्रिया को (n-1)/2 बार दोहराना होगा।

आप किसी भी विषम संख्या में प्रतीकों के साथ एक संतुलित खेल बना सकते हैं, लेकिन कभी-कभी आप मूल प्रतीक पर बहुत जल्दी वापस लौट जाएँगे। ऐसा होने पर, आपको छूटे हुए प्रतीकों से शुरू करके दूसरे लूप बनाने होंगे।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

आप डोमिनोज़ के एक मानक (28 टाइल) सेट को फेरबदल करते हैं और यादृच्छिक रूप से एक टाइल निकालते हैं। आप ध्यान से एक तरफ़ खोलते हैं तो 6 दिखाई देता है। इसकी क्या प्रायिकता है कि यह डबल 6 वाली टाइल हो?

Gialmere

डोमिनोज़ से परिचित न होने वालों के लिए, डोमिनोज़ के दो पहलू होते हैं, प्रत्येक पर 0 से 6 तक की संख्याएँ अंकित होती हैं। प्रत्येक संभावित डोमिनोज़ का एक सेट होता है। यानी कुल 7 में से बिना प्रतिस्थापन के, संख्याएँ चुनने के 21 तरीके, और दोनों संख्याओं को एक ही तरफ रखने के सभी 7 तरीके।

यहां उनमें से सभी 28 हैं: 0-0, 0-1, 0-2, 0-3, 0-4, 0-5, 0-6, 1-1, 1-2, 1-3, 1-4, 1-5, 1-6, 2-2-2, 2-3, 2-4, 2-5, 2-6, 3-3, 3-4, 3-5, 3-6, 4-4, 4-5, 4-6, 5-5, 5-6, 6-6।

इस स्पष्टीकरण के बाद, यहां उत्तर और समाधान दिया गया है।

1/4 = 25%

प्रश्न को सरल शब्दों में इस प्रकार लिखें: यादृच्छिक रूप से चुने गए डोमिनोज़ के दोनों ओर एक ही संख्या होने की क्या प्रायिकता है? इसका उत्तर है 7/28 = 1/4.

आप कह सकते हैं कि उत्तर 1/7 होना चाहिए, क्योंकि दूसरी तरफ़ सात संभावित संख्याओं में से कोई भी हो सकती है। यह सच है कि यह सात संख्याओं में से कोई भी हो सकती है, लेकिन सभी समान रूप से संभावित नहीं हैं। 6-6 डोमिनोज़ को दो बार गिना जाना चाहिए, क्योंकि इसमें दो तरफ़ एक छक्का है। इसलिए, दूसरी तरफ़ दो छक्कों में से कोई भी हो सकता है और सेट में कुल आठ छक्के हैं। इस प्रकार उत्तर 2/8 = 1/4 है।

यह प्रश्न मेरे फ़ोरम विज़ार्ड ऑफ़ वेगास में पूछा और चर्चा किया गया है। यह प्रश्न एलन मेंडेलसन की स्मृति को समर्पित है।

एलन और बॉब तब तक टेनिस खेलने का फैसला करते हैं जब तक कि उनमें से कोई एक लगातार दो गेम नहीं जीत लेता। एलन के किसी भी दिए गए गेम को जीतने की संभावना 2/3 है। एलन के टूर्नामेंट जीतने की संभावना क्या है?

गुमनाम

उत्तर 16/21 = 76.1905% है।

[स्पॉइलर=समाधान]

एलन के किसी व्यक्तिगत खेल को जीतने की किसी भी संभावना के लिए निम्नलिखित समाधान दिया गया है।

मान लें कि p = प्रायिकता a की जीत है।
मान लें कि a = एलन द्वारा अंतिम गेम जीतने के बाद एलन द्वारा टूर्नामेंट जीतने की संभावना।
मान लीजिए b = संभावना है कि बॉब के अंतिम गेम जीतने के बाद एलन टूर्नामेंट जीतेगा।

(1) ए = पी + (1-पी)*बी
(2) बी = पी*ए

समीकरण (2) को समीकरण (1) में प्रतिस्थापित करने पर:

a = p + (1-p)*pa
ए = पी + पा - पी ² *ए
a - pa + p ² *a = p
ए(1-पी+पी ² ) = पी
(3) a = p/(1-p+p ² )

समीकरण (3) को समीकरण (2) में प्रतिस्थापित करने पर:

बी = पी ² /(1-पी+पी ² )

पहला गेम यह निर्धारित करेगा कि टूर्नामेंट जीतने की संभावना a है या b:

उत्तर = pa + (1-p)b
= पी ² /(1-पी+पी ² ) + (1-पी)*पी ² /(1-पी+पी ² )
= (2a ² -a ³ )/(a ² -a+1)

a=2/3 लगाने पर टूर्नामेंट जीतने की संभावना 16/21 आती है।

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

आपके पास 5 फीट की एक सीढ़ी है। आप इसे दीवार से जितना हो सके उतना ऊपर टिकाना चाहते हैं। लेकिन, एक 1x1x1 घन फुट का बक्सा है जिस पर आपको सीढ़ी रखनी है। नहीं, आप बक्सा नहीं हिला सकते। सीढ़ी का ऊपरी हिस्सा अधिकतम कितनी ऊँचाई तक पहुँच सकता है?

गुमनाम

उत्तर है (1 + sqrt(26) - sqrt(23-2*sqrt(26)))/2 =~ लगभग 4.838501 फीट।

यहाँ मेरा समाधान (पीडीएफ) है।

किस मान पर x ^1/x अधिकतम है?

गुमनाम

उत्तर है e =~ 2.71828182845905.

वहाँ, e^(1/e) का मान =~ 1.44466786100977.

यहाँ मेरा समाधान (पीडीएफ) है।

1944 में समाचार पत्रों ने इस अविश्वसनीय संयोग पर ध्यान दिया:

संयोग

क्या यह एक बड़ा संयोग है या इसमें कोई गणितीय नौटंकी शामिल है?

Gialmere

यह एक गणितीय नौटंकी है और एक ज्ञात जादू की चाल का आधार है।

1944 में जीवित सभी लोगों की आयु (उनके जन्मदिन के बाद) और उनके जन्म वर्ष का योग 1944 था। ज़रा सोचिए। अगर आपकी आयु x वर्ष थी, तो आपका जन्म 1944-x में हुआ था। योग x + (1944-x) = 1944 है।

यह 1944 में "कार्यालय में बिताए गए वर्षों" के समान ही है। यदि आप y वर्षों से कार्यालय में थे, तो आपने 1944-y में कार्य प्रारंभ किया होगा। y + (1944-y) = 1944.

1944 + 1944 का योग = 3,888. हर बार काम करता है.

इसे 2023 में काम करने वाली जादुई चाल में बदलने के लिए, निम्नलिखित चार चीजों का योग एक विषय के रूप में लें:

उनके जन्म का वर्ष
इस वर्ष उनकी आयु कितनी हो जाएगी?
वर्ष कोई महत्वपूर्ण घटना घटी (जैसे पहले बच्चे का जन्म)।
इस वर्ष उस महत्वपूर्ण घटना की वर्षगांठ है।

इसका योग हमेशा 2023 + 2023 = 4046 होगा।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

विज़ार्ड अनुशंसा करता है

$11000 स्वागत बोनस

खेल
समीक्षा पढ़ें
$3000 स्वागत बोनस

खेल
समीक्षा पढ़ें
$777 तक बोनस

खेल
समीक्षा पढ़ें

एक्स	ए(एक्स)	बी(एक्स)	सी(एक्स)	डी(एक्स)
0	1	1	1
5	2	2	0
10	3	4	0
15	4	6	0
20	5	9	0
25	6	12	13
30	7	16	0
35	8	20	0
40	9	25	0
45	10	30	0
50	11	36	49	50
55	12	42	0
60	13	49	0
65	14	56	0
70	15	64	0
75	16	72	121
80	17	81	0
85	18	90	0
90	19	100	0
95	20	110	0
100	21	121	242	292

एक्स	ए(एक्स)	बी(एक्स)	सी(एक्स)	डी(एक्स)
0	1	1	1
5	2	2	0
10	3	4	0
15	4	6	0
20	5	9	0
25	6	12	13
30	7	16	0
35	8	20	0
40	9	25	0
45	10	30	0
50	11	36	49	50
55	12	42	0
60	13	49	0
65	14	56	0
70	15	64	0
75	16	72	121
80	17	81	0
85	18	90	0
90	19	100	0
95	20	110	0
100	21	121	242	292

विज़ार्ड अनुशंसा करता है

संभावना - सामान्य प्रश्न

लाल बालों का अनुपात

2013 WSOP फाइनल टेबल चिप स्टैक

2013 WSOP फाइनल टेबल पुरस्कार राशि

ड्राइंग टिकट प्रयोग

उदासीनता खेलने की राशि

संशोधित जैक या बेहतर रिटर्न तालिका

2014 अवधि जीवन तालिका मृत्यु पूल

2+ लोगों के लिए सामान्य जन्मदिन

3+ लोगों के लिए सामान्य जन्मदिन

4+ लोगों के सामान्य जन्मदिन

5+ लोगों के सामान्य जन्मदिन

2+ लोगों के सामान्य जन्मदिन

बदलाव लाने के तरीके

खिलाड़ी द्वारा कुल अंक

अभाज्य संख्याओं के बीच औसत दूरी

अभाज्य संख्याओं के बीच औसत दूरी

वर्ग संख्याओं का अंतिम अंक

मूल संख्या का अंतिम अंक

वर्गमूल का पहला भाग

सीरियल नंबर दांव

वर्डले में अक्षरों की आवृत्ति

वर्डले में सर्वश्रेष्ठ शुरुआती शब्द

सम और विषम संख्या में चक्करों की संभावना

इसे साझा करें

एक्स	ए(एक्स)	बी(एक्स)	सी(एक्स)	डी(एक्स)
0	1	1	1
5	2	2	0
10	3	4	0
15	4	6	0
20	5	9	0
25	6	12	13
30	7	16	0
35	8	20	0
40	9	25	0
45	10	30	0
50	11	36	49	50
55	12	42	0
60	13	49	0
65	14	56	0
70	15	64	0
75	16	72	121
80	17	81	0
85	18	90	0
90	19	100	0
95	20	110	0
100	21	121	242	292