WOO logo

विज़ार्ड अनुशंसा करता है

संभावना - पासा

यदि आप 6 छः-पक्षीय मानक पासे फेंक रहे हैं तो एक ही प्रकार के 6 पासे आने की संभावना क्या है?

Jeff B. से Miami, Florida

उत्तर है 6*(1/6) 6 = 6/46,656 = 1/7,776 =~ 0.0001286 .

एक शूटर के "सेवन आउट" होने तक रोल की औसत संख्या कितनी होती है? मुझे पता है कि हर 6 रोल पर 7 आएगा, लेकिन कम-आउट 7-11 और क्रेप्स के साथ-साथ शूटरों द्वारा कई पॉइंट बनाने की संभावना के कारण, मुझे लगता है कि रोल की औसत संख्या अपेक्षा से ज़्यादा हो सकती है। क्या इस पर कोई गणितीय संदर्भ सामग्री उपलब्ध है?

Grshooter से Kansas City, Missouri

प्रति शूटर रोल की औसत संख्या 8.525510 है। ठीक 2 से 200 रोल की संभावना के लिए, कृपया मेरा क्रेप्स सर्वाइवल प्रायिकता पृष्ठ देखें।

पासों के 100,000 रोल (क्रेप्स/डोंट पास लाइन) में डीपी दांव 2x, 3x, 4x, 5x, 6x, 7x, 8x या 9x लगातार हारने की संभावना (और आवृत्ति) क्या है।

Derick से Minneapolis, USA

मेरा क्रेप्स परिशिष्ट दिखाता है कि किसी एक दांव के ऑड्स कैसे निकाले जाते हैं। वहाँ आप देखेंगे कि डोंट पास बेट हारने की प्रायिकता 2928/5940 है। लगातार n बेट हारने की प्रायिकता (2928/5940) n है। 100,000 में ठीक n हारने की आवृत्ति को लगभग 100,000 * (2928/5940) n+2 के रूप में अनुमानित किया जा सकता है।

एक ही बार में छह पासों से एक ही संख्या आने की संभावना क्या है?

Kyle Hill से Colstrip, Montana

छह पासों से एक ही संख्या के छह आने की संभावना 6*(1/6) 6 =1/7776 =~ 0.01286% है।

आप कितनी बार एक पासे को 28 बार घुमाकर 7 नहीं पाते? आप इसका अंदाज़ा कैसे लगाते हैं? आपकी साइट के लिए बधाई, यह बहुत अच्छी है।

Arturo G. से Mexico City, Mexico

तारीफ़ के लिए शुक्रिया। मेरा मतलब है कि आपका मतलब एक पासे को 28 बार उछालने पर 7 न आने की प्रायिकता क्या है। किसी एक बार भी 7 न आने की प्रायिकता 5/6 है। 28 बार उछालने पर 7 न आने की प्रायिकता (5/6) 28 = 0.006066, यानी लगभग 165 में 1 है।

एक पूर्वी पासा खेल के बारे में बस एक प्रश्न, जहाँ खिलाड़ियों को यह अनुमान लगाना होता है कि पासे का कौन सा पक्ष दिखाई देता है। खिलाड़ी पहले 1, 2, 3, 4, 5, 6 (रूलेट की तरह) पर अपना दांव लगाएँगे और फिर "डीलर" एक साथ 3 पासे फेंकेगा। यदि चुनी गई संख्या एक बार (तीनों पासों में से किसी पर भी) दिखाई देती है, तो भुगतान 1:1 होगा, यदि चुनी गई संख्या दो बार दिखाई देती है, तो 2:1 होगा, और यदि चुनी गई संख्या तीनों पासों पर दिखाई देती है, तो 3:1 होगा। चूँकि खिलाड़ी बोर्ड पर कितने भी दांव लगा सकता है, तो दांव लगाने की इष्टतम संख्या क्या होगी? (यह मानते हुए कि मेरे सभी दांव बराबर आकार के हैं)

Jansen से Toronto, Canada

तीन मिलान की संभावना 1/216 है। दो मिलान की संभावना 3*5/216 है। एक मिलान की संभावना 25*5/216 है। 0 मिलान की संभावना 5*5*5/216 है। इसलिए अपेक्षित रिटर्न 3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7.87% है। दांव लगाने की कोई इष्टतम संख्या नहीं है, आप चाहे जो भी करें, कुल दांव पर लगाई गई राशि का अपेक्षित 7.87% ही हारेंगे।

ये दांव सिक बो और चक अ लक दोनों में लगाए जा सकते हैं।

श्रीमान जादूगर, चार पासे फेंकने पर दो जोड़ी पासे आने की संभावना क्या है?

Brian से St. Catherines, Canada

संयोजन (6,2) = 15 अलग-अलग युग्मों के समूह संभव हैं। संयोजन (4,2) = 6 तरीके हैं जिनसे पासे किसी भी विशिष्ट दो युग्म को फेंक सकते हैं। चार पासे फेंकने के 6^4 = 1296 तरीके हैं। इसलिए प्रायिकता 90/1296 = 6.9444% है।

अगर मैं एक पासा फेंकता हूँ, तो छक्का आने की मेरी संभावना 1/6 है। अगर मैं दो पासे फेंकता हूँ, तो क्या उनमें से एक पर छक्का आने की मेरी संभावना बढ़ जाती है, या यह 1/6 पर ही रहती है?

Mike R. से Rosemount

यदि आपने x पासे फेंके, तो कम से कम एक 6 आने की संभावना 1-(5/6) 2 है। दो पासों के मामले में यह 30.56% है।

6 पासों का उपयोग करके 3 इकाईयाँ फेंकने के कितने अलग-अलग तरीके हैं?

Jamie से Croydon, England

सबसे पहले, कॉम्बिन (6,3) = 20 तरीके हैं जिनसे आप तीन इकाइयों के लिए 6 में से तीन पासे चुन सकते हैं। फिर बाकी तीन में से प्रत्येक पाँच संख्याओं में से कोई भी हो सकता है। तो, कुल तरीके 20×5 3 = 2500 हैं। सभी पासों को फेंकने के कुल तरीके 6 6 = 46,656 हैं, इसलिए ठीक तीन इकाइयाँ आने की प्रायिकता 2500/46656 = 0.0536 है। कॉम्बिन फ़ंक्शन की सहायता के लिए , पोकर में मेरी प्रायिकताएँ अनुभाग देखें।

तीन पासों को एक साथ उछालने पर किसी एक पासे के एक आने की प्रायिकता क्या है? मेरी समझ से इसकी संभावना 50% होनी चाहिए (1/6+1/6+1/6=1/2 -->50%) लेकिन आपकी ऑड्स तालिका में यह 34.72% दिखाई गई है। कृपया मदद करें।

John C. से Singapore

तीन पासों में से ठीक एक पासा आने की संभावना 3*(5/6) 2 *(1/6) = 75/216 = 34.72% है।

4 पासे उछालने पर एक "जोड़ा" आने की संभावना क्या है?

Anthony से Toronto, Canada

जोड़ी 6 संख्याओं में से कोई भी हो सकती है। अन्य दो एकल संख्याएँ अन्य पाँच संख्याओं में से हो सकती हैं। अतः पहले से ही 6*combin(5,2)=60 संयोजन हैं। पासों के संयोजन(4,2)=6 संयोजन हैं जिन पर जोड़ी आ सकती है। दो एकल संख्याओं को दो तरीकों से व्यवस्थित किया जा सकता है। अतः जोड़ी को फेंकने के 60*12=720 तरीके हैं। पासों को फेंकने के सभी तरीकों की कुल संख्या 6 4 =1296 है। अतः प्रायिकता 720/1296 =~ 55.56% है।

मेरे दोस्त का एक बार है और वह "शेक ऑफ़ द डे" का आयोजन करता है, जिसमें एक टपरवेयर कंटेनर में दस पासे होते हैं। एक शेक में 10 में से 8 पासे मिलने की संभावना कितनी है? आपके समय के लिए धन्यवाद।

August से Oshkosh, USA

यदि आप 10 पासे फेंकते हैं और ठीक 8 संख्याएँ समान हों, तो इसकी प्रायिकता 6*combin(10,8)*(1/6) 8 *(5/6) 2 = 1/8957.952 है। कम से कम 8 संख्याओं के मेल खाने की प्रायिकता 6*[combin(10,8)*(1/6) 8 *(5/6) 2 + combin(10,9)*(1/6) 9 *(5/6) + (1/6) 10 ] = 1/8569.469 है।

हाल ही में, बैकगैमौन के एक खेल में, मैंने लगातार चार बार दोहरा छक्का मारा। क्या ऐसा दोबारा होने की संभावना है?

David से Sunland, USA

प्रत्येक नए रोल के साथ अगले चार रोल के सभी दोहरे छक्के होने की संभावना (1/36) 4 = 1679616 में 1 है।

5 पासों को एक बार फेंकने पर सीधी रेखा आने की संभावना क्या है?

Teodoro C. Deocares से Dagupan, Philippines

दो संभावित अवधियाँ हैं: 1 से 5 और 2 से 6। इनमें से प्रत्येक अवधि को 5! = 120 तरीकों से क्रमबद्ध किया जा सकता है। पाँच पासों को फेंकने के 6 5 = 7776 तरीके हैं। इसलिए संभावना 2*120/7776 = 3.09% है। याहत्ज़ी के खेल के दौरान बड़े स्ट्रेट के लिए 0 का निशान लगाने के ठीक बाद इसकी संभावना बहुत अधिक प्रतीत होती है।

एक निष्पक्ष पक्ष वाले पासे को 30 बार उछाला जाता है। संख्या 1 के आने की अपेक्षित संख्या क्या है? संख्या 1 के अपेक्षित संख्या में आने की प्रायिकता क्या है?

गुमनाम

अपेक्षित इकाईयों की संख्या 30*(1/6) = 5 है। ठीक 5 इकाईयों की संभावना combin(30,5)*(1/6) 5 *(5/6) 25 = 19.21% है।

यदि मेरे पास कोई निश्चित संख्या में पासे हों तो क्या संभावना है कि यदि मैं उन सभी को उछालूं तो कम से कम एक पासा एक पर आएगा?

गुमनाम

सभी पासों के एक न आने की प्रायिकता (5/6) n है। इसलिए, कम से कम एक पासे के 1 आने की प्रायिकता 1-(5/6) n है। आइए पाँच पासों का उदाहरण लेते हैं। उत्तर 1-(5/6) 5 = 59.81% होगा।

यदि मैं 36 पासे फेंकूं तो कम से कम एक पर छक्का आने की संभावना क्या है?

गुमनाम

1-(5/6) 36 = 99.86%

यदि मैं लगातार पासे फेंकता रहूं और हर बार सभी छक्के हटा दूं, तो मैं एक निश्चित संख्या में पासे फेंकने के बाद शेष बचे पासों की सैद्धांतिक संख्या का अनुमान कैसे लगाऊंगा?

गुमनाम

हर बार पासे फेंकने पर 5/6 पासे बचे रहने की उम्मीद होती है। इसलिए n बार फेंकने के बाद बचे पासों की अपेक्षित संख्या 36*(5/6) n होगी। उदाहरण के लिए, 10 बार फेंकने के बाद आपके पास औसतन 5.81 पासे बचेंगे।

यदि मैं तीन पासे फेंकता हूँ, तो कम से कम दो संख्याएँ समान आने की संभावना क्या है?

गुमनाम

सभी संख्याओं के अलग-अलग होने की प्रायिकता (5/6)*(4/6)=20/36 है। इसलिए कम से कम दो संख्याओं के समान होने की प्रायिकता 1-(20/36) = 16/36 = 44.44% है।

अगर दो लोग पासों का एक जोड़ा फेंकते हैं, तो क्या संभावना है कि दोनों पासे एक ही संख्या के हों? क्या इसका पता लगाने का कोई सूत्र है?

गुमनाम

हाँ। आप बस 2 से 12 तक के सभी योगों को देखें और प्रत्येक के दो बार आने की प्रायिकता ज्ञात करें। तो उत्तर होगा (1/36) 2 +(2/36) 2 +(3/36) 2 +(4/36) 2 +(5/36) 2 +(6/36) 2 +(5/36) 2 +(4/36) 2 +(3/36) 2 +(2/36) 2 +(1/36) 2 = 11.27%।

मैं हाल ही में एक अस्पताल के उत्सव में गया था। अगर सात पासों से एक ही बार में सात छक्के निकल आएँ तो इनाम में एक नई कार थी। एक पासा 1.00 पाउंड का था। इसकी संभावना ज़रूर ज़्यादा होगी, लेकिन कितनी ज़्यादा?

गुमनाम

सात पासों में सात छक्के आने की प्रायिकता (1/6) 7 = 279,936 में 1 है। इसलिए इस दांव को सही साबित करने के लिए कार की कीमत £279,936 या उससे ज़्यादा होनी चाहिए। आपकी औसत रोल्स रॉयस भी इतनी कीमत की नहीं होती, इसलिए मैं कहूँगा कि यह एक बहुत ही बुरा दांव था।

[ब्लूजे आगे कहते हैं: हाँ, लेकिन मुझे लगता है कि मुद्दा यह था कि यह दान के लिए था। क्या ज़्यादा मज़ेदार है: दान के लिए £1.00 दान करना और बदले में कुछ न पाना, सिर्फ़ मदद करने का अच्छा एहसास, या £1.00 दान करना और अच्छा एहसास के साथ-साथ कार जीतने का सुनहरा मौका?]

पांच पासों को फेंकने पर एक ही प्रकार के 5, एक ही प्रकार के 4, एक ही प्रकार के 3, फुल हाउस, 2 जोड़ी, जोड़ी, स्ट्रेट और कुछ नहीं आने की संभावनाएं क्या हैं?

गुमनाम

  • एक ही तरह के पाँच: 6/6 5 = 0.08% (स्पष्ट)
  • एक ही तरह के चार: 5*6*5 = 1.93% (सिंगलटन के लिए पांच संभावित स्थान * एक ही तरह के चार के लिए 6 रैंक * सिंगलटन के लिए 5 रैंक)।
  • फुल हाउस: कॉम्बिन(5,3)*6*5/6 5 = 3.86% (एक तरह के तीन के लिए कॉम्बिन(5,3) स्थिति * एक तरह के तीन के लिए 6 रैंक * जोड़ी के लिए 2 रैंक)।
  • एक तरह के तीन: COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15.43%. (एक तरह के तीन के लिए combin(5,3) स्थिति * बड़े सिंगलटन के लिए combin(2,1) स्थिति * एक तरह के तीन के 6 रैंक * दो सिंगलटन के लिए combin(5,2) रैंक.
  • दो जोड़ी: COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23.15% (उच्च जोड़ी के लिए combin(5,2) स्थिति * निम्न जोड़ी के लिए combin(3,2) स्थिति * दो जोड़ी के लिए combin(6,4) रैंक * सिंगलटन के लिए 4 रैंक।
  • जोड़ी: COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46.30% (जोड़ी के लिए combin(5,2) स्थिति * तीन सिंगलटन के लिए fact(3) स्थिति * जोड़ी के लिए 6 रैंक * सिंगलटन के लिए combin(5,3) रैंक।
  • सीधे: 2*fact(5) / 6 5 = 3.09% (सीधे {1-5 या 2-6} * fact(5) क्रम व्यवस्थित करने के तरीकों के लिए 2 स्पैन)।
  • कुछ नहीं: ((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6.17% (combin(6,5) छह में से 5 रैंक चुनने के तरीके, स्ट्रेट्स के लिए 2 कम, * क्रम व्यवस्थित करने के तथ्य(5) तरीके।

नमस्ते जादूगर, मैं जानना चाहता था कि क्या आप इसका उत्तर दे सकते हैं। 17वीं शताब्दी के फ़्रांस में एक लोकप्रिय जुए के खेल में, एक खिलाड़ी पासों के एक जोड़े को 24 बार उछालता था। अगर इनमें से कम से कम एक बार छक्का दोहरा आता, तो वह अपनी बाजी जीत जाता था। उस समय इस बात पर बहस चल रही थी कि जीतने की संभावना 50% से ऊपर है या नीचे। क्या आप मेरी मदद कर सकते हैं?

गुमनाम

ज़रूर, यह आसान है। 24 बार में कम से कम एक 12 आने की प्रायिकता 1-(35/36) 24 = 49.14% है। इसलिए, 12 के विरुद्ध दांव लगाने के पक्ष में संभावनाएँ हैं। यह एक चतुर दांव है क्योंकि 24 बार में बारह आने की अपेक्षित संख्या 2/3 है। हालाँकि, इसका मतलब यह नहीं है कि 12 आने की प्रायिकता 2/3 है, क्योंकि कभी-कभी एक से ज़्यादा 12 आएँगे, और 12 पर दांव लगाने वाला खिलाड़ी पहले वाले के बाद अतिरिक्त बारह आने पर और नहीं जीतता। यदि किसी दिए गए प्रयास में जीतने की प्रायिकता p है, प्रयासों की संख्या n है, और कम से कम एक जीत की प्रायिकता w है, तो n को p और w के पदों में हल करने पर हमें...

w=1-(1-p) n
1-w = (1-p) n
लॉग(1-w) = लॉग((1-p) n )
लॉग(1-w) = n*लॉग(1-p)
n= लॉग(1-w)/लॉग(1-p)

तो आपके उदाहरण में n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051. इसलिए यदि 24.6 रोल में सफलता की संभावना 50% है, तो 24 रोल में यह थोड़ी कम होनी चाहिए।

छः पासों से लगातार छः बार 1,2,3,4,5,6 आने की प्रायिकता क्या है?

गुमनाम

छह पासों को एक साथ फेंकने पर 123456 आने की प्रायिकता इस प्रकार व्यक्त की जा सकती है: प्रायिकता (दूसरा पासा पहले पासे से मेल नहीं खाता) * प्रायिकता (तीसरा पासा पहले या दूसरे पासे से मेल नहीं खाता) * ... = 1*(5/6)*(4/6)*(3/6)*(2/6)*(1/6) = 0.015432। इसलिए, लगातार छह बार ऐसा होने की प्रायिकता 0.015432 है। 6 = 74,037,208,411 में 1।

यदि मैं एक ही पासे को 6 बार घुमाऊं, तो ठीक 4 बार "2" आने की संभावना क्या है?

गुमनाम

संयोजित करें(6,2)*(1/6) 4 *(5/6) 2 = 0.008037551.

यदि आपको अपने पासे में सबसे बड़े तीन पासे रखने की अनुमति दी जाए, तो 3, 4 और 5 पासों के साथ 13 या अधिक पासे आने की संभावना क्या है?

गुमनाम

संभावनाएं इस प्रकार हैं:

3 पासे: 25.93%
4 पासे: 48.77%
5 पासे: 66.13%.

मान लीजिए हम तीन निष्पक्ष छह-पक्षीय पासे फेंकते हैं। पहले पासे पर 4 आने की सशर्त प्रायिकता क्या है, जबकि तीनों संख्याओं का योग 12 है?

Shikha से North Ryde

A के B दिए जाने की प्रायिकता, A और B की प्रायिकता को B की प्रायिकता से भाग देने पर प्राप्त होती है। इस स्थिति में, पहले पासे पर 4 आने और फिर बाकी दो पासों पर कुल 8 आने की प्रायिकता (1/6)*(5/36) = 5/216 है। 3 पासों से 12 का कोई भी योग आने की प्रायिकता 25/216 है, जैसा कि मेरे सिक बो भाग में दिखाया गया है। तो उत्तर है (5/216)/(25/216) = 5/25 = 20%।

हाल ही में एक प्रोग्रामिंग अभ्यास में मुझे और अन्य छात्रों को कोड में छह-तरफा पासे का वर्णन करने के लिए कहा गया था, और फिर सरल गेम खेलने के लिए हमारे पासे का उपयोग करना था। खेल का उद्देश्य तब तक पासे को फेंकना था जब तक कि टॉस का योग ठीक 100 तक न पहुंच जाए। कोई भी टॉस जो कुल को 100 से ऊपर रखता था उसे जोड़ा नहीं जाता था और केवल आंकड़ों में जोड़ा जाता था। जल्दी से यह निर्धारित किया गया कि 100 तक पहुंचने के लिए 17 फेंक कम से कम संख्या में होंगे। हालांकि ऐसा होने की संभावना की गणना करना मायावी साबित हुआ है। फेंकने के एक विशिष्ट अनुक्रम की संभावनाओं की गणना करना सीधा है, लेकिन फेंकने के गैर-विशिष्ट क्रम, और 17 फेंक में 100 तक पहुंचने के विभिन्न तरीकों (16 * 6 + 1 * 4 और 15 * 6 + 2 * 5) को कैसे कारक बनाया जा सकता है?

Björn से Göteborg, Sweden

आपने जिन दो तरीकों का उल्लेख किया है, वे 17 फेंकों में कुल 100 फेंकने के एकमात्र तरीके हैं। 16 छक्के और एक चौका फेंकने की संभावना 17 * (1/6) 17 है। 4 की 17 संभावित स्थितियाँ हैं और प्रत्येक अनुक्रम की 17 पदों के साथ (1/6) * (1/6) * ... * (1/6) संभावना है। 15 छक्के और 2 फाइव प्राप्त करने के तरीकों की संख्या (17,2) = 136 है। इसलिए 15 छक्के और 2 फाइव की संभावना 136 * (1/6) 17 है। इसलिए कुल संभावना (17 + 136) * (1/6) 17 है। = 110,631,761,077 में 1।

तीन पासे हैं, जिनमें से दो सही छह-तरफा पासे हैं, जबकि एक ऐसा पासा है जिसके सभी पक्षों पर छह-छह का निशान है। सभी पासे मेरी जेब में हैं। मैं बेतरतीब ढंग से एक पासा निकालता हूँ और उसे उछालता हूँ। परिणाम 6 आता है। क्या संभावना है कि वह पासा सही छह अलग-अलग मानों वाले पासों में से एक हो?

Annojh से Toronto

मान लीजिए A = सामान्य पासा चुनना
मान लीजिए B = यादृच्छिक रूप से चुने गए पासे से 6 आना
उत्तर = Pr(A दिया गया B) = Pr(A और B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4.

यदि आप छह पासे केवल एक बार ही फेंक सकते हैं, तो किसी भी क्रम में 6,6,6,6,1, और 4 आने की संभावना क्या है?

Aubrey से Kokomo

इन संख्याओं को किसी भी क्रम में व्यवस्थित करने के 6!/(4!*1!*1!) = 30 तरीके हैं। इसे देखने का एक और तरीका यह है कि 1 को रखने के लिए 6 स्थान हैं, और 4 को रखने के लिए 5 स्थान बचे हैं, इसलिए 6*5=30। 666614 के ठीक इसी क्रम में आने की प्रायिकता 6 में 1 है। 6 = 46656 में 1। 30 संभावित क्रमों के लिए इसे 30 से गुणा करें और उत्तर 30/46656 = 0.0643%, या 1552.2 में 1 है।

किसी घटना के लिए "प्रतीक्षा समय" की मेरी समझ उस घटना की प्रायिकता का व्युत्क्रम है। मैं एक पासे का उपयोग करके लगातार 2 आने के लिए प्रतीक्षा समय की गणना करने में रुचि रखता हूँ। एक सिमुलेशन में मुझे औसतन 42 पासे आते हैं। मैं लगातार 2 आने की प्रायिकता के साथ इसका संबंध कैसे जोड़ूँ?

Lee से Andover

यह सत्य है कि एकल घटनाओं के लिए यदि प्रायिकता p है, तो औसत प्रतीक्षा समय 1/p है। हालाँकि, क्रमागत घटनाओं के साथ यह और अधिक जटिल हो जाता है। मान लीजिए x वह स्थिति है जहाँ अंतिम रोल दो नहीं था। यह शुरुआत की स्थिति भी है। मान लीजिए y वह स्थिति है जहाँ अंतिम रोल दो था। पहले रोल के बाद, हमारे x अवस्था में रहने की 5/6 संभावना है, और y अवस्था में रहने की 1/6 संभावना है। मान लीजिए Ex(x) अवस्था x से रोल की अपेक्षित संख्या है, और Ex(y) अवस्था y से रोल की अपेक्षित संख्या है। तो...

Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), और
एक्स(y) = 1 + (5/6)*एक्स(x)

इन दो समीकरणों को हल करने पर...

उदाहरण(x) = 1 + (5/6)*उदाहरण(x) + (1/6)*( 1 + (5/6)*उदाहरण(x))
उदाहरण(x) = 7/6 + (35/36)*उदाहरण(x)
(1/36)*एक्स(x) = 7/6
उदाहरण(x) = 36*(7/6) = 42

अतः लगातार दो बार दो आने के लिए औसत प्रतीक्षा समय 42 बार है।

मेरे पास भी इसी प्रकार की समस्या है, केवल दो सिर पाने के लिए अपेक्षित फ्लिप, गणित की समस्याओं की मेरी साइट में, समस्या 128 देखें।

क्या आप मुझे बता सकते हैं कि दो पासों, तीन पासों और चार पासों से एक ही संख्या के दो पासे आने की संभावना क्या है? मैं सोच रहा हूँ कि एक बार में कितने पासे फेंकने होंगे ताकि संभावनाएँ पासे फेंकने वाले के पक्ष में हों। (इससे कोई फ़र्क नहीं पड़ता कि कौन सी संख्या दोगुनी होती है।)

Mary से Minneapolis, MN

रोल की संख्या के अनुसार कम से कम एक संख्या के एक से अधिक बार आने की संभावना इस प्रकार है:

एक जोड़ी या अधिक की संभावना

रोल्स संभावना
2 रोल 16.67%
3 रोल 44.44%
4 रोल 72.22%
5 रोल 90.74%
6 रोल 98.46%
इसलिए यदि आप इसे बुक करना चाहते हैं तो आपको 3 रोल पर हाँ या 4 रोल पर ना कहना चाहिए।

20 पासे फेंकने पर 100 से ज़्यादा का योग आने की क्या संभावना है? सादर प्रणाम

Terje से Stockholm

मैंने इसे हल करने के लिए सामान्य सन्निकटन का उपयोग करना शुरू किया, लेकिन 100 से ज़्यादा बिंदुओं की संभावना उस विधि के सटीक होने के लिए बहुत कम है। इसलिए मैंने 8.25 मिलियन परीक्षणों का एक यादृच्छिक सिमुलेशन किया और 101 या उससे ज़्यादा बिंदुओं वाले परीक्षणों की संख्या 127 थी। इसलिए संभावना लगभग 65,000 में से 1 है।

जादूगर, क्या आप कैलिफ़ोर्निया सुपरलोट्टो प्लस (41.4 मिलियन में 1) के बराबर ऑड्स का वर्णन कर सकते हैं, लगातार 7 या 11 आने की संख्या के संदर्भ में? मैंने इसे पहले कहीं सुना था। ज़्यादातर लोग लॉटरी ऑड्स को समझ नहीं पाते। लेकिन, पासे के लुढ़कने से - वे समझ सकते हैं।

Tim से Belmont, CA

मान लीजिए आपका उत्तर n है। 7 या 11 आने की प्रायिकता 8/36 है। n का हल निकालने के लिए:

(8/36) n = 1/41,400,000

लॉग((8/36) n ) = लॉग(1/41,400,000)

एन × लॉग(8/36) = लॉग(1/41,400,000)

n = लॉग(1/41,400,000)/लॉग(8/36)

एन = -7.617 / -0.65321

एन = 11.6608

तो लीजिए, सुपरलोट्टो जीतने की संभावना लगातार 11.66 बार सात या ग्यारह फेंकने के बराबर है। जो लोग आंशिक फेंक को नहीं समझ पा रहे हैं, उनके लिए मैं इसे इस तरह से कहूँगा कि संभावना लगातार 11 से 12 बार फेंकने के बीच है।

हम कर्मचारियों के बीच मतभेद में हैं। गली के नीचे एक बार है जहाँ दिन में एक शेक मिलता है। यानी आपको एक साथ पाँच पासे फेंकने होते हैं और सभी पाँचों पासे एक जैसे होने चाहिए, "याहत्ज़ी की तरह", लेकिन वह आपको इसके लिए तीन मौके देता है। लेकिन आपको तीनों बार सारे पासे उठाने होते हैं। तो सवाल यह है कि एक शेक में पासा फेंकने की संभावना क्या है और तीन शेक में पासा फेंकने की संभावना क्या है। धन्यवाद, अगर आपने पहले ही इसका उत्तर दे दिया है तो मुझे माफ़ करना, लेकिन मैं इसे ढूँढ नहीं पाया।

Dan and co workers at maple island से Forest Lake

एक ही बार में पाँच-एक-तरह के आने की प्रायिकता 6*(1/6) 5 = 1/1,296 है। ऐसा इसलिए है क्योंकि छह अलग-अलग पाँच-एक-तरह के (एक से छह) पासे होते हैं और प्रत्येक पासे पर वह संख्या आने की प्रायिकता (1/6) है। पाँच-एक-तरह के न आने की प्रायिकता 1-(1/1,296)=1,295/1,296 है। तीन बार बिना तीन-तरह के आने की प्रायिकता (1,295/1,296) 3 =99.77% है। इसलिए तीन प्रयासों में कम से कम एक पाँच-एक-तरह के आने की प्रायिकता 100%-99.77% = 0.23% है।

एक निष्पक्ष 6 भुजाओं वाले पासे पर प्रत्येक संभावित परिणाम में से कम से कम एक परिणाम प्राप्त करने के लिए अपेक्षित उछालों की संख्या क्या है?

Michael से Melbourne

यदि किसी चीज़ की प्रायिकता p है, तो पहली बार घटित होने में औसतन 1/p प्रयास लगेंगे। ज़ाहिर है, पहली बार में आप एक संख्या काट देंगे। अगली बार बाकी पाँच संख्याओं में से किसी एक के आने की प्रायिकता 5/6 है। इसलिए ऐसा होने में औसतन 1/(5/6)=6/5=1.2 प्रयास लगेंगे। इस तर्क का अंत तक पालन करने पर, अपेक्षित प्रयासों की संख्या (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14.7 है।

जब 5 संतुलित पासे फेंके जाते हैं तो कुल 12 आने की शास्त्रीय संभावना क्या है?

Kennith H. से Winters

मुझे उम्मीद है कि आप खुश होंगे, मैंने अभी-अभी 1 से 25 पासों के लिए इस तरह के सवालों के जवाब देने वाला एक नया खंड जोड़ा है। जैसा कि पाँच पासों वाली तालिका दिखाती है, कुल 12 पासे आने की संभावना 0.039223251028807 है।

यदि दो पासों को बार-बार तब तक घुमाया जाए जब तक कि निम्नलिखित में से कोई घटना घटित न हो जाए, तो किसके पहले घटित होने की अधिक संभावना है:

  • कुल छह और आठ, किसी भी क्रम में, लुढ़काए जाते हैं, डुप्लिकेट की अनुमति है।
  • कुल सात दो बार लुढ़का है।

किसी ने मुझसे शर्त लगाई कि छह और आठ पहले आएँगे। मैंने मान लिया क्योंकि सात सबसे ज़्यादा संभावित योग है। लेकिन बार-बार ऐसा करने से मैं 2,500 डॉलर हार गया। क्या संभावना है?

Anthony से Indiana

मुझे डर है कि आपने इस शर्त का वर्गाकार पक्ष चुना है। छह और आठ से पहले दो सात आने की संभावना 45.44% है। यहाँ सभी संभावित परिणाम दिए गए हैं। पहला कॉलम शर्त के परिणाम के लिए संभावित रोल का क्रम है, बाकी सभी को छोड़कर।

छह और आठ की बाजी से पहले दो सात

रिलेवेंट रोल्स संभावना FORMULA नतीजा
6,8 0.142045 (5/16)*(5/11) खोना
8,6 0.142045 (5/16)*(5/11) खोना
6,7,8 0.077479 (5/16)*(6/11)*(5/11) खोना
7,6,8 0.053267 (6/16)*(5/16)*(5/11) खोना
8,7,6 0.077479 (5/16)*(6/11)*(5/11) खोना
7,8,6 0.053267 (6/16)*(5/16)*(5/11) खोना
7,7 0.140625 (6/16)*(6/16) जीतना
6,7,7 0.092975 (5/16)*(6/11)*(6/11) जीतना
8,7,7 0.092975 (5/16)*(6/11)*(6/11) जीतना
7,6,7 0.06392 (6/16)*(5/16)*(6/11) जीतना
7,8,7 0.06392 (6/16)*(5/16)*(6/11) जीतना

मूलतः, 6 और 8 के बेहतर होने का कारण यह है कि आप इन संख्याओं को किसी भी क्रम में प्राप्त कर सकते हैं: 6 फिर 8, या 8 फिर 6। दो सात के साथ केवल एक ही क्रम होता है, एक 7 और फिर एक और 7।

कृपया दो प्रश्न पूछें: 1) (6) 6-पक्षीय पासे से एक बार में 6,6,6,6,6,6 आने की प्रायिकता क्या है? 2) (6) 6-पक्षीय पासे से एक बार में 1,2,3,4,5,6 आने की प्रायिकता क्या है? धन्यवाद! यह तो मुझे बहुत परेशान कर रहा है!

Heather से Petaluma

छह छक्कों की संभावना (1/6) 6 = 46656 में 1 है। छह पासों से 1,2,3,4,5,6 आने की संभावना 6 है ! /6 6 = 64.8 में 1

यदि आप एक पासे को दस बार उछालते हैं तो किसी दी गई संख्या के एक से अधिक बार आने की संभावना क्या है?

Ryan से Silay

1-(5/6) 10 -10 × (1/6) × (5/6) 9 = 51.55%.

कराधान और चोरी नामक खेल में, एक खिलाड़ी पासों का एक जोड़ा फेंकता है। किसी भी बार यदि योग 7, 11, या 12 आता है, तो खिलाड़ी का ऑडिट होता है; अन्य किसी भी राशि पर वे करों से बचते हैं। यदि कोई खिलाड़ी पासों का जोड़ा 5 बार फेंकता है, तो क्या संभावना है कि वह करों से बच जाता है?

George P. से Stevens Point, WI

7, 11, या 12 आने की प्रायिकता (6+2+1)/36 = 9/36 = 1/4 है। मैं इस आंकड़े तक कैसे पहुँचा, यह जानने के लिए मेरे पासे की प्रायिकता की मूल बातें वाले अनुभाग को देखें। किसी और चीज़ के आने की प्रायिकता 3/4 है। 7, 11, या 12 आए बिना पाँच बार पासा फेंकने की प्रायिकता (3/4) 5 = 23.73% है।

एक पासे को कितनी बार फेंकने पर यह संभव है कि आपने 1, 2, 3, 4, 5, और 6 में से प्रत्येक को कम से कम एक बार फेंका हो? इसे n-पक्षीय पासे के लिए सामान्यीकृत करने के कोई विचार हैं?

Asif से Columbia, SC

ऐसा नहीं है कि आपने पूछा है, लेकिन पहले मैं माध्य पर बात करूँ। छह-पक्षीय पासे के लिए, प्रत्येक फलक को कम से कम एक बार प्राप्त करने के लिए अपेक्षित उछालों की संख्या (6/6) + (6/5) + (6/4) + (6/3) + (6/2) + (6/1) = 14.7 है। n-पक्षीय पासे के लिए अपेक्षित उछालों की संख्या (n/n) + (n/(n-1)) + (n/(n-2)) + ... + n है। आवश्यक उछालों की माध्यिका संख्या 13 है। 13 या उससे कम बार उछालने की संभावना 51.4% है, और 13 या उससे अधिक बार उछालने की संभावना 56.21% है।

मुझे पता है कि आपको पासा नियंत्रण पर संदेह है। मैं पिछले तीन महीनों से पासा सेट करने और नियंत्रित शूटिंग का अभ्यास कर रहा हूँ। 655 बार यादृच्छिक रूप से फेंकने पर 78 सात आने की प्रायिकता क्या है? मदद के लिए धन्यवाद :)

Eric B. से Boston, MA

बड़ी संख्या में फेंकों के लिए हम गॉसियन वक्र सन्निकटन का उपयोग कर सकते हैं। 655 फेंकों में सातों की अपेक्षित संख्या 655 × (1/6) = 109.1667 है। प्रसरण 655 × (1/6) × (5/6) = 90.9722 है। मानक विचलन sqr(90.9722) = 9.5379 है। आपके 78 सात अनुमान से 109.1667 − 78 = 31.1667 कम हैं। यह (31.1667 - 0.5)/9.5379 = 3.22 मानक विचलन अपेक्षा से कम है। अपेक्षा से 3.22 या अधिक मानक विचलन कम होने की संभावना 0.000641, या 1,560 में 1 है। मुझे यह आंकड़ा एक्सेल में normsdist(-3.22) सूत्र का उपयोग करके मिला।

यह क्रेप्स में पासों को नियंत्रित करने के बारे में है। आपने पहले स्टैनफोर्ड वोंग प्रयोग पर चर्चा की थी, जिसमें कहा गया था, "शर्त की शर्तें यह थीं कि क्या सटीक निशानेबाज़ 500 पासों में 79.5 से कम सात फेंक सकते हैं। एक यादृच्छिक खेल में अपेक्षित संख्या 83.33 होगी। 500 यादृच्छिक पासों में 79 या उससे कम सात आने की संभावना 32.66% है.... 500 यादृच्छिक पासों में 74 या उससे कम सात आने की संभावना 14.41% है।"

इस शर्त के बारे में मेरा प्रश्न यह है कि 14.41% अभी भी "सांख्यिकीय रूप से महत्वपूर्ण" नहीं है [अर्थात p < 0.05], जिसे आमतौर पर माध्य से दो मानक विचलन से अधिक माना जाता है - या श्रृंखला के किसी भी छोर पर यादृच्छिक रूप से घटना घटित होने की *संयुक्त* 5% से कम संभावना।

500 बार रोल करने पर कितने सात आने चाहिए, इससे पहले कि आप कह सकें कि इस बात की 2.5% से भी कम संभावना है कि परिणाम पूर्णतः यादृच्छिक था (अर्थात् परिणाम सांख्यिकीय रूप से महत्वपूर्ण था)?

बहुत धन्यवाद और वैसे, जुआ बाधाओं और संभावनाओं के विषय पर आपकी वेबसाइट निश्चित रूप से सबसे अच्छी वेबसाइट है जो मैंने पाई है .... अच्छा काम जारी रखें !!!

Plexus से Warwick, Rhode Island

आपके दयालु शब्दों के लिए धन्यवाद। आपको यह नहीं बताना चाहिए कि फेंके गए गैर-यादृच्छिक होने की प्रायिकता p है। इसे इस तरह से लिखा जाना चाहिए कि एक यादृच्छिक खेल में ऐसा परिणाम आने की प्रायिकता p है। किसी ने भी यह उम्मीद नहीं की थी कि 500 बार फेंके जाने से कुछ भी सिद्ध या असत्य सिद्ध हो जाएगा। मैंने 79.5 सेवन की रेखा निर्धारित नहीं की थी, लेकिन मुझे संदेह है कि इसे सांख्यिकीय रूप से महत्वपूर्ण होने के लिए चुना गया था; बल्कि, मुझे संदेह है कि यह एक ऐसा बिंदु था जिस पर दोनों पक्ष शर्त पर सहमत होंगे।

2.5% सार्थकता स्तर अपेक्षाओं से 1.96 मानक विचलन है। इसे एक्सेल में सूत्र =normsinv(0.025) से ज्ञात किया जा सकता है। 500 रोल का मानक विचलन sqr(500*(1/6)*(5/6)) = 8.333 है। अतः 1.96 मानक विचलन 1.96 * 8.333 = अपेक्षाओं से 16.333 रोल कम है। 500 रोल में सात की अपेक्षित संख्या 500*(1/6) = 83.333 है। अतः इससे 1.96 मानक विचलन कम होने पर 83.333 − 16.333 = 67 है। द्विपद वितरण का उपयोग करके इसकी जाँच करने पर, 67 या उससे कम सात की सटीक प्रायिकता 2.627% है।

याहत्ज़ी प्राप्त करने के लिए अपेक्षित रोल की संख्या कितनी है?

Ian F. से Provo

यह मानते हुए कि खिलाड़ी के पास हमेशा सबसे ज़्यादा दर्शाई गई संख्या होती है, औसत 11.09 है। यहाँ एक तालिका दी गई है जो 82.6 मिलियन परीक्षणों के एक यादृच्छिक सिमुलेशन में रोल की संख्या के वितरण को दर्शाती है।

याहत्ज़ी प्रयोग

रोल्स पुनरावृत्तियां संभावना
1 63908 0.00077371
2 977954 0.0118396
3 2758635 0.0333975
4 4504806 0.0545376
5 5776444 0.0699327
6 6491538 0.0785901
7 6727992 0.0814527
8 6601612 0.0799227
9 6246388 0.0756221
10 5741778 0.0695131
11 5174553 0.0626459
12 4591986 0.0555931
13 4022755 0.0487016
14 3492745 0.042285
15 3008766 0.0364257
16 2577969 0.0312103
17 2193272 0.0265529
18 1864107 0.0225679
19 1575763 0.019077
20 1329971 0.0161013
21 1118788 0.0135446
22 940519 0.0113864
23 791107 0.00957757
24 661672 0.00801056
25 554937 0.00671837
26 463901 0.00561624
27 387339 0.00468933
28 324079 0.00392347
29 271321 0.00328476
30 225978 0.00273581
31 189012 0.00228828
32 157709 0.00190931
33 131845 0.00159619
34 109592 0.00132678
35 91327 0.00110565
36 76216 0.00092271
37 63433 0.00076795
38 52786 0.00063906
39 44122 0.00053417
40 36785 0.00044534
41 30834 0.00037329
42 25494 0.00030864
43 21170 0.0002563
44 17767 0.0002151
45 14657 0.00017745
46 12410 0.00015024
47 10299 0.00012469
48 8666 0.00010492
49 7355 0.00008904
50 5901 0.00007144
51 5017 0.00006074
52 4227 0.00005117
53 3452 0.00004179
54 2888 0.00003496
55 2470 0.0000299
56 2012 0.00002436
57 1626 0.00001969
58 1391 0.00001684
59 1135 0.00001374
60 924 0.00001119
61 840 0.00001017
62 694 0.0000084
63 534 0.00000646
64 498 0.00000603
65 372 0.0000045
66 316 0.00000383
67 286 0.00000346
68 224 0.00000271
69 197 0.00000238
70 160 0.00000194
71 125 0.00000151
72 86 0.00000104
73 79 0.00000096
74 94 0.00000114
75 70 0.00000085
76 64 0.00000077
77 38 0.00000046
78 42 0.00000051
79 27 0.00000033
80 33 0.0000004
81 16 0.00000019
82 18 0.00000022
83 19 0.00000023
84 14 0.00000017
85 6 0.00000007
86 4 0.00000005
87 9 0.00000011
88 4 0.00000005
89 5 0.00000006
90 5 0.00000006
91 1 0.00000001
92 6 0.00000007
93 1 0.00000001
94 3 0.00000004
95 1 0.00000001
96 1 0.00000001
97 2 0.00000002
102 1 0.00000001
कुल 82600000 1

एक काल्पनिक खेल पर विचार करें जो पासे के उछाल पर आधारित है। यदि पासा 1 पर आता है, तो खिलाड़ी $1 हार जाता है और खेल समाप्त हो जाता है। यदि पासा किसी और चीज़ पर आता है, तो खिलाड़ी $1 जीत जाता है। इस बिंदु पर खिलाड़ी इसे छोड़ सकता है, या खेल छोड़ सकता है। खिलाड़ी तब तक खेल जारी रख सकता है, प्रत्येक दांव को दोगुना करता हुआ, जब तक कि वह हार न जाए या खेल छोड़ न दे। सबसे अच्छी रणनीति क्या है?

Byron P. से Newington, CT

केवल अपेक्षित मूल्य को अधिकतम करने के संदर्भ में, खिलाड़ी को हमेशा खेलना चाहिए। हालाँकि खिलाड़ी के अंततः हारने की संभावना 1 है, लेकिन किसी भी निर्णय बिंदु पर अपेक्षित मूल्य हमेशा दोबारा खेलने के पक्ष में होता है। यह एक विरोधाभास जैसा लगता है। इसका उत्तर इस तथ्य में निहित है कि कुछ घटनाओं की संभावना 1 होती है, लेकिन फिर भी घटित नहीं हो सकती है। उदाहरण के लिए, यदि आप 0 से 10 तक की संख्या रेखा पर एक तीर फेंकते हैं, तो पाई पर ठीक से न पहुँचने की संभावना 1 है, लेकिन फिर भी ऐसा हो सकता है।

हालाँकि, व्यावहारिक रूप से, इसमें कुछ रुकावटें ज़रूर हैं। ऐसा इसलिए क्योंकि पैसा जितनी खुशी देता है, वह उसकी मात्रा के अनुपात में नहीं होती। हालाँकि यह आम तौर पर स्वीकार किया जाता है कि ज़्यादा पैसा ज़्यादा खुशी देता है, लेकिन आप जितने अमीर होते जाते हैं, हर अतिरिक्त डॉलर आपको उतनी ही कम खुशी देता है।

मेरा मानना है कि इस प्रश्न का उत्तर देने का एक अच्छा तरीका इस समस्या पर केली मानदंड लागू करना है। केली के अनुसार, खिलाड़ी को हर निर्णय दांव के बाद अपने बैंकरोल के अपेक्षित लॉग को अधिकतम करने के लक्ष्य के साथ लेना चाहिए। इस निष्कर्ष पर पहुँचने के लिए (मैंने बहुत सारे गणित को हटा दिया है), खिलाड़ी को तब तक दोगुना करते रहना चाहिए जब तक कि दांव की राशि उसकी कुल संपत्ति के 96.5948% से अधिक न हो जाए। संपत्ति को जीती गई राशि और पहला दांव लगाने से पहले खिलाड़ी के पास जो भी धन था, उसके योग के रूप में परिभाषित किया जाना चाहिए। उदाहरण के लिए, यदि खिलाड़ी के पास शुरुआत में $100,000 थे, तो उसे 23 बार तक दोगुना करते रहना चाहिए, जिससे उसकी जीत $4,194,304 हो जाएगी। उस समय खिलाड़ी की कुल संपत्ति $4,294,304 होगी। उसे अपनी कुल संपत्ति का 4,194,304/4,294,304 = 96.67% दांव पर लगाने के लिए कहा जाएगा, जो कि 96.5948% रोक बिंदु से अधिक है, इसलिए उसे छोड़ देना चाहिए।

खिलाड़ी A और B पासों का एक जोड़ा फेंकते हैं। खिलाड़ी A जीतता है यदि वह B के कुल 7 फेंकने से पहले कुल 6 फेंकता है, और B जीतता है यदि वह A के 6 फेंकने से पहले 7 फेंकता है। यदि A शुरू करता है, तो दर्शाइए कि A के जीतने की संभावना 30/61 है।

Sangeeta से Mumbai, India

मान लीजिए कि इस प्रश्न का उत्तर p है। कुल छह आने की प्रायिकता 5/36 है, और कुल सात आने की प्रायिकता 6/36 है। अगर आपको समझ नहीं आ रहा है कि क्यों, तो कृपया पासा प्रायिकता की मूल बातें पर मेरा अनुभाग देखें। हम p को इस प्रकार परिभाषित कर सकते हैं:

p = संभावना (पहले रोल पर 6) + संभावना (पहले रोल पर कोई 6 नहीं) * संभावना (दूसरे रोल पर कोई 7 नहीं) * p.

ऐसा इसलिए है, क्योंकि यदि पहले दो रोल के बाद कोई भी खिलाड़ी नहीं जीतता है, तो खेल मूल स्थिति में वापस आ जाता है, और खिलाड़ी ए के जीतने की संभावना वही रहती है।

तो, हमारे पास है:

पी = (5/36) + (31/36)×(30/36)×पी
पी = 5/36 + (930/1296)×पी
पी * (1-(930/1296)) = 5/36.
पी * (366/1296) = 5/36
पी = (5/36)×(1296/366) = 30/61.

n छह-पक्षीय, अस्पष्ट पासों को फेंकने के कितने तरीके हैं? जैसा कि बताया गया है, पासे अस्पष्ट हैं, इसलिए पाँच पासों के साथ, उदाहरण के लिए, 1-1-3-5-6 और 1-6-5-1-3 को एक ही तरह से फेंका जाएगा। दो पासों के साथ, यह निर्धारित करना आसान है कि उत्तर 21 है, लेकिन मैं कोई सुंदर, सामान्यीकृत समाधान नहीं निकाल पा रहा हूँ।

Don से New York

उत्तर को इस प्रकार व्यक्त किया जा सकता है: combin(n+5,n) = (n+5)!/(120×n!). यहाँ 1 से 20 पासों का उत्तर दिया गया है।

गैर-विशिष्ट पासा संयोजन

पासा युग्म
1 6
2 21
3 56
4 126
5 252
6 462
7 792
8 1287
9 2002
10 3003
11 4368
12 6188
13 8568
14 11628
15 15504
16 20349
17 26334
18 33649
19 42504
20 53130
21 65780
22 80730
23 98280

श्रेय एप्लाइड कॉम्बिनेटोरिक्स के लेखक एलन टकर को जाता है।

क्या आप गणना कर सकते हैं कि पासे के एक ही बार में दो संख्याओं के एक के बाद एक आने की क्या प्रायिकता है? यानी, दो 4, दो 6 या दो 7 आने की प्रायिकता क्या है? मुझे पता है कि भूतकाल भविष्य की भविष्यवाणी नहीं कर सकता, लेकिन क्या 7/36 x 7/36 को एक के बाद एक आने की गणना करने का कोई तरीका है? मुझे उम्मीद है कि यह समझ में आया होगा।

James से Birmingham

ज़रूर। यह Pr(2) 2 + Pr(3) 2 + ... + Pr(12) 2 = (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (2/36) 2 + (1/36) 2 = 11.27% होगा।

पासे के लगातार 180 बार फेंकने पर, मैं निम्नलिखित को कितनी बार देखने की उम्मीद कर सकता हूँ:

लगातार दो सात?
लगातार तीन सात?
लगातार चार सात?

समय देने के लिए आपको धन्यवाद :-)।

Melanie D. से Elizabeth City, NC

मैं इस जानकारी को जानने का कोई उपयोगी कारण नहीं सोच पा रहा हूँ, लेकिन मुझसे इस तरह की बातें अक्सर पूछी जाती हैं, इसलिए मैं आपकी बात मान लूँगा।

पहले रोल से शुरू होकर या आखिरी रोल पर खत्म होने वाले सातों का एक निर्दिष्ट क्रम प्राप्त करना थोड़ा आसान होता है, क्योंकि यह क्रम एक तरफ से घिरा होता है। विशेष रूप से, पहले रोल से शुरू होकर या आखिरी रोल पर खत्म होने वाले s सातों का एक क्रम प्राप्त करने की प्रायिकता (1/6) s × (5/6) है। 5/6 पद इसलिए है क्योंकि आपको क्रम के खुले सिरे पर एक गैर-7 प्राप्त करना है।

अनुक्रम के मध्य में किसी भी बिंदु पर s सेवन का अनुक्रम शुरू करने की प्रायिकता (1/6) s × (5/6) 2 है। हम 5/6 पद का वर्ग करते हैं, क्योंकि खिलाड़ी को अनुक्रम के दोनों सिरों पर एक गैर-7 प्राप्त करना होगा।

यदि r रोल हैं, तो अंदर के क्रम के लिए 2 स्थान होंगे, और n सातों के क्रम के लिए rn-1 स्थान होंगे। इन समीकरणों को एक तालिका में रखने पर, 1 से 10 तक, सातों के क्रम की अपेक्षित संख्या यहाँ दी गई है। "अंदर" कॉलम 2*(5/6)*(1/6) r है, और "बाहर" कॉलम (179-r)*(5/6) 2 *(1/6) r है, जहाँ r क्रम में सातों की संख्या है। इसलिए, हम दो सातों के 3.46 रन, तीन सातों के 0.57 रन और चार सातों के 0.10 रन की अपेक्षा कर सकते हैं।

180 रोल में सेवन्स के अपेक्षित रन

दौड़ना अंदर बाहर कुल
1 0.277778 20.601852 20.87963
2 0.046296 3.414352 3.460648
3 0.007716 0.565844 0.57356
4 0.001286 0.093771 0.095057
5 0.000214 0.015539 0.015754
6 0.000036 0.002575 0.002611
7 0.000006 0.000427 0.000433
8 0.000001 0.000071 0.000072
9 0 0.000012 0.000012
10 0 0.000002 0.000002

दो पासों को तब तक फेंका जाता है जब तक या तो कुल 12 न आ जाए या दो बार लगातार कुल 7 न आ जाए। इसकी क्या संभावना है कि 12 पहले आए?

गुमनाम

इसका उत्तर और समाधान मेरी सहयोगी साइट mathproblems.info पर समस्या 201 पर पाया जा सकता है।

मैं एक टेबलटॉप गेमर हूँ, और अपने दोस्तों के साथ नॉन-क्यूबिकल प्लेटोनिक सॉलिड पासों (अगर आप बड़े शौकीन हैं, तो इसका मतलब है d4, d8, d12, और d20) के बारे में चर्चा कर रहा था। उनका तर्क था कि सिर्फ़ यही पासे प्रदर्शनात्मक रूप से निष्पक्ष होंगे। मैंने तर्क दिया कि इन्हें निष्पक्ष बनाने के लिए इनका निर्माण करना बहुत मुश्किल होगा। इसके अलावा, केवल क्रेप्स के ही वे संस्करण होंगे जो अतिरिक्त परिणामों की संख्या के कारण अत्यधिक बोझिल हो जाते हैं। क्या किसी कैसीनो में कभी ऐसा खेल हुआ है जिसमें गैर-पारंपरिक छह-तरफा पासों का इस्तेमाल किया गया हो?

Bayani से Carnagie, PA


यह लिसा फुरमैन हैं, मेरे एम कैसीनो रिव्यू की मॉडल। जब मैंने उन्हें यह कहकर प्रभावित करने की कोशिश की कि बाईं ओर की गुब्बारे वाली आकृति एक कटा हुआ इकोसाहेड्रोन है, तो उन्होंने बस मुस्कुराकर आँखें घुमा लीं।

मेरी गणित की प्रतिभा को चुनौती देने की हिम्मत मत करना! जब मैं हाई स्कूल में दूसरे वर्ष का छात्र था, तो मैंने पोस्टर बोर्ड और इलेक्ट्रीशियन टेप से न केवल सभी प्लेटोनिक ठोस आकृतियाँ बनाई थीं, बल्कि सभी आर्किमिडीयन ठोस आकृतियाँ भी बनाई थीं।

अगर आप खुद को नियमित बहुभुजों तक सीमित रखते हैं, और चाहते हैं कि हर फलक की प्रायिकता समान हो, तो आप प्लेटोनिक ठोसों तक ही सीमित हैं। हालाँकि, अगर आप नियमित बहुभुज की आवश्यकता को हटा सकते हैं, तो आप 13 कैटलन ठोसों को भी जोड़ सकते हैं।

आपके दूसरे सवाल का जवाब देते हुए, नहीं, मैंने असल में कभी किसी कसीनो में ऐसा कोई खेल नहीं देखा जिसमें क्यूब्स के अलावा किसी और पासे का इस्तेमाल हुआ हो। लगभग दस साल पहले मैंने अटलांटिक सिटी के एक गेमिंग शो में एक खेल का प्रदर्शन देखा था, जिसमें मुझे लगता है कि कैटलन सॉलिड्स में से एक, रॉम्बिक ट्रायकॉन्टाहेड्रॉन का इस्तेमाल किया गया था, लेकिन मुझे नहीं लगता कि वह कभी कसीनो में आया। ग्लोबल गेमिंग एक्सपो में मैं हर साल एक ऐसा खेल देखता हूँ जिसमें स्पिनिंग टॉप (ड्राइडल जैसा) का इस्तेमाल होता है, लेकिन अफ़सोस, मैंने उसे भी कभी कसीनो में नहीं देखा।

यदि मैं तीन छः-पक्षीय पासे फेंकता हूँ, तो सीधी रेखा आने की क्या सम्भावना है, तथा एक समान तीन आने की क्या सम्भावना है?

Mark से Fargo, ND

तीन पासों को फेंकने के 6 3 = 216 तरीके हैं। इनमें से छह संयोजनों से एक जैसा तीन (1-1-1 से 6-6-6) आएगा। इसलिए एक जैसा तीन होने की प्रायिकता 6/216 = 1/36 है। एक सीधी रेखा के लिए चार संभावित फैलाव हैं (1-2-3 से 4-5-6)। तीनों पासों को एक सीधी रेखा में व्यवस्थित करने के 3! = 6 तरीके भी हैं। इसलिए, 4*6 = 24 सीधी रेखाएँ हैं। इस प्रकार एक सीधी रेखा की प्रायिकता 24/216 = 1/9 है।

चार छह-पक्षीय पासों को फेंकने पर सबसे कम परिणाम (जिसे 4d6-L कहते हैं) को घटाने के बाद औसत योग क्या होगा? इस पासे को फेंकने के लिए मानक विचलन क्या है?

Aaron से New York

निम्नलिखित तालिका 3 से 18 तक सभी संभावित योगों के लिए संयोजनों की संख्या दर्शाती है।

4d6-L में संयोजन

नतीजा युग्म
3 1
4 4
5 10
6 21
7 38
8 62
9 91
10 122
11 148
12 167
13 172
14 160
15 131
16 94
17 54
18 21
कुल 1296

औसत परिणाम 12.2446 है, और मानक विचलन 2.8468 है।

मेरा प्रश्न पासे के ऑड्स पर आधारित है। मुझे पता है कि 7 आने के छह तरीके हैं और 12 आने का एक तरीका, लेकिन एक 12 से पहले छह 7 आने की क्या संभावना है? क्या वे सम हैं, और यदि नहीं, तो समीकरण को सम बनाने के लिए इसमें कितने बारह जोड़ने चाहिए?

nick

7 आने की प्रायिकता 1/6 है, और 12 आने की प्रायिकता 1/36 है। 7 आने की प्रायिकता, बशर्ते कि 7 या 12 आए, (1/6)/((1/6)+(1/36)) = 6/7 है। इसलिए, पहली छह बार 6 या 12 आने पर हर बार 6 आने की प्रायिकता (6/7) 6 = 39.66% है।

यदि आप प्रश्न को इस प्रकार बदलें कि 12 से पहले पाँच 6 आने की प्रायिकता क्या है, तो उत्तर (6/7) 5 = 46.27% है। चार बार आने पर यह (6/7) 4 = 53.98% है। इसलिए 12 से पहले 7 की कोई भी संख्या 50/50 नहीं है। यदि आप एक अच्छा दांव लगाना चाहते हैं, तो मेरा सुझाव है कि आप 12 से पहले चार 7 या पाँच 7 से पहले 12 लाएँ।

यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।

क्या d 6-पक्षीय पासे के साथ कुल t फेंकने की संभावना की गणना करने का कोई आसान तरीका है?

Anon E. Mouse

समरसेट, यूके के रॉबर्ट गुडहैंड की सौजन्य से, यहाँ एक आसान तरकीब दी गई है। सबसे पहले, एक पंक्ति में छह इकाईयाँ रखें, जिनके दोनों ओर पाँच शून्य हों, इस प्रकार:

एक-पासा संभावनाएँ

पासा कुल 1 2 3 4 5 6
एक मरा 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0

यह एक पासे से 1 से 6 तक आने वाले संयोजनों की संख्या दर्शाता है। मुझे पता है, यह बिलकुल स्पष्ट है। फिर भी, मेरी बात पर कायम रहिए। दो पासों के लिए, नीचे एक और पंक्ति जोड़ें, और प्रत्येक खाने के लिए ऊपर वाली पंक्ति और उसके बाईं ओर के पाँच खाने का योग निकालें। फिर, अगर आप आगे बढ़ना चाहते हैं, तो दाईं ओर पाँच और नकली शून्य जोड़ें। यह कुल 2 से 12 आने वाले संयोजनों को दर्शाता है।

दो पासों की संभावनाएँ

पासा कुल 2 3 4 5 6 7 8 9 10 11 12
एक मरा 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
दो पासे 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0

तीन पासों के लिए, बस यही दोहराएँ। यह 3 से 18 तक के संयोजनों की संख्या दर्शाएगा।

तीन पासों की संभावनाओं का विस्तार

पासा कुल 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
एक मरा 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
दो पासे 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0
तीन पासे 0 0 0 0 0 1 3 6 10 15 21 25 27 27 25 21 15 10 6 3 1 0 0 0 0 0

किसी भी दिए गए योग की प्रायिकता ज्ञात करने के लिए, उस योग के संयोजनों की संख्या को संयोजनों की कुल संख्या से भाग दें। तीन पासों के मामले में, योग 216 है, जिसे आसानी से 6 3 के रूप में भी ज्ञात किया जा सकता है। उदाहरण के लिए, तीन पासों से कुल 13 आने की प्रायिकता 21/216 = 9.72% है।

तो d पासों के लिए, आपको 1 से d-1 पासों तक काम करना होगा। यह किसी भी स्प्रेडशीट में बहुत आसानी से किया जा सकता है।

कम से कम एक पासा 12 आने की 50/50 सम्भावना के लिए दो पासों को कितनी बार फेंकना होगा?

Maff

प्रायिकता के क्षेत्र के इतिहास में यह एक क्लासिक समस्या है। कई लोग गलती से इसका उत्तर 18 मान लेते हैं, क्योंकि 12 आने की प्रायिकता 36 में 1 है, और 18×(1/36)=50% है। हालाँकि, इस तर्क से, 36 बार आने पर 12 आने की प्रायिकता 100% होगी, जो स्पष्ट रूप से नहीं है। यहाँ सही समाधान है। मान लीजिए r आने की संख्या है। 12 न आने की प्रायिकता 35/36 है। r आने पर 0 12 आने की प्रायिकता (35/36) r है। इसलिए हमें निम्नलिखित समीकरण में r का मान ज्ञात करना है:

(35/36) आर = 0.5
लॉग(35/36) आर = लॉग(0.5)
आर × लॉग(35/36) = लॉग(0.5)
आर = लॉग(0.5)/लॉग(35/36)
आर = 24.6051

तो इसका कोई गोल उत्तर नहीं है। 24 बार फेंकने पर 12 आने की प्रायिकता 1-(35/36) 24 = 49.14% है। 25 बार फेंकने पर 12 आने की प्रायिकता 1-(35/36) 25 = 50.55% है।

अगर आप इस पर दांव लगाना चाहते हैं, तो मान लीजिए कि आप 25 बार में 12 ला सकते हैं, या कोई और 24 बार में नहीं ला सकता। किसी भी तरह से आपको सम राशि पर फ़ायदा होगा।

डाइस वॉर्स में, किसी भी निश्चित संख्या में हमलावर और बचाव करने वाले पासों की सफलता की संभावना क्या है? एक हमलावर के रूप में, किस अनुपात में सबसे अधिक अपेक्षित लाभ होता है?

odiousgambit

जो लोग इस खेल से परिचित नहीं हैं, उनके लिए बता दें कि हमलावर और बचाव पक्ष, युद्ध के उस समय उनके पास मौजूद सेनाओं की संख्या के अनुसार, 1 से 8 पासे फेंकेंगे। जो पासा ज़्यादा होगा, वही जीतेगा। बराबरी पर बचाव पक्ष जीतेगा। अगर हमलावर हार जाता है, तो भी उसकी एक सेना उस क्षेत्र में बनी रहेगी जहाँ से उसने हमला शुरू किया था। इसलिए, उसके पास हमला करने के लिए कम से कम दो सेनाएँ होनी चाहिए, ताकि अगर वह जीत जाए, तो एक सेना जीते हुए क्षेत्र में रह सके और एक पीछे रह सके।

निम्नलिखित तालिका कुल पासों के सभी 64 संयोजनों के अनुसार हमलावर की जीत की संभावना दर्शाती है।

हमलावर की जीत की संभावना

हमलावर रक्षक
1 सेना 2 सेनाएँ 3 सेनाएँ 4 सेनाएँ 5 सेनाएँ 6 सेनाएँ 7 सेनाएँ 8 सेनाएँ
2 0.837963 0.443673 0.152006 0.035880 0.006105 0.000766 0.000071 0.000005
3 0.972994 0.778549 0.453575 0.191701 0.060713 0.014879 0.002890 0.000452
4 0.997299 0.939236 0.742831 0.459528 0.220442 0.083423 0.025450 0.006379
5 0.999850 0.987940 0.909347 0.718078 0.463654 0.242449 0.103626 0.036742
6 0.999996 0.998217 0.975300 0.883953 0.699616 0.466731 0.259984 0.121507
7 1.000000 0.999801 0.994663 0.961536 0.862377 0.685165 0.469139 0.274376
8 1.000000 0.999983 0.999069 0.989534 0.947731 0.843874 0.673456 0.471091

अगली तालिका हमलावर द्वारा अपेक्षित लाभ दर्शाती है, जिसे pr(हमलावर जीतता है)*(रक्षक पासा)+pr(रक्षक जीतता है)*(हमलावर पासा -1) के रूप में परिभाषित किया गया है। यह दर्शाता है कि 5 पासा वाले प्रतिद्वंद्वी के विरुद्ध 8 पासा से हमला करने पर सबसे अधिक अपेक्षित लाभ होता है।

हमलावर की जीत का शुद्ध लाभ

हमलावर रक्षक
1 सेना 2 सेनाएँ 3 सेनाएँ 4 सेनाएँ 5 सेनाएँ 6 सेनाएँ 7 सेनाएँ 8 सेनाएँ
2 0.675926 0.331019 -0.391976 -0.820600 -0.963370 -0.994638 -0.999432 -0.999955
3 0.918982 1.114196 0.267875 -0.849794 -1.575009 -1.880968 -1.973990 -1.995480
4 0.989196 1.696180 1.456986 0.216696 -1.236464 -2.249193 -2.745500 -2.929831
5 0.999250 1.927640 2.365429 1.744624 0.172886 -1.575510 -2.860114 -3.559096
6 0.999976 1.987519 2.802400 2.955577 1.996160 0.134041 -1.880192 -3.420409
7 1.000000 1.998408 2.951967 3.615360 3.486147 2.221980 0.098807 -2.158736
8 1.000000 1.999847 2.990690 3.884874 4.372772 3.970362 2.428384 0.066365

पासों के n रोल तक याहत्ज़ी बनने की संभावना क्या है?

गुमनाम

अन्य पाठकों की जानकारी के लिए, याहत्ज़ी पाँच पासों वाला एक ही तरह का पाँच होता है। याहत्ज़ी के खेल में खिलाड़ी अपनी इच्छानुसार कोई भी पासा पकड़ सकता है और बाकी पासों को दोबारा घुमा सकता है। वह ऐसा तीन बार तक कर सकता है।

खिलाड़ी चाहे तो पहले से रखे हुए पासों को दोबारा भी फेंक सकता है। उदाहरण के लिए, अगर खिलाड़ी की पहली बारी 3-3-4-5-6 है और उसके पास तीन हैं और दूसरी बार फेंकने पर उसके पास 3-3-5-5-5 हैं, तो वह पाँचों को अपने पास रख सकता है और तीसरी बार फेंकने पर तीन को दोबारा फेंक सकता है।

निम्नलिखित तालिका 1 से 20 बार घुमाने पर एक ही फलक वाले पासों की अधिकतम संख्या दर्शाती है। तालिका दर्शाती है कि तीन बार घुमाने पर याहत्ज़ी आने की संभावना लगभग 4.6% है।

याहत्ज़ी संभावनाएँ

रोल्स एक ही फलक के अधिकतम पासे
एक दो तीन चार पाँच
1 0.092593 0.694444 0.192901 0.019290 0.000772
2 0.008573 0.450103 0.409022 0.119670 0.012631
3 0.000794 0.256011 0.452402 0.244765 0.046029
4 0.000074 0.142780 0.409140 0.347432 0.100575
5 0.000007 0.079373 0.337020 0.413093 0.170507
6 0.000001 0.044101 0.263441 0.443373 0.249085
7 0.000000 0.024501 0.199279 0.445718 0.330502
8 0.000000 0.013612 0.147462 0.428488 0.410438
9 0.000000 0.007562 0.107446 0.398981 0.486011
10 0.000000 0.004201 0.077416 0.362855 0.555528
11 0.000000 0.002334 0.055317 0.324175 0.618174
12 0.000000 0.001297 0.039279 0.285674 0.673750
13 0.000000 0.000720 0.027757 0.249063 0.722460
14 0.000000 0.000400 0.019543 0.215313 0.764744
15 0.000000 0.000222 0.013720 0.184883 0.801175
16 0.000000 0.000124 0.009610 0.157896 0.832371
17 0.000000 0.000069 0.006719 0.134258 0.858954
18 0.000000 0.000038 0.004692 0.113753 0.881517
19 0.000000 0.000021 0.003272 0.096100 0.900607
20 0.000000 0.000012 0.002280 0.080994 0.916714


यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।

मैं सोच रहा हूं कि पासा फेंकने पर कौन सा परिणाम अधिक आएगा - विषम या सम?

relaxmax

उत्तर है 50/50. यह किसी भी संख्या में फेंके गए पासों के लिए सही होगा, सिर्फ़ दो के लिए नहीं।

विषय से थोड़ा हटकर, लेकिन मैंने हमेशा सोचा है कि क्रेप्स में 6/8 के बड़े दांवों की जगह विषम/सम दांव लगाना एक अच्छा तरीका होगा। घर को फ़ायदा पहुँचाने के लिए, यहाँ मेरी प्रस्तावित भुगतान तालिकाएँ और विश्लेषण दिए गए हैं।

विषम शर्त

आयोजन भुगतान करता है युग्म संभावना वापस करना
3 या 11 1.5 4 0.111111 0.166667
5 या 9 1 8 0.222222 0.222222
7 0.5 6 0.166667 0.083333
यहां तक की -1 18 0.500000 -0.500000
कुल 36 1.000000 -0.027778

सम शर्त

आयोजन भुगतान करता है युग्म संभावना वापस करना
2 या 12 3 2 0.055556 0.166667
4 या 10 1 6 0.166667 0.166667
6 या 8 0.5 10 0.277778 0.138889
विषम -1 18 0.500000 -0.500000
कुल 36 1.000000 -0.027778


कृपया ध्यान दें कि मैं इस प्रकाशन के सभी अधिकारों का दावा करता हूं।

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।

हॉट रोल बोनस में, खिलाड़ी दो पासों के योग के अनुसार निम्नलिखित संख्या में सिक्के जीतता है:

  • 2 या 12: 1000
  • 3 या 11: 600
  • 4 या 10: 400
  • 5 या 9: 300
  • 6 या 8: 200


वह तब तक रोल करता रहता है जब तक उसे कुल सात नहीं मिल जाते, जिससे बोनस खत्म हो जाता है। अगर पहली बार में उसे सात मिलता है, तो उसे 700 सिक्कों का सांत्वना पुरस्कार मिलता है। प्रति बोनस जीते गए सिक्कों की औसत संख्या क्या है?

गुमनाम

रोल की औसत संख्या बोनस-समाप्ति घटना के व्युत्क्रम के बराबर होती है, जिसकी प्रायिकता 1/6 होती है, इसलिए खिलाड़ी औसतन छह बार रोल करेगा। हालाँकि, अंतिम रोल सात होगा, इसलिए प्रत्येक बोनस में औसतन पाँच विजयी रोल होंगे।

इसके बाद, यहां प्रत्येक योग की संभावना दी गई है, यह मानते हुए कि कोई सात नहीं है:

  • 2 या 12: 1/30
  • 3 या 11: 2/30
  • 4 या 10: 3/30
  • 5 या 9: 4/30
  • 6 या 8: 5/30


इसलिए, प्रति रोल औसत जीत, यह मानते हुए कि कोई सात नहीं है, 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373.33 है।

सांत्वना पुरस्कार का मूल्य (1/6)*700 = 116.67 है।

इस प्रकार, औसत बोनस जीत 116.67 + 5×373.33 = 1983.33 है।

जादूगर से पूछें कॉलम #179 में पासा समस्या का उत्तर क्या होगा, यदि खिलाड़ी बारी-बारी से पासा फेंकें और केवल पासा फेंकने वाला खिलाड़ी ही रोल के आधार पर आगे बढ़ सकता है?

गुमनाम

कॉलम #179 में मूल प्रश्न यह था: यदि दो पासों को बार-बार तब तक घुमाया जाता है, जब तक कि निम्नलिखित में से कोई एक घटना घटित न हो जाए, तो किसके पहले घटित होने की अधिक संभावना है:

  • कुल छह और आठ, किसी भी क्रम में, लुढ़काए जाते हैं, डुप्लिकेट की अनुमति है।
  • कुल सात दो बार लुढ़का है।

आपकी चाल यह है कि एक ही रोल दोनों खिलाड़ियों के काम नहीं आ सकता। इसके बजाय, वे बारी-बारी से रोल करते हैं और केवल रोल करने वाला ही रोल का इस्तेमाल कर सकता है।

जवाब इस बात पर निर्भर करता है कि पहले कौन रोल करता है। अगर छह और आठ की ज़रूरत वाला खिलाड़ी पहले रोल करता है, तो उसके जीतने की संभावना 57.487294% है। अगर दो सात की ज़रूरत वाला खिलाड़ी पहले रोल करता है, तो छह और आठ की ज़रूरत वाले खिलाड़ी के जीतने की संभावना 52.671614% है। मैंने इसे एक सरल मार्कोव श्रृंखला प्रक्रिया का उपयोग करके हल किया।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मान लीजिए आपके पास 12 छह-तरफा पासे हैं। आप उन्हें उछालते हैं और अपनी इच्छानुसार कोई भी पासा अलग रख सकते हैं। फिर आप दूसरे पासे को दोबारा उछालते हैं। दोनों बार एक ही तरह के 12 पासे आने की प्रायिकता क्या है?

गुमनाम

प्रारंभिक रोल पर 58 विभिन्न प्रकार के अनुक्रम होते हैं। मैं प्रत्येक को इस प्रकार पहचानता हूँ कि पहले फलक की संख्या सबसे अधिक होती है, फिर दूसरे फलक के पासों की कुल संख्या, इत्यादि। उदाहरण के लिए, 3,3,3,3,6,6,6,5,5,2 के रोल को 4-3-2-1 के रूप में दर्शाया जाएगा। निम्न तालिका प्रत्येक अनुक्रम के संयोजनों की संख्या, उसे रोल करने की प्रायिकता, दूसरे रोल में एक ही प्रकार के 12 आने की प्रायिकता और दोनों का गुणनफल दर्शाती है। दूसरे रोल पर प्रायिकता के लिए, मैं मानता हूँ कि खिलाड़ी के पास वह पासा है जिसका प्रारंभिक रोल पर सबसे बड़ा योग है। निचला दायाँ कोष्ठ 0.0000037953 की समग्र प्रायिकता दर्शाता है, जो 263,486 में 1 के बराबर है।

12 पासा प्रश्न

अनुक्रम युग्म संभावना
अनुक्रम		 सशर्त
संभावना		 कुल
संभावना
12-0-0-0-0-0 6 0.0000000028 1.0000000000 0.0000000028
11-1-0-0-0-0 360 0.0000001654 0.1666666667 0.0000000276
10-2-0-0-0-0 1,980 0.0000009096 0.0277777778 0.0000000253
10-1-1-0-0-0 7,920 0.0000036384 0.0277777778 0.0000001011
9-3-0-0-0-0 6,600 0.0000030320 0.0046296296 0.0000000140
9-2-1-0-0-0 79,200 0.0000363840 0.0046296296 0.0000001684
9-1-1-1-0-0 79,200 0.0000363840 0.0046296296 0.0000001684
8-4-0-0-0-0 14,850 0.0000068220 0.0007716049 0.0000000053
8-3-1-0-0-0 237,600 0.0001091519 0.0007716049 0.0000000842
8-2-2-0-0-0 178,200 0.0000818639 0.0007716049 0.0000000632
8-2-1-1-0-0 1,069,200 0.0004911837 0.0007716049 0.0000003790
8-1-1-1-1-0 356,400 0.0001637279 0.0007716049 0.0000001263
7-5-0-0-0-0 23,760 0.0000109152 0.0001286008 0.0000000014
7-4-1-0-0-0 475,200 0.0002183039 0.0001286008 0.0000000281
7-3-2-0-0-0 950,400 0.0004366077 0.0001286008 0.0000000561
7-3-1-1-0-0 2,851,200 0.0013098232 0.0001286008 0.0000001684
7-2-2-1-0-0 4,276,800 0.0019647348 0.0001286008 0.0000002527
7-2-1-1-1-0 5,702,400 0.0026196464 0.0001286008 0.0000003369
7-1-1-1-1-1 570,240 0.0002619646 0.0001286008 0.0000000337
6-6-0-0-0-0 13,860 0.0000063672 0.0000214335 0.0000000001
6-5-1-0-0-0 665,280 0.0003056254 0.0000214335 0.0000000066
6-4-2-0-0-0 1,663,200 0.0007640635 0.0000214335 0.0000000164
6-4-1-1-0-0 4,989,600 0.0022921906 0.0000214335 0.0000000491
6-3-3-0-0-0 1,108,800 0.0005093757 0.0000214335 0.0000000109
6-3-2-1-0-0 19,958,400 0.0091687624 0.0000214335 0.0000001965
6-3-1-1-1-0 13,305,600 0.0061125083 0.0000214335 0.0000001310
6-2-2-2-0-0 4,989,600 0.0022921906 0.0000214335 0.0000000491
6-2-2-1-1-0 29,937,600 0.0137531436 0.0000214335 0.0000002948
6-2-1-1-1-1 9,979,200 0.0045843812 0.0000214335 0.0000000983
5-5-2-0-0-0 997,920 0.0004584381 0.0000035722 0.0000000016
5-5-1-1-0-0 2,993,760 0.0013753144 0.0000035722 0.0000000049
5-4-3-0-0-0 3,326,400 0.0015281271 0.0000035722 0.0000000055
5-4-2-1-0-0 29,937,600 0.0137531436 0.0000035722 0.0000000491
5-4-1-1-1-0 19,958,400 0.0091687624 0.0000035722 0.0000000328
5-3-3-1-0-0 19,958,400 0.0091687624 0.0000035722 0.0000000328
5-3-2-2-0-0 29,937,600 0.0137531436 0.0000035722 0.0000000491
5-3-2-1-1-0 119,750,400 0.0550125743 0.0000035722 0.0000001965
5-3-1-1-1-1 19,958,400 0.0091687624 0.0000035722 0.0000000328
5-2-2-2-1- 59,875,200 0.0275062872 0.0000035722 0.0000000983
5-2-2-1-1-1 59,875,200 0.0275062872 0.0000035722 0.0000000983
4-4-4-0-0-0 693,000 0.0003183598 0.0000005954 0.0000000002
4-4-3-1-0-0 24,948,000 0.0114609530 0.0000005954 0.0000000068
4-4-2-2-0-0 18,711,000 0.0085957147 0.0000005954 0.0000000051
4-4-2-1-1-0 74,844,000 0.0343828589 0.0000005954 0.0000000205
4-4-1-1-1-1 12,474,000 0.0057304765 0.0000005954 0.0000000034
4-3-3-2-0-0 49,896,000 0.0229219060 0.0000005954 0.0000000136
4-3-3-1-1-0 99,792,000 0.0458438119 0.0000005954 0.0000000273
4-3-2-2-1-0 299,376,000 0.1375314358 0.0000005954 0.0000000819
4-3-2-1-1-1 199,584,000 0.0916876238 0.0000005954 0.0000000546
4-2-2-2-2-0 37,422,000 0.0171914295 0.0000005954 0.0000000102
4-2-2-2-1-1 149,688,000 0.0687657179 0.0000005954 0.0000000409
3-3-3-3-0-0 5,544,000 0.0025468784 0.0000000992 0.0000000003
3-3-3-2-1-0 133,056,000 0.0611250826 0.0000000992 0.0000000061
3-3-3-1-1-1 44,352,000 0.0203750275 0.0000000992 0.0000000020
3-3-2-2-2-0 99,792,000 0.0458438119 0.0000000992 0.0000000045
3-3-2-2-1-1 299,376,000 0.1375314358 0.0000000992 0.0000000136
3-2-2-2-2-1 149,688,000 0.0687657179 0.0000000992 0.0000000068
2-2-2-2-2-2 7,484,400 0.0034382859 0.0000000165 0.0000000001
कुल 2,176,782,336 1.0000000000 0.0000037953

औसतन, प्रत्येक फलक को कम से कम दो बार घुमाने के लिए एक निष्पक्ष पासे को कितनी बार घुमाना पड़ता है?

Ace2

उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

उत्तर है 1,172,906,043 / 48,600,000 = लगभग 24.13387

मेरा समाधान यहां है (पीडीएफ)

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मान लीजिए कि एक निष्पक्ष छह-पक्षीय पासे को तब तक उछाला जाता है जब तक कि 1, 2, 3, या 6 न आ जाए। अगर खेल के अंत में आने वाली इन संख्याओं में से पहली संख्या 1, 2, या 3 आती है, तो आप कुछ भी नहीं जीतेंगे। अगर खेल के अंत में आने वाली इन संख्याओं में से पहली संख्या 6 आती है, तो आप पासे के हर बार लुढ़कने पर $1 जीतेंगे। इस खेल में औसत जीत कितनी है?

Klopp

कुछ अनंत श्रेणी सूत्रों के लिए नीचे दिए गए बटन पर क्लिक करें जो आपके लिए उपयोगी हो सकते हैं।

[स्पॉइलर=संकेत]

संकेत 1: i = 0 से n के ∞ तक का योग i = 1 / (1-n)

संकेत 2: i = 0 से i × n के ∞ तक का योग i = n / (1-n) 2

[/spoiler]

उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

उत्तर 3/4 है।

समाधान के लिए नीचे दिए गए बटन पर क्लिक करें।

[स्पॉइलर=समाधान]

मान लीजिए कि एक निष्पक्ष छह-पक्षीय पासे को तब तक उछाला जाता है जब तक कि 1, 2, 3, या 6 न आ जाए। अगर खेल के अंत में आने वाली इन संख्याओं में से पहली संख्या 1, 2, या 3 आती है, तो आप कुछ भी नहीं जीतेंगे। अगर खेल के अंत में आने वाली इन संख्याओं में से पहली संख्या 6 आती है, तो आप पासे के हर बार लुढ़कने पर $1 जीतेंगे। इस खेल में औसत जीत कितनी है?

संकेत 1: i = 0 से n के ∞ तक का योग i = 1 / (1-n)

संकेत 2: i = 0 से i × n के ∞ तक का योग i = n / (1-n) 2

अपेक्षित जीत को i = 0 से ∞ तक (1 + i) * (1/3) i * (1/6) के योग के रूप में व्यक्त किया जा सकता है।

(1/6) * i = 0 से ∞ तक (1/3) i का योग + (1/6) * i = 0 से ∞ तक (i * (1/3) i ) का योग।

आइये एक-एक करके इनका मूल्यांकन करें।

i = 0 से ∞ (1/3) i = का योग

1 / (1 - (1/3)) =

1 / (2/3) =

3/2

i = 0 से ∞ तक का योग (i * (1/3) i ) =

(1/3) / (1 - (1/3)) 2 =

(1/3) / (4/9) =

(1/3) * (9/4) =

3/4

इन सबको एक साथ रखकर उत्तर यह है

(1/6) * (3/2) + (1/6)*(3/4) =

(1/4) + (1/8) =

3/8

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

एक निष्पक्ष पासे के प्रत्येक फलक को कम से कम दो बार घुमाने के लिए अपेक्षित संख्या क्या है?

Ace2

उत्तर है 390968681 / 16200000 = लगभग 24.13386919753086

[स्पॉइलर=समाधान]

हालाँकि इसे एक लंबी और थकाऊ मार्कोव श्रृंखला से हल किया जा सकता है, मैं एक समग्र समाधान को प्राथमिकता देता हूँ। मैं फ़ायर बेट और बोनस क्रेप्स पर अपने पृष्ठों में इस विधि का उपयोग कैसे करें, यह समझाता हूँ।

कल्पना कीजिए कि महत्वपूर्ण घटनाओं को पासे के उछाल से, एक-एक करके, निर्धारित करने के बजाय, उन्हें समय के एक क्षण के रूप में मानिए। मान लीजिए कि घटनाओं के बीच का समय स्मृति-रहित है, यानी घटनाओं के बीच का औसत समय समय की एक इकाई है। दूसरे शब्दों में, घटनाओं के बीच का समय एक घातांकीय वितरण का अनुसरण करता है जिसका माध्य 1 है। बाजी तय करने के लिए यह मायने नहीं रखेगा, क्योंकि घटनाएँ फिर भी एक-एक करके घटित होती हैं।

पॉइसन वितरण के अनुसार, पासे के किसी भी दिए गए पक्ष को समय की x इकाई में शून्य बार घुमाए जाने की संभावना exp(-x/6)*(x/6) 0 /0! = exp(-x/6) है। पॉइसन का यह भी कहना है कि किसी भी पक्ष को ठीक एक बार घुमाए जाने की संभावना exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6) है। इस प्रकार, किसी भी पक्ष को समय की x इकाई में दो या अधिक बार घुमाए जाने की संभावना 1 - exp(-x/6)*(1 + (x/6)) है। सभी छह पक्षों को कम से कम दो बार घुमाए जाने की संभावना (1 - exp(-x/6)*(1 + (x/6))) 6 है। कम से कम एक पक्ष को कम से कम दो बार घुमाए जाने की संभावना निम्न के बराबर है:

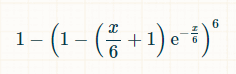
हर तरफ दो बार रोल करें

हमें इसे समग्र समय में एकीकृत करने की आवश्यकता है, ताकि पता चल सके कि औसतन कितना समय बीत जाएगा, जब वांछित लक्ष्य प्राप्त नहीं हुआ होगा।

सौभाग्य से, इस बिंदु पर हम एक समाकल कैलकुलेटर का उपयोग कर सकते हैं। लिंक किए गए कैलकुलेटर के लिए, "का समाकलन परिकलित करें" के बाद वाले टेक्स्ट बॉक्स में 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = लगभग 24.1338692 लिखें और कस्टम के अंतर्गत, समाकलन की सीमा 0 से ∞ तक निर्धारित करें।

उत्तर है 390968681 / 16200000 = लगभग 24.13386919753086

[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

आप एक निष्पक्ष 6-पक्षीय पासे से शुरुआत करते हैं और उसे छह बार घुमाते हैं, और हर बार के परिणाम लिखते हैं। फिर आप इन संख्याओं को एक और बिना लेबल वाले निष्पक्ष पासे के छह फलकों पर लिखते हैं। उदाहरण के लिए, अगर आपके छह फलकों पर 3, 5, 3, 6, 1 और 2 आए, तो आपके दूसरे पासे पर 4 नहीं, बल्कि दो 3 होंगे।

इसके बाद, आप इस दूसरे पासे को छह बार घुमाते हैं। आप उन छह संख्याओं को एक और निष्पक्ष पासे के फलकों पर लिखते हैं, और पिछले पासे से एक नया पासा बनाने की प्रक्रिया जारी रखते हैं।

अंततः, आपके पास एक ऐसा पासा होगा जिसके सभी छह फलकों पर एक ही संख्या होगी। इस स्थिति तक पहुँचने के लिए एक पासे से दूसरे पासे में संक्रमणों की औसत संख्या (या कुल पासों को 6 से भाग देने पर) कितनी होगी?

rsactuary

लगभग 9.65599148388557

[स्पॉइलर=समाधान]

भ्रम से बचने के लिए, आइए प्रारंभिक पासे को संख्याओं के बजाय अक्षरों से चिह्नित करें। आइए प्रत्येक संभावित पासे की स्थिति को अक्षरों से चिह्नित करें। उदाहरण के लिए, AAABBC का अर्थ होगा एक अक्षर के तीन, दूसरे के दो और तीसरे के एक। प्रारंभिक स्थिति स्पष्ट रूप से ABCDEF होगी।

मान लीजिए E(ABCDEF) राज्य ABCDEF से रोल की अपेक्षित संख्या है।

ई(एबीसीडीईएफ) = 1 + [180 × ई(एएएएएबी) + 450 × ई(एएएएबीबी) + 300 × ई(एएएबीबीबी) + 1800 × ई(एएएएबीसी) + 7200 × ई(एएएबीबीसी) + 1800 × ई(एएबीबीसीसी) + 7200 × ई(एएएबीसीडी) + 16200 × ई(एएबीबीसीडी) + 10800 × ई(एएबीसीडीई) + 720 × ई(एबीसीडीईएफ)]/46656

एक अवस्था से दूसरी अवस्था में जाने के संयोजनों की संख्या के आधार पर, निम्नलिखित संक्रमण मैट्रिक्स दर्शाता है कि प्रत्येक प्रारंभिक अवस्था (बाएँ स्तंभ) से प्रत्येक नई अवस्था में जाने के कितने तरीके हैं। वैसे, इसे ठीक से बनाने में कुछ घंटे लगे।

संक्रमण मैट्रिक्स A

राज्य
पहले		 आआआआ आआआआब आआआआब एएएबीबीबी एएएएबीसी एएएबीबीसी एएबीबीसीसी एएएबीसीडी एएबीबीसीडी एएबीसीडीई एबीसीडीईएफ
आआआआब 15,626 18,780 9,750 2,500 - - - - - - -
आआआआब 4,160 13,056 19,200 10,240 - - - - - - -
एएएबीबीबी 1,458 8,748 21,870 14,580 - - - - - - -
एएएएबीसी 4,098 12,348 8,190 2,580 7,920 10,080 1,440 - - - -
एएएबीबीसी 794 5,172 8,670 5,020 6,480 17,280 3,240 - - - -
एएबीबीसीसी 192 2,304 5,760 3,840 5,760 23,040 5,760 - - - -
एएएबीसीडी 732 4,464 4,140 1,680 7,920 14,400 2,520 4,320 6,480 - -
एएबीबीसीडी 130 1,596 3,150 1,940 5,280 16,800 3,600 4,800 9,360 - -
एएबीसीडीई 68 888 1,380 760 3,960 11,520 2,520 7,200 14,040 4,320 -
एबीसीडीईएफ 6 180 450 300 1,800 7,200 1,800 7,200 16,200 10,800 720

मैं मैट्रिक्स बीजगणित पर लंबा व्याख्यान नहीं दूंगा, सिवाय इसके कि मान लीजिए मैट्रिक्स B इस प्रकार है:

मैट्रिक्स बी

राज्य
पहले		 आआआआब आआआआब एएएबीबीबी एएएएबीसी एएएबीबीसी एएबीबीसीसी एएएबीसीडी एएबीबीसीडी एएबीसीडीई एबीसीडीईएफ
आआआआब -27876 9750 2500 0 0 0 0 0 0 -46656
आआआआब 13056 -27456 10240 0 0 0 0 0 0 -46656
एएएबीबीबी 8748 21870 -32076 0 0 0 0 0 0 -46656
एएएएबीसी 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
एएएबीबीसी 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
एएबीबीसीसी 2304 5760 3840 5760 23040 -40896 0 0 0 -46656
एएएबीसीडी 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
एएबीबीसीडी 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
एएबीसीडीई 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
एबीसीडीईएफ 180 450 300 1800 7200 1800 7200 16200 10800 -46656

उत्तर मैट्रिक्स B का मैट्रिक्स A के निर्धारक के बराबर है:

निर्धारित करें(A) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000

निर्धारित करें (B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000

निर्धारित करें(B) / निर्धारित करें(A) = लगभग 9.65599148388557

[/spoiler]

यदि आप एक ही पासे को 20 बार घुमाते हैं, तो क्या संभावना है कि कम से कम एक बार सभी छह पक्षों पर पासा गिरेगा?

Ace2

उत्तर लगभग 0.847987541 है

[स्पॉइलर=समाधान]

उत्तर को इस प्रकार व्यक्त किया जा सकता है 1 - (संभावना (कोई 1 नहीं) + संभावना (कोई 2 नहीं) + ... + संभावना (कोई 6 नहीं)) = 1 - 6*(5/6)^20 = लगभग 0.84349568.

हालाँकि, इससे उन स्थितियों को दोगुना घटाया जा सकेगा जहाँ दो अलग-अलग भुजाएँ कभी नहीं निकलीं। छह में से दो भुजाएँ चुनने के लिए combin(6,2)=15 तरीके हैं। किसी भी दो दी गई भुजाओं के कभी न निकलने की प्रायिकता (4/6)^20 है। हमें उन्हें प्रायिकता में जोड़ना होगा, क्योंकि पिछले चरण में उन्हें दो बार घटाया गया था। तो, अब हम 1 - 6*(5/6)^20 + 15*(4/6)^20 = लगभग 0.84800661 पर हैं।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

हालाँकि, अगर तीन भुजाओं का कोई भी समूह, जो कभी नहीं लुढ़का होता, पहले चरण में तीन गुना घटाया गया होता और दूसरे चरण में तीन गुना जोड़ा गया होता। हमें उन्हें वापस घटाना होगा क्योंकि ऐसी स्थिति में सभी छह भुजाएँ नहीं लुढ़की थीं। छह में से तीन भुजाएँ चुनने के लिए संयोजन (6,3) = 20 तरीके हैं। किसी भी विशिष्ट तीन भुजाओं के कभी नहीं लुढ़कने की प्रायिकता (3/6)^20 है। तो, अब हम 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 = लगभग 0.847987537 पर हैं।

हालाँकि, यदि चार भुजाओं का कोई भी समूह, जिसे कभी नहीं घुमाया गया था, पहले चरण में चौगुना घटाया गया होगा, दूसरे चरण में चौगुना जोड़ा गया होगा, और तीसरे चरण में चौगुना घटाया गया होगा। हमें उन्हें वापस जोड़ना होगा, क्योंकि ऐसी प्रत्येक स्थिति पहले ही दो बार घटाई जा चुकी है। छह में से चार भुजाएँ चुनने के लिए संयोजन (6,4) = 15 तरीके हैं। किसी भी विशिष्ट चार भुजाओं के कभी नहीं लुढ़कने की प्रायिकता (2/6)^20 है। तो, अब हम 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = लगभग 0.84798754089 पर हैं।

हालाँकि, अगर सभी 20 रोल एक जैसे होते, तो यह स्थिति पहले चरण में पाँच गुना घटाव, पहले चरण में पाँच गुना जोड़, तीसरे चरण में पाँच गुना घटाव और चौथे चरण में पाँच गुना जोड़ वाली होती। हमें उन्हें वापस घटाना होगा। तो, अब हम 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = लगभग 0.84798754089 पर हैं।

तो जवाब है 1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = लगभग 0.84798754089. [/spoiler]

आपके पास दो पासे हैं। आप दोनों पासों के प्रत्येक पक्ष को अपनी इच्छानुसार संख्या दे सकते हैं, बशर्ते कि प्रत्येक पक्ष एक पूर्णांक हो और एक से बड़ा या बराबर हो। आप एक ही पासे पर एक ही संख्या दोहरा सकते हैं और अपनी इच्छानुसार ऊपर जा सकते हैं। मानक पासे बनाने के अलावा, आप उन्हें कैसे संख्या दे सकते हैं ताकि किसी भी दिए गए योग की प्रायिकता मानक पासों के समान हो?

गुमनाम

पासा 1 = 1,2,2,3,3,4.
पासा 2 = 1,3,4,5,6,8.

मुझे डर है कि इस समस्या का मेरा समाधान काफी हद तक परीक्षण और त्रुटि पर आधारित था।

2 से 12 तक का कुल योग प्राप्त करने के लिए दो पासों को औसतन कितनी बार घुमाना पड़ेगा?

गुमनाम

उत्तर है 769767316159 / 12574325400 = लगभग 61.2173847639572.

[स्पॉइलर=समाधान]

इसका उत्तर देने के लिए मार्कोव श्रृंखला का उपयोग किया जा सकता है, लेकिन मुझे कैलकुलस ज़्यादा पसंद है। मुख्य बात यह है कि यदि रोल के बीच का समय घातांकीय रूप से वितरित हो और माध्य एक हो, तो उत्तर वही होगा। अतः, उत्तर को 0 से अनंत तक के समाकलन के रूप में व्यक्त किया जा सकता है:

1-(1-एक्सप(-x/36))^2*(1-एक्सप(-x/18))^2*(1-एक्सप(-x/12))^2*(1-एक्सप(-x/9))^2*(1-एक्सप(-5*x/36))^2*(1-एक्सप(-x/6))

आप ऐसे समाकलों को समाकल कैलकुलेटर से आसानी से हल कर सकते हैं।

आप मेरी अपेक्षित परीक्षण कैलकुलेटर के साथ ऐसी किसी भी समस्या को हल कर सकते हैं।

[/spoiler]

ड्रॉप डेड पाँच मानक पासों से खेला जाने वाला एक खेल है। आप अपनी बारी की शुरुआत सभी पाँच पासों को फेंककर करते हैं। अगर उनमें से कोई भी 2 या 5 नहीं आता है, तो आप पासों का योग करें, उस योग को अपने अंक में जोड़ें और फिर से फेंकें। अगर कोई 2 या 5 आता है, तो उस फेंके गए पासे का आपका स्कोर शून्य होता है। 2 या 5 दिखाने वाले सभी पासों को मृत घोषित कर दिया जाता है और अलग रख दिया जाता है। फिर आप बचे हुए पासों को फिर से फेंकते हैं। खेल आगे बढ़ता है, या तो आप अंक अर्जित करते हैं या पासे हटाते हैं। आपकी बारी तब समाप्त होती है जब आपके सभी पासे हटा दिए जाते हैं, जिसके बाद आपको ड्रॉप डेड घोषित कर दिया जाता है। आपके सभी स्कोरिंग पासों को जोड़कर आपका अंतिम अंक प्राप्त किया जाता है। सबसे ज़्यादा अंक जीतने वाला विजेता होता है।

इस खेल के लिए आपका अपेक्षित स्कोर क्या है?

Gialmere

16.064662

[स्पॉइलर=समाधान]

आइए एक पासा शेष रहने पर परिदृश्य से शुरू करें और पीछे की ओर बढ़ें।

मान लीजिए चर a एक पासा शेष रहने पर अपेक्षित अतिरिक्त अंक है।

औसत रोल जो 2 या 5 नहीं है वह (1+3+4+6)/4 = 7/2 है।

ए = (2/3)×(ए + 7/2).

ए/3 = 7/3.

ए = 7.

अब, आइए b की गणना करें, जो कि दो पासे शेष रहने पर अपेक्षित अंक है।

बी = (2/3) 2 ×(बी + 2 × (7/2)) + 2×(2/3)×(1/3)×ए.

बी = 11.2.

अब, आइए c की गणना करें, जो कि तीन पासे शेष रहने पर अपेक्षित अंक है।

सी = (2/3) 3 ×(सी + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×बी + 3×(2/3)×(1/3) 2 ×बी.

सी = 1302/95 = 13.705263.

अब, आइए d की गणना करें, जो कि चार पासे शेष रहने पर अपेक्षित अंक है।

डी = (2/3) 4 ×(डी + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×सी + 6×(2/3) 2 ×(1/3) 2 ×बी + 4×(2/3)×(1/3) 3 ×ए.

डी = 3752/247 = 15.190283.

अंत में, आइए e की गणना करें, जो कि पांच पासे शेष रहने पर अपेक्षित अंक है।

ई = (2/3) 5 ×(ई + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×डी + 10×(2/3) 3 ×(1/3) 2 ×सी + 10×(2/3) 2 ×(1/3) 3 ×बी + 5×(2/3)×(1/3) 4 ×ए।

ई = 16.064662.

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

[/spoiler]

दो पासे, एक लाल और एक नीला, बार-बार घुमाएँ। हर पासे के घुमावों का योग ध्यान में रखें। जब तक इन दोनों का संचयी योग बराबर न हो जाए, तब तक कितनी बार घुमावों की अपेक्षित संख्या होगी?

teliot

उत्तर अनंत है।

यह समझाना मुश्किल है कि उत्तर अनंत क्यों है। बात को और भी उलझाने वाली और विरोधाभासी बनाने के लिए, कुल योग के बराबर होने की संभावना 1 है।

निम्नलिखित तालिका 1 से 16 रोल के बाद पहली बार कुल योग समान होने की संभावना दर्शाती है।

पहली बार समान योग की संभावना

रोल्स संभावना
1 0.166667
2 0.112654
3 0.092850
4 0.080944
5 0.072693
6 0.066539
7 0.061722
8 0.057819
9 0.054573
10 0.051819
11 0.049443
12 0.047367
13 0.045532
14 0.043895
15 0.042423
16 0.041089

एक्सेल इस वक्र के बहुत करीब फिट को y = 0.1784*x-1.011 दिखाता है, जहां x = रोल की संख्या और y = संभावना है।

इस अनंत श्रृंखला का योग अनंत है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

पाँच लाल और पाँच नीले पासे फेंके गए हैं। क्या संभावना है कि क्रम की परवाह किए बिना, दोनों पासों के एक जैसे ही पासे फेंके जाएँ? उदाहरण के लिए, दोनों पासे 1-2-3-3-6 हैं।

गुमनाम

3,557 / 559,872 = 0.006353238, या लगभग 1 / 157.

[स्पॉइलर=समाधान]

किसी भी प्रकार के रोल के लिए निम्नलिखित तालिका दर्शाई गई है:

  • इस रोल को प्राप्त करने के कई अलग-अलग तरीके हैं। उदाहरण के लिए, एक फुल हाउस के लिए, तीन एक जैसे के लिए छह संयोजन होते हैं और जोड़ी के लिए पाँच, यानी कुल 30 अलग-अलग फुल हाउस।
  • आदेशों की संख्या। उदाहरण के लिए, फुल हाउस के लिए, तीन एक जैसे पासों के लिए पाँच में से तीन पासों को चुनने के लिए combin(5,3)=10 तरीके हैं। बाकी दो के पास जोड़ी होनी चाहिए।
  • दिए गए हाथ को रोल करने के तरीकों की संख्या। यह पहले दो स्तंभों का गुणनफल है। उदाहरण के लिए, फुल हाउस रोल करने के 30 * 10 = 300 तरीके हैं।
  • हाथ की संभावना। उदाहरण के लिए, फुल हाउस के लिए संभावना 300/6 5 = 0.038580 है।
  • दोनों रोल के एक जैसे होने और दिए गए हाथ के होने की प्रायिकता। यह चौथे वर्ग के कॉलम से प्राप्त प्रायिकता को दूसरे कॉलम से भाग देने पर प्राप्त होती है। उदाहरण के लिए, दोनों रोल के फुल हाउस होने की प्रायिकता 0.038580 2 है। हालाँकि, दोनों रोल के एक ही फुल हाउस होने की प्रायिकता 1/30 है। इसलिए, दोनों रोल के एक ही फुल हाउस होने की प्रायिकता 0.038580 2 /30 = 0.00004961 है।

निचले दाएं सेल में दोनों रोल के समान होने की कुल संभावना 0.00635324 दर्शाई गई है।

मिलान रोल

प्रकार
रोल का		 अलग
प्रकार		 आदेश कुल
युग्म		 संभावना
एक रोल		 संभावना
दो रोल
एक तरह के पाँच 6 1 6 0.00077160 0.00000010
एक तरह के चार 30 5 150 0.01929012 0.00001240
पूरा घर 30 10 300 0.03858025 0.00004961
तीन हास्य अभिनेता 60 20 1,200 0.15432099 0.00039692
दो जोड़ी 60 30 1,800 0.23148148 0.00089306
जोड़ा 60 60 3,600 0.46296296 0.00357225
पाँच एकल 6 120 720 0.09259259 0.00142890
कुल 7,776 1.00000000 0.00635324
[/spoiler]

एक छह-पक्षीय पासा तब तक फेंका जाता है जब तक कि निम्नलिखित में से कोई घटना घटित न हो जाए:

A) कोई भी पक्ष छह बार सामने आया है।
बी) प्रत्येक पक्ष कम से कम एक बार उपस्थित हुआ है।

घटना A के पहले घटित होने की प्रायिकता क्या है?

Ace2

जैसा कि मैंने किया, कैलकुलस का उपयोग करते हुए, इसका उत्तर देने के लिए मैं integral-calculator.com/ जैसे इंटीग्रल कैलकुलेटर की अनुशंसा करता हूं।

लगभग 0.252635881662548

यहां मेरा समाधान (पीडीएफ) है।

यह समस्या (थोड़े अलग शब्दों में) मेरे फोरम विज़ार्ड ऑफ़ वेगास में पूछी गई है और इस पर चर्चा की गई है।

आप एक ऐसा खेल खेलना चाहते हैं जिसमें एक साधारण छह-तरफा पासा शामिल हो। दुर्भाग्य से, आप पासा हार गए। हालाँकि, आपके पास चार इंडेक्स कार्ड हैं, जिन पर आप अपनी इच्छानुसार निशान लगा सकते हैं। खिलाड़ी को चार में से दो कार्ड बिना बदले, यादृच्छिक रूप से चुनने होंगे और उन दोनों कार्डों का योग निकालना होगा।

आप कार्डों को किस प्रकार क्रमांकित कर सकते हैं ताकि दो अलग-अलग कार्डों का योग एक पासे के रोल को दर्शाए?

Gialmere

उन्हें 0, 1, 2, और 4 संख्या दें।

चार में से दो कार्ड निकालने के छह तरीके इस प्रकार हैं।

  • 0+1 = 1
  • 0+2 = 2
  • 1+2 = 3
  • 0+4 = 4
  • 1+4 = 5
  • 2+4 = 6

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

एक छह-पक्षीय पासे को तब तक बार-बार घुमाया जाता है जब तक कि सभी पासों का योग 13 या उससे अधिक न हो जाए। अंतिम योग का माध्य, माध्यिका और बहुलक क्या है?

Gialmere

माध्य = 14.690219
माध्यिका = 14
मोड = 13

[स्पॉइलर=समाधान]

मुझे इसके लिए मार्कोव श्रृंखला का उपयोग करना पड़ा। नीचे दी गई तालिका बाएँ स्तंभ में दिए गए चलित योग के अनुसार प्रत्येक अंतिम योग की प्रायिकता दर्शाती है। 13 से 18 के योग के लिए स्पष्ट मामलों से शुरुआत करें। फिर, 0 से 12 के चलित योग के लिए, नीचे दिए गए छह कक्षों का औसत निकालें।

प्रारंभिक अवस्था की संभावनाएं पहली पंक्ति में 0 के योग के लिए पाई जा सकती हैं।

मार्कोव श्रृंखला

रोल का योग 13 14 15 16 17 18
0 0.279263 0.236996 0.192313 0.145585 0.097371 0.048472
1 0.290830 0.230791 0.188524 0.143842 0.097114 0.048899
2 0.293393 0.241931 0.181893 0.139625 0.094943 0.048215
3 0.289288 0.245178 0.193717 0.133678 0.091410 0.046728
4 0.280369 0.242560 0.198450 0.146988 0.086950 0.044682
5 0.268094 0.235687 0.197878 0.153768 0.102306 0.042267
6 0.253604 0.225827 0.193419 0.155611 0.111500 0.060039
7 0.360232 0.193566 0.165788 0.133380 0.095572 0.051462
8 0.308771 0.308771 0.142104 0.114326 0.081919 0.044110
9 0.264660 0.264660 0.264660 0.097994 0.070216 0.037809
10 0.226852 0.226852 0.226852 0.226852 0.060185 0.032407
11 0.194444 0.194444 0.194444 0.194444 0.194444 0.027778
12 0.166667 0.166667 0.166667 0.166667 0.166667 0.166667
13 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000
14 0.000000 1.000000 0.000000 0.000000 0.000000 0.000000
15 0.000000 0.000000 1.000000 0.000000 0.000000 0.000000
16 0.000000 0.000000 0.000000 1.000000 0.000000 0.000000
17 0.000000 0.000000 0.000000 0.000000 1.000000 0.000000
18 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000
[/spoiler]

यह प्रश्न मेरे फोरम ' विजार्ड ऑफ वेगास' में पूछा गया और इस पर चर्चा की गई।

जैसा कि आप जानते हैं, क्रेप्स में ऑल बेट तभी जीतता है जब 7 को छोड़कर 2 से 12 तक का प्रत्येक योग 7 से पहले फेंका जाता है। इस बेट को जीतने के लिए औसतन कितने रोल लगते हैं, जब यह जीतता है?

Ace2

20.989727251191...

यहाँ मेरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मैं देख रहा हूँ कि कोई व्यक्ति क्रेप्स टेबल पर लगातार 18 (कुल 11) साल के बच्चों के होने का दावा कर रहा है। इसे देखने के लिए औसतन कितने रोल लगेंगे?

Ace2

41,660,902,667,961,039,785,742 रोल.

यहां मेरा समाधान (पीडीएफ) है।

दो निष्पक्ष छह-पक्षीय पासों के जोड़े को तब तक बार-बार घुमाया जाता है जब तक कि निम्नलिखित दो घटनाओं में से एक घटना घटित न हो जाए:

A) कुल 12 आया है।
B) कुल 7 लगातार दो बार आया है।

किसके पहले घटित होने की अधिक सम्भावना है?

गुमनाम

कुल 12.

> [स्पॉइलर=समाधान]

होने देना:

  • p = संभावना है कि प्रारंभिक अवस्था से पहले 12 लुढ़का है या जब भी पिछला रोल 7 नहीं था।
  • q = संभावना है कि 12 पहले आएगा, जबकि पिछली बार 7 आया था।

इसे मार्कोव श्रृंखला समस्या के नाम से जाना जाता है।

इससे पहले कि हम इस पर आएं, याद रखें कि कुल 7 आने की संभावना 1/6 है और 12 आने की संभावना 1/36 है।

हम p और q को एक दूसरे के संदर्भ में इस प्रकार परिभाषित कर सकते हैं:

  • (1) पी = (1/36) + (6/36)q + (29/36)पी
  • (2) क्यू = (1/36) + (29/36)पी

आइए समीकरण (1) को 36 से गुणा करें:

36पी = 1 + 6q + 29पी
(3) 7p = 1 + 6q

आइए (2) में q का मान (3) में प्रतिस्थापित करें:

7पी = 1 + 6*((1/36) + (29/36)पी)
7पी = 1 + (1/6) + (29/6)पी
42पी = 6 + 1 + 29पी
13पी = 7
क्यू = 7/13

तो, पहले 12 आने की संभावना 7/13 =~ 53.85% है।

इस प्रकार, दो लगातार 7 आने की संभावना 46.15% है।

इस प्रकार, यह अधिक संभावना है कि कुल 12 पहले आएगा।