संभावना - सिक्के
यदि एक सिक्के को 1000 बार उछाला जाए तो क्या संभावना है कि कुल चितों की संख्या 452 से 548 के बीच होगी?
इस समस्या के लिए हम द्विपद वितरण के सामान्य सन्निकटन का उपयोग कर सकते हैं। सिरों की संख्या का प्रसरण 1000*(1/2)*(1/2)=250 है। अतः मानक विचलन 250 1/2 =15.8114 है। 548 से कम सिरों की प्रायिकता normdist((548+0.5-500)/15.8114) = 0.998920 है, जहाँ normdist, माध्य 0 और मानक विचलन 1 वाले सामान्य वितरण वाले किसी यादृच्छिक चर के दिए गए Z स्कोर के अंतर्गत आने की प्रायिकता के लिए Excel फ़ंक्शन है। इसके बाद हम 452 से कम सिरों की प्रायिकता घटाते हैं। यह normdist((452-0.5-500)/15.8114) = 0.001080 है। अतः उत्तर 0.99892-0.00108 = 0.997840 है। फिर से, यह एक अनुमान है। वास्तविक उत्तर 0.997856 है, लेकिन इसे निकालना ज़्यादा कठिन है। औसतन, क्रेप्स में एक बिंदु स्थापित करने के बाद खिलाड़ी कितनी बार बिंदु बनाएगा?
यह देखते हुए कि 5/12 बार एक बिंदु बनाया गया था, वह 6 या 8 होगा, 4/12 बार 5 या 9 होगा, और 3/12 बार 4 या 10 होगा। 6 या 8 बनने की प्रायिकता 5/11 है, 5 या 9 बनने की प्रायिकता 4/10 है, और 4 या 10 बनने की प्रायिकता 3/9 है। इसलिए, यह देखते हुए कि एक बिंदु स्थापित किया गया था, एक बिंदु बनने की प्रायिकता है: (5/12)*(5/11)+(4/12)*(4/10)+(3/12)*(3/9) = 40.61%।
जादूगर महोदय, अगर 50 अलग-अलग लोग एक सिक्के को 8 बार हवा में उछालें, तो 50 लोगों में से कितने प्रतिशत लोग लगातार 8 बार चित या पट उछालेंगे? अग्रिम धन्यवाद।
किसी भी व्यक्ति द्वारा 8 बार चित या पट आने की प्रायिकता 2*(1/2) 8 = 128 में 1 है। यदि 50 लोग ऐसा करते हैं, तो औसतन 0.39 लोगों को सभी चित या पट मिलेंगे। कम से कम एक व्यक्ति के सभी चित या पट आने की प्रायिकता 32.44% है।
मेरे पास 100 सिक्कों का एक थैला है, उनमें से एक सिक्का दो मुँह वाला है। मैं बेतरतीब ढंग से एक सिक्का उठाता हूँ और देखता हूँ कि सिक्के पर लगातार 10 बार चित आता है। क्या संभावना है कि मैंने दो मुँह वाला सिक्का चुना?
यह एक पाठ्यपुस्तक बेयसियन सशर्त प्रायिकता प्रश्न है। सामान्य तौर पर, दिए गए B के A की प्रायिकता, A और B की प्रायिकता को B की प्रायिकता से विभाजित करके प्राप्त होती है। इस स्थिति में A लगातार 10 बार चित्त उछाल रहा है और B दो-मुख वाला सिक्का उठा रहा है। A और B की प्रायिकता 1/100 है। ऐसा इसलिए है क्योंकि दो-मुख वाला सिक्का चुनने की संभावना 100 में से 1 है, और यदि आप ऐसा करते हैं तो लगातार 10 बार चित्त उछालने की संभावना 100% है। एक यादृच्छिक रूप से उठाए गए सिक्के को मानते हुए, लगातार 10 बार चित्त उछालने की प्रायिकता (1/100)*1 + (99/100)*(1/2) 10 है। ऐसा इसलिए है क्योंकि दो-मुख वाला सिक्का चुनने की 1% संभावना है, जिसमें 10 बार चित्त आने की 100% संभावना है, और एक निष्पक्ष सिक्का चुनने की 99% संभावना है, जिसमें लगातार 10 बार चित्त उछालने की (1/2) 10 संभावना है। अतः, यदि आपने लगातार 10 बार सिर उछाला है तो आपके द्वारा दो सिर वाला सिक्का चुनने की संभावना 0.01/(0.01*1 + 0.99* 0.000977) = 0.911843 है।
क्या आपके पास सिक्के के उछाल पर दांव लगाने के लिए कोई सलाह है?
हाँ! मेरी सलाह है कि उछाल की शुरुआत में ऊपर वाले हिस्से पर दांव लगाएं। साइंस न्यूज़ ऑनलाइन के अनुसार, सिक्के के उसी तरफ गिरने की संभावना 51% है जिस तरफ से वह शुरू हुआ था। लेख में कहा गया है कि इसका कारण यह है कि उछाला गया सिक्का अपनी धुरी पर पूरी तरह से नहीं घूमता है और कभी-कभी ऐसा लगता है कि वह उछल रहा है, जबकि वास्तव में ऐसा नहीं होता है। यह परिकल्पना तभी लागू होती है जब सिक्का हाथ की हथेली में पकड़ा हो, ताकि उछलने में कोई समस्या न हो। लेख में यह भी कहा गया है कि घूमता हुआ सिक्का 80% बार पट पर गिरेगा, क्योंकि भारी चित्त वाला भाग पहले नीचे गिरने की ओर आकर्षित होता है। हालाँकि, मुझे इस पर संदेह है। मैंने इसे 20 बार आजमाया और 11 बार चित्त और 9 पट आए। 80% सफलता की संभावना के साथ 20 घुमावों में 9 या उससे कम पट आने की संभावना 1775 में 1 है।
मुझे लगता है कि घूमते हुए पैसे का जवाब शायद मेरे पास है। एक दशक से भी ज़्यादा पहले, छठी कक्षा में मैंने पैसे के घूमने पर एक विज्ञान प्रोजेक्ट किया था। मैंने ओमनी पत्रिका में पढ़ा था कि बहुत तेज़ी से घुमाने पर लगभग हमेशा पूँछ ऊपर की ओर नहीं जाती क्योंकि उसके किनारे चित की ओर झुके होते हैं। मैंने इसे सैकड़ों बार आज़माया और लगभग निष्पक्ष परिणाम मिले, सिवाय दो बार जब वह किनारे पर खड़ा था।
कई घंटे बर्बाद करने के बाद, आखिरकार मुझे एहसास हुआ कि मैं इसे बहुत तेज़ घुमा रहा था, और धीरे घुमाने पर मुझे मनचाहे नतीजे मिले, यानी पूंछ ऊपर की ओर। इसके अलावा, पैसा पूरी तरह से एक समान नहीं है और सबसे पतले हिस्से से घुमाना शुरू करने से इसकी एकरूपता और बढ़ गई। कुछ बेकार चार्ट और पैसे की तरह सजाए गए एक विशाल कार्डबोर्ड सर्कल ने मुझे विज्ञान में A ग्रेड दिलाया और बाकी सभी कक्षाओं में फेल कर दिया क्योंकि मैंने अपना सारा होमवर्क अनदेखा कर दिया था।
अतः मैंने दस वर्ष पूर्व किए गए एक प्रयोग से निर्णायक रूप से सिद्ध कर दिया है, जिसके बारे में मुझे कुछ भी याद नहीं है और मुझे इस बात की कोई वास्तविक समझ नहीं थी कि मैं उस समय क्या कर रहा था, कि शायद आप अपनी सोच को थोड़ा अधिक तेजी से बदल रहे हैं।
ठीक है, मैंने फिर से कोशिश की और पैसे को धीरे-धीरे 100 बार घुमाया। धीरे-धीरे से मेरा मतलब है कि घुमाने और परिणाम स्पष्ट होने के बीच का समय कम से कम दो सेकंड था, लेकिन पाँच सेकंड से कम। मैंने एक चमकदार 2004-डी सिक्का इस्तेमाल किया। मेरे परिणाम 52 चित और 48 पट आए। इसलिए मैं अभी भी इस बात से सहमत नहीं हूँ कि किसी भी गति से घूमता हुआ पैसा पट की ओर ज़्यादा झुका होता है।
किसी घटना के लिए "प्रतीक्षा समय" की मेरी समझ उस घटना की प्रायिकता का व्युत्क्रम है। मैं एक पासे का उपयोग करके लगातार 2 आने के लिए प्रतीक्षा समय की गणना करने में रुचि रखता हूँ। एक सिमुलेशन में मुझे औसतन 42 पासे आते हैं। मैं लगातार 2 आने की प्रायिकता के साथ इसका संबंध कैसे जोड़ूँ?
यह सत्य है कि एकल घटनाओं के लिए यदि प्रायिकता p है, तो औसत प्रतीक्षा समय 1/p है। हालाँकि, क्रमागत घटनाओं के साथ यह और अधिक जटिल हो जाता है। मान लीजिए x वह स्थिति है जहाँ अंतिम रोल दो नहीं था। यह शुरुआत की स्थिति भी है। मान लीजिए y वह स्थिति है जहाँ अंतिम रोल दो था। पहले रोल के बाद, हमारे x अवस्था में रहने की 5/6 संभावना है, और y अवस्था में रहने की 1/6 संभावना है। मान लीजिए Ex(x) अवस्था x से रोल की अपेक्षित संख्या है, और Ex(y) अवस्था y से रोल की अपेक्षित संख्या है। तो...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), और
एक्स(y) = 1 + (5/6)*एक्स(x)
इन दो समीकरणों को हल करने पर...
उदाहरण(x) = 1 + (5/6)*उदाहरण(x) + (1/6)*( 1 + (5/6)*उदाहरण(x))
उदाहरण(x) = 7/6 + (35/36)*उदाहरण(x)
(1/36)*एक्स(x) = 7/6
उदाहरण(x) = 36*(7/6) = 42
अतः लगातार दो बार दो आने के लिए औसत प्रतीक्षा समय 42 बार है।
मेरे पास भी इसी प्रकार की समस्या है, केवल दो सिर पाने के लिए अपेक्षित फ्लिप, गणित की समस्याओं की मेरी साइट में, समस्या 128 देखें।
मान लीजिए हम एक जुआ खेल रहे हैं। एक निष्पक्ष सिक्का बार-बार उछाला जाता है। हर बार उछालने पर हमें 1 रुपया देना होता है। इसके दो संभावित परिणाम हैं: H या T। अगर चित और पट के बीच का अंतर 3 हो जाता है, तो हमें जुआरी से 8 रुपये मिलेंगे। क्या हमें यह खेल खेलना चाहिए और क्यों? हमारे जीतने की संभावना कितनी है? जब हमें 7 या 9 रुपये मिल रहे हों, तो जीतने की संभावना पर क्या प्रभाव पड़ेगा?
आइए x को प्रारंभिक बिंदु से फ़्लिप की अपेक्षित संख्या कहें।
यदि एक पक्ष बहुमत में एक फ्लिप है, तो शेष फ्लिप की अपेक्षित संख्या को y कहें।
यदि एक पक्ष बहुमत में दो फ़्लिप है, तो शेष फ़्लिप की अपेक्षित संख्या को z कहें।
ई(एक्स) = 1 + ई(वाई)
ई(वाई) = 1 + 0.5*ई(एक्स) + 0.5*ई(जेड)
ई(जेड) = 1 + 0.5*ई(वाई)
मैट्रिक्स बीजगणित की मदद से यह देखना आसान है कि E(x) = 9, E(y) = 8, और E(z) = 5. तो औसतन चित और पट के बीच का अंतर 3 होने के लिए 9 उछाल लगेंगे। इसलिए 8 रुपये पर यह उस व्यक्ति के लिए एक अच्छा दांव है जो प्रति उछाल एक रुपया इकट्ठा करता है, क्योंकि उसे औसतन 9 रुपये मिलेंगे, लेकिन केवल 8 रुपये वापस मिलेंगे। जुआरी के लिए हाउस एज 11.11% है। 9 रुपये पर यह एक उचित दांव है, जबकि 7 रुपये पर हाउस एडवांटेज 22.22% है।
कई लोगों ने मुझसे मेरे उत्तर को विस्तार से बताने के लिए कहा। इस समाधान के लिए बुनियादी मैट्रिक्स बीजगणित की आवश्यकता है।
x को उत्तर के रूप में परिभाषित करके शुरू करें, या जब तक सिर और पूंछ के बीच असमानता 3 न हो जाए, तब तक फ्लिप की औसत संख्या निर्धारित करें।
मान लीजिए y उस बिंदु से अपेक्षित फ़्लिप की संख्या है जहां एक पक्ष एक फ़्लिप से ऊपर है।
मान लीजिए z उस बिंदु से अपेक्षित फ़्लिप की संख्या है जहां एक पक्ष दो फ़्लिप से ऊपर है।
पहली पलटी के बाद एक पक्ष एक पलटी से बहुमत में आ जाएगा। इसलिए x=1+y.
जब कोई भी पक्ष एक फ़्लिप आगे हो, तो दूसरा फ़्लिप या तो शुरुआती बराबरी की स्थिति में होगा, या एक पक्ष दो फ़्लिप से आगे होगा। दोनों परिणाम समान रूप से संभावित हैं। इसलिए y=1+0.5*x + 0.5*z
जब कोई भी पक्ष दो फ़्लिप आगे हो, तो एक और फ़्लिप के परिणामस्वरूप या तो एक पक्ष एक फ़्लिप से आगे हो जाएगा, या खेल समाप्त हो जाएगा। फिर से, दोनों परिणाम समान रूप से संभावित हैं। इसलिए z=1+0.5*y
अतः हमारे पास तीन समीकरण और तीन अज्ञात हैं:
(1) एक्स= 1+y
(2) वाई = 1+ 0.5x + 0.5z
(3) Z = 1+ 0.5y
इसे हल करने के लिए सबसे पहले अंतिम दो समीकरणों को 2 से गुणा करके दशमलव से छुटकारा पाएं।
(1) एक्स= 1+y
(2) 2Y = 2+ x + z
(3) 2Z = 2+ y
आइए (1) से (2) में x के स्थान पर 1+y प्रतिस्थापित करें।
2Y = 2 + 1 + y + z
(4) y = 3 + z
(3) में y के स्थान पर 3+z का कोई प्रतिस्थापन नहीं
2z = 2 + 3 + z
ज़ेड = 5
अब (4) में z के स्थान पर 5 प्रतिस्थापित करें
(5) y = 3+ 5 = 8
(1) में y = 8 को प्रतिस्थापित न करें
(6) x = 9
एक दोस्त चित या पट का 3-पलट क्रम चुनता है, और मुझे अपना (अलग) 3-पलट क्रम चुनने का विकल्प देता है। हम एक निष्पक्ष सिक्के को तब तक जितनी बार चाहें उतनी बार उछालते हैं जब तक कि हमारा कोई क्रम न आ जाए। अगर वह HHH चुनता है, तो मुझे कौन सा क्रम चुनना चाहिए, और इस दांव पर मेरा क्या फ़ायदा है? उसके चुने हुए क्रम के आधार पर मैं कौन सा क्रम चुनूँ, इसकी गणना कैसे करूँ?
निम्नलिखित तालिका खिलाड़ी A और खिलाड़ी B के सभी संभावित चुने गए पैटर्न के अनुसार खिलाड़ी A के जीतने की संभावना को दर्शाती है।
खिलाड़ी A के जीतने की संभावना
| खिलाड़ी A | खिलाड़ी बी | |||||||
| एचएचएच | एचएचटी | एचटीएच | एचटीटी | टीएचएच | टीएचटी | टीटीएच | टीटीटी | |
| एचएचएच | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| एचएचटी | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| एचटीएच | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| एचटीटी | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| टीएचएच | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| टीएचटी | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| टीटीएच | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| टीटीटी | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 | |
सर्वोत्तम पैटर्न चुनने के लिए एक मेमोरी डिवाइस यह है कि उसकी पहली और दूसरी पसंद क्रमशः आपकी दूसरी और तीसरी पसंद होनी चाहिए। आपकी पहली पसंद आपकी तीसरी पसंद के विपरीत होनी चाहिए। उदाहरण के लिए, यदि आपका प्रतिद्वंद्वी HTT चुनता है, तो आपकी दूसरी और तीसरी पसंद HT होनी चाहिए। आपकी अंतिम पसंद T है, इसलिए HHT पैटर्न के लिए आपकी पहली पसंद H होनी चाहिए। इस रणनीति का पालन करने पर आपके जीतने की संभावना 2/3 से 7/8 तक होगी, जो इस बात पर निर्भर करती है कि आपका प्रतिद्वंद्वी कौन सा पैटर्न चुनता है।
नमस्ते, मेरा नाम पैटी है। आपकी साइट बहुत अच्छी है और आप बहुत जानकार इंसान लगते हैं। बिलकुल वैसा ही आदमी जिसे मैं कैसीनो में अपने साथ चाहती हूँ!!!!!!! मैं सोच रही थी कि क्या आप मेरी मदद कर सकते हैं। मैंने अपने बॉयफ्रेंड से कहा था कि मैं इंटरनेट पर एक समस्या का समाधान ढूँढूँगी। अगर आप मेरी मदद करेंगे, तो मैं वाकई बहुत अच्छी दिखूँगी।
मेरा एक बॉयफ्रेंड सिक्के इकट्ठा करता है। उसने गेहूँ के सिक्कों से भरा एक थैला खरीदा। मुझे खुद सिक्कों के बारे में ज़्यादा जानकारी नहीं है। (वो मुझे समय के साथ सिखा रहा है) लेकिन उसने कहा कि उसे हैरानी है कि थैले में एक खास साल का नाम नहीं था, क्योंकि वो तो बहुत आम हैं। उसने कहा कि ऐसा होने की संभावना एक अरब में एक है। मैंने उससे कहा कि मैं अपने ऑफिस के लोगों (स्वयंभू प्रतिभाशाली लोगों से!) से पूछने की कोशिश करूँगा और अगर उन्हें पता नहीं है, तो मैं ऑनलाइन थोड़ी रिसर्च करूँगा। मुझे आप मिले।
खैर, अगर आप मदद कर सकें तो। मैं बहुत आभारी रहूँगा। बैग में लगभग 5,500 पेनीज़ थे। सभी अमेरिकी टकसालों द्वारा ढाले गए गेहूँ के पेनीज़ की कुल संख्या 24,267,000,000 थी। 1955 के जो पेनीज़ ढाले गए थे (वह जिसकी तलाश में था) उनकी संख्या 330,000,000 थी। मेरे कार्यालय के कुछ लोगों का कहना है कि इसके पीछे और भी कारण हैं, जैसे; जनसांख्यिकी, यह तथ्य कि टकसालों ने शायद सभी पेनीज़ वितरित नहीं किए होंगे आदि। ...................... मैं मान लूँगा कि वे सही हैं, लेकिन मैं (और मुझे यकीन है कि मेरा मित्र भी) अनुमानित ऑड्स जानने पर सहमत हो जाऊँगा!!!!!!!!! मुझे आशा है आप मदद कर सकते हैं।
आपके टकसाल के आंकड़े माउंटेन व्यू सिक्कों के करीब हैं। यह मानते हुए कि अब तक ढाले गए हर गेहूँ के सिक्के के बैग में होने की संभावना समान है, किसी भी एक सिक्के के 55 न होने की संभावना (24,267,000,000-330,000,000)/24,267,000,000 = 0.986401286 है। 5500 सिक्कों के 55 न होने की संभावना लगभग 0.986401286 के रूप में अनुमानित की जा सकती है। 5500 = 507,033,772,284,213,000,000,000,000,000,000 में से 1।
मेरे पिताजी सिक्के इकट्ठा करते हैं, इसलिए मैंने उनसे इस बारे में मदद माँगी। उन्होंने जो कहा, वह इस प्रकार है:
मेरा अनुमान यह है। 1955 में, फिलाडेल्फिया में कुछ लिंकन सेंट थे जिन पर तारीख दो बार अंकित थी। कोई नहीं जानता कि कितने सेंट प्रचलन में थे, इससे पहले कि यह त्रुटि पकड़ी गई, उन्हें प्रचलन में लाने के लिए अन्य सेंटों के साथ मिला दिया गया। आज एक अप्रचलित नमूने की कीमत लगभग $2000 से $6000 है। मुझे संदेह है कि "गेहूँ" के उस थैले से 1955 के सभी सेंट पहले ही किसी ने डबल-डाई नमूनों की तलाश में निकाल लिए थे। यहाँ एक का चित्र है: 1955 डबल्ड डाई ऑब्वर्स वन सेंट ।
ध्यान दें कि यह वेबसाइट "गेहूँ" बेच रही है और आप शर्त लगा सकते हैं कि डीलर द्वारा सिक्के एकत्र किए जाने के बाद, तारीखों में कुछ कटौती पहले ही हो चुकी होगी। मुझे लगता था कि 1955 के सिक्के, जो डबल-डाई वाले नहीं थे, संग्रह में वापस कर दिए गए होंगे, लेकिन शायद वे अलग से बेचे जाते हैं, या पिघला दिए जाते हैं। गेहूँ के पेनी में मौजूद तांबे का मूल्य आज एक सेंट से कहीं ज़्यादा है। इसीलिए कुछ दशक पहले तांबे की परत चढ़े जिंक सेंट का चलन शुरू हुआ। ऐसी संभावना है कि टकसाल ने ही 1955 के कई सिक्कों को वितरित न करने का फैसला किया हो, और दुर्लभ डबल-डाई नमूनों के लिए होड़ से बचने के लिए, ढलाई के बाद उन्हें पिघला दिया हो। टकसाल और डाकघर हमेशा से मुद्रण त्रुटियों से शर्मिंदा रहे हैं, और उन्हें प्रचलन से बाहर रखने की कोशिश करते हैं।
अपने पिछले कॉलम में आपने कहा था कि "5500 सिक्कों के 55 न होने की संभावना को बहुत करीब से इस प्रकार अनुमानित किया जा सकता है: 0.9864012865500 = 507,033,772,284,213,000,000,000,000,000,000 में 1।"
मैं "अनुमानित" मान रहा हूँ क्योंकि जैसे-जैसे आप 5500 सिक्कों को हटाते हैं, निष्कासन का प्रभाव बढ़ता जाता है। निष्कासन के नगण्य प्रभाव की बात करें! यह एक अच्छा उदाहरण है कि जैसे-जैसे आप गैर-लक्ष्य सिक्कों को हटाते हैं, लक्ष्य सिक्कों के कम होने की संभावना कम होती जाती है, क्योंकि निष्कासन का प्रभाव एक टेढ़े खेल की बहुत बड़ी संभावना की तुलना में बहुत कम होता है, यानी लक्ष्य सिक्के हटा दिए गए हैं।
हाँ, मैंने "करीब-करीब अनुमानित" कहा क्योंकि दुनिया में पैसे बहुत कम हैं। बैग से एक गैर-55 वाला पैसा निकाल दें और इस हटाने के प्रभाव से बैग में मौजूद हर दूसरे पैसे के 55 होने की संभावना बढ़ जाती है। अगर मैंने "करीब-करीब अनुमानित" नहीं कहा होता, तो कम से कम तीन लोग मुझे सही करने के लिए लिख देते। बेशक, यह एक बहुत ही सूक्ष्म प्रभाव है, लेकिन मेरे कई पाठक पूर्णतावादी हैं, और छोटी-सी गलती पर भी मुझ पर टूट पड़ते हैं।
एक कमरे में दो मेज़ें हैं। दाईं ओर वाली मेज़ पर 100 सिक्के रखे हैं, जिनमें से 20 सिक्के H की तरफ ऊपर की ओर और बाकी (80) सिक्के T की तरफ ऊपर की ओर रखे हैं। दूसरी मेज़ पर कोई सिक्का नहीं है। लक्ष्य किसी तरह सिक्कों को इस तरह हिलाना है कि दोनों मेज़ों पर H की तरफ ऊपर की ओर रखे सिक्कों की संख्या बराबर हो जाए। आप सिक्कों को देख नहीं सकते (अंधेरे कमरे में) और न ही उन्हें छूकर बता सकते हैं कि वे ऊपर की तरफ हैं या नीचे की तरफ।
समाधान के लिए मेरी दूसरी साइट mathproblems.info पर जाएं (स्पॉइलर चेतावनी!)
मेरे दोस्त ने मुझसे $20.00 की शर्त लगाने की पेशकश की और मुझे 3 में से 1 का ऑड्स दिया कि अगर मैं एक सिक्का 100 बार उछालूँ, तो ठीक 50 बार चित और 50 बार पट आएगा। अगर ऐसा हुआ, तो मैं $60.00 जीत जाऊँगा और अगर ऐसा नहीं हुआ, तो मुझे उस पर $20.00 देने होंगे। क्या मुझे शर्त लगानी चाहिए थी? इसके अलावा, अगर 50/50 सबसे संभावित परिणाम नहीं है, तो क्या कोई और परिणाम (जैसे 51/49) है जिसकी संभावना अधिक है?
प्रत्येक के ठीक 50 आने की संभावना (100,50)*(1/2) 100 = 7.96% है । उचित ऑड्स 11.56 से 1 होंगे। इसलिए, 3 से 1 पर, यह एक बहुत ही खराब दांव है, जिसमें हाउस एज 68.2% है। यह आपके लिए एक अच्छा दोस्त है। 50/50 चित और पट के बीच सबसे अधिक संभावित सटीक विभाजन है। एक दिलचस्प दांव यह है कि चित/पटल की संख्या 47 और 53 के बीच आएगी या नहीं। इस सीमा के अंदर आने की संभावना 51.59% है। अगर आपको कोई ऐसा व्यक्ति मिल जाए जो यह दांव लगा सके कि कुल योग उस सीमा के बाहर आएगा, तो सम धन पर आपको 3.18% का लाभ होगा।
निम्नलिखित तालिका 30 से 70 चित/पूंछ की संभावना दर्शाती है।
100 फ़्लिप में कुल चित/पूंछ की संभावना
| चित्त पट | संभावना |
|---|---|
| 30, 70 | 0.000023 |
| 31, 69 | 0.000052 |
| 32, 68 | 0.000113 |
| 33, 67 | 0.000232 |
| 34, 66 | 0.000458 |
| 35, 65 | 0.000864 |
| 36, 64 | 0.001560 |
| 37, 63 | 0.002698 |
| 38, 62 | 0.004473 |
| 39, 61 | 0.007111 |
| 40, 60 | 0.010844 |
| 41, 59 | 0.015869 |
| 42, 58 | 0.022292 |
| 43, 57 | 0.030069 |
| 44, 56 | 0.038953 |
| 45, 55 | 0.048474 |
| 46, 54 | 0.057958 |
| 47, 53 | 0.066590 |
| 48, 52 | 0.073527 |
| 49, 51 | 0.078029 |
| 50 | 0.079589 |
n परीक्षणों में से w जीत की संभावना के लिए सामान्य सूत्र, जहां प्रत्येक जीत की संभावना p है, संयोजन (n, w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw) है ।
यदि मैं एक सिक्का 1,000 बार उछालूं, तो क्या संभावना है कि मुझे लगातार कम से कम 10 बार चित या पट आने की संभावना दिखे?
यह अजीब है कि आपने पूछा; एक अन्य पाठक ने मुझे अभी-अभी इस विषय पर एक अकादमिक पेपर भेजा है। इस पेपर में निम्नलिखित ग्राफ़ शामिल है, जो लगभग 62% संभावना दर्शाता है।
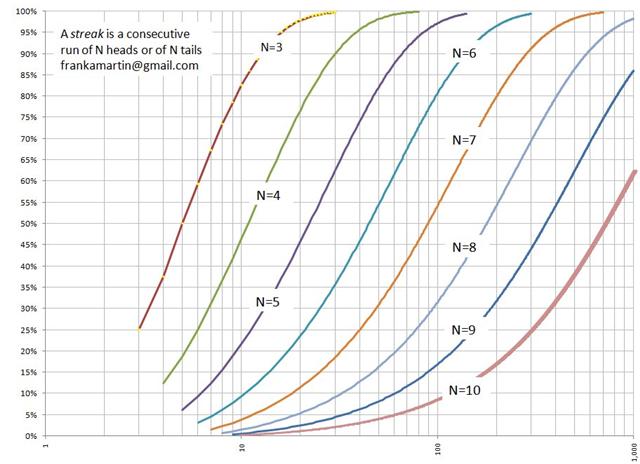
इस विषय पर अधिक जानकारी के लिए कृपया देखें कैसीनो में इतना भयानक क्रम होने की क्या संभावना थी? (483K) लेखक: फ्रैंक मार्टिन।
यदि एक सिक्के को 100 बार उछाला जाए, तो कम से कम एक बार लगातार 7 बार सिर आने की संभावना क्या है?
अगर इस उत्तर के लिए कोई आसान, गैर-पुनरावर्ती व्यंजक है, तो मुझे उसकी जानकारी नहीं है। हालाँकि, एक आसान पुनरावर्ती उत्तर ज़रूर है।
f(n)= pr(पहले फ्लिप में पूंछ)×f(n-1) +
pr(पहली फ़्लिप में हेड, दूसरी फ़्लिप में टेल)×f(n-2) +
pr(पहले 2 फ़्लिप में हेड, तीसरे फ़्लिप में टेल)×f(n-3) +
pr(पहले 3 फ़्लिप में हेड, तीसरे फ़्लिप में टेल)×f(n-4) +
pr(पहले 4 फ़्लिप में हेड, चौथे फ़्लिप में टेल)×f(n-5) +
pr(पहले 5 फ़्लिप में हेड, पाँचवें फ़्लिप में टेल)×f(n-6) +
pr(पहले 6 फ़्लिप में हेड, छठे फ़्लिप में टेल)×f(n-7) +
pr(पहले 7 फ़्लिप में हेड) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
कहाँ:
f(n)=n फ़्लिप के भीतर सफलता की संभावना।
pr(x)=x घटित होने की संभावना.
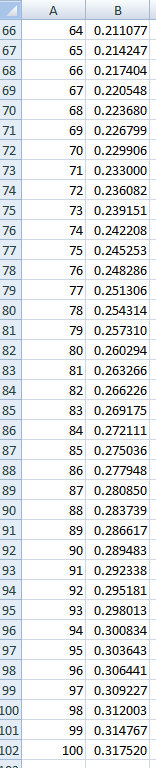
स्प्रेडशीट ऐसी समस्याओं के लिए एकदम सही हैं। नीचे दिए गए स्प्रेडशीट के स्क्रीनशॉट में, मैंने सेल B2 से B8 के लिए 0 की प्रायिकता दी है, क्योंकि 6 या उससे कम बार उछालने पर लगातार 7 चित नहीं आ सकते। सेल B9 के लिए, मैंने यह सूत्र दिया है:
=(1/2)*बी8+(1/2)^2*बी7+(1/2)^3*बी6+(1/2)^4*बी5+(1/2)^5*बी4+(1/2)^6*बी3+(1/2)^7*बी2+(1/2)^7
फिर मैंने इसे सेल B10 से सेल B102 में कॉपी और पेस्ट किया, जो 100 फ़्लिप के बराबर है। इसकी प्रायिकता 0.317520 है। एक यादृच्छिक सिमुलेशन इसकी पुष्टि करता है।
 |  |
इसके मूल प्रकाशन के बाद, रिक पर्सी ने अपना मैट्रिक्स अलजेब्रा का हल मेरे साथ साझा किया। यहाँ मेरे अपने शब्दों में है। मुझे लगता है कि पाठक मैट्रिक्स अलजेब्रा की मूल बातें पहले से ही जानते होंगे।
सबसे पहले, फ्लिपर किसी भी एक बिंदु पर आठ संभावित स्थितियों में हो सकता है:
p 1 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 7 और सिर की आवश्यकता हो।
p 2 = सफलता की संभावना, यह देखते हुए कि आपको वर्तमान बिंदु से 6 और सिर की आवश्यकता है।
p 3 = सफलता की संभावना, यह देखते हुए कि आपको वर्तमान बिंदु से 5 और सिर की आवश्यकता है।
p 4 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 4 और सिर की आवश्यकता हो।
p 5 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 3 और सिर की आवश्यकता हो।
p 6 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 2 और सिर की आवश्यकता हो।
p 7 = सफलता की संभावना, बशर्ते कि आपको वर्तमान बिंदु से 1 और सिर की आवश्यकता हो।
p 8 = सफलता की संभावना, बशर्ते कि आपको और अधिक सिर की आवश्यकता न हो = 1.
आइए अधिकतम S n को n वें फ़्लिप के बाद प्रत्येक अवस्था में होने की प्रायिकता के रूप में परिभाषित करें। S 0 पहले फ़्लिप से पहले की प्रायिकताओं को दर्शाता है, जहाँ अवस्था 0 में होने की 100% संभावना होती है। अतः S 0 =
| 1 0 0 0 0 0 0 0 |
मान लीजिए T दो लगातार फ़्लिप से परिवर्तन मैट्रिक्स है, या S n से S n+1 तक, जहाँ S n+1 = T × S n
- यदि आप अवस्था 1 में हैं तो एक पलटी के बाद आपके पास अवस्था 2 (चित के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में पहुंचने की 0.5 संभावना है।
- यदि आप अवस्था 2 में हैं तो एक पलटी के बाद आपके पास अवस्था 3 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 3 में हैं तो एक पलटी के बाद आपके पास अवस्था 4 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 4 में हैं तो एक पलटी के बाद आपके पास अवस्था 5 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 5 में हैं तो एक पलटी के बाद आपके पास अवस्था 6 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप अवस्था 6 में हैं तो एक पलटी के बाद आपके पास अवस्था 7 (सिर के साथ) में पहुंचने की 0.5 संभावना है, तथा अवस्था 1 (पूंछ के साथ) में लौटने की 0.5 संभावना है।
- यदि आप स्थिति 7 में हैं तो एक पलटी के बाद आपके पास स्थिति 8 (सिर के साथ) में होने की 0.5 संभावना है, और स्थिति 1 (पूंछ के साथ) में वापस आने की 0.5 संभावना है।
- यदि आप अवस्था 8 में हैं तो आपने सफलता प्राप्त कर ली है, और 1.0 की संभावना के साथ आप अवस्था 8 में ही बने रहेंगे।
इन सबको संक्रमण मैट्रिक्स T = के रूप में रखने पर
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
एक फ्लिप के बाद प्रत्येक स्थिति की संभावना जानने के लिए...
(1) एस 1 = एस 0 × टी
दो फ़्लिप के बाद क्या होगा?
(2) एस 2 = एस 1 × टी
आइए समीकरण (1) को समीकरण (2) में प्रतिस्थापित करें...
(3) एस 2 = एस 0 × टी × टी = एस 0 × टी 2
तीन फ़्लिप के बाद क्या होगा?
(4) एस 3 = एस 2 × टी
समीकरण (3) को (4) में प्रतिस्थापित करने पर...
(5) एस 3 = एस 0 × टी 2 × टी = एस 0 × टी 3
हम 100वें फ्लिप के बाद भी राज्य तक ऐसा करते रह सकते हैं...
एस 100 = एस 0 × टी 100
तो, T 100 क्या है? कंप्यूटर से पहले ऐसी चीज़ों को समझना बहुत मुश्किल रहा होगा। हालाँकि, एक्सेल के MMULT फ़ंक्शन और काफ़ी कॉपी-पेस्ट करने पर हमें T 100 = मिलता है।
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
ऊपरी दाईं ओर दिया गया शब्द हमें 100 फ़्लिप के बाद स्थिति 8 में होने की संभावना दर्शाता है, जो 0.317520 है।
क्या आपने उस ऑस्ट्रेलियाई क्रिकेट खिलाड़ी की कहानी सुनी है जिसने लगातार 35 मैचों तक सिक्के की उछाल गलत बताई, और 36वीं बार सही फैसला सुनाया? ऐसा होने की कितनी संभावना है?
जब तक आपने इसका ज़िक्र नहीं किया, मैंने इसके बारे में नहीं सुना था। आप मैगपाईज़ की एक किशोर क्रिकेट खिलाड़ी क्रिस्टी पेरिन की अद्भुत कहानी का ज़िक्र कर रहे हैं, जिसने लगातार 35 बार सिक्का उछालना ग़लत बताया था। ठीक 35 या उससे ज़्यादा बार गलत होने की संभावना (1/2) 35 = 34,359,738,368 में 1 है। इसे समझने के लिए, पावरबॉल पर हिट होने की संभावना 195,249,054 में 1 है। यह लगातार 35 बार सिक्का उछालने से चूकने की संभावना से 176 गुना ज़्यादा है।
क्या आपके पास सिक्के के उछाल पर दांव लगाने के लिए कोई सलाह है?
हाँ! फ़्लिपर के हाथ में जो पक्ष ऊपर की ओर हो, उस पर दांव लगाएँ। पर्सी डायकोनिस, सुसान होम्स और रिचर्ड मोंटगोमरी द्वारा लिखित अकादमिक शोधपत्र "डायनेमिक बायस इन द कॉइन टॉस" का निष्कर्ष है कि 51% बार सिक्का उसी ओर गिरेगा जिस ओर से वह शुरू हुआ था।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
औसतन, 50/50 के खेल में लगातार दो मैच हारने के लिए कितने प्रयास करने होंगे? लगातार 3, 4, n के बारे में क्या ख्याल है?
आइये पहले दो हानि वाले मामले को हल करें।
मान लीजिए x किसी भी जीत के बाद या शुरुआत से शुरू होने वाले भविष्य के फ़्लिप की अपेक्षित संख्या है।
मान लीजिए कि y एक हार के बाद भविष्य में होने वाली फ़्लिप की अपेक्षित संख्या है।
हम निम्नलिखित दो समीकरण बना सकते हैं:
(1) x = 1 + .5x + .5y
एक यह दर्शाता है कि खिलाड़ी को अवस्था बदलने के लिए सिक्का उछालना होगा। अवस्था x में बने रहने पर जीत की संभावना 50% है। अवस्था y में आगे बढ़ने पर हार की संभावना 50% है।
(2) y = 1 + .5x
स्थिति y से फिर से, 1 उस बिंदु पर फ़्लिप को दर्शाता है। स्थिति x पर वापस लौटने पर जीत की संभावना 50% है। हार की संभावना 50% है, जिससे खेल समाप्त हो जाता है और अतिरिक्त फ़्लिप की आवश्यकता नहीं होती, इसलिए यह एक निहित 0.5*0 है।
दोनों समीकरणों को 2 से गुणा करें और पुनः क्रमित करें:
(3) x - y =2
(4) -x + 2y = 2
दोनों समीकरणों को जोड़ने पर प्राप्त होगा:
(5) y = 4
इसे (1) से (4) तक किसी भी समीकरण में डालें और x=6 प्राप्त करें।
तीन हानि वाले मामले के लिए, तीन संभावित स्थितियों को इस प्रकार परिभाषित करें:
मान लीजिए x किसी भी जीत के बाद या शुरुआत से शुरू होने वाले भविष्य के फ़्लिप की अपेक्षित संख्या है।
मान लीजिए कि y एक हार के बाद भविष्य में होने वाली फ़्लिप की अपेक्षित संख्या है।
मान लीजिए z दो हार के बाद भविष्य में होने वाली फ़्लिप की अपेक्षित संख्या है।
प्रारंभिक समीकरण इस प्रकार हैं:
x = 1 + .5x + .5y
y = 1 + .5x + .5z
z = 1 + .5x
हम प्रारंभिक अवस्थाओं को मैट्रिक्स रूप में इस प्रकार सेट कर सकते हैं:
| 0.5 | -0.5 | 0 | 1 |
| -0.5 | 1 | -0.5 | 1 |
| -0.5 | 0 | 1 | 1 |
यदि आपको अपना मैट्रिक्स बीजगणित याद है, तो हम x को निर्धारक (A)/निर्धारक (B) के रूप में हल कर सकते हैं जहाँ
ए =
| 1 | -0.5 | 0 |
| 1 | 1 | -0.5 |
| 1 | 0 | 1 |
बी =
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
एक्सेल में एक आसान निर्धारक फ़ंक्शन है: =mdeterm(रेंज)। इस स्थिति में x = mdeterm(मैट्रिक्स A)/mdeterm(मैट्रिक्स B) = 1.75/0.125 = 14.
हम अतिरिक्त लगातार नुकसान के लिए रिकर्सन का उपयोग कर सकते हैं। आइए 4 पर विचार करें। ऊपर से हम जानते हैं कि लगातार 3 नुकसान पाने के लिए औसतन 14 बार उछालना पड़ेगा। उस बिंदु पर सिक्का फिर से उछाला जाएगा, और फिर से शुरू होने की 50% संभावना होगी। तो:
x = 14 + 1 + x/2
x/2 = 15
एक्स = 30
दूसरे शब्दों में, पिछले उत्तर में एक जोड़ें और फिर उसे दोगुना करें।
पैटर्न देखना मुश्किल नहीं है। एक पंक्ति में n नुकसान पाने के लिए अपेक्षित फ़्लिप की संख्या 2 n+1 -2 है।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया और इस पर चर्चा की गई।
यह देखते हुए कि एक निष्पक्ष सिक्के को n बार उछाला जाता है, कम से कम एक बार t-पुच्छ की लकीर देखने की संभावना क्या है?
उत्तर है 1-F (t) n+2 /2 n , जहाँ F (t) n, t-चरणीय फिबोनाची अनुक्रम में n-वीं संख्या है।
आप पूछ सकते हैं कि फ़िबोनाची अनुक्रम क्या है? पहली संख्या एक होती है। t-चरण अनुक्रम में, प्रत्येक बाद की संख्या पिछली t संख्याओं का योग होती है। मान लीजिए कि पहली संख्या से पहले की कोई भी संख्या शून्य है।
आइए दो-चरणीय अनुक्रम देखें। पहली संख्या 1 है। दूसरी संख्या पिछली दो संख्याओं का योग है। मान लीजिए कि एक से पहले शून्य है, तो दूसरी संख्या 0+1=1 है। तीसरी संख्या 1+1=2 है, चौथी संख्या 1+2=3 है, और पाँचवीं संख्या 2+3=5 है।
प्रथम बारह 2-चरणीय फिबोनाची संख्याएँ हैं: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144।
आइए एक उदाहरण लेते हैं। दस बार उछालने पर कम से कम एक बार लगातार दो पट आने की प्रायिकता क्या है?
हम दो-चरणीय फ़िबोनाची अनुक्रम का उपयोग करते हैं, क्योंकि हमें केवल दो पटों की आवश्यकता है। अनुक्रम में 12वीं संख्या (पलटों की संख्या से दो अधिक) 144 है। अतः, उत्तर है 1-F (2) 10+2 /2 10 = 1 - 144/2 10 = 1 - 144/1024 = 85.94%।
20 बार उछालने पर लगातार पांच बार पट आने की संभावना क्या है?
प्रथम 22 5-चरणीय फिबोनाची संख्याएँ हैं 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, 464, 912, 1793, 3525, 6930, 13624, 26784, 52656, 103519, 203513, 400096, 786568।
इस प्रकार उत्तर है 1 - F (5) 20+2 /2 20 = 1 - 786,568/1,048,576 = 1 - 75.01% = 24.99%.
इस प्रश्न पर विज़ार्ड ऑफ़ वेगास में मेरे मंच पर चर्चा की गई है।
एक पक्षपाती सिक्का है जिसके चित आने की 60% संभावना है। इसे तब तक उछाला जाता है जब तक कि लगातार दो चित या दो पट न आ जाएँ। पहले दो चित आने की क्या संभावना है?
यहां उत्तर और समाधान (पीडीएफ) दिया गया है।
इस समस्या पर चर्चा के लिए कृपया मेरे फोरम विज़ार्ड ऑफ़ वेगास पर जाएँ।
जादूगर, मैं तुम्हें एक शर्त के लिए चुनौती देता हूँ। नियम ये हैं:
- आप अपनी पसंद का कोई भी पैटर्न चुन सकते हैं, जैसे कि चित (H) और पट (T)। उदाहरण के लिए, HTT।
- आपका पैटर्न बताने के बाद मैं अपना पैटर्न चुनूंगा।
- हम एक सिक्का तब तक बार-बार उछालेंगे जब तक कि एक क्रम में एक पैटर्न न आ जाए। जो उस पैटर्न को चुन लेगा, वही जीतेगा।
- मैं आपको 3 से 2 का ऑड्स दूंगा।
क्या आप स्वीकार करते हैं? मैं इसे जितनी बार चाहें उतनी बार करूँगा।
नहीं। फिर भी, कोशिश अच्छी है। दूसरे नंबर पर आने वाले खिलाड़ी को स्थितिगत तौर पर बहुत बड़ा फ़ायदा होता है। यहाँ दूसरे नंबर पर आने वाले खिलाड़ी के लिए रणनीति और उसकी जीत की संभावना दी गई है।
ओडियसगैम्बिट गेम रणनीति
| खिलाड़ी 1 | खिलाड़ी 2 | प्रमुख खिलाड़ी 2 जीतता है |
|---|---|---|
| एचएचएच | टीएचएच | 87.50% |
| एचएचटी | टीएचएच | 75.00% |
| एचटीएच | एचएचटी | 66.67% |
| एचएचटी | टीएचएच | 75.00% |
| टीएचएच | एचटीटी | 75.00% |
| टीएचटी | टीटीएच | 66.67% |
| टीटीएच | एचटीटी | 75.00% |
| टीटीटी | एचटीटी | 87.50% |
जैसा कि ऊपर दी गई तालिका में दिखाया गया है, मेरे जीतने की सबसे अच्छी संभावना, या आपकी सबसे कम संभावना, तब होगी जब मैं या तो THT या HTH चुनूंगा, जहां मेरे जीतने की संभावना अभी भी 3 में से केवल 1 है। इसे उचित दांव बनाने के लिए मुझे 2 से 1 मिलना चाहिए, इसलिए केवल 3 से 2 प्राप्त करने पर, आपके पास 16.67% बढ़त होगी।
खिलाड़ी दो की रणनीति को याद रखने का एक तरीका यह है। मान लीजिए कि खिलाड़ी 1 ने स्थिति x के लिए P(x) चुना है। मान लीजिए कि खिलाड़ी 1 ने स्थिति x के लिए O(x) चुना है, जो खिलाड़ी 1 के विपरीत है। खिलाड़ी 2 को हमेशा यह चुनना चाहिए: O(2) - P(1) - P(2)।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
यदि आप एक निष्पक्ष सिक्के को 40 बार उछालते हैं, तो 5 बार चित और 5 बार पट आने की क्या संभावना है? "एक धारी" का मतलब कम से कम 1 और "5" का मतलब कम से कम 5 है। चित और पट की धारियों का आस-पास होना ज़रूरी नहीं है।
कृपया उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।
यहां मेरा समाधान (पीडीएफ) है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
हेनरी और टॉम सिक्का उछालने पर दांव लगाने का फैसला करते हैं। चित आने पर हेनरी जीतता है, और पट आने पर टॉम जीतता है।
प्रति फ़्लिप $1 है और वे सचमुच ऊब चुके हैं, इसलिए वे दस लाख फ़्लिप करने का फैसला करते हैं। सत्र के अंत में, हारने वाला विजेता को अंतिम शेष राशि के लिए एक चेक लिखेगा। चेक की अपेक्षित राशि क्या है?
उत्तर के लिए सामान्य सूत्र sqrt(प्रसरण * (2/pi)) है।
इस स्थिति में प्रसरण 1,000,000 है। इसलिए, वास्तविक और अपेक्षित परिणामों के बीच अपेक्षित निरपेक्ष अंतर sqrt(1,000,000 × (2/pi)) =~ 797.88456080286535587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903 269161506119450728546416733918695654340599837 28381269120656178667772134093073.
मैं Ask the Wizard #358 में एक संबंधित प्रश्न पूछता हूं, जो यह दिखाने में मदद करेगा कि मुझे sqrt(2/pi) शब्द कहां से मिला।
[/spoiler]यह प्रश्न विज़ार्ड ऑफ़ वेगास फोरम में पूछा गया और इस पर चर्चा की गई।
मान लीजिए कि एक कैसीनो में एक निष्पक्ष सिक्का उछालने पर आधारित खेल है जिसमें बराबर राशि का भुगतान होता है। एक खिलाड़ी $1 प्रति दांव पर दस लाख बार खेलना चाहता है। दिवालिया न होने की 50% संभावना के लिए उसे कितना पैसा लाना चाहिए?
आइए सबसे पहले इस प्रश्न का उत्तर दें कि एक मिलियन फ़्लिप के बाद खिलाड़ी के x यूनिट से अधिक नीचे होने की क्या संभावना है, यह मानते हुए कि खिलाड़ी के पास असीमित बैंकरोल है।
चूँकि यह एक निष्पक्ष दांव है, इसलिए दस लाख फ़्लिप के बाद औसत जीत शून्य है। प्रत्येक फ़्लिप का प्रसरण 1 है, इसलिए दस लाख फ़्लिप का प्रसरण दस लाख होगा। इस प्रकार एक मानक विचलन sqrt(1,000,000) = 1000 है।
हम एक्सेल फ़ंक्शन =norm.inv(संभावना, माध्य, मानक विचलन) से आवश्यक बैंकरोल ज्ञात कर सकते हैं। उदाहरण के लिए, यदि हम =norm.inv(.25,0,1000) डालें, तो हमें -674.49 प्राप्त होता है। इसका अर्थ है कि यदि एक मिलियन फ़्लिप के बाद, खिलाड़ी के 674 या उससे अधिक अंक प्राप्त करने की 25% संभावना है। कृपया ध्यान रखें कि यह एक अनुमान है। सही उत्तर प्राप्त करने के लिए, हमें द्विपद वितरण का उपयोग करना चाहिए, जो एक मिलियन फ़्लिप के साथ बहुत कठिन होगा।
ऐसा हो सकता है कि अगर खिलाड़ी $674 लेकर टेबल पर गया, तो मिलियन फ़्लिप होने से पहले ही उसके पैसे खत्म हो जाएँ। अगर वह क्रेडिट पर खेलता रहे, तो हो सकता है कि उसकी रिकवरी हो जाए और वह $674 से कम की गिरावट के साथ समाप्त हो। दरअसल, एक बार जब खिलाड़ी -674 पर पहुँच जाता है, तो भविष्य में किसी भी समय उसके -674 से ऊपर या नीचे होने की 50/50 संभावना होती है।
इसलिए, यदि खिलाड़ी क्रेडिट पर खेल सकता है, तो तीन संभावित परिणाम हैं।
- खिलाड़ी कभी भी -674 से नीचे नहीं गिरता।
- खिलाड़ी किसी समय -674 से नीचे चला जाता है, लेकिन फिर उबरकर -674 से ऊपर समाप्त करता है।
- खिलाड़ी किसी समय -674 से नीचे चला जाता है, खेलता रहता है और और भी अधिक हार जाता है।
हमने यह स्थापित किया है कि परिदृश्य 3 की संभावना 25% है।
परिदृश्य 2 की संभावना परिदृश्य 3 के समान ही होनी चाहिए, क्योंकि एक बार जब खिलाड़ी -674 से नीचे होता है, तो उसके पास एक मिलियन फ़्लिप के बाद उस बिंदु से ऊपर या नीचे समाप्त होने की 50/50 संभावना होती है।
परिदृश्य 1 एकमात्र अन्य विकल्प है, जिसकी संभावना 100%-25%-25% = 50% होनी चाहिए।
यदि खिलाड़ी के 674 से नीचे न गिरने की संभावना 50% है, तो नीचे गिरने का विकल्प 100%-50% = 50% होना चाहिए।
तो, मूल प्रश्न का हमारा उत्तर यही है, $674।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।


