संभावना - कार्ड
मैं ऑनलाइन बैकारेट खेल रहा था और 75 हाथों में से बैंकर ने 52 जीते और खिलाड़ी ने 23। यह 29 का अंतर है, ऐसा होने की संभावना क्या है?
सबसे पहले, मैं यह मानकर चल रहा हूँ कि आप बराबरी की गिनती नहीं कर रहे हैं। दूसरे शब्दों में, आपका मतलब है कि 75 बाजी सुलझ गई हैं। बिना बराबरी के 75 हाथ चलना बहुत ही असंभव है। 75 बाजी सुलझने पर बैंकर की जीत की अपेक्षित संख्या 38.00913745 है। मानक विचलन 75, बैंकर की जीत की प्रायिकता और खिलाड़ी की जीत की प्रायिकता के गुणनफल का वर्गमूल है। यह देखते हुए कि कोई बराबरी नहीं हुई है, बैंकर की जीत की प्रायिकता 0.506788499 है और खिलाड़ी की जीत की प्रायिकता 0.493211501 है। इस प्रकार मानक विचलन 4.329727904 है। फिर आपको द्विपद वितरण के लिए आधा अंक का सुधार करना होगा और मानक सामान्य तालिका में Z आँकड़ा देखना होगा (यह चरण पाठक पर छोड़ दिया गया है)। अंतिम उत्तर यह है कि बैंकर के 52 या अधिक जीत हासिल करने की प्रायिकता .0009 है। आपके प्रश्न में बैंकर के 23 या उससे कम बार जीतने की संभावना (और 29 अधिक का अंतर) को भी शामिल किया गया है, जिसकी प्रायिकता .0004 है। इसलिए अंतिम उत्तर यह है कि 29 या उससे अधिक के अंतर की प्रायिकता .0013, यानी 769 में 1 है।
जब मैं कैरिबियन स्टड पोकर के लिए खिलाड़ी और डीलर के हाथों के कॉम्बो की गणना करता हूँ, तो मुझे आपके 19, आदि के मुकाबले केवल 3,986,646,103,440 मिलते हैं। मैं ठीक 5 के कारक से चूक गया हूँ। मैंने कॉम्बिन (52,5)*कॉम्बिन (47,5) का उपयोग किया था। मुझसे कहाँ गलती हुई? धन्यवाद और मुझे लगता है कि आपकी साइट बहुत अच्छी है।
तारीफ़ के लिए शुक्रिया। आप पाँच गुना ग़लत हैं क्योंकि डीलर पाँच में से किसी एक कार्ड को खुला रख सकता है। दूसरे शब्दों में, डीलर के हाथ में क्रम मायने रखता है, क्योंकि पहला कार्ड खुला ही दिया जाता है। कुल संयोजनों की सही व्युत्पत्ति संयोजन (52,5)*47*संयोजन (46,4) = 19,933,230,517,200 है।
पांच-कार्ड ड्रॉ पोकर में तीन कार्डों को एक जोड़ी में खींचने और फुल हाउस प्राप्त करने की क्या संभावनाएं हैं?
इस स्थिति में फुल हाउस पाने के दो तरीके हैं: (1) एक तरह का तीन कार्ड बनाएँ या (2) जोड़ी में एक और कार्ड बनाएँ और एक और जोड़ी बनाएँ। मैं मान रहा हूँ कि आप तीन सिंगलटन कार्ड हटा देंगे।
सबसे पहले, (1) के अंतर्गत संयोजनों की संख्या ज्ञात करते हैं। 3 रैंक हैं जिनमें केवल 3 सूट बचे हैं (याद रखें कि आपने 3 सिंगलटन हटा दिए हैं) और 9 रैंक हैं जिनमें 4 सूट बचे हैं। इस प्रकार संयोजनों की संख्या 3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39 है।
अब, आइए (2) के अंतर्गत संयोजनों की संख्या ज्ञात करें। मौजूदा जोड़ी में जोड़ने के लिए 2 सूट बचे हैं। 3 कार्ड शेष रहने पर 3 रैंक से जोड़ी बनाने के लिए (3,2) संयोजन तरीके हैं और 4 कार्ड शेष रहने पर रैंक से जोड़ी बनाने के लिए (4,2) संयोजन तरीके हैं। तो 2 के अंतर्गत कुल संयोजन 2*(3*combin(3,2)+9*combin(4,2)) = 2*(3*3 + 9*6) = 126 हैं। फुल हाउस बनाने के तरीकों की कुल संख्या (1) और (2) के अंतर्गत योग है, या 39+126=165 है। दूसरे ड्रॉ में 3 कार्डों को व्यवस्थित करने के लिए (47,3)=16,215 संयोजन तरीके हैं। फुल हाउस निकालने की संभावना, फुल हाउस निकालने के तरीकों की संख्या को कुल संयोजनों से विभाजित करने पर प्राप्त होती है, या 165/16,215 = 0.0101758, या लगभग 98 में से 1 होती है।
कॉम्बिन() फ़ंक्शन के बारे में अधिक जानकारी के लिए कृपया पोकर पृष्ठ में संभावनाओं पर मेरा अनुभाग देखें।
मैंने हफ़्ते में एक बार अपने दोस्तों के साथ पोकर खेलना शुरू किया (पाँच पत्तों का ड्रॉ, स्टड, सात पत्तों का स्टड)। हमारे पास टेबल पर सात खिलाड़ी होते हैं। मुझे लगता है कि 52 पत्तों की गड्डी से जितने खिलाड़ियों को पत्ते दिए जाएँगे, उनके जीतने की संभावना उतनी ही कम हो जाएगी। क्या आपके पास कोई गणितीय सूत्र है जो मुझे सही दिशा दिखा सके?
नहीं, किसी भी दिए गए हाथ के मिलने की संभावना एक समान होती है, चाहे टेबल पर कितने भी खिलाड़ी हों। एक अनदेखा कार्ड तो अनदेखा ही रहता है, इससे कोई फ़र्क़ नहीं पड़ता कि वह किसी और खिलाड़ी के पास है या डेक में अभी भी है।
हाल ही में मुझे एक ऐसी कहानी सुनाई गई जिस पर मुझे यकीन नहीं हुआ!! मेरे एक दोस्त ने बताया कि उसके घर पर एक दोस्ताना पोकर गेम में, उसने और उसके दोस्त ने बिना कोई कार्ड निकाले, एक ही हाथ में नेचुरल स्ट्रेट फ्लश जीत लिया!! (पाँच पत्तों के ड्रॉ में) मुझे इस पर यकीन करना मुश्किल लग रहा है और आपकी साइट से मैंने एक स्ट्रेट फ्लश के ऑड्स की गणना लगभग 65,000 से एक की है, तो खेल में 6 खिलाड़ियों के साथ (बिना कोई कार्ड निकाले) एक हाथ में 2 के ऑड्स क्या होंगे?
मैं यह मानकर एक अनुमानित उत्तर देने जा रहा हूँ कि प्रत्येक खिलाड़ी को अलग-अलग डेक से एक हाथ दिया गया था। इससे ऑड्स में ज़्यादा बदलाव नहीं आना चाहिए। पोकर में प्रायिकताओं पर मेरे अनुभाग में दिए गए अनुसार, किसी एक खिलाड़ी द्वारा स्ट्रेट फ्लश निकालने की प्रायिकता 36/2,598,960 है। आइए इस प्रायिकता को p कहते हैं। दो खिलाड़ियों द्वारा स्ट्रेट फ्लश निकालने की प्रायिकता (6,2)*p 2 *(1-p) 4 = .0000000028779 का संयोजन है। दूसरे शब्दों में, ऐसा होने के विरुद्ध ऑड्स 347,477,740 से 1 हैं।
तीन कार्ड पोकर में (1) रानी उच्च, (2) राजा उच्च, और (3) इक्का उच्च प्राप्त करने के लिए आप अलग-अलग संभावनाओं पर कैसे काम करते हैं?
मैं सबसे पहले किंग हाई का पता लगाऊंगा और संक्षेप में अन्य दो के लिए सूत्र दिखाऊंगा। संभावना किंग हाई हाथों की संख्या को कुल हाथों की संख्या से विभाजित करके प्राप्त होगी। राजा से कम रैंकों की संख्या 11 है। किंग हाई हाथ में इन रैंकों में से दो अलग-अलग होने चाहिए। 11 में से 2 को व्यवस्थित करने के तरीकों की संख्या संयोजन (11,2) = 55 है। हालांकि, इनमें से एक संयोजन राजा-रानी-जैक है, जिसके परिणामस्वरूप एक सीधा (स्ट्रेट) बनता है, इसलिए इस संयोजन को घटाने पर 54 बचते हैं जो एक सीधा (स्ट्रेट) नहीं बनाते हैं। इसके बाद, प्रत्येक रैंक के लिए चार सूट हैं, या 4 3 = 64 सूट के संभावित संयोजन हैं। हालांकि, इन 64 में से चार फ्लश का परिणाम देते हैं इसलिए 64-4 = 60 सूट के संयोजन बचते हैं। 52 में से 3 पत्तों को व्यवस्थित करने के लिए कुल कॉम्बिनेशन (52,3) = 22,100 हैं। इसलिए, किंग हाई बनने की प्रायिकता 3,240/22,100 = 0.1466063 है। ऐस हाई बनने की प्रायिकता है: (कॉम्बिनेशन (12,2) -2)*(4 3 -4)/कॉम्बिनेशन (52,3) = 0.1737557। ध्यान दें कि -1 के बजाय -2 है क्योंकि दोनों a-2-3 और qka स्ट्रेट्स हैं।
रानी के उच्च होने की संभावना है: (कॉम्बिन(10,2)-1)*(4 3 -4)/कॉम्बिन(52,3)=0.119457.
रॉयल फ्लश मिलने की कितनी संभावना है? क्रमिक रॉयल फ्लश मिलने की (आगे या पीछे)?
किसी भी रॉयल फ्लश की प्रायिकता संभावित रॉयल्स की संख्या होती है, जो चार (प्रत्येक सूट के लिए एक) होती है, जिसे 52 में से 5 कार्ड चुनने के तरीकों की संख्या से विभाजित किया जाता है, जो कि (52,5) = 2,598,960 है। तो, उत्तर 4/2,598,960 = 0.00000153908, या 649,740 में 1 है।
अनुक्रमिक रॉयल फ्लश की प्रायिकता बराबर है (सूट की संख्या) * (दिशाओं की संख्या) / (52 में से 5 पत्तों के कुल क्रमपरिवर्तन) = 4 * 2 / क्रमपरिवर्तन (52,5) = 8 / 311,875,200 = 8 / संभावित रॉयल्स की संख्या, जो चार (प्रत्येक सूट के लिए एक) है, दिशाओं की संख्या का गुणा, 52 में से 5 पत्ते चुनने के तरीकों की संख्या से विभाजित, जो क्रमपरिवर्तन (52,5) = 311,875,200 है। तो, उत्तर है 4/311,875,200 = 0.00000002565, या 38,984,400 में 1।
मुझे डॉलर के नोटों से "लायर्स पोकर" खेलना पसंद है। किसी नोट पर एक ही संख्या के 1,2,3,4, या 5 आने की प्रायिकता क्या है? धन्यवाद। अगर मैं 3 लोगों के साथ खेल रहा हूँ, तो किसी एक संख्या के आने की प्रायिकता क्या है?
सबसे पहले, मैं इस अनपूछे गए प्रश्न का उत्तर दूँगा कि किसी विशिष्ट संख्या के किसी यादृच्छिक बिल पर n बार आने की प्रायिकता क्या है। एक बिल में 8 अंक होते हैं, इसलिए किसी विशिष्ट संख्या के n की प्रायिकता combin(8,n)*0.1 n *0.9 8-n /10 8 है। यहाँ एक तालिका दी गई है जो किसी विशिष्ट संख्या के 0 से 8 तक की प्रायिकता दर्शाती है।
झूठे पोकर में विशिष्ट संख्या की संभावनाएँ
| संख्या | संभावना |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| कुल | 1.00000000 |
अगली तालिका हर संभावित प्रकार के बिल की प्रायिकता दर्शाती है, जिसे प्रत्येक n-of-a-kind की संख्या के आधार पर वर्गीकृत किया गया है। उदाहरण के लिए, सीरियल नंबर 66847680 में एक तीन एक तरह के, एक जोड़ा और तीन एकल होंगे, जिसकी प्रायिकता 0.1693440 है।
झूठे पोकर में सामान्य संभावनाएँ
| 8 ओक | 7 ओक | 6 ओक | 5 ओक | 4 ओक | 3 ओक | 2 ओक | 1 ओक | संभावना |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| कुल | 1.0000000 | |||||||
ओक = "एक प्रकार का"
अधिक जानकारी के लिए, झूठे पोकर पर मेरा पेज देखें।
52 पत्तों की गड्डी में जैक की जोड़ी निकलने की क्या सम्भावना है?
मान लें कि आप पांच कार्ड खींचते हैं, और सभी हाथों को ठीक दो जैक के साथ गिनते हैं, तो संभावना होगी combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3.99%.
पाई गौ पोकर में तीन जोड़ी मिलने की संभावना क्या है? क्या संभावनाएँ एक तरह के तीन से कम या ज़्यादा हैं?
एक तरह के तीन और दो जोड़े को छोड़कर, तीन जोड़े और संयोजनों की संख्या प्राप्त करने के तरीके निम्नलिखित हैं।
कोई वाइल्ड कार्ड नहीं: combin(13,3)*10*6 3 *4 =2471040
इक्कों की जोड़ी को प्रतिस्पर्धा करने के लिए इस्तेमाल किया गया वाइल्ड कार्ड: combin(12,2)*10*6 2 *4 2 = 380,160
सिंगलटन ऐस के रूप में प्रयुक्त वाइल्ड कार्ड: कॉम्बिन(12,3)*6 3 = 47,520
संयोजनों की कुल संख्या 2,898,720 है। यह एक तरह के तीन के लिए 747,0676 संयोजनों के आधे से भी कम है।
आपके फॉर्मूले के अनुसार, रॉयल फ्लश के लिए ऑड्स 4/2,598,960 = 1/649,740 हैं। इसलिए, अगर मैं डीलर के साथ कैरेबियन स्टड वन-ऑन-वन खेल रहा होता, तो मेरे और डीलर के हाथ 649,740*2 = 1,299,480 के बराबर होते। इसलिए, गणित के अनुसार, 1,299,480 हाथों के बाद दो रॉयल फ्लश होने चाहिए। कृपया मुझे बताएँ कि क्या मैं ऑड्स को सही ढंग से समझ पाया हूँ।
आप सही कह रहे हैं कि औसतन हर 649,740 हाथों में एक बार रॉयल फ्लश आएगा, और 1,299,480 हाथों में रॉयल फ्लश की अपेक्षित संख्या 2 है। हालाँकि, यह केवल औसत है। हर हाथ के साथ आप रॉयल फ्लश पाने के करीब नहीं पहुँचते। स्वतंत्र परीक्षणों के हर खेल में यह स्मृति-रहित गुण होता है, इसलिए रॉयल फ्लश कभी भी अतिदेय नहीं होता।
1,299,480 हाथों में शून्य रॉयल्स की संभावना 13.53% है।
नमस्ते, मैं पै गो पोकर का नियमित खिलाड़ी हूँ, और मैंने देखा कि आपकी साइट पर इस खेल के बारे में बहुत अच्छी जानकारी है। पिछले दिनों जब मैं अपने एक दोस्त के साथ खेल रहा था, तो उसे 9-हाई हैंड मिला, जो मेरे हिसाब से सबसे कम हैंड है। मैंने अब तक इस गेम को खेलते हुए सिर्फ़ एक बार ऐसा होते देखा था। फिर पाँच हैंड बाद उसे बिल्कुल वैसा ही हैंड मिला (2-3-4-5-7-8-9)। हमें यकीन नहीं हो रहा था और हम सोच रहे थे कि ऐसा होने की संभावना कितनी है, इसलिए हमने सोचा कि आपसे पूछ लेते हैं। आपके समय और आपकी बेहतरीन साइट के लिए धन्यवाद।
9 हाई हैंड बनाने के लिए रैंक्स को व्यवस्थित करने के दो तरीके हैं, आपने जो बताया और 2-3-4-6-7-8-9। फ्लश बनाए बिना सूट के संयोजनों की संख्या 4 7 -4*(combin(7,5)*3^2+6*3+1) = 15,552 है। इसलिए 9 हाई हैंड की संभावना 2*15,552/combin(53,7) = 31,104/154,143,080, या 9,911 में 1 है। अगर आप सिर्फ़ पाँच बार खेलें, तो 2 9-हाई हैंड मिलने की संभावना 9,826,685 में 1 होगी। मेरा मानना है कि ऐसा होना एक संयोग है, न कि रैंडम नंबर जनरेटर या प्रोग्राम की कोडिंग में कोई गड़बड़ी।
मेरा सवाल कैसीनो नियाग्रा नियमों के तहत कैसीनो वॉर के लिए हाउस एज और जोखिम तत्व की गणना से संबंधित है (अर्थात, 3-1 की बढ़ोतरी पर भुगतान और मूल दांव हारना)। आपने ये संख्याएँ कैसे निकालीं, मैं अभी इनकी गणना करने की कोशिश कर रहा हूँ? मुझे परेशानी हो रही है। आपकी मदद के लिए धन्यवाद।
मान लीजिए d डेक की संख्या है। पहले राउंड में बराबरी की संभावना (4*d-1)/(52*d-1)= 0.073955 है। दूसरे राउंड में बराबरी की संभावना 12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0.073974 है। मान लीजिए p 1 पहले राउंड में बराबरी की संभावना है और p 2 दूसरे राउंड में बराबरी की संभावना है। तब प्लेयर रिटर्न p 1 *(2*p 2 +(1-p 2 )/2*(1-2))= -0.023301 है। -1 से गुणा करें और आपको 2.33% हाउस एज मिलेगा। मुझे आशा है कि मैंने इस पर बहुत जल्दी नहीं कहा।
क्या आप मुझे बता सकते हैं कि कैरिबियन में कुल 19,933,230,517,200 संयोजन कैसे प्राप्त होते हैं? मैंने आपके 5-कार्ड पोकर संयोजनों का अनुसरण करके 2,598,960 प्राप्त किए। अब मैं आगे कैसे बढ़ूँ? अग्रिम धन्यवाद।
आपने खिलाड़ियों के संयोजनों की संख्या सही ढंग से गणना की है, जैसे कि संयोजन (52,5) = 2,598,960। इसके बाद, डीलर के पास संयोजन (47,5) = 1,533,939 संभावित हाथ हो सकते हैं। तब डीलर के पाँच कार्डों में से कोई भी एक कार्ड खुला हो सकता है। तो 2,598,960*1,533,959*5=19,933,230,517,200।
सबसे पहले, मैं यह कहना चाहता हूँ कि मुझे आपकी वेबसाइट वाकई बहुत अच्छी लगती है। मैंने कुछ लोगों को इसके बारे में बताया है, और उम्मीद करता हूँ कि वे भी इसे आज़माएँगे। मैं कामना करता हूँ कि आपको इसमें निरंतर सफलता मिले। मुझे WinPoker का लिंक भी पसंद आया। मुझे WinPoker इतना पसंद आया कि मैंने इसे ऑर्डर कर दिया। यह एक बेहतरीन प्रोग्राम है। मेरा एक सवाल है, उम्मीद है आप मेरी मदद कर सकते हैं। मैं यह पता लगाने की कोशिश कर रहा हूँ कि सात पत्तों वाले स्टड में हर हाथ में कितनी बार स्ट्रेट आते हैं। मेरे पास आपकी सात पत्तों वाली टेबल की एक कॉपी है, लेकिन मुझे उन संख्याओं तक पहुँचने के गणित में दिलचस्पी है। मैं पाँच पत्तों वाले नंबर तो बता सकता हूँ, लेकिन सात पत्तों वाले नंबर मुझे बिलकुल समझ नहीं आते। मैं अपने नंबरों के साथ एक Excel 2000 फ़ाइल भेजना चाहता हूँ। मैं यह भी जानना चाहता हूँ कि जोकर वाले 53 पत्तों वाले डेक में स्ट्रेट की संख्या कैसे पता करें। मदद ! ! !
आपके स्नेहपूर्ण शब्दों के लिए धन्यवाद। मैं मानता हूँ कि सात पत्तों वाले स्टड के लिए संख्याओं की गणना करना कठिन है। इसलिए मैं इसे अपने कंप्यूटर पर करता हूँ। मेरा प्रोग्राम सभी संभावित संयोजनों की जाँच करता है और प्रत्येक को अंक देता है। पाई गो पोकर में वाइल्ड स्ट्रेट्स की संख्या 11*(4 4 -4)+10*3*(4 4 -4)=10332 है। 10200 प्राकृतिक स्ट्रेट्स के साथ कुल योग 20532 होता है।
मैं समझता हूँ कि कैरिबियन स्टड पोकर या लेट इट राइड टेबल पर किसी भी व्यक्ति के लिए रॉयल, स्ट्रेट फ्लश मिलने की संभावना क्या है और यह कैसे निर्धारित होती है। लेकिन मेरा सवाल यह है: खेल देखने वाले एक तीसरे पक्ष के रूप में, किसी भी डील पर टेबल पर किसी खिलाड़ी को इनमें से कोई भी हैंड मिलने की संभावना क्या है? मुझे लगता है कि यह खेल में मौजूद हाथों की संख्या पर निर्भर करता है... क्या यह सिर्फ़ व्यक्ति के ऑड्स को खेल में मौजूद हाथों की संख्या से गुणा करने पर निर्भर करता है? यानी, टेबल पर 4 खिलाड़ियों के साथ किसी खास हैंड पर रॉयल मिलने का मतलब है कि रॉयल मिलने की संभावना 4* है? मैं थोड़ा उलझन में हूँ!
आपकी विधि एक अच्छा अनुमान है। हालाँकि उस तर्क से, जब एक सिक्का उछाला जाता है, तो 3 में से कम से कम एक व्यक्ति के सिर उछालने की संभावना 3 * 50% = 150% होगी। स्वतंत्र घटनाओं को मानते हुए n प्रयासों में से कम से कम एक सफलता की संभावना, जहां प्रत्येक सफलता की संभावना p है, 1-(1-p) n है। सिक्का उछालने के उदाहरण के मामले में यह 1-.5 3 = 0.875 होगा। कैरेबियन स्टड पोकर के चार खिलाड़ियों के मामले में कम से कम एक रॉयल फ्लश की संभावना 1-(1-4/2598960) 4 = 0.00000615629 होगी। हालाँकि चूंकि सभी कार्ड एक ही डेक से निपटाए जाते हैं, इसलिए घटनाएँ स्वतंत्र नहीं हैं।
पै गो पोकर में नेचुरल सेवन कार्ड स्ट्रेट फ्लश मिलने की संभावना क्या है? मैं एक कैसीनो में काम करता हूँ और पिछले 15 सालों में पहली बार ऐसा देखा है। भाग्यशाली ग्राहक ने $40,000 जीते।
32 संभावित प्राकृतिक स्ट्रेट फ्लश हैं (4 रैंक गुणा 7 कार्डों के 8 संभावित स्पैन)। 53 में से 7 कार्ड निकालने के लिए कॉम्बिनेशन (53,7) = 154143080 संभावित तरीके हैं। तो उत्तर है 32/154143080, या 4816971 में 1।
थ्री कार्ड पोकर में लगातार दो हाथों में दो समान स्ट्रेट फ्लश (दोनों रैंक और सूट में) प्राप्त होने की संभावना क्या है?
पहले हाथ में स्ट्रेट फ्लश मिलने की संभावना 4*12/combin(52,3) = 48/22100 =~ 0.0022 है। अगले हाथ में भी ठीक वैसा ही होने की संभावना 1/22100 है। तो उत्तर है (48/22100)*(1/22100) = 48/488410000, यानी 10,175,208 में से 1। यह 6/49 लॉटरी जीतने की संभावना से 1.37 गुना ज़्यादा है, जिसकी संभावना 13983816 में से 1 है।
8 डेक बैकारेट में, एक ही सौदे में खिलाड़ी और बैंकर दोनों के लिए एक इक्का और ईंट का 8 प्राप्त करने की संभावना क्या है?
(8 2 /कॉम्बिन(416,2))* (7 2 /कॉम्बिन(414,2)) = 0.00000043, या 2308093 में 1
हाल ही में मैंने एक अजीबोगरीब घटना देखी। मैं फाइव कार्ड ड्रॉ पोकर देख रहा था, जहाँ आप अधिकतम 2 कार्ड ही निकाल सकते थे। एक खिलाड़ी ने एक कार्ड निकाला और हार्ट फ्लश पूरा किया। डीलर ने एक कार्ड निकाला और हुकुम का फ्लश निकाला। स्वाभाविक रूप से, डीलर का फ्लश ज़्यादा था। खेल में 3 और खिलाड़ी थे। एक ही हाथ में दो फ्लश होने की संभावना क्या है?
आइए फ्लश की प्रायिकता को परिभाषित करें, या तो डील पर एक कार्ड मिलने या 4-कार्ड फ्लश ड्रॉ होने की। सरलता के लिए, हम मान लेंगे कि कोई खिलाड़ी पैट पेयर या 4 फ्लश ड्रॉ होने पर स्ट्रेट ड्रॉ करेगा। डील पर फ्लश मिलने की प्रायिकता (स्ट्रेट/रॉयल फ्लश को छोड़कर) 4*(कॉम्बिनेशन(13,5)-10)/कॉम्बिनेशन(52,5) = 5108/2598960 = 0.0019654 है। 4-कार्ड फ्लश मिलने की प्रायिकता 4*3*कॉम्बिनेशन(13,4)*13/कॉम्बिनेशन(52,5) = 111540/2598960 = 0.0429172 है। ड्रॉ पर फ्लश पूरा होने की प्रायिकता 9/47 है। तो 4-कार्ड फ्लश मिलने और उसे पूरा करने की कुल प्रायिकता 0.0429172*(9/47) = 0.0082182 है। तो फ्लश मिलने की कुल प्रायिकता 0.0019654 + 0.0082182 = 0.0101836 है। 5 में से ठीक 2 खिलाड़ियों को फ्लश मिलने की प्रायिकता combin(5,2)* 0.0101836 2 *(1-00.0101836) 3 = 0.001006 है, यानी लगभग 994 में से 1।
मुझे यह जानना है कि पाँच खिलाड़ियों और एक डेक के साथ 7 कार्ड स्टड के हाथ में किसी को एक ही तरह के 4 कार्ड मिलने की कितनी संभावना है? मुझे उम्मीद है कि आप मेरी मदद कर सकते हैं, और आपके समय के लिए धन्यवाद।
52 में से 7 पत्तों को व्यवस्थित करने के लिए combin(52,7) = 133,784,560 तरीके हैं। एक तरह के चार पत्तों सहित 7 पत्तों के सेट की संख्या 13*combin(48,3) = 224,848 है। 13 एक तरह के 4 पत्तों के लिए रैंक की संख्या है और combin(48,3) उन तरीकों की संख्या है जिनसे आप बचे हुए 48 पत्तों में से 3 पत्ते चुन सकते हैं। इसलिए प्रायिकता 224,848/133,784,560 = 0.0017, या 595 में 1 है।
जब आप ताश के पत्तों का एक नया डेक खोलते हैं, तो उसमें हर सूट का इक्का से लेकर बादशाह तक होता है। ताश के पत्तों के एक फेंटे हुए डेक को लेकर उसे इक्का से बादशाह तक की स्थिति में लाने की क्या संभावना है?
52 फैक्टोरियल में 1, या 80,658,175,170,943,900,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 में 1।
यदि दस व्यक्तियों को एक ही डेक से दो-दो कार्ड दिए जाएं तो क्या संभावना है कि दो खिलाड़ियों को इक्कों की जोड़ी मिलेगी?
सबसे पहले, 10*9/2=45 तरीके हैं जिनसे आप 10 में से 2 खिलाड़ी चुन सकते हैं। दो विशिष्ट खिलाड़ियों द्वारा चार इक्के मिलने की प्रायिकता 1/combin(52,4)=1/270725 है। इसलिए किन्हीं दो खिलाड़ियों द्वारा इक्कों का एक जोड़ा मिलने की प्रायिकता 45/270725=0.0001662 है।
यदि सात खिलाड़ियों में से प्रत्येक को सात कार्ड मिलते हैं, तो क्या संभावना है कि कम से कम एक व्यक्ति को 7-कार्ड फ्लश मिलेगा?
किसी एक खिलाड़ी द्वारा 7-कार्ड फ्लश प्राप्त करने की संभावना 4*कॉम्बिन(13,7)/कॉम्बिन(52,7) = 19491 में 1 है। 7 में से कम से कम एक खिलाड़ी द्वारा 7-कार्ड फ्लश प्राप्त करने की संभावना लगभग 2785 में 1 है।
मुझे पता है कि गणितीय रूप से कुछ भी संभव है, लेकिन उस रात कैसीनो में मुझे लगता है कि मैंने कुछ ऐसा देखा जो एक शॉट में एक अरब के बराबर होगा, ऐसा नहीं है कि ऐसा कभी नहीं होता। हुआ यूँ: लेट इट राइड टेबल पर 40 हाथों (5 खिलाड़ियों के साथ लगभग 8 राउंड में 40 सिंगल 3 कार्ड डील) के दौरान, 3 चार-चार कार्ड बाँटे गए। एक चार-चार कार्ड लगभग 4100-1 के अनुपात में होने पर, 40 डील में उनमें से तीन कार्ड बाँटने की संभावना क्या होगी? कृपया उत्तर दें क्योंकि यह मुझे परेशान कर रहा है। पुराना प्रशंसक हूँ।
सरलता के लिए मान लें कि प्रत्येक हाथ में एक नया डेक है। एक तरह के चार की संभावना 13*48/combin(52,5) = 624/2598960 है। 40 में से ठीक 3 एक तरह के चार की संभावना combin(40,3)*p 3 *(1-p) 37 = 7378135 में 1 है, जहाँ p = 624/2598960 है। तो यह 70 लाख में 1 शॉट जैसा है।
सबसे पहले मैं आपको बताना चाहता हूँ कि मैं आपकी वेबसाइट को कितना देखता हूँ और कितना पसंद करता हूँ, और आपके गणित कौशल का कितना प्रशंसक हूँ। मैं ब्लैकजैक खेलने के लिए 6 डेक इस्तेमाल करता हूँ, और 3 जोकर इसलिए जोड़े हैं क्योंकि मैं आपका समय बर्बाद नहीं करूँगा, लेकिन एक खिलाड़ी को एक ही पंक्ति में तीनों जोकर खेलने की संभावना कितनी है? बहुत-बहुत धन्यवाद।
आपका स्वागत है, आपकी तारीफ़ों के लिए शुक्रिया। छह डेक वाले जूते (और तीन जोकर) से लगातार तीन जोकर मिलने की प्रायिकता 1/combin(315,3) = 5,159,805 में 1 है। दूसरा हल (3/315)*(2/314)*(1/313) है।
52 पत्तों वाली डेक का इस्तेमाल करके चार खिलाड़ियों को 13-13 पत्ते बाँटने की क्या संभावना है, और चारों खिलाड़ियों के पास इक्के से लेकर दो तक का सीधा पत्ता हो? पत्तों का एक ही सूट का होना ज़रूरी नहीं है।
उत्तर है (4 13 /COMBIN(52,13))* (3 13 /COMBIN(39,13))* (2 13 /COMBIN(26,13)) = 61,204,166,001 में 1.
एक रॉयल को चार कार्ड दिए जाने की संभावना क्या है?
रॉयल के लिए चार संभावित सूट हैं। पाँच संभावित लुप्त कार्ड हैं। पाँचवाँ कार्ड 47 अन्य कार्डों में से एक हो सकता है। इसलिए रॉयल में चार कार्ड पाने के 4*5*47=940 तरीके हैं। कुल संयोजन (52,5) = 2,598,960 हैं। इसलिए संभावना 940/2,598,960 = 2,765 में 1 है।
प्रिय विद्वान, मान लीजिए 52 पत्तों की एक गड्डी को फेंटा जाता है, और हम 52 में से 18 पत्ते यादृच्छिक रूप से निकालते हैं, और उन्हें 3-3 पत्तों वाली 6 ढेरियों में रखते हैं। क्या संभावना है कि उनमें से एक ढेर में ठीक 3 (4 में से) इक्के हों?
इस समस्या को हल करने का आसान तरीका यह है कि पहली ढेरी में तीन इक्के होने की प्रायिकता (4/52)*(3/51)*(2/50) = 1/5525 है। हालाँकि, प्रत्येक ढेरी में तीन इक्के होने की प्रायिकता समान है, इसलिए हम इसे 6 से गुणा करते हैं, जिससे 6/5525 = 0.001086 प्राप्त होता है।
पांच कार्ड स्टड में सभी फेस कार्ड आने की संभावना क्या है?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0.00030474, या लगभग 3282 में 1.
लेट इट राइड खेलते हुए दो घंटे की अवधि में एक ही प्रकार के दो चार कार्ड प्राप्त होने की संभावना क्या है?
किसी भी दिए गए हाथ में एक तरह के चार की संभावना 13*48/combin(52,5) = 0.0002401 है। मान लीजिए कि आप दो घंटों में 120 हाथ खेल सकते हैं। ठीक दो बार एक तरह के चार की संभावना combin(120,2) × 0.0002401 2 × (1-0.0002401) 118 = 0.000400095 = 2499.41 में 1 होगी।
चार-कार्ड पोकर में, स्ट्रेट या फ्लश की संभावना अधिक होती है?
स्ट्रेट फ्लश और रॉयल फ्लश को छोड़कर, स्ट्रेट की संभावना 1.02% और फ्लश की 1.04% है। इसलिए फ्लश की संभावना थोड़ी ज़्यादा है।
दस लाख हाथों के दौरान, 2,00,000 हाथों तक रॉयल फ्लश का सूखा पड़ने की क्या संभावना है? मुझे जवाब से ज़्यादा समाधान में दिलचस्पी है।
मैं अक्सर ऐसा नहीं कहता, लेकिन मैंने घंटों कोशिश की, लेकिन इस सवाल का गणित मेरे बस से बाहर था। इसलिए मैंने अपने दोस्त और गणित के प्रोफ़ेसर गैबर मेग्येसी से सलाह ली। किसी भी "सूखे" की समस्या के लिए उनका सूत्र यहाँ दिया गया है।
- मान लीजिए कि किसी भी दिए गए हाथ को जीतने की संभावना p है।
- मान लीजिए d सूखे की अवधि है।
- मान लीजिए कि खेले गए हाथों की संख्या n है।
- k=dp और x=np सेट करें।
- यदि k=1 तो a=-1 मान लें, अन्यथा a को इस प्रकार ज्ञात करें कि k=-ln(-a)/(1+a). (a एक ऋणात्मक संख्या है, यदि k>1 तो -1 < a < 0, यदि k < 1 तो a < -1, तथा a की गणना उच्च परिशुद्धता से की जानी चाहिए।) [विज़ार्ड का नोट: इस प्रकार का समाधान एक्सेल में टूल मेनू के अंतर्गत लक्ष्य खोज सुविधा का उपयोग करके आसानी से पाया जा सकता है।]
- यदि k=1 तो A=2 मान लें, अन्यथा A=(1+a)/(1+ak) मान लें।
- n हाथों में d लंबाई के सूखे की संभावना लगभग Ae a x है।
इस विशिष्ट समस्या में p=1/40391, d=200000, n=1000000, k=4.9516, x=24.758, a=-0.0073337, A=1.03007 है। अतः सूखे की संभावना 1.03007*e -0.0073337*24.758 = 0.859042 है। इस प्रकार कम से कम एक बार सूखे की संभावना 1-0.859042 = 0.140958 है।
यहाँ गैबर मेग्येसी का पूरा 5-पृष्ठ का समाधान (पीडीएफ़) है। आपकी मदद के लिए धन्यवाद गैबर।
मैंने दस लाख हाथों के 32,095 सेटों का एक यादृच्छिक सिमुलेशन किया। कम से कम एक बार सूखे की स्थिति वाले लोगों की संख्या 4558 थी, जिसकी प्रायिकता 14.20% थी।
मान लीजिए आपके पास अलग-अलग डेक से बाँटे गए दो पाँच-पत्तों वाले पोकर हाथ हैं। आपको बताया जाता है कि हाथ A में कम से कम एक इक्का है। आपको बताया जाता है कि हाथ B में हुकुम का इक्का है। किस हाथ में कम से कम एक और इक्का होने की संभावना ज़्यादा है?
निम्नलिखित तालिका पूर्णतः यादृच्छिक हाथ में 0 से 4 इक्कों की संभावना दर्शाती है।
इक्का संभावनाएँ - यादृच्छिक हाथ
| इक्के | FORMULA | युग्म | संभावना |
|---|---|---|---|
| 0 | कॉम्बिन(48,5) | 1712304 | 0.658842 |
| 1 | कॉम्बिन(4,1)×कॉम्बिन(48,4) | 778320 | 0.299474 |
| 2 | कॉम्बिन(4,2)×कॉम्बिन(48,3) | 103776 | 0.03993 |
| 3 | कॉम्बिन(4,3)×कॉम्बिन(48,2) | 4512 | 0.001736 |
| 4 | कॉम्बिन(4,4)×कॉम्बिन(48,1) | 48 | 0.000018 |
| कुल | 2598960 | 1 |
1 से 4 इक्कों का योगफल लें, तो कम से कम एक इक्का आने की प्रायिकता 0.341158 है। दो या अधिक इक्कों की प्रायिकता 0.041684 है।
कम से कम एक और इक्का होने की संभावना, बशर्ते कि कम से कम एक इक्का हो, को बेयस के प्रमेय के अनुसार इस प्रकार पुनः व्यक्त किया जा सकता है: संभावना (कम से कम एक इक्का दिए जाने पर दो और इक्के) = संभावना (दो या अधिक इक्के)/संभावना (कम से कम एक इक्का) = 0.041684/0.341158 = 0.122185.
बेयस प्रमेय से परिचित लोगों के लिए, यह बताता है कि B दिए जाने पर A की संभावना, A और B की संभावना को B की संभावना से विभाजित करने के बराबर होती है, या Pr(A दिया गया B) = Pr(A और B)/Pr(B)।
अगली तालिका अन्य इक्कों की प्रत्येक संख्या के लिए संयोजन और संभावना को दर्शाती है, बशर्ते कि हुकुम का इक्का डेक से हटा दिया गया हो।
इक्का की संभावनाएँ - इक्का हटा दिया गया हाथ
| इक्के | FORMULA | युग्म | संभावना |
|---|---|---|---|
| 0 | कॉम्बिन(3,0)×कॉम्बिन(48,4) | 194580 | 0.778631 |
| 1 | कॉम्बिन(3,1)×कॉम्बिन(48,3) | 51888 | 0.207635 |
| 2 | कॉम्बिन(3,2)×कॉम्बिन(48,2) | 3384 | 0.013541 |
| 3 | कॉम्बिन(3,3)×कॉम्बिन(48,1) | 48 | 0.000192 |
| कुल | 249900 | 1 |
इससे पता चलता है कि कम से कम एक और इक्का आने की संभावना 0.221369 है।
मज़े के लिए, चलिए बेयस प्रमेय का उपयोग करके इसी प्रश्न को हल करते हैं। मान लीजिए कि यादृच्छिक हाथों को तब तक बांटा जाता है जब तक कि एक ऐसा हाथ न मिल जाए जिसमें हुकुम का इक्का हो। कम से कम एक अतिरिक्त इक्के की संभावना, बशर्ते कि हाथ में हुकुम का इक्का हो, को इस प्रकार लिखा जा सकता है: प्रायिकता (यदि हाथ में हुकुम का इक्का है तो कम से कम दो इक्के)। बेयस प्रमेय के अनुसार, यह प्रायिकता (हाथ में हुकुम का इक्का और कम से कम एक और इक्का है) / Pr (हाथ में हुकुम का इक्का है) के बराबर है। हम अंश को इस प्रकार विभाजित कर सकते हैं: प्रायिकता (हुकुम के इक्का सहित 2 इक्के) + प्रायिकता (हुकुम के इक्का सहित 3 इक्के) + प्रायिकता (4 इक्के)। पहली तालिका का उपयोग करने पर यह 0.039930×(2/4) + 0.001736×(3/4) + 0.000018 = 0.021285 के बराबर है। हुकुम के इक्के की प्रायिकता 5/52 = 0.096154 है। इसलिए, हुकुम के इक्के दिए जाने पर कम से कम दो इक्के आने की प्रायिकता 0.021285/0.096154 = 0.221369 है।
अतः कम से कम एक इक्का दिए जाने पर दो या अधिक इक्के आने की संभावना 12.22% है, तथा हुकुम का इक्का दिए जाने पर 22.14% है।
ठीक है, मुझे आपके नंबरों पर यकीन है, लेकिन फिर भी मुझे समझ नहीं आ रहा। मुझे लगता है कि संभावनाएँ बराबर होंगी। आपको जो एक इक्का दिया गया है, उसके सूट से क्या फ़र्क़ पड़ता है?
आइए एक और सरल स्थिति पर विचार करें। मान लीजिए महिला A कहती है, "मेरे दो बच्चे हैं और कम से कम एक लड़का है।" महिला B कहती है, "मेरे दो बच्चे हैं और बड़े बच्चे का नाम जॉन है।" हम मान सकते हैं कि जॉन नाम की कोई भी लड़की नहीं है और कोई भी महिला एक से ज़्यादा बच्चों का एक ही नाम नहीं रखती। सशर्त प्रायिकता का उपयोग करते हुए, महिला A के दोनों बच्चों के लड़का होने की प्रायिकता pr(दोनों लड़के)/pr(कम से कम एक लड़का) = pr(दोनों लड़के)/(1-pr(दोनों लड़कियाँ)) = (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3 है। हालाँकि, महिला B के छोटे बच्चे के लड़का होने, या दोनों बच्चों के लड़के होने की प्रायिकता ? है, क्योंकि बड़े बच्चे का नाम जॉन रखने से हमें छोटे बच्चे के बारे में कुछ नहीं पता चलता।
एक और उदाहरण लेते हैं, मान लीजिए आप जिफ़ी ल्यूब जाते हैं और वे एक ही कीमत पर दो सौदे पेश करते हैं। सौदा A यह है कि वे चार पुर्ज़ों की जाँच करेंगे और केवल पहला खराब पुर्ज़ा ही बदलेंगे। सौदा B यह है कि वे केवल एक समस्या की जाँच करेंगे और अगर कोई समस्या पाई जाती है तो उसे ठीक कर देंगे। क्या आप सौदा A नहीं लेना चाहेंगे? आपकी कार अपेक्षित खराब पुर्ज़ों की समान संख्या के साथ आई थी, लेकिन सौदा A के तहत समस्या मिलने की संभावना ज़्यादा है, और इस प्रकार आप उस योजना के तहत अपेक्षित खराब पुर्ज़ों की एक छोटी संख्या के साथ वापस जाएँगे। इसी तरह, किसी भी इक्के की जाँच में संभवतः केवल इक्का ही निकलेगा, जबकि हुकुम के इक्के की जाँच में अन्य तीन सूटों की जाँच नहीं की जाती, जिससे उनके इक्के होने की संभावना ज़्यादा रहती है।
फोर कार्ड पोकर में 5 में से 4 कार्ड का उपयोग करके स्ट्रेट फ्लश की संख्या 2072 पर आप कैसे पहुंचे?
सबसे पहले मैंने स्ट्रेट फ्लश को दो प्रकारों में विभाजित किया, एक में चार लगातार सूट वाले कार्ड और दूसरे में पांच। पांच कार्ड के स्ट्रेट फ्लश की संख्या सूट की संख्या * स्पैन की संख्या (सबसे कम कार्ड के रूप में इक्का से 10 तक) = 4*10 = 40 है। चार कार्ड के स्ट्रेट फ्लश में 11 अलग-अलग स्पैन होते हैं (सबसे कम कार्ड के रूप में इक्का से जैक तक)। A234 और JQKA स्ट्रेट फ्लश के मामले में पांचवां कार्ड 47 में से एक हो सकता है (52 में से पहले से हटाए गए 4 कार्ड और पांचवां कार्ड जो 5 कार्ड का स्ट्रेट फ्लश बनाता है, जिनका पहले से ही हिसाब लगाया गया है, को घटाकर)। तो स्पैन A234 या JQKA के 4*2*47=376 स्ट्रेट फ्लश हैं। अन्य नौ में से पांचवें कार्ड के लिए 46 संभावित कार्ड हैं अतः 4-कार्ड स्ट्रेट फ्लश की कुल संख्या 40+376+1656=2072 है।
चाहे जो भी हो, 17वें कार्ड पर फ्लश 100% संभव है। कौन से कार्ड पर स्ट्रेट 100% कब संभव है?
स्ट्रेट की गारंटी केवल 45 पत्तों पर ही मिलती है। उदाहरण के लिए, आप A, 2, 3, 4, 6, 7, 8, 9, JQ, और K, इन सभी पत्तों को मिलाकर कुल 44 पत्ते बाँट सकते हैं, फिर भी स्ट्रेट नहीं मिलेगा।
प्रिय, अद्भुत श्रीमान, Wizard of Odds , मैं आपकी सांख्यिकीय कुशाग्रता से पूरी तरह अभिभूत हूँ। क्या आप संयोग से मेरे लिए सात पत्तों वाले स्टड में सात पत्तों वाले स्ट्रेट - यानी A, 2, 3, 4, 5, 6, 7 या 2, 3, 4, 5, 6, 7, 8 या 7, 8, 9, 10, जैक, क्वीन, किंग - की प्रायिकता की गणना कर सकते हैं? हम जानते हैं कि यह असली पोकर हैंड नहीं है; हालाँकि, जब हम खेल रहे थे, तब यह बात सामने आई और हम सोच रहे थे कि क्या सात पत्तों वाले स्टड में सामान्य फुल हाउस की तुलना में इसकी प्रायिकता कम है। वाह, हे ज्ञानी!
जब आपने मुझे इतनी अच्छी तरह से खुश किया, तो मैं कैसे मना कर सकता हूँ? सबसे पहले, 52 में से 7 पत्तों को चुनने के लिए, क्रम की परवाह किए बिना, संयोजन (52,7) = 133,784,560 तरीके हैं। 7 पत्तों वाले स्ट्रेट के लिए 8 संभावित स्पैन हैं (सबसे छोटा पत्ता A से 8 तक हो सकता है)। अगर हमारे पास 7 अलग-अलग रैंक हों, तो सूट को व्यवस्थित करने के 4 7 = 16384 तरीके हैं। ध्यान दें कि इसमें सभी एक ही सूट के पत्ते शामिल हैं, जिससे एक स्ट्रेट फ्लश बनेगा। तो प्रायिकता 8*16,384/133,784,560 = 1020.6952 में 1 है।
यदि मैं एक ही डेक से 4 पत्ते बाँटता हूँ तो क्या सम्भावना है कि कम से कम 1 पत्ता हुकुम का हो?
शून्य हुकुम की प्रायिकता (39/52)*(38/51)*(37/50)*(36/49) = 0.303818 है। इसलिए कम से कम एक हुकुम की प्रायिकता 1-0.303818 = 0.696182 है।
एकल-डेक खेल में, चार पत्तों में से कम से कम एक इक्का और एक ड्यूस आने की प्रायिकता क्या है? ओमाहा खेल के लिए यह जानना उपयोगी है।
प्रायिकता 101 से हम जानते हैं कि Pr(A या B) = Pr(A) + Pr(B) - Pr(A और B)। अतः Pr(A और B) = Pr(A) + Pr(B) - Pr(A या B)। मान लीजिए A को एक इक्का और B को एक ड्यूस मिलता है। Pr(A) = Pr(कम से कम एक इक्का) = 1-Pr(कोई इक्का नहीं) = 1-संयोजन (48,4)/ संयोजन (52,4) = 1-0.7187 = 0.2813। कोई ड्यूस न आने की प्रायिकता स्पष्ट रूप से समान होगी। इसी तर्क से pr(A या B) = Pr(कम से कम एक इक्का या दुक्की) = 1-Pr(न कोई इक्का न दुक्की) = 1-combin(44,4)/combin(52,4) = 1 - 0.501435 = 0.498565। इसलिए, कम से कम एक इक्का और दुक्की आने की प्रायिकता 0.2813 + 0.2813 - 0.498565 = 0.063962 है।
छह पत्तों वाले खेल में लगातार 27 हाथों में ईंट का गुलाम मिलने की संभावना क्या है?
किसी एक हाथ में इसे पाने की प्रायिकता 6/52 है। लगातार 27 हाथों में इसे पाने की प्रायिकता (6/52) है। 27 = 20,989,713,842,161,800,000,000,000 में 1।
"मृत व्यक्ति का हाथ" अर्थात् इक्के और आठ की दो जोड़ी प्राप्त होने की संभावना क्या है?
प्रत्येक जोड़ी के लिए चार में से दो सूट व्यवस्थित करने के छह तरीके हैं। फिर सिंगलटन के लिए 44 कार्ड हैं। तो सफल संयोजनों की संख्या 6*6*44 = 1584 है। कुल 2,598,960 संयोजन हैं, इसलिए संभावना 0.0609% है।
मैं समझता हूं कि आपने पहले ही उत्तर दे दिया है कि 3 अप्रैल, 2005 को "मृत व्यक्ति का हाथ", इक्के और आठ की दो जोड़ी, प्राप्त होने की संभावना 0.0609% है, लेकिन मेरा मानना है कि मृत व्यक्ति का हाथ "दो काले इक्के, दो काले आठ और क्लब की रानी" है, एक एकल मानक डेक से उस सटीक हाथ को खींचने की संभावना क्या है?
उस सटीक हाथ को पाने का सिर्फ़ एक ही तरीका है। तो संभावना कॉम्बिन(52,5) में 1 या 2,598,960 में 1 होगी।
एक मानक 52-ताश के डेक से, जहाँ एक हाथ में एक ही, बिना नकल वाले पत्ते के सूट को सामान्य माना जाता है, प्रत्येक संभावित पाँच-ताश के हाथ की संभावनाएँ/संभावनाएँ क्या हैं? उदाहरण के लिए, A♠ A♣ A हाथ पर विचार करें।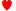 ए
ए 2. इस हाथ में 2 के सूट को नज़रअंदाज़ कर दिया गया है और यह डेक में मौजूद चार 2 में से किसी एक को दर्शाता है। एक और उदाहरण AJ-8-6-5 है। इस हाथ में सभी 5 पत्तों के सूट को नज़रअंदाज़ कर दिया गया है ताकि केवल एक ही ऐसा संयोजन बन सके। एक और उदाहरण: 3♠ 3
2. इस हाथ में 2 के सूट को नज़रअंदाज़ कर दिया गया है और यह डेक में मौजूद चार 2 में से किसी एक को दर्शाता है। एक और उदाहरण AJ-8-6-5 है। इस हाथ में सभी 5 पत्तों के सूट को नज़रअंदाज़ कर दिया गया है ताकि केवल एक ही ऐसा संयोजन बन सके। एक और उदाहरण: 3♠ 3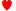 7♣ 7♠ Q. इस हाथ में दो 3 और दो 4 के सूट को नज़रअंदाज़ नहीं किया जाता क्योंकि हाथ में एक से ज़्यादा कार्ड हैं, लेकिन Q का सूट सामान्य है। दूसरे शब्दों में, किसी भी कार्ड के सूट को नज़रअंदाज़ कर दिया जाता है जो हाथ में दोहराया नहीं गया है और उस हाथ को संभावित हाथों में से एक माना जाता है, हालाँकि अगर हर कार्ड के सूट को नज़रअंदाज़ न किया जाए, तो उस हाथ के दोबारा होने की कई संभावनाएँ होंगी। इस प्रकार, पाँच विशिष्ट कार्डों से बना एक स्ट्रेट या फ्लश; मान लीजिए Q
7♣ 7♠ Q. इस हाथ में दो 3 और दो 4 के सूट को नज़रअंदाज़ नहीं किया जाता क्योंकि हाथ में एक से ज़्यादा कार्ड हैं, लेकिन Q का सूट सामान्य है। दूसरे शब्दों में, किसी भी कार्ड के सूट को नज़रअंदाज़ कर दिया जाता है जो हाथ में दोहराया नहीं गया है और उस हाथ को संभावित हाथों में से एक माना जाता है, हालाँकि अगर हर कार्ड के सूट को नज़रअंदाज़ न किया जाए, तो उस हाथ के दोबारा होने की कई संभावनाएँ होंगी। इस प्रकार, पाँच विशिष्ट कार्डों से बना एक स्ट्रेट या फ्लश; मान लीजिए Q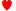 जे♣ 10
जे♣ 10 9
9 8♠ या A♠ J♠ 8♠ 7♠ 3♠ केवल एक बार ही हो सकता है क्योंकि उन्हीं पत्तों का कोई भी अन्य संयोजन, भले ही वह किसी अलग सूट का हो, दोहराव होगा। इसलिए, इस मानदंड का उपयोग करते हुए, किसी भी एक हाथ का O/P क्या है? दूसरे शब्दों में, मानक 52 पत्तों के डेक में ऐसे कितने पाँच पत्तों वाले हाथ होते हैं? आपके इनपुट के लिए धन्यवाद।
8♠ या A♠ J♠ 8♠ 7♠ 3♠ केवल एक बार ही हो सकता है क्योंकि उन्हीं पत्तों का कोई भी अन्य संयोजन, भले ही वह किसी अलग सूट का हो, दोहराव होगा। इसलिए, इस मानदंड का उपयोग करते हुए, किसी भी एक हाथ का O/P क्या है? दूसरे शब्दों में, मानक 52 पत्तों के डेक में ऐसे कितने पाँच पत्तों वाले हाथ होते हैं? आपके इनपुट के लिए धन्यवाद।
मैं इस अवधारणा से अच्छी तरह वाकिफ़ हूँ। कुल 134,459 अनोखे पाँच-पत्तों वाले हाथ होते हैं। मुझे यह इसलिए पता है क्योंकि यह मेरा पहला वीडियो पोकर प्रोग्राम है जिसने सभी 2,598,960 संभावित हाथों का विश्लेषण किया और पे टेबल पर इसे चलाने में कई दिन लगे। हालाँकि, 134,459 हाथों की श्रेणियों में से प्रत्येक में से केवल एक को चलाकर, उस श्रेणी के सभी हाथों की संख्या के आधार पर, आप रन टाइम को 95% तक कम कर सकते हैं। कभी-कभी जब कोई खेल सूट-विशिष्ट होता है, जैसे कि ब्लैक जैक बोनस पोकर का मेरा हालिया विश्लेषण, तो मुझे अपने पुराने प्रोग्राम की धूल झाड़नी पड़ती है और उसे धीरे-धीरे चलाना पड़ता है।
4 के बजाय 5 सूट वाले डेक का उपयोग करके पांच कार्ड स्टड में क्या संभावनाएं हैं?
फाइव सूट पोकर में संयोजन
| हाथ | युग्म | संभावना | FORMULA |
| एक तरह के पाँच | 13 | 0.000002 | 13 |
| स्ट्रेट फ्लश | 50 | 0.000006 | 5*10 |
| एक तरह के चार | 3900 | 0.000472 | 13*12* कॉम्बिन (5,4)*5 |
| लालिमा | 6385 | 0.000773 | 5*(कॉम्बिन(13,5)-10) |
| पूरा घर | 15600 | 0.001889 | 13*12*कॉम्बिन(5,3)*कॉम्बिन(5,2) |
| सीधा | 31200 | 0.003777 | 10*(5^5-5) |
| तीन हास्य अभिनेता | 214500 | 0.025969 | 13*कॉम्बिन(12,2)*कॉम्बिन(5,3)*5^2 |
| दो जोड़ी | 429000 | 0.051938 | कॉम्बिन(13,2)*11*कॉम्बिन(5,2)^2*5 |
| जोड़ा | 3575000 | 0.432815 | 13*कॉम्बिन(12,3)*कॉम्बिन(5,3)*5^3 |
| कुछ नहीं | 3984240 | 0.48236 | (कॉम्बिन(13,5)-10)*(5^5-5) |
| कुल | 8259888 | 1 |
ध्यान दें कि मैंने फुल हाउस और फ्लश का क्रम उलट दिया है।
एक मानक ताश के डेक के कितने पांच-कार्ड संयोजनों में ठीक दो सूट के कार्ड होते हैं?
दोनों सूटों को 4 और 1 या 3 और 2 में विभाजित किया जा सकता है। आइए पहले 4/1 के बंटवारे को देखें। जिसके पास 4 पत्ते हैं, उसके लिए 4 सूट चुनने हैं, और जिसके पास 1 पत्ता है, उसके लिए 3 सूट। 13 में से 4 रैंक चुनने के लिए कॉम्बिन (13,4) = 715 तरीके हैं। एक रैंक चुनने के 13 तरीके हैं। तो दोनों सूटों के बीच 4/1 का बंटवारा करने के 4×3×715×13 = 111,540 तरीके हैं। इसी तर्क से, 3/2 का बंटवारा करने के 4×3×कॉम्बिन (13,3)×कॉम्बिन (13,2) = 267,696 तरीके हैं। तो कुल संभावना (111540+267696)/कॉम्बिन (52,5) = 14.59% है।
2-3-4-5-7 अनसूटेड होने की संभावना कितनी है? बहुत-बहुत धन्यवाद, साइट बहुत बढ़िया है!
धन्यवाद. (4 5 -4)/combin(52,5) = 1020/2598960 = 2,548 में 1.
मैं पिछले दिनों फॉक्सवुड्स में था और फॉक्सवुड्स पोकर क्लासिक की आखिरी दो टेबलों पर दांव देख रहा था। जब विन्स वैन पैटन (वर्ल्ड पोकर टूर के मेज़बानों में से एक) देखने आए, तो उन्होंने आसपास मौजूद कुछ पोकर विशेषज्ञों के साथ तरह-तरह के प्रॉप दांव लगाने शुरू कर दिए। वे किसी को भी 20 में से 1 का दांव लगाने की पेशकश कर रहे थे, अगर वे ताश के पत्तों के पूरे डेक को क्रम से घुमाते हुए और इक्का, 2, 3, 4, और इसी तरह बादशाह तक हर पत्ते को खोलते हुए ज़ोर से बोलें और फिर इक्का से शुरू करें, बिना वह पत्ता सामने आए जिसकी घोषणा वे कर रहे थे। कोई भी पूरी तरह से सफल नहीं हुआ और विन्स ने लगभग 10 मिनट में कुछ सौ डॉलर जीत लिए, उसके बाद सभी ने हार मान ली। मुझे पता है कि यह संभव होना चाहिए, लेकिन मुझे शक है कि विन्स इस पर केवल 20 में से 1 का दांव लगाकर बहुत मेहनत कर रहे हैं। वास्तव में पूरे डेक को पार करने की संभावना क्या है?
जीतने की संभावना का अनुमान लगाने का एक आसान तरीका यह मान लेना है कि हर कार्ड के बताए गए रैंक से मेल न खाने की संभावना 12/13 है। इस शर्त को जीतने के लिए, पीड़ित को इसे 52 बार सफलतापूर्वक करना होगा। 52 बार जीतने की संभावना (12/13) 52 = 1.56% है। उचित मूल्य 63.2 से 1 होगा। 20 से 1 के अनुपात में विंस को 67.3% का फायदा था (ओह!)।
जीएम के अनुसार, जो मुझसे बेहतर गणितज्ञ हैं, वास्तविक संभावना 1.6232727% है। इस अंतर का कारण यह है कि प्रत्येक चयन का परिणाम पिछले चयनों से सकारात्मक रूप से सहसंबद्ध होता है।
कल रात खेलते हुए, एक बूढ़ा, चालाक, बदमिजाज़ और आक्रामक खिलाड़ी, टेबल को फ्लॉप पर बराबर पैसे वाले साइड बेट लगाने की चुनौती दे रहा था। यह बूढ़ा कंजूस शर्त लगा रहा था कि फ्लॉप के तीन पत्तों में से एक इक्का, दुक्का या गुलाम होगा (कभी-कभी वह तीनों पहचाने जा सकने वाले पत्ते बदल देता था)। इस शर्त के क्या ऑड्स हैं? आपकी बुद्धिमानी भरी सलाह का बहुत-बहुत स्वागत है।
किसी भी कार्ड को देखे जाने से पहले, फ्लॉप पर किसी भी तीन रैंक के न आने की संभावना कॉम्बिन (40,3)/कॉम्बिन (52,3) = 9880/22100 = 44.71% है। तो इस लड़के को 10.59% का फायदा हुआ।
मान लीजिए कि 52 पत्तों वाली एक गड्डी में से पाँच पत्ते बाँटे गए हैं और पहला पत्ता बादशाह है। कम से कम एक और बादशाह आने की क्या संभावना है? मैंने भी आपके द्वारा हल किया जा रहा एक इक्के का सवाल देखा था, लेकिन मैं उसे ठीक से समझ नहीं पाया। किसी भी मदद के लिए धन्यवाद।
प्रायिकता संबंधी प्रश्नों के उत्तर देने के लिए मैं संयोजन फलन का उपयोग करना पसंद करता हूँ। इस प्रकार, डेक में मौजूद 48 गैर-राजा पत्तों में से चार गैर-राजा पत्ते चुनने के लिए संयोजन (48,4) = 194,580 तरीके हैं। डेक में बचे हुए 51 पत्तों में से कोई भी चार पत्ते चुनने के लिए संयोजन (51,4) = 249,900 तरीके हैं। इसलिए, अगले चार पत्तों में कोई राजा न मिलने की प्रायिकता 194,580/249,900 = 77.86% है। इस प्रकार, कम से कम एक प्रकार का पत्ता मिलने की प्रायिकता 100% - 77.86% = 22.14% है।
कई लोगों ने कहा है कि संयोजक फलन शायद उन लोगों के लिए समझ से परे है जो इस तरह के सरल प्रायिकता संबंधी प्रश्न पूछते हैं। मैं इससे असहमत नहीं हूँ, लेकिन इस साइट का एक प्रमुख उद्देश्य मेरे पाठकों को गणित के बारे में कुछ सिखाने का प्रयास करना है। संयोजक फलन प्रायिकता में अत्यंत उपयोगी है, और बहुत समय बचाता है। हालाँकि, इस प्रश्न का उत्तर इसके बिना भी आसानी से दिया जा सकता है।
दूसरे पत्ते के बादशाह न होने की प्रायिकता 48/51 है। ऐसा इसलिए है क्योंकि डेक में 48 बिना बादशाह वाले पत्ते बचे हैं, और कुल 51 पत्ते बचे हैं। अगर दूसरा पत्ता बादशाह नहीं है, तो तीसरे पत्ते के भी बादशाह न होने की प्रायिकता 47/50 (47 बिना बादशाहों को बचे 50 पत्तों से भाग देने पर) है। इसके बाद अंत तक, बाकी चार पत्तों में से किसी के भी बादशाह न होने की प्रायिकता (48/51)×(47/50)×(46/49)×(45/48) = 77.86% है। ऐसा न होने की, यानी कम से कम एक बादशाह होने की, प्रायिकता 100% - 77.86% = 22.14% है।
सबसे पहले, 52 पत्तों वाली एक ही गड्डी से 5 पत्ते चुनें। फिर, उनके ब्लैकजैक मानों को जोड़ें (T,J,Q,K = 10, A = 1)। योग के सम/विषम होने की क्या संभावना है? मुझे लगता है कि सम पत्तों की अधिकता के कारण, योग के सम होने की संभावना ज़्यादा होगी।
आश्चर्य की बात है कि 52 में से 30 पत्ते सम होने के बावजूद, विषम योग की संभावना 50.03% ज़्यादा है। नीचे दी गई तालिका प्रत्येक सम/विषम विभाजन की संभावना दर्शाती है।
विषम/सम प्रश्न
| इवेंस | कठिनाइयाँ | युग्म | संभावना | जोड़ |
| 0 | 5 | 15504 | 0.005965 | विषम |
| 1 | 4 | 155040 | 0.059655 | यहां तक की |
| 2 | 3 | 565440 | 0.217564 | विषम |
| 3 | 2 | 942400 | 0.362607 | यहां तक की |
| 4 | 1 | 719200 | 0.276726 | विषम |
| 5 | 0 | 201376 | 0.077483 | यहां तक की |
| कुल | 2598960 | 1 |
यदि आप डेक से तीन पत्ते निकालते हैं तो क्या सम्भावना है कि उनमें से एक पत्ता हुकुम का होगा?
पहला पत्ता हुकुम का हो और बाकी दो पत्ते न हों, इसकी प्रायिकता (13/52)×(39/51)×(38/50) = 14.53% है। फिर आपको इसे 3 से गुणा करना चाहिए, क्योंकि हुकुम का पत्ता तीनों में से कोई भी हो सकता है। तो उत्तर है 3×14.53% = 43.59%। जो लोग संयोजन फलन पसंद करते हैं, उनके लिए उत्तर है 13×combin(39,2)/ combin (52,3) = 9,633/22,100 = 43.59%।
0 और 1 के बीच दो यादृच्छिक संख्याएँ चुनें (समान रूप से वितरित)। अब दोनों में से छोटी संख्या चुनें। चयन का औसत क्या है? n संख्याओं के सामान्य मामले के बारे में क्या?
दो संख्याओं के लिए, उत्तर 1/3 है, और n संख्याओं के लिए यह 1/(n+1) है। मैंने अपने गणित की समस्याओं वाले पेज पर प्रश्न 194 और 195 के हल पोस्ट किए हैं।
आप एक ऐसा खेल खेल रहे हैं जिसमें तीन लोग शामिल हैं: (क) आप स्वयं, (ख) आपका प्रतिद्वंद्वी, और (ग) एक रेफरी। आप में से प्रत्येक गुप्त रूप से 0 और 1 के बीच एक वास्तविक संख्या चुनता है। सभी संख्याएँ चुनने के बाद, उन्हें प्रकट किया जाता है। जो खिलाड़ी रेफरी की संख्या के सबसे करीब, बिना उससे आगे बढ़े, अनुमान लगाता है, वह जीत जाता है। यदि आप उससे करीब हैं, तो आप $1 जीतते हैं। यदि आपका प्रतिद्वंद्वी उससे करीब है, तो आप $1 हारते हैं। यदि दोनों खिलाड़ी उससे आगे निकल जाते हैं, या बराबरी हो जाती है, तो खेल बराबरी पर होता है।
क्या कोई ऐसी संख्या है जिसे आप चुनकर अपने अपेक्षित रिटर्न को अधिकतम कर सकते हैं, अगर दूसरा खिलाड़ी बेतरतीब ढंग से चुनता है? अगर दूसरे खिलाड़ी के पास भी कोई रणनीति हो तो क्या होगा?
मुझे उम्मीद है आप खुश होंगे, मैंने पूरा दिन दूसरे भाग पर बिताया, और मेरा उत्तर फिर भी गलत निकला। कहीं ऐसा न हो कि मैं अपने पाठकों को उसी आनंद से वंचित कर दूँ, इसलिए मैं यहाँ उत्तर यूँ ही नहीं लिख दूँगा। मैंने इसे दो समस्याओं में बाँट दिया है, और mathproblems.info पर उत्तर और समाधान पोस्ट किए हैं, समस्या 196 और 197।
यदि आप मानक 52-कार्ड डेक से यादृच्छिक रूप से पांच कार्ड चुनते हैं, तो क्या संभावना है कि सभी चार सूट का प्रतिनिधित्व किया जाएगा?
एक सूट में दो पत्ते और तीन सूट में एक-एक पत्ता होना चाहिए। जिस सूट को दो बार दर्शाया गया है, उसके लिए चार संभावित सूट हैं। दो बार दर्शाए गए सूट के लिए, 13 में से 2 रैंक चुनने के लिए संयोजन (13,2) = 78 तरीके हैं। अन्य तीन सूटों में से प्रत्येक के लिए, प्रत्येक के लिए 13 संभावित रैंक हैं। इसलिए, संयोजनों की कुल संख्या 4 × 78 × 13 × 13 × 13 = 685,464 है। 52 में से 5 पत्ते चुनने के लिए संयोजन (52,5) = 2,598,960 तरीके हैं। इसलिए प्रायिकता 685,464/2,598,960 = 26.37% है।
इसकी क्या संभावना है कि कोई भी दो चुनी हुई रैंक, उदाहरण के लिए रानी और राजा, किसी यादृच्छिक डेक में लगातार दिखाई दें? किसी ने मुझे सम-धन की शर्त लगाने की चुनौती दी थी कि ऐसा होगा।
एक यादृच्छिक सिमुलेशन के अनुसार, संभावना 48.64% है। तो, मैं यह शर्त लगा लेता।
क्या आप 52 पत्तों वाली डेक से किन्हीं पांच पत्तों को 0 से 2,598,959 तक के पूर्णांक में मैप करने के लिए कोई फ़ंक्शन सुझा सकते हैं?
हाँ। पहले प्रत्येक कार्ड को 0 से 51 तक का मान दें। कार्डों को c1 से c5 तक नाम दें, उन्हें c1 को सबसे छोटा और c5 को सबसे बड़ा क्रम दें। फिर निम्नलिखित फ़ंक्शन को कॉल करें:
int GetIndex(int c1, int c2, int c3, int c4, int c5)
{
रिटर्न कॉम्बिन(सी5,5) + कॉम्बिन(सी4,4)+ कॉम्बिन(सी3,3) + कॉम्बिन(सी2,2) + कॉम्बिन(सी1,1);
}
जहां कॉम्बिन पारंपरिक मान लौटाता है, सिवाय इसके कि यदि पहला मान दूसरे मान से कम है, तो 0 लौटाता है, इस प्रकार:
int संयोजन(int x, int y)
{
यदि (y>x)
0 लौटाएँ;
अन्य
{
int i,n;
एन=1;
(i=x-y+1; i<=x; i++) के लिए
एन*=i;
(i=2; i<=y; i++) के लिए
एन/=i;
वापसी n;
}
}
यदि आप किसी ऐरे तत्व तक पहुंचने के लिए ऐसा कर रहे हैं, तो ऐरे को निम्नानुसार लोड करें।
गिनती=0;
(c5 = 4; c5 < 52; c5++) के लिए
{
(c4 = 3; c4 < c5; c4++) के लिए
{
(c3 = 2; c3 < c4; c3++) के लिए
{
के लिए (c2 = 1; c2 < c3; c2++)
{
(c1 = 0; c1 < c2; c1++) के लिए
{
index_array[गिनती]=जो भी आप चाहते हैं;
गिनती++;
}
}
}
}
}
10 में से 3 स्ट्रेट फ्लश निकालने की संभावना क्या है, जिसमें एक गैप के साथ तीन स्ट्रेट फ्लश हों?

यह एक द्विपद वितरण प्रकार की समस्या है। सामान्य सूत्र यह है कि यदि किसी घटना की प्रायिकता p है, और प्रत्येक परिणाम स्वतंत्र है, तो t परीक्षणों में से ठीक w पर उसके घटित होने की प्रायिकता (t,w)×p w ×(1-p) tw के संयोजन से होती है।
इस स्थिति में, स्ट्रेट फ्लश बनाने के दो तरीके हैं। आपको ईंटों का 8 और ईंटों का 6 या J का एक और पत्ता चाहिए। डेक में बचे 47 पत्तों में से 2 पत्ते निकालने के लिए combin(47,2)=1,081 तरीके हैं। इसलिए, किसी एक हाथ में स्ट्रेट फ्लश मिलने की प्रायिकता 2/1,081 = 0.0018501 है। 10 में से 3 पत्ते निकलने की प्रायिकता combin(10,3)×0.0018501 3 ×(1-0.0018501) 7 = 0.000000750178, या 1,333,017 में 1 है।
54 पत्तों वाली दो गड्डियाँ (दो जोकर सहित) एक साथ मिलाई जाती हैं। एक खिलाड़ी को उनमें से आधी गड्डियाँ दी जाती हैं। क्या प्रायिकता है कि खिलाड़ी को चारों लाल तीन मिलें?
चार लाल तीन और 104 अन्य कार्ड हैं। चारों लाल तीन पाने का केवल एक ही तरीका है। संयोजन (104,50) = 1.46691 × 10 28 तरीके हैं जिनसे खिलाड़ी अन्य 104 कार्डों में से 50 प्राप्त कर सकता है। संयोजनों की कुल संख्या संयोजन (108,54) = 2.48578 × 10 30 है। संयोजन (104,50)/संयोजन (108,54) = 0.059012।
अगर आपको इतनी बड़ी संख्याओं से निपटना पसंद नहीं है, तो यहाँ एक वैकल्पिक उपाय है। चारों लाल तीन पत्तों को 1 से 4 तक संख्या दें। खिलाड़ी के पास पहला लाल तीन पत्ता होने की प्रायिकता 54/108 है। अब पहले तीन पत्तों को हटा दें। खिलाड़ी के पास दूसरा लाल तीन पत्ता होने की प्रायिकता 53/107 है, क्योंकि खिलाड़ी के पास 53 पत्ते बचे हैं, और शेष 107 पत्ते हैं। इसी तरह, खिलाड़ी के पास तीसरा लाल तीन पत्ता होने की प्रायिकता 52/106 है, और चौथा लाल तीन पत्ता होने की प्रायिकता 51/105 है। (54/108) × (53/107) × (52/106) × (51/105) = 0.059012।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
अपने 14 दिसंबर, 2010 के कॉलम में आपने लिखा था कि AAAAAKK हैंड, जिसका ख़ास तौर पर हाउस वे में ज़िक्र किया गया है, शायद खेल के इतिहास में कभी नहीं आया। एक अन्य डीलर के अनुसार, नवंबर 2010 में मेन स्ट्रीट स्टेशन पर एक खिलाड़ी को यह हैंड मिला था।
दिलचस्प बात है। जैसा कि मैंने लिखा, मेरा अनुमान है कि नेवादा में कहीं भी यह घटना लगभग हर 23.7 साल में एक बार घटित होती है। मैं कहूँगा कि वह भी ऐसी ही एक घटना थी।
मान लीजिए आप दो रैंक चुनते हैं, उदाहरण के लिए राजा और रानी। क्या संभावना है कि बेतरतीब ढंग से फेंटे गए 52 पत्तों वाले डेक में कम से कम एक बार राजा और रानी एक-दूसरे के बगल में होंगे?
मुझे 48.6279% मिलता है। अगर आप इस पर दांव लगाना चाहते हैं, तो "हाँ" पर उचित ऑड्स 1.0564 से 1 होंगे।
मैंने सुना है कि हाल ही में ब्रिज का एक "परफेक्ट" खेल हुआ था, जिसमें हर खिलाड़ी को चार सूट में से किसी एक के 13 कार्ड मिले थे। इसकी संभावना क्या है?
2011 में वार्विकशायर में व्हिस्ट के खेल में भी ऐसा होने की अफवाहें हैं। अन्य पाठकों के लाभ के लिए, यह पूछा जा रहा है कि 52-कार्ड डेक को 13-13 कार्ड के चार समूहों में विभाजित करने की संभावना क्या है, जहां प्रत्येक सेट पूरी तरह से एक सूट के 13 कार्डों से बना है।
52 पत्तों को चार 13 पत्तों के सेट में व्यवस्थित करने के लिए combin(52,13)*combin(39,13)*combin(26,13) = 53,644,737,765,488,800,000,000,000,000 संभावित तरीके हैं। 4! = 24 जीतने वाले संयोजनों की संख्या होगी, क्योंकि आप चारों सूटों को चारों खिलाड़ियों में अपनी इच्छानुसार वितरित कर सकते हैं। इसलिए ऑड्स 2,235,197,406,895,370,000,000,000,000 में 1 के बराबर हैं। इस संख्या को कुछ परिप्रेक्ष्य देने के लिए, यदि पृथ्वी पर सभी 7.5 बिलियन लोग प्रति सेकंड एक की दर से ब्रिज हैंड निपटाते हैं, तो 5 बिलियन वर्षों में सूर्य के विस्फोट से पहले किसी व्यक्ति द्वारा तथाकथित परफेक्ट हैंड निपटाने की संभावना 16,558 में 1 है।
हालाँकि, कुछ लोग "परफेक्ट" हाथ को इस तरह परिभाषित करते हैं कि एक खिलाड़ी को किसी भी सूट के सभी 13 पत्ते मिल जाएँ। मैं बताता हूँ कि इसकी संभावना 39,688,347,497 खेलों में से 1 है। ऐसा शायद धरती पर कभी-कभार ही होता है।
टेक्सास होल्ड-एम में दो खिलाड़ियों द्वारा एक ही हाथ पर फ्लश प्राप्त करने की संभावना क्या है, जबकि दोनों खिलाड़ी अपने दोनों होल कार्ड का उपयोग कर रहे हैं?
सबसे पहले, आइए खिलाड़ी और बोर्ड कार्ड के उन संयोजनों की संख्या निर्धारित करें जहाँ ऐसा हो सकता है। स्पष्टतः चार सूट हैं। फिर, दिए गए सूट के 13 में से चार कार्ड चुनने के लिए संयोजन(13,4)=715 तरीके हैं।
दूसरा, ऐसा होने का एक तरीका यह है कि खिलाड़ियों के पास बोर्ड पर एक ही सूट के तीन पत्ते हों और बाकी दो पत्ते बाकी 39 पत्तों में से हों। कॉम्बिन(9,3)=84 तरीके हैं जिनसे बोर्ड पर चुने हुए सूट के बचे हुए 9 पत्तों में से तीन पत्ते निकल सकते हैं। फिर, कॉम्बिन(39,2)=741 तरीके हैं जिनसे बाकी तीन सूट के 39 पत्तों में से दो और पत्ते निकल सकते हैं। इस तरह, बोर्ड पर एक ही सूट के तीन पत्ते होने पर 84*741=62,244 तरीके हैं।
तीसरा, ऐसा एक और तरीके से हो सकता है जब खिलाड़ियों के पास बोर्ड पर एक ही सूट के चार कार्ड हों और दूसरा 39 अन्य कार्डों में से एक हो। बोर्ड पर चुने हुए सूट के बचे हुए 9 कार्डों में से चार को रखने के लिए कॉम्बिन(9,4)=126 तरीके हैं। फिर अन्य तीन सूटों के 39 में से एक और कार्ड चुनने के 39 तरीके हैं। हालांकि, इनमें से सभी का परिणाम यह नहीं होगा कि दोनों खिलाड़ी दोनों होल कार्ड का उपयोग करें। उस शर्त को पूरा करने के लिए, संबंधित सूट का सबसे छोटा कार्ड बोर्ड पर होना चाहिए। खेल में उस सूट के 8 कार्डों में से इसकी संभावना 4/8 = 1/2 है। तो, बोर्ड पर संबंधित सूट के चार के साथ 126*39*(1/2)=2,457 तरीके हैं।
चौथा, ऐसा होने का आखिरी तरीका है बोर्ड पर खिलाड़ियों के पास मौजूद एक ही सूट के पाँच कार्ड। बोर्ड पर चुने हुए सूट के बचे हुए 9 कार्डों में से पाँच कार्ड रखने के लिए कॉम्बिन (9,5) = 126 तरीके हैं। हालाँकि, इन सभी तरीकों से दोनों खिलाड़ी दोनों होल कार्ड का इस्तेमाल नहीं करेंगे। इस शर्त को पूरा करने के लिए, संबंधित सूट के सबसे निचले दो कार्ड बोर्ड पर होने चाहिए। खेल में मौजूद उस सूट के 9 कार्डों में से, इसकी प्रायिकता कॉम्बिन (5,2)/कॉम्बिन (9,2) = 10/36 = 5/18 है। तो, बोर्ड पर संबंधित सूट के चार कार्ड रखने के लिए 126*(5/18) = 35 तरीके हैं।
तो, ऐसे संयोजनों की संख्या जहां ऐसा होगा 715*(62,244 + 2,457 + 35) = 46,286,240 है।
खिलाड़ी के होल कार्ड के लिए 52 में से चार कार्ड चुनने तथा फिर बोर्ड पर बचे 48 में से 5 और कार्ड चुनने के तरीकों के संयोजनों की कुल संख्या है कॉम्बिन (52,4) * कॉम्बिन (48,5) = 463,563,500,400.
इस प्रकार, संभावना 46,286,240 / 463,563,500,400 = 0.000399395 = 2,504 में 1 है।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर पूछा गया और इस पर चर्चा की गई।
एक कैसीनो डीलर थ्री कार्ड पोकर के एक नए संस्करण पर काम कर रहा है। वह एक मानक डेक से सभी फेस कार्ड्स लेती है और उन्हें अच्छी तरह से फेंटती है। फिर वह खिलाड़ी #1 को 3 कार्ड, खिलाड़ी #2 को तीन कार्ड, खिलाड़ी #3 को तीन कार्ड और खिलाड़ी #4 को अंतिम तीन कार्ड देती है। क्या संभावना है कि सभी चार हाथों में एक स्ट्रेट (किसी भी सूट का JQK) होगा?
[स्पॉइलर=समाधान]
एक समय में एक ही खिलाड़ी को बाँटें। पहले खिलाड़ी को प्रत्येक रैंक में से एक मिलने की प्रायिकता 4^3/combin(12,3) = 64/220 है।
मान लीजिए कि पहले खिलाड़ी को एक सीधी रेखा मिली है, तो प्रत्येक रैंक के तीन-तीन खाली कार्ड बचे हैं। दूसरे खिलाड़ी को प्रत्येक रैंक का एक कार्ड मिलने की प्रायिकता 3^3/combin(9,3) = 27/84 है।
मान लीजिए कि पहले दो खिलाड़ियों को एक स्ट्रेट मिला है, तो प्रत्येक रैंक के दो-दो खाली कार्ड बचे हैं। तीसरे खिलाड़ी को प्रत्येक रैंक का एक कार्ड मिलने की संभावना 2^3/combin(6,3) = 8/20 है।
मान लीजिए कि पहले तीन खिलाड़ियों को एक स्ट्रेट मिला है, तो हर रैंक के एक-एक कार्ड का डेक खाली हो जाता है। ये तीन कार्ड ज़ाहिर तौर पर एक स्ट्रेट बनाते हैं।
इस प्रकार, सभी चार खिलाड़ियों को सीधा मिलने की संभावना (64/220) * (27/84) * (8/20) * 1 = 216/5775 = 72/1925 = 3.74% है।
[/spoiler]यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है, जिसकी शुरुआत इस पोस्ट से होती है।
मान लीजिए मेरे पास 48 पत्तों का एक डेक है, चार सूट, हर सूट में बारह पत्ते। अगर मैं 15 पत्ते निकालता हूँ, तो क्या संभावना है कि मैं हर सूट में कम से कम एक पत्ता निकालूँ?
आइए 100% से शुरू करें और उन संभावनाओं को घटा दें जिनके परिणामस्वरूप चार से कम सूट हों।
उदाहरण के लिए, 48 पत्तों में चित न होने की प्रायिकता क्या है? 36 पत्ते ऐसे हैं जिनमें चित नहीं है। 36 में से 15 पत्ते चुनने के तरीकों की संख्या combin(36,15) = 5,567,902,560 है। सभी 48 पत्तों में से 15 पत्ते चुनने के तरीकों की संख्या 1,093,260,079,344 है। इसलिए, 15 पत्तों में चित न होने की प्रायिकता 5,567,902,560 / 1,093,260,079,344 = 0.005093 है।
अब, आइए इसे चार से गुणा करें, ताकि केवल दिल ही नहीं, बल्कि किसी भी सूट के छूटने की संभावना प्राप्त हो सके: 4 × कॉम्बिन (36,15) / कॉम्बिन (48,15) = 0.02037174.
हालाँकि, इससे कुछ स्थितियों में गिनती दोगुनी हो जाती है। मान लीजिए कि आपको 15 काले पत्ते मिलते हैं। इससे पान के पत्ते और ईंट के पत्ते दोनों छूट जाएँगे। उस स्थिति में हमारी गिनती दोगुनी हो जाती। इसलिए, हमें इसे ठीक करना होगा। चार में से दो सूट चुनने के लिए कॉम्बिन(4,2) = 6 तरीके हैं। सभी 15 पत्तों के किन्हीं दो विशिष्ट सूट के होने की प्रायिकता कॉम्बिन(24,15)/कॉम्बिन(48,15) = 1307504/1,093,260,079,344 = 0.00000120 है। जैसा कि बताया गया है, चार में से दो सूट चुनने के छह तरीके हैं, इसलिए सभी पत्तों के दो सूट के होने के तरीकों की संख्या 6 × कॉम्बिन(24,15)/कॉम्बिन(48,15) = 0.00000718 है।
हमने जो दोगुना गिना है उसे घटाने पर, हमें दो या तीन सूटों के प्रतिनिधित्व की संभावना 0.02037174 - 0.00000718 = 0.02036456 प्राप्त होती है।
ध्यान दें कि हमें एक सूट के बारे में चिंता करने की आवश्यकता नहीं है, क्योंकि 12 में से 15 कार्ड चुनना असंभव है।
अंतिम चरण के रूप में, सभी चार सूटों के प्रतिनिधित्व की संभावना प्राप्त करने के लिए 2 या 3 सूटों की संभावना को 100% से घटाएं: 1.00000000 - 0.02037174 = 0.97963544.
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
यदि मुझे ताश के पत्तों के एक मिश्रित (अनुमानित यादृच्छिक) डेक से 13 पत्ते बांटने हों, तो मुझे कितने अलग-अलग रैंक देखने की उम्मीद करनी चाहिए?
यदि कभी कोई मार्कोव श्रृंखला जैसी समस्या थी तो यह वही है।
निम्नलिखित तालिका 1 से 52 तक बांटे गए सभी कार्डों के लिए 0 से 4 कार्डों के साथ अपेक्षित रैंकों की संख्या दर्शाती है।
बांटे गए कार्डों के आधार पर अपेक्षित रैंक
| कार्ड | 0 रैंक | 1 रैंक | 2 रैंक | 3 रैंक | 4 रैंक | अपेक्षित रैंक |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0.058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0.169412 | 0.002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0.324994 | 0.009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0.519088 | 0.022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0.745498 | 0.044178 | 0.000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0.075630 | 0.001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0.003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0.173445 | 0.006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0.324850 | 0.015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0.422569 | 0.023770 | 8.611525 |
| 13 | 3.949628 | 5.705018 | 2.775414 | 0.535606 | 0.034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0.664202 | 0.048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0.065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0.968067 | 0.087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0.146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0.186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0.232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0.287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0.351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0.983193 | 3.775462 | 5.009748 | 2.721345 | 0.510252 | 12.016807 |
| 25 | 0.842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 26 | 0.717887 | 3.246098 | 5.072029 | 3.246098 | 0.717887 | 12.282113 |
| 27 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0.842737 | 12.392557 |
| 28 | 0.510252 | 2.721345 | 5.009748 | 3.775462 | 0.983193 | 12.489748 |
| 29 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 30 | 0.351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0.287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 32 | 0.232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0.186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 34 | 0.146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 35 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 36 | 0.087395 | 0.968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 37 | 0.065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 38 | 0.048067 | 0.664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 39 | 0.034334 | 0.535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0.023770 | 0.422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0.015846 | 0.324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 42 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0.006050 | 0.173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 44 | 0.003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0.001681 | 0.075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0.000720 | 0.044178 | 0.745498 | 4.373589 | 7.836014 | 12.999280 |
| 47 | 0.000240 | 0.022569 | 0.519088 | 3.893157 | 8.564946 | 12.999760 |
| 48 | 0.000048 | 0.009220 | 0.324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0.002353 | 0.169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0.058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
किसी ने मुझे निम्नलिखित शर्त लगाने की चुनौती दी। मुझे एक मानक पोकर डेक से कोई भी तीन रैंक चुननी होती हैं, अपनी भविष्यवाणी लिखनी होती है, लेकिन उसे अंत तक छिपाए रखना होता है। उदाहरण के लिए, 7-इक्का-2। फिर उसने मुझसे बराबर की शर्त लगाने की पेशकश की कि अगर वह तीन अनुमान लगाता है तो वह मेरी कम से कम एक रैंक बता सकता है। मेरे जीतने की संभावना क्या थी?
जीतने के लिए, आपके प्रतिद्वंद्वी को तीनों भविष्यवाणियों में गलत होना होगा। पहली भविष्यवाणी के गलत होने की संभावना 10/13 है। दूसरी भविष्यवाणी के गलत होने की संभावना 9/12 है, क्योंकि हम संभावना के रूप में अनुमानित पहली रैंक को हटा सकते हैं। तीसरी भविष्यवाणी के गलत होने की संभावना 8/11 है, क्योंकि हम संभावना के रूप में अनुमानित पहली दो रैंक को हटा सकते हैं।
जीतने के लिए ये तीनों चीज़ें होनी ज़रूरी हैं। इस प्रकार, आपके जीतने की संभावना (10/13) * (9/12) * (8/11) = 720/1716 = 41.96% है।
सम राशि पर, इस दांव पर आपकी ओर से हाउस एज 16.08% है (ओह!)।
यह प्रश्न ओवेन ई'शे (संख्या 7) द्वारा लिखित द बुक ऑफ प्रोपोज़िशन बेट्स से लिया गया था।
किसी ने मुझे शर्त लगाने की चुनौती दी थी कि वह 27 पासों में दो पासों से कुल 12 पासे फेंक सकता है। अगर वह ऐसा नहीं करता, तो मैं बराबर पैसे जीत जाता। चूँकि 12 आने की संभावना 1/36 है, तो क्या उसे 12 आने में औसतन 36 पासे नहीं लगाने चाहिए? ऐसा लगता है कि अगर मेरे प्रतिद्वंद्वी को सिर्फ़ 27 पासे ही फेंके जाते, तो संभावनाएँ मेरे पक्ष में होतीं। क्या मैं सही हूँ या मेरे गणित में कोई खामी है?
12 के बीच औसत प्रतीक्षा समय वास्तव में 36 रोल के बराबर है, जिसमें 12 का रोल भी शामिल है। हालाँकि, इसका मतलब यह नहीं है कि वे हर 36 रोल पर आते हैं। 12 न आने की संभावना (35/36) है। 27 रोल में ऐसा न होने की संभावना (35/36)^27 है। इसलिए, कम से कम 12 आने की संभावना 1-(35/36)^27 = 53.26% है।
नीचे दी गई तालिका 20 से 36 रोल के लिए कम से कम 12 रोल की संभावना दर्शाती है। ध्यान दें कि सम-धन पर लाभ के लिए 25 रोल की आवश्यकता होती है।
संभावना 12
| रोल्स | संभावना |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |
हम जानते हैं कि 52 में से पांच कार्डों के संयोजन (52,5) = 2,598,960 संभावित संयोजन हैं। मेरा प्रश्न यह है कि पांच-डेक के जूते से कितने संभावित पांच-कार्ड हाथ संभव हैं?
आइए एक समय में एक ही प्रकार का हाथ लें।
- एक ही कार्ड के पांच: एक डेक में 52 संयोजनों के लिए 52 अलग-अलग कार्ड होते हैं।
- एक जैसे चार पत्ते: एक जैसे चार पत्तों के लिए 52 संभावित पत्ते हैं और एक जैसे पत्तों के लिए 51। तो, एक जैसे चार पत्तों के लिए 52*51 = 2,652 संभावित संयोजन हैं।
- एक ही पत्ते के तीन और दूसरे पत्ते के दो: तीन समान पत्तों के लिए 52 संभावित पत्ते हैं और जोड़ी के लिए 51। तो, फुल हाउस के लिए 52*51 = 2,652 संभावित संयोजन हैं।
- एक जैसे तीन पत्ते और दो अलग-अलग सिंगलटन: तीन समान पत्तों के लिए 52 संभावित संयोजन हैं और दो सिंगलटन के लिए संयोजन (51,2) = 1,275 है। इसलिए, एक जैसे तीन पत्तों के लिए 52*1,275 = 66,300 संभावित संयोजन हैं।
- एक ही पत्ते के दो जोड़े और एक सिंगलटन: दो अलग-अलग पत्तों के जोड़े बनाने के लिए कॉम्बिन (52,2) = 1,326 संयोजन हैं। फिर सिंगलटन के लिए 50 बचते हैं। इसलिए, दो जोड़े के लिए 1,326*50 = 66,300 संभावित संयोजन हैं।
- एक ही पत्ते का एक जोड़ा और तीन सिंगलटन: इस जोड़े के लिए 52 संभावित पत्ते हैं। तो सिंगलटन के लिए बचे 51 पत्तों में से 3 पत्ते चुनने के लिए संयोजन (51,3) = 20,825 तरीके हैं। इसलिए, एक जोड़े के लिए संयोजनों की संख्या 52*20,825 = 1,082,900 है।
- पांच सिंगलटन: 52 में से पांच कार्ड चुनने के लिए संयोजन(52,5)=2,598,960 तरीके हैं।
इन सभी संयोजनों का योग 3,819,816 है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।


