क्रेप्स - पासा और रोलिंग
मैं सोच रहा था कि क्रेप्स के खेल में पासा को कैसे बदला जाए ताकि हर बार 7 या 11 आए, क्या आप मदद कर सकते हैं। धन्यवाद।
फिर इसे इस प्रकार बदलें कि एक पासे के सभी ओर छः हो, तथा दूसरे पासे के सभी ओर इकाई और पाँच हो।
क्या आप मानते हैं कि खिलाड़ियों की "इच्छाधारी सोच" खेल के नतीजे को प्रभावित कर सकती है? ध्यान दें कि मुझे प्रभाव के आकार से कोई सरोकार नहीं है, बस आपकी दार्शनिक राय से। इसके अलावा, क्या आपको लगता है कि क्रेप्स में खिलाड़ी जिस तरह से पासा उछालता है, उससे नतीजे में कोई पूर्वाग्रह (अच्छा या बुरा) पैदा हो सकता है? हमेशा की तरह, आपकी साइट शानदार है।
आपके दयालु शब्दों के लिए शुक्रिया। नहीं, मुझे नहीं लगता कि कैसीनो में, बाकी सब चीज़ें समान होने पर, इच्छाधारी सोच से कोई फायदा होता है।
पासे के प्रभाव पर सवाल एक गरमागरम बहस का विषय है। निजी तौर पर, मैं बहुत संशय में हूँ। 2013 में इस जवाब की समीक्षा करते हुए, मुझे अभी तक कोई ठोस सबूत नहीं मिला है कि कोई इतना प्रभाव डाल सके कि उसे फ़ायदा हो।
मैं बस यह जानना चाहता हूँ कि क्रेप्स में पासों को पूर्व-सेट करके आवृत्ति तालिका में परिवर्तन करने के बारे में आपकी क्या राय है।
मुझे इस पर बहुत संदेह है। मैंने अपने क्रेप्स परिशिष्ट 3 में इस विषय पर कुछ प्रयोग बताए हैं।
हाल ही में मुझे क्रेप्स में पासा सेट करने की रणनीतियों के बारे में कुछ जानकारी मिली। कुछ लोगों का मानना है कि आप पासे को फेंकने से पहले एक खास तरीके से सेट कर सकते हैं, और पासों को घुमाव के एक ही अक्ष पर रखकर, कुछ पासों के सेट में कम से कम सात आने की संभावना हो सकती है। मैं जानना चाहता था कि क्या इसमें कोई सच्चाई है या यह सिर्फ़ एक भ्रांति है।
मैं इसमें विश्वास नहीं करता। अभी तक मुझे कोई ऐसा नाम नहीं मिला है जिसका मैं सम्मान करता हूँ और न ही ऐसा कोई प्रमाण मिला है कि यह तरीका कारगर है। हालाँकि मैं इस संभावना को पूरी तरह से खारिज नहीं करता, लेकिन मुझे इस पर बहुत संदेह है। मैं भले ही नेवादा में रहता हूँ, लेकिन जब पासा सेट करने जैसी चीज़ों की बात आती है, तो मैं मिसौरी से हूँ, "मुझे दिखाओ" कि यह काम करता है।
क्या पासे सचमुच निष्पक्ष होते हैं? ऐसा लगता है कि बड़ी संख्याओं वाले और ज़्यादा छेद वाले पक्ष, छोटी संख्याओं और कम छेद वाले पक्षों की तुलना में हल्के होंगे। इससे लगता है कि भारी पक्ष ज़्यादा संभावना से नीचे की ओर गिरेंगे और बड़ी संख्याओं वाले पासे ज़्यादा संभावना से ऊपर की ओर गिरेंगे। मैं एक क्रेप्स प्रणाली की कल्पना कर सकता हूँ जो इस सिद्धांत का लाभ उठाने की कोशिश कर सकती है, लेकिन मुझे आश्चर्य है कि क्या यह वास्तव में काम करेगी। आप क्या सोचते हैं?
साधारण पासों के साथ, जैसे कि आपको बोर्ड गेम में मिलते हैं, यह बात सच है। हालाँकि, कैसीनो के पासों में जड़े हुए धब्बे होते हैं। कारखाने में, वे धब्बों के लिए छेद करते हैं और फिर छेदों में सफेद रंग के धब्बे डालते हैं, जिनका घनत्व पासे के समान होता है। इसलिए पासा अनिवार्य रूप से एक पूर्ण घन होता है। अगर उन्होंने बोर्ड गेम के साधारण पासों का भी इस्तेमाल किया होता, तो भी मुझे संदेह है कि उनका पूर्वाग्रह हाउस एज को पार करने के लिए पर्याप्त होगा।
क्या आप मानते हैं कि कैसीनो क्रेप्स टेबल पर पासा फेंकना वास्तव में यादृच्छिक है, जैसा कि RNG होगा, या क्या पासा "यांत्रिकी" या सादे मैला फेंकने (उदाहरण के लिए छोटी फेंक) के माध्यम से अच्छे निशानेबाज और बुरे निशानेबाज होते हैं, यदि वास्तविक दुनिया कैसीनो क्रेप्स वास्तव में यादृच्छिक नहीं है, तो मैं इसका लाभ कैसे उठाऊंगा?
मुझे लगता है कि स्वाभाविक रूप से खराब शूटर जैसी कोई चीज़ नहीं होती। कुछ पेशेवरों को छोड़कर, सभी पासों की फेंक को पूरी तरह से यादृच्छिक माना जा सकता है। क्रेप्स में प्रिसेशन थ्रोइंग द्वारा हाउस एज को कैसे पार किया जाए, इस पर सेमिनार होते हैं, लेकिन मैं उनके पक्ष या विपक्ष में कोई दावा नहीं करता। मुझे अभी तक किसी भी तरह के पर्याप्त प्रमाण नहीं मिले हैं।
कैसीनो प्लेयर पत्रिका के अक्टूबर अंक में, फ्रैंक स्कोबलेट ने नियंत्रित पासा शूटिंग पर एक लेख लिखा था, जिसमें आपने बताया था कि आप स्टैनफोर्ड वोंग से $1800 हार गए थे, जबकि उन्होंने 500 पासों में केवल 74 सात फेंके थे। आपने इतने छोटे नमूने (500) पर दांव क्यों लगाया? जो व्यक्ति पासों को नियंत्रित करने का दावा करता है, उसे कम से कम 50,000 पासों के साथ अपने कौशल का प्रदर्शन करने के लिए तैयार रहना चाहिए। क्या मैं यह सोचने में गलत हूँ कि 500 पासे इतने छोटे नमूने हैं कि कुछ भी हो सकता है?
मैंने स्टैनफोर्ड से नहीं, बल्कि किसी दूसरे जुआ लेखक से $1800 हारे। मैं ज़्यादा पासे फेंकना पसंद करता, लेकिन समय की स्पष्ट कमी थी। प्रति मिनट एक पासा फेंकने की बात मानकर, 50,000 बार पासा फेंकने में 34.7 दिन लगेंगे। मैंने 500 पासे फेंकने का फैसला नहीं किया था, लेकिन बड़े नमूने और समय के बीच यह एक उचित समझौता लग रहा था। आप सही कह रहे हैं कि पासे को प्रभावित करने के पक्ष या विपक्ष में कोई ठोस तर्क देने के लिए 500 पासे बहुत कम हैं, लेकिन 500 पासे फेंकना शून्य से बेहतर है।
मुझे पता है कि आपको पासा नियंत्रण पर संदेह है। मैं पिछले तीन महीनों से पासा सेट करने और नियंत्रित शूटिंग का अभ्यास कर रहा हूँ। 655 बार यादृच्छिक रूप से फेंकने पर 78 सात आने की प्रायिकता क्या है? मदद के लिए धन्यवाद :)
बड़ी संख्या में फेंकों के लिए हम गॉसियन वक्र सन्निकटन का उपयोग कर सकते हैं। 655 फेंकों में सातों की अपेक्षित संख्या 655 × (1/6) = 109.1667 है। प्रसरण 655 × (1/6) × (5/6) = 90.9722 है। मानक विचलन sqr(90.9722) = 9.5379 है। आपके 78 सात अनुमान से 109.1667 − 78 = 31.1667 कम हैं। यह (31.1667 - 0.5)/9.5379 = 3.22 मानक विचलन अपेक्षा से कम है। अपेक्षा से 3.22 या अधिक मानक विचलन कम होने की संभावना 0.000641, या 1,560 में 1 है। मुझे यह आंकड़ा एक्सेल में normsdist(-3.22) सूत्र का उपयोग करके मिला।
यह क्रेप्स में पासों को नियंत्रित करने के बारे में है। आपने पहले स्टैनफोर्ड वोंग प्रयोग पर चर्चा की थी, जिसमें कहा गया था, "शर्त की शर्तें यह थीं कि क्या सटीक निशानेबाज़ 500 पासों में 79.5 से कम सात फेंक सकते हैं। एक यादृच्छिक खेल में अपेक्षित संख्या 83.33 होगी। 500 यादृच्छिक पासों में 79 या उससे कम सात आने की संभावना 32.66% है.... 500 यादृच्छिक पासों में 74 या उससे कम सात आने की संभावना 14.41% है।"
इस शर्त के बारे में मेरा प्रश्न यह है कि 14.41% अभी भी "सांख्यिकीय रूप से महत्वपूर्ण" नहीं है [अर्थात p < 0.05], जिसे आमतौर पर माध्य से दो मानक विचलन से अधिक माना जाता है - या श्रृंखला के किसी भी छोर पर यादृच्छिक रूप से घटना घटित होने की *संयुक्त* 5% से कम संभावना।
500 बार रोल करने पर कितने सात आने चाहिए, इससे पहले कि आप कह सकें कि इस बात की 2.5% से भी कम संभावना है कि परिणाम पूर्णतः यादृच्छिक था (अर्थात् परिणाम सांख्यिकीय रूप से महत्वपूर्ण था)?
बहुत धन्यवाद और वैसे, जुआ बाधाओं और संभावनाओं के विषय पर आपकी वेबसाइट निश्चित रूप से सबसे अच्छी वेबसाइट है जो मैंने पाई है .... अच्छा काम जारी रखें !!!
आपके दयालु शब्दों के लिए धन्यवाद। आपको यह नहीं बताना चाहिए कि फेंके गए गैर-यादृच्छिक होने की प्रायिकता p है। इसे इस तरह से लिखा जाना चाहिए कि एक यादृच्छिक खेल में ऐसा परिणाम आने की प्रायिकता p है। किसी ने भी यह उम्मीद नहीं की थी कि 500 बार फेंके जाने से कुछ भी सिद्ध या असत्य सिद्ध हो जाएगा। मैंने 79.5 सेवन की रेखा निर्धारित नहीं की थी, लेकिन मुझे संदेह है कि इसे सांख्यिकीय रूप से महत्वपूर्ण होने के लिए चुना गया था; बल्कि, मुझे संदेह है कि यह एक ऐसा बिंदु था जिस पर दोनों पक्ष शर्त पर सहमत होंगे।
2.5% सार्थकता स्तर अपेक्षाओं से 1.96 मानक विचलन है। इसे एक्सेल में सूत्र =normsinv(0.025) से ज्ञात किया जा सकता है। 500 रोल का मानक विचलन sqr(500*(1/6)*(5/6)) = 8.333 है। अतः 1.96 मानक विचलन 1.96 * 8.333 = अपेक्षाओं से 16.333 रोल कम है। 500 रोल में सात की अपेक्षित संख्या 500*(1/6) = 83.333 है। अतः इससे 1.96 मानक विचलन कम होने पर 83.333 − 16.333 = 67 है। द्विपद वितरण का उपयोग करके इसकी जाँच करने पर, 67 या उससे कम सात की सटीक प्रायिकता 2.627% है।
तीन साल पहले, " आस्क द विज़ार्ड" कॉलम में, आपने लिखा था: "आप सही कह रहे हैं कि पासों को प्रभावित करने के पक्ष या विपक्ष में 500 पासे बहुत कम हैं, लेकिन 500 पासे फेंकना शून्य से बेहतर है।" क्या आप बता सकते हैं कि किसी प्रयोग में, किसी कथित पासा प्रभावित करने वाले से आपको क्या अपेक्षा करनी होगी, ताकि आप उस पर अच्छी-खासी रकम दांव पर लगाने के लिए पर्याप्त आश्वस्त हो सकें? मैं इसलिए पूछ रहा हूँ क्योंकि कुछ ब्लैकजैक सिम्स में "विश्वसनीय" परिणामों के लिए एक अरब पासे एक अच्छा मानक हैं। सबसे कुशल (अर्थात कम से कम पासे फेंकने वाले) प्रायोगिक डिज़ाइन के साथ, शूटर को परिणामों को प्रभावित करने का भरोसा दिलाने के लिए कितने पासे फेंकने होंगे? मुझे पता है कि जवाब शूटर के कौशल पर निर्भर करेगा, लेकिन आप मेरी बात समझ रहे होंगे। अगर आपको सबसे अच्छी स्थिति में भी दस लाख पासे फेंकने की ज़रूरत है, तो यह कोई सार्थक प्रयास नहीं होगा।
आत्मविश्वास अर्जित करने का कोई निश्चित बिंदु नहीं है। यह डिग्री का मामला है। सबसे पहले, मैं पूछूँगा कि किस चीज़ के लिए परीक्षण किया जा रहा है, और निशानेबाज़ का अनुमान क्या होगा। किसी भी परीक्षण में दो संभावित त्रुटियाँ होती हैं। एक कुशल निशानेबाज़ दुर्भाग्य के कारण असफल हो सकता है, या कोई यादृच्छिक निशानेबाज़ अच्छे भाग्य के कारण उत्तीर्ण हो सकता है। इन दोनों में से, मैं गलत सकारात्मक परिणाम से बचना पसंद करूँगा। मुझे लगता है कि एक उचित परीक्षण में गलत नकारात्मक परिणाम की संभावना लगभग 5% और गलत सकारात्मक परिणाम की संभावना लगभग 1% निर्धारित की जाएगी।
उदाहरण के लिए, मान लीजिए दावेदार कहता है कि वह पासों को हर सात बार फेंकने पर औसतन एक सात का योग प्राप्त कर सकता है। एक यादृच्छिक निशानेबाज औसतन हर छह बार फेंकने पर एक सात फेंकेगा। परीक्षण और त्रुटि के आधार पर, मुझे पता चला है कि इन दोनों मानदंडों को पूरा करने वाला एक परीक्षण 3,600 बार पासे फेंकने और पास होने के लिए 547 या उससे कम सात की आवश्यकता होगी, या 6.58 बार फेंकने पर एक सात।
सात में से एक निशानेबाज़ को औसतन 514.3 सात फेंकने चाहिए, जिसका मानक विचलन 21.00 है। गॉसियन सन्निकटन का उपयोग करते हुए, ऐसे कुशल निशानेबाज़ द्वारा 548 या अधिक सात फेंकने की संभावना (एक मिथ्या नकारात्मक) 5.7% है। एक यादृच्छिक निशानेबाज़ को औसतन 600 सात फेंकने चाहिए, जिसका मानक विचलन 22.36 है। एक यादृच्छिक निशानेबाज़ के परीक्षण में उत्तीर्ण होने की संभावना (एक मिथ्या सकारात्मक) 0.94% है। नीचे दिया गया ग्राफ़ कुशल और यादृच्छिक निशानेबाज़ों के संभावित परिणाम दर्शाता है। यदि परिणाम हरी रेखा के बाईं ओर हैं, तो मैं मान लूँगा कि निशानेबाज़ ने परीक्षण पास कर लिया है, और मैं उस पर दांव लगाऊँगा।
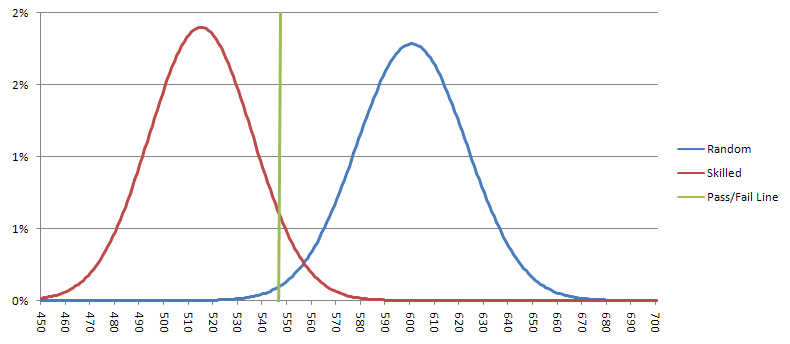
व्यावहारिक दुविधा यह है कि अगर हम प्रति मिनट दो थ्रो मान लें, तो परीक्षण करने में 30 घंटे लगेंगे। शायद मैं समय की आवश्यकता को कम करने के लिए महत्व के स्तर के बारे में अधिक उदार हो सकता था, लेकिन परिणाम उतने विश्वसनीय नहीं होंगे। मुझे लगता है कि 500-रोल वोंग प्रयोग से भी बड़े परीक्षण का समय आ गया है।
आज समाचार में, अटलांटिक सिटी की एक महिला ने बोरगाटा में सात आने से पहले लगातार 154 बार पासा फेंका। इसका मतलब है कि उसने दो पासों को 154 बार फेंका, जिसमें कोई सात नहीं था। इसलिए मैंने (30/36) 154 लिया, और 1.5 ट्रिलियन से 1 के अंतर पर पहुंचा। एक व्यक्ति के मेगा मिलियन्स लॉटरी जीतने की संभावना 154-लगातार गैर-सात पासा रोल मैराथन को पूरा करने की तुलना में लगभग 9,000 गुना अधिक है। यह देखते हुए कि यह कितना खगोलीय रूप से असंभव है, और यह देखते हुए कि लोगों को डीएनए सबूत पर दोषी ठहराया जाता है जो कि झूठे मिलान के खिलाफ केवल एक अरब में एक है, आपको धोखाधड़ी का कितना संदेह होगा, और क्या आप इस बारे में बोरगाटा से परामर्श करना चाहेंगे? मैंने पहले ही उन्हें फोन किया, और उन्हें अपना नाम दिया,
सबसे पहले, उसने कुल 154 बार पासा फेंका, जिसमें 154वां रोल सात था ( स्रोत: NJ.com )। हालांकि, इसका मतलब यह नहीं है कि उसने पहले 153 रोल में कभी सात नहीं फेंका। वह उनमें से बहुत से रोल आउट रोल पर कर सकती थी। जैसा कि मैंने 3 मई, 2003 के कॉलम में दिखाया है, 154 वें रोल तक पहुंचने की संभावना 5.6 बिलियन में 1 है। मेगा मिलियन्स जीतने की संभावना संयुक्त (56,5) * 46 = 175,711,536 में 1 है। इसलिए 154 या अधिक बार रोल करना लगभग 32 गुना कठिन है। पर्याप्त समय और तालिकाओं को देखते हुए, जो मुझे लगता है कि मौजूद हैं, ऐसा कुछ जल्द या बाद में होने के लिए बाध्य था। इसलिए, मुझे धोखाधड़ी का संदेह नहीं होगा। मैं अनुमान लगाता हूं कि किसी भी वर्ष ऐसा होने की संभावना लगभग 1% है।
कृपया mathproblems.info पर मैट्रिसेस में व्यक्त मेरा समाधान, समस्या 204 भी देखें।
मुझे लगता है कि लास वेगास के कुछ कैसिनो एक तरफ से भारी पासों का इस्तेमाल कर रहे हैं। सबूत के तौर पर, मैं स्ट्रिप कैसिनो में इकट्ठा किए गए 244 पासों के नतीजे पेश कर रहा हूँ। क्या संभावना है कि निष्पक्ष पासों से इतने भारी नतीजे आ सकते हैं?
| पासा परीक्षण डेटा | |
| पासा कुल | टिप्पणियों |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 36 |
| 9 | 37 |
| 10 | 27 |
| 11 | 14 |
| 12 | 7 |
| कुल | 244 |
7.7%.
इस प्रकार के प्रश्नों के लिए काई-स्क्वेयर परीक्षण सर्वथा उपयुक्त है। इस परीक्षण के लिए, प्रत्येक श्रेणी के लिए (ae) 2 /e मान लें, जहाँ a वास्तविक परिणाम है और e अपेक्षित परिणाम है। उदाहरण के लिए, 244 बार फेंकने पर 2 आने की अपेक्षित संख्या 244×(1/36) = 6.777778 है। यदि आपको समझ नहीं आ रहा है कि 2 आने की प्रायिकता 1/36 क्यों है, तो कृपया पासा प्रायिकता मूल बातें पर मेरा पृष्ठ पढ़ें। कुल 2 के लिए काई-स्क्वेयर मान के लिए, a=6 और e=6.777778, इसलिए (ae) 2 /e = (6-6.777778) 2 /6.777778 = 0.089253802।
काई-स्क्वेयर्ड परिणाम
| पासा कुल | टिप्पणियों | अपेक्षित | ची-चुकता |
| 2 | 6 | 6.777778 | 0.089253 |
| 3 | 12 | 13.555556 | 0.178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 36 | 33.888889 | 0.131512 |
| 9 | 37 | 27.111111 | 3.607013 |
| 10 | 27 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0.014572 |
| 12 | 7 | 6.777778 | 0.007286 |
| कुल | 244 | 244 | 16.889344 |
फिर काई-स्क्वेयर्ड कॉलम का योगफल लें। इस उदाहरण में, योगफल 16.889344 है। इसे काई-स्क्वेयर्ड सांख्यिकी कहते हैं। "स्वतंत्रता की कोटि" की संख्या, आँकड़ों में श्रेणियों की संख्या से एक कम है, इस स्थिति में 11-1=10। अंत में, या तो किसी सांख्यिकी तालिका में 10.52 और 10 स्वतंत्रता की कोटि वाला काई-स्क्वेयर्ड सांख्यिकी देखें, या एक्सेल में सूत्र =chidist(16.889344,10) का उपयोग करें। दोनों में से कोई भी आपको 7.7% परिणाम देगा। इसका अर्थ है कि निष्पक्ष पासे द्वारा इतने विषम या उससे अधिक परिणाम देने की संभावना 7.7% है। सार यह है कि हालाँकि ये परिणाम अपेक्षा से अधिक विषम हैं, लेकिन इतने विषम नहीं हैं कि कोई आश्चर्य करे। यदि आप इस परीक्षण को जारी रखते हैं, तो मेरा सुझाव है कि योगफल के बजाय प्रत्येक पासे का अलग-अलग परिणाम एकत्र करें। यह भी ध्यान रखना चाहिए कि यदि किसी श्रेणी के परिणामों की अपेक्षित संख्या कम है, तो काई-स्क्वेयर परीक्षण उपयुक्त नहीं है। न्यूनतम अपेक्षित संख्या 5 है, जिसके बारे में आमतौर पर चर्चा होती रहती है।
अगर दोनों पासे क्रेप्स में एक साथ गिरें तो क्या होगा? क्या यह वैध रोल होगा? अगर हाँ, तो डीलर कैसे बताएगा कि नीचे वाला पासा किस नंबर पर गिरा?
इसे वैध रोल कहा जाए या नहीं, यह इस बात पर निर्भर करता है कि आप कहाँ हैं। न्यू जर्सी गेमिंग विनियमन 19:47-1.9(a) में कहा गया है:
जब भी कोई एक या दोनों पासे मेज से बाहर चले जाएं या जब भी एक पासा दूसरे के ऊपर आ जाए तो पासे का फेंकना अमान्य हो जाएगा। -- NJ 19:47-1.9(a)
पेंसिल्वेनिया में भी ठीक यही विनियमन है, धारा 537.9(ए) :
जब भी कोई एक या दोनों पासे टेबल से बाहर चले जाएं या जब भी एक पासा दूसरे के ऊपर आ जाए तो पासे का फेंकना अमान्य हो जाएगा। - पीए 537.9(ए)
मैंने लास वेगास के एक पासा विक्रेता से पूछा, तो उसने बताया कि अगर यह सही थ्रो होता, तो इसे यहाँ वैध रोल कहा जाता। हालाँकि उसने ऐसा होते कभी नहीं देखा, लेकिन उसने बताया कि अगर ऐसा होता, तो डीलर बस ऊपर वाले पासे को हिलाकर देखते कि नीचे वाला पासा किस नंबर पर आता है। हालाँकि, ऊपर वाले पासे को छुए या देखे बिना भी नीचे वाले पासे का परिणाम पता किया जा सकता है। यह कैसे किया जाता है, यह यहाँ बताया गया है। सबसे पहले, चारों तरफ़ देखकर आप ऊपर की संभावनाओं को दो तक सीमित कर सकते हैं। तीन संभावनाओं के आधार पर कैसे पता लगाया जाए, यह यहाँ बताया गया है।
- 1 या 6: 3 को देखें। अगर सबसे ऊँचा बिंदु 5 के किनारे पर है, तो 1 सबसे ऊपर है। अगर वह 2 के किनारे पर है, तो 6 सबसे ऊपर है।
- 2 या 5: 3 को देखें। अगर सबसे ऊँचा बिंदु 6 के किनारे पर है, तो 2 सबसे ऊपर है। अगर वह 1 के किनारे पर है, तो 5 सबसे ऊपर है।
- 3 या 4: 2 को देखें। अगर सबसे ऊँचा बिंदु 6 के किनारे पर है, तो 3 सबसे ऊपर है। अगर वह 1 के किनारे पर है, तो 4 सबसे ऊपर है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
2 से 12 तक प्रत्येक योग के लिए कम से कम एक बार दो पासों के लुढ़कने की अपेक्षित संख्या क्या है?
यह प्रश्न TwoPlusTwo.com पर पूछा गया था और BruceZ ने इसका सही उत्तर दिया था। निम्नलिखित समाधान BruceZ के समाधान जैसा ही है, जो इसके लिए पूरी तरह से श्रेय के पात्र हैं। यह एक कठिन उत्तर है, इसलिए ध्यान दें।
सबसे पहले, कुल दो प्राप्त करने के लिए अपेक्षित रोल की संख्या पर विचार करें। दो की संभावना 1/36 है, इसलिए पहले 2 प्राप्त करने के लिए औसतन 36 रोल लगेंगे।
इसके बाद, दो और तीन दोनों प्राप्त करने के लिए पासों की अपेक्षित संख्या पर विचार करें। हम पहले से ही जानते हैं कि दो प्राप्त करने के लिए औसतन 36 पासे फेंकने होंगे। यदि दो का इंतज़ार करते हुए तीन प्राप्त हो जाता है, तो 3 के लिए अतिरिक्त पासों की आवश्यकता नहीं होगी। हालाँकि, यदि ऐसा नहीं होता है, तो तीन प्राप्त करने के लिए पासों को और अधिक बार फेंकना होगा।
तीन आने की प्रायिकता 1/18 है, इसलिए अगर दो पहले आए तो तीन आने के लिए औसतन 18 अतिरिक्त रोल लगेंगे। यह देखते हुए कि दो आने का एक तरीका है और तीन आने के दो तरीके हैं, दो आने की प्रायिकता 1/(1+2) = 1/3 है।
तो, 1/3 संभावना है कि हमें तीन पाने के लिए अतिरिक्त 18 रोल की ज़रूरत पड़ेगी। इस प्रकार, दो और तीन दोनों पाने के लिए अपेक्षित रोल की संख्या 36+(1/3)×18 = 42 है।
इसके बाद, विचार करें कि चार आने के लिए आपको कितनी बार और पासे फेंकने होंगे। जब तक आप दो और तीन फेंकते हैं, अगर आपको चार नहीं मिला है, तो आपको एक आने के लिए औसतन 12 बार और पासे फेंकने होंगे। ऐसा इसलिए है क्योंकि चार आने की संभावना 1/12 है।
दो और तीन प्राप्त करने से पहले चार प्राप्त करने की प्रायिकता क्या है? सबसे पहले, आइए प्रायिकता के एक सामान्य नियम की समीक्षा करें जब A और B परस्पर अनन्य न हों:
पीआर(ए या बी) = पीआर(ए) + पीआर(बी) - पीआर(ए और बी)
आप pr(A और B) घटाते हैं क्योंकि वह आकस्मिकता pr(A) + pr(B) में दोगुनी गिनी जाती है। इसलिए,
pr(2 या 3 से पहले 4) = pr(2 से पहले 4) + pr(3 से पहले 4) - pr(2 और 3 से पहले 4) = (3/4)+(3/5)-(3/6) = 0.85.
दो और तीन तक पहुँचने के दौरान चार न आने की संभावना 1.0 - 0.85 = 0.15 है। इसलिए, अतिरिक्त 12 रोल की आवश्यकता पड़ने की संभावना 15% है। इस प्रकार, दो, तीन और चार आने के लिए अपेक्षित रोल की संख्या 42 + 0.15*12 = 43.8 है।
इसके बाद, विचार करें कि पाँच आने के लिए आपको कितनी बार और पासे फेंकने होंगे। जब तक आप दो से चार तक पासे फेंकते हैं, अगर आपको अभी तक पाँच नहीं मिला है, तो आपको एक पासा पाने के लिए औसतन 9 बार और पासे फेंकने होंगे, क्योंकि पाँच आने की संभावना 4/36 = 1/9 है।
दो, तीन या चार तक पहुँचने से पहले पाँच आने की संभावना क्या है? सामान्य नियम यह है:
pr (A या B या C) = pr(A) + pr(B) + pr(C) - pr(A और B) - pr(A और C) - pr(B और C) + pr(A और B और C)
तो, pr(2 या 3 या 4 से पहले 5) = pr(2 से पहले 5)+pr(3 से पहले 5)+pr(4 से पहले 5)-pr(2 और 3 से पहले 5)-pr(2 और 4 से पहले 5)-pr(3 और 4 से पहले 5)+pr(2, 3 और 4 से पहले 5) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90। दो से चार तक पहुँचने के दौरान चार न आने की प्रायिकता 1 - 83/90 = 7/90 है। इसलिए, अतिरिक्त 7.2 रोल की आवश्यकता होने की 7.78% संभावना है। इस प्रकार, दो, तीन, चार और पाँच पाने के लिए रोल की अपेक्षित संख्या 43.8 + (7/90)*9 = 44.5 है।
छह से बारह तक के योग के लिए इसी तर्क का पालन करें। अगली संख्या आने से पहले उसकी प्रायिकता ज्ञात करने के लिए आवश्यक गणनाओं की संख्या, क्योंकि पिछली संख्या हर बार लगभग दोगुनी हो जाती है। बारह तक पहुँचने तक, आपको 1,023 गणनाएँ करनी होंगी।
यहाँ pr(A या B या C या ... या Z) के लिए सामान्य नियम दिया गया है
pr(A या B या C या ... या Z) =
पीआर(ए) + पीआर(बी) + ... + पीआर(जेड)
- pr (A और B) - pr(A और C) - ... - pr(Y और Z) दो घटनाओं के प्रत्येक संयोजन की संभावना घटाएँ
+ pr (A और B और C) + pr(A और B और D) + ... + pr(X और Y और Z) तीन घटनाओं के प्रत्येक संयोजन की संभावना जोड़ें
- pr (A और B और C और D) - pr(A और B और C और E) - ... - pr(W और X और Y और Z) चार घटनाओं के प्रत्येक संयोजन की संभावना घटाएँफिर दोहराते रहें, याद रखें कि विषम संख्या वाली घटनाओं के लिए प्रायिकताएँ जोड़ें और सम संख्या वाली घटनाओं के लिए प्रायिकताएँ घटाएँ। संभावित घटनाओं की बड़ी संख्या के लिए यह स्पष्ट रूप से थकाऊ हो जाता है, जिसके लिए व्यावहारिक रूप से स्प्रेडशीट या कंप्यूटर प्रोग्राम की आवश्यकता होती है।
निम्न तालिका रास्ते में प्रत्येक चरण के लिए अपेक्षित संख्या दर्शाती है। उदाहरण के लिए, दो प्राप्त करने के लिए 36, दो और तीन प्राप्त करने के लिए 42। निचले दाएँ कक्ष में सभी 11 योग प्राप्त करने के लिए अपेक्षित रोल की संख्या 61.217385 दर्शाई गई है।
रोल की अपेक्षित संख्या की समस्या
| उच्चतम आवश्यक संख्या | संभावना | यदि आवश्यक हो तो अपेक्षित रोल | संभावना की आवश्यकता नहीं | संभावना की आवश्यकता | अपेक्षित कुल रोल |
|---|---|---|---|---|---|
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
जादूगर का कहना है कि वेबसाइट पर बहुत ज़्यादा बकवास और बकवास भरी बातें हैं, लेकिन आरोपों को सही ठहराने के लिए कोई भी विश्वसनीय सबूत नहीं है। अगर मेरे पास पक्षपातपूर्ण पासों का इस्तेमाल करने वाले किसी भी कैसीनो का पर्दाफाश करने में कोई सबूत होता, तो मुझे खुशी होती।
अगर किसी के पास पक्षपातपूर्ण पासों का कोई ठोस सबूत है, तो मुझे उसकी जाँच करके अपने निष्कर्ष प्रकाशित करने में खुशी होगी। मैं जो सबूत देखना चाहूँगा, वह या तो पासों के रोल की लॉग फ़ाइलें हैं, या फिर, इससे भी बेहतर, कुछ वास्तविक कथित पक्षपातपूर्ण पासे।
इसके अलावा, यदि कैसीनो वास्तव में ऐसे पासों का उपयोग कर रहे थे, जो अपेक्षित संख्या से अधिक सात उत्पन्न कर रहे थे, तो फिर इन जासूसों को उस षड्यंत्र की जानकारी क्यों नहीं है, जो दांव लगा रहे थे कि पास नहीं होगा और दांव लगा रहे थे?
स्लॉट मशीनों पर हॉट रोल बोनस राउंड में खिलाड़ी को दो पासों के योग के अनुसार निम्नलिखित संख्या में सिक्के मिलते हैं। खिलाड़ी तब तक सिक्के जमा करता रहता है जब तक कि उसके पास कुल सात न आ जाएँ, और बोनस समाप्त हो जाता है। अगर पहली बार सात आता है, तो उसे 70 सिक्कों का सांत्वना पुरस्कार मिलता है। सात के अलावा बाकी सभी पासों के योग के लिए निम्नलिखित पुरस्कार हैं:
- 2 या 12: 1,000
- 3 या 11: 600
- 4 या 10: 400
- 5 या 9: 300
- 6 या 8: 200
मेरा प्रश्न यह है कि औसत बोनस जीत क्या है?
उत्तर के लिए निम्नलिखित बटन पर क्लिक करें।
समाधान के लिए निम्नलिखित बटन पर क्लिक करें।
[स्पॉइलर] मान लीजिए कि उत्तर x है। जब तक खिलाड़ी सात नहीं फेंकता, तब तक वह पिछली सभी जीतों के अलावा, भविष्य की जीत के x होने की उम्मीद कर सकता है। दूसरे शब्दों में, पासे फेंकने का एक स्मृति-रहित गुण है कि चाहे आपने कितने भी पासे फेंके हों, आप सात के उतने ही करीब पहुँचते हैं जितने आप शुरुआत में थे।मैं पासा की संभावनाओं के मूल में नहीं जाऊंगा, लेकिन सिर्फ इतना कहूंगा कि प्रत्येक कुल की संभावना इस प्रकार है:
- 2: 1/36
- 3: 2/36
- 4: 3/36
- 5: 4/36
- 6: 5/36
- 7: 6/36
- 8: 5/36
- 9: 4/36
- 10: 3/36
- 11: 2/36
- 12: 1/36
सांत्वना पुरस्कार पर विचार करने से पहले, x का मान इस प्रकार व्यक्त किया जा सकता है:
x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)इसके बाद, दोनों पक्षों को 36 से गुणा करें:
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)36x = 11,200 + 30x
6x = 11,200
x = 11,200/6 = 1866.67.
इसके बाद, सांत्वना पुरस्कार का मूल्य 700*(6/36) = 116.67 है।
इस प्रकार, बोनस की औसत जीत 1866.67 + 116.67 = 1983.33 है।
[/spoiler]


