WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #427

केक को इस प्रकार विभाजित किया जाता है:

  • पहले व्यक्ति को 1% मिलता है
  • दूसरे व्यक्ति को बचे हुए हिस्से का 2% मिलता है
  • तीसरे व्यक्ति को बचे हुए भाग का 3% मिलता है
  • और इसी तरह।

सबसे ज़्यादा केक किस व्यक्ति को मिलेगा? स्प्रेडशीट या बलपूर्वक गणना की अनुमति नहीं है।

गुमनाम

दसवें व्यक्ति को सबसे अधिक केक मिलेगा।

यहां मेरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

मैं इस गणित पहेली के लिए माइंड योर डिसीजन्स यूट्यूब चैनल को श्रेय देना चाहूंगा।

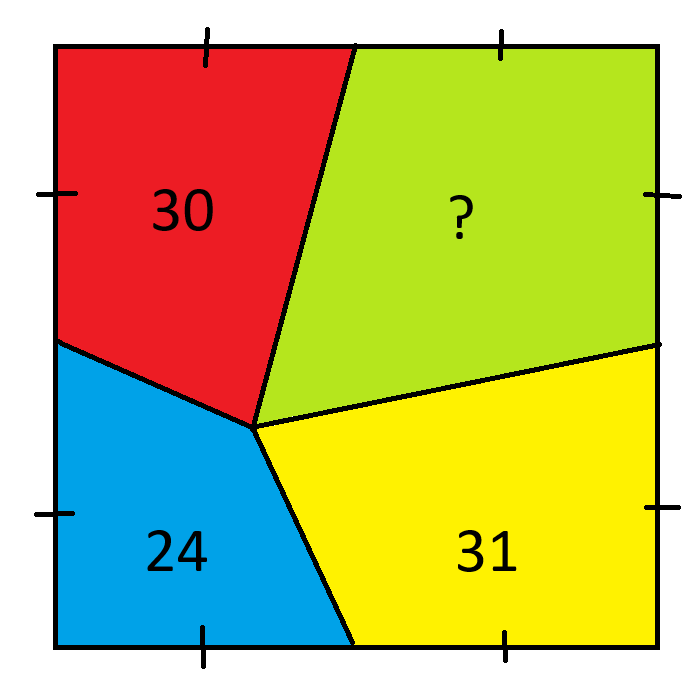
हरित क्षेत्र का क्षेत्रफल कितना है?

गुमनाम

38

[स्पॉइलर=समाधान]

सबसे पहले, चारों टुकड़ों के प्रतिच्छेद बिंदु से प्रत्येक कोने तक चार रेखाएँ खींचें। फिर आठों टुकड़ों पर निम्नलिखित नाम लिखें।

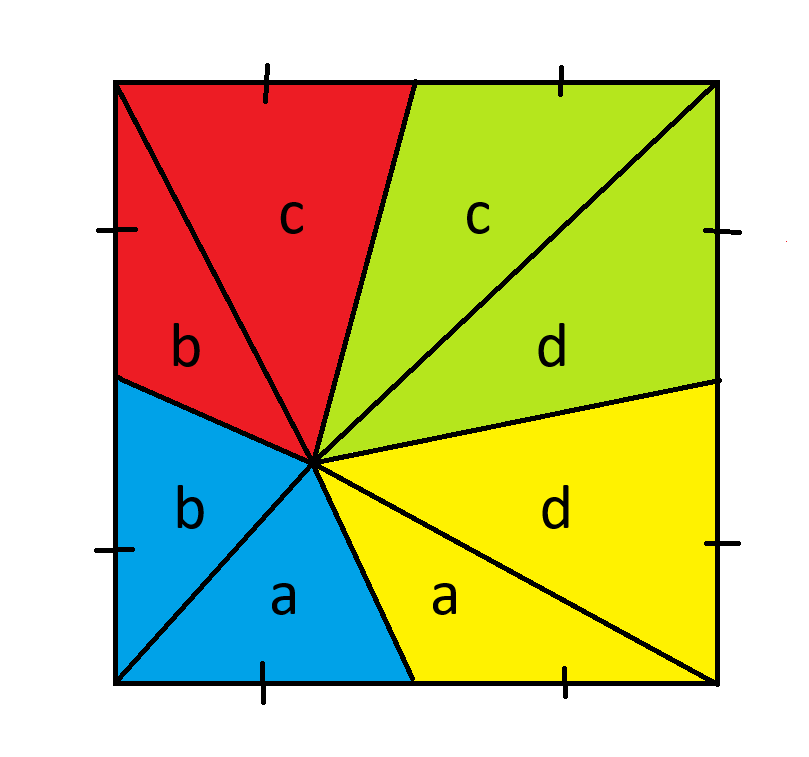
याद रखें कि त्रिभुज का क्षेत्रफल आधार*ऊँचाई/2 होता है। चूँकि सभी त्रिभुजों का आधार समान होता है, इसलिए हम समान ऊँचाई वाले त्रिभुजों को समान क्षेत्रफल वाले त्रिभुजों के रूप में जोड़ सकते हैं।

इस बिंदु पर हम जानते हैं:

  • (1) ए+बी = 34
  • (2) बी+सी = 42
  • (3) ए+डी = 30

समीकरण (2) और (3) को जोड़ने पर:

ए+बी+सी+डी = 72

आइए इसमें से समीकरण (1) घटाएं:

C+D = 38, जो हमारा उत्तर है।

[/spoiler]

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर पूछा गया और इस पर चर्चा की गई।

इस पहेली का स्रोत यूट्यूब वीडियो है जिसका शीर्षक है "98% लोग इस गणित की समस्या को हल करने में असफल रहे।"

मान लीजिए कि आप कई मानों का माध्य ज्ञात करना चाहते हैं। ओलंपिक में जिम्नास्टिक स्कोरिंग की तरह, उच्चतम और निम्नतम मानों को छोड़ने के बारे में आपकी क्या राय है? मान लीजिए कि उद्देश्य किसी खास इलाके के प्रति वर्ग फुट का माध्य ज्ञात करना है।

गुमनाम

अच्छा सवाल। आप जिस बारे में बात कर रहे हैं उसे ट्रिम्ड माध्य कहते हैं। मुझे ट्रिम्ड माध्य और वास्तविक माध्य के बीच के विचरण के किसी आँकड़े की जानकारी नहीं है। कोई बेहतर जानकारी न होने के कारण, मैंने अपना प्रयोग स्वयं किया।

आपके प्रश्न का उत्तर देने के लिए, मैंने मानों के दस सेटों के 1,00,000 नमूने लिए। प्रत्येक मान को मानक सामान्य वितरण के अनुसार वितरित किया गया था, जिसका अर्थ है 0 का माध्य और 1 का प्रसरण। फिर मैंने सभी दस मानों के माध्य के साथ-साथ छांटे गए आठ मानों के माध्य को भी देखा।

मैंने पाया कि सभी दस मानों के नमूने के लिए नमूना माध्य और वास्तविक माध्य के बीच औसत अंतर 0.003450 था। यही प्रक्रिया दोहराते हुए, लेकिन कटे हुए माध्य का औसत लेते हुए, औसत अंतर 0.003445 था। मेरी राय में, यह इतना महत्वपूर्ण अंतर नहीं है कि यह घोषित किया जा सके कि कौन सी विधि बेहतर है। इसके अलावा, जो मेरे प्रयोग के लिए सही हो सकता है, वह किसी अन्य अनुप्रयोग के लिए सही नहीं भी हो सकता है।

निष्कर्ष के तौर पर, मैं अक्सर ऐसा नहीं कहता, मेरे पास इसका कोई निश्चित गणितीय उत्तर नहीं है।

वर्गाकार या त्रिभुजाकार आधार वाले गोलों को एक साथ रखने का अधिक कुशल (अर्थात कम से कम स्थान बर्बाद करने वाला) तरीका क्या है?

गुमनाम

मैंने इसका उत्तर इस प्रकार दिया कि किस पिरामिड में गोलों के आयतन का अनुपात, उन्हें घेरने वाले पिरामिड के आयतन से सबसे अधिक था, क्योंकि गोलों की संख्या अनंत के करीब पहुंच गई थी।

वे समान रूप से कुशल हैं, जिनकी दक्षता 74.05% है।

यहां मेरा समाधान (पीडीएफ) है।

मुझे बाद में पता चला कि यह सवाल Ask the Wizard #350 में भी पूछा गया था। हालाँकि, मुझे लगता है कि यह समाधान बेहतर है।