WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #426

मान लीजिए कि कुछ क्रम संख्याएँ 1 से शुरू होकर क्रमिक रूप से अंकित हैं। प्रचलन में अधिकतम संख्या अज्ञात है। n संख्याओं का एक यादृच्छिक नमूना दिया गया है, तो अधिकतम क्रम संख्या का सर्वोत्तम अनुमान क्या है?

गुमनाम

मैं इस उत्तर के बारे में जिस तरह से सोचना पसंद करता हूँ, वह है क्रम संख्याओं के बीच औसत अंतराल ज्ञात करना। इसकी गणना करने का तरीका यह है कि अधिकतम मान लें और उसे नमूने के आकार से भाग दें। उदाहरण के लिए, यदि आपके नमूने में सबसे बड़ी वस्तु 1,000 है और आपके नमूने का आकार 5 है, तो औसत अंतराल 1000/5 = 200 होगा। फिर अनुमानित उच्चतम संख्या प्राप्त करने के लिए उस अंतराल को अधिकतम प्रेक्षण में जोड़ें। इस उदाहरण में, 1000+200 = 1200।

समान संख्या प्राप्त करने के लिए दिया गया सामान्य सूत्र M*(k+1)/k है, जहाँ M = अधिकतम मान और k = प्रेक्षणों की संख्या। हमारे उदाहरण में, यह 1000*(6/5) = 1200 देता है।

ABCD एक वर्ग है जिसकी भुजा की लंबाई 10 है। इसके अंदर एक अर्धवृत्त और एक चौथाई वृत्त अंकित है, जैसा कि निम्नलिखित चित्र में दिखाया गया है।

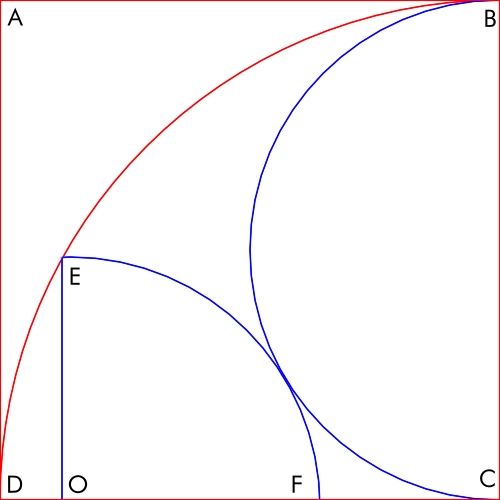
OE की लम्बाई कितनी है?

ThatDonGuy

5

[स्पॉइलर=समाधान]

निम्नलिखित आरेख पर विचार करें।

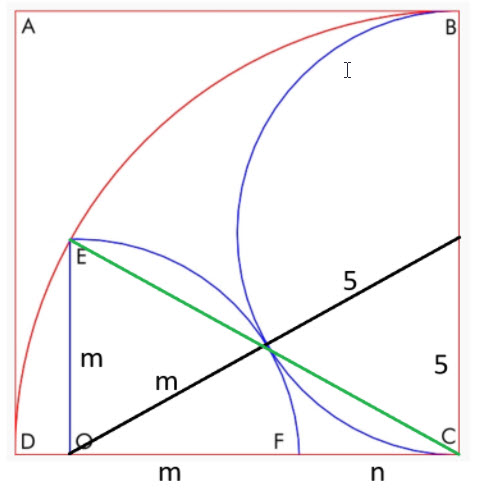
यहाँ हमारे पास दो समकोण त्रिभुज हैं, एक का कर्ण हरा है और दूसरे का काला। आइए दो पाइथागोरस समीकरण बनाएँ:

  • हरा कर्ण: m 2 + (m+n) 2 = 10 2
  • काला कर्ण: 5 2 + (m+n) 2 = (m+5) 2

आइए पहले समीकरण को (m+n) 2 = 10 2 - m 2 में पुनर्व्यवस्थित करें

आइए उस मान को (m+n) 2 के लिए दूसरे समीकरण में प्रतिस्थापित करें:

5 2 + 10 2 - मी 2 = (मी+5) 2

25 + 100 - मी 2 = मी 2 + 10मी + 25

2मी 2 + 10मी - 100 = 0

मी 2 + 5मी - 50 = 0

m को हल करने के लिए पाइथागोरस सूत्र का उपयोग करें:

एम = (-5 +/- sqrt(25 + 200))/2

m = 5 या -10. 5 ही एकमात्र उचित उत्तर है।

[/बिगाड़ने वाला]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

बड़ी संख्या में छात्र 10 प्रश्नों वाली एक परीक्षा दे रहे हैं। प्रत्येक प्रश्न सत्य या असत्य है। अधिकतम कितने छात्र इस परीक्षा में शामिल हो सकते हैं ताकि कोई भी दो परीक्षाएँ एक-दूसरे से कम से कम दो प्रश्नों से भिन्न हों?

ThatDonGuy

512

[स्पॉइलर=समाधान]

एक परीक्षण लें जिसे हम मुख्य परीक्षण कहेंगे।

समूह 1 = अन्य परीक्षण मुख्य परीक्षण से ठीक 2 प्रश्नों से भिन्न हो सकते हैं, इसकी संख्या combin(10,2)=45 है।

मैं मुख्य परीक्षण से 3 से भिन्न होने के तरीकों की संख्या की गणना नहीं करने जा रहा हूं, क्योंकि उनमें से कुछ तरीके समूह 1 के परीक्षण से 10 में से 9 मेल खाएंगे।

समूह 2 = अन्य परीक्षण मुख्य परीक्षण से ठीक 4 प्रश्नों से भिन्न हो सकते हैं, इसकी संख्या संयोजन (10,4) = 210 है। इनमें से कोई भी परीक्षण समूह 1 के किसी भी परीक्षण से कम से कम 2 प्रश्नों से भिन्न होगा।

इस तर्क को दोहराते हुए...

  • समूह 3 = अन्य परीक्षण मुख्य परीक्षण से ठीक 6 प्रश्नों से भिन्न हो सकते हैं, इसकी संख्या combin(10,6)=210 है।
  • समूह 4 = अन्य परीक्षण मुख्य परीक्षण से ठीक 8 प्रश्नों से भिन्न हो सकते हैं, इसकी संख्या combin(10,8)=45 है।
  • समूह 5 = अन्य परीक्षण मुख्य परीक्षण से ठीक 10 प्रश्नों से भिन्न हो सकते हैं, इसकी संख्या combin(10,10)=1 है।

तो, उत्तर है समूह 1 से 5 का योग + मुख्य परीक्षण के लिए एक = 1+45+210+210+45+1 = 512.

यह संख्या 2^9 के बराबर है। क्या यह संयोग हो सकता है? नहीं!

एक बड़े समूह से विषम संख्या में वस्तुएँ निकालने के तरीकों की संख्या, सम संख्या निकालने के तरीकों की संख्या के समान ही होती है। ऐसा इसलिए है क्योंकि बड़े समूह की प्रत्येक वस्तु को या तो चुना जा सकता है या नहीं चुना जा सकता है। n वस्तुओं के समूह में प्रत्येक सदस्य के चुने जाने या न चुने जाने के 2^n संयोजन होते हैं। यदि आप उन्हें बाइनरी क्रम में व्यवस्थित रूप से सूचीबद्ध करें, तो चुने गए संयोजनों की संख्या सम और विषम के बीच बारी-बारी से होगी। समूह की कुल संख्या 2^n है, जो स्वयं सम है, इसलिए 2^n का आधा सम होगा।

तो, समूह 1 से 5 का योग, मुख्य परीक्षा से मेल खाने वाले प्रश्नों की सम संख्या चुनने के तरीकों की संख्या है। यह मुख्य परीक्षा से मेल खाने वाले विषम संख्या में प्रश्नों को चुनने के तरीकों की संख्या के बराबर होगा। मुख्य परीक्षा से मेल खाने या न मिलने के तरीकों की कुल संख्या 2^10 = 1024 है। इनमें से आधे सम संख्या में मेल खाएँगे। तो, उत्तर 1024/2 = 512 है।[/spoiler]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।