WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #422

तर्क के लिए, मान लीजिए कि एक ब्लैकजैक गेम में अनगिनत डेक हैं, तो अनंत बार पुनः-विभाजन की अनुमति है, और खिलाड़ी किसी भी जोड़ी को विभाजित कर देगा। खिलाड़ी द्वारा खेले जाने वाले किसी भी अंतिम हाथ की प्रायिकता क्या है?

गुमनाम

n हाथों में पुनः विभाजित होने की संभावना (combin(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n है। उस पहले पद के बारे में अधिक जानकारी के लिए, जिसके लिए मुझे कुछ मदद की ज़रूरत थी, कैटलन संख्याएँ देखें।

निम्नलिखित तालिका 1 से 20 अंतिम हाथों की संभावना दर्शाती है। सेकंड कॉलम "पेड़ों" की संख्या है, जो ऊपर दिए गए व्यंजक में कैटलन संख्या है।

हाथ पेड़ संभावना
1 1 0.9230769230769
2 1 0.0655439235321
3 2 0.0093080128093
4 5 0.0016523099661
5 14 0.0003285065968
6 42 0.0000699777366
7 132 0.0000156163334
8 429 0.0000036037693
9 1430 0.0000008529631
10 4862 0.0000002059225
11 16796 0.0000000505114
12 58786 0.0000000125531
13 208012 0.0000000031540
14 742900 0.0000000007998
15 2674440 0.0000000002045
16 9694845 0.0000000000526
17 35357670 0.0000000000136
18 129644790 0.0000000000035
19 477638700 0.0000000000009
20 1767263190 0.0000000000002

मैंने सुना है कि पाइथागोरस त्रिकों की संख्या अनंत है। क्या उन्हें ज्ञात करने का कोई सूत्रबद्ध तरीका है?

गुमनाम

हाँ, अनगिनत अद्वितीय पाइथागोरस त्रिक हैं! जो लोग इस शब्द से परिचित नहीं हैं, उनके लिए बता दें कि ये समकोण त्रिभुज होते हैं जिनकी प्रत्येक भुजा एक पूर्णांक होती है। 3-4-5 इनमें सबसे प्रसिद्ध है। एक अद्वितीय (दूसरे शब्दों में, अपरिमेय) समुच्चय प्राप्त करने के लिए, a और b के लिए कोई भी पूर्णांक मान चुनें, जहाँ a < b हो और एक विषम और एक सम हो।

  • पैर 1 = b 2 - a 2
  • पैर 2 = 2ab
  • कर्ण = a 2 + b 2

निम्नलिखित तालिका में सभी गैर-अपचयनीय पाइथागोरस त्रिक दर्शाए गए हैं, जहां सभी भुजाएं 101 या उससे कम हैं।

ए, बी चरण 1 चरण 2 कर्ण
1,2 3 4 5
1,4 8 15 17
1,6 12 35 37
1,8 16 63 65
1,10 20 99 101
2,3 5 12 13
2,5 20 21 29
2,7 28 45 53
2,9 36 77 85
3,4 7 24 25
3,6 27 36 45
3,8 48 55 73
4,5 9 40 41
4,7 33 56 65
4,9 65 72 97
5,6 11 60 61
5,8 39 80 89
6,7 13 84 85

सात के अलावा अन्य दो पासों से प्रत्येक योग पर कम से कम दो बार सात आने की संभावना क्या है?

Garrison

इस तरह के प्रश्नों की युक्ति यह है कि यदि रोल के बीच का समय 1 के माध्य के साथ घातांकीय वितरण का अनुसरण करता है, तो संभावना समान होती है। इस मामले में, इसे निम्नलिखित सूत्र द्वारा दिया जा सकता है।

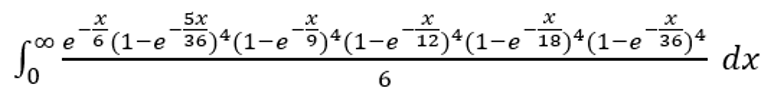
इसे टेक्स्ट फॉर्म में लिखने के लिए: exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6

ऐसे समाकलों को हल करने के लिए, मैं इस समाकल कैलकुलेटर की अनुशंसा करता हूँ।

उत्तर आता है 7864581698887803455719/10946915593544650625105200 =~ 0.0007184290069364848.