WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #418


छवि स्रोत: यूट्यूब

स्क्विड गेम के सीज़न 2 में रॉक पेपर सिज़र्स माइनस वन नाम का एक गेम है, जिसे इस वीडियो में समझाया गया है। इसके नियम रॉक पेपर सिज़र्स के क्लासिक संस्करण पर आधारित हैं, जिनमें कुछ बदलाव किए गए हैं।

  • एक ही समय में, दोनों खिलाड़ी दो प्रतीक खेलते हैं, प्रत्येक हाथ से एक।
  • दोनों खिलाड़ी यह जांचने के बाद कि क्या फेंका गया था, तीन की गिनती पर, प्रत्येक खिलाड़ी अपने हाथ से एक प्रतीक वापस ले लेता है, तथा दूसरा हाथ छोड़ देता है।
  • खेल में मानक नियमों के अनुसार अंक दिए जाते हैं: पत्थर कैंची को हराता है, कागज पत्थर को हराता है, कैंची कागज को हराती है।

यूट्यूब वीडियो में भर्तीकर्ता निम्नलिखित स्थिति को उदाहरण के रूप में उपयोग करता है:

  • त्रिकोण कैंची और कागज़ खेलता है
  • सर्कल रॉक और पेपर खेलता है

रिक्रूटर कहता है कि त्रिभुज को कागज़ खेलना चाहिए क्योंकि वह हार नहीं सकता। क्या यह रणनीति सही है? मुझे लगता है कि वृत्त शायद इस रणनीति का अनुमान लगाएगा और कागज़ खेलकर भी बराबरी की स्थिति में पहुँच जाएगा। इसलिए, शायद त्रिभुज को कम से कम एक मौका लेकर कैंची खेलने पर विचार करना चाहिए। दोनों खिलाड़ियों के लिए सबसे अच्छी रणनीति क्या है?

गुमनाम

कुछ गणना करने के बाद, मुझे पता चला कि दोनों पक्षों के लिए इष्टतम रणनीति इस प्रकार है:

  • त्रिभुज: कागज़ की संभावना 2/3, कैंची की संभावना 1/3।
  • वृत्त: कागज़ की संभावना 2/3, पत्थर की संभावना 1/3।

यदि कम से कम एक खिलाड़ी इस रणनीति का पालन करता है, तो त्रिभुज के लिए प्रत्येक परिणाम की संभावना निम्नलिखित होगी:

  • जीत = 4/9
  • टाई = 4/9
  • हानि = 1/9

सर्कल के लिए यह विपरीत है, इस प्रकार:

  • जीत = 1/9
  • टाई = 4/9
  • हानि = 4/9

कुल मिलाकर, रिक्रूटर अपनी सलाह में बिल्कुल ग़लत है। किसी भी स्थिति के लिए मेरी सामान्य सलाह यह है:

  • शुरुआत में हमेशा दो अलग-अलग प्रतीकों से खेलें।
  • अगर आप अपने प्रतिद्वंद्वी के समान दो चिन्ह खेलते हैं, तो वह चिन्ह खेलें जो आपके द्वारा खेले गए दूसरे चिन्ह को हरा दे। उदाहरण के लिए, अगर दोनों पत्थर और कागज़ खेलते हैं, तो कागज़ खेलें।
  • यदि दोनों खिलाड़ी एक समान प्रतीक पर खेलते हैं, तो दोनों पक्षों को उस समान प्रतीक पर 2/3 तथा दूसरे पक्ष को 1/3 संभावना के साथ खेलना चाहिए।

लिंक

छह-पक्षीय पासे पर एक ही पक्ष को दो बार घुमाने के लिए अपेक्षित रोलों की संख्या कितनी है? अन्य प्लेटोनिक ठोसों के बारे में क्या? क्या किसी n-पक्षीय पासे के लिए कोई सूत्र है?

गुमनाम

छह-पक्षीय पासे का उत्तर 1223/324 = ~ 3.774691 रोल है।

निम्नलिखित तालिका विभिन्न भुजाओं के लिए उत्तर दर्शाती है।

पक्षों अपेक्षित
रोल्स
4 3.218750
6 3.774691
8 4.245018
12 5.036074
20 6.293585
50 9.543127
100 13.209961
200 18.398444

यहाँ छह-पक्षीय पासे के लिए एक सूत्र दिया गया है। किसी भी अन्य पक्षीय पासे के लिए, 6 को वांछित भुजाओं की संख्या में बदलें।

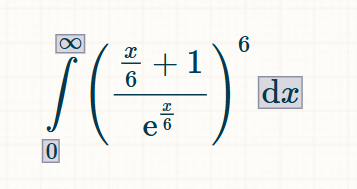
ऐसे कठिन समाकलों को हल करने के लिए मैं integral-calculator.com की अनुशंसा करता हूँ।

इस प्रश्न पर सहायता के लिए मैं विजार्ड ऑफ वेगास के सदस्य ऐस2 को धन्यवाद देता हूं।

मान लीजिए आपको एक पासा तब तक उछालने का मौका दिया जाता है जब तक कि वह 6 पर न आ जाए। आप जितने पासे उछालने होंगे, उसका वर्ग (डॉलर में) जीतेंगे। उदाहरण के लिए, अगर 6 बार पासा उछाला गया तो आप $25 जीतेंगे। इस खेल में अपेक्षित जीत क्या है?

गुमनाम

$66

यहाँ मेरा समाधान (पीडीएफ) है।