WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #417

मुझे पता है कि आप पहले सरकारी एक्चुअरी हुआ करते थे। तो क्या इस तालिका में दिए गए आँकड़े, जो कथित तौर पर अमेरिका में आयात और अमेरिकी उत्पादों के निर्यात पर लगाए गए टैरिफ दिखाते हैं, सही हैं?

गुमनाम

नहीं।

मैं इन आँकड़ों के स्रोत के बारे में जानने को उत्सुक था। अमेरिका पर लगाए गए टैरिफ़ वाले कॉलम से शुरुआत करते हुए, मैंने पाया कि ये टैरिफ़ के बारे में नहीं, बल्कि व्यापार घाटे के बारे में हैं। नीचे दी गई तालिका 2024 में सूची में शामिल शीर्ष दस देशों द्वारा अमेरिका को किए जाने वाले आयात और निर्यात के मूल्य को दर्शाती है। "व्यापार घाटा अनुपात" कॉलम आयात में से निर्यात को घटाकर आयात का अनुपात है। आयात और निर्यात लाखों डॉलर में दर्शाए गए हैं। ध्यान दें कि यह ट्रम्प द्वारा पकड़े गए टेबल पर दिए गए आँकड़ों से बिल्कुल मेल खाता है।

देश निर्यात आयात व्यापार
घाटा
अनुपात		 "टैरिफ
आरोपी
संयुक्त राज्य अमेरिका के लिए"
चीन $143,546 $438,947 67% 67%
यूरोपीय संघ $370,189 $605,760 39% 39%
वियतनाम $13,098 $136,561 90% 90%
ताइवान $42,337 $116,264 64% 64%
जापान $79,741 $148,209 46% 46%
भारत $41,753 $87,416 52% 52%
दक्षिण कोरिया $65,542 $131,549 50% 50%
थाईलैंड $17,719 $63,328 72% 72%
स्विट्ज़रलैंड $24,962 $63,425 61% 61%
इंडोनेशिया $10,202 $28,085 64% 64%

आयात और निर्यात का स्रोत: संयुक्त राज्य अमेरिका जनगणना ब्यूरो ।

इसलिए, राष्ट्रपति के चार्ट में "अमेरिका पर लगाए गए टैरिफ" कॉलम का टैरिफ से कोई संबंध नहीं है, बल्कि यह केवल आयात के प्रतिशत के रूप में व्यापार घाटा है।

आप पूछ सकते हैं, "'यूएसए डिस्काउंटेड रेसिप्रोकल टैरिफ' कॉलम के सुनहरे कॉलम का क्या?" यह बस टैरिफ चार्ज कॉलम के आधे और 10% में से जो ज़्यादा है, वह है। इसे तालिका देखकर ही समझा जा सकता है।

इससे बस यही पता चलता है कि सिर्फ़ इसलिए कि कोई आपके सामने ढेर सारे आँकड़े और आँकड़ों की बौछार कर देता है, इसका मतलब यह नहीं कि वह सच बोल रहा है। दरअसल, लोगों को बेवकूफ़ बनाने का एक आम तरीका है कि उन पर आँकड़ों की बौछार कर दी जाए मानो किसी फ़ायरहॉउस से आ रही हो और उम्मीद की जाए कि सुनने वाला उनकी सच्चाई की जाँच करने में आलस करेगा। मैंने मनुष्य बनाम भालू बहस पर यह वीडियो देखने के बाद से आँकड़ों का इतना ज़बरदस्त दुरुपयोग नहीं देखा। दरअसल, यह "पारस्परिक शुल्क" तालिका तो और भी बदतर है।

मान लीजिए मैंने एक अनंत-डेक ब्लैकजैक गेम में $100 का दांव लगाया और मुझे डीलर के तीन के मुकाबले दो-दो का जोड़ा दिया गया। विभाजित करने के बाद दोगुना करने की अनुमति है और खिलाड़ी अनंत बार फिर से विभाजित कर सकता है। यह मानते हुए कि मैं जितना संभव हो सके उतना विभाजित करूँ और अगर मेरे दो-कार्ड का कुल योग 9 से 11 है, तो दोगुना करने के लिए अपेक्षित अंतिम कुल दांव क्या होगा?

Ace2

आइए पहले गणना करें कि आप कितने हाथों में पुनः-विभाजन की उम्मीद कर सकते हैं। मान लीजिए n, पुनः-विभाजन के बाद एक कार्ड से प्राप्त होने वाले हाथों की संख्या है।

एन=(12/13)×1 + (1/13)×2एन
13एन = 12 + 2एन
11एन = 12
एन = 12/11 =~ 1.090909...

दो शुरुआती दो के साथ, खिलाड़ी 2×(12/11) = 24/11 =~ 2.181818 हाथों में पुनः विभाजित होने की उम्मीद कर सकता है।

किसी भी दिए गए दो में से 7 से 9 निकालने की प्रायिकता 3×(1/12) = 3/12 = 1/4 है। मैं 12 से भाग दे रहा हूँ, 13 से नहीं, क्योंकि अगर खिलाड़ी 2 निकालता है, तो वह जोड़ी को फिर से बाँट देगा। इसलिए, दोबारा बाँटने के बाद प्रति हाथ औसत दांव (3/4)×1 + (1/4)×2 = 5/4 = 1.25 है।

$100 के आधार दांव के साथ, औसत अंतिम दांव $100×(24/11)×(5/4) = $272.73 है।

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर पूछा गया और इस पर चर्चा की गई।

मान लीजिए कि दो खिलाड़ी निम्नलिखित नियमों के तहत रूसी रूलेट खेलना चाहते हैं।

  • बंदूक एक रिवॉल्वर है जिसमें छह कक्ष होते हैं।
  • किसी भी ट्रिगर को दबाने के लिए चैम्बर में एक से पांच गोलियां डालनी पड़ती हैं।
  • प्रत्येक खींचने से पहले बंदूक में गोलियों की संख्या बदल सकती है।
  • प्रत्येक खींचने के बाद बंदूक को आगे-पीछे करना होगा।
  • बंदूक के अलावा किसी अन्य यादृच्छिकीकरण विधि का उपयोग नहीं किया जा सकता।

प्रत्येक खिलाड़ी के जीवित बचने की 50% संभावना सुनिश्चित करने का तरीका क्या है?

गुमनाम

यह सिर्फ़ मेरा जवाब है। मुझे यकीन है कि और भी जवाब होंगे।

  1. पहले खिलाड़ी के लिए बंदूक में दो गोलियाँ रखें। अगर वह बच जाता है, तो चरण 2 पर जाएँ।
  2. दूसरे खिलाड़ी के लिए बंदूक में तीन गोलियाँ रखें। अगर वह बच जाता है, तो चरण 1 पर वापस जाएँ।

यदि हम p को खिलाड़ी 1 के हारने की संभावना मानें, तो इसकी गणना निम्न प्रकार से की जा सकती है:

पी = (2/6) + (4/6)*(3/6)पी
36पी = 12 + 12पी
24पी = 12
पी = 12/24 = 1/2

मान लीजिए कि भुजा लंबाई a वाले एक वर्ग की भुजाओं को वर्ग के नीचे एक रेखा पर बढ़ाया जाता है, जिससे रेखा पर 2 और 5 की दूरी बनती है।

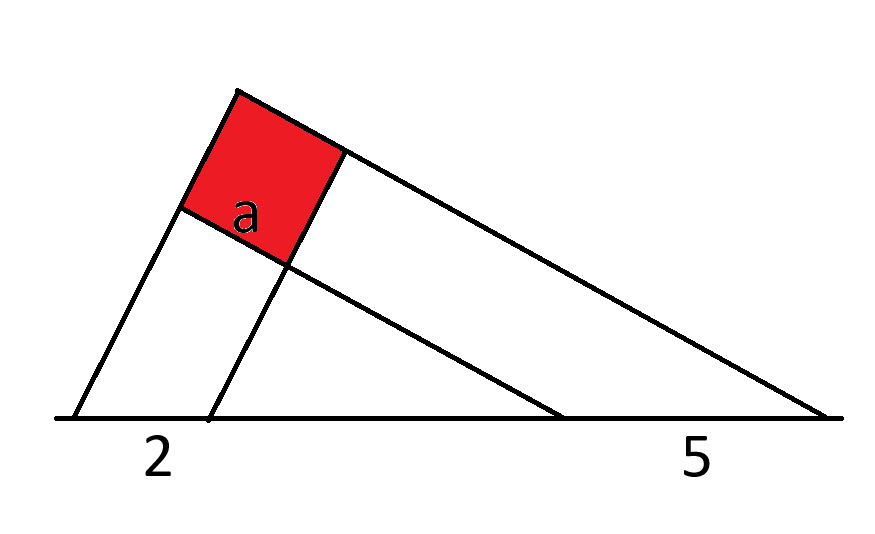
वर्ग का क्षेत्रफल क्या है?

गुमनाम

[स्पॉइलर=उत्तर]100/29 =~3.448276 [/स्पॉइलर]

[स्पॉइलर=समाधान]

सबसे पहले, रेखा को ऊपर की ओर इस प्रकार ले जाएँ कि वह वर्ग के कोने को छू ले। इससे रेखा पर बनी दूरियों पर कोई असर नहीं पड़ेगा। फिर, दोनों त्रिभुजों की अज्ञात भुजाओं को चिह्नित करें।

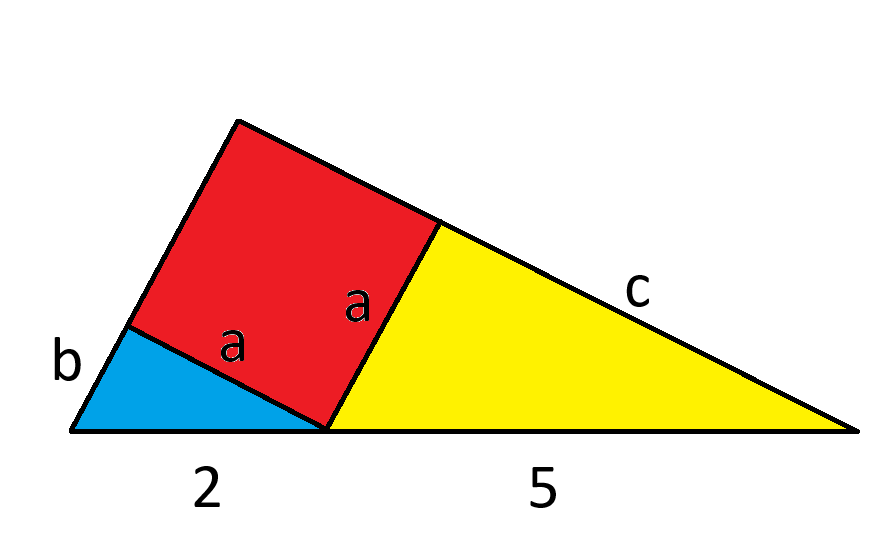
नीले और पीले त्रिकोण समकोण त्रिकोण हैं।

नीले त्रिभुज पर पाइथागोरस सूत्र का उपयोग:

बी 2 + ए 2 = 4
बी = sqrt(4-a 2 )

पीले त्रिभुज पर पाइथागोरस सूत्र का उपयोग:

सी 2 + ए 2 = 25
c = sqrt(25-a 2 )

नीले और पीले त्रिभुज समरूप हैं। इस प्रकार, a और b का अनुपात c और a के अनुपात के बराबर है:

a/sqrt(4-a 2 ) = sqrt(25-a 2 )/a
a 2 = sqrt(4-a 2 ) * sqrt(25-a 2 )

दोनों पक्षों का वर्ग करने पर:

ए 4 = (4 - ए 2 ) * (25 - ए 2 )

मान लीजिए x = a 2

x 2 = (4-x)(25-x)
x 2 = 100 - 29x + x 2
29x = 100
x = 100/29

ए = sqrt(x) = sqrt(100/29)

प्रश्न में लाल वर्ग का क्षेत्रफल पूछा गया था, जो कि 2 = (sqrt(100/29)) 2 = 100/29 है।

[/बिगाड़ने वाला]