जादूगर से पूछो #415
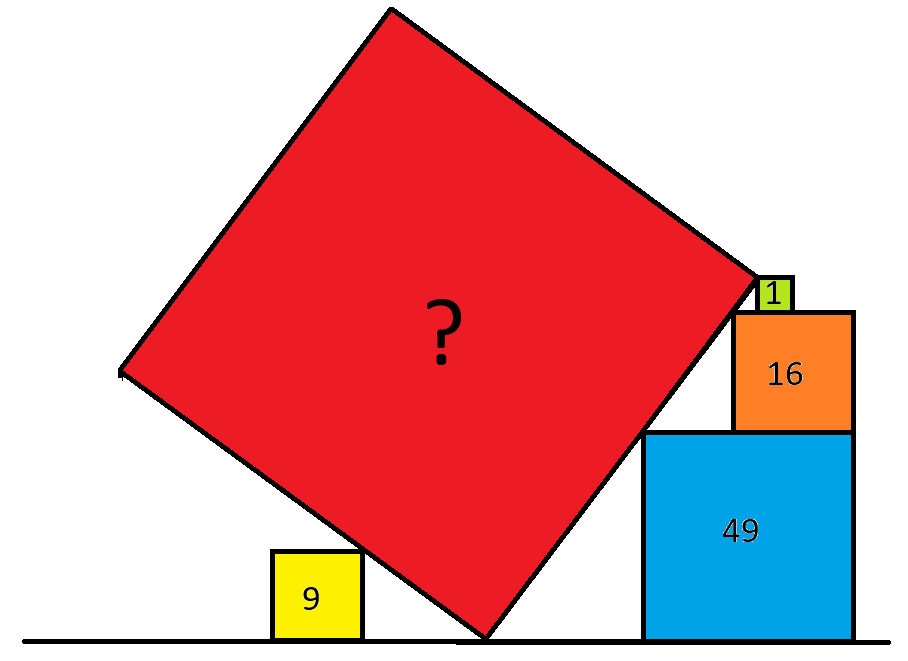
ऊपर दी गई छवि में, संख्याएँ चार वर्गों के क्षेत्रफलों को दर्शाती हैं। लाल वर्ग का क्षेत्रफल क्या है?
सबसे पहले, पीला वर्ग हमारी बिल्कुल भी मदद नहीं करता। यह एक भ्रामक बात है, इसलिए इसे नज़रअंदाज़ कर दें।
इसके बाद, नारंगी वर्ग के बाईं ओर स्थित त्रिभुज पर विचार करें, जैसा कि निम्नलिखित चित्र में दिखाया गया है।
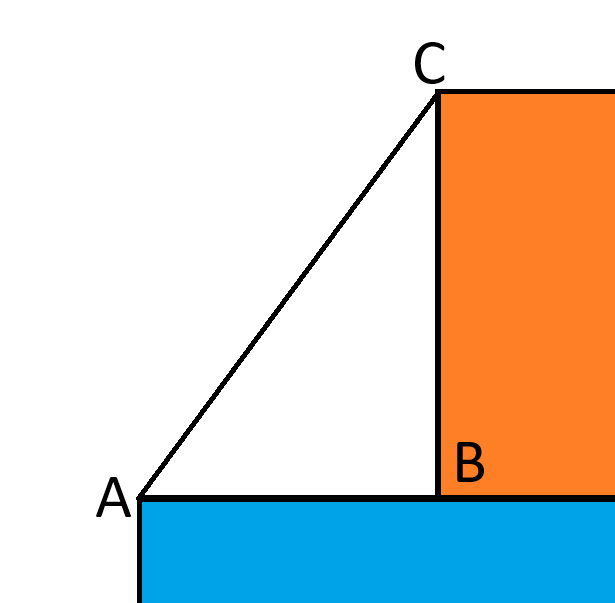
बीसी = sqrt(16) = 4.
एबी = वर्ग(49) - वर्ग(16) = 7-4 = 3.
पाइथागोरस सूत्र से, AC 2 = 4 2 + 3 2 = 25.
एसी = sqrt(25) = 5.
दाईं ओर के तीनों वर्गों की ऊंचाई sqrt(49) + sqrt(16) + sqrt(1) = 12 है।
लाल वर्ग की भुजा की लंबाई और दाईं ओर के तीन वर्गों की ऊंचाई का अनुपात AC और BC के अनुपात = 5/4 के समान होगा।
तो, लाल वर्ग की भुजा की लंबाई (5/4)*12 = 15 है।
इस प्रकार, लाल वर्ग का क्षेत्रफल 15 2 = 225 है।
विज़ार्ड ऑफ़ वेगास में मेरे मंच पर एक समान पहेली पूछी और चर्चा की गई है।
माइंड योर डिसीजन्स यूट्यूब चैनल पर भी ऐसी ही एक पहेली है।
[/spoiler]वह सबसे छोटा संभावित आयत कौन सा है जिसका क्षेत्रफल परिमाप के बराबर हो?
माना आयत की विमाएँ x और y हैं।
हमें दिया गया है: xy = 2x + 2y.
2y - xy = 2x
y(2-x) = 2x
y=2x/(2-x)
मान लीजिए f(x) = आयत का क्षेत्रफल = x*y =
x*2x/(2-x) = 2x 2 /(2-x)
न्यूनतम क्षेत्रफल ज्ञात करने के लिए, भागफल नियम का उपयोग करके व्युत्पन्न निकालें:
f'(x) = 4x(2-x) + 2x 2 / (2-x) 2 = 0
4x(2-x) + 2x 2 = 0
8x = 2x 2
एक्स=4
यदि x=4, y = 2*4/(4-2) = 8/2 = 4.
आइए 4 के निकट x के अन्य मानों के लिए y का हल निकालें।
यदि x=3, y=6, क्षेत्रफल 18
यदि x=5, y = 10/3, क्षेत्रफल 16+(2/3) के लिए।
यह देखना आसान है कि x=4 और y=4 पर हल न्यूनतम प्राप्त होता है। इस प्रकार, सबसे छोटा संभव आयत 4x4 = 16 है।
[/spoiler]कैसीनो ड्रॉ में टिकट धारक के ड्रम में निम्नलिखित संख्या में टिकट होते हैं:
- खिलाड़ी 1 के पास 6 टिकट हैं।
- खिलाड़ी 2 के पास 2 टिकट हैं।
- खिलाड़ी 3 के पास 1 टिकट है।
- 21 अन्य खिलाड़ियों के पास 21 टिकट हैं।
कैसीनो पाँच बराबर पुरस्कारों के लिए पाँच टिकट निकालेगा। प्रत्येक खिलाड़ी केवल एक बार ही जीत सकता है। अगर कोई टिकट किसी ऐसे खिलाड़ी द्वारा निकाला जाता है जो पहले ही जीत चुका है, तो वह टिकट फेंक दिया जाएगा और एक नया टिकट निकाला जाएगा।
खिलाड़ी 1, 2 और 3 ड्रॉ में अपनी इक्विटी के अनुसार जीत को बाँटने के लिए सहमत होते हैं। उचित बंटवारा क्या है?
मैं इस समस्या को सरल बनाने के लिए यह मानकर चल रहा हूँ कि अगर कोई टिकट किसी ऐसे खिलाड़ी द्वारा निकाला जाता है जो पहले ही जीत चुका है, तो वह पुरस्कार रद्द हो जाएगा। अन्यथा, गणित बहुत ज़्यादा उलझ जाएगा, और एक यादृच्छिक सिमुलेशन की आवश्यकता होगी।
n टिकट रखने वाले खिलाड़ी द्वारा पुरस्कार न जीतने की संभावना combin(30-n,5)/combin(30,n) है।
इस प्रकार खिलाड़ी A द्वारा पुरस्कार जीतने की संभावना 1-कॉम्बिन (24,5) / कॉम्बिन (30,5) = 0.701739 है।
इस प्रकार खिलाड़ी बी द्वारा पुरस्कार जीतने की संभावना 1-कॉम्बिन (28,5) / कॉम्बिन (30,5) = 0.310345 है।
इस प्रकार खिलाड़ी सी द्वारा पुरस्कार जीतने की संभावना 1-कॉम्बिन (29,5) / कॉम्बिन (30,5) = 0.166667 है।
इन संभावनाओं का योग 1.178750 है। यानी समूह को कितनी जीत मिलने की उम्मीद है।
मेरे विचार में, प्रत्येक खिलाड़ी को पुरस्कार जीतने की उसकी संभावना के बराबर हिस्सा मिलना चाहिए, जिसे समूह की अपेक्षित कुल जीत से विभाजित किया जाना चाहिए।
A को 0.701739/1.178750 = 0.595324 शेयर मिलता है।
बी को 0.310345/1.178750 = 0.263283 शेयर मिलता है।
सी को 0.166667/1.178750 = 0.141393 शेयर मिलता है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।


