विज़ार्ड अनुशंसा करता है
-
$11000 स्वागत बोनस -
$3000 स्वागत बोनस -
$777 तक बोनस
जादूगर से पूछो #413
क्या सीक्रेट सांता उपहार विनिमय करने का कोई तरीका है जो निम्नलिखित आवश्यकताओं को पूरा करता है:
- कोई भी अपने आप को उपहार नहीं देता।
- इसमें दोबारा कुछ करने का विकल्प नहीं है।
- किसी को भी कुछ नहीं पता सिवाय इसके कि उन्हें किसके लिए खरीदना है।
- प्रत्येक मिलान समान रूप से संभावित है।
हाँ! मैं इसे हन्ना फ्राई विधि कहता हूँ।
- नीचे दिखाए अनुसार कार्डों का एक सेट बनाएँ। प्रत्येक कार्ड के ऊपर और नीचे एक अलग संख्या होनी चाहिए। नीचे दिए गए उदाहरण में, संख्या 23 है।
- कार्डों को फेंटें और उन्हें पुनः व्यवस्थित करें।
- ढेर को यथावत रखते हुए, प्रत्येक कार्ड को बीच में राइड लाइन के साथ काटें, जिससे दो ढेर बन जाएं।
- एक स्टैक को काटें और पूरा करें।
- प्रत्येक ढेर के शीर्ष कार्ड को एक-एक करके प्रत्येक प्रतिभागी को वितरित करें।
- एक क्रमांकित सूची बनाएं और सभी से उस पर अपना नंबर लिखने को कहें।
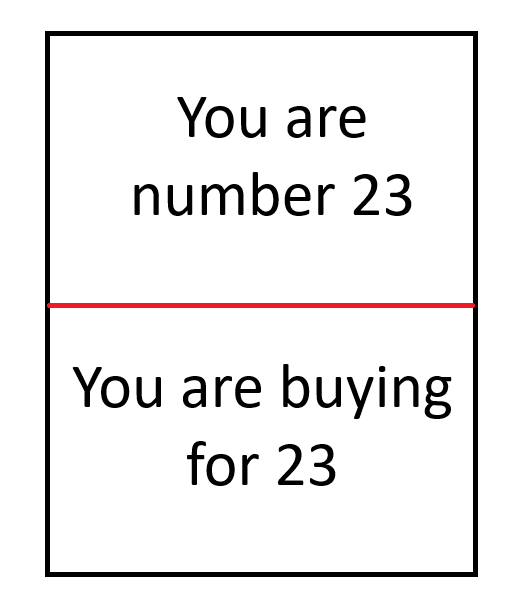
इस प्रक्रिया के बाद, सभी के पास दो कार्ड होंगे जिन पर लिखा होगा, उदाहरण के लिए, "आप 13वें नंबर पर हैं" और "आप 7वें नंबर के लिए खरीदारी कर रहे हैं।" एक बार सूची भर जाने के बाद, सभी को पता चल जाएगा कि किसके लिए खरीदारी करनी है, लेकिन उन्हें यह नहीं पता होगा कि उनके लिए कौन खरीदारी कर रहा है।
एक स्विमिंग पूल खारे पानी से भरा है। पूल में 1000 घन मीटर पानी समा सकता है। एक बगीचे की नली एक घन मीटर प्रति घंटे की दर से ताज़ा पानी पूल में छोड़ती है। जैसे-जैसे ताज़ा पानी अंदर आता है, दूसरी तरफ़ से पानी उसी दर से बाहर निकलता है। पूल में केवल 1% खारा पानी होने में कितना समय लगता है?
यहाँ मेरा समाधान (पीडीएफ) है।
औसतन, प्रत्येक प्लेटोनिक ठोस को पहले से रोल किए गए किसी भी पक्ष को रोल करने के लिए कितने रोल लगते हैं?
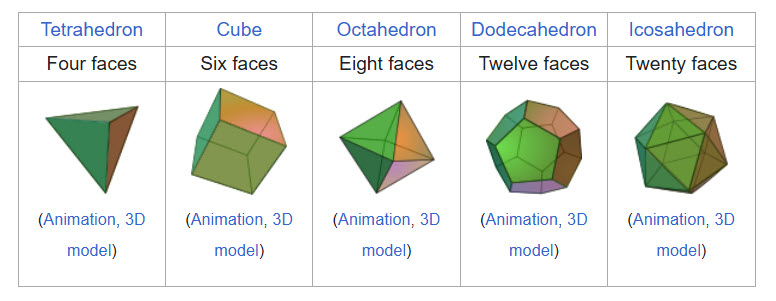
छवि स्रोत: विकिपीडिया
यहाँ पक्षों की संख्या के अनुसार उत्तर दिया गया है।
| पक्षों | औसत रोल |
|---|---|
| 4 | 3.218750 |
| 6 | 3.774691 |
| 8 | 3.846558 |
| 12 | 5.036074 |
| 20 | 6.293585 |
आइये, हम छः भुजाओं वाले घन के मामले पर विचार करें।
- प्रयोग के दो बार समाप्त होने की संभावना 1/6 है।
- प्रयोग के तीन रोल में समाप्त होने की संभावना (5/6)*(2/6) है।
- प्रयोग के चार रोल में समाप्त होने की संभावना (5/6)*(4/6)*(3/6) है।
- प्रयोग के पांच रोल में समाप्त होने की संभावना (5/6)*(4/6)*(3/6)*(4/6) है।
- प्रयोग के छह रोल में समाप्त होने की संभावना (5/6)*(4/6)*(3/6)*(2/6)*(5/6) है।
- प्रयोग के सात रोल में समाप्त होने की संभावना (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) है।
मान लें कि pr(n) = संभावना है कि प्रयोग n रोल में समाप्त होता है।
अपेक्षित रोल है: 2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =
2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3.774691358.