जादूगर से पूछो #411
मेरा मानना है कि अगर कैसिनो में हर खेल पर 0% हाउस एज होता, तो भी वे पैसा कमा सकते थे। ऐसा खिलाड़ियों के खराब धन प्रबंधन और कैसिनो की तुलना में खिलाड़ियों के पास सीमित बैंकरोल के कारण होता है। क्या आप सहमत हैं?
नहीं, मैं असहमत हूं।
धन प्रबंधन को ज़रूरत से ज़्यादा महत्व दिया जाता है। रूलेट जैसे भाग्य के खेल में खिलाड़ी चाहे जैसे भी खेलें, घर की बढ़त को किसी भी दिशा में कम नहीं किया जा सकता।
इस तर्क के अनुसार कि कैसीनो खिलाड़ी के दिवालिया होने तक उससे ज़्यादा समय तक टिक सकता है, यह संभव है कि कैसीनो पहले दिवालिया हो। किसी भी MGM-Mirage कैसीनो के खिलाफ $10,000 के बैंकरोल वाले खिलाड़ी पर विचार करें। इस लेखन के समय, MGM-Mirage का बाज़ार पूंजीकरण $11,168,000,000 है। इसके अलावा, तर्क के लिए, मान लें कि कंपनी के पास उसके 100% शेयर हैं। यदि खिलाड़ी तब तक खेलता है जब तक कि कोई भी पक्ष दिवालिया न हो जाए, तो उसके पास पूरी कंपनी जीतने का 1,116,801 में 1 मौका होगा। खिलाड़ियों की बड़ी संख्या को देखते हुए, अंततः कोई न कोई खिलाड़ी सफल होगा।
मुझे पता है कि हर राज्य को उसकी जनसंख्या के हिसाब से कांग्रेस की सीटें मिलती हैं। लेकिन, वे ऐसा कैसे करते हैं? इसका कोई न कोई तरीका ज़रूर होगा। क्या यह संभव है कि किसी राज्य की जनसंख्या बढ़ जाए, जबकि कुल जनसंख्या वही रहे, और वह एक सीट खो दे?
संक्षिप्त उत्तर यह है कि प्रत्येक राज्य कम से कम एक सीट से शुरुआत करता है। फिर, प्रत्येक अतिरिक्त सीट उस राज्य को एक-एक करके दी जाती है जिसे उस सीट से "सबसे ज़्यादा लाभ" होगा।
"सबसे ज़्यादा लाभ" की गणना कैसे की जाती है, यह और भी जटिल हो जाता है। विवरण इस प्रकार है:
- "गुणक" की गणना (1) अतिरिक्त सीट के साथ कुल सीटों में प्रतिशत वृद्धि और (2) यदि राज्य में वास्तविक सीट से एक सीट अधिक होती, तो कुल सीटों में प्रतिशत वृद्धि के ज्यामितीय माध्य के रूप में करें। इसे सूत्र में कहें तो, यदि n वर्तमान सीटों की संख्या है, तो गुणक 1/sqrt(n*(n+1)) है।
- गुणक और राज्य की जनसंख्या के गुणनफल के रूप में "प्राथमिकता मूल्य" की गणना करें।
हर राज्य के लिए यह गणना करें। सबसे ज़्यादा प्राथमिकता वाले राज्य को अगली सीट मिलेगी।
उदाहरण के लिए, नेवादा को ही लीजिए। 2020 की जनसंख्या 3,104,614 थी और इसमें पहले से ही 4 सीटें हैं। गुणक 1/sqrt(4*5) = 1/sqrt(20) = 0.223607 है। प्राथमिकता मान 3,104,614 * 0.223607 = 694,213 है।
ऐसा नहीं है कि आपने पूछा था, लेकिन अगर कांग्रेस 436वीं सीट जोड़ दे, तो वह न्यूयॉर्क को मिल जाएगी। नीचे दी गई तालिका क्रम से सभी 50 राज्यों के लिए प्राथमिकता मान दर्शाती है।
| राज्य | जनसंख्या | वर्तमान सीटें | गुणक | प्राथमिकता मूल्य |
|---|---|---|---|---|
| न्यूयॉर्क | 20,201,249 | 26 | 0.037743 | 762,447 |
| ओहियो | 11,799,448 | 15 | 0.064550 | 761,651 |
| टेक्सास | 29,145,505 | 38 | 0.025976 | 757,090 |
| फ्लोरिडा | 21,538,187 | 28 | 0.035093 | 755,842 |
| एरिज़ोना | 7,151,502 | 9 | 0.105409 | 753,835 |
| कैलिफोर्निया | 39,538,223 | 52 | 0.019048 | 753,143 |
| वर्जीनिया | 8,631,393 | 11 | 0.087039 | 751,266 |
| इडाहो | 1,839,106 | 2 | 0.408248 | 750,812 |
| मिशिगन | 10,077,331 | 13 | 0.074125 | 746,981 |
| न्यू जर्सी | 9,288,994 | 12 | 0.080064 | 743,715 |
| पेंसिल्वेनिया | 13,002,700 | 17 | 0.057166 | 743,315 |
| मैसाचुसेट्स | 7,029,917 | 9 | 0.105409 | 741,018 |
| जॉर्जिया | 10,711,908 | 14 | 0.069007 | 739,192 |
| वाशिंगटन | 7,705,281 | 10 | 0.095346 | 734,670 |
| इलिनोइस | 12,812,508 | 17 | 0.057166 | 732,442 |
| वेस्ट वर्जीनिया | 1,793,716 | 2 | 0.408248 | 732,281 |
| यूटा | 3,271,616 | 4 | 0.223607 | 731,556 |
| टेनेसी | 6,910,840 | 9 | 0.105409 | 728,466 |
| मैरीलैंड | 6,177,224 | 8 | 0.117851 | 727,993 |
| मिसौरी | 6,154,913 | 8 | 0.117851 | 725,363 |
| ओकलाहोमा | 3,959,353 | 5 | 0.182574 | 722,876 |
| उत्तरी केरोलिना | 10,439,388 | 14 | 0.069007 | 720,386 |
| लुइसियाना | 4,657,757 | 6 | 0.154303 | 718,708 |
| इंडियाना | 6,785,528 | 9 | 0.105409 | 715,257 |
| आयोवा | 3,190,369 | 4 | 0.223607 | 713,388 |
| डेलावेयर | 989,948 | 1 | 0.707107 | 699,999 |
| केंटकी | 4,505,836 | 6 | 0.154303 | 695,266 |
| विस्कॉन्सिन | 5,893,718 | 8 | 0.117851 | 694,581 |
| नेवादा | 3,104,614 | 4 | 0.223607 | 694,213 |
| दक्षिण कैरोलिना | 5,118,425 | 7 | 0.133631 | 683,978 |
| कोलोराडो | 5,773,714 | 8 | 0.117851 | 680,439 |
| अर्कांसस | 3,011,524 | 4 | 0.223607 | 673,397 |
| मिनेसोटा | 5,706,494 | 8 | 0.117851 | 672,517 |
| अलाबामा | 5,024,279 | 7 | 0.133631 | 671,398 |
| मिसिसिपी | 2,961,279 | 4 | 0.223607 | 662,162 |
| कनेक्टिकट | 3,605,944 | 5 | 0.182574 | 658,352 |
| कान्सास | 2,937,880 | 4 | 0.223607 | 656,930 |
| ओरेगन | 4,237,256 | 6 | 0.154303 | 653,823 |
| दक्षिणी डकोटा | 886,667 | 1 | 0.707107 | 626,968 |
| न्यू मैक्सिको | 2,117,522 | 3 | 0.288675 | 611,276 |
| हवाई | 1,455,271 | 2 | 0.408248 | 594,112 |
| नेब्रास्का | 1,961,504 | 3 | 0.288675 | 566,237 |
| न्यू हैम्पशायर | 1,377,529 | 2 | 0.408248 | 562,374 |
| मैंने | 1,362,359 | 2 | 0.408248 | 556,181 |
| नॉर्थ डकोटा | 779,094 | 1 | 0.707107 | 550,903 |
| अलास्का | 733,391 | 1 | 0.707107 | 518,586 |
| वरमोंट | 643,077 | 1 | 0.707107 | 454,724 |
| रोड आइलैंड | 1,097,379 | 2 | 0.408248 | 448,003 |
| MONTANA | 1,084,225 | 2 | 0.408248 | 442,633 |
| व्योमिंग | 576,851 | 1 | 0.707107 | 407,895 |
| कुल | 330,759,736 | 435 | 0.002296 | 759,495 |
आपके दूसरे प्रश्न के संबंध में, हाँ, यह संभव है। मुझे ऐसी स्थिति ढूँढ़ने में काफ़ी देर तक मशक्कत करनी पड़ी जहाँ ऐसा हुआ हो। सबसे पहले, एक काल्पनिक देश पर विचार करें जिसमें निम्नलिखित छह राज्य हों। कुल 15 सीटों के साथ, आवंटन इस प्रकार होगा:
| राज्य | जनसंख्या | वर्तमान सीटें | गुणक | प्राथमिकता मूल्य |
|---|---|---|---|---|
| भ्रम | 900 | 3 | 0.288675 | 259.807621 |
| इनकार | 800 | 3 | 0.288675 | 230.940108 |
| परम आनंद | 700 | 3 | 0.288675 | 202.072594 |
| अवसाद | 600 | 2 | 0.408248 | 244.948974 |
| लीम्बो | 500 | 2 | 0.408248 | 204.124145 |
| चिंता | 400 | 2 | 0.408248 | 163.299316 |
| कुल | 3,900 | 15 |
इसके बाद मान लें कि जनगणना हुई और जनसंख्या में काफी बदलाव आया, लेकिन कुल संख्या 3,900 ही रही और एंग्जाइटी की जनसंख्या 400 से बढ़कर 401 हो गई। इसे 15 राज्यों में केवल एक सीट मिलेगी।
| राज्य | जनसंख्या | वर्तमान सीटें | गुणक | प्राथमिकता मूल्य |
|---|---|---|---|---|
| भ्रम | 1,885 | 7 | 0.133631 | 251.893721 |
| इनकार | 405 | 2 | 0.408248 | 165.340558 |
| परम आनंद | 404 | 2 | 0.408248 | 164.932309 |
| अवसाद | 403 | 2 | 0.408248 | 164.524061 |
| लीम्बो | 402 | 1 | 0.707107 | 284.256926 |
| चिंता | 401 | 1 | 0.707107 | 283.549819 |
| कुल | 3,900 | 15 |
मैं इस बात पर ज़ोर देना चाहता हूँ कि मुझे ऐसी स्थिति ढूँढ़ने के लिए काफ़ी देर तक आँकड़ों के साथ छेड़छाड़ करनी पड़ी जहाँ ऐसा हुआ हो। कुल मिलाकर, मुझे यह तरीका काफ़ी उचित लगता है।
81 ऊँचाई वाले एक आयत में दो वृत्त अंकित हैं। दोनों वृत्तों के किनारे तक 56 लंबाई का एक रेखाखंड है जो वृत्तों के मिलने वाले स्थान से होकर गुजरता है तथा आयत के ऊर्ध्वाधर किनारे के समानांतर है।
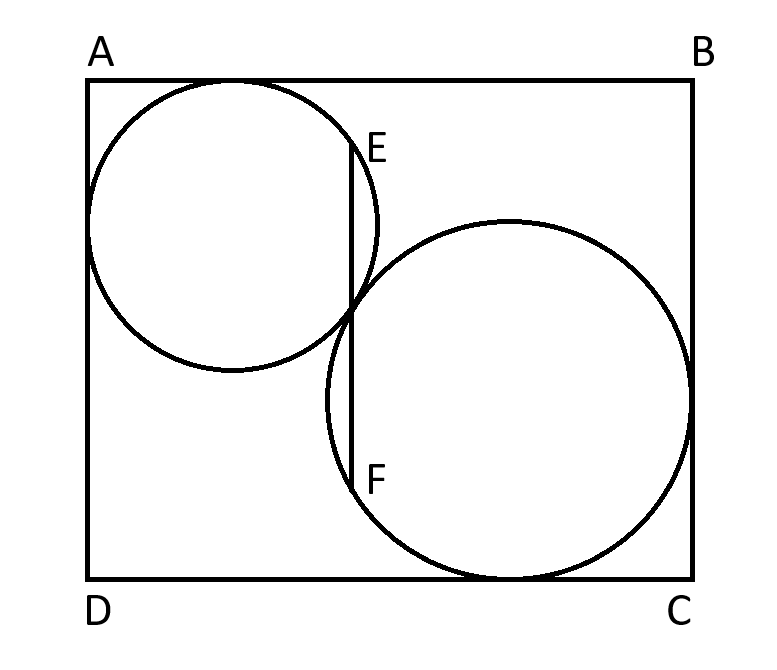
आयत कितनी चौड़ी है?
यहाँ मेरा समाधान (पीडीएफ) है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।


