विज़ार्ड अनुशंसा करता है
-
$11000 स्वागत बोनस -
$3000 स्वागत बोनस -
$777 तक बोनस
जादूगर से पूछो #410
मैंने देखा कि आपने "प्राइज़ इज़ राइट " कॉलम #115 में "आस्क द विज़ार्ड" में प्लिंको गेम के बारे में एक प्रश्न का उत्तर दिया है। हालाँकि, कभी-कभी विशेष शो के लिए पुरस्कार राशि बदल दी जाती है। उदाहरण के लिए, बिग मनी वीक में, बाएँ से दाएँ पुरस्कार $500, $1000, $2500, $0, $200000, $0, $2500, $1000, $500 थे। पक को जिस भी स्थिति से गिराया जाएगा, उसका अपेक्षित मूल्य क्या होगा? किसी भी प्रारंभिक स्थिति में पक के किसी भी पुरस्कार में गिरने की प्रायिकता क्या है?
पक को गिराने के लिए नौ शुरुआती पोज़िशन हैं। हालाँकि, हमें केवल पाँच पर ही ध्यान देना होगा क्योंकि पुरस्कार और खूँटी का लेआउट सममित है। आइए, बाएँ किनारे से शुरू करते हुए, उन्हें 1 से 5 तक लेबल करें।
इसमें नौ अंतिम स्थितियां भी हैं, आइए पहले पांच को लेबल करें, बाएं से शुरू करते हुए, 1 से 5 तक भी।
निम्नलिखित तालिका किसी भी स्थान (बाएं स्तंभ) पर उतरने की संभावना को दर्शाती है, जो कि गिराए गए स्थान (शीर्ष पंक्ति) के अनुसार है।
| लैंडिंग स्पॉट | 1 या 9 छोड़ें | 2 या 8 गिराएँ | 3 या 7 गिराएँ | 4 या 6 गिराएँ | ड्रॉप 5 |
|---|---|---|---|---|---|
| 1 या 9 | 0.225586 | 0.193359 | 0.121094 | 0.056641 | 0.032227 |
| 2 या 8 | 0.386719 | 0.346680 | 0.250000 | 0.153320 | 0.113281 |
| 3 या 7 | 0.242188 | 0.250000 | 0.257813 | 0.250000 | 0.242188 |
| 4 या 6 | 0.113281 | 0.153320 | 0.250000 | 0.346680 | 0.386719 |
| 5 | 0.032227 | 0.056641 | 0.121094 | 0.193359 | 0.225586 |
| कुल | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
अगली तालिका आपके द्वारा पूछे गए बिग मनी वीक के लिए प्रत्येक ड्रॉपिंग पोजीशन से अपेक्षित मूल्य दर्शाती है। जैसा कि अपेक्षित था, खिलाड़ी को पक को सबसे बड़े पुरस्कार की दिशा में गिराना चाहिए।
| ड्रॉप स्थान | अपेक्षित जीत |
|---|---|
| 1 या 9 | $7,550.29 |
| 2 या 8 | $12,396.48 |
| 3 या 7 | $25,173.83 |
| 4 या 6 | $39,478.52 |
| 5 | $45,852.05 |
गेब्रियल हॉर्न विरोधाभास क्या है?
सबसे पहले, 1 से अनंत तक x के मानों के लिए समीकरण y=1/x द्वारा बनाए गए वक्र पर विचार करें। x से 17 तक के मानों के लिए यह ग्राफ़ इस प्रकार दिखाई देगा।
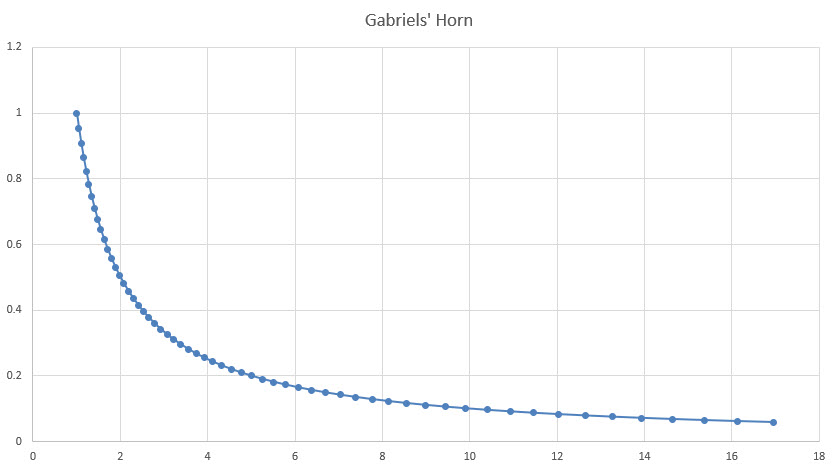
अब, कल्पना कीजिए कि उस वक्र को x-अक्ष पर घुमाया जा रहा है। इससे एक सींग जैसा आकार बनेगा, जिसका सिरा अनंत लंबा होगा। गणितज्ञ इसे ही गेब्रियल का सींग कहते हैं?
छवि स्रोत: गणित की आत्मा ।
अब, गेब्रियल हॉर्न के बारे में प्रश्नों पर विचार करें:
- आयतन क्या है?
- सतह क्षेत्र क्या है?
उत्तर इस प्रकार हैं:
[स्पॉइलर=उत्तर]- आयतन = π = पाई.
- सतह क्षेत्र = अनंत
इन उत्तरों को दर्शाने वाला मेरा कार्य यहां (पीडीएफ) पाया जा सकता है।
विरोधाभास की प्रकृति यह पूछती है कि आयतन सीमित होते हुए भी सतह का क्षेत्रफल अनंत कैसे हो सकता है?
यह विरोधाभास तब होता है जब हम दो आयामों को तीन आयामों से भ्रमित कर देते हैं। हमें ऐसा नहीं करना चाहिए। 1 त्रिज्या वाले वृत्त A और 1.1 त्रिज्या वाले वृत्त B पर विचार करें, जहाँ वृत्त A, वृत्त B के अंदर है।
वृत्त A की परिधि 2*π =~= 6.283185 है और वृत्त B का क्षेत्रफल 1.1^2 *π =~ 3.801327 है। ध्यान दें कि वृत्त B, वृत्त A से बड़ा है, फिर भी इसका क्षेत्रफल B की परिधि से कम है। ऐसा नहीं है कि B की परिधि, A के क्षेत्रफल का हिस्सा है। क्षेत्रफल और परिधि अलग-अलग आयामों में अलग-अलग माप हैं और इनकी तुलना नहीं की जानी चाहिए।
इसे देखने का एक अन्य तरीका यह है कि यदि हम वृत्त A से अनंत संख्या में खांचों वाला एक रिकार्ड बनाएं, तो उन खांचों की लंबाई अनंत होगी।
गैब्रियल हॉर्न पर वापस आते हुए, इसे 1, 1/2, 1/3, 1/4 ... त्रिज्या वाले वृत्तों के विवेकपूर्ण मामले में सरल बनाने पर विचार करें।
इन वृत्तों के आयतनों का योग pi*(1/1 + 1/4 + 1/9 + 1/16 + ...) होगा। एक प्रसिद्ध अनंत श्रेणी है जो कहती है:
1/1 + 1/4 + 1/9 + 1/16 + ... = पाई^2/6 =~ 1.644934.
एक और पाई पद जोड़ने पर, वृत्तों के क्षेत्रफलों का योग pi^3/6 =~ 5.167713 है।
इस बीच, परिधियों का योग 2*pi(1/1 + 1/2 + 1/3 + 1/4 + ...) है।
यह गणित में एक और प्रसिद्ध अनंत श्रृंखला है जिसे हार्मोनिक श्रृंखला कहा जाता है जो कहती है:
1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = अनंत.
2*pi*∞ अभी भी ∞ के बराबर है।
यदि हम इस तर्क को वृत्तों के बीच असीम रूप से छोटी दूरियों तक विस्तारित करें, तो हमें गेब्रियल हॉर्न प्राप्त होता है।
नाथन 100 पाउंड बीन्स खरीदती है। बीन्स में वज़न के हिसाब से 99% पानी होता है। वह उन्हें धूप में सूखने के लिए छोड़ देती है। अगले दिन, उसे पता चलता है कि उनमें 98% पानी है। उनका नया वज़न क्या है?
होने देना:
- w = मूल जल भार.
- w' = फलियों को सुखाने के बाद पानी का वजन।
- x = बीन्स में बाकी सब चीजों का वजन.
हमें पहले दिन के लिए दिया गया है:
w + x = 100
w/(w+x) = 0.99
पहले समीकरण को दूसरे में प्रतिस्थापित करने पर:
w/100 = 0.99
w = 99
इस प्रकार, x=1.
अगले दिन हमें दिया गया:
w'/(w'+x) = 0.98
w' = 0.98*(w'+x)
0.02w' = 0.98x
हम जानते हैं कि x=1 इसलिए:
0.02w' = 0.98
w' = 0.98/0.02 = 49
अगले दिन कुल वजन x+w' = 1+49 = 50 होगा।
[/बिगाड़ने वाला]