WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #407

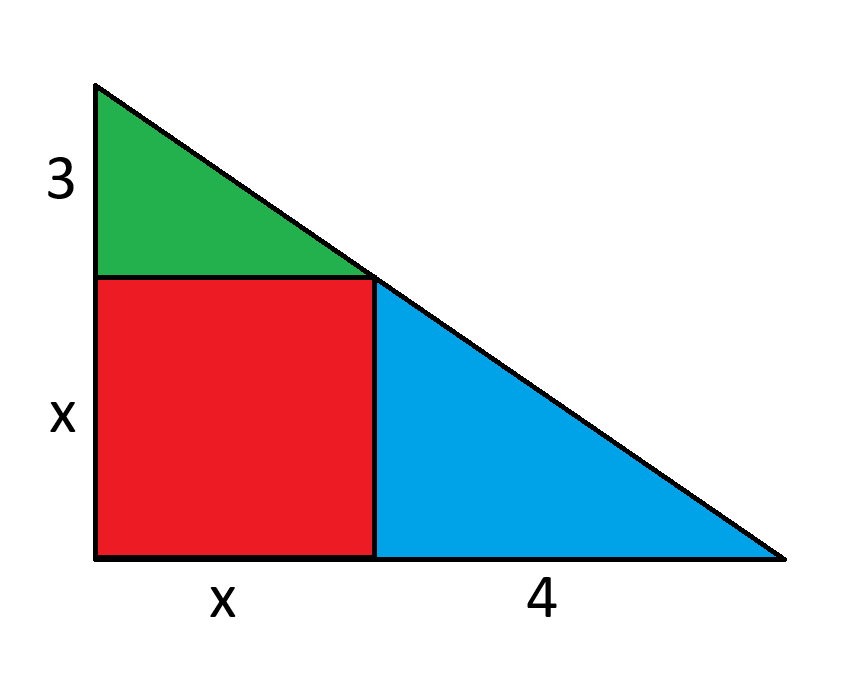
x ज्ञात करें।

गुमनाम

आइए, पूरे त्रिभुज के अलग-अलग भागों के क्षेत्रफल से मिलान करने वाला समीकरण बनाएं:

हरा + नीला + लाल = कुल
3x/2 + 4x/2 + x^2 = (x+3)*(x+4)/2
3x + 4x + 2x^2 = (x+3)*(x+4)
7x + 2x^2 = x^2 + 7x + 12
2x^2 = x^2 + 12 x^2 = 12 x = 2*sqrt(3) =~ 3.464102

यह प्रश्न "माइंड योर डिसीजन्स" यूट्यूब चैनल के प्रेश टॉकवाल्कर द्वारा पूछे गए एक समान प्रश्न पर आधारित है, विशेष रूप से इस वीडियो की पहली समस्या पर। प्रेश मेरे प्रश्न से एक चतुर और अलग समाधान प्रस्तुत करते हैं।

आप रेगिस्तान में एक मरुद्यान में हैं। आपका काम है कि आप 100 मील दूर एक पत्र जितनी जल्दी हो सके पहुँचाएँ। आपका ऊँट तीन दिन तक का पानी ढो सकता है और प्रतिदिन 20 मील की यात्रा कर सकता है। रेगिस्तान में पानी का भण्डार छोड़ना जायज़ है। आप पत्र कितनी जल्दी पहुँचा सकते हैं?

गुमनाम

"फ़ॉलोइंग" बटन पर क्लिक करने से मेरा उत्तर पता चल जाएगा। यह मेरा सबसे तेज़ समय दिखाता है, लेकिन मैं यह साबित नहीं कर सकता कि इससे बेहतर कोई तरीका नहीं है।

11.8 दिन

[स्पॉइलर=समाधान]
  1. 8 मील दूर एक चौकी तक चार चक्कर लगाएँ। आप पहली तीन यात्राओं में 44 गैलन और चौथी यात्रा में 52 गैलन और जमा कर पाएँगे, यानी कुल 184 गैलन पानी पहुँचाया जाएगा। इसमें 7*8=56 मील पैदल चलना होगा, जिसमें 56/20 = 2.8 दिन लगेंगे।
  2. 12 मील दूर एक चौकी तक तीन चक्कर लगाएँ। आप पहली दो यात्राओं में 36 गैलन और तीसरी में 48 गैलन और जमा कर पाएँगे, यानी कुल 120 गैलन पानी पहुँचाया जाएगा। इसके लिए आपको 5*12=60 मील पैदल चलना होगा, जिसमें 60/20 = 3.0 दिन लगेंगे।
  3. 20 मील दूर एक चौकी तक दो चक्कर लगाएँ। पहली बार में आप 20 गैलन और दूसरी बार में 40 गैलन जमा कर पाएँगे, यानी कुल 60 गैलन पहुँचाया जाएगा। इसमें 3*20=60 मील पैदल चलना होगा, जिसमें 60/20 = 3.0 दिन लगेंगे।
  4. 60 मील दूर किसी चौकी तक एक यात्रा करें। इसमें 60 मील पैदल चलना होगा, जिसमें 60/20 = 3.0 दिन लगेंगे।

चौकी तक की दूरी 8+12+20+60 = 100 मील है। कुल समय 2.8 + 3.0 + 3.0 + 3.0 = 11.8 दिन लगेगा।

[/बिगाड़ने वाला]

आपके पास 4 इंच ऊंचा एक मार्टिनी ग्लास है। आधा गिलास परोसने के लिए आपको इसे कितना ऊंचा भरना चाहिए?

गुमनाम

4×(1/2)^(1/3) = 3.174802" ऊँचा.

[स्पॉइलर=समाधान]

दिलचस्प बात यह है कि त्रिज्या क्या है, इससे कोई फ़र्क़ नहीं पड़ता। मान लीजिए कि त्रिज्या r है। मान लीजिए कि बारटेंडर को गिलास में जितनी ऊँचाई भरनी है, उसे h कहते हैं। ज़ाहिर है कि आधे हिस्से की त्रिज्या दोनों ऊँचाइयों के अनुपात के बराबर है। दूसरे शब्दों में, आधे हिस्से की त्रिज्या r*(h/4) है।

याद करें कि शंकु का आयतन (1/3)*h*pi*r 2 है।

आइए आधे भाग को पूर्ण भाग के आधे भाग के बराबर मानें:

(1/2)*(1/3)*4*pi*r 2 = (1/3)*h*pi*(rh/4) 2

(1/2)*4*r 2 = h*(rh/4) 2

2*आर 2 = एच*आर 2 *एच 2 /16

2 = एच 3 /16

32 = एच 3

h = 32 1/3 =~ 3.174802"

[/बिगाड़ने वाला]